Abstract
In recent years, the need for high-performance computing solutions has increased due to the growing complexity of computational tasks. The use of parallel processing techniques has become essential to address this demand. In this study, an Open Computing Language (OpenCL)-based parallelization algorithm is implemented for the Constant Neighbors (CNe) and CNe with Predictor–Corrector (CpC) numerical methods, which are recently developed explicit and stable numerical algorithms to solve the heat conduction equation. The CPU time and error rate performance of these two methods are compared with the sequential implementation and Euler’s explicit method. The results demonstrate that the parallel version’s CPU time remains nearly constant under the examined circumstances, regardless of the number of spatial mesh points. This leads to a remarkable speed advantage over the sequential version for larger data point counts. Furthermore, the impact of the number of timesteps on the crossover point where the parallel version becomes faster than the sequential one is investigated.
1. Introduction
Parallel computing has emerged as a key approach to meet the increasing demand for high-performance computing solutions. By dividing computational tasks into smaller sub-tasks that can be executed simultaneously, parallel computing offers the potential to significantly improve the speed and efficiency of numerical methods [1]. One popular framework for parallel computing is OpenCL, which allows the utilization of heterogeneous computing platforms, including CPUs, GPUs, and FPGAs.
Several methods are used and processed for solving the equations related to heat transfer and diffusion, e.g., semi-analytical methods [2], domain-decomposition methods [3], and finite-element solvers [4].
The most frequent approach may be the spatial discretization of the equation by the central difference formula and then the solution of the obtained ODE (ordinary differential equation) system by either an explicit or an implicit finite difference [5] algorithm. The most well-known explicit methods, however, such as the Runge–Kutta family, are only conditionally stable, and the solution is expected to diverge whenever the timestep size is above a threshold [6], which is called the CFL (Courant–Friedrichs–Lewy) limit. The advantage of the explicit schemes is that they can execute a timestep quite quickly and they can be easily coded and parallelized.
Implicit methods have much fewer problems with stability; thus, they are commonly used by many scientists and software [7,8,9]. However, the unknown values cannot be expressed explicitly; hence, a system of algebraic equations must be solved in each timestep. This is computationally challenging, especially in multiple space dimensions, where the matrix is enormous and non-tridiagonal. Semi-explicit or semi-implicit algorithms, as combinations of explicit and implicit algorithms, are also developed [10,11,12,13].
However, we believe that the trend toward increasing parallelization can be followed using explicit schemes, which can be more efficient even if short timesteps have to be used. For example, Essongue et al. showed that the explicit Euler time integration can be faster than the implicit one for 3D thermal simulations [14]. Moreover, not all explicit methods suffer from severe stability issues. A new suite of robust techniques has been created by our group for addressing the non-stationary heat equation, which is explicit and unconditionally stable at the same time. In our original works [15,16], the new algorithms were theoretically examined, verified, and tested. Most importantly, it has been analytically proven that when using these schemes, the temperature values at the new time level are the convex combination of those at the old time level, which implies the stability of the arbitrary time step size and arbitrary space discretization. The main weakness of these explicit and stable schemes is that their accuracy does not always match the standard methods with the same order of convergence. Even with this, these non-conventional methods can severely outperform the standard ones, see, e.g., [17]. In those papers, we frequently mentioned that they are easily parallelizable. The novelty of this research is that this is the first occasion the implementation is completed, which delves into examining how OpenCL-based parallelization affects two of these methods, namely, the Constant Neighbors and the CNe with Predictor–Corrector (which is a two-stage version of the CNe similar to second-order Runge–Kutta schemes).
In this study, the methods being investigated are tested with a couple of initial conditions using various temporal and spatial scales. For each test, a reference solution is used to measure the error. The error is collected as a function of the CPU time required to run the algorithm. The error–runtime functions of the parallel versions of CNe and CpC are compared with the sequential counterparts, as well as with Euler’s explicit time integration. Additionally, we aim to investigate the impact of the number of timesteps on the crossover point where the parallel version becomes faster than the sequential one. The crossover point typically occurs due to the overhead associated with parallelization, which can be higher for small problem sizes but becomes advantageous as the problem size increases [18,19]. By analyzing the performance characteristics of these parallel implementations, we can gain insights into the benefits and limitations of utilizing OpenCL-based parallelization in numerical methods for solving heat equations.
2. Equation and Methods
2.1. The Numerical Methods Being Investigated
This work focuses on the heat conduction equation. It is mathematically analogous to the diffusion equation. The homogenous version of them is as follows:
which is to be used with an initial condition, and where
- f is the temperature [°C, K] —or, in the case of diffusion, concentration,
- t is the simulated time [s],
- is the position vector [m],
- D is the diffusion coefficient [m2/s], and
- is the Laplacian operator.
As for the concentration term, one should note that the mass concentration [kg/m3], molar concentration [mol/m3], and particle count concentration [m−3] are all applicable as long as the same type of concentration is used consistently on both side of the equation.
After expanding the Laplacian, we have the following equation:
In this study, the equations are applied to simple, rectangle-like domains and a fixed Dirichlet’s condition is used at the boundaries (see Equations (12) and (13) in Section 2.3).
The algorithms mentioned in Section 1 belong to the family of finite difference methods, which makes spatial and temporal discretization necessary. The spatial discretization divides the domain into a grid (with initial points Xinit, Yinit, and Zinit and endpoints Xfin, Yfin, and Zfin):
where the spatial step sizes are
the index ranges are
and Nx, Ny, and Nz are the number of nodes along the spatial mesh, i.e., the data point counts. It should be mentioned that in Section 3.1, the notation Nr is used as the total number of spatial grid-points, which is
for a 1-dimensional measurement and
for 2-dimensional data.
Similarly, the temporal discretization divides the time interval into smaller timesteps as follows:
where the step size and index range are
Euler’s method, which serves as a reference in this paper, uses a straightforward conception to produce the data point values of timestep n + 1 as an explicit function of the values of timestep n. Approximating the Laplacian operator with the central difference formula, the stepper formula is (for ease of understanding, in 2 dimensions) as follows:
where the index ranges are
This method is susceptible to numerical instability and requires a small timestep size for accuracy. To eliminate stability problems, CNe method uses a convex combination of the function values to calculate the values of the next timestep. First, an average temperature value of the neighboring datapoints is calculated, and then this value is used as an ambient or terminal temperature to apply Newton’s law of heat transfer (i.e., to calculate the exponentially converging value after the timestep has elapsed):
where
is the time constant of the node and
is the asymptotic value to which the node temperature tends.
The bottleneck of this method is its relatively poor accuracy. To mitigate this problem, CpC method combines it with a predictor–corrector approach, namely the second-order Runge–Kutta scheme. In the first stage, an approximating value is calculated at a fractional timestep using the CNe formula. In the second stage, a linear combination of the original value and the result of the first stage is used as the terminal temperature for CNe to calculate the full-timestep value as follows:
where 0 < p ≤ 1 is the step fraction.
It is mathematically proven in [15] that the above algorithm with coefficients 1 – 1/2p and 1/2p indeed yields to a second-order error term. The results of [15] also show that the accuracy does not depend significantly on the value of parameter p; hence, p = 1/2 is a good choice to simplify calculations. By doing so, the coefficient of the pre-step value becomes zero, enabling the result of the first stage to be used directly in the second stage without having to calculate the linear combination:
which yields an algorithm analog to the midpoint method.
2.2. Parallelization and Applying OpenCL
Both the CNe and CpC methods are parallelizable, and the same applies to the Euler’s method. When determining whether an algorithm is parallelizable, several key criteria must be considered. One important criterion is the independence of tasks, often referred to as data parallelism. This refers to the extent to which tasks or operations can be performed independently of each other. If the algorithm’s tasks do not depend on the results of other tasks, they can be executed in parallel. Another crucial factor is task granularity, which refers to the size of the tasks being parallelized. Fine-grained tasks, which involve small and fast operations, can create overhead in managing parallel tasks, whereas coarse-grained tasks, involving larger and more complex operations, may reduce overhead but require careful balancing. Communication overhead is also a key consideration. This involves the amount of data exchange or synchronization required between parallel tasks. Algorithms that require minimal communication between tasks are easier to parallelize. Load balancing, which is the ability to distribute the workload evenly across all available computing units, is another important criterion. For effective parallelization, the workload should be balanced to avoid situations where some processors are idle while others are overloaded. Scalability is another critical factor, referring to how well the algorithm’s performance improves with the addition of more processing units. An algorithm is considered scalable if its performance continues to improve as more cores or processors are added. A scalable algorithm might demonstrate near-linear speedup as the number of processors increases, such as in parallel matrix multiplication. Synchronization needs must also be considered. These involve the need for synchronization between tasks during execution. Memory access patterns are also important. The way an algorithm accesses memory can affect parallelization, with algorithms that have predictable and non-conflicting memory access patterns being easier to parallelize. For example, algorithms with regular, sequential memory access patterns, such as matrix operations, are easier to optimize for parallel execution compared to those with irregular access patterns that may cause contention. In this research, a cell-by-cell parallelization is carried out, which means that each kernel invocation calculates one cell value.
In this paper, OpenCL [20] was used. Open Computing Language is a framework for writing programs that execute across heterogeneous platforms, including CPUs, GPUs, DSPs, and FPGAs. Its primary purpose is to facilitate parallel computing by allowing developers to harness the computational power of diverse hardware architectures within a unified programming model. By leveraging parallelization, OpenCL aims to significantly enhance performance in various computational tasks, from scientific simulations to real-time data processing. OpenCL is widely used for high-performance computing [21]. Its cross-platform nature [22] makes it useful in various domains of application. Parallelization was used in [23] for solving nonlinear ordinary differential equations. A sparse matrix-vector multiplication is presented in [24]. Parallel computing in the modeling of fractional-order state–space systems is presented by [25]. The Smith–Waterman implementation is shown in [26].
The kernel function for Euler’s method, as well as for the CNe method, can be found in Listing 1 (in 2 dimensions, supposing a GPU supports Khronos-style 64-bit floating point arithmetic [27]):
where
| Listing 1: Kernel of CNe and the 1st stage of CpC. |
| #pragma OPENCL EXTENSION cl_khr_fp64 : enable |
| __kernel void calc_cell_2D( |
| __global const double *before, __global double *after, |
| double2 coeffs, uint2 size, long4 neighbours) { |
| const size_t index = get_global_id(0) + size.x * get_global_id(1); |
| __global const double *old_cell = before + index; |
| after[index] = (1 − 2 * (coeffs.x + coeffs.y)) * *old_cell |
| + coeffs.x * |
| (old_cell[neighbours.even.x] + |
| old_cell[neighbours.odd.x]) |
| + coeffs.y * |
| (old_cell[neighbours.even.y] + |
| old_cell[neighbours.odd.y]); |
| } |
- before, after are pointers to the array containing data before and after the timestep;
- coeffs is a vector containing numerical coefficients for computation;
- size is a vector containing the [Nx, Ny] number of datapoints;
- neighbours is a vector containing pointer differences between the current datapoint and its neighbours (introduced to simplify handling boundary conditions).
During each timestep, the calculation uses the value of the neighboring cells. To ensure that none of these neighboring values has been updated by parallel cell computation—i.e., the before-step value of all the neighbors is used—two memory buffers are necessary [28]. During odd timestep computations, buffer 1 is read while buffer 2 is written to. During even timestep computations, buffer 2 is read while buffer 1 is written to, as follows (Figure 1):
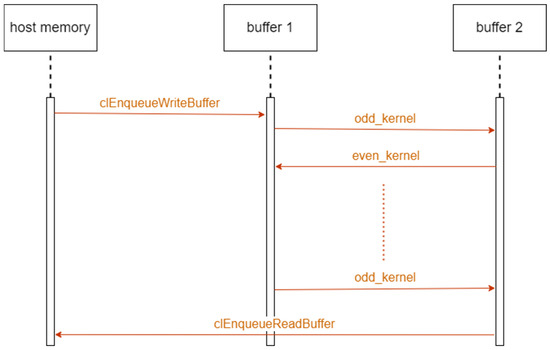
Figure 1.
Using memory buffers with CNe and the 1st stage of CpC.
This is an explicit buffer parallelization technique [29]. Its advantage is that the programmer controls when and how data are moved, optimizing the data transfer to minimize latency and maximize throughput. It allows the use of device-specific features and capabilities, potentially enabling hardware-specific optimizations [30] that are not possible with a more abstracted approach. The first stage of the CpC method can also use the same kernel as shown in Listing 1, but this algorithm also needs a second-stage kernel, as well (Listing 2):
where
| Listing 2: Kernel of the 2nd stage of CpC. |
| __kernel void stage2p05_calc_cell_2D( |
| __global const double *stage0, |
| __global const double *stage1, |
| __global double *after, |
| double2 coeffs, uint2 size, long4 neighbours) { |
| const size_t index = get_global_id(0) + size.x * get_global_id(1); |
| __global const double *old_cell = stage0 + index; |
| __global const double *midpoint = stage1 + index; |
| after[index] = (1 − 2 * (coeffs.x + coeffs.y)) * *old_cell |
| + coeffs.x * |
| (midpoint[neighbours.even.x] + |
| midpoint[neighbours.odd.x]) |
| + coeffs.y * |
| (midpoint[neighbours.even.y] + |
| midpoint[neighbours.odd.y]); |
| } |
- stage0 is a pointer to the array containing data before stage 1;
- stage1 is a pointer to the array containing the result of stage 1;
- after is a pointer to the array containing data after all the stages;
- coeffs is a vector containing numerical coefficients for computation;
- size is a vector containing the [Nx, Ny] number of datapoints;
- neighbours is a vector containing pointer differences between the current datapoint and its neighbours (introduced to possibly simplify handling boundary conditions).
Method CpC also requires 2 memory buffers, but they are used in a different way. The computation of each step uses both buffers. The first stage reads buffer 1 and writes the result to buffer 2. The second stage reads both buffer 1 (stage0) and buffer 2 (stage1) and stores the result in buffer 1 (after), as shown in Figure 2.
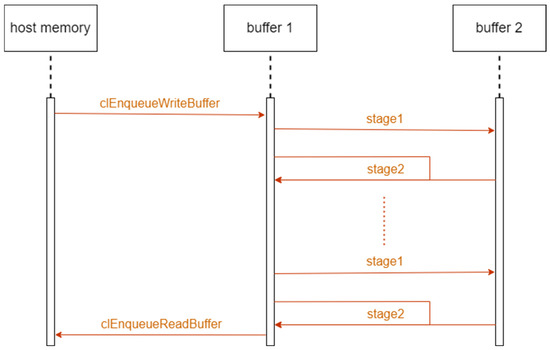
Figure 2.
Using memory buffers with CpC.
2.3. Initial and Boundary Conditions, Scale Parameters, and the Method of Investigation
In this study, fixed Dirichlet boundaries [31] are assumed, meaning that the initial value of the boundaries is kept constant during the calculation, and no calculation is involved on these boundaries, as follows:
in 1 dimension, and
in 2 dimensions.
To deal with the initial values, four different problems are created using two initial condition functions for both 1- and 2-dimensional measurements. In the case of one type of the initial function, we have the analytical solution, which is used as a reference. The other problem does not have an analytical solution; hence, a numerical reference solution is used instead. This reference solution is generated using the built-in ode15s function of MATLAB [32]. These initial value functions are the following (assuming Xinit = 0, Yinit = 0 and Tinit = 0):
- A 1D sine with nodes at the boundaries iswhereare arbitrarily chosen parameters and the analytical solution is
- A 1D Gaussian function [33] iswhereare arbitrarily chosen parameters. In this case, a numerical reference solution is used.
- In 2D, the product of sinewaves for each dimension with nodes at the boundaries iswhereare arbitrarily chosen parameters and the analytical solution is
- A 2D planar wave, propagating at an angle [34] iswhereare arbitrarily chosen parameters. In this case, a numerical reference solution is used.
The timescales and data grids used together with these functions are listed in Table 1, Table 2, Table 3 and Table 4. During the measurement, each row of the timescale tables is combined with each row of the appropriate spatial mesh–grid table (i.e., the rows of Table 1 with the rows of Table 2 and the rows of Table 3 with the rows of Table 4) and one of the 2 appropriate initial functions. For each combination, the measurement is repeated 4 times, and the mean value along with the standard deviation of the CPU time is calculated. The maximal absolute value of the difference between the output data points and the reference solution values (mathematically spoken, the l∞ distance of the output vector and the reference vector) is considered as the error of the algorithm as follows:
for 1 dimensional calculations and
for 2 dimensional calculations. (This value is expected to be the same for all the 4 repetitions, since the examined algorithms are deterministic.)

Table 1.
The timescales used with 1D data.

Table 2.
The 1D spatial grids.

Table 3.
The timescales used with 2D data.

Table 4.
The 2D spatial grids.
2.4 The Specifications of the Applied Computer, Further Circuimstances of the Investigation
The aforementioned algorithms can be found at the repository mentioned in Supplementary Materials. These were executed on a personal computer (PC) to validate their performance and functionality. The specifications of the PC used for this purpose are as follows:
- CPU—Gen11 Intel Core i7-11700F, 2.5 GHz;
- RAM—64 GB;
- OS—Windows 10 Professional (22H2), ×64;
- GPU—NVIDIA;
- Open CL—Intel v2020.3.494.
3. Results
The results presented in this section refer to the cases described in Section 2.3.
In this examination, the problem sizes had to be limited to the size that can be practically calculated during the experiments, given the computational resources available, such as the GPU and CPU used. These circumstances include the number of spatial mesh points and the scale of the computational task that the hardware could handle efficiently. In traditional, sequential algorithms, the CPU time typically increases as the number of spatial mesh points grows because more calculations are required. However, in the parallel version of the algorithm studied, the CPU time remained nearly constant across the range of mesh points tested. This means that within the practical limits of the problem sizes tested, the parallel implementation was able to efficiently distribute the workload across multiple processing units (like GPU cores), allowing it to handle larger problem sizes without a corresponding increase in computation time.
3.1. The Dependency of CPU Time on the Number of Data Points
In the following subsections, the CPU time of the given implementation (i.e., CNe in Section 3.1.1 and CpC in Section 3.1.2) is plotted as the function of the total number of spatial grid points (see Equations (3) and (4) for a definition of Nr) for a fixed number of timesteps, along with the CPU time of Euler’s method. For ease of comparison, the 1-dimensional and 2-dimensional data are plotted on the same graph. Each data point in Figure 3, Figure 4, Figure 5 and Figure 6 contains both the problems with analytical and numerical reference solutions, meaning that the average of eight CPU time values is used instead of four values.
On Figure 3, Figure 4, Figure 5 and Figure 6, one can observe, that in the parallel case, the CPU time remains unaffected by the data point count (presumably due to no depletion of the GPU capability in these measurements), whereas in the sequential case, it increases with the data point number. For most cases under examination at two-dimensional levels and all one-dimensional instances, the system size consistently falls below a critical cross-over point threshold, and hence finer space grids (i.e., greater datapoint count) are required.
The position of the cross-over point shifts towards lower data point counts as timestep numbers rise. With 500 timesteps, OpenCL demonstrates greater efficiency within a range of 6000–8000 data points; meanwhile, with 900,000 timesteps, the transition happens at around 3000 data points.
3.1.1. The CNe Method Compared to Euler’s Method
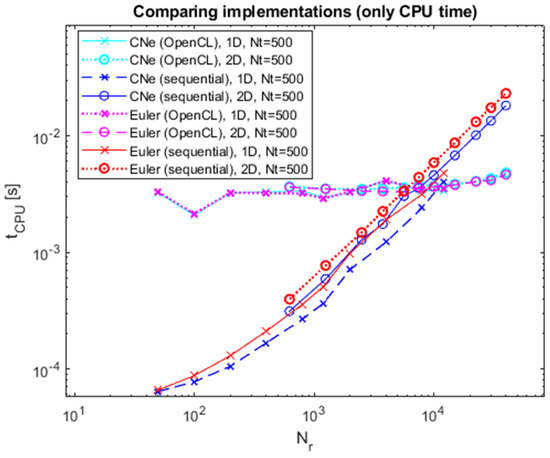
Figure 3.
The CPU time of CNe and Euler’s methods as a function of the number of spatial mesh points for 500 timesteps.
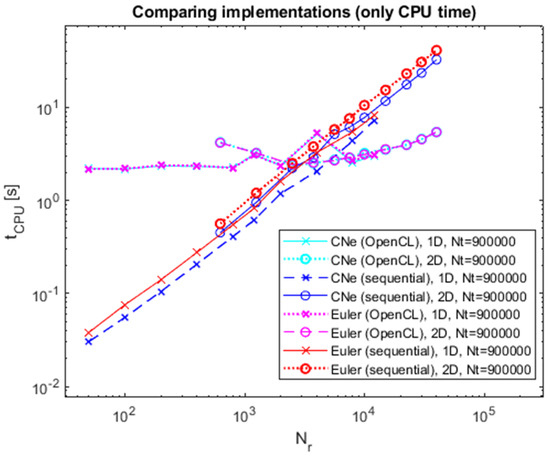
Figure 4.
The CPU time of CNe and Euler’s methods as a function of the number of spatial mesh points for 900,000 timesteps.
3.1.2. The CpC Method Compared to Euler’s Method
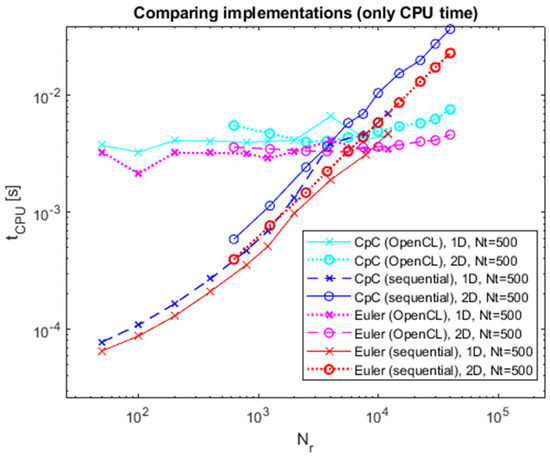
Figure 5.
The CPU time of CpC and Euler’s methods as a function of the number of datapoints for 500 timesteps.
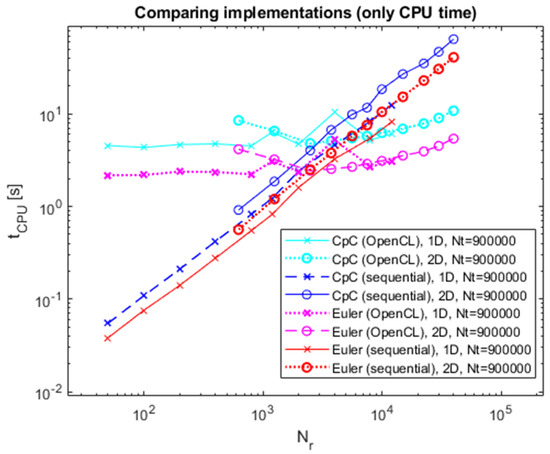
Figure 6.
The CPU time of CpC and Euler’s methods as a function of the number of data points for 900,000 timesteps.
3.2. The Error as a Function of the Timestep Size
In this section, the error is plotted as a function of the CPU time necessary to execute the algorithm. (For the definition of ErrMax, see Equations (20) and (21).) This technique enables a sophisticated comparison of the examined methods (CNe in Section 3.2.1 and CpC in Section 3.2.2) with Euler’s method.
As it can be expected based on Section 3.1, on Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14, it is noticeable that better performance with OpenCL is only achieved in two dimensions for large data grids. It can also be seen that the errors of both the parallel and the sequential algorithms are similar. This confirms that the OpenCL-based and sequential implementations conduct identical mathematical operations, and they differ at most in scheduling.
3.2.1. The CNe Method Compared to Euler’s Method
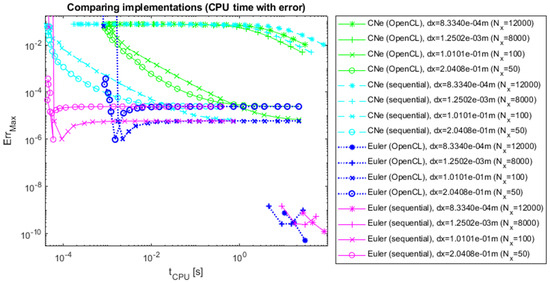
Figure 7.
The errors of CNe and Euler’s methods as a function of CPU time, 1D with analytical reference.
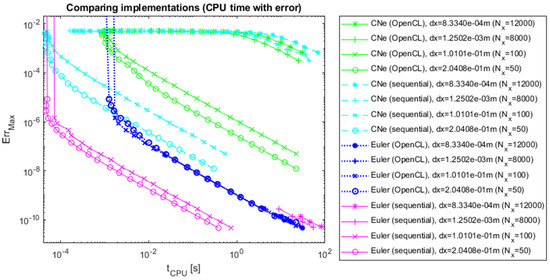
Figure 8.
The errors of CNe and Euler’s methods as a function of CPU time, 1D with numerical reference.
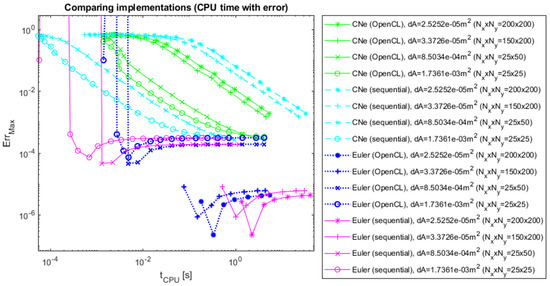
Figure 9.
The errors of CNe and Euler’s methods as a function of CPU time, 2D with analytical reference.
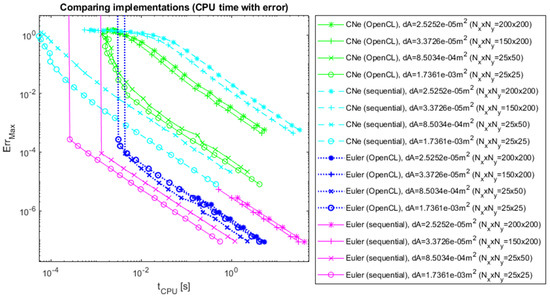
Figure 10.
The errors of CNe and Euler’s methods as a function of CPU time, 2D with numerical reference.
3.2.2. The CpC Method Compared to Euler’s Method
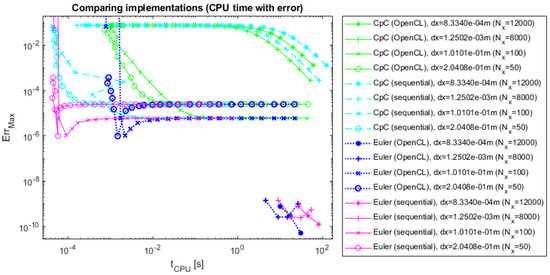
Figure 11.
The errors of CpC and Euler’s methods as a function of CPU time, 1D with analytical reference.
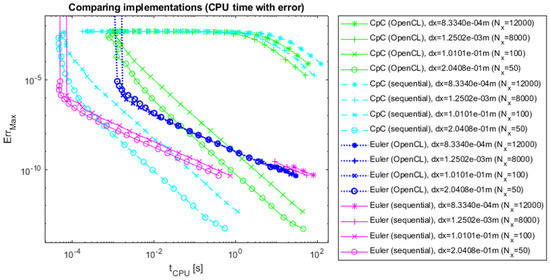
Figure 12.
The errors of CpC and Euler’s methods as a function of CPU time, 1D with numerical reference.
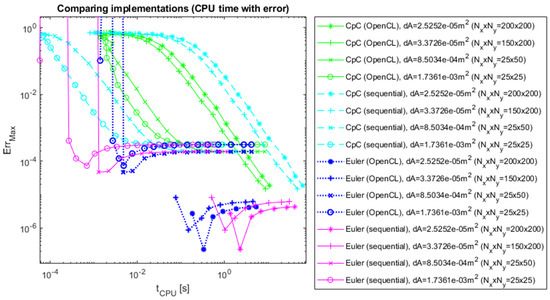
Figure 13.
The errors of CpC and Euler’s methods as a function of CPU time, 2D with analytical reference.
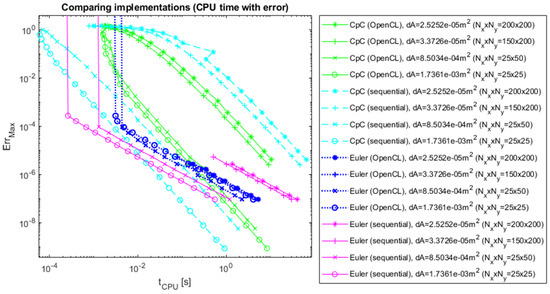
Figure 14.
The errors of CpC and Euler’s methods as a function of CPU time, 2D with numerical reference.
4. Discussion and Conclusions
According to this research, it can be argued that employing OpenCL has the potential to achieve improved performance; however, whether such enhanced performance is realized depends on certain conditions. The size of the data grids examined in this study is not enough to deplete the parallel computing capacity of the computer used for the calculation. As a result, the CPU time required by OpenCL-based algorithms is determined mostly by the number of timesteps and only to a much smaller extent by the number of data points. Consequently, OpenCL becomes more efficient than its sequential counterpart only when a sufficiently high number of data points is employed (which appears to decrease as the number of timesteps increases). In our investigation, only certain 2-dimensional scenarios meet this criterion; in other cases, it has been demonstrated that sequential calculation outperforms parallel processing.
The constancy in CPU time is likely due to the parallel nature of the algorithm, where the computational load is spread out across multiple processors. However, this effect is observed only up to the point where the problem size is within the capabilities of the hardware. Beyond this point, or with extremely large mesh sizes, the CPU time might increase as the computational resources become a limiting factor. The key takeaway is that for the problem sizes tested, which the hardware could manage effectively, the parallel implementation showed a significant advantage in maintaining a consistent CPU time, making it particularly suitable for larger-scale problems.
Future experiments should utilize finer data grids to illustrate the effectiveness of OpenCL compared to sequential computing. In one dimension, a minimum of 300 to 400 data points is required, while in two dimensions, a grid size of at least 150 × 150 would be suitable for the upper limit of test cases.
Supplementary Materials
The repository of the implementation of the examined algorithms can be found at https://www.bitbucket.org/koicsd/diffusion2, accessed on 19 September 2024. The snapshots of the code used in this investigation can be found by the following tag-names: Sequential Euler’s method, bison04Apr2024_seqEuler; OpenCL-based Euler’s method, bison04Apr2024_clEuler; sequential CNe method, bison04Apr2024_seqCNe; OpenCL-based CNe method, bison05Apr2024_clCNe; sequential CpC method, bison02Apr2024_seqCpC; and OpenCL-based CpC method, bison03Apr2024_clCpC. The test framework used is hosted at https://www.bitbucket.org/koicsd/test-tool, accessed on 19 September 2024.
Author Contributions
Conceptualization, methodology, supervision, project administration, and resources, E.K. and O.H.; software, validation, investigation, visualization, and writing—original draft preparation, D.K.; writing—review and editing, D.K., E.K., and O.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are available from the first author on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Robert, E.T.; Larson, E. Parallel Processing Algorithms for the Optimal Control of Nonlinear Dynamic Systems. IEEE Trans. Comput. 1973, 100, 777–786. [Google Scholar]
- Patel, Y.F.; Dhodiya, J.M. Efficient algorithm to study the class of Burger’s Fisher equation. Int. J. Appl. Nonlinear Sci. 2022, 3, 179–266. [Google Scholar] [CrossRef]
- Xue, G.; Gao, Y. A Samarskii domain decomposition method for two-dimensional convection-diffusion equations. Comput. Appl. Math. 2022, 41, 283. [Google Scholar] [CrossRef]
- Kumar, V.; Chandan, K.; Nagaraja, K.V.; Reddy, M.V. Heat conduction with Krylov subspace method using FEniCSx. Energies 2022, 15, 8077. [Google Scholar] [CrossRef]
- Köroğlu, C.; Aydin, A. Exact and nonstandard finite difference schemes for the Burgers equation B(2,2). Turk. J. Math. 2021, 45, 3. [Google Scholar] [CrossRef]
- Ruan, C.; Dong, C.; Zhang, Z.; Chen, B.; Liu, Z. Finite difference-peridynamic differential operator. Comput. Model. Eng. Sci. 2024, 140, 2707–2728. [Google Scholar]
- Yang, J.; Kim, J. Consistently and unconditionally energy-stable linear method for the diffuse-interface model of narrow volume reconstruction. Eng. Comput. 2024, 40, 2617–2627. [Google Scholar] [CrossRef]
- Mbroh, N.A.; Munyakazi, J.B. A robust numerical for singularly perturbed parabolic reaction-diffusion problems via the method of lines. Comput. Math. 2021, 99, 1139–1158. [Google Scholar] [CrossRef]
- Aydin, A.; Koroglu, C. A nonstandard numerical method for the modified KdV equa-tion. Pramana—J. Phys. 2017, 89, 72. [Google Scholar] [CrossRef]
- Beuken, L.; Cheffert, O.; Tutueva, A.; Butusov, D.; Legat, V. Numerical stability and performance of semi-explicit and semi-implicit predictor-corrector methods. Mathematics 2022, 10, 2015. [Google Scholar] [CrossRef]
- Ji, Y.; Xing, Y. Highly accurate and efficient time integration methods with unconditional stability and flexible numerical dissipation. Mathematics 2023, 11, 593. [Google Scholar] [CrossRef]
- Dou, N.; Dlamini, P.; Jacobs, B.A. Enhanced unconditionally positive finite difference method for advection-diffusion-reaction equations. Mathematics 2022, 10, 2639. [Google Scholar] [CrossRef]
- Jaglan, J.; Singh, A.; Maurya, V.; Yadav, V.S.; Rajpoot, M.K. Strong stability preserving multiderivative time marching methods for stiff reaction-diffusion systems. Math. Comput. Simul. 2024, 225, 267–282. [Google Scholar] [CrossRef]
- Essongue, S.; Ledoux, Y.; Ballu, A. Speeding up mesoscale thermal simulations of powder bed additive manufacturings thanks to the forward Euler time integration scheme: A critical assesment. Finite Elem. Anal. Des. 2022, 211, 103825. [Google Scholar] [CrossRef]
- Kovács, E.; Nagy, Á.; Saleh, M. A set of new, stabl, explicit, second-order schemes for the nonsationary heat conduction equation. Mathematics 2021, 9, 2284. [Google Scholar] [CrossRef]
- Kovács, E. A Class of New Stable, Explicit Methods to Solve the Non-Stationary Heat Equation. Numer. Methods Partial Differ. Equ. 2020, 37, 2469–2489. [Google Scholar] [CrossRef]
- Askar, A.H.; Nagy, Á.; Barna, I.F.; Kovács, E. Analytical and numerical results for the diffusion-reaction equation when the reaction coefficient depends on simultaneously the space and time coordinates. Computation 2023, 11, 127. [Google Scholar] [CrossRef]
- Midkiff, S.P. Automatic Parallelization: An Overview of Fundamental Compiler Techniques; Springer Nature: Cham, Switzerland, 2022. [Google Scholar]
- Parhami, B. Introduction to Parallel Processing: Algorithms and Architectures; Springer Science & Business Media: Cham, Switzerland, 2006. [Google Scholar]
- Munshi, A. The OpenCL specification. In 2009 IEEE Hot Chips 21 Symposium (HCS); IEEE: Stanford, CA, USA, 2009; pp. 1–314. [Google Scholar] [CrossRef]
- Kang, P. Programming for high-performance computing on edge accelerators. Mathematics 2023, 11, 1055. [Google Scholar] [CrossRef]
- Takáč, M.; Petráš, I. Cross-Platform GPU-Based Implementation of Lattice Boltzmann Method Solver Using ArrayFire Library. Mathematics 2021, 9, 1793. [Google Scholar] [CrossRef]
- Tavakkoli, V.; Mohsenzadegan, K.; Chedjou, J.C.; Kyamakya, K. Contribution to Speeding-Up the Solving of Nonlinear Ordinary Differential Equations on Parallel/Multi-Core Platforms for Sensing Systems. Sensors 2020, 20, 6130. [Google Scholar] [CrossRef]
- Baskaran, M.M.; Bordawekar, R. Optimizing Sparse Matrix-Vector Multiplication on GPUs. IBM Research Report RC24704, (W0812–047) 2009. Available online: https://dominoweb.draco.res.ibm.com/reports/rc24704.pdf (accessed on 19 September 2024).
- Stanisławski, R.; Kozioł, K. Parallel Implementation of Modeling of Fractional-Order State-Space Systems Using the Fixed-Step Euler Method. Entropy 2019, 21, 931. [Google Scholar] [CrossRef]
- Di Tucci, L.; O’Brien, K.; Blott, M.; Santambrogio, M.D. Architectural optimizations for high performance and energy efficient Smith-Waterman implementation on FPGAs using OpenCL. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Lausanne, Switzerland, 27–31 March 2017; pp. 716–721. [Google Scholar]
- Khronos Group. OpenCL 3.0 Specification. 2020. Available online: https://www.khronos.org/registry/OpenCL/specs/3.0-unified/html/OpenCL_API.html (accessed on 19 September 2024).
- Jo, G.; Jung, J.; Park, J.; Lee, J. Memory-Access-Pattern Analysis Techniques for OpenCL Kernels. In International Workshop on Languages and Compilers for Parallel Computing; Springer International Publishing: Cham, Switzerland, 2017; pp. 109–126. [Google Scholar]
- Jääskeläinen, P.; de La Lama, C.S.; Schnetter, E.; Raiskila, K.; Takala, J.; Berg, H. pocl: A performance-portable OpenCL implementation. Int. J. Parallel Program. 2015, 43, 752–785. [Google Scholar] [CrossRef]
- Wang, Z.; He, B.; Zhang, W.; Jiang, S. A performance analysis framework for optimizing OpenCL applications on FPGAs. In Proceedings of the 2016 IEEE International Symposium on High Performance Computer Architecture (HPCA), Barcelona, Spain, 12–16 March 2016; pp. 114–125. [Google Scholar]
- Smith, G.D. Numerical Solution of Partial Differential Equations: Finite Difference Methods; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- MathWorks. MATLAB—ODE15S. 2023. Available online: https://www.mathworks.com/help/matlab/ref/ode15s.html (accessed on 19 September 2024).
- Weisstein, E.W. (n.d.). Gaussian Function. In MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/GaussianFunction.html (accessed on 19 September 2024).
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).