Abstract
Mutual exclusion is a fundamental problem in concurrent/parallel/distributed systems. The first pure-software solution to this problem for two processes, which is not based on hardware instructions like test-and-set, was proposed in 1965 by Th.J. Dekker and communicated by E.W. Dijkstra. The correctness of this algorithm has generally been studied under the strong memory model, where the read and write operations on a memory cell are atomic or indivisible. In recent years, some variants of the algorithm have been proposed to make it RW-safe when using the weak memory model, which makes it possible, e.g., for multiple read operations to occur simultaneously to a write operation on the same variable, with the read operations returning (flickering) a non-deterministic value. This paper proposes a novel approach to formal modeling and reasoning on a mutual exclusion algorithm using Timed Automata and the Uppaal tool, and it applies this approach through exhaustive model checking to conduct a thorough analysis of the Dekker’s algorithm and some of its variants proposed in the literature. This paper aims to demonstrate that model checking, although necessarily limited in the scalability of the number of the processes due to the state explosions problem, is effective yet powerful for reasoning on concurrency and process action interleaving, and it can provide significant results about the correctness and robustness of the basic version and variants of the Dekker’s algorithm under both the strong and weak memory models. In addition, the properties of these algorithms are also carefully studied in the context of a tournament-based binary tree for processes.
1. Introduction
This paper focuses on software-based mutual exclusion algorithms [1,2,3,4] which are at the core of concurrent/parallel and distributed systems. Such algorithms are the fundamental support to high-level mutual exclusion constructs (e.g., semaphores [5]) that are often exposed by operating systems and multi-threading libraries of programming languages like Java [6]. Ensuring the correctness of these algorithms is of utmost importance. However, mutual exclusion algorithms can be very hard to analyze by intuitive reasoning due to non-determinism and interleaving, which affect the order that actions are executed in the involved processes. Formal means for automated reasoning are represented by theorem provers (e.g., [7]), which can be difficult to use in practical cases for necessary mathematical characterization. In addition, a theorem prover usually cannot deal with timing issues. In this paper, the use of model checkers [8,9] is advocated because they not only provide the formal modeling required by a mutual exclusion algorithm, but they can also enable the possibility of investigating a model’s behavior using a symbolic simulator (as in [9]) which animates the execution of the chosen algorithm, thus helping in the preliminary phase of understanding and debugging the operations of the algorithm. For a precise analysis, though, exhaustive model checking is used, which relies on constructing a model state graph, which contains all the possible execution states that the model can assume during its dynamic evolution. A temporal logic can then be exploited for expressing the safety and liveness properties of the model through suitable formal queries, thus enabling the state graph to be explored to check whether the properties hold or not, and possibly generating a counterexample showing why a given property/query is not satisfied. In this work, timed automata [10], as implemented in the Uppaal toolbox [9], are exploited to model and analyze mutual exclusion algorithms. Uppaal was chosen because it supports intuitive graphical yet formal modeling and can handle temporal aspects using clocks. This paper argues that properly using the timing dimension is a key for observing the overtaking factor of a mutual exclusion algorithm, that is, the number of times other competing processes precede a given competing process before is finally allowed to enter its critical section. Another benefit Uppaal provides concerns the possibility of studying a mutual exclusion algorithm according to either the strong or weak memory model [1,2,11,12]. In the strong model, read/write operations on a memory cell are guaranteed to be atomic or indivisible. In the weak memory model, which now naturally occurs in low-cost multi-processor hardware devices [13,14], read/write operations can be simultaneous on the same variable. An algorithm that is robust enough to execute under the weak memory model is said to be RW-safe. It is a widespread opinion that a mutual exclusion algorithm should be correct and safe to execute regardless of the underlying memory model.
As a specific contribution, this paper proposes a novel modeling and verification approach based on Uppaal and applies it to conduct a thorough investigation of Dekker’s algorithm [15] for two processes, which is only supposed to be safe under the strong memory model. Two variants of this algorithm were proposed in [12,16] to improve Dekker’s solution specifically. The proposal in [12] was guided by the goal of making it RW-safe. However, as the model checking experimental work reported in this paper demonstrates, the basic Dekker’s algorithm is RW-safe as well as the variants in [12,16]. As a further study, the basic Dekker’s algorithm and the two variants in [12,16] are investigated in the more general scenario of processes using a tournament-based implementation [17,18,19]. It was found that the general solution based on Dekker’s algorithm is still RW-safe and ensures a bounded overtaking. The other two solutions become RW-safe by fencing the write operation on a shared variable in pairs of sibling processes (see Section 5.2 and Section 5.3). In addition, both variants incur in an unbounded overtaking.
As it is based on model checking, the applicability of the proposed approach is limited in the practical case by the state explosion problem, which occurs when the number of processes grows beyond a given threshold (e.g., or, more often, a lower value), which depends on (i) the particular exploited algorithm, (ii) its adopted data variables, and (iii) the memory model used. Despite this scalability restriction, the approach proves valuable for predicting the properties of a mutual exclusion solution, including quantifying the overtaking bound.
The rest of this paper is organized as follows. Section 2 highlights some basic concepts about mutual exclusion algorithms, memory constraints, and the Uppaal Timed Automata modeling language. Section 3 describes the proposed modeling and verification approach used for studying mutual exclusion algorithms. The approach is concretely applied to dive into Dekker’s solution, which is shown to be RW-safe. Section 4 is devoted to a deep property checking of two variants of Dekker’s algorithm. Section 5 proposes a tournament binary tree as a standard mutual exclusion solution for processes, where the studied algorithms for two processes are used to arbitrate pairs of sibling processes. Section 6 compares the experimental results, which are more favorable for the Dekker-based solution. Finally, Section 7 concludes the paper with an indication of on-going and future work.
2. Background
2.1. The Concepts of a Mutual Exclusion Algorithm
A mutual exclusion algorithm (MEA) [1,2,15] aims to enforce to a group of processes competing for a common shared resource that only one process is granted access to it. All of the remaining processes have to wait until the resource is finally released. After that, another competing process should be allowed to enter and use the resource, and so forth. The actions executed by a process when it is permitted to enter and use the resource are said to be its critical section (CS). Therefore, the mission of an MEA is to guarantee that only one CS can be executed at a time.
Concretely, an MEA consists of a protocol which processes have to follow when they want to access the resource (Entry-part of the protocol) and when they abandon the resource (Exit-part of the protocol). A process that is not interested in accessing the resource is said to execute its non-critical section (NCS). In the NCS, a process can remain for an arbitrary time, even an infinite time, to model the fact that the process can stop being executed in the NCS and would no longer compete to use the resource. The typical structure of a never-ending process involved in a mutual exclusion problem is shown in Algorithm 1. In the Entry-part (and sometimes also in the Exit-part), a process can undergo a busy-waiting phase (spinning and wasting processor cycles) until some shared variables change their values, causing the exiting from the busy-waiting.
The protocol of an MEA consists of wisely using a (hopefully minimal) set of shared variables. Almost always, an MEA is the happy result of a clever design that is not easy to understand, and it has to prove its correctness against the non-determinism and action interleaving that characterize the execution of a concurrent/parallel system.
| Algorithm 1. The pseudo-code of a mutual exclusion algorithm. |
| shared communication variables Process(i) local variables repeat NCS; Entry-part; CS; Exit-part; forever |
An MEA should satisfy the following properties:
- (a)
- The absence of a deadlock: The protocol execution must not determine a fatal reciprocal lockout of the processes in any cases in which no one can prosecute. In a deadlocked state, every process awaits someone to do something that never occurs.
- (b)
- Only one process can execute its CS at a time (the essence of mutual exclusion).
- (c)
- The absence of individual starvation: No competing process, that is, the one executing the Entry-part of the protocol, should wait for an unbounded time before entering its CS.
- (d)
- A process in the NCS should not impede another process from entering its CS.
- (e)
- No hypothesis should be made on the relative speed of processes.
2.2. Memory Model Constraints
As pointed out in [1,2,12] a mutual exclusion algorithm (MEA) should be robust under both the strong and weak memory models. In the strong model, the read/write operations on a memory cell (shared variable) are supposed to be atomic. Consequently, a read operation always returns the most recent value assigned to the variable. Of course, non-determinism can affect this value, which ultimately depends on the latest process which assigns a value to the variable. Under the weak model, multiple operations can occur simultaneously.
The weak model is a reality due to the diffusion of low-cost multi-processor hardware, e.g., based on multi-port memories (e.g., [13,14]). In the following, compiler and hardware optimizations that can alter the order of operations are ignored, as in [12], and two significant cases about read/write operations are considered. The first relates to one writer and multiple readers of the same variable. In this case, any reader who simultaneously reads a variable under writing receives a flickering value, which is a non-deterministic value belonging to the type of the variable. Of course, a read that precedes or follows the write operation, respectively, returns the previous value or the new value assigned to the variable. The second case refers to multiple writers who simultaneously try to change the value of the same variable. In this case, a subsequent reader can achieve a scrambled value, which is a value that is possibly not coincident with any one written by writers.
It is worth noting that many mutual exclusion algorithms depend on a set of shared communication variables where each variable is controlled by a separate process. In other words, every process writes on “its” variable, which all the remaining processes can then consult. Kessels in [18] calls these exterior variables. The use of exterior variables implies that the algorithm can be affected by flickering, which causes an increase in the non-determinism and partial order among the process actions. Scrambling can ruin the logic and properties of the algorithm and its model instead. Scrambling can be avoided by fencing the write operation, which ensures that the write operations on a shared variable occur in sequence, although they can occur in any order (see Section 5.2 and Section 5.3).
2.3. Modeling Language
In this work, the Uppaal [9] Timed Automata (UTA) [10] are used as the modelling language for a formal specification of a mutual exclusion algorithm. UTA’s original mission is modeling and property assessment by performing model checking of real-time systems and, more in general, of timed systems. Clock variables control time. A clock can be reset. At any moment, a clock measures the time elapsed from its last reset. All the clocks of a model grow according to the same rate.
A UTA model is a network of instantiable processes (said template or parameterized automata) that proceed concurrently and can interact and synchronize with one another through instantaneous signals exchanged by unicast or broadcast channels. Unicast channels ensure two-way or rendezvous synchronizations: the sender (!) and the receiver (?) must be both ready for the signal to be exchanged. The first one who arrives at the synchronization point is blocked until the partner arrives. Following synchronization, both the sender and the receiver resume their concurrent execution. A broadcast channel, instead, models asynchronous or one-way communications. The sender can synchronize with zero, one, or multiple receivers which are ready to accept the signal. If no receiver is available, the sender immediately prosecutes. In other terms, the sender of a broadcast channel never blocks. Neither kind of channel synchronization carries any data/parameter. If the data are to be transmitted, they can be easily mediated by global variables.
The data of a UTA model are represented by global variables of the primitive data types int and bool. Arrays and structs of primitive types are allowed. In addition, each process can have local or private variables, which are exclusively used in the process. C-like functions are supported, which can significantly contribute to defining compact and easy-to-understand models.
The dynamic behavior of a process is an automaton made up of locations and connecting arrowed edges. An edge is marked by a guarded command constituted by three optional attributes: a guard (a logical condition based on data and/or clock constraints), synchronization (a ! or ? operation on a channel), and an update (an ordered list of variable assignments and clock resets). The update of a channel sender precedes that of a receiver. In addition, a non-deterministic selection of a value to be assigned to a variable can also be specified in a command. Guarded commands represent the atomic concurrency units of a UTA model. The evolution of a model is the result of the non-deterministic or interleaved execution of its commands.
Figure 1 shows a simple example of a command used to switch from location L1 to L2. The edge is not enabled when the clock x is less than two time units, measured from when L1 was entered. If the command is taken, a communication over the channel c is signaled, and the assignment of a value v belonging to its ordinal type (e.g., int[0,3]) is assigned to var. As a matter of graphical evidence, a guard is shown in green, a synchronization is depicted in azure, the update is portrayed in blue, and a non-deterministic selection is shown in yellow.
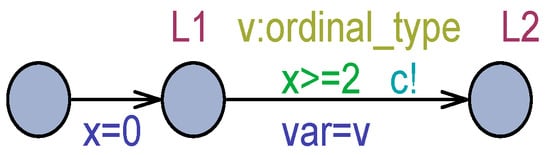
Figure 1.
A command example.
In Figure 1, although the command is enabled, the sender remains blocked in L1 if c is a unicast channel and the receiver is not ready. If the receiver is ready, the command is not executed until the clock value is less than 2. If the receiver is ready and x >= 2, the command can be taken but not necessarily soon, similar to transitions in classical Petri nets [20,21]. Locations L1 and L2 in Figure 1 are normal locations. A process can remain in a normal location for an arbitrary amount of time, and even for an infinite time. To constrain a process to exit from a normal location, an invariant can be added to it, as shown in Figure 2. In this case, the process can remain in L1 for five time units at most from the time the instant L1 is entered. In the situation modeled in Figure 2, after five time units, L1 must be abandoned; otherwise, a deadlock will occur. In other words, invariants (logical conditions) have to be continually satisfied for the automaton to remain in the location. The actual time taken to exit L1 in Figure 2 is any instant in the interval [2,5], as measured from when L1 was entered.
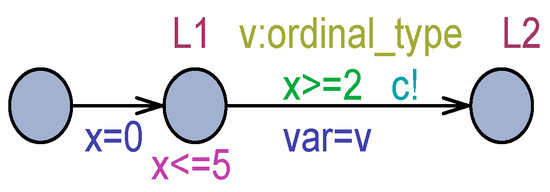
Figure 2.
Improving progress from L1 through invariant.
Particular cases of exiting from a location occur when the location is flagged as urgent (U) or committed (C). An urgent or committed location must be abandoned without any time passage. In Figure 3, when L1 is entered, it must immediately exit; otherwise, a deadlock will occur. If c is a broadcast channel, there will be no problem in abandoning L1 immediately.
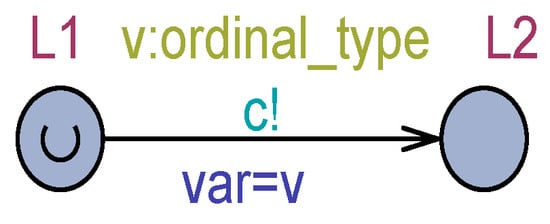
Figure 3.
A use case for an urgent location.
Despite the urgency, in the case when multiple processes are simultaneously in urgent locations, their exiting process obeys a non-deterministic order. Committed locations are similar to urgent ones, but the UTA recognizes committed locations with greater priority. Committed locations are always abandoned before urgent ones. Among multiple committed locations, the exiting process follows a non-deterministic order.
Another way to “accelerate” progress in a UTA model is to use urgent channels. By turning L1 in Figure 3 to a normal location and making c an urgent channel, the switch to L2 will occur as soon as the receiver of c is ready to synchronize. If c is a broadcast urgent channel, L1 will be exited immediately, independently from the readiness of any receiver. It is important to stress that the UTA will non-deterministically serve all events with the same urgency (priority).
The formal semantics of a UTA model can be given by a Timed Transition System (TTS), , where is a set of execution states for the model, is the initial state, and is a transition relation, which moves the TTS from one state to the next one. Two kinds of transitions exist: a delay and an action transition. Action transitions are instantaneous and are always executed before any delay transition. When no action transition exists to be executed at the current time, a delay transition is chosen to advance the system time of a minimal quantity . The amount of the delay must comply with all of the model invariants, which can never be falsified. Following a delay transition, all of the clocks of the model are increased by . In a correct model, following a delay transition, some action transitions are enabled to be taken. The construction of the TTS is a fundamental part of an Uppaal model and constitutes its state graph. Each node of the state graph admits a data component and a time component (zone or firing domain). The zone component is a system of clock inequalities describing a geometrical polyhedra (e.g., [22]) of all the time instants the state can actually reach.
Queries belonging to (a subset of) the Timed Computational Tree Logic (TCTL) [9] can be issued to the Uppaal model checker () for state graph navigation and property assessment. The hard work of the verifier involves conducting a systematic examination of all of the execution paths which originated from the initial state and are driven by non-determinism and the interleaving of the involved concurrent actions.
The following are some query examples: (a) checks if it is always true (invariantly) that there is no deadlocked state (a typical safety property); (b) is satisfied if (existentially) at least one state can be reached where is fulfilled (a liveness property). An can include a state predicate (a process is found in a given location) and/or a data/clock predicate. A particular query is built with the leads-to operator : , which aims to assess whether it always follows (inevitably) that a subsequent state is reached where is satisfied when starting from a state where holds. The or queries, e.g., , are also useful as they can be issued to find the maximum (respectively the minimum) value of a clock or data variable in the states of the state graph where the holds. The reader can refer to the Uppaal documentation [9] for further details.
3. Modeling and Verification Approach
A mutual exclusion algorithm (see Algorithm 1) can be modeled in Uppaal according to the following points:
- (a)
- Each process is an instance of a basic Process (const pid i) parameterized automaton, where pid is the type of the process identifiers and i is the unique id of the process instance.
- (b)
- Elementary actions in the Entry/Exit parts (see Algorithm 1) are assumed to consume no time and are modeled by commands exiting from urgent locations.
- (c)
- Busy-waiting actions in the Entry/Exit parts are mapped onto normal locations from which the exit is commanded as soon as the busy-waiting condition ceases to hold. To force an immediate exit from the busy-waiting location, an urgent and broadcast channel () is used, whose signal is sent, but it is not received by any other process.
- (d)
- The non-critical section (NCS in Algorithm 1) is represented by a normal location with a spontaneous exit (i.e., with a void guarded command). This way, the NCS can be abandoned after an arbitrary dwell time. An infinite dwell time models the process that stops being executed and will no longer compete to access the shared resource.
- (e)
- The critical section (CS in Algorithm 1) is expressed by a normal location, which is abandoned after exactly one time unit has elapsed. Time-sensitive behavior is achieved by associating one clock per process instance, which is reset at the entrance to the CS. The invariant of the CS location is x[i] <= 1, and the guard for exiting CS is x[i] >= 1.
- (f)
- The repeat-forever loop of Algorithm 1 is achieved by re-entering the NCS location after exiting the CS location. Before entering the NCS, all the Exit-part actions must be executed.
The above-proposed modeling schema permits the modeler to investigate all the (safety and liveness) properties of the mutual exclusion algorithm through model checking. In particular, the so-called overtaking factor () can be observed by quantifying the maximum (suprema) number of critical sections that a competing process must suffer before it obtains the grant to enter its critical section. Since all the process instances are identical, any process can be chosen as the target process (), and the can be measured by monitoring the value of the clock x[tp] just before entering the CS.
The modeling approach can be best understood through a practical example. Below, the original Dekker’s algorithm for processes [15], numbered 1 and 2, is considered and then modeled into Uppaal. The algorithm logic is expressed in pseudo-code in Algorithm 2. The following global shared variables are used:
- bool flag[N]; //all false initially by default;
- pid turn; //initial value is immaterial.
| Algorithm 2. Pseudo-code for Dekker’s mutual exclusion for two processes. |
| Process(i): local pid j = 3−i; //partner process repeat NCS //Entry-part flag[i] = true; while(flag[j]){ if(turn == j){ flag[i] = false; await(turn ! = j); //busy-waiting/spin-lock flag[i] = true; } } CS //Exit-part turn = j; flag[i] = false; forever |
Process i writes on its global variable flag[i], which is then checked by the partner process, j = 3 − i. The turn variable is only written by the process which exits its critical section and possibly checked by the partner. Therefore, the variables flag[1] and flag[2] and the turn are exterior variables [18]. Variable turn cannot suffer from scrambling because it is written by one process only. The following are the global declarations of the Uppaal model corresponding to Algorithm 2:
- const int N = 2;
- typedef int[1,N] pid;
- bool flag[pid]; //all false initially by default;
- pid turn; //default initialization;
- urgent broadcast chan synch;
- clock x[pid]; //one clock per process instance.
Some further global declarations are related to the chosen target process used for monitoring the overtaking factor:
- const pid tp = 1; //target process;
- void reset(const pid i){;
- if(i == tp) x[tp] = 0;
- }//reset.
Figure 4 reports the Uppaal model of Dekker’s algorithm according to the strong memory model. Location C is a choice point. BW is the busy-waiting location. The condition for exiting BW occurs when the turn variable has a value that is different from the partner process, j, that is, when the turn is found to be equal to the current process, i. In choice point C, if the partner is not interested in the CS (flag[j] = false), the current process enters its CS. When it exits the CS, the first turn is assigned to the partner, and then the process releases its current interest to the CS.
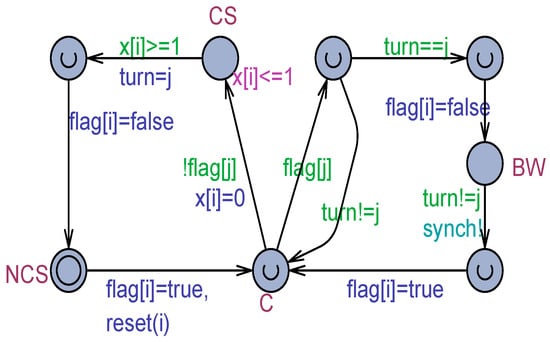
Figure 4.
The Uppaal model for Dekker’s algorithm for two processes.
The model in Figure 4 has a zeno-cycle [23], which occurs when the partner process j has issued its interest in accessing the resource, and the turn is assigned to the current process. The current process i cycles continually (even an infinite number of times and in zero time units) around C. As a side benefit provided by the use of Uppaal, a model like that shown in Figure 4 can be inspected in animation using a symbolic simulator [9]. Figure 5 shows a snapshot witnessing the zeno-cycle. The animation can also be exploited to study a diagnostic trace of events that brings the model into a particular state, e.g., an unexpected state (see later in this paper). Thus, the symbolic simulator can help to understand the logical behavior of a mutual exclusion algorithm, which can intrinsically be challenging to master from its pseudo-code (see Algorithm 2) due to non-determinism and the partial order of concurrency.
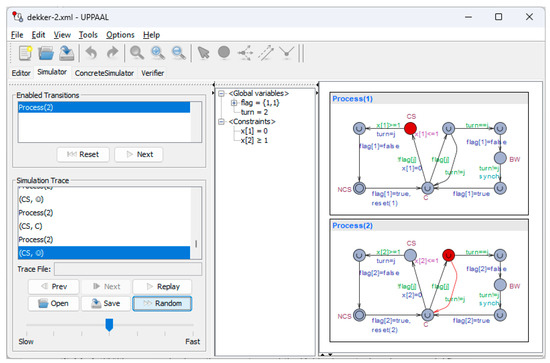
Figure 5.
A snapshot of Dekker’s solution in the Uppaal symbolic simulator.
Table 1 reports some basic TCTL queries and their answers, demonstrating that Dekker’s model is a correct mutual exclusion algorithm (see also Section 2.1).

Table 1.
TCTL queries checking the correctness of Dekker’s mutual exclusion model.
Query 2 simultaneously ensures that the number of processes in CS is always less than or equal to 1, which is the fundamental property of a mutual exclusion algorithm (see point (b) in Section 2.1). Queries 3 and 4 guarantee that each process can effectively enter its CS (liveness property). Query 5 states that a process in NCS does not forbid the partner from entering its critical section (point d) in Section 2.1). Queries 6 and 7 check that a process in the C or BW location eventually enters the CS (liveness or progress property). Both queries are not satisfied because of the model’s zeno-cycle. Finally, query 8 checks the maximal time (number of executed critical sections) which elapses before the target process enters its CS. This query furnishes the bound to the overtaking factor (), which is just 1 (a competing process only has to wait one turn). It should be noted that since the prediction is based on time, the zeno-cycle existing in the model (and in the algorithm in Algorithm 2) has no consequence.
As a final remark, it is worth noting that the arbitrary time spent by a process in the NCS location does not interfere with the computation of the overtaking bound. In fact, the worst-case scenario occurs when a process remains in the NCS by a zero-time duration. In this case, the process is immediately ready to start a new competition and then contributes to the definition of the bound. Any other duration in the NCS can only favor the partner process for reaching its CS.
Checking the Dekker’s Solution on a Weak Memory
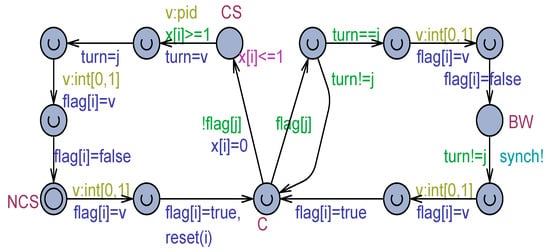
Figure 6.
Dekker’s model adapted for checking RW safeness.
For the reasons discussed in Section 3, the new model only considers the effects of flickering. Flickering is modeled by anticipating each change to flag[1], flag[2], and the turn by an assignment, which temporarily sets the variable to a non-deterministically value selected in the variable data type, which is int[0,1] for a flag[] bool variable (0 is false, 1 is true) and pid for a turn. These provisions make it possible in non-determinism for a process to effectively read the flickered value of a variable instead of the correct value that is subsequently assigned.
4. Analysis of Dekker’s Variants
The following considers two variants of Dekker’s algorithm. The first one was proposed by Doran and Thomas (DT) in [16], which simplified Dekker’s solution by making it loop-free, except for the busy-waiting cycles. The second one was designed by Buhr, Dice, and Hesselink (BDH) [12]. Both variants were studied in [12] using invariants and the UNITY logic. As a result, the DT variant was deemed to be RW-unsafe, whereas the BDH was found to be RW-safe. The DT and BDH algorithms were modeled and carefully verified using the Uppaal-based approach described in Section 3.
4.1. Doran and Thomas’s Variant
Algorithm 3 illustrates this variant in pseudo-code, which relies on the same shared communication variables in Dekker’s algorithm (see Section 3).
| Algorithm 3. The Doran and Thomas variant of the Dekker’s algorithm. |
| Process(i): local pid j = 3−i; //partner process repeat NCS //Entry-part flag[i] = true; if(flag[j]){ if(turn ! = i){ flag[i] = false; await(turn == i); //1st busy-waiting flag[i] = true; } await(!flag[j]); //2nd busy-waiting } CS //Exit-part turn = j; flag[i] = false; forever |
Figure 7 shows the Uppaal model corresponding to Algorithm 3 when the read and write operations are supposed to be atomic.
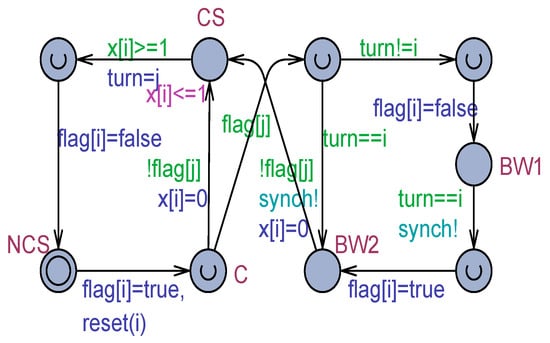
Figure 7.
The Uppaal model corresponding to the Doran and Thomas (DT) algorithm of Algorithm 3.
The more elegant solution of the model in Figure 7 was exhaustively model-checked using the same queries (with some obvious adaptations because there are now two busy-waiting locations) in Table 1. All of the fundamental queries were found to be satisfied. In particular, e.g., the target process in BW1 or BW2 eventually reaches its critical section, and it is now satisfied. This fact mirrors the absence, in this variant, of the zeno-cycle observed in Dekker’s solution. As another difference, the overtaking bound measured from BW2 was found to be 2. To justify this non-intuitive result, the following query was issued to the model checker in a quest to generate a diagnostic trace as follows:
- E<> Process(tp).BW2 && x[tp] == 2
A careful inspection of the generated trace in the symbolic simulator made it possible to observe the following sequence of events: “A first CS of the partner process is executed while the target process is in its BW1 (and has lowered its flag). After exiting the CS, the partner gives the turn to the target process but, for non-determinism (exiting from BW1 by the target process and reaching NCS by the partner are equally urgent and can occur in any order), the partner reaches NCS and exits it in zero time thus entering again its CS. Due to the time-sensitive CS of the partner, now the target process is forced to abandon BW1, set to true its flag thus reaching BW2. After this, when the partner process exits its 2nd CS, and again decides to compete, it will find the flag of the target process to true and thus necessarily it moves to its BW1 (by first changing its flag to false), whereas the target process certainly now exits its BW2 and enters its CS”.
The next step was studying the DT variant under the weak memory model. The adapted model is reported in Figure 8. The model checking work confirmed that the new model satisfies exactly the same queries as the basic model shown in Figure 7. Then, the new model with flickering confirmed that the DT variant is RW-safe, which is different from what is indicated in [12].
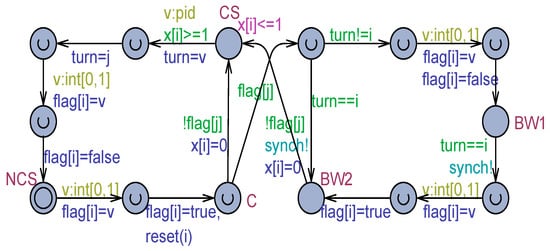
Figure 8.
The DT variant model with flickering.
4.2. Buhr, Dice, and Hesselink’s Variant
Algorithm 4 reproduces the Buhr, Dice, and Hesselink (BDH) variant in pseudo-code. The Entry-part is realized in a nested loop, which can be interrupted by a instruction. Each time the inner loop is broken, the CS enters.
| Algorithm 4. The Buhr, Dice, and Hesselink variant of Dekker’s algorithm. |
| Process(i): local pid j = 3−i; //partner process repeat NCS repeat //Entry-part flag[i] = true; if(!flag[j]) break; if(turn == i){ await(!flag[j]); //1st busy-waiting break; } flag[i] = false; await turn == i); //2nd busy-waiting forever CS //Exit-part turn = j; flag[i] = false; forever |
Figure 9 depicts the Uppaal model of the BDH variant. The model satisfies, as for the DT variant, all of the mutual exclusion queries, including the liveness queries based on the leads-to: from C, BW1, or BW2, it is always guaranteed that the process eventually reaches the CS, which, in turn, excludes the existence, as for the DT variant, of an internal zeno-cycle.
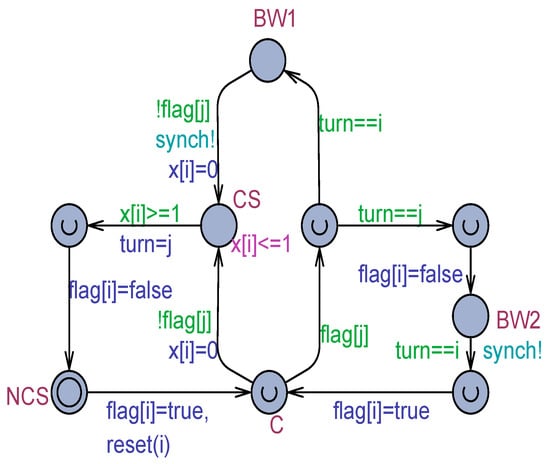
Figure 9.
The Uppaal model corresponding to the Buhr, Dice, and Hesselink (BDH) algorithm of Algorithm 4.
Figure 10 shows the BDH model when flickering is considered. It exhibits exactly the same behavior and properties as the basic model with atomic read/write.
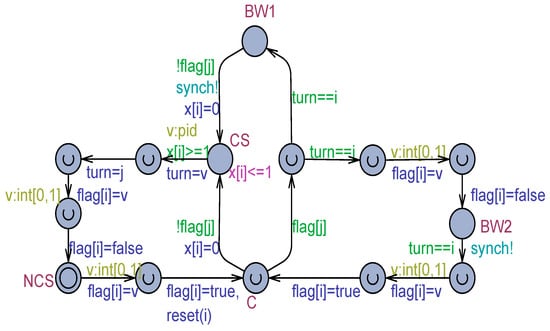
Figure 10.
The BDH variant model with flickering.
In light of the carried analysis work, it was found that both proposed variants only improve the basic Dekker’s mutual exclusion algorithm by eliminating the internal zeno-cycle. From the point of view of the overtaking bound, both the DT and the BDH algorithms have a worst-case bound of 2 instead of 1, as exhibited by Dekker’s solution. Moreover, all three algorithms proved to be RW-safe, that is, they all are resilient to flickering.
5. Embedding Algorithms in a Tournament Tree
All three algorithms studied in the preceding sections were extended to the more general and challenging case of processes by using a tournament tree (TT) [17,18,19]. The use of tournament trees is often advocated as an efficient yet standard solution for managing processes [11].
A binary tree is used here, where the arriving processes occupy the leaves of the latest level given by . All of the intermediate nodes, including the root one, play the role of arbitration loci for (maximum) two sibling processes. Each arbitration is regulated by a mutual exclusion algorithm for two processes, which can be the basic Dekker’s solution or the DT or BDH variants that were previously investigated. The winner of an arbitration moves to and occupies the father node and can thus attend a new arbitration with a new sibling. The process that first arrives at the root wins and enters its critical section. At the exit from the critical section, the path followed by the winner process is traversed in the opposite direction to reset all of the previously occupied nodes. Such resets can unblock waiting processes, which can resume their upward movement in the TT. The releasing process then reaches its NCS position from which a new competition can, possibly, recommence by using the same leaf node assigned to the specific process. Multiple and concurrent arbitrations can occur in the TT at a given time.
The global shared communication variables are two arrays: and . There is a flag for each node in the TT, and there is a turn for each intermediate node, including the root, with each one serving a distinct arbitration. These arrays are supposed to be initialized with their default values, that is, false for a flag and 1 for a turn.
The TT is linearized into the same array that is usually employed to support the heap sort. Slot 1 corresponds to the root node (level 0). Then, indexes 2 and 3 host the nodes of level 1 and so forth. The last level is at the end of the array. Two processes occupying the positions j and k are siblings if they share the same ancestor node (i.e., j/2 == k/2). The adopted organization makes it possible for a process to not have a sibling at a given node (e.g., a leaf). In this case, the arbitration immediately ends with the process moving up in the TT. As processes move along a path toward the root, arbitrations always tend to have two siblings.
5.1. Tournament Tree Based on Dekker’s Algorithm
Figure 11 shows the Uppaal model of the generic Process(i) in the context of a TT solution, which depends on Dekker’s algorithm for two processes.
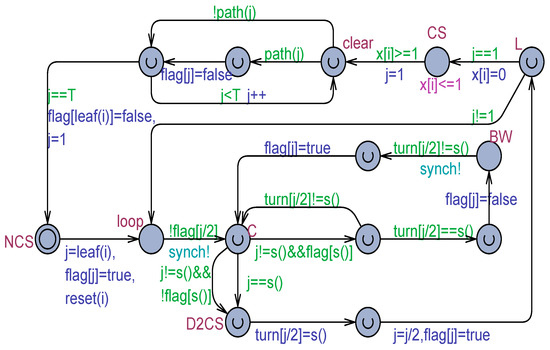
Figure 11.
The tournament tree model for N > 2 processes, which is based on Dekker’s algorithm for 2 processes.
At its arrival (exiting from the NCS location), the process identifies its leaf position j. Then, flag[j] is set to true to witness that the node is occupied by the process i. The main part of the model realizes a loop that finishes when j becomes 1 (root index). To minimize the number of local variables and thus reduce the memory footprint required by the state graph used by the model checker, the sibling’s identity is computed “on-the-fly” using the s() function. As shown in Figure 11, a process can participate in its current arbitration provided that the ancestor node is not yet occupied (i.e., flag[j/2] is false). If the arbitration is open and the process does not have a sibling, it immediately moves to the D2CS location, which denotes the critical section of the arbitration. Of course, in the context of the TT, this location can be urgent because the duration of one time unit will be spent in the critical section (see the CS location in Figure 11) of the whole TT. If both the siblings exist and the partner has not expressed its interest in the local critical section (flag[s()] is false), the process in node j moves directly to D2CS. Otherwise (see the right part of the location C of Figure 11), the normal behavior of Dekker’s algorithm can easily be retrieved. In the case where the process reaches D2CS, the turn of the ancestor node (turn[j/2]) is first assigned to the sibling, and then the process moves (j = j/2) and occupies the ancestor node by setting the flag[j/2] to true.
From L, the loop location is reached if a new iteration is needed (j! = 1), and the story repeats. When j becomes 1, the CS is entered, and the clock x[i] is reset. After one time unit, the CS exits and the traversed path is visited in the opposite direction by assigning false to all of the flag[] slots of the nodes that were previously occupied, including the leaf node. The L location is the natural point for measuring the overtaking bound suffered by the adopted target process (tp).
Model checking the model in Figure 11 confirmed that all of the basic mutual exclusion queries are satisfied. Only the following liveness/progress query is not satisfied due to the internal zeno-cycle existing around the C location:
Process(1).loop --> Process(1).CS
The overtaking bound was assessed through the following query:
sup{ Process(tp).L }: x[tp]
Since the bound is independent of the dwell time a process spends in the NCS, the worst-case of process arrivals was studied by making the NCS an urgent location. This provision allowed us to model check the model for ranging from 2 to 8. Table 2 collects the values of the resultant overtaking bound .

Table 2.
Overtaking bound vs. for the tournament-based model in Figure 11.
The dependency rule, , is clearly shown in Table 2, which implies that there is a linear trend of when the tournament tree is perfectly balanced (all the leaves of the last level of the tree are occupied). To give an idea of the execution performance, the query when terminates after 886 sec with a RAM memory usage of about 13 GB. All of the experimental runs were carried out on a Win11 Pro desktop platform, Dell XPS 8940, Intel i7-10700 (8 physical cores), CPU@2.90 GHz, with 32 GB RAM using the Uppaal tool version 64-4.1.26-2, 64 bit.
The same behavior was retrieved by model checking the model in Figure 11, which was adapted to weak memory by flickering (see Figure 12). The adapted model, though, witnessed an execution degradation due to the higher degree of non-determinism introduced by the flickering operations. In particular, the exhaustive verification cannot go over . For , the query that checks for the absence of deadlocks terminates after 325 sec with a memory usage of 5 GB.
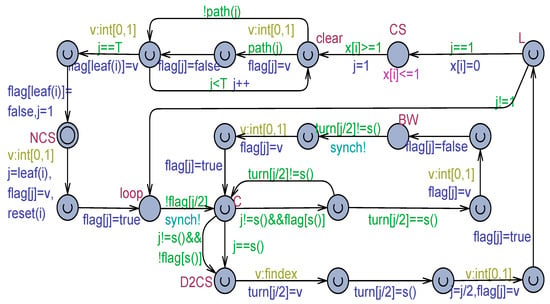
Figure 12.
The Uppaal model of Dekker’s algorithm in Figure 11 adapted to work with a weak memory.
5.2. Tournament Tree Based on Doran and Thomas Variant Algorithm
Figure 13 depicts the Uppaal model of the tournament-based algorithm for processes, which embeds the Doran and Thomas (DT) variant of Dekker’s algorithm.
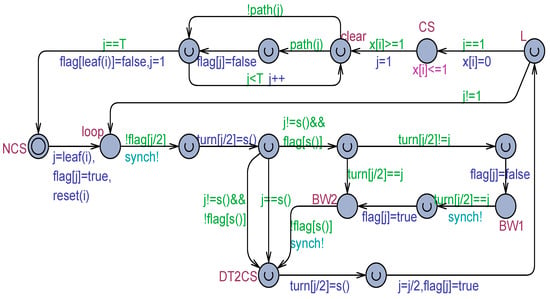
Figure 13.
The tournament tree model for processes based on the Doran and Thomas variant of Dekker’s solution for 2 processes.
With respect to the model in Figure 11, the necessity of initializing the turn variable of the ancestor node (turn[j/2]), e.g., by assigning it to the sibling process, should be noted. The remaining details can easily be retraceable according to the DT algorithm. The model in Figure 13 was found to be correct from the point of view of mutual exclusion basic properties. However, the overtaking factor emerged to be unbounded [12]. Figure 14 shows the adapted model used for working with a weak memory, which was confirmed to show the exact same behavior observed in the model in Figure 13.
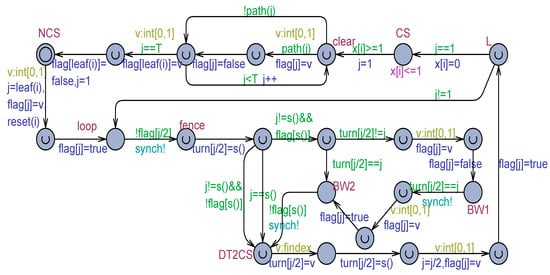
Figure 14.
The Uppaal model of the Doran and Thomas variant shown in Figure 13 adapted to work with a weak memory.
5.3. Tournament Tree Based on Buhr, Dice, and Hesselink Variant Algorithm
For completeness, Figure 15 shows the tournament-based model, which embeds the Buhr, Dice, and Hesselink algorithm for two processes.
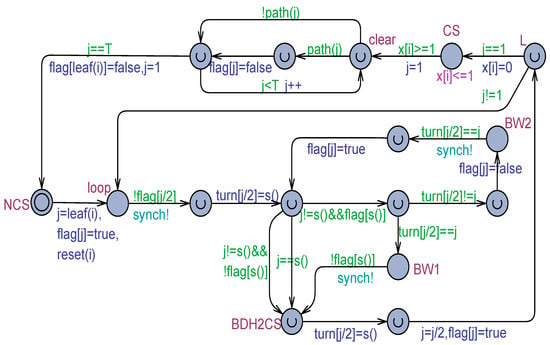
Figure 15.
The tournament tree model for processes based on the Buhr, Dice, and Hesselink variant of Dekker’s solution for 2 processes.
Similarly to the model in Figure 13, before engaging arbitration, the new model also initializes the turn variable of the ancestor node provided that the node is not already occupied. Figure 16 portrays the adapted Uppaal model used for working with a weak memory and flickering. The two models fulfill the basic mutual exclusion properties, although with an unbounded overtaking.
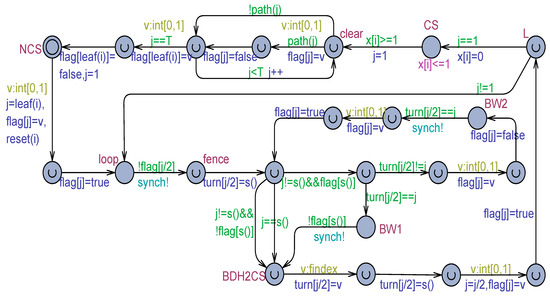
Figure 16.
The Uppaal model of the Buhr, Dice, and Hesselink variant in Figure 15 adapted to work with a weak memory.
A key point of both the models in Figure 13 and Figure 15 is the necessity of fencing (see the location named fence in Figure 14 and Figure 16) in the write operation, which initializes the turn variable of the ancestor node. This requirement originates from the fact that such initialization could be scrambled by the two sibling processes, which could simultaneously execute the write operation. Fencing has to be ensured by some hardware control mechanism. In Uppaal models, fencing is automatically ensured because the write operations are necessarily executed one after the other in any order. In contrast, no fencing is required by the tournament-based model, which embodies Dekker’s mutual exclusion algorithm (see Figure 11).
6. Summary of the Results
The carried model checking work provided some important information about the correctness assessment of Dekker’s mutual exclusion algorithm for two processes and its variants proposed by Doran and Thomas in [16] and by Buhr, Dice, and Hesselink in [12] with the goal of improving Dekker’s solution. It emerged that all three basic algorithms are correct and RW-safe. The only difference brought on by the two variants with respect to Dekker’s algorithm is the elimination of an internal zeno-cycle that physically cannot possibly exist since actions have a non-zero duration in a practical case. In addition, the overtaking bound was found to be 1 for Dekker’s solution and 2 in both the proposed variants.
Another set of interesting results emerged by separately using the three algorithms as the arbitration strategy in a tournament-based, standard, and efficient mutual exclusion scenario capable of handling processes. Here, the three tournament implementations were also found to be both logically correct and RW-safe, but with more positive aspects on the side of the Dekker-based realization. In fact, this implementation was more scalable than the other two when the strong memory model was used as it enabled its model checking until . Moreover, and most importantly, the overtaking factor for the Dekker-based realization emerged to be bounded and equal to , whereas in the other two cases, it was unbounded. Finally, adapting tournament-based solutions to work with a weak memory only requires managing the flickering, which occurs when one or more read operations are issued concurrently with a write operation for the Dekker-based solution, but it also requires fencing a write operation in the other two cases to avoid scrambling the value generated by simultaneous write operations.
7. Conclusions
This paper proposes a modeling and verification approach for a careful study of mutual exclusion algorithms for processes by model checking. The approach is based on the Uppaal toolbox [9] and its timed automata [10], a very flexible modeling language. Uppaal is well known to be a mature yet powerful tool for the formal specification and exhaustive model checking of real-time and distributed systems. This novel approach is concretely applied for a thorough investigation of Dekker’s mutual exclusion algorithm for two processes [15] and some of its variants proposed in the literature to improve the behavior of Dekker’s solution. This paper analyzes the algorithms both in the context of the strong memory model with atomic read/write operations on memory cells and with the weak memory model [1,2,12], where multiple read/write operations can occur simultaneously on the same memory cell.
The experimental work reported in this paper confirms that Dekker’s algorithm is RW-safe and that the proposed variants did not really improve it. The same conclusions also emerged in the case where the algorithms for two processes were embedded in a tournament tree, which delivered mutual exclusion in the more general scenario of processes, where the Dekker-based solution was distinguished for having a bounded overtaking.
Our future research will aim to develop the following points: First, we will aim to extend the application of the modelling and verification approach for proving properties of other algorithms for 2 processes, e.g., refs. [17,18,24,25] embodied in a tournament-based implementation for processes. Second, we will aim to develop an agent-based parallel simulation framework [26] to investigate, e.g., in a timed context, where stochastic behavior replaces non-determinism, general, and scalable mutual exclusion algorithms for processes on a modern multi/many-core machine.
Author Contributions
Methodology, L.N.; Validation, L.N., F.C. and F.P.; Formal analysis, L.N.; Investigation, F.C.; Data curation, L.N.; Writing – original draft, L.N.; Writing – review & editing, F.C. and F.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author/s.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lamport, L. The mutual exclusion problem: Part I—A theory of interprocess communication. In Concurrency: The Works of Leslie Lamport; Association for Computing Machinery: New York, NY, USA, 2019; pp. 227–245. [Google Scholar]
- Lamport, L. The mutual exclusion problem: Part II—Statement and solutions. In Concurrency: The Works of Leslie Lamport; Association for Computing Machinery: New York, NY, USA, 2019; pp. 247–276. [Google Scholar]
- Misra, J. A Discipline of Multiprogramming; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Raynal, M. Concurrent Programming: Algorithms, Principles, and Foundations; Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Silbershatz, A.; Galvin, P.B.; Gagne, G. Operating System Concepts, 10th ed.; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Goetz, B. Java Concurrency in Practice; Pearson Education: Singapore, 2006. [Google Scholar]
- Aravind, A.A.; Hesselink, W.H. A queue based mutual exclusion algorithm. Acta Inform. 2009, 46, 73–86. [Google Scholar] [CrossRef]
- Clarke, E.M.; Grumberg, O.; Peled, D.A. Model Checking; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Behrmann, G.; David, A.; Larsen, K.G. A tutorial on UPPAAL. In Formal Methods for the Design of Real-Time Systems; Bernardo, M., Corradini, F., Eds.; LNCS 3185; Springer: Berlin/Heidelberg, Germany, 2004; pp. 200–236. [Google Scholar]
- Alur, R.; Dill, D.L. A theory of timed automata. Theor. Comput. Sci. 1994, 126, 183–235. [Google Scholar] [CrossRef]
- Buhr, P.A.; Dice, D.; Hesselink, W.H. High-performance N-thread software solutions for mutual exclusion. Concurr. Comput. Pract. Exp. 2014, 27, 651–701. [Google Scholar] [CrossRef]
- Buhr, P.A.; Dice, D.; Hesselink, W.H. Dekker’s mutual exclusion algorithm made RW-safe. Concurr. Comput. Pract. Exp. 2016, 28, 144–165. [Google Scholar] [CrossRef]
- Frenzel, L.E. Dual-port SRAM accelerates smart-phone development. In Electronic Design; Endeavor Business Media LLC: Nashville, TN, USA, 2004. [Google Scholar]
- Wang, Z.; Zuo, Q.; Li, J. An intelligent multi-port memory. In International Symposium on Intelligent Information Technology Application Workshops; IEEE: Piscataway, NJ, USA, 2008; pp. 251–254. [Google Scholar]
- Dijkstra, E.W. Co-operating sequential processes. In Programming Languages; Genuys, F., Ed.; NATO Advanced Study Institute, Academic Press: London, UK; New York, NY, USA, 1968; pp. 43–112, Also EWD123 1965. [Google Scholar]
- Doran, R.W.; Thomas, L.K. Variants of the software solution to mutual exclusion. Inf. Process. Lett. 1980, 10, 206–208. [Google Scholar] [CrossRef]
- Peterson, G.L.; Fischer, M.J. Economical solutions for the critical section problem in a distributed system. In Proceedings of the Ninth Annual ACM Symposium on Theory of Computing, El Paso, TX, USA, 4–6 May 1977; pp. 91–97. [Google Scholar]
- Kessels, D.E. Arbitration without common modifiable variables. Acta Inform. 1982, 17, 135–141. [Google Scholar] [CrossRef]
- Hesselink, W.H. Tournaments for mutual exclusion: Verification and concurrent complexity. Form. Asp. Comput. 2017, 29, 833–852. [Google Scholar] [CrossRef]
- Murata, T. Petri nets: Properties, analysis and applications. Proc. IEEE 1989, 77, 541–580. [Google Scholar] [CrossRef]
- Nigro, L.; Cicirelli, F. Formal modeling and verification of embedded real-time systems: An approach and practical tool based on Constraint Time Petri Nets. Mathematics 2024, 12, 812. [Google Scholar] [CrossRef]
- Cicirelli, F.; Furfaro, A.; Nigro, L. Model checking time-dependent system specifications using time stream Petri nets and Uppaal. Appl. Math. Comput. 2012, 218, 8160–8186. [Google Scholar] [CrossRef]
- Bowman, H.; Gomez, R.; Su, L. A tool for the syntactic detection of zeno-timelocks in Timed Automata. Electron. Notes Theor. Comput. Sci. 2005, 139, 25–47. [Google Scholar] [CrossRef]
- Peterson, G.L. Myths about the mutual exclusion problem. Inf. Process. Lett. 1981, 12, 115–116. [Google Scholar] [CrossRef]
- Knuth, D.E. Additional comments on a problem in concurrent programming control. Commun. ACM 1966, 9, 321–322. [Google Scholar] [CrossRef]
- Nigro, L. Parallel Theatre: An actor framework in Java for high performance computing. Simul. Model. Pract. Theory 2021, 106, 102189. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).