Learning-Oriented QoS- and Drop-Aware Task Scheduling for Mixed-Criticality Systems
Abstract
:1. Introduction
- Presenting a novel adaptive technique with high QoS to schedule MC tasks at run-time.
- Proposing a learning-based drop-aware MC task scheduling mechanism, called SOLID, to improve the QoS by exploiting the generated dynamic slacks rigorously, during run-time with no HC tasks’ deadline misses.
- Extending the proposed mechanism (SOLID) to a mechanism that uses accumulated dynamic slack moderately, called LIQUID.
2. Related Works
3. System Model
4. Motivational Example and Problem Statement
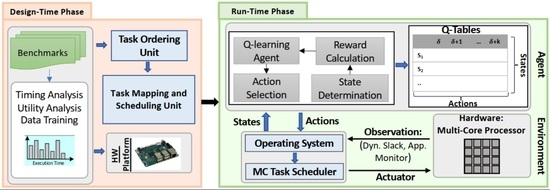
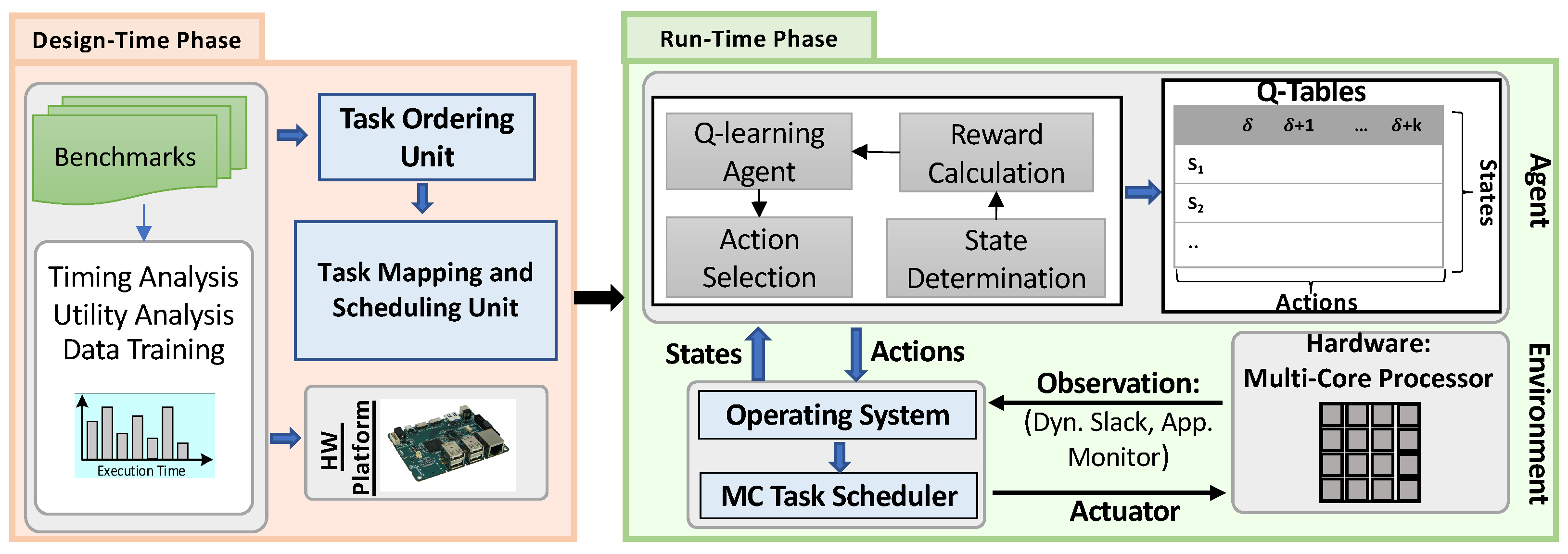
5. Proposed Method in Detail
5.1. An Overview of the Design-Time Approach
5.2. Run-Time Approach: Employment of SOLID
5.2.1. Learning-Based System Properties Optimization
5.2.2. SOLID Optimization
5.3. LIQUID Approach
| Algorithm 1 Proposed Learning-Based Scheme at Run-Time |
| Input:Task Set, Cores, Q-table |
| Output:QoS, Scheduled Tasks |
| 1: procedure LEARNING-BASED QoS OPTIMIZATION() |
| 2: for each cr in Cores do = 0; |
| 3: for t = 1 to Time do |
| 4: [,] = TaskStatusCheck(Tasks) |
| 5: [] = EDF-VD (, Cores) |
| 6: if = = 1 then |
| 7: for each released LC do |
| 8: + = 1; |
| 9: if mod(,) = = 0 then + = 1; |
| 10: end if |
| 11: end for |
| 12: else |
| 13: for each do = 0; |
| 14: end for |
| 15: end if |
| 16: = TaskOutputCheck(Tasks) |
| 17: if = = 1 then = |
| 18: end if |
| 19: if mod(t,) = = 0 then |
| 20: State = Deter-State (,) |
| 21: k = rand (1); //(0<k<1) //ϵ-Greedy Policy |
| 22: if then = argrand |
| 23: else = argmax |
| 24: end if |
| 25: Set the new task’s drop-rate based on the action |
| 26: R = CompReward () // Equation (5) |
| 27: //Equation (4) |
| 28: = 0; = 0; |
| 29: end if |
| 30: end for |
| 31: end for |
| 32: end procedure |
6. System Setup and Evaluation
6.1. Evaluation with Real-Life Benchmarks
6.2. Evaluation with Synthetic Task Sets
6.2.1. Effects of System Utilization
6.2.2. Effects of HC Tasks’ Run-Time Behaviour
6.2.3. Impacts of Task Mixtures
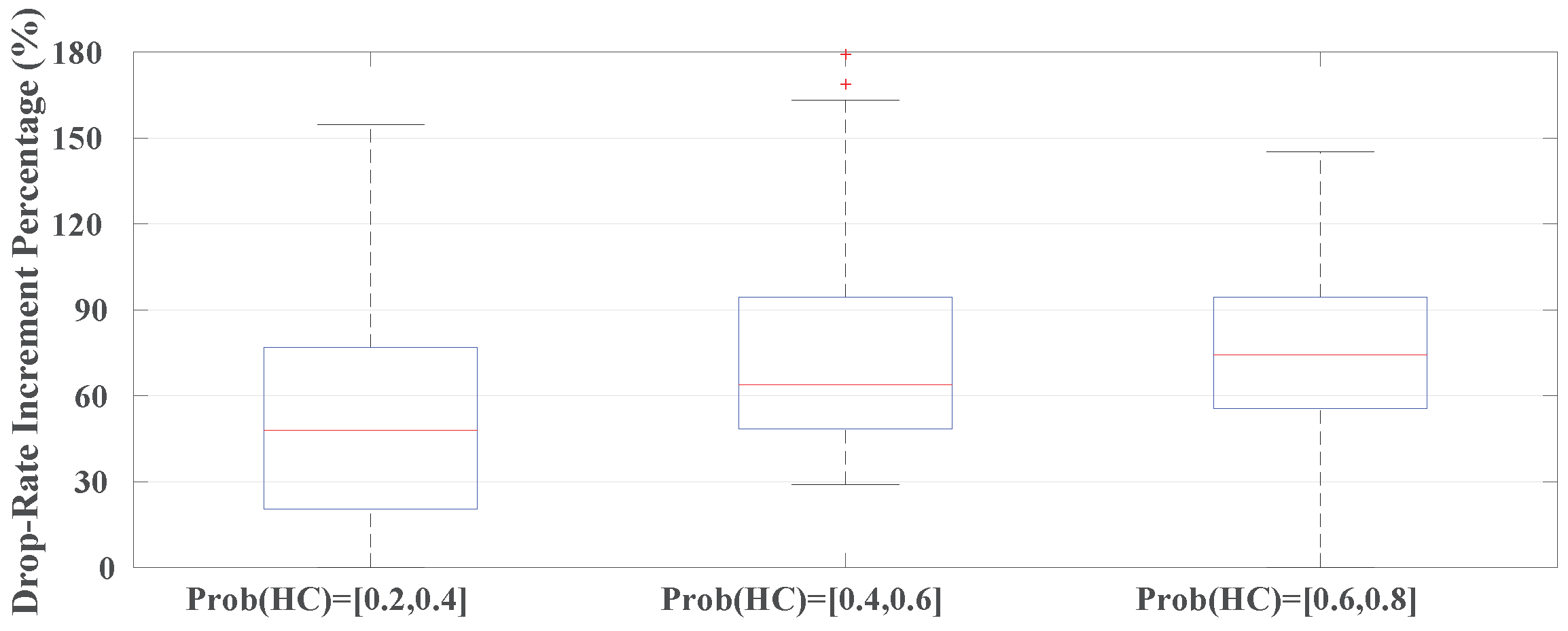
6.2.4. Investigating the LC Tasks’ Drop-Rate Parameter
6.3. Investigating the Timing and Memory Overheads of ML Technique
7. Conclusions and Future Studies
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BF | Best-Fit |
| DC | Decreasing Criticality |
| DU | Decreasing Utilization |
| EDF | Earliest-Deadline-First |
| EDF-VD | EDF with Virtual Deadline |
| FF | First-Fit |
| HC | High-Criticality |
| HI mode | HIgh-criticality mode |
| LC | Low-Criticality |
| LCM | Least Common Multiple |
| LO mode | LOw-criticality mode |
| MC | Mixed-Criticality |
| ML | Machine Learning |
| NDM | Number of Deadline Misses |
| QoS | Quality-of-Service |
| RL | Reinforcement Learning |
| UAV | Unmanned Aerial Vehicles |
| WCET | Worst Case Execution Time |
| WF | Worst-Fit |
References
- Baruah, S.; Bonifaci, V.; D’angelo, G.; Li, H.; Marchetti-Spaccamela, A.; Van Der Ster, S.; Stougie, L. Preemptive uniprocessor scheduling of mixed-criticality sporadic task systems. J. ACM (JACM) 2015, 62, 1–33. [Google Scholar] [CrossRef] [Green Version]
- Burns, A.; Davis, R.I. A Survey of Research into Mixed Criticality Systems. ACM Comput. Surv. 2017, 50, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, S.S.; Ranjbar, B.; Kumar, A. Reliability-Aware Resource Management in Multi-/Many-Core Systems: A Perspective Paper. J. Low Power Electron. Appl. 2021, 11, 7. [Google Scholar] [CrossRef]
- Lee, J.; Chwa, H.S.; Phan, L.T.X.; Shin, I.; Lee, I. MC-ADAPT: Adaptive Task Dropping in Mixed-Criticality Scheduling. ACM Trans. Embed. Comput. Syst. (TECS) 2017, 16, 1–21. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, K.; Vaidhun, S.; Arefin, S.; Das, S.K.; Xiong, H. Uniprocessor Mixed-Criticality Scheduling with Graceful Degradation by Completion Rate. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Nashville, TN, USA, 11–14 December 2018; pp. 373–383. [Google Scholar]
- Baruah, S.; Li, H.; Stougie, L. Towards the Design of Certifiable Mixed-criticality Systems. In Proceedings of the IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS), Stockholm, Sweden, 12–15 April 2010; pp. 13–22. [Google Scholar]
- Ranjbar, B.; Safaei, B.; Ejlali, A.; Kumar, A. FANTOM: Fault Tolerant Task-Drop Aware Scheduling for Mixed-Criticality Systems. IEEE Access 2020, 8, 187232–187248. [Google Scholar] [CrossRef]
- Huang, L.; Hou, I.H.; Sapatnekar, S.S.; Hu, J. Improving QoS for global dual-criticality scheduling on multiprocessors. In Proceedings of the IEEE International Conference on Embedded and Real-Time Computing Systems and Applications (RTCSA), Hangzhou, China, 18–21 August 2019; pp. 1–11. [Google Scholar]
- Liu, D.; Guan, N.; Spasic, J.; Chen, G.; Liu, S.; Stefanov, T.; Yi, W. Scheduling Analysis of Imprecise Mixed-Criticality Real-Time Tasks. IEEE Trans. Comput. (TC) 2018, 67, 975–991. [Google Scholar] [CrossRef] [Green Version]
- Baruah, S.; Bonifaci, V.; DAngelo, G.; Li, H.; Marchetti-Spaccamela, A.; van der Ster, S.; Stougie, L. The Preemptive Uniprocessor Scheduling of Mixed-Criticality Implicit-Deadline Sporadic Task Systems. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Pisa, Italy, 11–13 July 2012; pp. 145–154. [Google Scholar]
- Gettings, O.; Quinton, S.; Davis, R.I. Mixed Criticality Systems with Weakly-Hard Constraints. In Proceedings of the International Conference on Real Time and Networks Systems (RTNS), Lille, France, 4–6 November 2015; pp. 237–246. [Google Scholar]
- Li, Z.; Ren, S.; Quan, G. Dynamic Reservation-Based Mixed-Criticality Task Set Scheduling. In Proceedings of the IEEE Conf. on High Performance Computing and Communications, Cyberspace Safety and Security, Embedded Software and System (HPCC,CSS,ICESS), Paris, France, 20–22 August 2014; pp. 603–610. [Google Scholar]
- Ranjbar, B.; Hoseinghorban, A.; Sahoo, S.S.; Ejlali, A.; Kumar, A. Improving the Timing Behaviour of Mixed-Criticality Systems Using Chebyshev’s Theorem. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 1–5 February 2021; pp. 264–269. [Google Scholar]
- Ramanathan, S.; Easwaran, A. Mixed-criticality scheduling on multiprocessors with service guarantees. In Proceedings of the IEEE International Symposium on Real-Time Distributed Computing (ISORC), Singapore, 29–31 May 2018; pp. 17–24. [Google Scholar]
- Pathan, R.M. Improving the quality-of-service for scheduling mixed-criticality systems on multiprocessors. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Dubrovnik, Croatia, 27–30 June 2017. [Google Scholar]
- Pathan, R.M. Improving the schedulability and quality of service for federated scheduling of parallel mixed-criticality tasks on multiprocessors. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Barcelona, Spain, 3–6 July 2018. [Google Scholar]
- Sigrist, L.; Giannopoulou, G.; Huang, P.; Gomez, A.; Thiele, L. Mixed-criticality runtime mechanisms and evaluation on multicores. In Proceedings of the IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS), Seattle, WA, USA, 13–16 April 2015; pp. 194–206. [Google Scholar]
- Hu, B.; Huang, K.; Huang, P.; Thiele, L.; Knoll, A. On-the-fly fast overrun budgeting for mixed-criticality systems. In Proceedings of the International Conference on Embedded Software (EMSOFT), Pittsburgh, PA, USA, 2–7 October 2016; pp. 1–10. [Google Scholar] [CrossRef] [Green Version]
- Bate, I.; Burns, A.; Davis, R.I. A Bailout Protocol for Mixed Criticality Systems. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Lund, Sweden, 7–10 July 2015; pp. 259–268. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Ma, X.; Singh, K.; Schulz, M.; de Supinski, B.R.; McKee, S.A. Machine learning based online performance prediction for runtime parallelization and task scheduling. In Proceedings of the IEEE Symposium on Performance Analysis of Systems and Software, Boston, MA, USA, 26–28 April 2009; pp. 89–100. [Google Scholar]
- Eom, H.; Juste, P.S.; Figueiredo, R.; Tickoo, O.; Illikkal, R.; Iyer, R. Machine Learning-Based Runtime Scheduler for Mobile Offloading Framework. In Proceedings of the IEEE/ACM International Conference on Utility and Cloud Computing, Dresden, Germany, 9–12 December 2013; pp. 17–25. [Google Scholar]
- Horstmann, L.P.; Hoffmann, J.L.C.; Fröhlich, A.A. A Framework to Design and Implement Real-time Multicore Schedulers using Machine Learning. In Proceedings of the IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Zaragoza, Spain, 10–13 September 2019; pp. 251–258. [Google Scholar]
- Buttazzo, G.C. Hard Real-TIME Computing Systems: Predictable Scheduling Algorithms and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 24. [Google Scholar]
- Huang, P.; Kumar, P.; Giannopoulou, G.; Thiele, L. Energy efficient DVFS scheduling for mixed-criticality systems. In Proceedings of the International Conference on Embedded Software (EMSOFT), New Delhi, India, 12–17 October 2014; pp. 1–10. [Google Scholar]
- Li, Z.; He, S. Fixed-Priority Scheduling for Two-Phase Mixed-Criticality Systems. ACM Trans. Embed. Comput. Syst. (TECS) 2018, 17, 1–20. [Google Scholar] [CrossRef]
- Ranjbar, B.; Hosseinghorban, A.; Salehi, M.; Ejlali, A.; Kumar, A. Toward the Design of Fault-Tolerance-and Peak-Power-Aware Multi-Core Mixed-Criticality Systems. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2022, 41, 1509–1522. [Google Scholar] [CrossRef]
- Su, H.; Zhu, D.; Mossé, D. Scheduling algorithms for Elastic Mixed-Criticality tasks in multicore systems. In Proceedings of the International Conference on Embedded and Real-Time Computing Systems and Applications (RTCSA), Taipei, Taiwan, 19–21 August 2013; pp. 352–357. [Google Scholar]
- Pagani, S.; Manoj, P.D.S.; Jantsch, A.; Henkel, J. Machine Learning for Power, Energy, and Thermal Management on Multicore Processors: A Survey. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. (TCAD) 2020, 39, 101–116. [Google Scholar] [CrossRef]
- Bithas, P.S.; Michailidis, E.T.; Nomikos, N.; Vouyioukas, D.; Kanatas, A.G. A survey on machine-learning techniques for UAV-based communications. Sensors 2019, 19, 5170. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Safaei, B.; Mohammadsalehi, A.; Khoosani, K.T.; Zarbaf, S.; Monazzah, A.M.H.; Samie, F.; Bauer, L.; Henkel, J.; Ejlali, A. Impacts of mobility models on rpl-based mobile iot infrastructures: An evaluative comparison and survey. IEEE Access 2020, 8, 167779–167829. [Google Scholar] [CrossRef]
- Dinakarrao, S.M.P.; Joseph, A.; Haridass, A.; Shafique, M.; Henkel, J.; Homayoun, H. Application and thermal-reliability-aware reinforcement Learning based multi-core power management. ACM J. Emerg. Technol. Comput. Syst. (JETC) 2019, 15, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Lin, M.; Yang, L.T.; Zhang, Q. Autonomous Power Management with Double-Q Reinforcement Learning Method. IEEE Trans. Ind. Inform. (TII) 2020, 16, 1938–1946. [Google Scholar] [CrossRef]
- Dey, S.; Singh, A.K.; Wang, X.; McDonald-Maier, K. User interaction aware reinforcement learning for power and thermal efficiency of CPU-GPU mobile MPSoCs. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2020; pp. 1728–1733. [Google Scholar]
- Rummery, G.A.; Niranjan, M. On-Line Q-Learning Using Connectionist Systems; Department of Engineering Cambridge, University of Cambridge: Cambridge, UK, 1994; Volume 37. [Google Scholar]
- Kim, T.; Sun, Z.; Cook, C.; Gaddipati, J.; Wang, H.; Chen, H.; Tan, S.X.D. Dynamic reliability management for near-threshold dark silicon processors. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Austin, TX, USA, 7–10 November 2016; pp. 1–7. [Google Scholar]
- Biswas, D.; Balagopal, V.; Shafik, R.; Al-Hashimi, B.M.; Merrett, G.V. Machine learning for run-time energy optimisation in many-core systems. In Proceedings of the Design, Automation & Test in Europe Conference Exhibition (DATE), Lausanne, Switzerland, 27–31 March 2017; pp. 1588–1592. [Google Scholar]
- Zhu, D.; Aydin, H. Reliability-Aware Energy Management for Periodic Real-Time Tasks. IEEE Trans. Comput. (TC) 2009, 58, 1382–1397. [Google Scholar]
- Su, H.; Zhu, D. An Elastic Mixed-Criticality task model and its scheduling algorithm. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 18–22 March 2013; pp. 147–152. [Google Scholar]
- Guthaus, M.R.; Ringenberg, J.S.; Ernst, D.; Austin, T.M.; Mudge, T.; Brown, R.B. MiBench: A free, commercially representative embedded benchmark suite. In Proceedings of the IEEE International Workshop on Workload Characterization. WWC-4 (Cat. No.01EX538), Austin, TX, USA, 2 December 2001; pp. 3–14. [Google Scholar]
- Ranjbar, B.; Hosseinghorban, A.; Sahoo, S.S.; Ejlali, A.; Kumar, A. BOT-MICS: Bounding Time Using Analytics in Mixed-Criticality Systems. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. (TCAD) 2021, 1. [Google Scholar] [CrossRef]
- Brandenburg, B.B.; Calandrino, J.M.; Anderson, J.H. On the Scalability of Real-Time Scheduling Algorithms on Multicore Platforms: A Case Study. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Barcelona, Spain, 8 December 2008; pp. 157–169. [Google Scholar]
- Ranjbar, B.; Nguyen, T.D.A.; Ejlali, A.; Kumar, A. Power-Aware Run-Time Scheduler for Mixed-Criticality Systems on Multi-Core Platform. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. (TCAD) 2021, 40, 2009–2023. [Google Scholar] [CrossRef]








| # | S/M-Core | MC Tasks | Run-/Design-Time | QoS Opt. | Use of ML | |
|---|---|---|---|---|---|---|
| 1 | Gettings’15 [11], Ranjbar’20a [7], Liu’18 [9] Guo’18 [5], Ranjbar’21 [13] | S-Core | ✓ | Design-Time | offline | None |
| 2 | Ramanathan’18 [14], Pathan’17 [15], Pathan’18 [16] | M-Core | ✓ | Design-Time | offline | None |
| 3 | Sigrist’15 [17] | M-Core | ✓ | Run-Time | None | None |
| 4 | Huang’19 [8], Lee’17 [4], Li’14 [12], Hu’16 [18], Bate’15 [19] | S/M-Core | ✓ | Run-Time | online | None |
| 5 | Li’09 [20], Eom’13 [21], Horstmann’19 [22] | M-Core | × | Run-Time | None | ✓ |
| 6 | Proposed Work | M-Core | ✓ | Run-Time | offline & online | ✓ |
| Symbol | Description | Symbol | Description |
|---|---|---|---|
| Criticality level of task | Skip parameter of task | ||
| Optimistic WCET of task | Pessimistic WCET of task | ||
| Actual deadline of task | Virtual deadline of task | ||
| Period of task | Hyper-period of task set | ||
| A released job (j) of task | Finish Time of task | ||
| Number of all LC tasks | Number of executed LC tasks |
| Task Function | |||||||
|---|---|---|---|---|---|---|---|
| engine control | HI | 2 | 7 | 24 | 11 | ∞ | |
| collision avoidance | HI | 2 | 4 | 48 | 22 | ∞ | |
| video capturing and transferring | LO | 2 | 2 | 8 | - | 3 | |
| sensor data recording | LO | 2 | 2 | 6 | - | 4 | |
| navigation | HI | 0.8 | 1 | 12 | 6 | ∞ |
| Metrics | LIQUID | Gettings’15 [11], Ranjbar’20 [7] | Liu’18 [9] | Li’14 [12] | Huang’19 [8] |
|---|---|---|---|---|---|
| NDM | 0.009 | 0.010 | 1 | 0.341 | 0.999 |
| QoS | 99.67% | 96.92% | 64.33% | 87.83% | 64.36% |
| LIQUID | SOLID | Gettings’15 [11], Ranjbar’20 [7] | Liu’18 [9] | Li’14 [12] | Huang’19 [8] | |
|---|---|---|---|---|---|---|
| = [0.2,0.4] | 0.38, 0.82 | 0.42, 0.83 | 0.46, 0.84 | 1.00, 1.00 | 0.70, 0.99 | 1.00, 0.95 |
| = [0.4,0.6] | 0.36, 0.80 | 0.41, 0.81 | 0.47, 0.83 | 0.96, 0.99 | 0.71, 0.97 | 0.96, 0.94 |
| = [0.6,0.8] | 0.29, 0.78 | 0.34, 0.79 | 0.38, 0.80 | 0.80, 0.94 | 0.58, 0.93 | 0.80, 0.90 |
| LIQUID | SOLID | Gettings’15 [11], Ranjbar’20 [7] | Liu’18 [9] | Li’14 [12] | Huang’19 [8] | |
|---|---|---|---|---|---|---|
| = [0.6,0.8] | 0.15, 0.49 | 0.29, 0.50 | 0.32, 0.51 | 0.76, 0.93 | 0.68, 0.87 | 0.76, 0.92 |
| = [0.4,0.6] | 0.25, 0.78 | 0.38, 079 | 0.46, 0.80 | 1.00, 0.95 | 0.79, 0.90 | 0.99, 0.94 |
| = [0.2,0.4] | 0.25, 0.78 | 0.35, 0.78 | 0.47, 0.79 | 0.99, 1.00 | 0.68, 0.95 | 0.99, 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ranjbar, B.; Alikhani, H.; Safaei, B.; Ejlali, A.; Kumar, A. Learning-Oriented QoS- and Drop-Aware Task Scheduling for Mixed-Criticality Systems. Computers 2022, 11, 101. https://doi.org/10.3390/computers11070101
Ranjbar B, Alikhani H, Safaei B, Ejlali A, Kumar A. Learning-Oriented QoS- and Drop-Aware Task Scheduling for Mixed-Criticality Systems. Computers. 2022; 11(7):101. https://doi.org/10.3390/computers11070101
Chicago/Turabian StyleRanjbar, Behnaz, Hamidreza Alikhani, Bardia Safaei, Alireza Ejlali, and Akash Kumar. 2022. "Learning-Oriented QoS- and Drop-Aware Task Scheduling for Mixed-Criticality Systems" Computers 11, no. 7: 101. https://doi.org/10.3390/computers11070101
APA StyleRanjbar, B., Alikhani, H., Safaei, B., Ejlali, A., & Kumar, A. (2022). Learning-Oriented QoS- and Drop-Aware Task Scheduling for Mixed-Criticality Systems. Computers, 11(7), 101. https://doi.org/10.3390/computers11070101