1. Introduction
In the current technology era, many multimedia applications are on demand, which creates a huge amount of video and image data just at a finger click. There is a high demand for data compression techniques to handle those data. The data compression can be achieved by reducing or removing the redundant information from the original data. There are two types of image compression techniques: lossy and lossless image compression. In the medical diagnosis process, we need a reconstructed image, which has the exact replica of the original image. That is, no information is lost and the type of compression is known as the lossless image compression. Meanwhile, in lossy image compression techniques, some data loss is acceptable, such as a photograph where a minor loss in redundant data from the original image is acceptable to contain a better bit rate.
The details of different image compression techniques can be found in the literature [
1,
2] and the techniques can be classified as direct and transform domain methods. In direct techniques, such as block truncation coding [
2] and vector quantization [
3], compression is applied directly to the spatial domain data. However, in the transform domain techniques, the image is transformed to a different domain before the compression. Principal component analysis (PCA), discrete wavelet transform (DWT) and discrete cosine transform (DCT) [
4,
5,
6] are the most popular transform domain methods found in the literature. In these transform domain methods, the information content of the image is concentrated in a few blocks, making them suitable for data reduction. The DWT method poses a better reconstructed image than any other methods. According to image and video compression quality measure standards, PSNR of a DWT-based approach is much better than a DCT-based approach. However, due to lower complexity, DCT-based approaches are preferred in multimedia devices.
The simple and efficient encoding and decoding structure of JPEG standard is making it most popular among all compression standards [
7,
8]. This standard is used in digital cameras and various equipment that are used to take photographs for data storage and transmission worldwide. As DCT is applicable in a block-wise manner, for the encoding process, we have considered the 8 × 8 block size in the proposed method. For each block, a 2D DCT is obtained following quantization and zig-zag scanning.
DCT [
9] based JPEG is the most widely used transform domain algorithm that is used today, with various modifications. In JPEG, the quantization matrix (QM) plays a major role that decides the compression ratio and, hence, the bpp of the compressed image. The JPEG depends on adaptive quantization and a scanning method has been developed by Messaoudi et al. [
10]. There are JPEG papers based on saliency, which is generating a low bit rate [
11]. Some image compression methods have used the feature extraction technique for bit rate reduction using block truncation coding (BTC) [
12,
13]. BTC methods are mostly acceptable for low-complexity applications, but the bit rate is still very high for this method. The high bit rate is reduced by using multi-grouping techniques [
14,
15]. The compression algorithms developed based on DWT [
16], H264 [
17], H265 [
18], and JPEG2000 [
19,
20] have effective compression, but, due to the high complexity, these methods have high computational requirements. Low-complexity saliency-based DCT has better compression but is not applied for the entire image [
21]. The Walsh–Hadamard Transform (WHT) is used for image compression [
22] due to the high speed of operation and its ability to reduce bit rate and, hence, with higher compression ratio.
To reduce the correlation between the RGB bands, Touil et al. [
23] proposed a DCT-based compression method where the authors used three different uncorrelated spaces by using the Bat algorithm, which gives better performance than standard JPEG. This method is capable of reducing the number of small energy coefficients of the DCT by optimizing the cost function. In [
24], a homogeneous texture region (HTR)-based block allocation for the DCT compression is proposed. The blocks with high HTR are given larger block-size to perform the DCT and vice versa.
Motivated by the popularity and simplicity of the DCT-based compression approach, in this paper, we have proposed a DCT-based framework followed by bi-level quantization for image compression. Here, the quantization matrix is not fixed for the entire image blocks. The value of the quantization matrix is decided based on the feature strength of the blocks extracted using Walsh–Hadamard kernel.
The unique contributions for this paper are as follows:
Deployed Walsh–Hadamard transform kernel (WHTK)-based feature extraction for image compression. This enables faster implementation.
Generation of block feature strength (BFS) based on a weighted combination of color, edge, and texture strength extracted using Walsh–Hadamard transform kernel. This enhances the compression performance.
Automatic selection of the quantization level of the blocks using BFS and K-means [
25] algorithm. This ensures easy implementation.
The proposed DCT-based framework using bi-level quantization is efficient and faster as compared to standard JPEG and other recent algorithms, such as H264, H265, JPEG 2000, and others.
The remainder of the paper is organized as follows.
Section 2 describes the materials and methods, including an overview of Walsh–Hadamard Transform and its properties, and the proposed methods in detail.
Section 3 describes the simulations, results, and analysis. Finally, some concluding remarks are given in
Section 4.
2. Materials and Methods
This section describes the overview of Walsh–Hadamard Transforms (WHT) and its properties, Walsh Basis Vector, and Walsh-Basis-Vector-based feature extraction, followed by details of the proposed algorithm.
2.1. Overview of Walsh–Hadamard Transforms
The DCT, DWT, and WHT transform methods are used in various signal and image processing fields. These methods are popular due to their compaction of the energy in the lower frequency components and the quality of reconstruction. Through analyzing and classifying the coefficients of linear image transform and the frequency components of the image, we obtain the edge information. The kernels or the bases of the image transform, which give the edge information, can also provide energy information of an image, which gives the local properties of an image, such as texture and color. WHT is very useful due to its simplicity of operation over other linear transform methods. WHT has reduced computational complexity due to its +1 and −1 orthogonal components. WHT is an average but non-sinusoidal image transform method. The Walsh–Hadamard Transform matrix (WHTM) can be defined as with N sets of rows. The properties of the are defined as follows:
- (i)
= 1 or ,
- (ii)
for all ,
- (iii)
has all zero crossing. The size of the WHTM is of power of 2.
The WHT matrix is valid for
N > 2 and
N mod 4 = 0.
WHTM for
N = 8 is given by:
The row of WHTM is known as the 1D Walsh–Hadamard Basis Vector and is ortho-normal. By using the tensor of 1D-basis vector from
WHTM, we obtain the 2D WHT kernel by multiplying the corresponding row with the column of the WHT [
26]. The basis WHT kernel can be used as the basis vectors
k of the
WHTM. We can obtain the basis vectors as
according to the number of WHT kernel.
2.2. Properties of Walsh–Hadamard Transform
Consider an image block of size
and pixels of
, we can find the 2D WHTM as:
where
are the Walsh transform results and the
g(
x,
y ,
u ,
v) are the kernels. The very first kernel is
and the next kernel is
. The 1st kernel is the zero sequencing kernel.
Below are some interesting properties of WHT:
(i) Property 1: The zero sequencing term is a measure of average brightness of the image block, which gives color strength of the image.
Property 1 gives the brightness of the image by using the statistics of zero sequencing term (). This gives the color strength of an image.
(ii) Property 2: There exists an energy conservation property among the transform domain and the spatial domain of a block [
26].
This property can be deployed for extracting edge information based on the non-zero sequencing terms , , and . Property 2 gives the idea of conservation of energy in the transform domain, which gives the edge information based on the nonzero sequencing terms , , and .
(iii) Property 3: The property of energy compaction indicates that the energy of the image is distributed to only a few transform coefficients. This shows that the few coefficients have the significant values. Property 3 gives the energy compaction of the image in the transform coefficients, which give the information of the texture strength of the image block.
Motivated by the properties of Walsh–Hadamard Transform [
26], we have considered the energy, texture, and color properties to obtain the better visual features of an image in the proposed method.
In the preprocessing stage, we have converted the image block from RGB to YCbCr model and generated one color component (
) from which we can extract the features of an image.
value can be generated by considering the average of the two planes as follows:
where
and
;
indicates the size of the image.
,
, and
indicate YCbCr planes where Y is the luminance/brightness of the color, and
,
are the blue component and the red component related to the chrominance of color. The image is divided into 8 × 8 blocks. Feature extraction has been done by applying the basis vector on the
values.
2.3. Walsh Basis Vectors
Walsh basis vectors are n-dimensional basis vectors that depend on the kernel of the WHT [
26]. The idea of using the basis vector for feature extraction has been discussed in [
26]. The low frequencies and high frequencies define important features of the image, as low frequencies capture the brightness of the image, whereas high frequencies capture the edge features of the image. The basis kernel (
) has the capability to capture the low-frequency components and the basis kernels
have the capability to capture the high-frequency components of the image, where
n is the total number of kernels in the WHTM. In this paper, for feature extraction, we have considered only
basis kernel for capturing the low-frequency information and
. basis kernels for capturing the high-frequency information. To capture the texture information, we have considered
and
basis kernels. While selecting the basis vectors, we need to ensure that one vector should not be the transform of the other. In [
26], Lakshmipriya et al. selected a basis kernel of dimension 4 × 4 for feature extraction by considering
and
basis kernels of the
WHTM. In contrast to this, in our work, we have considered
WHTM basis kernel
and
, as illustrated in
Figure 1, with a dimension of
for feature extraction.
, and
are the vector representation of the Walsh basis kernels, which are orthogonal vectors, as they are representing the Walsh–Hadamard kernel, and are calculated based on (6), (7), and (8) as follows.
Color strength is extracted by applying the basis vector on the image block, which has low-frequency information. Edge strength is extracted by applying and basis vectors on the image block, which have high-frequency information. Texture strength is extracted by applying , and basis vectors on the image block. The procedure for feature extraction using basis vectors is described in the following subsection.
2.4. Feature Extraction and Generation of Block Feature Strength (BFS) Using Walsh Basis Vector
In this section, we describe the block-based color feature, edge feature, and texture feature extraction techniques using the three Walsh basis vectors defined in the previous subsection.
Let
,
, no. of blocks.
represents the inner product of block
with Walsh basis vector
. Then:
where,
;
p represents the number of elements in a block,
represents the
cth value of the block, and
represents the
cth value of the
Walsh basis vector.
The block-based color feature strength, edge feature strength, and texture feature strength denoted as and , respectively, are obtained as follows:
Block color strength (
): It is defined as the amount of brightness in the image block which can be calculated as given in (10):
Block edge strength (
): Block edge strength is computed by using the magnitude of gradient vectors
and
as given in (11):
For efficient implementation, (11) can be approximated as:
Block texture strength (
): The spatial occurrence of the pixel intensities in a specified region denoted as
is given by (13):
is texture strength of the
block, where
XT is defined in (14):
By combining the value of
,
, and
, a block feature strength (BFS) is generated as given in (15):
where, the
, and
are three constants known as feature scaling factor and their values range between 0 and 1, such that:
2.5. Proposed Method
In this section, we describe the details of the proposed algorithm. Literature review revealed that the YCbCr model provides a better quality of image and it catches more human-eye-sensitive intensity colors. Therefore, it is preferably used in JPEG compression. Moreover, the RGB model is less acceptable due to its redundant nature [
23]. As a result, we also processed the image in YCbCr color space. After conversion to the YCbCr model, the image is divided into
N ×
N non-overlapping blocks. For each block, the block color strength, the block edge strength, and the block texture strength are extracted using Walsh–Hadamard basis [
16] vectors as given in (10), (12), and (13), respectively. The complete feature content of the block is generated by considering weighted combination of individual feature strengths using (15), known as block feature strength (BFS) of the block. After generation of the BFS, a block selection is made by comparing the BFS with automatically generated threshold (Th) using k-means algorithm. If the BFS exceeds the threshold value, then that particular block will be compressed by a high value of Q-Marix chosen from (17), where
F ranges from 10 to 100 or else the block will be compressed by the least value of the Q-Matrix,
, which offers the highest compression. In this technique, the low feature content blocks are compressed to a fixed level by
, which ensures the minimum quality of the reconstructed image. To improve the quality of the reconstruction, the Q-Matrix assigned to the high BFS block should be higher than 10. For the decoding process, the respective block Q-Matrix is taken into consideration and followed by inverse-DCT process. Algorithm 1 represents the encoding process of the proposed method.
| Algorithm 1 Proposed algorithm |
| Divide the image into N non-over lapping blocks. |
|
|
| ) using K-Means algorithm |
| in Q-Matrix (High Q-Matrix for DCT compression) |
| |
| in Q-Matrix for DCT Compression |
| of If block |
| of for loop. |
The details of the proposed method work flow are shown in
Figure 2. In the encoding and the decoding process of JPEG compression, the Q-Matrix plays a major role. The required bit rate can be achieved by the quantization step in the JPEG framework. The QM (Q-Matrix) [
27], also known as quality factor matrix, can be varied to change the bit rate. So, the bpp of the image is configured by the series of quantization tables developed in JPEG to obtain a different PSNR.
The quantization table is given by
:
A different Q-factor matrix can be generated by varying the F parameter in (17). To evaluate the performance of the proposed method for different bpp, we have used a different QM. To obtain the different Q, we have used F values from 1 to 100 in (17).
3. Simulations and Result Analysis
The performance of the proposed algorithm is measured based on objective and subjective evaluation criteria. The objective evaluation is made based on PSNR [
28] and SSIM [
29] at a given bpp. To evaluate the efficacy of the proposed method, we have considered seven standard images, such as Lena, Airplane, Peppers Boat, Zelda, Girl, and Couple [
30], in the first comparative study by using different quantization matrices, such as
, and
. In the second comparative study, the performance of the proposed method is evaluated for different images from KODAK dataset [
31] having 25 images. The different images are 24 bits color images of sizes ranging from 256 × 256 to 1024 × 1024. During simulations, we have experimented with different sets of values of
, and
for five images and observed that optimum performance is obtained by considering values of
, and
as 0.3, 0.3, and 0.4, respectively. Therefore, all simulations are made by considering this set of values only. In our experiments, we have considered only the color images. For illustration purposes, the KODAK dataset images are given in
Figure 3.
The performance measurements of the proposed method and the JPEG method based on the different QM are illustrated in
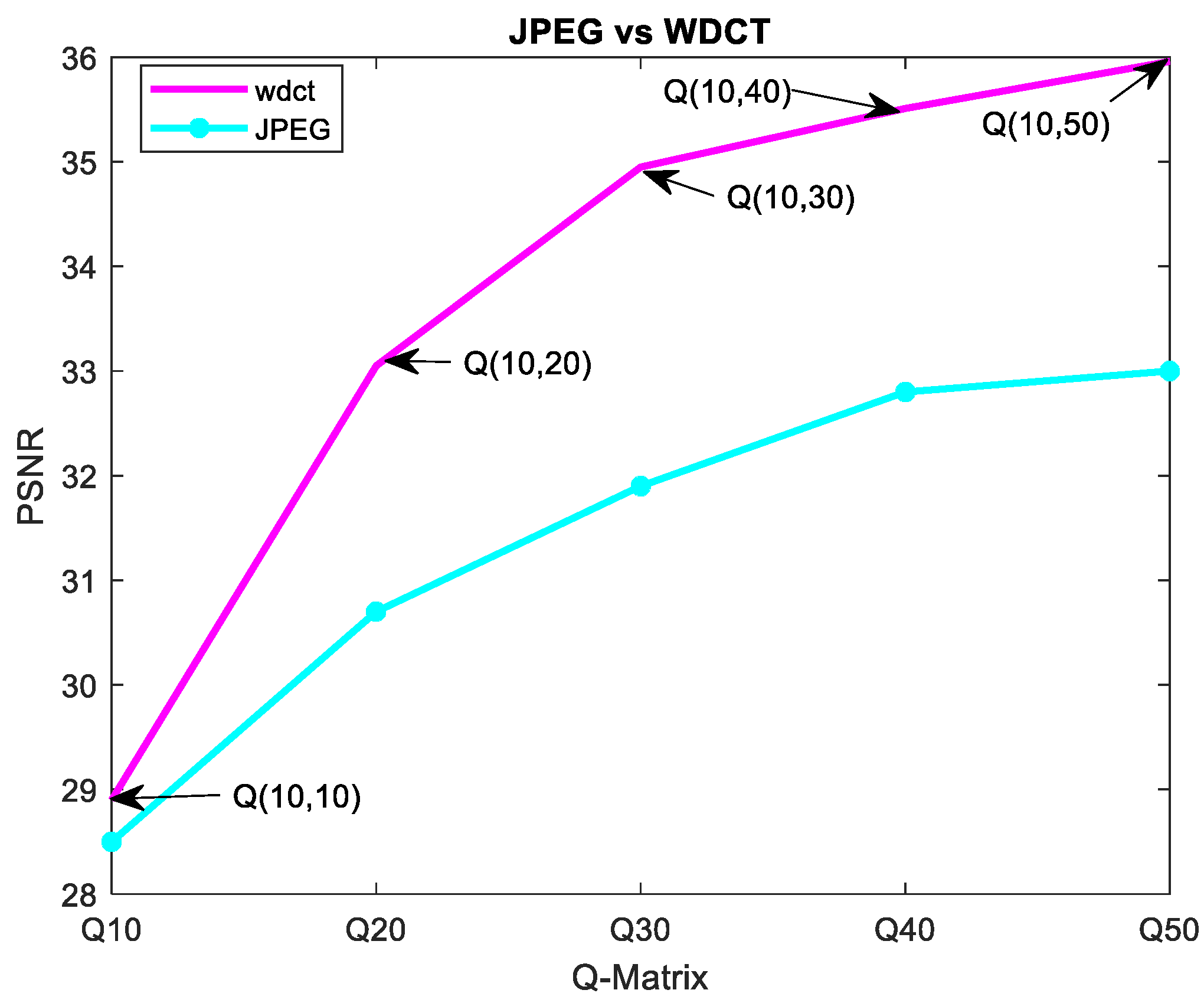
Figure 4. In
Figure 4, the pink color graph shows the variation in PSNR by considering a fixed quantization of
for blocks with lower BFS and
for blocks with higher BFS values. By varying the
F parameter in (17) from
to
with an increment of 10 units, different QM are generated. In
Figure 4, Q(
x,
y) indicates the two QM values
x and
y used in the two-level quantization process by the proposed algorithm, as shown in the pink color line. The
x value is kept fixed to 10, corresponding to blocks with low BFS, and the
y can take value from {10, 20, 30, 40, 50}. Again, the variation in the PSNR with respect to the single QM as used in standard JPEG is shown in cyan color. From
Figure 4, we have illustrated that the proposed method has improved the PSNR value as compared to the JPEG baseline method. It is observed from
Figure 4 that, with the increase in QM value, there is an increase in the PSNR value for both the methods. However, using two quantization matrices for encoding by the proposed method has ensured lower bpp than the corresponding JPEG counterpart.
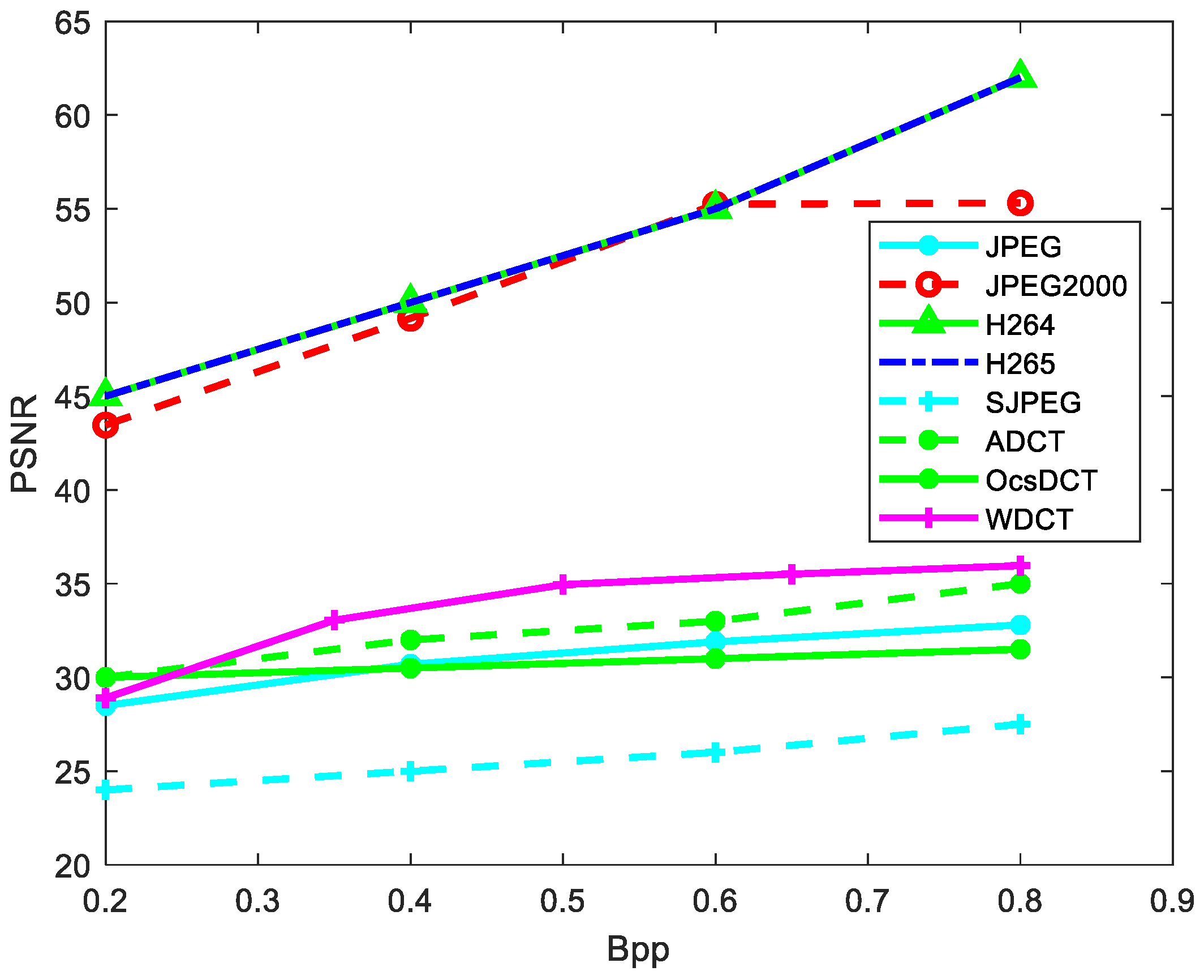
Variation in the quantization matrix controls the degree of compression resulting in variation in compression ratio and bpp of the image and, hence, the PSNR of the image. The variation in the PSNR with respect to bpp for JPEG [
8], JPEG2000 [
20], H264 [
17], H265 [
18], and AMBTC [
2] are shown in
Figure 5. It is observed from
Figure 5 that, for a fixed bpp, the proposed WDCT method has a better PSNR than JPEG [
8], ADCT [
10], SJPEG [
11], and, OcsDCT [
23]. Again, PSNR comparisons for different DCT-based methods, such as ADCT [
10], SJPEG [
11] and OcsDCT [
23], at constant QM of Q30 are shown in
Table 1. In the ADCT [
10] method, block-wise adaptive scanning technique was used to generate the compressed image, and the adaptive scanning improved the bpp and PSNR values. In the saliency-based SJPEG [
11], a saliency-based compression framework is proposed where the salient blocks are encoded separately and the non-salient region blocks are encoded individually, which ensured improved quality of the image at lower bpp. In OcsDCT [
23], the BAT algorithm was used to optimize the cost function to compute the threshold partially, which reduced the numberless significant DCT coefficients having lesser energy. In this way, it managed to reduce the bit rate with a higher PSNR value. From
Figure 5, we can observe that our proposed method, as well as JPEG, ADCT, OcsDCT, and SPJEG are not as good as H264, H265, and JPEG2000. However, our method has the lowest complexity. The comparison of execution times will be shown in a later section.
It is observed from
Table 1 that, for a fixed quantization matrix, the proposed WDCT method outperformed, having the lowest average bpp of 0.53 and highest average PSNR of 35.61 as compared to those methods (ADCT, JPEG, and OcsDCT) with similar complexity. From
Table 1, it is clearly observed that the proposed method outperformed most of the cases, except for the Lena and Girl images. The reason behind lower PSNR for these two images is that these images have a smaller area having more detailed information and larger areas having less detailed information, which is treated as background. Lena image has detailed information content only in the face area and the remaining portion has very low details. Similarly, the Girl image has detailed information near her face area, near the table area, and near the drawer region only. Less detailed areas undergo higher compression than high detailing areas, resulting in lower reconstruction quality of the image. This clearly illustrates that the proposed WDCT is well capable of handling images having detailed information content by maintaining a good quality of reconstruction with high compression level.
The proposed method is also compared with different BTC-based approaches, such as ImgAMBTC [
14] and ADMG [
15], and the results are included in
Table 2. Evaluation of SSIM at constant bpp of 0.6 and variation of bpp by using different levels of QM are shown in the
Figure 6 and
Figure 7, respectively.
It is observed from
Figure 6 that the proposed method has an SSIM value similar to that of ADCT and has an SSIM value 0.03 units less than that of the JPEG method at constant bpp of 0.6, whereas the proposed method leads in SSIM value by 0.14 units compared to the SJPEG method.
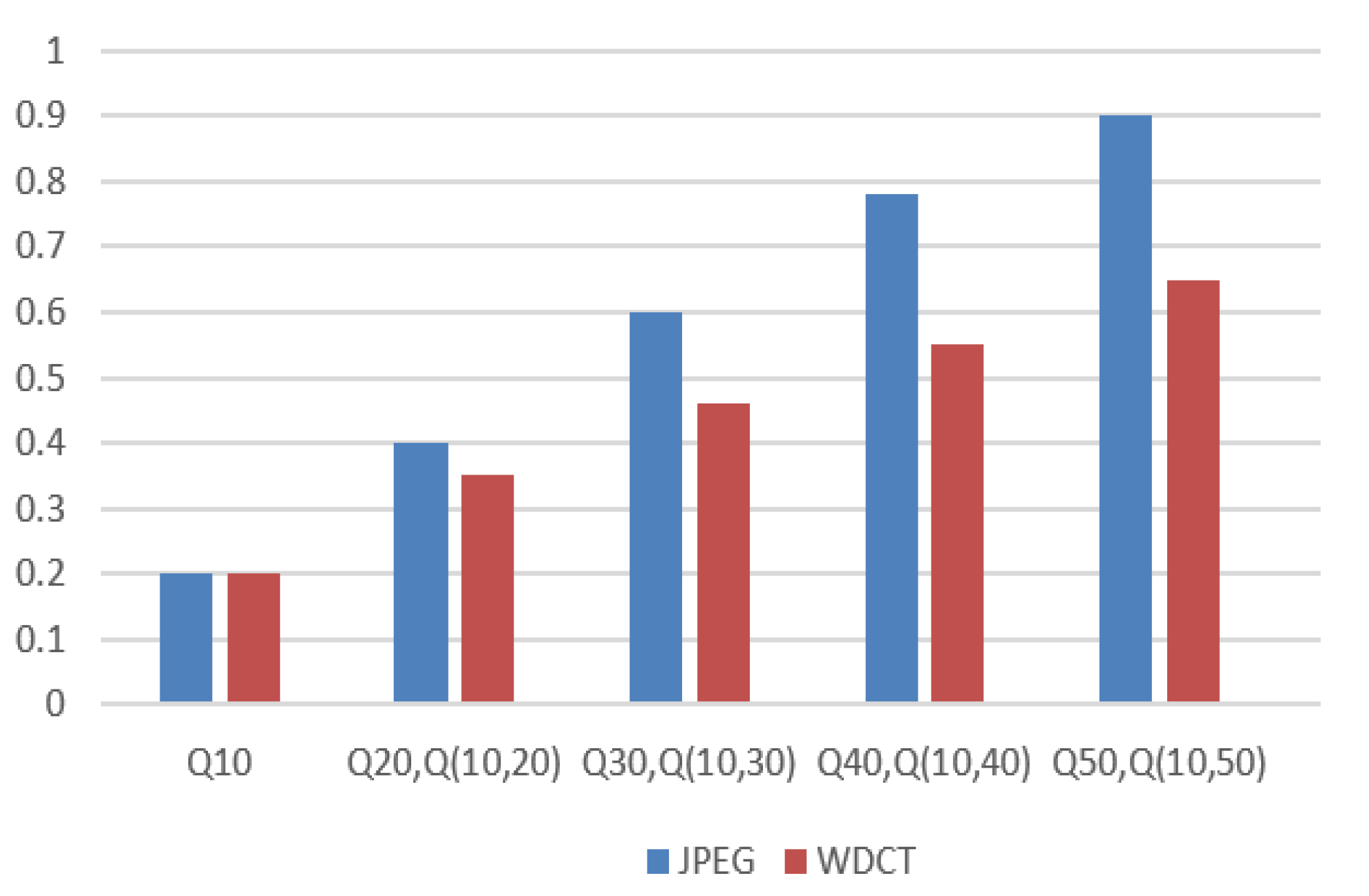
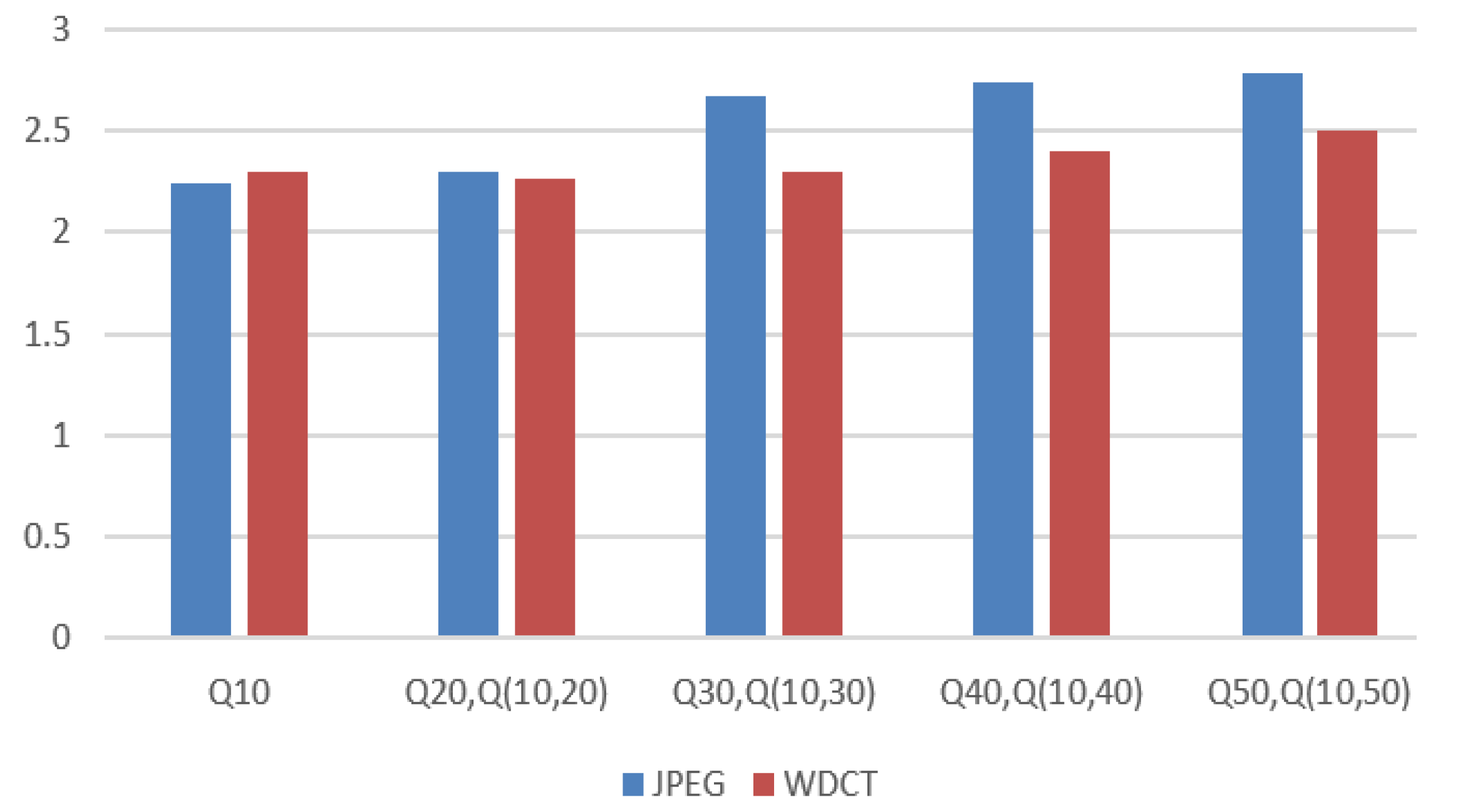
Figure 7 illustrates the comparison of the bpp values of the JPEG method and the proposed method by using a fixed QM. From
Figure 8, it can be observed that, for a QM of
Q10, the proposed WDCT and the JPEG method has equal bpp. However, with the increase in the quality factor of the QM, there is an increase in the bpp for both the methods. For higher value of the QM, the proposed method has lower bpp than the corresponding JPEG counterpart that ensured higher compression rate for the proposed method.
All simulations are carried out using a platform powered by an i5 CPU with 8 GB RAM in MatlabR2017a environment, and execution times are measured. The execution time of the proposed WDCT- and DCT-based JPEG method are compared and plotted in
Figure 8. It is observed from
Figure 8 that the WDCT method has lower computation time than JPEG for all QM.
Performance comparison of different methods in terms of average execution time in seconds is shown in
Figure 9. It is observed from
Figure 9 that the proposed method has the lowest execution time compared to H264, H265, JPEG 2000, and JPEG considering all the images. It is noted that JPEG 2000 is a wavelet-based approach and it is more complex than our proposed method. Although, H264, H265, JPEG, and the proposed WDCT- are DCT-based approaches, due to two-level quantization of the proposed WDCT algorithm in contrast to the fixed quantization of the JPEG, have lower execution times.
The subjective evaluation of the proposed WDCT and other DCT-based approaches are made based on the perceptual quality of the reconstructed image.
Figure 10 shows the reconstructed image of Lena of size 256 × 256 by using the proposed WDCT method and JPEG at 0.4 bpp. The WDCT-based reconstructed image has a PSNR of 34.8 dB, and the JPEG-based reconstructed image has a PSNR of 31.5 dB. For the proposed WDCT approach, the main feature-containing blocks are compressed by using the
, and the remaining blocks are compressed by using the fixed QM of
, while JPEG is compressed by using a QM of
. The variation in QM for the illustration of the two reconstruction approaches are just to maintain constant bpp. It is observed from
Figure 10 that the proposed method has fewer artifacts at 0.4 bpp than the direct JPEG method at 0.4 bpp. The high feature-containing areas are compressed by using the high QM and the low feature content blocks compressed by using the low QM ensures improved bpp, while maintaining appreciable PSNR and SSIM values. The proposed WDCT method has lower bpp with better reconstruction image quality than other DCT-based approaches.
The ADMG method used a combination of multi-grouping and AMBTC [
2] with a predefined threshold to reduce the bit rate. The bpp of this method is 1.99. In ImgAMBTC [
14], the ADMG [
15] grouping is applied to the selected blocks having higher edge features, and the rest of the blocks are compressed by using the AMBTC [
2] method. In order to compare the proposed WDCT method with the BTC-based approaches, we have considered a higher QM to obtain a comparable bpp, which is shown in
Table 2. On average, our method has the highest PSNR and lowest bpp. It is emphasized that high PSNR and low bpp mean better performance.