Abstract
Monitoring the development of infectious diseases is of great importance for the prevention of major outbreaks. Syndromic surveillance aims at developing algorithms which can detect outbreaks as early as possible by monitoring data sources which allow to capture the occurrences of a certain disease. Recent research mainly concentrates on the surveillance of specific, known diseases, putting the focus on the definition of the disease pattern under surveillance. Until now, only little effort has been devoted to what we call non-specific syndromic surveillance, i.e., the use of all available data for detecting any kind of infectious disease outbreaks. In this work, we give an overview of non-specific syndromic surveillance from the perspective of machine learning and propose a unified framework based on global and local modeling techniques. We also present a set of statistical modeling techniques which have not been used in a local modeling context before and can serve as benchmarks for the more elaborate machine learning approaches. In an experimental comparison of different approaches to non-specific syndromic surveillance we found that these simple statistical techniques already achieve competitive results and sometimes even outperform more elaborate approaches. In particular, applying common syndromic surveillance methods in a non-specific setting seems to be promising.
1. Introduction
The surveillance of health-related data is of major importance to preserve public health. In particular, the early detection of infectious disease outbreaks enables to apply control measures at an early stage, which indeed can save lives and reduce suffering [1]. In this regard, syndromic surveillance has been introduced which aims to identify clusters of infected people before final diagnosis are confirmed and reported to public health agencies [2]. The fundamental concept of syndromic surveillance is to define indicators for a particular infectious disease on the given data, also referred to as syndromes, which are monitored over time to be able to detect unexpectedly high numbers of infections which might indicate an outbreak of that disease. This can be done in many different ways, e.g., by tracking over-the-counter sales of specific pharmaceuticals or by observing the number of patients arriving at an emergency department with a particular medical condition [3].
Depending on the available data sources and the disease under surveillance, the definition of syndromes is a challenging task, since symptoms are often shared by different diseases and a particular disease can have different disease patterns in the early phase of an infection. Moreover, this kind of filtering is a highly handcrafted approach and only allows to monitor known infectious diseases.
Rather than developing highly specialized algorithms which are based on specific indicators and assume particular characteristics of outbreak shapes [4], we argue that the task of outbreak detection should be viewed as a general anomaly detection problem, where an outbreak alarm is triggered if the distribution of the incoming data changes in an unforeseen and unexpected way. On the one hand, this interpretation does not require manual specification of suitable syndromes in advance, while, on the other hand, the algorithms are able to capture individual behaviour for each given data source. For example, the reporting of chief complaints (the documented reason for patient visit) can vary between different hospital staff, making it difficult to monitor a particular syndrome across different emergency departments. Moreover, approaches to interpretable machine learning [5] can be leveraged for syndromic surveillance to support epidemiologists after an anomaly has been detected to ease the investigation of the raised signal.
Therefore, we distinguish between specific syndromic surveillance, where factors related to a specific disease are monitored, and non-specific syndromic surveillance, where general, universal characteristics of the stream of data are monitored for anomalies. However, until now, only few approaches have been proposed which make use of available data to detect any kind of infectious disease outbreaks.
In this paper, we revisit approaches which can be used for non-specific syndromic surveillance and propose a general framework in which these can be integrated. Even though most of the previous works present extensive evaluations, we found it difficult to assess the actual performance of these algorithms. In particular, only little effort has been spent on implementing appropriate benchmarks which serve as reference to judge the ability of how well the algorithms can detect outbreaks. Therefore, we also propose a set of benchmarks relying on simple statistical assumptions, which have been widely used in syndromic surveillance before. Moreover, to close the gap between specific and non-specific syndromic surveillance, our framework also allows to apply well-studied statistical algorithms for outbreak detection in the setting of non-specific syndromic surveillance. For comparability, we evaluate the techniques on the same synthetic data which have been used in previous works [6,7]. In addition, we have performed extensive evaluations on real data of a German emergency department to which we injected synthetic outbreaks with a controlled number of infections, in order to assess the sensitivity of the algorithms.
1.1. Contributions
In summary, in this paper we make the following contributions: (1) We formulate and motivate the problem of syndromic surveillance from the perspective of machine learning to make it more attractive for the machine learning community. (2) We present a local and a global modeling strategy for non-specific syndromic surveillance in an unified framework. (3) We review the few available machine learning approaches for non-specific syndromic surveillance in face of our proposed modeling framework. (4)We propose a set of benchmarks for non-specific syndromic surveillance relying on simple distributions which have been widely used in syndromic surveillance. Moreover, we introduce a way how specific syndromic surveillance methods can be applied to the nonspecific setting. (5) We analyze previous proposed approaches and our benchmarks using an extensive experimental evaluation based on synthetic and real data and demonstrate that simple statistical approaches, which have been disregarded in previous works, are in fact quite effective.
A preliminary version of this paper has previously appeared as [8] which focuses on the comparison of our proposed benchmarks with respect to more elaborate machine learning approaches addressing the task of non-specific syndromic surveillance, including common anomaly detection algorithms. New to this version are, in particular, a detailed survey of related work in syndromic surveillance, the novel modeling framework for non-specific syndromic surveillance, and a considerably more extensive description and analysis of the experimental results.
1.2. Outline
The remainder of this paper is organized as follows: In Section 2, we first give an overview of syndromic surveillance and its relation to data mining and machine learning. Afterwards, we explain the framework for non-specific syndromic surveillance in Section 3, proposing a local and a global modeling strategy. We then show how existing approaches for non-specific syndromic surveillance can be categorized by this framework in Section 4, and propose a set of benchmarks in Section 5. Section 6 presents the results of a comparative evaluation of the performance of various known approaches in comparison to our benchmarks using synthetic and real data. Finally, we conclude and planned future extensions in Section 7.
2. Syndromic Surveillance
The main objective of syndromic surveillance is to monitor the presence of an infectious disease over time and to allow to conduct an investigation by epidemiologists if an unexpectedly high number of infections is observed. Rather than tracking the confirmed cases, which can take up to several days until the laboratory results are available, syndromic surveillance focuses on early indicators of a disease to allow a more timely detection of outbreaks [4]. In the context of syndromic surveillance, such indicators are usually encapsulated as syndromes:
Definition 1
(Syndrome [9]). A syndrome is a set of symptoms or conditions that occur together and suggest the presence of a certain disease or an increased chance of developing the disease.
Notably, this definition differs slightly from the original meaning of a syndrome, which is only described by a set of symptoms, to also include the monitoring of nonclinical data sources [2]. For example, the sales of a specific pharmaceutical product against flu could be used for the detection of influenza outbreaks, but cannot be described as a symptom directly. In general, syndromic surveillance can be defined as:
Definition 2
(Syndromic Surveillance [10]). Syndromic surveillance is an investigational approach where health department staff, assisted by automated data acquisition and generation of statistical alerts, monitor disease indicators in real-time or near real-time to detect outbreaks of disease earlier than would otherwise be possible with conventional reporting of confirmed cases.
The general approach to syndromic surveillance is to first decide on a disease under surveillance and based on that a syndrome is specified which needs to be monitored.
Definition 3
(Specific Syndromic Surveillance). We speak of specific syndromic surveillance if a specific syndrome for a given disease is monitored over time in order to be able to detect possible outbreaks of this particular disease early on.
However, for this approach the disease and the related syndrome need to be known in advance for which reason an outbreak of an unknown infectious disease might be missed due to a different disease pattern. Only little research has been put on what we refer to as non-specific syndromic surveillance, i.e., universal approaches to syndromic surveillance which aim to detect any suspicious anomalies in the given data, indicating an infectious disease outbreak.
Definition 4
(Non-Specific Syndromic Surveillance). We speak of non-specific syndromic surveillance if a data source is monitored over time in order to be able to detect possible outbreaks of any disease early on.
In particular, this universal approach can also be seen as the surveillance of all possible syndromes at the same time. Obviously, this comes with an increased computational complexity, but also allows to detect outbreaks with an, at this time, yet unknown disease pattern. Moreover, any anomaly is an indicator that something unexpected is happening, which does not necessarily relate to an infectious disease outbreak. For example, Rappold et al. [11] investigated the health effects associated with exposure to wildfire emissions in emergency department (ED) data. Therefore, non-specific syndromic surveillance could also be used as a general tool for public health surveillance to increase the preparedness for unexpected events.
2.1. Overview of Prior Work in Syndromic Surveillance
Most of the research in syndromic surveillance is devoted to monitoring specific syndromes. A survey of syndromic surveillance for influenza is provided by Hiller et al. [12]. However, many other infectious diseases have been monitored as well, such as pneumonia [13] or norovirus [14]. In contrast, we found only a few publications which relate to non-specific syndromic surveillance. Reis et al. [15,16] monitor the total number of patient visits in an emergency department rather than particular syndromes. However, a high number of patient visits can be caused by various reasons, making the resulting signal of the syndromic surveillance method noisy and unreliable. Furthermore, small outbreaks are hard to detect with such frequency-based approaches. On the other hand, it has been proposed to monitor a set of syndromes at the same time in order to be able to detect outbreaks of various known diseases, e.g., [17,18,19,20,21]. However, these works are more related to specific syndromic surveillance, since the syndromes need to be specified in advance and all of them are monitored and investigated individually. In particular, for syndromic surveillance based on emergency department data, it has been shown that the monitoring of multiple indicators for a particular disease in one data source can improve the ability for detecting outbreaks. For example, Reis and Mandl [22] show that the surveillance of chief complaints and diagnostic codes together yield better results than alone. The selection which information (e.g., diagnostic codes, discharge diagnosis or chief complaint) should be used to form syndromes is discussed in the works of Begier et al. [23], Fleischauer et al. [24] and Ivanov et al. [25]. Generally speaking, a clear preference cannot be stated since the usefulness depends on the disease under surveillance. However, the use of diagnostic codes (such as the International Classification of Diseases (ICD) codes) allows a more fine grained specification of diseases, but comes with the drawback of reporting delays up to several days due to laboratory testing [26].
In general, monitoring multiple syndromes or multiple data sources simultaneously facilitates the detection of outbreaks [27]. This area is known as multivariate syndromic surveillance and can be categorized as follows: (1) spatial surveillance (e.g., simultaneously monitoring of disease counts at different locations with possible spatial correlations), e.g., [19,20]; (2) simultaneous surveillance of a syndrome with respect to particular groups of patients which differ in their demographic characteristics (e.g., monitor the syndrome for children and adults separately), e.g., [28]; or (3) monitoring of different types of data sources at the same time (e.g., over-counter sales in pharmacies and emergency department visits), e.g., [29]. Non-specific syndromic surveillance can be seen as multivariate syndromic surveillance over all infectious diseases if we assume that all possible syndromes are monitored simultaneously. While the monitoring of different demographic characteristics is implicitly included in this scenario, non-specific syndromic surveillance methods can also be designed to include spatial information and multiple data sources. However, if multiple data sources are monitored at the same time, one needs to take into account the problem of autocorrelation and multiple testing [16], as we will discuss later in Section 3.2.2.
2.2. Data for Syndromic Surveillance
The presence of an infectious disease outbreak can only be determined through the actions of infected people. If an infected person does not contact any service that allows to collect information about the case, the infection remains unknown and cannot be detected by a syndromic surveillance system. Consequently, the data sources for syndromic surveillance can only be seen as a weak indicator for disease outbreaks.
Syndromic data can be obtained from (1) clinical data sources (e.g., diagnoses in an emergency department), which provide measurements of the symptoms of individuals, as well as (2) alternative data sources (e.g., internet-based health inquiries), which indirectly measure the presence of a disease [2]. A selected set of possible data sources is displayed in Table 1.

Table 1.
Exemplary data sources for syndromic surveillance.
An important property of syndromic data is that the underlying probability distribution can change over time. A specific characteristic of syndromic data is seasonality, in machine learning also known as cyclic drift [30], a special form of concept drift, in which the target concept changes over time with respect to a fixed time frame. For example, Hughes et al. [31] and Dirmyer [32] show that the cold weather in winter has an influence on the symptoms of the people arriving in emergency departments. Johnson et al. [33] capture seasonal patterns in emergency department data due to respiratory illnesses. In particular, this kind of drift is predictable, and appropriate outbreak detection algorithms can take advantage of it.
The evaluation of syndromic surveillance methods is usually difficult due to the lack of labeled data. In particular, for some scenarios of infectious disease outbreaks, such as the intentional release of Bacillus anthracis, none or only very few outbreaks happened in the past. In addition, a precise definition for the labeling of outbreaks does not exist, making it difficult to obtain standardized data sets on which algorithms can be evaluated. According to this, the evaluation data used for syndromic surveillance can be described by three categories: (1) wholly authentic, (2) wholly simulated, and (3) simulated outbreaks superimposed onto authentic data [34]. Most of the proposed algorithms in the literature are evaluated using data from categories (2) or (3), which allows a detailed analysis of the performance of the proposed algorithm in a controlled setting.
2.3. Relation to Data Mining and Machine Learning
Seen from a machine learning perspective, syndromic data are a constant stream of instances. For specific syndromic surveillance the data are pre-processed in order to extract only the information pertinent to the definition of the monitored syndrome, whereas for non-specific syndromic surveillance all available data are monitored for unusual distributional changes. To detect such changes in the data stream, which might indicate an outbreak, the instances are usually grouped together according to pre-specified time slots. For example, all patients which arrive at an emergency department on a specific day are grouped together as a set of instances. Hence, the stream can be represented as a time series of sets of instances. The goal of syndromic surveillance is to detect any major changes for the last observed set in the stream which might indicate an outbreak of an infectious disease.
Generally speaking, the main objective of syndromic surveillance can be described as anomaly detection, which refers to the problem of finding patterns in data that do not conform to expected behavior [35]. In particular, the focus is put on patterns which indicate an increasing number of infections over time which can be described by collective and sequential anomaly detection at the same time. Directly applying point anomaly detection, which aims to identify single instances as outliers, such as encountering a patient over a hundred years old in the ED, is not of interest for syndromic surveillance [36]. However, by forming a univariate time series of counts for a particular syndrome, as it is done in specific syndromic surveillance, the problem can be reduced to point anomaly detection. Most approaches to syndromic surveillance can be categorized as statistical anomaly detection techniques (e.g., EARS [37], Farrington [1], and many more).
In contrast, the area of emerging pattern mining [38], which aims to discover item sets whose support increases significantly from one data set to the other, directly relates to the problem of non-specific syndromic surveillance, in that each item set can be seen as a specific syndrome. Similarly, contrast set mining [39] aims to find conjunctions of attributes and values that differ meaningfully in their distributions across data sets. Such techniques can be used to compare the last observed set of instances to the previous sets of instances in order to detect significant changes in the frequencies of any group of instances. Both approaches have also been viewed as instantiations of a general framework for supervised descriptive rule learning [40], a generalization of the subgroup discovery [41], where labels (e.g., w.r.t. to a concrete syndrome) are assumed to be available.
Because of the lack of labeled data, most algorithms for syndromic surveillance are unsupervised. Apart from unsupervised anomaly detectors, generative machine learning algorithms can also be used for syndromic surveillance, such as sum-product networks [42] or Bayesian networks [43]. Such algorithms allow to capture the underlying probability distribution of the data source and, therefore, can capture the normal behavior. Afterwards an expectation can be created with the generative machine learning algorithm which is then compared to the current observed set of instances to detect anomalies. In this way, syndromic surveillance can also be seen from the perspective of exceptional model mining [44] in that it can be formulated as the identification of a subset of instances in which a model of the current set of instances differs substantially from the models for previous set of instances.
In general, the output of an anomaly detector for syndromic surveillance should be seen as a signal that an outbreak may be occurring which triggers a further investigation of the situation by public health officials [9]. To avoid unnecessary and costly interventions, the signal ideally includes information about the reason of the detected anomaly allowing the epidemiologist to quickly judge the importance of the alarm. Therefore, syndromic surveillance could also benefit from the area of interpretable machine learning, focusing on approaches which can provide explanations to their predictions [5].
Furthermore, machine learning can also be used to address data quality issues, which can be a major issue in health-related data due to the manual capturing. For example, the manually inserted initial assessments in an emergency department may experience gaps as the frequency of patient visits increases. In this respect, missing data imputation algorithms, such as generative adversarial networks [45] or mean-field-type filters [46], can be leveraged to improve data quality before syndromic surveillance methods are applied.
3. Non-Specific Syndromic Surveillance
In this section, we formulate the problem of non-specific syndromic surveillance from the perspective of machine learning and propose two modeling strategies. The used notation is summarized in Table 2.

Table 2.
Notation.
3.1. Problem Definition
Let us denote the population of instances as , to which we will also refer to as cases. For example, a case can be a patient arriving at the emergency department. As mentioned above, the cases are grouped together according to pre-specified time slots in order to detect sudden changes in the data. Hence, the cases for a specific time slot t are denoted as . Each case , is represented by a set of attributes , where each attribute can be either categorical (e.g., gender), continuous (e.g., age) or text (e.g., chief complaint). Following the notation of Wong et al. [6], we refer to such attributes which basically represent the information under surveillance as response attributes. Note that spatial information can also be included in the response attributes which can be used for spatial surveillance (e.g., postal code of the patients arriving in the emergency department).
While the cases are described by response attributes, information about external influences is represented by a set of environmental attributes . The environmental attributes are independent of the response attributes and represent external factors which might have an influence on the distribution of cases for a given time slot t. For example, during the winter, we expect to have a higher number of patients with flu symptoms than during the summer. In order to consider such effects, the season can be represented as an environmental attribute which can be used by the algorithms. Hence, the use of suitably chosen attributes allows to capture periodic trends for the population of instances . Depending on which information is available, the environmental attributes can be freely configured by the user based on their domain knowledge apart from the collected data .
From a machine learning perspective, the instances can be seen as a tabular data set, where a row represents a particular case and the columns represent the response attributes . In addition, each data set is associated with an environmental setting , defining external factors which might have an impact on the distribution of . Thus, the information available for time slot t can be represented by the tuple and the information about prior time slots can be denoted as . The main goal of non-specific syndromic surveillance is to detect any anomalies in the set of the current time slot t w.r.t. the previous time slots , which may indicate an outbreak of an infectious disease. Therefore, the history can be used to fit a model and the information given by environmental setting can be used to condition the model on the current time slot t.
3.2. Modeling
The general approach to non-specific syndromic surveillance is to model the normal activity by analyzing , which can be seen as an expected observation, and compare it to the set . A significant difference between the expectation to the actual observed set can indicate an outbreak of an infectious disease. Especially an increase in the number of instances following a particular syndrome can be a good indicator for an outbreak, while under normal circumstances the absence is not of interest. The difference between the expectation and the current observed subset can be modeled in two ways, namely via global and local modeling. While global modeling tries to solve the problem of outbreak detection with a single universal model, a local modeling approach breaks down the problem into many local tasks, each representing an expectation for a particular characteristic of . For example, the expectation could be an expected count for a specific syndrome which is then compared to the actual count of the syndrome in . The local tasks are executed independently and their results need to be aggregated afterwards, in contrast to the global modeling where the outcome is already a single result.
3.2.1. Global Modeling
The basic idea of global modeling is visualized in Figure 1. Given the information of prior time slots , which serve as training data, and the information about the environmental attributes of the current time slot , the learning objective of the model is to create an expectation for the distribution of cases . In the following step, the distribution is compared to the actual observation of cases . Depending on the used algorithm, the representation of and can have arbitrary forms. For example, the information about all cases for a particular time slot can be encapsulated as one vector, as it is done by Fanaee-T and Gama [7]. Depending on the representation of , statistical tests such as the normality [7] or the Fisher’s test [47,48] are typically used for assessing the difference between and . However, instead of making a binary final decision, it is much more preferable to directly use the p-value [49]. The complement of the p-value can be seen as the likelihood of being in an outbreak and, therefore, contain much more information about the belief of being in an outbreak than the binary decision. This allows us to analyze the performance of the model in the evaluation more precisely and, moreover, we are able to defer the specification of the significance level during the evaluation. Depending on the results, an appropriate significance level can be selected for applying the model in practice.
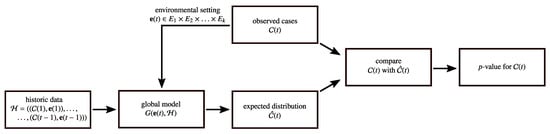
Figure 1.
Global modeling.
3.2.2. Local Modeling
The major drawback of global modeling is that all the information about the cases is summarized in one representation. Thus, information about individual cases, which could be a good indicator for an outbreak, might be lost. This is particularly important for detecting outbreaks of very rare diseases, for which a relative small increase of cases is already alerting. Therefore, local modeling breaks down the problem of non-specific syndromic surveillance into several local modeling tasks, each focusing on a different characteristic of the data (cf. Figure 2). The general idea of composing a global model from many local models has previously been proposed by Knobbe et al. [50].
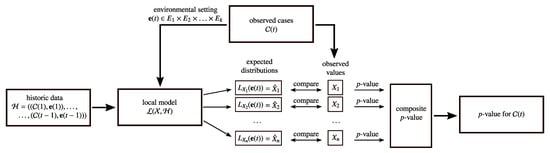
Figure 2.
Local modeling.
Problem Formulation
Given some information of prior days , local modeling generates a set of local models , each responsible for monitoring a specific pattern of the data. As we will discuss in more detail in Section 4, most of the algorithms differ in what patterns they monitor. For example, one can use high-frequency association rules, as in DMSS (Section 4.1), or all possible patterns up to a certain complexity, as in WSARE (Section 4.2). In dependence of the environmental attributes of the current time slot , each local model defines an expectation for their pattern. A local model can monitor any kind of pattern which might be helpful to detect an outbreak of an infectious disease. Subsequently, the expectation for the patterns are compared to the actual observations of the patterns obtained from the data set . Like for the global modeling, the comparison is usually performed with statistical tests which yield a p-value, as explained in the previous section. As each local model yields a single p-value, the results of the local models need to be aggregated to a final p-value for the respective time slot.
Aggregation of p-Values
Heard and Rubin-Delanchy [51] review multiple methods for combining p-values, such as Edgington’s and Fisher’s methods which have already been used for syndromic surveillance [52]. Each of the combination procedures have different statistical properties, not allowing to generally prefer one particular method. In addition to these methods, we introduce as a simple baseline the naive approach that reports the smallest p-value, which basically represents the most significant observation. We have to note that in this case the reported value for a time slot is not a valid p-value anymore. The complement should be seen as a mere score for being in an outbreak.
Problem of Multiple Testing
The aggregation of p-values is a difficult task due to the problem of multiple testing. In particular, with an increasing number of statistical tests executed at the same time, it becomes more likely that an extreme p-value for one of the tests is computed by chance, increasing the number of false positives.
Generally speaking, it is impossible to check whether a single extreme p-value is an indicator for an outbreak or just created by random noise if all tests are assumed to be independent of each other. In this case, several techniques can be used for controlling the likelihood of obtaining false positives, such as Bonferroni corrections or permutation tests [53]. The general concept is to make each individual underlying statistical test less sensitive to changes, so that chance false positives are less likely to occur. However, this also has the drawback that the sensitivity to detect events is reduced. Moreover, these kind of corrections are focused on determining whether to raise an alarm or not, while we are interested in obtaining an aggregated p-value. In particular, Roure et al. [27] argue that the Bonferroni correction corresponds to an aggregation of p-values based on the minimum function. Such correction methods do not have an influence on the performance if we evaluate our approaches using ROC-curves (cf. Section 6.1).
Specifically for contrast set mining, a modified version of the Bonferroni correction has been proposed by Bay and Pazzani [39]. Based on statistical significance pruning, tests performed on specifications of item sets are pruned if they have similar support to its parent item set or fail test of independence with respect to its parent item set.
If the executed statistical tests are correlated, which is true for a scenario in which we monitor all possible syndromes, this knowledge can be used to reduce the number of false alarms. For example, in the area of neuro-imaging, cluster-extent based thresholding techniques are used to identify areas of brain activity [53]. In this case, it is assumed that the statistical tests which are performed for areas which are close together are likely to correlate. However, not always such domain knowledge is available. Without any prior information about the correlations, the framework proposed by Leek and Storey [54] can be used, which captures the dependencies in the data before the statistical tests are conducted, and then adjust the data in a way so that the actually performed statistical tests are independent of each other.
In summary, if a relative assessment of the findings is sufficient our proposed aggregation of taking the minimum is sufficient. Nonetheless, more sophisticated approaches, such as the exploitation of correlations, can likewise be integrated in our proposed framework. We leave the investigation for future work.
Relation to Syndromic Surveillance
Viewed from the perspective of syndromic surveillance, a special case of the local modeling is to monitor all possible syndromes at the same time. The set of all possible syndromes can be defined as
where for is defined as . Hence, each local model is responsible for a pattern which represents the count of a particular syndrome . Therefore, of the local model represents the expectation for the count of syndrome s. In particular, by extracting the counts for the syndrome s from the historic data , we obtain a univariate time series which can be used to fit the local model. In fact, the most common outbreak detection algorithms in the literature of syndromic surveillance are based on univariate time series. Apart from the environmental attributes, most of these methods are able to consider effects such as seasonality and trend by just analyzing the change of the counts over time. The idea is to apply these well-studied syndromic surveillance methods in the setting of non-specific syndromic surveillance.
4. Machine Learning Approaches to Non-Specific Syndromic Surveillance
As mentioned above, only little research has been devoted to non-specific syndromic surveillance. In our literature research, we have identified only a few algorithms which we will discuss in this section from the point of view of our modeling framework.
4.1. Data Mining Surveillance System (DMSS)
Brossette et al. [47] have proposed the first algorithm which is able to identify new and interesting patterns in syndromic data. The algorithm is based on the concept of association rule mining and follows the local modeling approach where each local model is represented by an association rule X. The association rules are obtained by running an association rule mining algorithm on . Moreover, the authors propose to reduce the complexity of this process by focusing only on mining high-support association rules. In order to perform the comparison, a reference set of patients is created by merging the cases of a selected set of previous time slots. This is used for comparing the confidence of an association rule X on with the confidence computed on using a or a Fisher’s test. If the confidence has significantly increased on , the finding is reported as an unexpected event. The technique was evaluated on data collected in an emergency department using patients of the previous one, three or six months as the reference set , and the patients arriving at the ED in a single day as . The authors always report all findings for a day, since they only focus on identifying potentially interesting patterns. An aggregation is not performed. Moreover, environmental attributes are not considered by this approach.
4.2. What Is Strange about Recent Events? (WSARE)
The family of WSARE algorithms has been proposed by Wong et al. [48]. All algorithms share the same underlying concept, namely to monitor all possible syndromes having a maximum of two conditions at the same time. Again, these algorithms can be categorized as local modeling in which each local model is responsible for observing one particular syndrome , hence . The three WSARE algorithms only differ in the way how the reference set of patients is created, on which the expectation for a syndrome is estimated. For each local model , the proportion of the syndrome on the reference set is compared to the proportion of the syndromes observed on the set using the or Fisher’s exact test. In order to aggregate the p-values for one time slot, a permutation test with 1000 repetitions is performed. As for DMSS, the authors of the WSARE algorithm focused in their evaluation on patient data using single-day time slots.
The following three versions have been considered:
- WSARE 2.0
- merges the patients of the 35, 42, 49 and 56 prior days together. The authors have specifically selected these set sizes in order to consider the day-of-the-week effect which represents the occurrence of different observations depending on the day of the week. For example, this effect can have a significant impact on the number of emergency department visits [55].
- WSARE 2.5
- merges the patients of all prior days which have the same values for the environmental attributes as the current day . This has the advantage that the expectations are conditioned on the environmental attributes , and that more patients are contained in the reference set , allowing to obtain more precise results.
- WSARE 3.0
- learns a Bayesian network over all recent data from which the reference set of patients is sampled. For the learning of the network, all patients of all previous days are merged together and encapsulated in a data set where the rows represent the patients. Each patient is characterized by the response attributes as well as the environmental attributes of the respective day the patient arrived. Moreover, the authors make use of domain knowledge for the structure learning of the Bayesian network and restrict the nodes of environmental attributes to have parent nodes. This can be done because the environmental attributes only serve as evidence for the sampling, the prediction of their distribution is not of interest. For the reference set the authors choose to generate 10,000 samples given the environmental attributes as evidence.
4.3. Eigenevent
The Eigenevent algorithm proposed by Fanaee-T and Gama [7] can be categorized as a global modeling approach. Its key idea is to track changes in the data correlation structure using eigenspace techniques. Instead of monitoring all possible syndromes, as it is done for the family of WSARE algorithms, only overall changes and dimension-level changes are observed by the algorithm. This makes the Eigenevent algorithm less susceptible to noise resulting in a lower false alarm rate. However, this also reduces the sensitivity of detecting outbreaks which might be caused by only a few cases for a very rare syndrome.
The basic idea of the algorithm is to create a dynamic baseline tensor using the information of prior time slots which share the same values for the environmental attributes as . In the case that not enough prior time slots are available, time slots with the most frequent value combinations for the environmental attributes will be added. The conducted experiments showed that this mixing improves the detection power of the algorithm for unseen value combinations of environmental attributes. In the next step, information of the patients and the baseline tensor are decomposed to a lower-rank subspace in which the eigenvectors and eigenvalues are compared to each other, respectively. Any significant changes in the eigenvectors and eigenvalues between the baseline tensor and the information of patients indicate an outbreak.
5. Basic Statistical Approaches to Non-Specific Syndromic Surveillance
Of all works discussed in Section 4, only the WSARE algorithms have been compared to common anomaly detection algorithms [48]. These baselines monitor the total number of observations per time slot, and may thus be viewed as global modeling techniques. In our opinion, this provides only a very coarse assessment of the outbreak detection performance.
Therefore, we propose a set of local modeling benchmarks which monitor all possible syndromes simultaneously. The key idea of our benchmarks is to apply the same way of monitoring a particular syndrome to all syndromes at the same time and combine the p-values for each time slot by taking the minimum (cf. the problem of multiple testing described in Section 3.2.2). As a simple set of approaches, we first propose to use the parametric distributions in Section 5.1. For more advanced benchmarks, we additionally propose to use common and universal syndromic surveillance methods in Section 5.2. Since the monitoring for each of the syndromes is always performed in the same manner, we will focus on one syndrome and its time series of counts in the following explanations. Note that our proposed benchmarks do not make use of the environmental attributes.
5.1. Parametric Distributions
Similarly to the approaches of Section 4, we choose to use the entire history to fit the parametric distributions. Thus, we estimate the empirical mean and the empirical standard deviation as follows:
Given the fitted distribution and a new observed count , we perform a statistical significance test in order to identify an outbreak for the monitored syndrome. As only a suspicious increase in the number of cases is usually associated with an infectious disease outbreak, we rely on an one-tailed test. With the one-tailed test we only measure the deviation of the observed count from the estimated distribution with respect to high counts. Consequently, the one sided p-value estimates the probability of observing or higher counts.
- Gaussian.
- Not suitable for count data but often used is the Gaussian distribution . This distribution will serve as reference for the other distributions which are specifically designed for count data.
- Poisson.
- The Poisson distribution is directly designed for count data. For estimating the parameter , we use the maximum likelihood estimate which is the mean .
- Negative Binomial.
- Since the distributional assumptions of the Poisson distribution are often violated due to overdispersion, we also include the Negative Binomial distribution . This distribution includes an additional parameter, also referred to as the dispersion parameter, which allows to control the variance of the distribution [56]. We estimate the parameters with and .
- Fisher’s Test.
- Since the Fisher’s exact test has been used by most of the proposed approaches for non-specific syndromic surveillance, we also include it as a benchmark. It compares the proportion of cases with the syndrome to all cases on the previous data to the corresponding proportion on the current day based on the hypergeometric distribution. In particular, Fisher’s test is known to yield good results on small sample sizes [57], which is the case for the estimates derived from .
Modifications for Adapting the Sensitivity
Modeling count data with a statistical distribution is often challenging because of the different forms of count data and distributional assumptions [56]. Especially for our application scenario, in which we perform multiple statistical tests in parallel, a fitted distribution which is overly sensitive to changes can cause many false alarms. In fact, if the number of monitored syndromes is much higher than the average number of cases observed each time slot, most of the syndromes are rare. Statistical tests performed on these syndromes report a very low p-value if only one case is observed in . This problem becomes more frequent with an increasing number of rare syndromes which are monitored simultaneously, which results in reporting many unusual observations throughout the time slots. In addition, outbreaks are usually associated with a high number of infections, for which reason single unusual observations should have less weight. Therefore, we propose the following modifications for the benchmarks in order to reduce the sensitivity of statistical tests on rare syndromes.
For the Gaussian distribution, we propose to use a minimal value for the standard deviation to which we refer to as . Moreover, for the Poisson distribution, we use a minimal value for the lambda parameter . The Negative Binomial distribution is similarly lead by the mean number of cases. Hence, we assume a minimal mean for the Negative Binomial distribution before setting the parameters as indicated. We leave the standard deviation untouched since manipulating the overdispersion leads to extreme distortions in the estimation.
5.2. Syndromic Surveillance Methods
In principle, arbitrary outbreak detection methods which operate on univariate time series can be used in the setting of non-specific syndromic surveillance. Many traditional methods rely on sliding windows which use the w most recent counts of as reference values for fitting a particular parametric distribution. Therefore, the mean and the standard deviation can be computed over these w reference values as follows:
In the following, we will only focus on a selected set of outbreak detection methods which are universally applicable and serve as drop-in approaches for surveillance systems. In particular, we have chosen to base our work on the following methods which are all implemented in the R package surveillance [58]:
- EARS C1
- and EARS C2 are variants of the Early Aberration Reporting System [37,59] which rely on the assumption of a Gaussian distribution. The difference between C2 and C1 lies in the added gap of two time points between the reference values and the current observed count , so that the distribution of are assumed as in the following:
- EARS C3
- combines the result of the C2 method over a period of three previous observations. For convenience of notation, the incidence counts for the C3 method are transformed according to the statistics so that it fits a normal distribution.Despite the inaccurate assumption of the Gaussian distribution for low counts, the EARS variants are often included in comparative studies due to their simplicity and are still considered to be competitive baselines [59,60,61].
- Bayes method.
- In contrast to the family of EARS C-algorithms, the Bayes algorithm [62] relies on the assumption of a Negative Binomial distribution:With this initialization of parameters, the variance of the Negative Binomial distribution only depends on the window size. For small w a bigger variance is assumed due to insufficient data, while for big w it converges to a Poisson distribution.
- RKI method.
- Since the Gaussian distribution is not suitable for count data with a low mean, the RKI algorithm, as implemented by Salmon et al. [58], assumes a Poisson distribution:
6. Evaluation
The goal of the experimental evaluation reported in this section is to provide an overview of the performance of non-specific syndromic surveillance methods and to highlight the difficulties to detect outbreaks either with global or local modeling. Therefore, we compare the non-specific syndromic surveillance approaches of Section 4 to the simpler statistical methods discussed in Section 5. First we conducted experiments on synthetic data (cf. Section 6.2), which already have been used for the evaluation of the algorithms Eigenevent and WSARE [7,48]. In particular, this experiment allows us to replicate and double-check published results, and complement them with new statistical benchmarks, which provide a deeper insight into the performance of these algorithms. Thereafter, in Section 6.3, we have evaluated the algorithms and the benchmarks on real data of a German emergency department. Since no real outbreaks are known to us in advance, we injected synthetic outbreaks by adding cases with a particular disease pattern on certain days, which allows us to evaluate and compare the algorithms in a controlled environment. Table 3 and Table 4 show the attributes of the data sets. A detailed description of the evaluation data is provided in Section 6.2.1 and Section 6.3.1, respectively.

Table 3.
Information about the attributes of the synthetic data.

Table 4.
Information about the attributes of the real data.
6.1. Evaluation Setup
The evaluation of syndromic surveillance methods is usually performed on a set of data streams, to which we will refer as an evaluation set, since a single data stream does normally not contain enough outbreaks to draw conclusions about the performance of the evaluated algorithms.
For each single evaluation, the respective data stream is split into two parts, a training part, containing the first k time slots, and a test part, which contains the remainder of the data stream. The test part of the data stream contains exactly one outbreak which covers one or more successive time slots depending on the duration of the outbreak. Alarms raised during the outbreak are considered as true positives while all other raised alarms are considered as false positives. Note that the evaluation on the test part is performed incrementally, which means that for evaluating each time slot , the model will be newly fitted on the complete set of previously observed data points .
6.1.1. Evaluation Measures
The complement of the p-value, which we obtain for each time slot in the test part, can be interpreted as a score which is used for the evaluation measure. For the evaluation we rely on the activity monitor operating characteristic (AMOC) [63] which has been predominantly used in previous works. AMOC can be seen as an adaptation of the receiver operating characteristic (ROC), in which the true positive rate is replaced by the detection delay, i.e., the number of time points until an outbreak has been first detected by the algorithm. In case the algorithm does not raise an alarm during the period of the outbreak, the detection delay is equal to the length of the outbreak. Hence, the computation of the AMOC curves is based on the sorting of the composite p-values for each time slot in the test part and the detection delay that the particular time slots would cause if there was no alarm raised.
Contrary to the evaluation in [7,48], in which only specific scores have been evaluated to create the AMOC-curves, we evaluate the complete range of scores to allow a more precise analysis. Moreover, for syndromic surveillance, we are interested in a very low false-alarm rate for the algorithms, and therefore only report the partial area under AMOC-curve for a false alarm rate less than , to which we refer to as . Note that contrary to conventional AUC values, in this case lower values mean better results since small values for the detection delay are better.
Furthermore, in previous works, the computed scores of all evaluated data streams have been combined together, before the AMOC-curve has been created. This results in a micro-averaged measure. However, each data stream is handled by the algorithms independently, possibly resulting in different models across the data streams. Depending on the properties of the respective underlying data distribution, these models might perform differently. In order to consider such differences we propose to evaluate the AMOC-curve on each data stream individually and then take the average of all computed values representing the macro-averaged result. If not stated otherwise, the macro-averaged values are reported. However, as long as the streams share similar properties, which is the case for the WSARE synthetic data, the results of the micro-averaged and the macro-averaged values are quite similar.
6.1.2. Parameter Configurations
For our proposed benchmarks, all possible syndromes having a maximum of two conditions are evaluated as it is done in the WSARE algorithms. In addition, we have used a minimal standard deviation of one (), a minimal lambda of one () and minimal mean of one () as the standard setting. Since the implementation of the EARS algorithms allows to set a minimal standard deviation as well, we also choose to set it to one for these methods. For the DMSS algorithm two parameters need to be specified, the minimum support threshold for the rules, and the window size w, defining the number of recent time slots used for the reference set . For a fair comparison, we have evaluated all parameter settings for , as proposed in [47], and for . Since the described approaches all rely on a sliding window, we have evaluated the window sizes 7, 14, 28, 56, 112, 182 and 357 to further analyze the influence of amount of data used for fitting the distributions of the statistical methods.
6.1.3. Additional Baselines
Following Wong et al. [48], we have also included the control chart, the moving average and the linear regression algorithms. These baselines only monitor the total number of patients per time slot and can therefore be considered to be simple global modeling approaches. Note that this kind of surveillance can also be viewed as monitoring the universal syndrome, which is true for all observed cases. The control chart algorithm is essentially identical to our proposed Gaussian benchmark and the moving average algorithm corresponds to the EARS C1 algorithm using a window size of 7 except that both algorithms are only applied on the univariate time series of the universal syndrome. In contrast, the linear regression model fits a linear model which predicts the number of cases per time slot solely based on the environmental attributes. To apply linear regression on categorical features we create a one-hot encoded representation of using the information of the environmental attributes. Given the encoded data with binary features the linear regression model is fitted where Y represents the estimation for the total number of patients per time slot. The standard error of the model, which is computed on all recent time slots which share the same values for the environmental attributes as the current observed time slot, and the predicted value for the current time slot are used to fit a Gaussian distribution, on which a p-value is computed for the actually observed number of patients.
6.1.4. Implementation
For the Eigenevent algorithm, we rely on the code provided by the authors (https://github.com/fanaee/EigenEvent, accessed on 22 April 2020). Unfortunately, we have not been able to get access to the original code of WSARE and DMSS, and therefore re-implemented these algorithms in Python, using the libraries pyAgrum [64] for Bayesian networks and mlxtend [65] for association rule mining. To further compare our implementation of the WSARE algorithms, we have imported the pre-computed p-values of the WSARE and Eigenevent algorithms on the synthetic data which are also available in the Eigenevent repository. As an implementation baseline for the common syndromic surveillance methods, we have used the R package surveillance [58], and adapted the implementation of the methods EARS (C1, C2, and C3), Bayes, and RKI so that they also return p-values. Finally, for performing linear regression, we have used the Python library scikit-learn [66]. Our implementation is publicly available (https://github.com/MoritzKulessa/NSS, accessed on 9 March 2021).
6.2. Experiments on Synthetic Data
6.2.1. Data
The evaluation set consists of 100 data streams, generated with the synthetic data generator proposed by Wong et al. [6] (https://web.archive.org/web/20150920104314/ http://www.autonlab.org/auton_static/datsets/wsare/wsare3data.zip, accessed on 8 August 2020). The data generator is based on a Bayesian network and simulates a population of people living in a city of whom only a subset are reported to the data stream at each simulated time slot. Detailed information about the attributes in the data stream is given in Table 3. As WSARE, DMSS, and the benchmarks cannot take spatial attributes into account, such kind of attributes are considered as response attributes for these algorithms. Each data stream captures the information about the people on a daily basis over a time period of two years, i.e., each time slot contains the patients of one day. The first year is used for the training part while the second year serves as the evaluation part. The outbreak in the second year starts at a randomly chosen day and always lasts for 14 days. For simulating the outbreak, a randomly chosen number of cases with a particular disease pattern is added to the baseline distribution of patients in this time period. A total of syndromes are monitored at the same time for the WSARE algorithms and the benchmarks.
All of the 100 synthetically generated data streams share similar properties. As an example, we have visualized the total number of reported people for one of the data streams in Figure 3. As it can be seen, the number of daily cases is considerably low compared to the number of monitored syndromes for which reason most of the syndromes might be rare. To get an impression about the distribution of the observed counts according to the Gaussian model, we additionally visualized the z-scores (degree of deviation from the mean measured in number of standard deviations) for all syndromes (minimum standard deviation correction was not applied). As can be seen, extreme deviations are not uncommon (cf. discussion on the problem of multiple testing described in Section 3.2.2). As a consequence, we expect that we are only able to reliably detect injected outbreaks for which the syndrome counts differ more than six standard deviations from the respective mean.
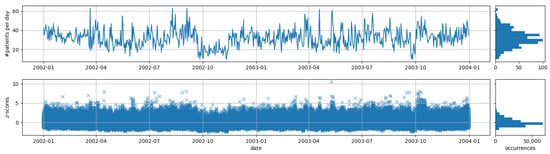
Figure 3.
Visualization of number of patients and z-scores of all syndromes of over time for one of the synthetic data streams.
6.2.2. Results
Comparison to the Benchmarks
First of all, we have evaluated the non-specific syndromic surveillance approaches (cf. Section 4) and compared them to our proposed distributional benchmarks (cf. Section 5.1). For the WSARE algorithms, we additionally evaluate the results of just reporting the minimal p-value for each day (min. p-value), instead of performing a permutation test with 1000 repetitions (permutation test). Moreover, we imported the pre-computed p-values for the data streams from the Eigenevent repository for the Eigenevent and WSARE algorithms (imported p-values) and rerun the Eigenevent algorithm (rerun). The results are presented in Table 5. For comparison, we also have included the evaluation of the micro-averaged measure.

Table 5.
Results on the synthetic data.
Rerunning the Eigenevent algorithm returns worse results than the imported p-values. In a personal communication, one of the authors of EigenEvent pointed out that the performance of EigenEvent depends on the random initialization of the used tensor decomposition, and suggested BetaNTF as an alternative [67]. However, even the imported p-values did not achieve competitive results compared to other algorithms, so we did not further investigate this issue. For the WSARE algorithms, we can observe that our implementation achieves better results than the imported p-values. In particular, if we omit the permutation test and only report the minimal p-value for each day, the results improve. Our investigations reveal that the number of repetitions of the permutation test is limiting the performance of the approaches. Firstly, the permutation test is based on randomization, only allowing to obtain precise results if the number of repetitions is high enough. Secondly, by performing 1000 repetitions with a permutation test the p-values are mapped onto a coarse grained scale, limited to only three digits after the decimal point, not allowing to consider fine-grained differences between the found anomalies. Both problems can be solved by increasing the number of repetitions of the permutation test. However, increasing the precision by one digit after the decimal point requires to perform ten times as many repetitions, which is often not feasible in practice. A discussion about the efficiency of the WSARE algorithm compared to the Eigenevent algorithm can be found in the work of Fanaee-T and Gama [7].
The results of the DMSS algorithm suggest that monitoring association rules is not as effective as monitoring syndromes. In particular, the space of possible association rules is much greater than the space of possible syndromes , which worsens the problem of multiple testing. In contrast to the other local modeling approaches which are limited to syndromes of maximum length of two, the number of statistical tests performed each day for the DMSS algorithm is regulated by the parameter . For around 980, around 220 and around 68 association rules are checked every day compared to . The worse results for can be explained by the high number of tests performed each day. Conversely, with and , we perform less tests in average but these thresholds seem to be too strict for detecting outbreaks early on. The effect of the window size on the results is discussed in the following experiment in which we have evaluated the syndromic surveillance methods with different window sizes.
In general, all approaches based on global modeling perform considerably worse than the local modeling approaches. Linear regression could achieve the best results among the global approaches, highlighting the importance of capturing seasonal patterns. A closer examination of the coefficients of a linear ridge regression, shown in Table 6, reveal that we expect slightly more patients on the weekend than during the week. In contrast, the analysis of the other coefficients is difficult due to the correlation among these attributes. For example, the flu season starts during the winter when it is cold. In particular, the coefficients of the weather attribute seem to complement the pattern for the season and the flu level. As the flu season also may overlap between seasons, we are not able to extract a precise pattern.

Table 6.
Coefficients of a linear ridge regression model build on the first year of a synthetic data stream. The associated intercept of the model is .
The proposed benchmarks do not take the environmental attributes into account but still are able to achieve results that are competitive to WSARE 3.0. We are surprised about the good results of the Gaussian benchmark since this modelling is not specifically designed for count data. The advantage may be explained with the setting of multiple testing, allowing the generation of more reliable p-values for the day. Moreover, Fisher’s test performs well without specification of any minimum standard deviation. In contrast to the other benchmarks, Fisher’s test also takes the total number of visits on a particular day into account, which might be an advantage.
Interestingly, the Fisher’s test achieves better results than the WSARE 2.5 algorithm. The only difference between these algorithms is that the WSARE 2.5 accounts for the environmental attributes and only computes the proportion for the respective syndrome on all previous days which match the same values for the environmental attributes. Using more data for performing the statistical test seems to be more appropriate on this data than considering environmental effects.
Evaluation of Syndromic Surveillance Methods
In this experiment, we have evaluated common syndromic surveillance methods (cf. Section 5.2) in the setting of non-specific syndromic surveillance, i.e., monitoring the syndromes of with outbreak detection methods in parallel using the local modeling approach. The results for the measure are represented in Table 7.

Table 7.
Results of the on the synthetic data for syndromic surveillance methods.
In general, we can observe that greater window sizes achieve better results, especially for the EARS algorithms. Moreover, we can observe that for very small window sizes, like 7 and 14, the RKI and the Bayes method are superior to the EARS algorithms. It seems that these methods are more suitable in the setting of non-specific syndromic surveillance if very few data are available. The reason why the results of window sizes 112 and 182 of all methods do not seem to improve over the results of window size 56 can be explained by the influence of environmental factors. Due to the annual seasonal pattern of the synthetic data, each season in the year follows a different underlying data distribution. If the window size spans over different seasons, like 112 and 180, we also include non-representative data for fitting the distributions. The reason that a window size of 357 again works much better for all methods is due to the inclusion of data for fitting the distributions of the same season one year ago.
Sensitivity of Statistical Tests
In this experiment, we have evaluated the influence of the , and parameters. The results are shown in Figure 4 where the x-axis depicts the respective minimum value and the y-axis the result of measure.
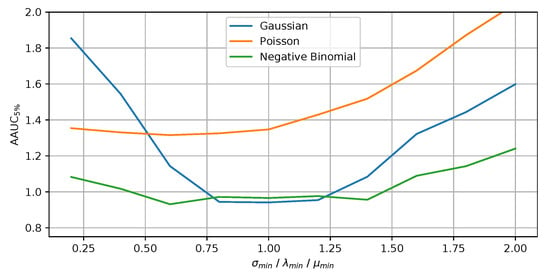
Figure 4.
Influence of the minimum parameter for the statistical test on the benchmarks.
It can be seen that dampening over-sensitive statistical tests does not have a major advantage for the Poisson benchmark. The implicit distributional assumptions already reduce the impact of the statistical tests on rare syndromes. In contrast, the other distributions benefit from adapting the respective minimum value, resulting in a top performance value of the slightly below one. In general, the minimum parameter has a stronger influence on the results for the Gaussian benchmark than for the other benchmarks. In addition, we have performed experiments in which we only monitor the syndromes with length of one and syndromes with a maximum length of three . Generally speaking, with an increasing number of syndromes monitored simultaneously, we observe that the value for the minimum parameter needs to increase as well, which compensates the problem of multiple testing.
6.3. Experiments on Real Data
6.3.1. Data
For an evaluation on real data, we rely on routinely collected, fully anonymized patient data of a German emergency department, collected over a time period of two years. We have extracted a set of response attributes from the emergency department data (cf. Table 4) which might allow an early detection of infectious disease outbreaks. Continuous attributes have been discretized, since all of the non-specific approaches can only operate on nominal data. In particular, we have discretized the temperature (normal , high , very high ), the respiration (low , normal , high ), the pulse (low , normal , high ), the oxygen level (low , normal ) and the systolic (normal , high , very high ) and diastolic (normal , high , very high ) blood pressure. Missing values are imputed with the value normal. In addition, we include the Manchester-Triage-System (MTS) [68] initial assessment, which is filled out for every patient on arrival. To reduce the number of values for the attribute MTS, we group classifications which do not relate to any infectious disease, such as to various kinds of injuries, into a single value. We did not include ICD codes as response attributes, since obtaining these values can take several days, hindering a timely detection of the outbreak [26]. For the WSARE algorithms and the benchmarks, a total of syndromes are monitored simultaneously.
The number of daily visits in the emergency department is shown in Figure 5. With a mean of 170 patients per day, these are much higher than the synthetic data, which have about 35 patients per day (cf. Figure 3). Again, we also show the z-scores of the syndromes to obtain an impression about the distribution of the observed counts, especially the extreme deviations. Compared to the synthetic data, we obtain much stronger deviations in the syndrome counts, which can be explained by the higher number of syndromes which are monitored simultaneously. In addition, the synthetic data seem to be very homogeneous while the real data seem to change a little bit over time (e.g., we can observe much higher deviations for the end of the second year). Such changes may be due to changes in the behaviour of the hospital staff that inputs the data into the emergency department management systems.
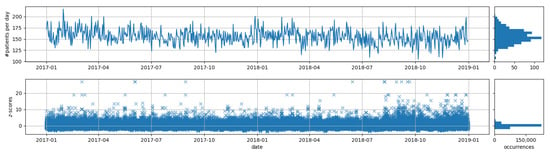
Figure 5.
Visualization of number of patients and z-scores of all syndromes of over time for the real ED data.
6.3.2. Evaluation Process
As the emergency department data do not contain any information about real outbreaks, we decided to inject synthetic outbreaks, which is common practice in the area of syndromic surveillance. Therefore, we have specified ten different scenarios of disease outbreaks, shown in Table 8, each represented by a particular syndrome. For a systematic evaluation, we have carefully selected these syndromes based on their daily occurrences in the emergency department data, ensuring a representative range of frequent and rare disease patterns. Again, we use the first year as the train part and the second year as evaluation part. To simulate an outbreak for one of the scenarios, we have drawn a fixed sized random sample of patients from the emergency department data, which have the respective syndrome, and added these to a randomly chosen single day in the second year, instead of simulating how the patients would arrive in the emergency department over time. This allows us to systematically assess the sensitivity of the algorithms to detect sudden outbreaks by running evaluations with a controlled number of infected people per outbreak.

Table 8.
Statistics about the scenarios.
For each scenario, we have created 25 data streams which differ from each other only by the day of the outbreak. To evaluate a particular outbreak size, we have added the same fixed number of patients to all outbreak days of these data streams. We evaluated all outbreak sizes from one to 20 infected patients per outbreak. Hence, for each scenario we obtain 20 evaluation sets, each containing 25 data streams. According to this, 500 data streams are evaluated for each of the 10 scenarios, resulting in a total of 5000 outbreaks.
For each evaluation set, the results for the measure can be computed for an algorithm, representing the ability to detect the respective outbreak size for the respective syndrome. Given the results of the measure for the different outbreak sizes, we can visualize the results of an algorithm as shown in Figure 6. Instead of reporting each single value for the outbreak sizes, we have chosen to report the area under this curve, encapsulating the overall ability to detect an outbreak for the respective scenario of an algorithm, to which we refer to as . Small values for the measure represent good results.
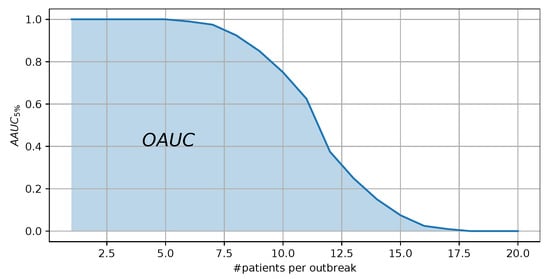
Figure 6.
Visualization of the results of an algorithm for different outbreak sizes. The area under this curve represents the measure.
6.3.3. Configuration of the Algorithms
Due to the better results in the experiments on synthetic data, we choose to report the minimal p-value for the WSARE algorithms instead of performing a permutation test. Unfortunately, we could not evaluate the DMSS algorithm, since the high number of cases each day causes the DMSS algorithm to find too many rules. For example, setting the minimum support to results in around rules for each day. Even by focusing on rules with a very high support, such as , we still obtain an average of 4000 rules each day, compared to syndromes. The configuration for all other algorithms remains the same.
6.3.4. Results
Comparison to the Benchmarks
For the following experiment, we have evaluated the non-specific syndromic surveillance algorithms on all ten scenarios. Table 9 shows the obtained measure for the algorithms, followed by the rank across all algorithms for each scenario (in round brackets). The last column of the table shows the average rank of the respective algorithms over all scenarios, so that better algorithms will show a low number in this column.

Table 9.
Results of the measure for all scenarios on the real data in which the algorithms have been applied in the setting of non-specific syndromic surveillance.
First of all, we can observe that global modeling improves over local modeling for the results on frequent syndromes (scenarios 1 to 3) while for the remaining rare syndromes it is vice versa. The observations on the frequent scenarios seems plausible, since for the local modeling the signal of the outbreak syndrome needs to surpass the signals of all other monitored syndromes, and as discussed for Figure 3, strong signals are not uncommon. Assuming a fixed outbreak size, the outbreak’s signal is obviously stronger for rare syndromes than for more frequent syndromes, which leads to the observed better performance of the global models for the frequent syndromes. On the other hand, the absolute numbers for the frequent syndromes are all close together and relatively high. This can be explained as we only used a maximum outbreak size of 20 in our evaluations, which is difficult to detect even for the global modeling approaches taking into account that an average of 170 patients arrive in the emergency department each day. This also explains why the global approaches are not able to improve much (in terms of absolute numbers) as the frequency of the evaluated syndromes decreases.
From scenario 4 onwards, the results of the local modeling approaches improve. In particular, the benchmark based on the Negative Binomial distribution, the Gaussian distribution and the EARS methods improve over all other algorithms. In contrast, the Fisher’s test benchmark only achieves competitive results for scenario 10. The same effect can be observed for the results of the WSARE algorithms, since they are all based on the Fisher’s test. While the WSARE 2.0 algorithm is not able to achieve good results at all due to the limited set of reference patients, the WSARE 2.5 and WSARE 3.0 can improve over the Fisher’s test benchmark. Directly comparing the Fisher’s test benchmark and WSARE 2.5 show that the environmental attributes can help to better detect the outbreaks. The improvement of including environmental variables can also be observed for the global modeling approaches, for which the Linear Regression algorithm achieve better results. The coefficients of a linear ridge regression, displayed in Table 10, show that during spring and winter we observe a slightly higher number of patients which may be caused by the flu season. Regarding the weekday, we expect a higher number of cases on Monday and Friday while on the weekend less patients are observed.

Table 10.
Coefficients of a linear ridge regression model build on the first year of a real data stream. The associated intercept of the model is .
The worse results of the approaches which are based on the Poisson distribution (e.g., Poisson benchmark and RKI method) suggest that this distribution might not be suitable for non-specific syndromic surveillance.
Evaluation of Syndromic Surveillance Methods
The results for all window sizes of the syndromic surveillance methods are shown in Figure 7. Since the all EARS algorithms obtain similar results, we only have visualized the results of EARS C1. In general we can observe that a very low window size of 7 and 14 achieves the worst results. However, already with a window size of 28 the statistical methods are competitive with the other algorithms presented in Table 9. They further improve with a window size of 56 and then stabilize for larger window sizes for all of the methods.
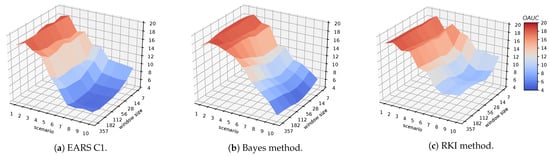
Figure 7.
Visualization of the results for the syndromic surveillance methods.
A closer look at the differences between the syndromic surveillance methods reveals that all EARS methods achieve similar results for all evaluations. The results of the Bayes and the RKI method are usually worse than the EARS methods. Only for scenario 10, the Bayes method can consistently improve over the EARS algorithms for all evaluated window sizes. In general, the results of the EARS methods with a window size of 56 are slightly better than the Gaussian benchmark. In contrast, for the synthetic data we observed that larger window sizes always improved the results. One reason for that difference could be the heterogeneity of the real data. While the synthetic data is consistently generated in a controlled environment, the reporting behaviour in the emergency department may change over time due to the different employees using the hospital system. Apparently, using a window size of 56 allows to adapt to these kind of changes.
Results on Specific Syndromic Surveillance
We have transformed the non-specific syndromic surveillance methods into specific syndromic surveillance methods by monitoring only the syndrome of the respective scenario. This allows us to assess the performance of the algorithms without the effect of the multiple testing. The results are shown in Table 11. Note that no results are reported for the global modeling algorithms since such a transformation is not possible for these algorithms.

Table 11.
Results of the measure for all scenarios on the real data in which the algorithms have been applied in the setting of specific syndromic surveillance.
It can be seen that all the algorithms perform almost equally well. In general, the outbreaks of rarer disease patterns are easier to detect by the algorithms, with the exception of scenario 2. The good results for scenario 2 can be explained by the lower standard deviation of the monitored syndrome, which indicates that the counts of that syndrome are more stable. This in turn results in fewer false positives, enabling the algorithms to better detect the outbreak.
Contrary to the results in the non-specific syndromic surveillance setting, the Poisson distribution seem to work much better than the Gaussian or Negative Binomial distribution. Moreover, we were surprised that the algorithms based on Fisher’s test obtain the best results, because this test is usually not used for specific syndromic surveillance. If we compare the results of specific and non-specific syndromic surveillance, we conclude that different distributions should be used depending on the setting at hand.
Sensitivity of Statistical Tests
We have again evaluated the influence of over-sensitive statistical tests by varying the minimum value parameters , , and for all scenarios. The results can be seen in Figure 8 where the x-axis depicts the value for the minimum parameter, the y-axis the scenario, and the color the value of the measure.
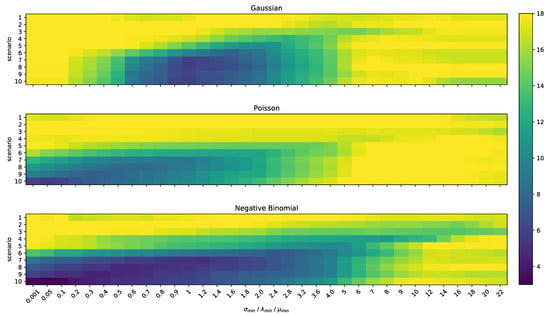
Figure 8.
Visualization of the influence of , and parameter for the benchmarks.
The plots of the Poisson and Negative Binomial benchmark show similar results when varying the minimum parameter. In particular, by adapting the parameter, we effectively set a minimal value for the mean as it is done with the parameter for the Negative Binomial distribution which explains the similarities of the results in the variation of these parameters. However, there is a clear gap between both score tables which can be explained by the ability of the Negative Binomial distribution to adapt to overdispersion. This statistical effect might be caused for instance by seasonality, or superspreading events, and different infectious diseases might be more or less prone to it. When surveilling a set of syndromes with different properties simultaneously, the adaptation to overdispersion leads to p-values which are better comparable between the different syndromes. This makes the Negative Binomial distribution generally preferable over the Poisson distribution for the scenario of non-specific syndromic surveillance.
However, the results also reveal the limitations in adapting to all syndromes simultaneously. A closer look at the results of the Negative Binomial benchmark shows a correlation between the value for the minimum parameter and the original frequency of the syndrome which was chosen in order to inject the artificial outbreaks. More specifically, the best result for a particular syndrome is achieved when the value for the parameter is close to the respective mean. This effect is reasonable since the sensitivity of all statistical tests on syndromes which actually have a lower mean is dampened by assuming a higher mean, while we maintain the sensitivity for the statistical test with which the outbreak can be detected. In particular, we reduce the number of false positives without reducing the ability to detect the outbreak. In contrast, if the value for the minimum parameter is higher than the mean of the syndrome which is responsible for the outbreak, we hinder the ability to detect the outbreak for which reason we obtain worse results again.
A similar behaviour can be observed for the Gaussian benchmark with the difference that we achieve the best performance for the syndromes whose standard deviations are closest to the value for the parameter. Moreover, we can observe that small values for the parameter do not work at all. In order to explain the reason for that behavior, we have visualized the results of scenarios 8 and 9 of the Gaussian benchmark in Figure 9, which depicts the results of the measure for different values for the parameter with respect to the outbreak size. It can be seen that for values , the results cannot obtain the optimal value of zero anymore, even if the outbreak size continues to increase. A closer look at this phenomenon reveals that such a low causes that non-outbreak days obtain a p-value of 0 due to the inclusion of very sensitive tests and numerical problems. A clear separation between these non-outbreak days and the outbreak day is impossible, resulting in a value above 0 for the measure. This problem can be solved by increasing the precision of the computed p-values or by reducing the number of statistical tests which are monitored at the same time.
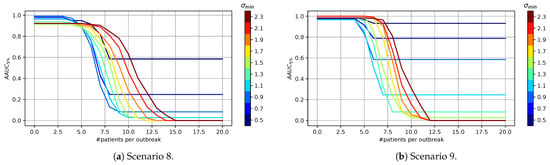
Figure 9.
Visualization of the influence of parameter for the Gaussian benchmark.
We conclude that the minimum parameter has a major influence on the ability to detect outbreaks and can be used to deliberately put the focus on a particular type of syndromes. In general, we could obtain the best results with the Negative Binomial distribution when properly configured.
7. Conclusions
In this work, we gave an overview about non-specific syndromic surveillance from the perspective of machine learning. Our main contribution is a unifying framework for this task based on two modeling strategies: global modeling solves the problem of outbreak detection with a single model, whereas local modeling breaks down the problem into many smaller, local tasks, which are executed independently and whose predictions eventually have to be aggregated into an overall prediction. In addition, we redefine previously proposed approaches to non-specific syndromic surveillance within this framework. This framework also allows us to define simple local modeling strategies based on statistical approaches, which essentially monitor all possible syndromes of the given data source at the same time.
The second main contribution of this work is an extensive empirical evaluation and experimental comparison of previously proposed algorithms as well as our newly proposed simple local modeling benchmarks. The experimental results on synthetic and real data show that these benchmarks already achieve competitive results or even outperform more elaborate approaches that have been previously proposed in the literature. Especially in the setting where multiple tests on count data are performed simultaneously, monitoring all possible syndromes with Negative Binomial distributions improves over all other approaches. Moreover, on heterogeneous data sources, simple window-based approaches can further improve the performance by adapting to concept drift. In general, the evaluated global modeling algorithms have problems in detecting significant changes for rare disease patterns and therefore perform worse than the local modeling approaches. However, the performance of the local modeling algorithms is limited by the total number of local tasks executed simultaneously, and suffers from the problem of multiple hypothesis testing.
This work can be seen as a foundation for non-specific syndromic surveillance and our proposed simple statistical approaches can serve as benchmarks for future works. As potential directions, the set of specific syndromic surveillance methods applied in the setting of non-specific syndromic surveillance can be enhanced since their results seem promising and these methods are already designed for outbreak detection. In particular, based on the statistical properties of the monitored syndromes, different methods could be used simultaneously. Furthermore, an interesting avenue for future work is the inclusion of geo-spatial information, which has not been addressed in detail in this work.
Author Contributions
Conceptualization, M.K., E.L.M. and J.F.; data curation, M.K.; formal analysis, M.K., E.L.M. and J.F.; funding acquisition, M.K. and E.L.M.; investigation, M.K., E.L.M. and J.F.; methodology, M.K., E.L.M. and J.F.; project administration, M.K., E.L.M. and J.F.; software, M.K.; validation, M.K.; writing—original draft, M.K., E.L.M. and J.F.; writing—review & editing, M.K., E.L.M. and J.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the German Innovation Committee of the Federal Joint Committee (G-BA) [ESEG project, grant number 01VSF17034].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Our code is publicly available at https://github.com/MoritzKulessa/NSS (accessed on 9 March 2021). The synthetic dataset proposed by Wong et al. [6] can be downloaded from https://web.archive.org/web/20150920104314/http://www.autonlab.org/auton_static/datsets/wsare/wsare3data.zip (accessed on 8 August 2020). The real data cannot be published due to privacy protection.
Acknowledgments
We thank our project partners the Health Protection Authority of Frankfurt, the Hesse State Health Office and Centre for Health Protection, the Hesse Ministry of Social Affairs and Integration, the Robert Koch-Institut, the Epias GmbH and especially the Sana Klinikum Offenbach GmbH. We acknowledge support by the German Research Foundation and the Open Access Publishing Fund of Technical University of Darmstadt.
Conflicts of Interest
The authors Moritz Kulessa and Eneldo Loza Mencía are funded by the German Innovation Committee of the Federal Joint Committee (G-BA).
References
- Noufaily, A.; Enki, D.; Farrington, P.; Garthwaite, P.; Andrews, N.; Charlett, A. An improved algorithm for outbreak detection in multiple surveillance systems. Stat. Med. 2013, 32, 1206–1222. [Google Scholar] [CrossRef]
- Henning, K.J. What is syndromic surveillance? Morb. Mortal. Wkly. Rep. Suppl. 2004, 53, 7–11. [Google Scholar]
- Buckeridge, D.L. Outbreak detection through automated surveillance: A review of the determinants of detection. J. Biomed. Inform. 2007, 40, 370–379. [Google Scholar] [CrossRef]
- Shmueli, G.; Burkom, H. Statistical challenges facing early outbreak detection in biosurveillance. Technometrics 2010, 52, 39–51. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning—A Guide for Making Black Box Models Explainable. 2020. Available online: http://christophm.github.io/interpretable-ml-book/ (accessed on 20 October 2020).
- Wong, W.K.; Moore, A.; Cooper, G.; Wagner, M. Bayesian Network Anomaly Pattern Detection for Disease Outbreaks. In Proceedings of the 20th International Conference on Machine Learning (ICML), Washington, DC, USA, 21–24 August 2003; Volume 2, pp. 808–815. [Google Scholar]
- Fanaee-T, H.; Gama, J. EigenEvent: An Algorithm for Event Detection from Complex Data Streams in Syndromic Surveillance. Intell. Data Anal. 2015, 19, 597–616. [Google Scholar] [CrossRef]
- Kulessa, M.; Loza Mencía, E.; Fürnkranz, J. Revisiting Non-Specific Syndromic Surveillance. In Proceedings of the 19th International Symposium Intelligent Data Analysis (IDA), Konstanz, Germany, 27–29 April 2021. [Google Scholar]
- Fricker, R.D. Syndromic surveillance. In Wiley StatsRef: Statistics Reference Online; American Cancer Society. 2014. Available online: https://onlinelibrary.wiley.com/doi/full/10.1002/9781118445112.stat03712 (accessed on 19 August 2020).
- Buehler, J.W.; Hopkins, R.S.; Overhage, J.M.; Sosin, D.M.; Tong, V. Framework for Evaluating Public Health Surveillance Systems for Early Detection of Outbreaks. 2008. Available online: https://www.cdc.gov/mmwr/preview/mmwrhtml/rr5305a1.htm (accessed on 14 July 2020).
- Rappold, A.G.; Stone, S.L.; Cascio, W.E.; Neas, L.M.; Kilaru, V.J.; Carraway, M.S.; Szykman, J.J.; Ising, A.; Cleve, W.E.; Meredith, J.T.; et al. Peat bog wildfire smoke exposure in rural North Carolina is associated with cardiopulmonary emergency department visits assessed through syndromic surveillance. Environ. Health Perspect. 2011, 119, 1415–1420. [Google Scholar] [CrossRef] [PubMed]
- Hiller, K.M.; Stoneking, L.; Min, A.; Rhodes, S.M. Syndromic surveillance for influenza in the emergency department—A systematic review. PLoS ONE 2013, 8, e73832. [Google Scholar] [CrossRef] [PubMed]
- Hope, K.; Durrheim, D.N.; Muscatello, D.; Merritt, T.; Zheng, W.; Massey, P.; Cashman, P.; Eastwood, K. Identifying pneumonia outbreaks of public health importance: Can emergency department data assist in earlier identification? Aust. N. Z. J. Public Health 2008, 32, 361–363. [Google Scholar] [CrossRef] [PubMed]
- Edge, V.L.; Pollari, F.; King, L.; Michel, P.; McEwen, S.A.; Wilson, J.B.; Jerrett, M.; Sockett, P.N.; Martin, S.W. Syndromic surveillance of norovirus using over the counter sales of medications related to gastrointestinal illness. Can. J. Infect. Dis. Med. Microbiol. 2006, 17. [Google Scholar] [CrossRef]
- Reis, B.Y.; Pagano, M.; Mandl, K.D. Using temporal context to improve biosurveillance. Proc. Natl. Acad. Sci. USA 2003, 100, 1961–1965. [Google Scholar] [CrossRef]
- Reis, B.Y.; Mandl, K.D. Time series modeling for syndromic surveillance. BMC Med. Inform. Decis. Mak. 2003, 3, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Ansaldi, F.; Orsi, A.; Altomonte, F.; Bertone, G.; Parodi, V.; Carloni, R.; Moscatelli, P.; Pasero, E.; Oreste, P.; Icardi, G. Emergency department syndromic surveillance system for early detection of 5 syndromes: A pilot project in a reference teaching hospital in Genoa, Italy. J. Prev. Med. Hyg. 2008, 49, 131–135. [Google Scholar]
- Wu, T.S.J.; Shih, F.Y.F.; Yen, M.Y.; Wu, J.S.J.; Lu, S.W.; Chang, K.C.M.; Hsiung, C.; Chou, J.H.; Chu, Y.T.; Chang, H.; et al. Establishing a nationwide emergency department-based syndromic surveillance system for better public health responses in Taiwan. BMC Public Health 2008, 8, 18. [Google Scholar] [CrossRef] [PubMed]
- Heffernan, R.; Mostashari, F.; Das, D.; Karpati, A.; Kulldorff, M.; Weiss, D. Syndromic Surveillance in Public Health Practice, New York City. Emerg. Infect. Dis. 2004, 10, 858–864. [Google Scholar] [CrossRef] [PubMed]
- Lober, W.B.; Trigg, L.J.; Karras, B.T.; Bliss, D.; Ciliberti, J.; Stewart, L.; Duchin, J.S. Syndromic surveillance using automated collection of computerized discharge diagnoses. J. Urban Health 2003, 80, i97–i106. [Google Scholar]
- Ising, A.I.; Travers, D.; MacFarquhar, J.; Kipp, A.; Waller, A.E. Triage note in emergency department-based syndromic surveillance. Adv. Dis. Surveill. 2006, 1, 34. [Google Scholar]
- Reis, B.Y.; Mandl, K.D. Syndromic surveillance: The effects of syndrome grouping on model accuracy and outbreak detection. Ann. Emerg. Med. 2004, 44, 235–241. [Google Scholar] [CrossRef] [PubMed]
- Begier, E.M.; Sockwell, D.; Branch, L.M.; Davies-Cole, J.O.; Jones, L.H.; Edwards, L.; Casani, J.A.; Blythe, D. The national capitol region’s emergency department syndromic surveillance system: Do chief complaint and discharge diagnosis yield different results? Emerg. Infect. Dis. 2003, 9, 393. [Google Scholar] [CrossRef]
- Fleischauer, A.T.; Silk, B.J.; Schumacher, M.; Komatsu, K.; Santana, S.; Vaz, V.; Wolfe, M.; Hutwagner, L.; Cono, J.; Berkelman, R.; et al. The validity of chief complaint and discharge diagnosis in emergency department–based syndromic surveillance. Acad. Emerg. Med. 2004, 11, 1262–1267. [Google Scholar]
- Ivanov, O.; Wagner, M.M.; Chapman, W.W.; Olszewski, R.T. Accuracy of three classifiers of acute gastrointestinal syndrome for syndromic surveillance. In Proceedings of the AMIA Symposium. American Medical Informatics Association, San Antonio, TX, USA, 9–13 November 2002; p. 345. [Google Scholar]
- Centers for Disease Control and Prevention. Syndrome Definitions for Diseases Associated with Critical Bioterrorism-Associated Agents. 2003. Available online: https://emergency.cdc.gov/surveillance/syndromedef/pdf/syndromedefinitions.pdf (accessed on 19 August 2020).
- Roure, J.; Dubrawski, A.; Schneider, J. A study into detection of bio-events in multiple streams of surveillance data. In NSF Workshop on Intelligence and Security Informatics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 124–133. [Google Scholar]
- Held, L.; Höhle, M.; Hofmann, M. A statistical framework for the analysis of multivariate infectious disease surveillance counts. Stat. Model. 2005, 5, 187–199. [Google Scholar] [CrossRef]
- Kulldorff, M.; Mostashari, F.; Duczmal, L.; Katherine Yih, W.; Kleinman, K.; Platt, R. Multivariate scan statistics for disease surveillance. Stat. Med. 2007, 26, 1824–1833. [Google Scholar] [CrossRef]
- Webb, G.I.; Hyde, R.; Cao, H.; Nguyen, H.L.; Petitjean, F. Characterizing concept drift. Data Min. Knowl. Discov. 2016, 30, 964–994. [Google Scholar] [CrossRef]
- Hughes, H.; Morbey, R.; Hughes, T.; Locker, T.; Shannon, T.; Carmichael, C.; Murray, V.; Ibbotson, S.; Catchpole, M.; McCloskey, B.; et al. Using an emergency department syndromic surveillance system to investigate the impact of extreme cold weather events. Public Health 2014, 128, 628–635. [Google Scholar] [CrossRef] [PubMed]
- Dirmyer, V.F. Using Real-Time Syndromic Surveillance to Analyze the Impact of a Cold Weather Event in New Mexico. J. Environ. Public Health 2018, 2018, 2185704. [Google Scholar] [CrossRef]
- Johnson, K.; Alianell, A.; Radcliffe, R. Seasonal patterns in syndromic surveillance emergency department data due to respiratory Illnesses. Online J. Public Health Inform. 2014, 6, e66. [Google Scholar] [CrossRef]
- Buckeridge, D.L.; Burkom, H.; Campbell, M.; Hogan, W.R.; Moore, A.W. Algorithms for rapid outbreak detection: A research synthesis. J. Biomed. Inform. 2005, 38, 99–113. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Wong, W.K.; Moore, A.; Cooper, G.; Wagner, M. Rule-Based Anomaly Pattern Detection for Detecting Disease Outbreaks. In Proceedings of the 18th National Conference on Artificial Intelligence (AAAI), Edmonton, AL, Canada, 28 July–1 August 2002; American Association for Artificial Intelligence: Menlo Park, CA, USA, 2002; pp. 217–223. [Google Scholar]
- Hutwagner, L.; Thompson, W.; Seeman, G.; Treadwell, T. The bioterrorism preparedness and response early aberration reporting system (EARS). J. Urban Health 2003, 80, i89–i96. [Google Scholar] [PubMed]
- Dong, G.; Li, J. Efficient mining of emerging patterns: Discovering trends and differences. In Proceedings of the 5th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 15–18 August 1999; pp. 43–52. [Google Scholar]
- Bay, S.; Pazzani, M. Detecting group differences: Mining contrast sets. Data Min. Knowl. Discov. 2001, 5, 213–246. [Google Scholar] [CrossRef]
- Novak, P.K.; Lavrač, N.; Webb, G.I. Supervised descriptive rule discovery: A unifying survey of contrast set, emerging pattern and subgroup mining. J. Mach. Learn. Res. 2009, 10, 377–403. [Google Scholar]
- Wrobel, S. An algorithm for multi-relational discovery of subgroups. In European Symposium on Principles of Data Mining and Knowledge Discovery; Springer: Berlin/Heidelberg, Germany, 1997; pp. 78–87. [Google Scholar]
- Poon, H.; Domingos, P. Sum-product networks: A New Deep Architecture. In Proceedings of the 27th Conference on Uncertainty in Artificial Intelligence (UAI), Barcelona, Spain, 14–17 July 2011; pp. 337–346. [Google Scholar]
- Jensen, F.V. An Introduction to Bayesian Networks; UCL Press: London, UK, 1996; Volume 210. [Google Scholar]
- Duivesteijn, W.; Feelders, A.J.; Knobbe, A. Exceptional model mining. Data Min. Knowl. Discov. 2016, 30, 47–98. [Google Scholar] [CrossRef]
- Li, S.C.X.; Jiang, B.; Marlin, B. Misgan: Learning from incomplete data with generative adversarial networks. arXiv 2019, arXiv:1902.09599. [Google Scholar]
- Gao, J.; Tembine, H. Distributed mean-field-type filters for big data assimilation. In Proceedings of the 2016 IEEE 18th International Conference on High Performance Computing and Communications; IEEE 14th International Conference on Smart City; IEEE 2nd International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Sydney, NSW, Australia, 12–14 December 2016; pp. 1446–1453. [Google Scholar]
- Brossette, S.; Sprague, A.; Hardin, J.; Waites, K.; Jones, W.; Moser, S. Association Rules and Data Mining in Hospital Infection Control and Public Health Surveillance. J. Am. Med. Inform. Assoc. 1998, 5, 373–381. [Google Scholar] [CrossRef] [PubMed]
- Wong, W.K.; Moore, A.; Cooper, G.; Wagner, M. What’s Strange About Recent Events (WSARE): An Algorithm for the Early Detection of Disease Outbreaks. J. Mach. Learn. Res. 2005, 6, 1961–1998. [Google Scholar]
- Amrhein, V.; Greenland, S.; McShane, B. Scientists rise up against statistical significance. Nature 2019, 567, 305–307. [Google Scholar] [CrossRef]
- Knobbe, A.; Crémilleux, B.; Fürnkranz, J.; Scholz, M. From local patterns to global models: The LeGo approach to data mining. In Workshop Proceedings: From Local Patterns to Global Models (Held in Conjunction with ECML/PKDD-08); Utrecht University: Antwerp, Belgium, 2008; Volume 8, pp. 1–16. [Google Scholar]
- Heard, N.A.; Rubin-Delanchy, P. Choosing between methods of combining-values. Biometrika 2018, 105, 239–246. [Google Scholar] [CrossRef]
- Vial, F.; Wei, W.; Held, L. Methodological challenges to multivariate syndromic surveillance: A case study using Swiss animal health data. BMC Vet. Res. 2016, 12, 288. [Google Scholar] [CrossRef]
- Lindquist, M.A.; Mejia, A. Zen and the art of multiple comparisons. Psychosom. Med. 2015, 77, 114. [Google Scholar] [CrossRef]
- Leek, J.T.; Storey, J.D. A general framework for multiple testing dependence. Proc. Natl. Acad. Sci. USA 2008, 105, 18718–18723. [Google Scholar] [CrossRef]
- Faryar, K.A. The Effects of Weekday, Season, Federal Holidays, and Severe Weather Conditions on Emergency Department Volume in Montgomery County, Ohio; Wright State University: Dayton, OH, USA, 2013. [Google Scholar]
- Hilbe, J.M. Modeling Count Data. In International Encyclopedia of Statistical Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 836–839. [Google Scholar]
- Fisher, R.A. Statistical Methods for Research Workers, 5th ed.; Oliver and Boyd: Edinburgh, UK; London, UK, 1934. [Google Scholar]
- Salmon, M.; Schumacher, D.; Höhle, M. Monitoring count time series in R: Aberration detection in public health surveillance. J. Stat. Softw. 2016, 70, 1–35. [Google Scholar] [CrossRef]
- Fricker, R., Jr.; Hegler, B.; Dunfee, D. Comparing syndromic surveillance detection methods: EARS’ versus a CUSUM-based methodology. Stat. Med. 2008, 27, 3407–3429. [Google Scholar] [CrossRef] [PubMed]
- Bédubourg, G.; Le Strat, Y. Evaluation and comparison of statistical methods for early temporal detection of outbreaks: A simulation-based study. PLoS ONE 2017, 12, e0181227. [Google Scholar] [CrossRef]
- Hutwagner, L.; Browne, T.; Seeman, G.; Fleischauer, A. Comparing aberration detection methods with simulated data. Emerg. Infect. Dis. 2005, 11, 314–316. [Google Scholar] [CrossRef] [PubMed]
- Riebler, A. Empirischer Vergleich von Statistischen Methoden zur Ausbruchserkennung bei Surveillance Daten. Bachelor’s Thesis, Department of Statistics, University of Munich, Munich, Germany, 2004. [Google Scholar]
- Fawcett, T.; Provost, F. Activity monitoring: Noticing interesting changes in behavior. In Proceedings of the 5th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 15–18 August 1999; pp. 53–62. [Google Scholar]
- Gonzales, C.; Torti, L.; Wuillemin, P.H. aGrUM: A Graphical Universal Model framework. In Proceedings of the 30th International Conference on Industrial Engineering, Other Applications of Applied Intelligent Systems, Arras, France, 27–30 June 2017; pp. 171–177. [Google Scholar]
- Raschka, S. MLxtend: Providing machine learning and data science utilities and extensions to Python’s scientific computing stack. J. Open Source Softw. 2018, 3, 638. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Fernandes, S.; Fanaee, T.H.; Gama, J. The Initialization and Parameter Setting Problem in Tensor Decomposition-Based Link Prediction. In Proceedings of the 2017 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Tokyo, Japan, 19–21 October 2017; pp. 99–108. [Google Scholar] [CrossRef]
- Gräff, I.; Goldschmidt, B.; Glien, P.; Bogdanow, M.; Fimmers, R.; Hoeft, A.; Kim, S.C.; Grigutsch, D. The German version of the Manchester Triage System and its quality criteria–first assessment of validity and reliability. PLoS ONE 2014, 9, e88995. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).