Enhancing Immunotherapy Response Prediction in Metastatic Lung Adenocarcinoma: Leveraging Shallow and Deep Learning with CT-Based Radiomics across Single and Multiple Tumor Sites
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design
2.2. Data Collection
2.2.1. Clinical Data
2.2.2. Pathological and Molecular Data
2.3. Radiomics Workflow (Figure 2)
2.3.1. CT Scan Post-Processing

2.3.2. Radiomics Features Extraction
2.3.3. Radiomics Features Filtering and Transformation
2.3.4. Summary Statistics Based on Radiomics Features
2.3.5. Quantification of Intra-Patient Inter-Tumoral Lesion Heterogeneity Using RFs
2.4. Statistical Analysis
2.4.1. Descriptive Statistics
2.4.2. Univariable Survival Analysis
2.4.3. Multivariable Survival Modeling
- -
- Stepwise Cox regression (SCR). This popular semi-parametric algorithm was used to benchmark more complex models. It assumes that the HRs are constant over time and the risks of experiencing an event are proportional over time for each level of the predictor variables (with a certain weighting) [16]. Herein, a stepwise backward process was added, based on the minimization of the Akaike information criterion, in order to select the final variables included in the model [32].
- -
- LASSO Cox regression. This variation of the Cox regression includes a penalty term (i.e., the λ hyperparameter) to perform variable selection and regularization, which forces some coefficients to shrink towards zero and leads to a more parsimonious model [17].
- -
- RSF. In this extension of random forests, multiple decision trees are created from a random bootstrapped subset of the training data and a random subset of predictors. At each split node of each tree, the algorithm selects the best split among the randomly selected predictors considering the time-to-event information (herein, according to log-rank score). After training, the predicted survival function for each patient is obtained by averaging the survival functions predicted by all trees in the forest [18]. The hyperparameters investigated in this work were: the number of variables to possibly split at each node (mtry) and the minimum size of terminal node (nodesize). The number of trees was set to 1000 and the splitting criterion to “log-rank”.
- -
- GBM. In this extension of gradient boosting machines, the model is built by combining multiple decisions trees sequentially and iteratively (instead of independently, as in RSF), with each tree attempting to correct the errors made by the previous tree. A Cox’s partial likelihood loss function is used to measure the difference between the predicted and observed survival times and to optimize the model at each iteration (i.e., to decrease the prediction error). Moreover, a regularization is applied to limit the complexity of individual trees. Finally, after training, the predicted survival function for each patient is also obtained by combining the predictions from all trees in the ensemble. The hyperparameters investigated comprised the interaction depth (i.e., the highest level of variable interactions allowed), the learning rate, and the minimum member of observations in the terminal nodes of the trees. The number of trees was set to 1000 [19,20].
- -
- Deepsurv. This recent deep-learning algorithm utilizes a multi-layer feed-forward neural network architecture to predict the hazard function from the input variables. Theoretically, it can learn complex and non-linear relationships between highly correlated covariates and survival times thanks to the optimization of a negative log partial likelihood Cox proportional hazards-based loss function and a gradient descent-based algorithm [21]. The hyperparameters investigated comprised the activation function, the optimizer, the number of hidden layers, and the number of nodes per layer. The number of epochs was set to 512 with early stopping to limit unneeded training, the batch size to 32 with a batch normalization, the momentum to 0.85, the learning rate to 0.01 with a learning rate decay of 0.001, the regularization to 15, and the drop out to 0.1, similar to the hyperparameters found in clinical datasets [21].
2.4.4. Visualization and Understanding
3. Results
3.1. Study Population (Table 1)
| Characteristics | Patients (N = 140, with 663 RTLs) |
|---|---|
| Sex | |
| Women | 51/140 (36.4) |
| Men | 89/140 (63.6) |
| Age (years) | |
| Mean ± SD | 64.26 ± 8.839 |
| Median [Q1–Q3] (range) | 65.2 [59.1–70.225] (42.5–87.9) |
| WHO-PS | |
| PS = 0 | 38/140 (27.1) |
| PS = 1 | 77/140 (55) |
| PS = 2 | 25/140 (17.9) |
| Tobacco addiction | |
| Never smoker | 6/140 (4.3) |
| Active smoker | 67/140 (47.9) |
| Former smoker | 67/140 (47.9) |
| Initial staging | |
| IIIB-IVA | 36/140 (25.7) |
| IVB | 104/140 (74.3) |
| PDL1 | |
| 0% | 43/140 (30.7) |
| 1–49% | 35/140 (25) |
| 50–100% | 62/140 (44.3) |
| No. of altered genes on routine screening | |
| 0 | 29/140 (20.7) |
| 1 | 73/140 (52.1) |
| ≥2 | 38/140 (27.1) |
| TP53 alteration | |
| Yes | 55/140 (39.3) |
| No or non-contributive | 85/140 (60.7) |
| KRAS alteration | |
| Yes | 67/140 (47.9) |
| No or non-contributive | 73/140 (52.1) |
| No. of distinct metastatic sites | |
| 1 | 35/140 (25) |
| 2 | 36/140 (25.7) |
| 3 | 29/140 (20.7) |
| ≥4 | 40/140 (28.6) |
| Bone metastasis | |
| No | 69/140 (49.3) |
| Yes | 71/140 (50.7) |
| Brain metastasis | |
| No | 108/140 (77.1) |
| Yes | 32/140 (22.9) |
| Liver metastasis | |
| No | 112/140 (80) |
| Yes | 28/140 (20) |
| No. of RTLs | |
| Mean ± SD | 4.7 ± 2.7 |
| Median [Q1–Q3] (range) | 4 [3–6] (2–15) |
| Size of RTLs (mm) | |
| Mean ± SD | 30 ± 18 |
| Median [Q1–Q3] (range) | 23 [18–35] (10–144) |
| Locations of RTLs | |
| Abdominal carcinosis | 33/663 (5) |
| Abdominal viscera | 118/663 (17.8) |
| Bone | 31/663 (4.7) |
| Brain | 19/663 (2.9) |
| Lung | 141/663 (21.3) |
| Lymph node | 294/663 (44.3) |
| Pleura and pericardium | 10/663 (1.5) |
| Soft tissue | 17/663 (2.6) |
| First-line treatment | |
| CPI + Chemotherapy | 110/140 (78.6) |
| CPI alone | 30/140 (21.4) |
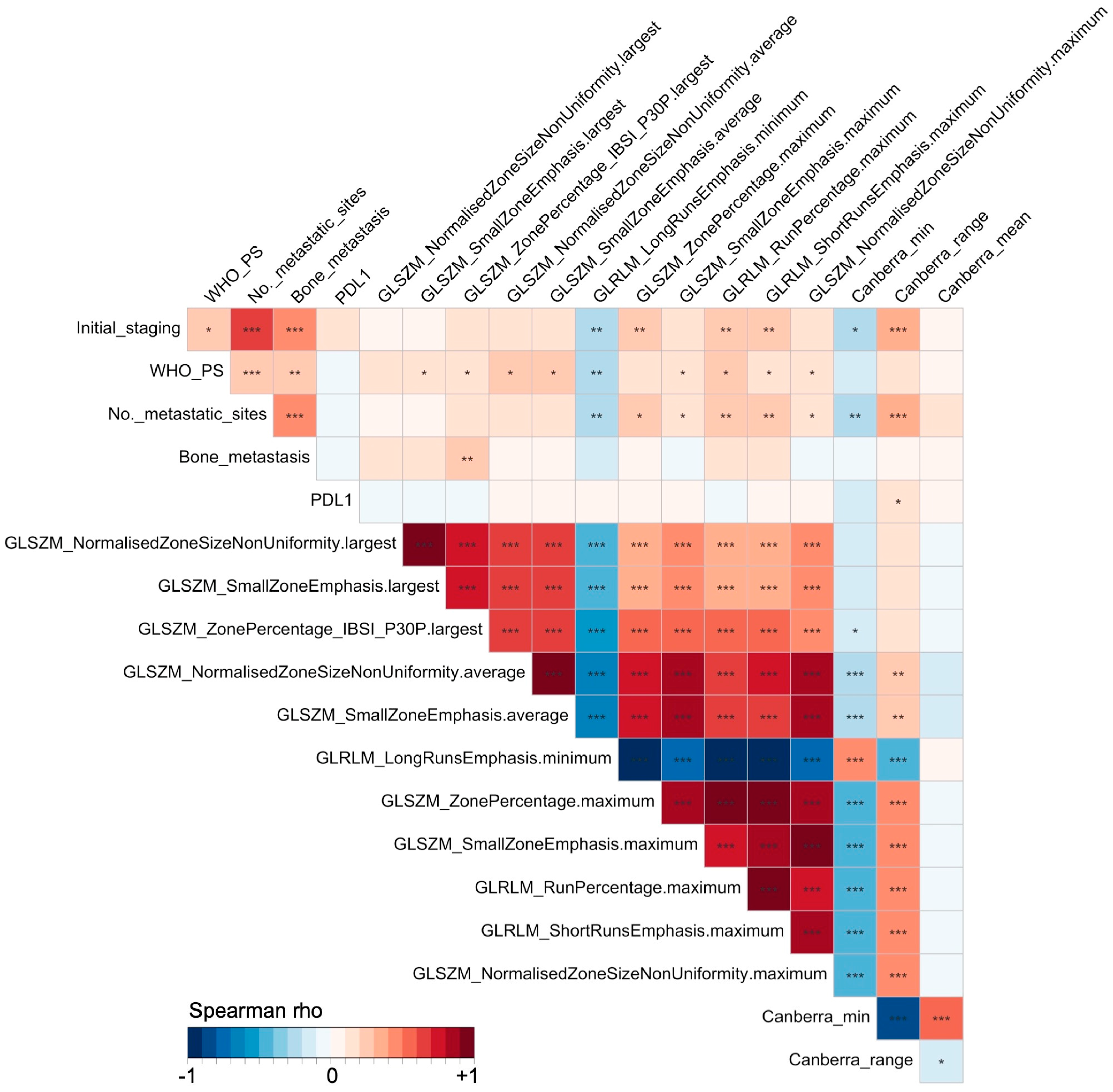
3.2. Univariable Assessment
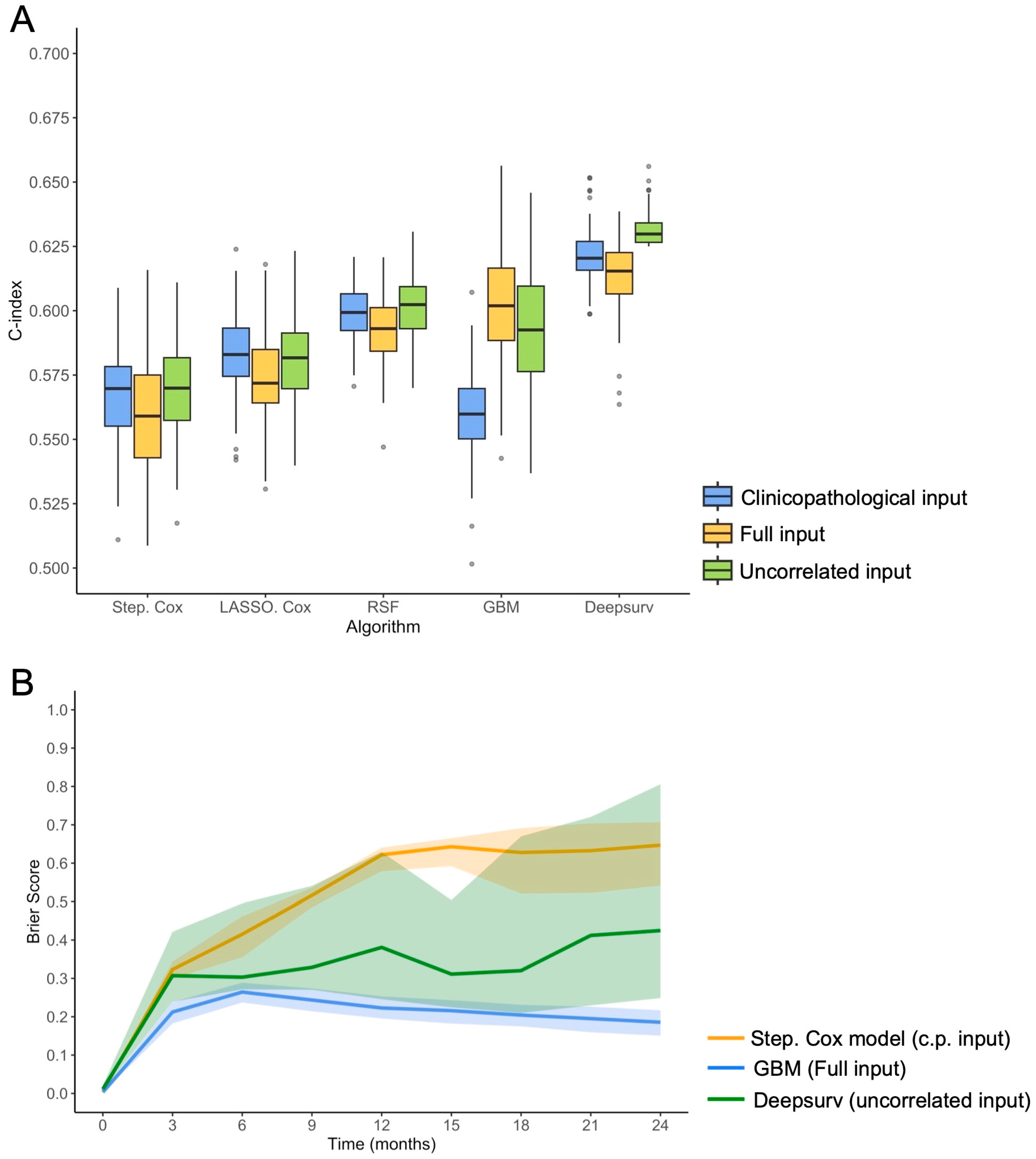
3.3. Performances of Survival Models in 100-Times Repeated 5-Fold Cross-Validation
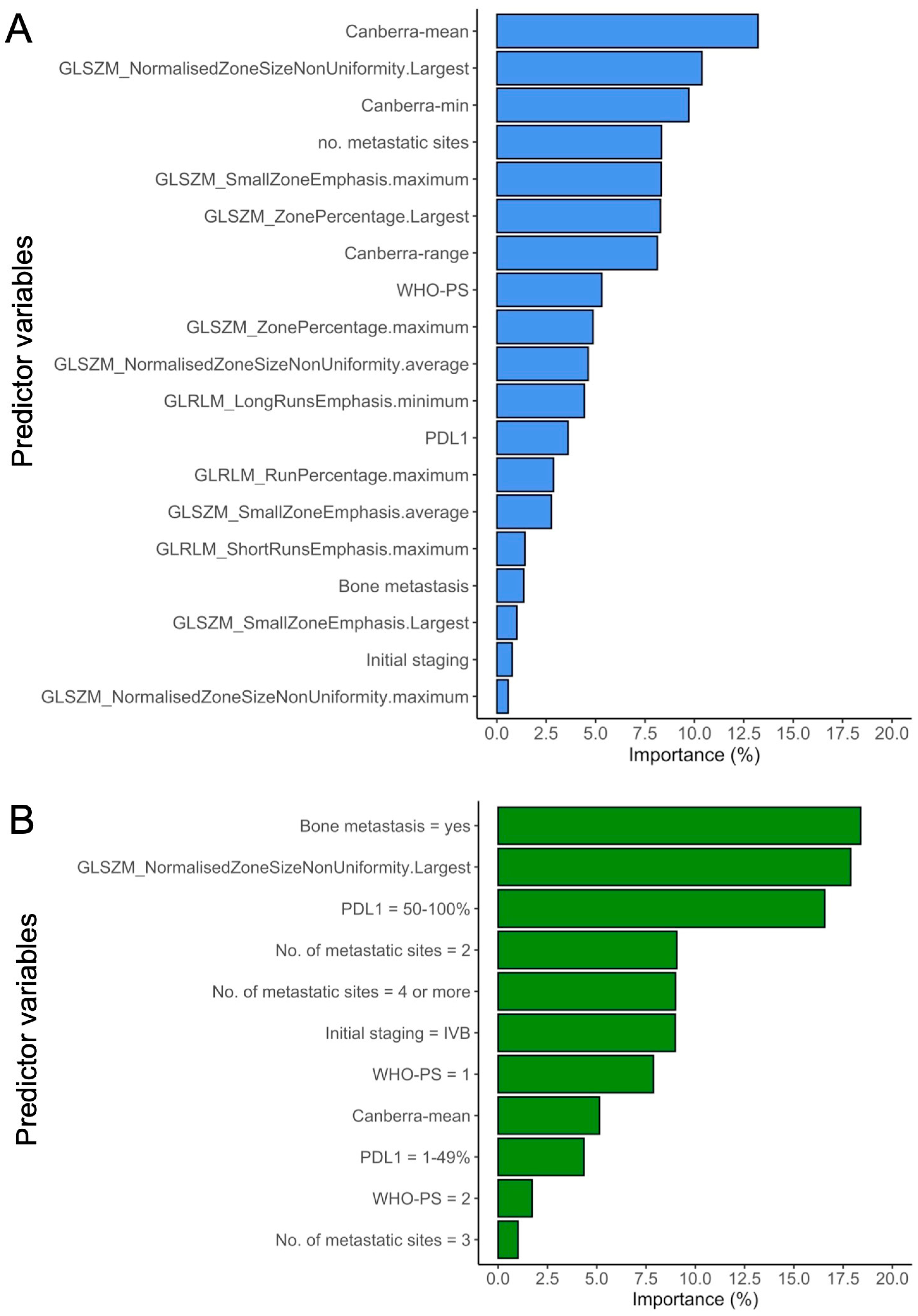
3.4. Understanding the Best-Performing Models
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global Cancer Statistics 2020: GLOBOCAN Estimates of Incidence and Mortality Worldwide for 36 Cancers in 185 Countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Vaccarella, S.; Morgan, E.; Li, M.; Etxeberria, J.; Chokunonga, E.; Manraj, S.S.; Kamate, B.; Omonisi, A.; Bray, F. Global Variations in Lung Cancer Incidence by Histological Subtype in 2020: A Population-Based Study. Lancet Oncol. 2023, 24, 1206–1218. [Google Scholar] [CrossRef] [PubMed]
- Planchard, D.; Popat, S.; Kerr, K.; Novello, S.; Smit, E.F.; Faivre-Finn, C.; Mok, T.S.; Reck, M.; Van Schil, P.E.; Hellmann, M.D.; et al. Metastatic Non-Small Cell Lung Cancer: ESMO Clinical Practice Guidelines for Diagnosis, Treatment and Follow-Up. Ann. Oncol. 2018, 29, iv192–iv237. [Google Scholar] [CrossRef] [PubMed]
- Garon, E.B.; Hellmann, M.D.; Rizvi, N.A.; Carcereny, E.; Leighl, N.B.; Ahn, M.-J.; Eder, J.P.; Balmanoukian, A.S.; Aggarwal, C.; Horn, L.; et al. Five-Year Overall Survival for Patients With Advanced Non–Small-Cell Lung Cancer Treated With Pembrolizumab: Results From the Phase I KEYNOTE-001 Study. J. Clin. Oncol. 2019, 37, 2518–2527. [Google Scholar] [CrossRef]
- Anagnostou, V.; Niknafs, N.; Marrone, K.; Bruhm, D.C.; White, J.R.; Naidoo, J.; Hummelink, K.; Monkhorst, K.; Lalezari, F.; Lanis, M.; et al. Multimodal Genomic Features Predict Outcome of Immune Checkpoint Blockade in Non-Small-Cell Lung Cancer. Nat. Cancer 2020, 1, 99–111. [Google Scholar] [CrossRef] [PubMed]
- van de Haar, J.; Mankor, J.M.; Hummelink, K.; Monkhorst, K.; Smit, E.F.; Wessels, L.F.A.; Cuppen, E.; Aerts, J.G.J.V.; Voest, E.E. Combining Genomic Biomarkers to Guide Immunotherapy in Non–Small Cell Lung Cancer. Clin. Cancer Res. 2024, 30, 1307–1318. [Google Scholar] [CrossRef] [PubMed]
- Vanhersecke, L.; Brunet, M.; Guégan, J.-P.; Rey, C.; Bougouin, A.; Cousin, S.; Moulec, S.L.; Besse, B.; Loriot, Y.; Larroquette, M.; et al. Mature Tertiary Lymphoid Structures Predict Immune Checkpoint Inhibitor Efficacy in Solid Tumors Independently of PD-L1 Expression. Nat. Cancer 2021, 2, 794–802. [Google Scholar] [CrossRef] [PubMed]
- Gillies, R.J.; Kinahan, P.E.; Hricak, H. Radiomics: Images Are More than Pictures, They Are Data. Radiology 2016, 278, 563–577. [Google Scholar] [CrossRef] [PubMed]
- Lambin, P.; Leijenaar, R.T.H.; Deist, T.M.; Peerlings, J.; de Jong, E.E.C.; van Timmeren, J.; Sanduleanu, S.; Larue, R.T.H.M.; Even, A.J.G.; Jochems, A.; et al. Radiomics: The Bridge between Medical Imaging and Personalized Medicine. Nat. Rev. Clin. Oncol. 2017, 14, 749–762. [Google Scholar] [CrossRef]
- Limkin, E.J.; Sun, R.; Dercle, L.; Zacharaki, E.I.; Robert, C.; Reuzé, S.; Schernberg, A.; Paragios, N.; Deutsch, E.; Ferté, C. Promises and Challenges for the Implementation of Computational Medical Imaging (Radiomics) in Oncology. Ann. Oncol. 2017, 28, 1191–1206. [Google Scholar] [CrossRef]
- Sun, R.; Limkin, E.J.; Vakalopoulou, M.; Dercle, L.; Champiat, S.; Han, S.R.; Verlingue, L.; Brandao, D.; Lancia, A.; Ammari, S.; et al. A Radiomics Approach to Assess Tumour-Infiltrating CD8 Cells and Response to Anti-PD-1 or Anti-PD-L1 Immunotherapy: An Imaging Biomarker, Retrospective Multicohort Study. Lancet Oncol. 2018, 19, 1180–1191. [Google Scholar] [CrossRef] [PubMed]
- Khorrami, M.; Khunger, M.; Zagouras, A.; Patil, P.; Thawani, R.; Bera, K.; Rajiah, P.; Fu, P.; Velcheti, V.; Madabhushi, A. Combination of Peri- and Intratumoral Radiomic Features on Baseline CT Scans Predicts Response to Chemotherapy in Lung Adenocarcinoma. Radiol. Artif. Intell. 2019, 1, e180012. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Zhang, L.; Mo, X.; You, J.; Chen, L.; Fang, J.; Wang, F.; Jin, Z.; Zhang, B.; Zhang, S. Current Status and Quality of Radiomic Studies for Predicting Immunotherapy Response and Outcome in Patients with Non-Small Cell Lung Cancer: A Systematic Review and Meta-Analysis. Eur. J. Nucl. Med. Mol. Imaging 2021, 49, 345–360. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Zhan, W.; Liu, L.; Xie, D.; Yao, L.; Yao, H.; Liao, G.; Huang, L.; Zhou, Y.; You, P.; et al. Pretreatment Radiomic Biomarker for Immunotherapy Responder Prediction in Stage IB–IV NSCLC (LCDigital-IO Study): A Multicenter Retrospective Study. J. Immunother. Cancer 2023, 11, e007369. [Google Scholar] [CrossRef] [PubMed]
- Trebeschi, S.; Drago, S.G.; Birkbak, N.J.; Kurilova, I.; Cǎlin, A.M.; Delli Pizzi, A.; Lalezari, F.; Lambregts, D.M.J.; Rohaan, M.W.; Parmar, C.; et al. Predicting Response to Cancer Immunotherapy Using Noninvasive Radiomic Biomarkers. Ann. Oncol. 2019, 30, 998–1004. [Google Scholar] [CrossRef] [PubMed]
- Cox, D.R. Regression Models and Life-Tables. J. R. Stat. Soc. Ser. B (Methodol.) 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Simon, N.; Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Cox’s Proportional Hazards Model via Coordinate Descent. J. Stat. Softw. 2011, 39, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Ishwaran, H.; Kogalur, U.B.; Blackstone, E.H.; Lauer, M.S. Random Survival Forests. Ann. Appl. Stat. 2008, 2, 841–860. [Google Scholar] [CrossRef]
- Hothorn, T.; Lausen, B.; Benner, A.; Radespiel-Tröger, M. Bagging Survival Trees. Stat. Med. 2004, 23, 77–91. [Google Scholar] [CrossRef]
- Ridgeway, G. Generalized Boosted Models: A Guide to the Gbm Package. 2006. Available online: https://pbil.univ-lyon1.fr/CRAN/web/packages/gbm/vignettes/gbm.pdf (accessed on 2 February 2024).
- Katzman, J.L.; Shaham, U.; Cloninger, A.; Bates, J.; Jiang, T.; Kluger, Y. DeepSurv: Personalized Treatment Recommender System Using a Cox Proportional Hazards Deep Neural Network. BMC Med. Res. Methodol. 2018, 18, 24. [Google Scholar] [CrossRef]
- Wiegrebe, S.; Kopper, P.; Sonabend, R.; Bischl, B.; Bender, A. Deep Learning for Survival Analysis: A Review. Artif. Intell. Rev. 2023, 57, 65. [Google Scholar] [CrossRef]
- Eisenhauer, E.A.; Therasse, P.; Bogaerts, J.; Schwartz, L.H.; Sargent, D.; Ford, R.; Dancey, J.; Arbuck, S.; Gwyther, S.; Mooney, M.; et al. New Response Evaluation Criteria in Solid Tumours: Revised RECIST Guideline (Version 1.1). Eur. J. Cancer 2009, 45, 228–247. [Google Scholar] [CrossRef] [PubMed]
- Kerr, K.M.; Tsao, M.-S.; Nicholson, A.G.; Yatabe, Y.; Wistuba, I.I.; Hirsch, F.R.; IASLC Pathology Committee. Programmed Death-Ligand 1 Immunohistochemistry in Lung Cancer: In What State Is This Art? J. Thorac. Oncol. 2015, 10, 985–989. [Google Scholar] [CrossRef] [PubMed]
- Lantuejoul, S.; Adam, J.; Girard, N.; Duruisseaux, M.; Mansuet-Lupo, A.; Cazes, A.; Rouquette, I.; Gibault, L.; Garcia, S.; Antoine, M.; et al. PD-L1 testing in non-small cell lung carcinoma: Guidelines from the PATTERN group of thoracic pathologists. Ann. Pathol. 2018, 38, 110–125. [Google Scholar] [CrossRef] [PubMed]
- Gandhi, L.; Rodríguez-Abreu, D.; Gadgeel, S.; Esteban, E.; Felip, E.; De Angelis, F.; Domine, M.; Clingan, P.; Hochmair, M.J.; Powell, S.F.; et al. Pembrolizumab plus Chemotherapy in Metastatic Non–Small-Cell Lung Cancer. N. Engl. J. Med. 2018, 378, 2078–2092. [Google Scholar] [CrossRef] [PubMed]
- Socinski, M.A.; Jotte, R.M.; Cappuzzo, F.; Orlandi, F.; Stroyakovskiy, D.; Nogami, N.; Rodríguez-Abreu, D.; Moro-Sibilot, D.; Thomas, C.A.; Barlesi, F.; et al. Atezolizumab for First-Line Treatment of Metastatic Nonsquamous NSCLC. N. Engl. J. Med. 2018, 378, 2288–2301. [Google Scholar] [CrossRef] [PubMed]
- Sholl, L.; Cooper, W.; Kerr, K.; Tan, D.; Tsao, M.; Yang, J. IASLC Atlas of Molecular Testing for Targeted Therapy in Lung Cancer; International Association for the Study of Lung Cancer: Denver, CO, USA, 2023; ISBN 9798987829202. [Google Scholar]
- Nioche, C.; Orlhac, F.; Boughdad, S.; Reuzé, S.; Goya-Outi, J.; Robert, C.; Pellot-Barakat, C.; Soussan, M.; Frouin, F.; Buvat, I. LIFEx: A Freeware for Radiomic Feature Calculation in Multimodality Imaging to Accelerate Advances in the Characterization of Tumor Heterogeneity. Cancer Res. 2018, 78, 4786–4789. [Google Scholar] [CrossRef] [PubMed]
- Zwanenburg, A.; Leger, S.; Vallières, M.; Löck, S. The Image Biomarker Standardization Initiative: Standardized Quantitative Radiomics for High-Throughput Image-based Phenotyping. Radiology 2020, 295, 328–338. [Google Scholar] [CrossRef]
- Drost, H.-G. Philentropy: Information Theory and Distance Quantification with R. J. Open Source Softw. 2018, 3, 765. [Google Scholar] [CrossRef]
- Harrell, F.E. Cox Proportional Hazards Regression Model. In Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis; Harrell, F.E., Ed.; Springer: New York, NY, USA, 2001; pp. 465–507. ISBN 978-1-4757-3462-1. [Google Scholar]
- Brier, G.W. Verification of Forecasts Expressed in Terms of Probability. Mon. Weather. Rev. 1950, 78, 1. [Google Scholar] [CrossRef]
- Wei, P.; Lu, Z.; Song, J. Variable Importance Analysis: A Comprehensive Review. Reliab. Eng. Syst. Saf. 2015, 142, 399–432. [Google Scholar] [CrossRef]
- Garassino, M.C.; Gadgeel, S.; Esteban, E.; Felip, E.; Speranza, G.; Domine, M.; Hochmair, M.J.; Powell, S.; Cheng, S.Y.-S.; Bischoff, H.G.; et al. Patient-Reported Outcomes Following Pembrolizumab or Placebo plus Pemetrexed and Platinum in Patients with Previously Untreated, Metastatic, Non-Squamous Non-Small-Cell Lung Cancer (KEYNOTE-189): A Multicentre, Double-Blind, Randomised, Placebo-Controlled, Phase 3 Trial. Lancet Oncol. 2020, 21, 387–397. [Google Scholar] [CrossRef]
- Reck, M.; Rodríguez-Abreu, D.; Robinson, A.G.; Hui, R.; Csőszi, T.; Fülöp, A.; Gottfried, M.; Peled, N.; Tafreshi, A.; Cuffe, S.; et al. Updated Analysis of KEYNOTE-024: Pembrolizumab Versus Platinum-Based Chemotherapy for Advanced Non–Small-Cell Lung Cancer With PD-L1 Tumor Proportion Score of 50% or Greater. J. Clin. Oncol. 2019, 37, 537–546. [Google Scholar] [CrossRef]
- Shukuya, T.; Carbone, D.P. Predictive Markers for the Efficacy of Anti–PD-1/PD-L1 Antibodies in Lung Cancer. J. Thorac. Oncol. 2016, 11, 976–988. [Google Scholar] [CrossRef] [PubMed]
- Kang, C.Y.; Duarte, S.E.; Kim, H.S.; Kim, E.; Park, J.; Lee, A.D.; Kim, Y.; Kim, L.; Cho, S.; Oh, Y.; et al. Artificial Intelligence-Based Radiomics in the Era of Immuno-Oncology. Oncologist 2022, 27, e471–e483. [Google Scholar] [CrossRef]
- Reck, M.; Rodríguez-Abreu, D.; Robinson, A.G.; Hui, R.; Csőszi, T.; Fülöp, A.; Gottfried, M.; Peled, N.; Tafreshi, A.; Cuffe, S.; et al. Pembrolizumab versus Chemotherapy for PD-L1–Positive Non–Small-Cell Lung Cancer. N. Engl. J. Med. 2016, 375, 1823–1833. [Google Scholar] [CrossRef]
- Hiraga, T. Immunotherapy Targeting PD-1/PD-L1: A Potential Approach for the Treatment of Cancer Bone Metastases (Review). Int. J. Oncol. 2024, 64, 35. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Wang, P.; Chen, Y.; Dai, W. 18F-FDG PET/CT for Evaluation of Metastases in Nonsmall Cell Lung Cancer on the Efficacy of Immunotherapy. Nucl. Med. Commun. 2023, 44, 900–909. [Google Scholar] [CrossRef] [PubMed]
- De Giglio, A.; Mezquita, L.; Auclin, E.; Blanc-Durand, F.; Riudavets, M.; Caramella, C.; Martinez, G.; Benitez, J.C.; Martín-Romano, P.; El-Amarti, L.; et al. Impact of Intercurrent Introduction of Steroids on Clinical Outcomes in Advanced Non-Small-Cell Lung Cancer (NSCLC) Patients under Immune-Checkpoint Inhibitors (ICI). Cancers 2020, 12, 2827. [Google Scholar] [CrossRef]
- Mok, T.S.K.; Wu, Y.-L.; Kudaba, I.; Kowalski, D.M.; Cho, B.C.; Turna, H.Z.; Castro, G.; Srimuninnimit, V.; Laktionov, K.K.; Bondarenko, I.; et al. Pembrolizumab versus Chemotherapy for Previously Untreated, PD-L1-Expressing, Locally Advanced or Metastatic Non-Small-Cell Lung Cancer (KEYNOTE-042): A Randomised, Open-Label, Controlled, Phase 3 Trial. Lancet 2019, 393, 1819–1830. [Google Scholar] [CrossRef]
- Leighl, N.B.; Hellmann, M.D.; Hui, R.; Carcereny, E.; Felip, E.; Ahn, M.-J.; Eder, J.P.; Balmanoukian, A.S.; Aggarwal, C.; Horn, L.; et al. Pembrolizumab in Patients with Advanced Non-Small-Cell Lung Cancer (KEYNOTE-001): 3-Year Results from an Open-Label, Phase 1 Study. Lancet Respir. Med. 2019, 7, 347–357. [Google Scholar] [CrossRef] [PubMed]
- Vargas, H.A.; Veeraraghavan, H.; Micco, M.; Nougaret, S.; Lakhman, Y.; Meier, A.A.; Sosa, R.; Soslow, R.A.; Levine, D.A.; Weigelt, B.; et al. A Novel Representation of Inter-Site Tumour Heterogeneity from Pre-Treatment Computed Tomography Textures Classifies Ovarian Cancers by Clinical Outcome. Eur. Radiol. 2017, 27, 3991–4001. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Kluge, K.; Papp, L.; Grahovac, M.; Yang, S.; Jiang, C.; Krajnc, D.; Spielvogel, C.P.; Ecsedi, B.; Haug, A.; et al. Multi-Lesion Radiomics of PET/CT for Non-Invasive Survival Stratification and Histologic Tumor Risk Profiling in Patients with Lung Adenocarcinoma. Eur. Radiol. 2022, 32, 7056–7067. [Google Scholar] [CrossRef] [PubMed]
- Mazieres, J.; Drilon, A.; Lusque, A.; Mhanna, L.; Cortot, A.B.; Mezquita, L.; Thai, A.A.; Mascaux, C.; Couraud, S.; Veillon, R.; et al. Immune Checkpoint Inhibitors for Patients with Advanced Lung Cancer and Oncogenic Driver Alterations: Results from the IMMUNOTARGET Registry. Ann. Oncol. 2019, 30, 1321–1328. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.-Y.; Zhang, J.-T.; Liu, S.-Y.; Su, J.; Zhang, C.; Xie, Z.; Zhou, Q.; Tu, H.-Y.; Xu, C.-R.; Yan, L.-X.; et al. EGFR Mutation Correlates with Uninflamed Phenotype and Weak Immunogenicity, Causing Impaired Response to PD-1 Blockade in Non-Small Cell Lung Cancer. Oncoimmunology 2017, 6, e1356145. [Google Scholar] [CrossRef]
- Soo, R.A.; Lim, S.M.; Syn, N.L.; Teng, R.; Soong, R.; Mok, T.S.K.; Cho, B.C. Immune Checkpoint Inhibitors in Epidermal Growth Factor Receptor Mutant Non-Small Cell Lung Cancer: Current Controversies and Future Directions. Lung Cancer 2018, 115, 12–20. [Google Scholar] [CrossRef] [PubMed]
- Astley, J.R.; Reilly, J.M.; Robinson, S.; Wild, J.M.; Hatton, M.Q.; Tahir, B.A. Explainable Deep Learning-Based Survival Prediction for Non-Small Cell Lung Cancer Patients Undergoing Radical Radiotherapy. Radiother. Oncol. 2024, 193, 110084. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Liu, C.; Wu, R.; Zhong, J.; Li, A.; Ma, L.; Zhong, J.; Yin, S.; Zhou, C.; Ge, Y.; et al. Development and Validation of a DeepSurv Nomogram to Predict Survival Outcomes and Guide Personalized Adjuvant Chemotherapy in Non-Small Cell Lung Cancer. Front. Oncol. 2022, 12, 895014. [Google Scholar] [CrossRef]
- Aggarwal, C.; Thompson, J.C.; Chien, A.L.; Quinn, K.J.; Hwang, W.-T.; Black, T.A.; Yee, S.S.; Christensen, T.E.; LaRiviere, M.J.; Silva, B.A.; et al. Baseline Plasma Tumor Mutation Burden Predicts Response to Pembrolizumab-Based Therapy in Patients with Metastatic Non-Small Cell Lung Cancer. Clin. Cancer Res. 2020, 26, 2354–2361. [Google Scholar] [CrossRef]


| Characteristics | No. at Risk | No. of Events | PFS Probability at 2 Years (95%CI) | Log-Rank p-Value | Univariable HR (95%CI) | p-Value |
|---|---|---|---|---|---|---|
| Age at diagnosis | ||||||
| <70 years | 103 | 85 | 31.07 (23.3–41.42) | 0.6447 | reference | - |
| ≥70 years | 37 | 31 | 29.73 (18.12–48.79) | 1.11 (0.73–1.67) | 0.6327 | |
| Sex | ||||||
| Women | 51 | 45 | 25.49 (15.94–40.75) | 0.4047 | reference | - |
| Men | 88 | 70 | 34.09 (25.5–45.58) | 0.86 (0.59–1.25) | 0.4262 | |
| WHO-PS | ||||||
| PS = 0 | 38 | 33 | 28.95 (17.59–47.64) | 0.0003 *** | reference | - |
| PS = 1 | 77 | 59 | 38.96 (29.46–51.53) | 0.92 (0.6–1.41) | 0.6921 | |
| PS = 2 | 25 | 24 | 8 (2.12–30.23) | 2.37 (1.39–4.05) | 0.0015 ** | |
| Tobacco addiction | ||||||
| Never smoker | 6 | 6 | 0 (NA–NA) | 0.3477 | reference | - |
| Active smoker | 67 | 52 | 35.82 (26–49.36) | 0.77 (0.33–1.8) | 0.5464 | |
| Former smoker | 67 | 58 | 28.36 (19.38–41.49) | 1.01 (0.43–2.35) | 0.9806 | |
| Initial staging | ||||||
| IIIB-IVA | 36 | 28 | 44.44 (30.85–64.04) | 0.0829 | reference | - |
| IVB | 104 | 88 | 25.96 (18.77–35.92) | 1.46 (0.95–2.23) | 0.0844 | |
| PDL1 | ||||||
| 0% | 43 | 38 | 27.91 (17.26–45.12) | 0.0779 | reference | - |
| 1–49% | 35 | 32 | 22.86 (12.44–42.01) | 0.81 (0.6–1.1) | 0.1826 | |
| 50–100% | 62 | 46 | 37.1 (26.83–51.3) | 0.74 (0.53–1.04) | 0.0825 | |
| No. of altered genes on routine screening | ||||||
| 0 | 29 | 25 | 24.14 (12.66–46.02) | 0.7005 | reference | - |
| 1 | 73 | 59 | 31.51 (22.47–44.19) | 0.87 (0.54–1.38) | 0.5484 | |
| ≥2 | 38 | 32 | 34.21 (22.01–53.17) | 0.8 (0.47–1.35) | 0.4032 | |
| TP53 alteration | ||||||
| No or non-contributive | 85 | 70 | 29.41 (21.16–40.88) | 0.8992 | reference | - |
| Yes | 55 | 46 | 32.73 (22.41–47.8) | 0.97 (0.67–1.41) | 0.8890 | |
| KRAS alteration | ||||||
| No or non-contributive | 73 | 62 | 26.03 (17.68–38.32) | 0.2002 | reference | - |
| Yes | 67 | 54 | 35.82 (26–49.36) | 0.79 (0.55–1.14) | 0.2003 | |
| No. of distinct metastatic sites | ||||||
| 1 | 35 | 27 | 37.14 (24.14–57.15) | 0.0587 | reference | - |
| 2 | 36 | 28 | 41.67 (28.31–61.33) | 0.91 (0.54–1.55) | 0.7304 | |
| 3 | 29 | 25 | 24.14 (12.66–46.02) | 1.41 (0.82–2.43) | 0.2183 | |
| ≥4 | 40 | 36 | 20 (10.76–37.17) | 1.66 (1.01–2.74) | 0.0462 * | |
| Bone metastasis | ||||||
| No | 69 | 53 | 37.68 (27.82–51.04) | 0.0427 * | reference | - |
| Yes | 71 | 63 | 23.94 (15.82–36.24) | 1.46 (1.01–2.11) | 0.0439 * | |
| Brain metastasis | ||||||
| No | 108 | 87 | 32.41 (24.68–42.55) | 0.1638 | reference | - |
| Yes | 32 | 29 | 25 (13.72–45.56) | 1.35 (0.88–2.06) | 0.1692 | |
| Liver metastasis | ||||||
| No | 112 | 92 | 33.04 (25.38–43) | 0.4336 | reference | - |
| Yes | 28 | 24 | 21.43 (10.54–43.55) | 1.2 (0.76–1.88) | 0.4351 | |
| First-line treatment | ||||||
| CPI + Chemotherapy | 110 | 93 | 30 (22.55–39.91) | 0.2766 | reference | - |
| CPI | 30 | 23 | 33.33 (20.1–55.29) | 0.78 (0.49–1.23) | 0.2812 |
| Type of Radiomics | Name of Radiomics-Based Feature (IBSI Reference Number) | HR (95%CI) | Univariable Cox p-Value |
|---|---|---|---|
| Largest | GLSZM_NormalisedZoneSizeNonUniformity (IBSI: VB3A) | 1.46 (1.11–1.94) | 0.0076 * |
| GLSZM_SmallZoneEmphasis(IBSI: 5QRC) | 1.44 (1.09–1.9) | 0.0092 * | |
| GLSZM_ZonePercentage (IBSI: P30P) | 1.25 (1–1.56) | 0.0495 * | |
| Average | GLSZM_NormalisedZoneSizeNonUniformity (IBSI: VB3A) | 1.25 (0.97–1.61) | 0.0887 |
| GLSZM_SmallZoneEmphasis (IBSI: 5QRC) | 1.25 (0.96–1.61) | 0.0921 | |
| Minimum | GLRLM_LongRunsEmphasis (IBSI: W4KF) | 0.65 (0.43–0.98) | 0.0417 * |
| GLSZM_ZonePercentage (IBSI: P30P) | 1.24 (1.01–1.51) | 0.0384 * | |
| Maximum | GLSZM_SmallZoneEmphasis (IBSI: 5QRC) | 1.21 (1.01–1.44) | 0.0403 * |
| GLRLM_RunPercentage (IBSI: 9ZK5) | 1.4 (1.01–1.93) | 0.0421 * | |
| GLRLM_ShortRunsEmphasis (IBSI: 22OV) | 1.38 (1.01–1.9) | 0.0437 * | |
| GLSZM_NormalisedZoneSizeNonUniformity (IBSI: VB3A) | 1.18 (1.01–1.39) | 0.0445 * | |
| IPITH | Canberra-min | 0.75 (0.63–0.88) | 0.0006 *** |
| Canberra-range | 1.30 (1.08–1.57) | 0.0049 ** | |
| Canberra-mean | 0.81 (0.64–1.03) | 0.0886 |
| Algorithms | Clinical Input | Full Input | Uncorrelated Input | |||
|---|---|---|---|---|---|---|
| rCV C-index | Hyperparameters | rCV C-index | Hyperparameters | rCV C-index | Hyperparameters | |
| Stepwise Cox Regression | 0.566 (0.525–0.601) | - | 0.560 (0.517–0.606) | - | 0.570 (0.538–0.602) | - |
| LASSO Cox Regression | 0.583 (0.549–0.613) | λ = 0.019 | 0.573 (0.535–0.613) | λ = 0.058 | 0.582 (0.554–0.616) | λ = 0.011 |
| Random Survival Forests | 0.599 (0.581–0.616) | mtry = 1, nodesize = 22 | 0.593 (0.567–0.618) | mtry = 1, nodesize = 20 | 0.602 (0.576–0.626) | mtry = 1, nodesize = 22 |
| Gradient Boosted Model | 0.560 (0.527–0.589) | shrinkage = 0.05, interaction depth = 2, MNOTN = 8 | 0.603 (0.557–0.646) | shrinkage = 0.01, interaction depth = 4, MNOTN = 11 | 0.594 (0.546–0.634) | shrinkage = 0.095, interaction depth = 1, MNOTN = 11 |
| Deepsurv | 0.622 (0.602–0.647) | no. layers = 3, no. nodes = 14, adam optimizer, ReLU activation | 0.613 (0.581–0.634) | no. layers = 2, no. nodes = 15, adam optimizer, SELU activation | 0.631 (0.625–0.647) | no. layers = 1, no. nodes = 15, adam optimizer, ReLU activation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masson-Grehaigne, C.; Lafon, M.; Palussière, J.; Leroy, L.; Bonhomme, B.; Jambon, E.; Italiano, A.; Cousin, S.; Crombé, A. Enhancing Immunotherapy Response Prediction in Metastatic Lung Adenocarcinoma: Leveraging Shallow and Deep Learning with CT-Based Radiomics across Single and Multiple Tumor Sites. Cancers 2024, 16, 2491. https://doi.org/10.3390/cancers16132491
Masson-Grehaigne C, Lafon M, Palussière J, Leroy L, Bonhomme B, Jambon E, Italiano A, Cousin S, Crombé A. Enhancing Immunotherapy Response Prediction in Metastatic Lung Adenocarcinoma: Leveraging Shallow and Deep Learning with CT-Based Radiomics across Single and Multiple Tumor Sites. Cancers. 2024; 16(13):2491. https://doi.org/10.3390/cancers16132491
Chicago/Turabian StyleMasson-Grehaigne, Cécile, Mathilde Lafon, Jean Palussière, Laura Leroy, Benjamin Bonhomme, Eva Jambon, Antoine Italiano, Sophie Cousin, and Amandine Crombé. 2024. "Enhancing Immunotherapy Response Prediction in Metastatic Lung Adenocarcinoma: Leveraging Shallow and Deep Learning with CT-Based Radiomics across Single and Multiple Tumor Sites" Cancers 16, no. 13: 2491. https://doi.org/10.3390/cancers16132491
APA StyleMasson-Grehaigne, C., Lafon, M., Palussière, J., Leroy, L., Bonhomme, B., Jambon, E., Italiano, A., Cousin, S., & Crombé, A. (2024). Enhancing Immunotherapy Response Prediction in Metastatic Lung Adenocarcinoma: Leveraging Shallow and Deep Learning with CT-Based Radiomics across Single and Multiple Tumor Sites. Cancers, 16(13), 2491. https://doi.org/10.3390/cancers16132491







