Toward Intraoperative Margin Assessment Using a Deep Learning-Based Approach for Automatic Tumor Segmentation in Breast Lumpectomy Ultrasound Images
Abstract
Simple Summary
Abstract
1. Introduction
- (1)
- Evaluation of the segmentation performance of eight individual pre-trained artificial neural network models on an external data set, applied to a new data set of US images acquired on BCS specimens with invasive carcinoma lesions (BCS-US data set).
- (2)
- Evaluation of the influence of an ensemble framework by combining multiple networks on the segmentation performance. Various methods for this ensemble approach were used, including different forms of voting, and weighted average.
- (3)
- Optimization of the best ensemble approach, in order to predict margin status with the highest accuracy.
2. Materials and Methods
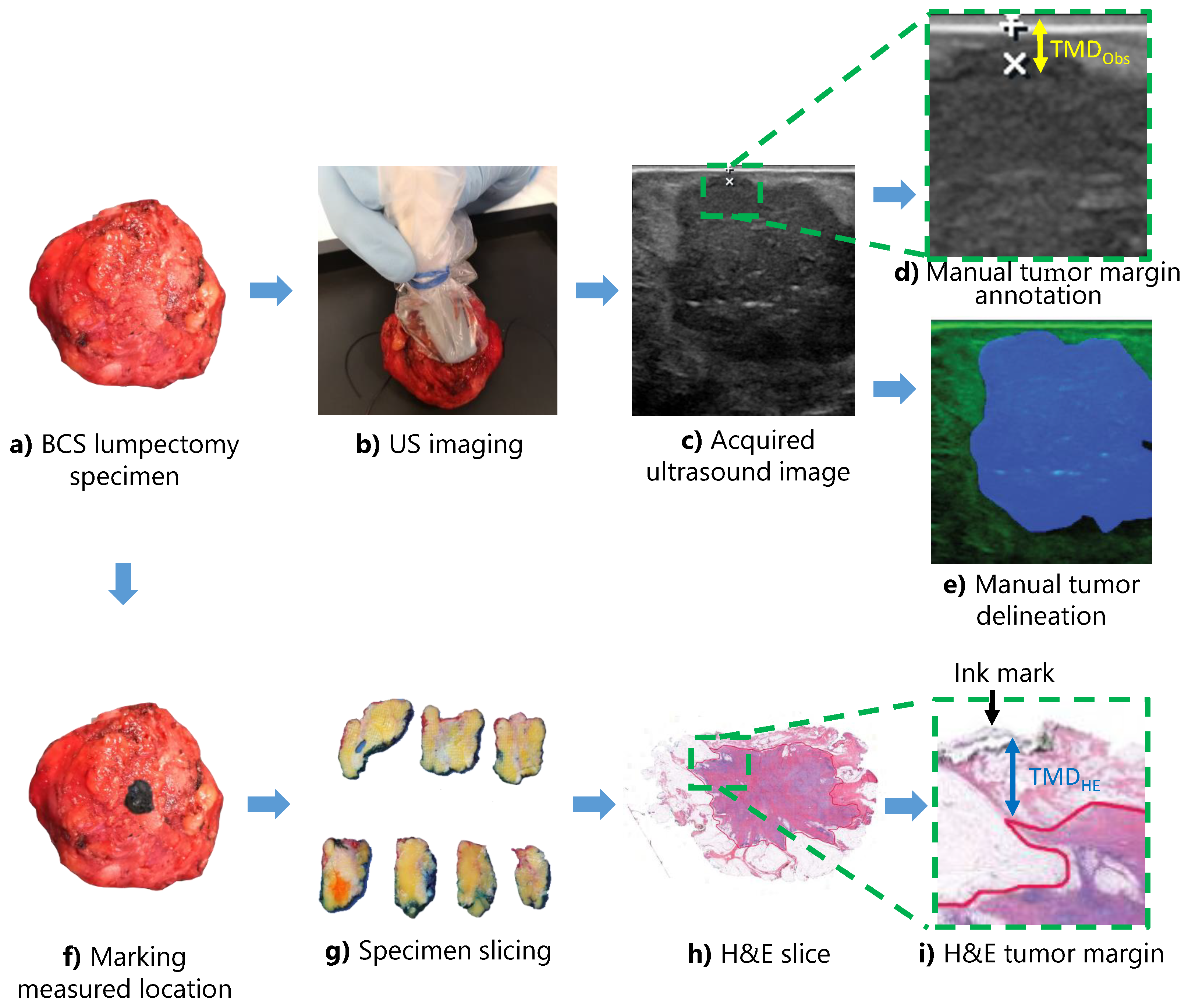
2.1. Data Acquisition
2.2. Data Labeling
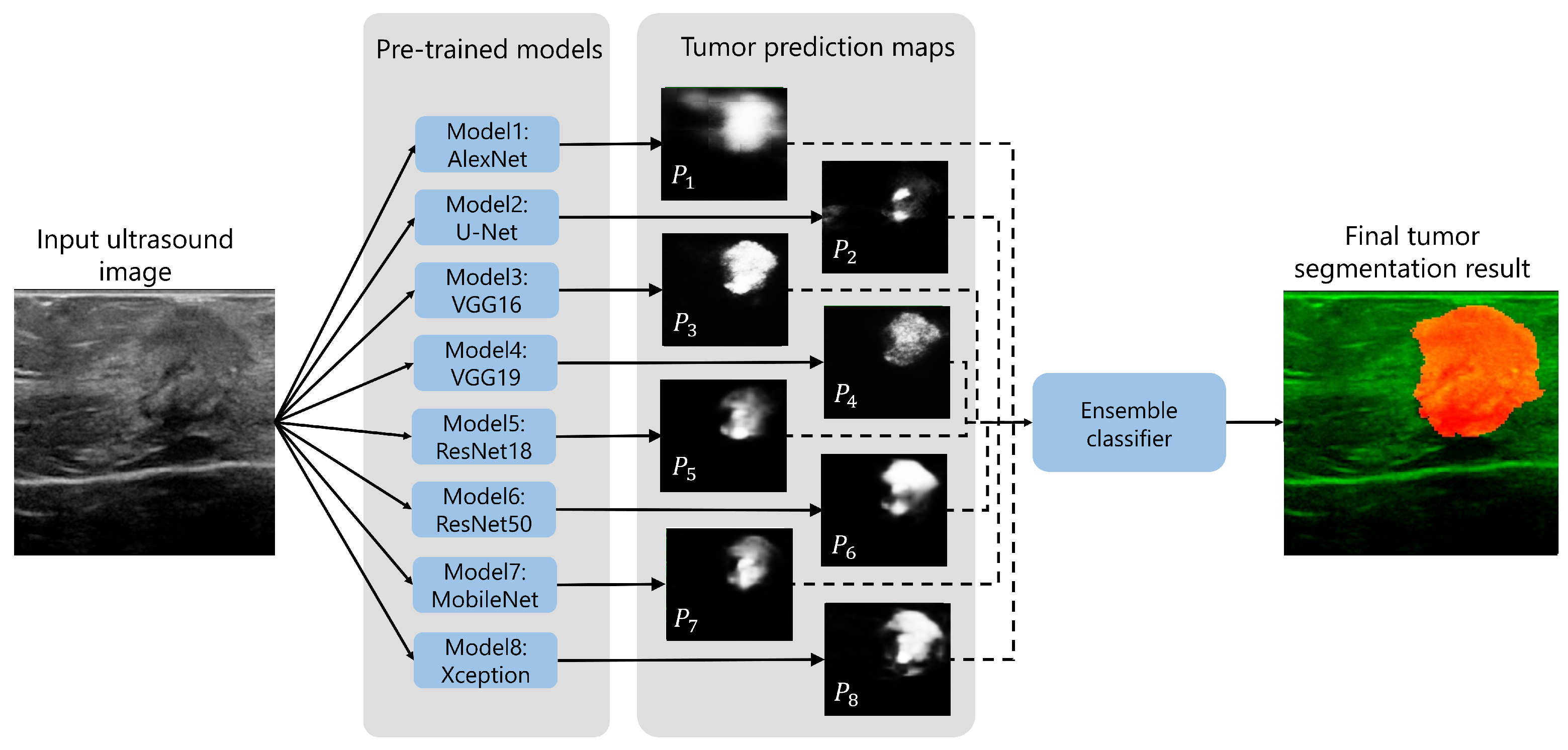
2.3. Tumor Segmentation Methodology
2.4. Ensemble Learning Framework
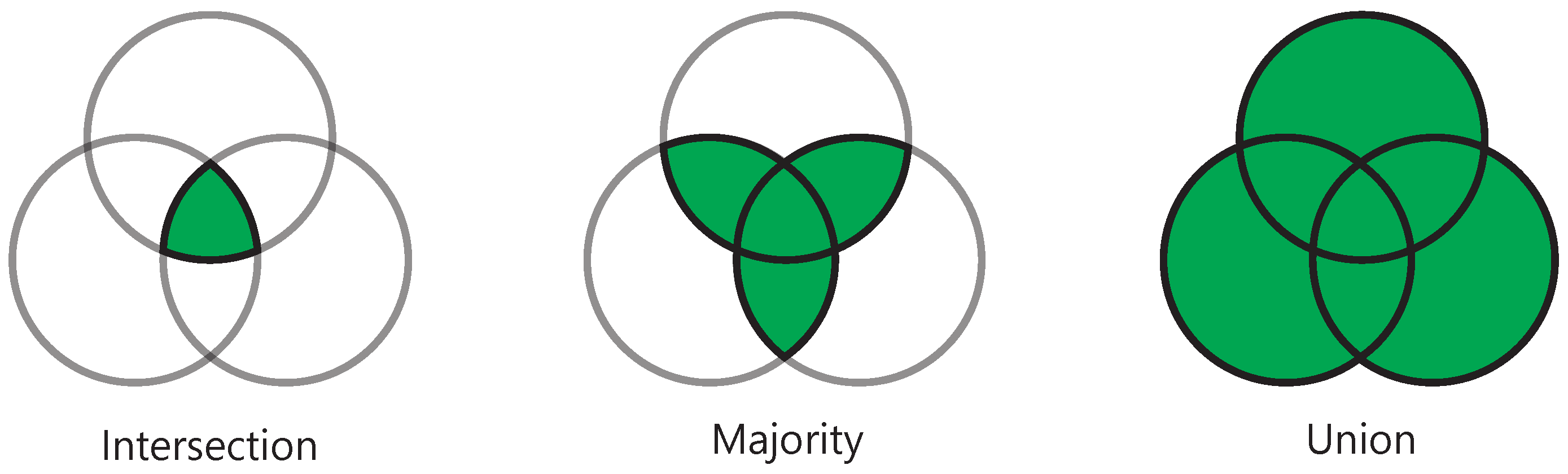
2.4.1. General Voting Method
2.4.2. Elective Voting Method
2.4.3. Weighted Average Method
2.5. Tumor Margin Distance Prediction
2.6. Performance Evaluation
2.6.1. Tumor Segmentation
2.6.2. Margin Assessment
3. Results
3.1. Tumor and Patient Characteristics
3.2. Tumor Segmentation
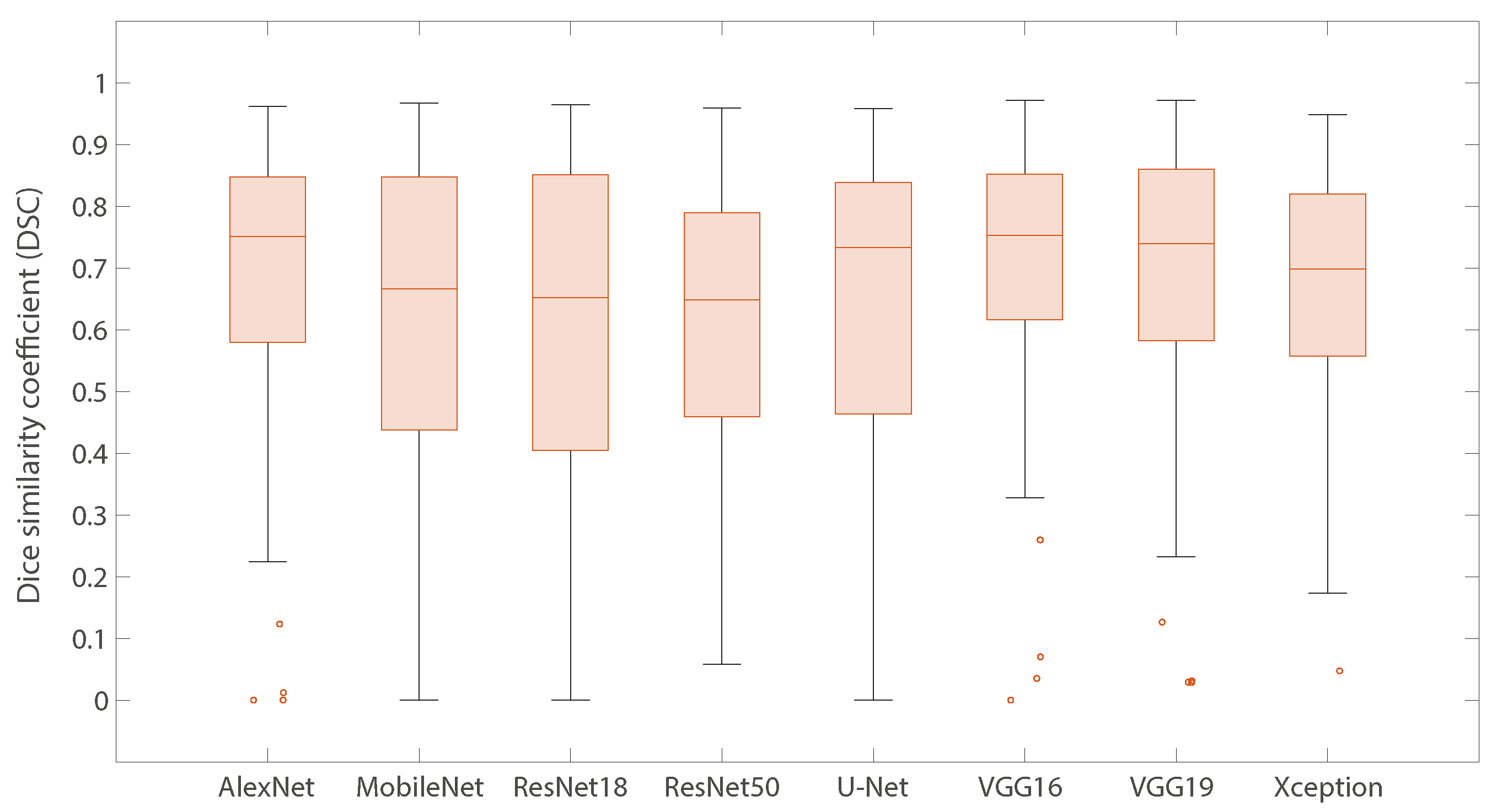
3.2.1. Individual Models
3.2.2. Ensemble Learning (Models Combinations)
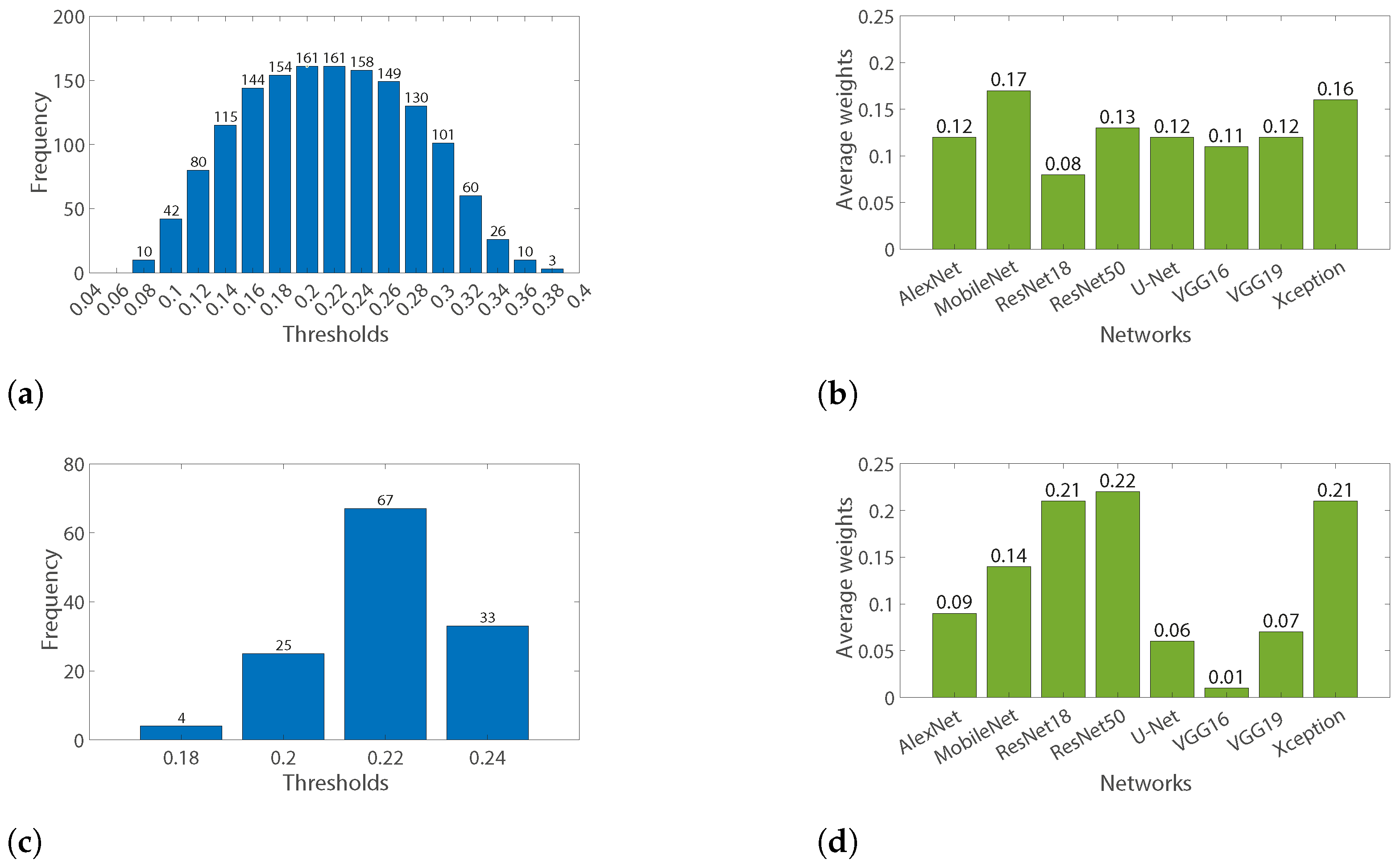
3.2.3. Weighting Average Parameters Optimization
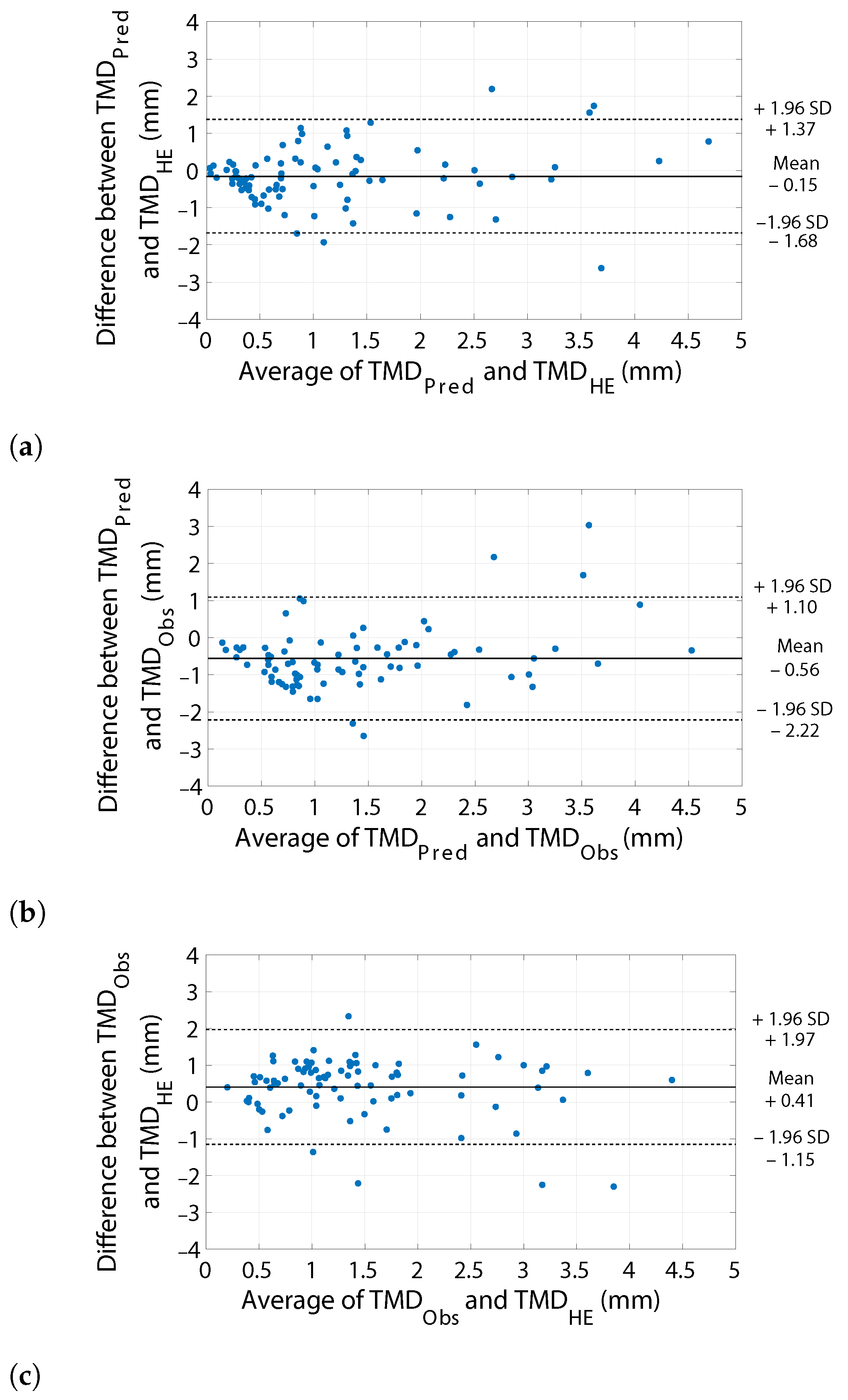
3.3. Margin Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- De la Cruz Ku, G.; Karamchandani, M.; Chambergo-Michilot, D.; Narvaez-Rojas, A.R.; Jonczyk, M.; Príncipe-Meneses, F.S.; Posawatz, D.; Nardello, S.; Chatterjee, A. Does breast-conserving surgery with radiotherapy have a better survival than mastectomy? A meta-analysis of more than 1,500,000 patients. Ann. Surg. Oncol. 2022, 29, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Fisher, B.; Anderson, S.; Bryant, J.; Margolese, R.G.; Deutsch, M.; Fisher, E.R.; Jeong, J.H.; Wolmark, N. Twenty-year follow-up of a randomized trial comparing total mastectomy, lumpectomy, and lumpectomy plus irradiation for the treatment of invasive breast cancer. N. Engl. J. Med. 2002, 347, 1233–1241. [Google Scholar] [CrossRef] [PubMed]
- Litière, S.; Werutsky, G.; Fentiman, I.S.; Rutgers, E.; Christiaens, M.R.; Van Limbergen, E.; Baaijens, M.H.; Bogaerts, J.; Bartelink, H. Breast conserving therapy versus mastectomy for stage I–II breast cancer: 20 year follow-up of the EORTC 10801 phase 3 randomised trial. Lancet Oncol. 2012, 13, 412–419. [Google Scholar] [CrossRef]
- Houssami, N.; Macaskill, P.; Luke Marinovich, M.; Morrow, M. The association of surgical margins and local recurrence in women with early-stage invasive breast cancer treated with breast-conserving therapy: A meta-analysis. Ann. Surg. Oncol. 2014, 21, 717–730. [Google Scholar] [CrossRef]
- Horst, K.C.; Smitt, M.C.; Goffinet, D.R.; Carlson, R.W. Predictors of local recurrence after breast-conservation therapy. Clin. Breast Cancer 2005, 5, 425–438. [Google Scholar] [CrossRef]
- De Koning, S.G.B.; Peeters, M.J.T.V.; Jóźwiak, K.; Bhairosing, P.A.; Ruers, T.J. Tumor resection margin definitions in breast-conserving surgery: Systematic review and meta-analysis of the current literature. Clin. Breast Cancer 2018, 18, e595–e600. [Google Scholar] [CrossRef]
- Nayyar, A.; Gallagher, K.K.; McGuire, K.P. Definition and management of positive margins for invasive breast cancer. Surg. Clin. 2018, 98, 761–771. [Google Scholar] [CrossRef]
- Olsen, M.A.; Nickel, K.B.; Margenthaler, J.A.; Wallace, A.E.; Mines, D.; Miller, J.P.; Fraser, V.J.; Warren, D.K. Increased risk of surgical site infection among breast-conserving surgery re-excisions. Ann. Surg. Oncol. 2015, 22, 2003–2009. [Google Scholar] [CrossRef]
- Collette, S.; Collette, L.; Budiharto, T.; Horiot, J.C.; Poortmans, P.M.; Struikmans, H.; Van den Bogaert, W.; Fourquet, A.; Jager, J.J.; Hoogenraad, W.; et al. Predictors of the risk of fibrosis at 10 years after breast conserving therapy for early breast cancer—A study based on the EORTC trial 22881–10882 ‘boost versus no boost’. Eur. J. Cancer 2008, 44, 2587–2599. [Google Scholar] [CrossRef]
- Wazer, D.E.; DiPetrillo, T.; Schmidt-Ullrich, R.; Weld, L.; Smith, T.; Marchant, D.; Robert, N. Factors influencing cosmetic outcome and complication risk after conservative surgery and radiotherapy for early-stage breast carcinoma. J. Clin. Oncol. 1992, 10, 356–363. [Google Scholar] [CrossRef] [PubMed]
- Heil, J.; Breitkreuz, K.; Golatta, M.; Czink, E.; Dahlkamp, J.; Rom, J.; Schuetz, F.; Blumenstein, M.; Rauch, G.; Sohn, C. Do reexcisions impair aesthetic outcome in breast conservation surgery? Exploratory analysis of a prospective cohort study. Ann. Surg. Oncol. 2012, 19, 541–547. [Google Scholar] [CrossRef]
- Hau, E.; Browne, L.; Capp, A.; Delaney, G.P.; Fox, C.; Kearsley, J.H.; Millar, E.; Nasser, E.H.; Papadatos, G.; Graham, P.H. The impact of breast cosmetic and functional outcomes on quality of life: Long-term results from the St. George and Wollongong randomized breast boost trial. Breast Cancer Res. Treat. 2013, 139, 115–123. [Google Scholar] [CrossRef]
- Waljee, J.F.; Hu, E.S.; Ubel, P.A.; Smith, D.M.; Newman, L.A.; Alderman, A.K. Effect of esthetic outcome after breast-conserving surgery on psychosocial functioning and quality of life. J. Clin. Oncol. 2008, 26, 3331–3337. [Google Scholar] [CrossRef]
- Volders, J.H.; Negenborn, V.L.; Haloua, M.H.; Krekel, N.M.; Jóźwiak, K.; Meijer, S.; van den Tol, P.M. Cosmetic outcome and quality of life are inextricably linked in breast-conserving therapy. J. Surg. Oncol. 2017, 115, 941–948. [Google Scholar] [CrossRef]
- Pataky, R.; Baliski, C. Reoperation costs in attempted breast-conserving surgery: A decision analysis. Curr. Oncol. 2016, 23, 314–321. [Google Scholar] [CrossRef]
- Abe, S.E.; Hill, J.S.; Han, Y.; Walsh, K.; Symanowski, J.T.; Hadzikadic-Gusic, L.; Flippo-Morton, T.; Sarantou, T.; Forster, M.; White Jr, R.L. Margin re-excision and local recurrence in invasive breast cancer: A cost analysis using a decision tree model. J. Surg. Oncol. 2015, 112, 443–448. [Google Scholar] [CrossRef]
- Eichler, C.; Hübbel, A.; Zarghooni, V.; Thomas, A.; Gluz, O.; Stoff-Khalili, M.; Warm, M. Intraoperative ultrasound: Improved resection rates in breast-conserving surgery. Anticancer Res. 2012, 32, 1051–1056. [Google Scholar] [PubMed]
- Pop, M.M.; Cristian, S.; Hanko-Bauer, O.; Ghiga, D.V.; Georgescu, R. Obtaining adequate surgical margin status in breast-conservation therapy: Intraoperative ultrasound-guided resection versus specimen mammography. Clujul Med. 2018, 91, 197. [Google Scholar] [CrossRef] [PubMed]
- Perera, N.; Bourke, A.G. The technique and accuracy of breast specimen ultrasound in achieving clear margins in breast conserving surgery. J. Med. Imaging Radiat. Oncol. 2020, 64, 747–755. [Google Scholar] [CrossRef]
- Tan, K.Y.; Tan, S.M.; Chiang, S.H.; Tan, A.; Chong, C.K.; Tay, K.H. Breast specimen ultrasound and mammography in the prediction of tumour-free margins. ANZ J. Surg. 2006, 76, 1064–1067. [Google Scholar] [CrossRef] [PubMed]
- Colakovic, N.; Zdravkovic, D.; Skuric, Z.; Mrda, D.; Gacic, J.; Ivanovic, N. Intraoperative ultrasound in breast cancer surgery—From localization of non-palpable tumors to objectively measurable excision. World J. Surg. Oncol. 2018, 16, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Rahusen, F.D.; Bremers, A.J.; Fabry, H.F.; Taets van Amerongen, A.; Boom, R.; Meijer, S. Ultrasound-guided lumpectomy of nonpalpable breast cancer versus wire-guided resection: A randomized clinical trial. Ann. Surg. Oncol. 2002, 9, 994–998. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Li, S.; Jiang, Y.; Wei, W.; Ji, Y.; Li, Q.; Jiang, Z. Intraoperative ultrasound-guided lumpectomy versus wire-guided excision for nonpalpable breast cancer. J. Int. Med. Res. 2020, 48, 0300060519896707. [Google Scholar] [CrossRef]
- Volders, J.; Haloua, M.; Krekel, N.; Negenborn, V.; Kolk, R.; Cardozo, A.L.; Bosch, A.; de Widt-Levert, L.; van der Veen, H.; Rijna, H.; et al. Intraoperative ultrasound guidance in breast-conserving surgery shows superiority in oncological outcome, long-term cosmetic and patient-reported outcomes: Final outcomes of a randomized controlled trial (COBALT). Eur. J. Surg. Oncol. (EJSO) 2017, 43, 649–657. [Google Scholar] [CrossRef] [PubMed]
- Volders, J.H.; Haloua, M.H.; Krekel, N.M.; Meijer, S.; van den Tol, P.M. Current status of ultrasound-guided surgery in the treatment of breast cancer. World J. Clin. Oncol. 2016, 7, 44. [Google Scholar] [CrossRef]
- Noble, J.A. Ultrasound image segmentation and tissue characterization. PRoceedings Inst. Mech. Eng. Part H J. Eng. Med. 2010, 224, 307–316. [Google Scholar] [CrossRef]
- Zhang, Y.; Xian, M.; Cheng, H.D.; Shareef, B.; Ding, J.; Xu, F.; Huang, K.; Zhang, B.; Ning, C.; Wang, Y. BUSIS: A Benchmark for Breast Ultrasound Image Segmentation. Healthcare 2022, 10, 729. [Google Scholar] [CrossRef]
- Maolood, I.Y.; Al-Salhi, Y.E.A.; Lu, S. Thresholding for medical image segmentation for cancer using fuzzy entropy with level set algorithm. Open Med. 2018, 13, 374–383. [Google Scholar] [CrossRef]
- Gomez-Flores, W.; Ruiz-Ortega, B.A. New fully automated method for segmentation of breast lesions on ultrasound based on texture analysis. Ultrasound Med. Biol. 2016, 42, 1637–1650. [Google Scholar] [CrossRef]
- Fan, H.; Meng, F.; Liu, Y.; Kong, F.; Ma, J.; Lv, Z. A novel breast ultrasound image automated segmentation algorithm based on seeded region growing integrating gradual equipartition threshold. Multimed. Tools Appl. 2019, 78, 27915–27932. [Google Scholar] [CrossRef]
- Lo, C.M.; Chen, R.T.; Chang, Y.C.; Yang, Y.W.; Hung, M.J.; Huang, C.S.; Chang, R.F. Multi-dimensional tumor detection in automated whole breast ultrasound using topographic watershed. IEEE Trans. Med. Imaging 2014, 33, 1503–1511. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.L.; Chen, D.R. Watershed segmentation for breast tumor in 2-D sonography. Ultrasound Med. Biol. 2004, 30, 625–632. [Google Scholar] [CrossRef]
- Xian, M.; Zhang, Y.; Cheng, H.D. Fully automatic segmentation of breast ultrasound images based on breast characteristics in space and frequency domains. Pattern Recognit. 2015, 48, 485–497. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, X.; Huang, Q. A multi-objectively-optimized graph-based segmentation method for breast ultrasound image. In Proceedings of the 2014 7th International Conference on Biomedical Engineering and Informatics, Dalian, China, 14–16 October 2014; pp. 116–120. [Google Scholar]
- Daoud, M.I.; Baba, M.M.; Awwad, F.; Al-Najjar, M.; Tarawneh, E.S. Accurate segmentation of breast tumors in ultrasound images using a custom-made active contour model and signal-to-noise ratio variations. In Proceedings of the 2012 Eighth International Conference on Signal Image Technology and Internet Based Systems, Naples, Italy, 25–29 November 2012; pp. 137–141. [Google Scholar]
- Kuo, H.C.; Giger, M.L.; Reiser, I.; Drukker, K.; Boone, J.M.; Lindfors, K.K.; Yang, K.; Edwards, A.V.; Sennett, C.A. Segmentation of breast masses on dedicated breast computed tomography and three-dimensional breast ultrasound images. J. Med. Imaging 2014, 1, 014501. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y. A modified spatial fuzzy clustering method based on texture analysis for ultrasound image segmentation. In Proceedings of the 2009 IEEE International Symposium on Industrial Electronics, Seoul, Republic of Korea, 5–8 July 2009; pp. 746–751. [Google Scholar]
- Liu, B.; Cheng, H.D.; Huang, J.; Tian, J.; Tang, X.; Liu, J. Fully automatic and segmentation-robust classification of breast tumors based on local texture analysis of ultrasound images. Pattern Recognit. 2010, 43, 280–298. [Google Scholar] [CrossRef]
- Yap, M.H.; Pons, G.; Marti, J.; Ganau, S.; Sentis, M.; Zwiggelaar, R.; Davison, A.K.; Marti, R. Automated breast ultrasound lesions detection using convolutional neural networks. IEEE J. Biomed. Health Inform. 2017, 22, 1218–1226. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.; Zhang, Y.; Cheng, H.D.; Xing, P.; Zhang, B. Semantic Segmentation of Breast Ultrasound Image with Pyramid Fuzzy Uncertainty Reduction and Direction Connectedness Feature. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milano, Italy, 10–15 January 2021; pp. 3357–3364. [Google Scholar]
- Hu, Y.; Guo, Y.; Wang, Y.; Yu, J.; Li, J.; Zhou, S.; Chang, C. Automatic tumor segmentation in breast ultrasound images using a dilated fully convolutional network combined with an active contour model. Med. Phys. 2019, 46, 215–228. [Google Scholar] [CrossRef]
- Xie, X.; Shi, F.; Niu, J.; Tang, X. Breast ultrasound image classification and segmentation using convolutional neural networks. In Proceedings of the Pacific Rim Conference on Multimedia; Springer: New York, NY, USA, 2018; pp. 200–211. [Google Scholar]
- Badawy, S.M.; Mohamed, A.E.N.A.; Hefnawy, A.A.; Zidan, H.E.; GadAllah, M.T.; El-Banby, G.M. Automatic semantic segmentation of breast tumors in ultrasound images based on combining fuzzy logic and deep learning—A feasibility study. PloS ONE 2021, 16, e0251899. [Google Scholar] [CrossRef]
- Stavros, A.T.; Thickman, D.; Rapp, C.L.; Dennis, M.A.; Parker, S.H.; Sisney, G.A. Solid breast nodules: Use of sonography to distinguish between benign and malignant lesions. Radiology 1995, 196, 123–134. [Google Scholar] [CrossRef]
- Zhang, S.; Liao, M.; Wang, J.; Zhu, Y.; Zhang, Y.; Zhang, J.; Zheng, R.; Lv, L.; Zhu, D.; Chen, H.; et al. Fully automatic tumor segmentation of breast ultrasound images with deep learning. J. Appl. Clin. Med. Phys. 2022, 24, e13863. [Google Scholar] [CrossRef]
- Gómez-Flores, W.; de Albuquerque Pereira, W.C. A comparative study of pre-trained convolutional neural networks for semantic segmentation of breast tumors in ultrasound. Comput. Biol. Med. 2020, 126, 104036. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Wang, K.y.; Chen, H.l.; Xu, Y.h.; Pan, T.; Chen, Y.d. Specimen mammography for intraoperative margin assessment in breast conserving surgery: A meta-analysis. Sci. Rep. 2022, 12, 18440. [Google Scholar] [CrossRef] [PubMed]
- Esbona, K.; Li, Z.; Wilke, L.G. Intraoperative imprint cytology and frozen section pathology for margin assessment in breast conservation surgery: A systematic review. Ann. Surg. Oncol. 2012, 19, 3236–3245. [Google Scholar] [CrossRef]
- Pleijhuis, R.; Langhout, G.; Helfrich, W.; Themelis, G.; Sarantopoulos, A.; Crane, L.; Harlaar, N.; De Jong, J.; Ntziachristos, V.; Van Dam, G. Near-infrared fluorescence (NIRF) imaging in breast-conserving surgery: Assessing intraoperative techniques in tissue-simulating breast phantoms. Eur. J. Surg. Oncol. (EJSO) 2011, 37, 32–39. [Google Scholar] [CrossRef] [PubMed]
- Haka, A.S.; Volynskaya, Z.I.; Gardecki, J.A.; Nazemi, J.; Shenk, R.; Wang, N.; Dasari, R.R.; Fitzmaurice, M.; Feld, M.S. Diagnosing breast cancer using Raman spectroscopy: Prospective analysis. J. Biomed. Opt. 2009, 14, 054023. [Google Scholar] [CrossRef] [PubMed]
- Thomas, G.; Nguyen, T.Q.; Pence, I.; Caldwell, B.; O’Connor, M.; Giltnane, J.; Sanders, M.; Grau, A.; Meszoely, I.; Hooks, M.; et al. Evaluating feasibility of an automated 3-dimensional scanner using Raman spectroscopy for intraoperative breast margin assessment. Sci. Rep. 2017, 7, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Ha, R.; Friedlander, L.C.; Hibshoosh, H.; Hendon, C.; Feldman, S.; Ahn, S.; Schmidt, H.; Akens, M.K.; Fitzmaurice, M.; Wilson, B.C.; et al. Optical coherence tomography: A novel imaging method for post-lumpectomy breast margin assessment—A multi-reader study. Acad. Radiol. 2018, 25, 279–287. [Google Scholar] [CrossRef]
- Foo, K.Y.; Kennedy, K.M.; Zilkens, R.; Allen, W.M.; Fang, Q.; Sanderson, R.W.; Anstie, J.; Dessauvagie, B.F.; Latham, B.; Saunders, C.M.; et al. Optical palpation for tumor margin assessment in breast-conserving surgery. Biomed. Opt. Express 2021, 12, 1666–1682. [Google Scholar] [CrossRef]
- Zysk, A.M.; Chen, K.; Gabrielson, E.; Tafra, L.; May Gonzalez, E.A.; Canner, J.K.; Schneider, E.B.; Cittadine, A.J.; Scott Carney, P.; Boppart, S.A.; et al. Intraoperative assessment of final margins with a handheld optical imaging probe during breast-conserving surgery may reduce the reoperation rate: Results of a multicenter study. Ann. Surg. Oncol. 2015, 22, 3356–3362. [Google Scholar] [CrossRef]
- Pappo, I.; Spector, R.; Schindel, A.; Morgenstern, S.; Sandbank, J.; Leider, L.T.; Schneebaum, S.; Lelcuk, S.; Karni, T. Diagnostic performance of a novel device for real-time margin assessment in lumpectomy specimens. J. Surg. Res. 2010, 160, 277–281. [Google Scholar] [CrossRef] [PubMed]
- Kupstas, A.; Ibrar, W.; Hayward, R.D.; Ockner, D.; Wesen, C.; Falk, J. A novel modality for intraoperative margin assessment and its impact on re-excision rates in breast conserving surgery. Am. J. Surg. 2018, 215, 400–403. [Google Scholar] [CrossRef] [PubMed]
- Dixon, J.M.; Renshaw, L.; Young, O.; Kulkarni, D.; Saleem, T.; Sarfaty, M.; Sreenivasan, R.; Kusnick, C.; Thomas, J.; Williams, L. Intra-operative assessment of excised breast tumour margins using ClearEdge imaging device. Eur. J. Surg. Oncol. (EJSO) 2016, 42, 1834–1840. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.Q.; Dorrius, M.D.; de Jongh, S.J.; Jansen, L.; de Vries, J.; Schröder, C.P.; Zhang, G.J.; de Vries, E.G.; van der Vegt, B.; van Dam, G.M. Micro-computed tomography (micro-CT) for intraoperative surgical margin assessment of breast cancer: A feasibility study in breast conserving surgery. Eur. J. Surg. Oncol. 2018, 44, 1708–1713. [Google Scholar] [CrossRef]
- Park, K.U.; Kuerer, H.M.; Rauch, G.M.; Leung, J.W.; Sahin, A.A.; Wei, W.; Li, Y.; Black, D.M. Digital breast tomosynthesis for intraoperative margin assessment during breast-conserving surgery. Ann. Surg. Oncol. 2019, 26, 1720–1728. [Google Scholar] [CrossRef]
- Wong, T.T.; Zhang, R.; Hai, P.; Zhang, C.; Pleitez, M.A.; Aft, R.L.; Novack, D.V.; Wang, L.V. Fast label-free multilayered histology-like imaging of human breast cancer by photoacoustic microscopy. Sci. Adv. 2017, 3, e1602168. [Google Scholar] [CrossRef]
- Li, R.; Wang, P.; Lan, L.; Lloyd, F.P.; Goergen, C.J.; Chen, S.; Cheng, J.X. Assessing breast tumor margin by multispectral photoacoustic tomography. Biomed. Opt. Express 2015, 6, 1273–1281. [Google Scholar] [CrossRef]
- Karni, T.; Pappo, I.; Sandbank, J.; Lavon, O.; Kent, V.; Spector, R.; Morgenstern, S.; Lelcuk, S. A device for real-time, intraoperative margin assessment in breast-conservation surgery. Am. J. Surg. 2007, 194, 467–473. [Google Scholar] [CrossRef]
- Lu, T.; Jorns, J.M.; Ye, D.H.; Patton, M.; Fisher, R.; Emmrich, A.; Schmidt, T.G.; Yen, T.; Yu, B. Automated assessment of breast margins in deep ultraviolet fluorescence images using texture analysis. Biomed. Opt. Express 2022, 13, 5015–5034. [Google Scholar] [CrossRef]
- Pradipta, A.R.; Tanei, T.; Morimoto, K.; Shimazu, K.; Noguchi, S.; Tanaka, K. Emerging technologies for real-time intraoperative margin assessment in future breast-conserving surgery. Adv. Sci. 2020, 7, 1901519. [Google Scholar] [CrossRef]
- Keating, J.J.; Fisher, C.; Batiste, R.; Singhal, S. Advances in intraoperative margin assessment for breast cancer. Curr. Surg. Rep. 2016, 4, 1–8. [Google Scholar] [CrossRef]
- St John, E.R.; Al-Khudairi, R.; Ashrafian, H.; Athanasiou, T.; Takats, Z.; Hadjiminas, D.J.; Darzi, A.; Leff, D.R. Diagnostic accuracy of intraoperative techniques for margin assessment in breast cancer surgery. Ann. Surg. 2017, 265, 300–310. [Google Scholar] [CrossRef] [PubMed]
- Heidkamp, J.; Scholte, M.; Rosman, C.; Manohar, S.; Fütterer, J.J.; Rovers, M.M. Novel imaging techniques for intraoperative margin assessment in surgical oncology: A systematic review. Int. J. Cancer 2021, 149, 635–645. [Google Scholar] [CrossRef] [PubMed]
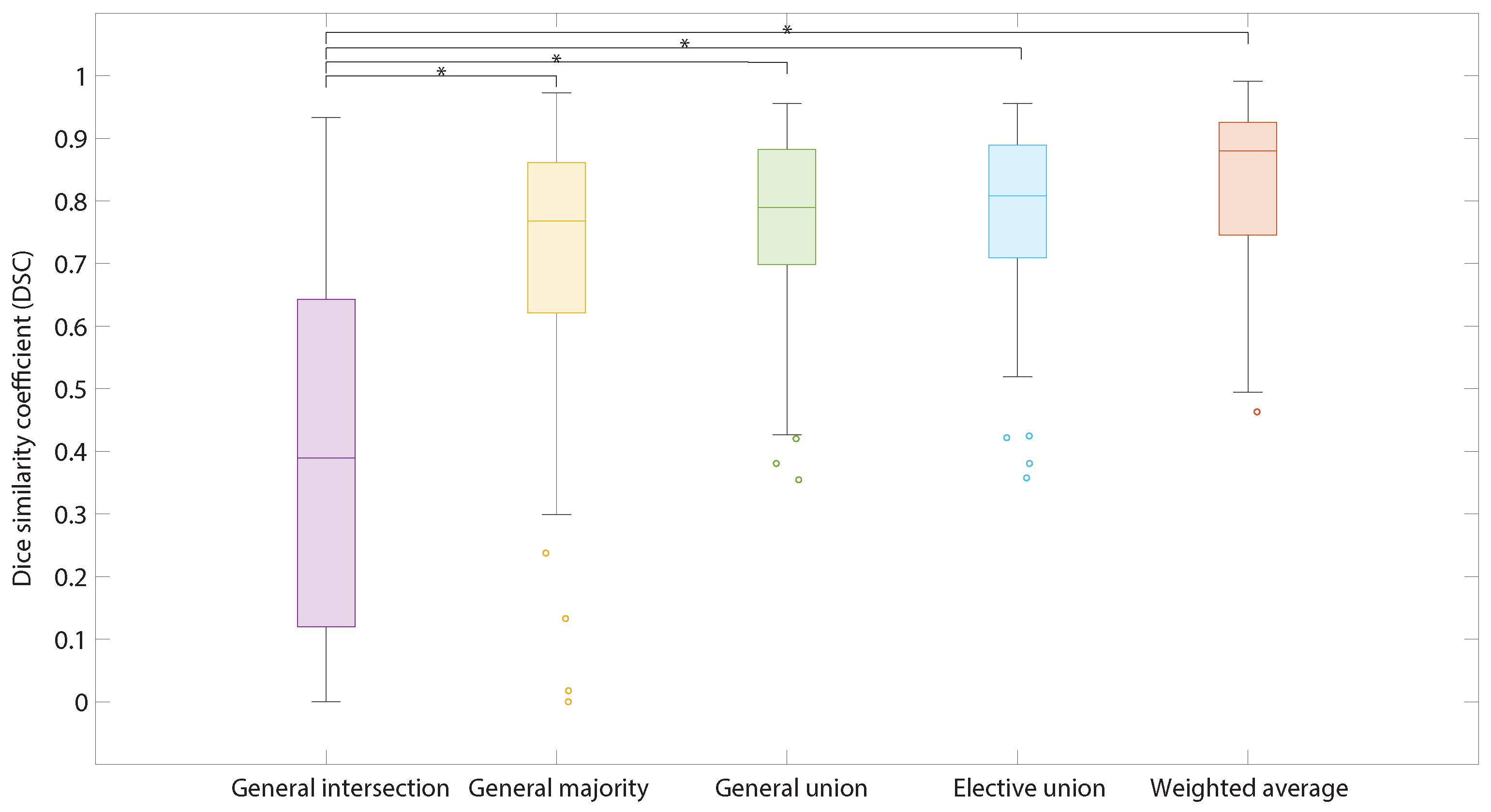

| Characteristic N = 86 | |
|---|---|
| Age (years) (median, SD) | 57 (12.4) |
| Menopausal status | |
| Pre | 26 (30%) |
| Post | 60 (70%) |
| BMI (kg/m2) (median, SD) | 25 (4.1) |
| Lesion diameter (mm) (median, min, max) | 1.5 (0.4, 5.5) |
| Specimen weight (gram) (median, SD) | 20 (19) |
| Histological tumor type | |
| IC NST | 35 (41%) |
| IC NST + DCIS | 43 (50%) |
| ILC | 3 (3%) |
| ILC + LCIS | 5 (6%) |
| T-stage | |
| pT1a | 8 (9%) |
| pT1b | 16 (19%) |
| pT1c | 38 (44%) |
| pT2 | 23 (27%) |
| pT3 | 1 (1%) |
| Histological tumor grade | |
| 1 | 36 (42%) |
| 2 | 44 (51%) |
| 3 | 6 (7%) |
| Hormonal receptor status | |
| ER+ | 81 (94%) |
| ER- | 5 (6%) |
| PR+ | 60 (70%) |
| PR- | 26 (30%) |
| HER2 status | |
| HER2+ | 8 (9%) |
| HER2- | 78 (91%) |
| Immunohistochemically defined subtype | |
| Luminal A-like | 54 (63%) |
| Luminal B-like/HER2-negative | 22 (26%) |
| Luminal B-like/HER2-positive | 7 (8%) |
| HER2-positive | 1 (1%) |
| TNBC | 2 (2%) |
| Neoadjuvant treatment | |
| Chemotherapy +/− targeted therapy | 16 (19%) |
| Endocrine therapy | 14 (16%) |
| None | 56 (65%) |
| AlexNet | MobileNet | ResNet18 | ResNet50 | U-Net | VGG16 | VGG19 | Xception | Threshold | |
|---|---|---|---|---|---|---|---|---|---|
| Maximizing DSC | 0.04 | 0.25 | 0 | 0.18 | 0.11 | 0.07 | 0.14 | 0.21 | 0.22 |
| Maximizing TDM sensitivity | 0.11 | 0.14 | 0.21 | 0.25 | 0.04 | 0 | 0.07 | 0.18 | 0.22 |
| Median DSC (IQR) | |
|---|---|
| Data subset 1 | 0.86 (0.15) |
| Data subset 2 | 0.85 (0.19) |
| Data subset 3 | 0.89 (0.19) |
| TMD Error | Margin Assessment Performance | t-Test | ||||
|---|---|---|---|---|---|---|
| MAE (mm) | NRMSE | PCC | Sensitivity | Specificity | p-Value | |
| vs. | 0.57 | 0.16 | 0.72 | 96% | 76% | 0.3736 |
| vs. | 0.83 | 0.21 | 0.70 | 95% | 57% | 0.0008 * |
| vs. | 0.73 | 0.19 | 0.69 | 87% | 82% | 0.0090 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veluponnar, D.; de Boer, L.L.; Geldof, F.; Jong, L.-J.S.; Da Silva Guimaraes, M.; Vrancken Peeters, M.-J.T.F.D.; van Duijnhoven, F.; Ruers, T.; Dashtbozorg, B. Toward Intraoperative Margin Assessment Using a Deep Learning-Based Approach for Automatic Tumor Segmentation in Breast Lumpectomy Ultrasound Images. Cancers 2023, 15, 1652. https://doi.org/10.3390/cancers15061652
Veluponnar D, de Boer LL, Geldof F, Jong L-JS, Da Silva Guimaraes M, Vrancken Peeters M-JTFD, van Duijnhoven F, Ruers T, Dashtbozorg B. Toward Intraoperative Margin Assessment Using a Deep Learning-Based Approach for Automatic Tumor Segmentation in Breast Lumpectomy Ultrasound Images. Cancers. 2023; 15(6):1652. https://doi.org/10.3390/cancers15061652
Chicago/Turabian StyleVeluponnar, Dinusha, Lisanne L. de Boer, Freija Geldof, Lynn-Jade S. Jong, Marcos Da Silva Guimaraes, Marie-Jeanne T. F. D. Vrancken Peeters, Frederieke van Duijnhoven, Theo Ruers, and Behdad Dashtbozorg. 2023. "Toward Intraoperative Margin Assessment Using a Deep Learning-Based Approach for Automatic Tumor Segmentation in Breast Lumpectomy Ultrasound Images" Cancers 15, no. 6: 1652. https://doi.org/10.3390/cancers15061652
APA StyleVeluponnar, D., de Boer, L. L., Geldof, F., Jong, L.-J. S., Da Silva Guimaraes, M., Vrancken Peeters, M.-J. T. F. D., van Duijnhoven, F., Ruers, T., & Dashtbozorg, B. (2023). Toward Intraoperative Margin Assessment Using a Deep Learning-Based Approach for Automatic Tumor Segmentation in Breast Lumpectomy Ultrasound Images. Cancers, 15(6), 1652. https://doi.org/10.3390/cancers15061652






