Effects of Interfraction Dose Variations of Target and Organs at Risk on Clinical Outcomes in High Dose Rate Brachytherapy for Cervical Cancer
Abstract
:Simple Summary
Abstract
1. Introduction
2. Methods and Materials
2.1. Calculating IDV and Determining IDV Uncertainty Distributions
2.2. Reference Dose Response Curves
2.3. Monte Carlo Simulation and Convolution
2.4. Determination of Treatment Response and Treatment Failure Rate
2.5. Utility Analysis
2.6. Statistical Analysis
2.7. Accuracy Testing of the Model
3. Results
3.1. HRCTV and OAR IDV Uncertainty
3.2. Effect of IDV Uncertainty on TCP and NTCP
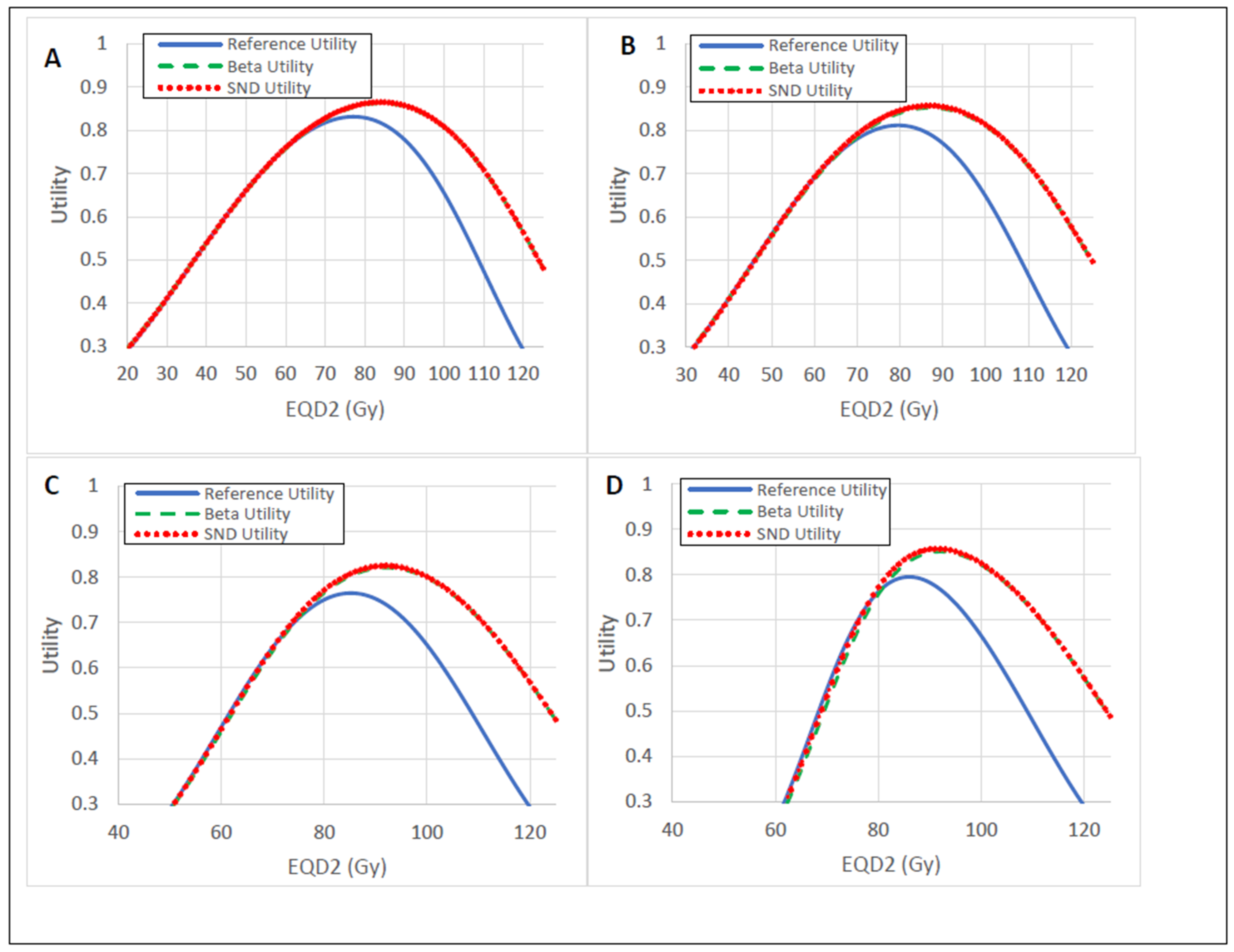
3.3. Utility Analysis
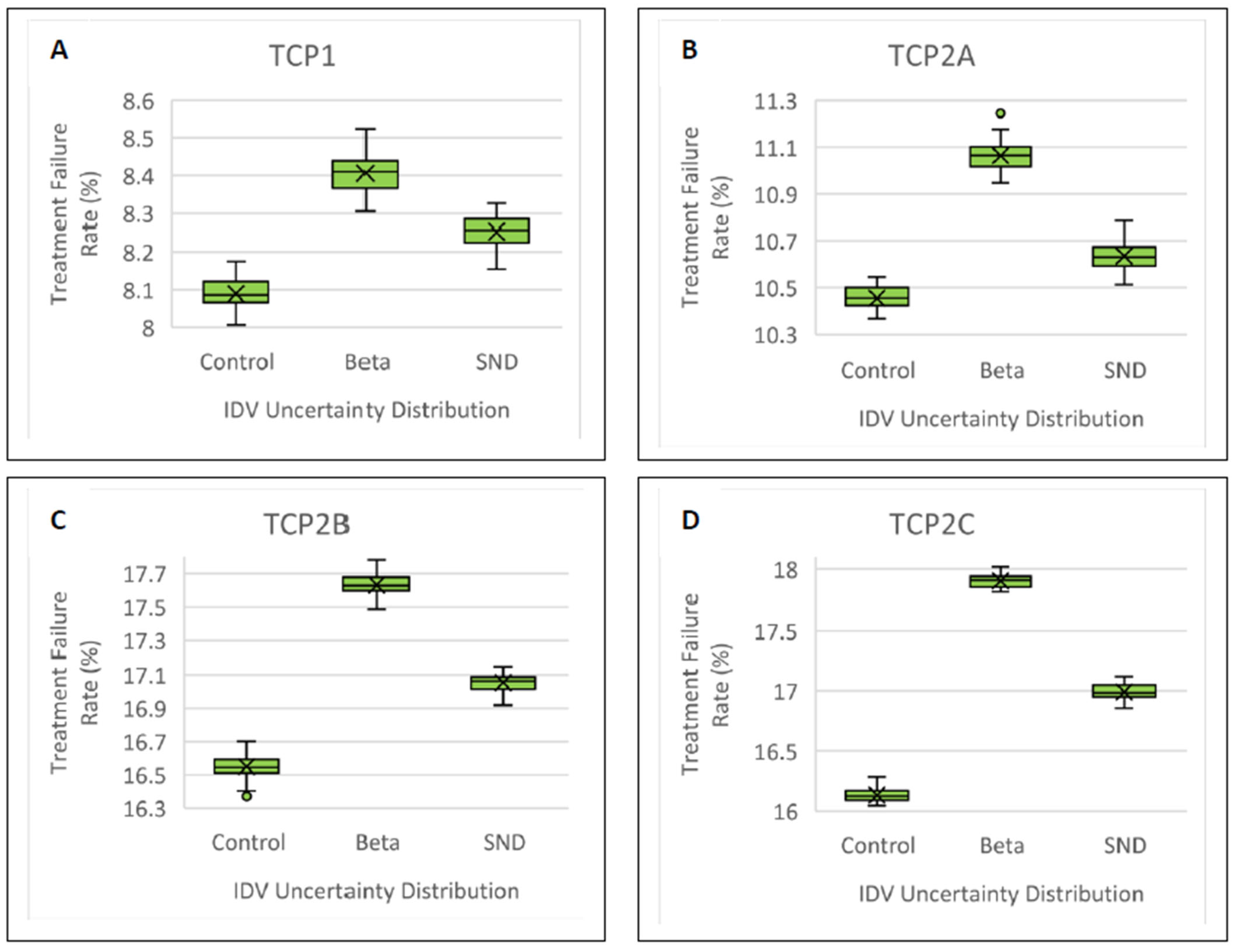
3.4. Treatment Failure Rate
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rivard, M.J.; Coursey, B.M.; DeWerd, L.A.; Hanson, W.F.; Huq, M.S.; Ibbott, G.S.; Mitch, M.G.; Nath, R.; Williamson, J.F. Update of AAPM Task Group No. 43 Report: A revised AAPM protocol for brachytherapy dose calculations. Med. Phys. 2004, 31, 633–674. [Google Scholar] [CrossRef] [PubMed]
- DeWerd, L.A.; Venselaar, J.L.; Ibbott, G.S.; Meigooni, A.S.; Stump, K.E.; Thomadsen, B.R.; Rivard, M.J. Overview on the dosimetric uncertainty analysis for photon-emitting brachytherapy sources, in the light of the AAPM Task Group No 138 and GEC-ESTRO report. Metrologia 2012, 49, S253–S258. [Google Scholar] [CrossRef]
- DeWerd, L.A.; Ibbott, G.S.; Meigooni, A.S.; Mitch, M.G.; Rivard, M.J.; Stump, K.E.; Thomadsen, B.R.; Venselaar, J.L.M. A dosimetric uncertainty analysis for photon-emitting brachytherapy sources: Report of AAPM Task Group No. 138 and GEC-ESTRO: AAPM TG-138 and GEC-ESTRO brachytherapy dosimetry uncertainty recommendations. Med. Phys. 2011, 38, 782–801. [Google Scholar] [CrossRef]
- Liu, H.; Kinard, J.; Maurer, J.; Shang, Q.; Vanderstraeten, C.; Hayes, L.; Sintay, B.; Wiant, D. Evaluation of offline adaptive planning techniques in image-guided brachytherapy of cervical cancer. J. Appl. Clin. Med. Phys. 2018, 19, 316–322. [Google Scholar] [CrossRef] [PubMed]
- Duane, F.K.; Langan, B.; Gillham, C.; Walsh, L.; Rangaswamy, G.; Lyons, C.; Dunne, M.; Walker, C.; McArdle, O. Impact of delineation uncertainties on dose to organs at risk in CT-guided intracavitary brachytherapy. Brachytherapy 2014, 13, 210–218. [Google Scholar] [CrossRef] [PubMed]
- Hellebust, T.P.; Tanderup, K.; Lervåg, C.; Fidarova, E.; Berger, D.; Malinen, E.; Pötter, R.; Petrič, P. Dosimetric impact of interobserver variability in MRI-based delineation for cervical cancer brachytherapy. Radiother. Oncol. 2013, 107, 13–19. [Google Scholar] [CrossRef] [PubMed]
- Bell, L.; Holloway, L.; Bruheim, K.; Petrič, P.; Kirisits, C.; Tanderup, K.; Pötter, R.; Vinod, S.; Lim, K.; Pogson, E.; et al. Dose planning variations related to delineation variations in MRI-guided brachytherapy for locally advanced cervical cancer. Brachytherapy 2020, 19, 146–153. [Google Scholar] [CrossRef] [PubMed]
- Saarnak, A.E.; Boersma, M.; van Bunningen, B.N.; Wolterink, R.; Steggerda, M.J. Inter-observer variation in delineation of bladder and rectum contours for brachytherapy of cervical cancer. Radiother. Oncol. 2000, 56, 37–42. [Google Scholar] [CrossRef]
- Arnesen, M.R.; Bruheim, K.; Malinen, E.; Hellebust, T.P. Spatial dosimetric sensitivity of contouring uncertainties in gynecological 3D-based brachytherapy. Radiother. Oncol. 2014, 113, 414–419. [Google Scholar] [CrossRef]
- Petrič, P.; Hudej, R.; Rogelj, P.; Blas, M.; Tanderup, K.; Fidarova, E.; Kirisits, C.; Berger, D.; Dimopoulos, J.C.A.; Pötter, R.; et al. Uncertainties of target volume delineation in MRI guided adaptive brachytherapy of cervix cancer: A multi-institutional study. Radiother. Oncol. 2013, 107, 6–12. [Google Scholar] [CrossRef]
- Patel, S.; Mehta, K.J.; Kuo, H.-C.G.; Ohri, N.; Patel, R.; Yaparpalvi, R.; Garg, M.K.; Guha, C.; Kalnicki, S. Do changes in interfraction organ at risk volume and cylinder insertion geometry impact delivered dose in high-dose-rate vaginal cuff brachytherapy? Brachytherapy 2016, 15, 185–190. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, K.; Murakami, N.; Wakita, A.; Nakamura, S.; Okamoto, H.; Umezawa, R.; Takahashi, K.; Inaba, K.; Igaki, H.; Ito, Y.; et al. Dosimetric variations due to interfraction organ deformation in cervical cancer brachytherapy. Radiother. Oncol. 2015, 117, 555–558. [Google Scholar] [CrossRef] [PubMed]
- Mazeron, R.; Champoudry, J.; Gilmore, J.; Dumas, I.; Goulart, J.; Oberlander, A.-S.; del Campo, E.R.; Diallo, I.; Lefkopoulos, D.; Haie-Meder, C. Intrafractional organs movement in three-dimensional image-guided adaptive pulsed-dose-rate cervical cancer brachytherapy: Assessment and dosimetric impact. Brachytherapy 2015, 14, 260–266. [Google Scholar] [CrossRef] [PubMed]
- Andersen, E.S.; Noe, K.; Sørensen, T.S.; Nielsen, S.K.; Fokdal, L.; Paludan, M.; Lindegaard, J.C.; Tanderup, K. Simple DVH parameter addition as compared to deformable registration for bladder dose accumulation in cervix cancer brachytherapy. Radiother. Oncol. 2013, 107, 52–57. [Google Scholar] [CrossRef] [PubMed]
- Huh, S.J.; Park, W.; Han, Y. Interfractional variation in position of the uterus during radical radiotherapy for cervical cancer. Radiother. Oncol. 2004, 71, 73–79. [Google Scholar] [CrossRef] [PubMed]
- Taylor, A.; Powell, M.E. Powell, An assessment of interfractional uterine and cervical motion: Implications for radio-therapy target volume definition in gynaecological cancer. Radiother. Oncol. 2008, 88, 250–257. [Google Scholar]
- Georgescu, M.T.; Moldoveanu, V.G.; Ileanu, B.V.; Anghel, R. Dosimetric influence of uterus position in cervix cancer high-dose-rate brachytherapy. Rom. J. Phys. 2016, 61, 1557–1566. [Google Scholar]
- Tanderup, K.; Nesvacil, N.; Pötter, R.; Kirisits, C. Uncertainties in image guided adaptive cervix cancer brachytherapy: Impact on planning and prescription. Radiother. Oncol. 2013, 107, 1–5. [Google Scholar] [CrossRef]
- Nesvacil, N.; Tanderup, K.; Hellebust, T.P.; De Leeuw, A.; Lang, S.; Mohamed, S.; Jamema, S.V.; Anderson, C.; Pötter, R.; Kirisits, C. A multicentre comparison of the dosimetric impact of inter- and intra-fractional anatomical variations in fractionated cervix cancer brachytherapy. Radiother. Oncol. 2013, 107, 20–25. [Google Scholar] [CrossRef]
- Boyer, A.L.; Schultheiss, T. Effects of dosimetric and clinical uncertainty on complication-free local tumor control. Radiother. Oncol. 1988, 11, 65–71. [Google Scholar] [CrossRef]
- Nesvacil, N.; Tanderup, K.; Lindegaard, J.C.; Pötter, R.; Kirisits, C. Can reduction of uncertainties in cervix cancer brachytherapy potentially improve clinical outcome? Radiother. Oncol. 2016, 120, 390–396. [Google Scholar] [CrossRef] [PubMed]
- Washington, B.; Randall, M.; Fabian, D.; Cheek, D.; Wang, C.; Luo, W. Statistical Analysis of Interfraction Dose Variations of High-Risk Clinical Target Volume and Organs at Risk for Cervical Cancer High-Dose-Rate Brachytherapy. Adv. Radiat. Oncol. 2022, 7, 101019. [Google Scholar] [CrossRef] [PubMed]
- Tanderup, K.; Fokdal, L.U.; Sturdza, A.; Haie-Meder, C.; Mazeron, R.; van Limbergen, E.; Jürgenliemk-Schulz, I.; Petric, P.; Hoskin, P.; Dörr, W.; et al. Effect of tumor dose, volume and overall treatment time on local control after radiochemotherapy including MRI guided brachytherapy of locally advanced cervical cancer. Radiother. Oncol. 2016, 120, 441–446. [Google Scholar] [CrossRef] [PubMed]
- Dimopoulos, J.C.; Pötter, R.; Lang, S.; Fidarova, E.; Georg, P.; Dörr, W.; Kirisits, C. Dose–effect relationship for local control of cervical cancer by magnetic resonance image-guided brachytherapy. Radiother. Oncol. 2009, 93, 311–315. [Google Scholar] [CrossRef] [PubMed]
- Georg, P.; Pötter, R.; Georg, D.; Lang, S.; Dimopoulos, J.C.; Sturdza, A.E.; Berger, D.; Kirisits, C.; Dörr, W. Dose Effect Relationship for Late Side Effects of the Rectum and Urinary Bladder in Magnetic Resonance Image-Guided Adaptive Cervix Cancer Brachytherapy. Int. J. Radiat. Oncol. 2012, 82, 653–657. [Google Scholar] [CrossRef] [PubMed]
- Schultheiss, T.E.; Orton, C.G. Models in radiotherapy: Definition of decision criteria. Med. Phys. 1985, 12, 183–187. [Google Scholar] [CrossRef] [PubMed]
- Kashihara, T.; Murakami, N.; Tselis, N.; Kobayashi, K.; Tsuchida, K.; Shima, S.; Masui, K.; Yoshida, K.; Takahashi, K.; Inaba, K.; et al. Hyaluronate gel injection for rectum dose reduction in gynecologic high-dose-rate brachytherapy: Initial Japanese experience. J. Radiat. Res. 2019, 60, 501–508. [Google Scholar] [CrossRef] [PubMed]
- Murakami, N.; Nakamura, S.; Kashihara, T.; Kato, T.; Shibata, Y.; Takahashi, K.; Inaba, K.; Okuma, K.; Igaki, H.; Nakayama, Y.; et al. Hyaluronic acid gel injection in rectovaginal septum reduced incidence of rectal bleeding in brachytherapy for gynecological malignancies. Brachytherapy 2020, 19, 154–161. [Google Scholar] [CrossRef]
- Gonzalez, Y.; Giap, F.; Klages, P.; Owrangi, A.; Jia, X.; Albuquerque, K. Predicting which patients may benefit from the hybrid intracavitary+interstitial needle (IC/IS) applicator for advanced cervical cancer: A dosimetric comparison and toxicity benefit analysis. Brachytherapy 2021, 20, 136–145. [Google Scholar] [CrossRef]
- Albuquerque, K.; Hrycushko, B.A.; Harkenrider, M.M.; Mayadev, J.; Klopp, A.; Beriwal, S.; Petereit, D.G.; Scanderbeg, D.J.; Yashar, C. Compendium of fractionation choices for gynecologic HDR brachytherapy—An American Brachytherapy Society Task Group Report. Brachytherapy 2019, 18, 429–436. [Google Scholar] [CrossRef]
- Moiseenko, V.; Song, W.Y.; Mell, L.K.; Bhandare, N. A comparison of dose-response characteristics of four NTCP models using outcomes of radiation-induced optic neuropathy and retinopathy. Radiat. Oncol. 2011, 6, 61. [Google Scholar] [CrossRef]
- van Heerden, L.E.; van Wieringen, N.; Koedooder, K.; Rasch, C.R.; Pieters, B.R.; Bel, A. Dose warping uncertainties for the accumulated rectal wall dose in cervical cancer brachytherapy. Brachytherapy 2018, 17, 449–455. [Google Scholar] [CrossRef]
- Zhen, X.; Chen, J.; Zhong, Z.; Hrycushko, B.; Zhou, L.; Jiang, S.; Albuquerque, K.; Gu, X. Deep convolutional neural network with transfer learning for rectum toxicity prediction in cervical cancer radiotherapy: A feasibility study. Phys. Med. Biol. 2017, 62, 8246–8263. [Google Scholar] [CrossRef]
- Mazeron, R.; Castelnau-Marchand, P.; Dumas, I.; del Campo, E.R.; Kom, L.K.; Martinetti, F.; Farha, G.; Tailleur, A.; Morice, P.; Chargari, C.; et al. Impact of treatment time and dose escalation on local control in locally advanced cervical cancer treated by chemoradiation and image-guided pulsed-dose rate adaptive brachytherapy. Radiother Oncol. 2015, 114, 257–263. [Google Scholar] [CrossRef]
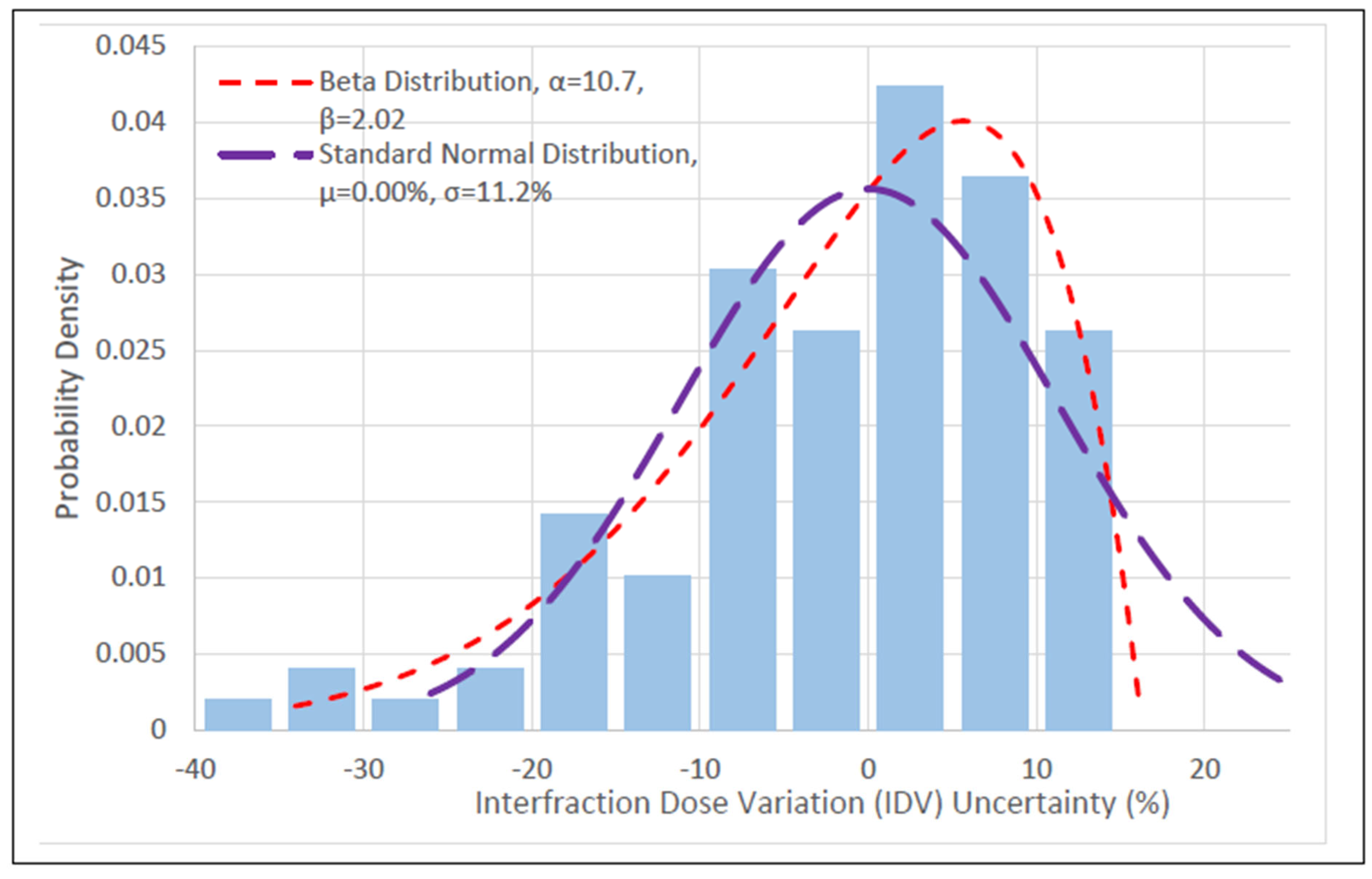
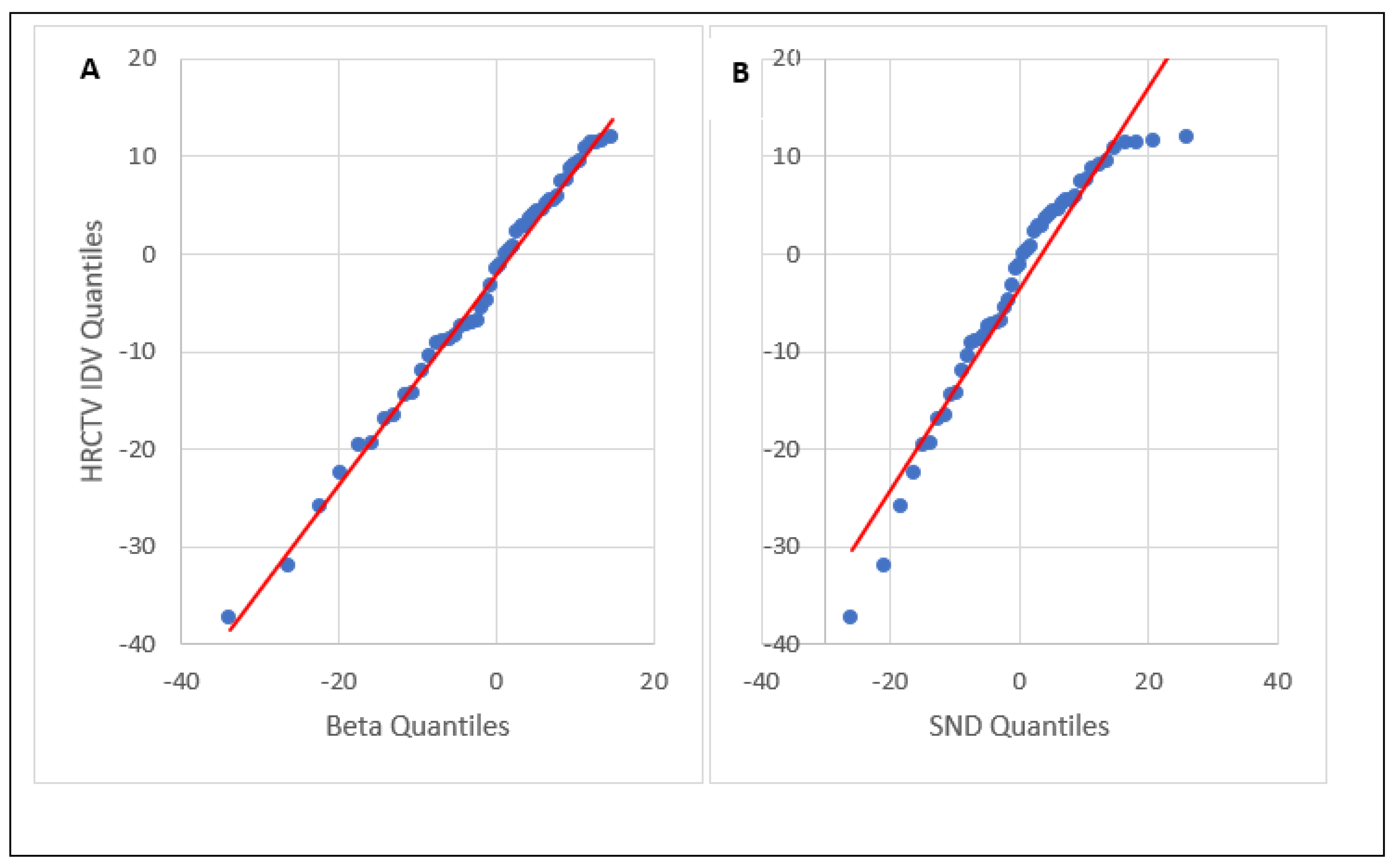
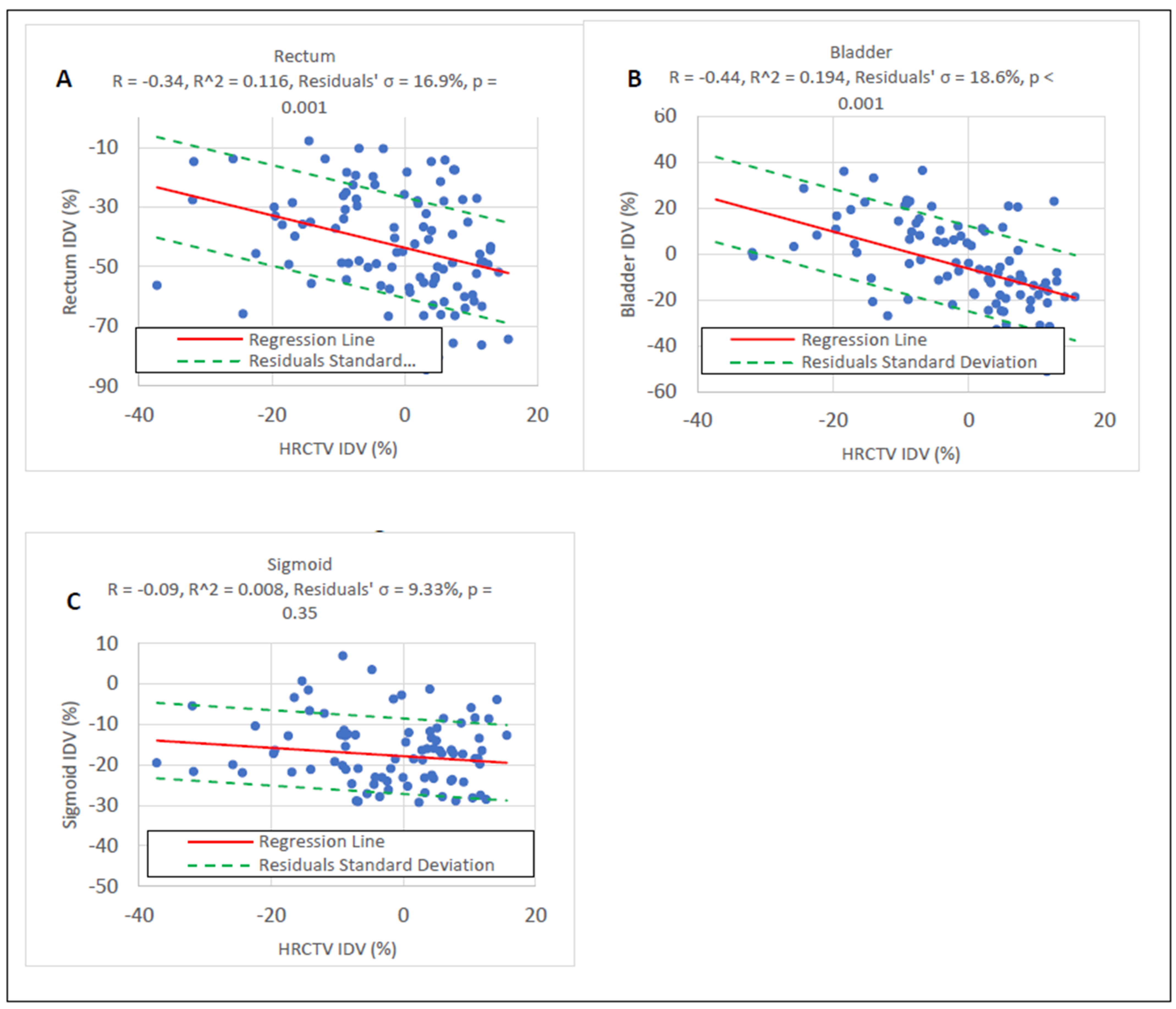


| Distribution | RSS Score | Mean IDV ± Std (%) | p |
|---|---|---|---|
| Beta | −1.53 ± 11.0 | >0.251 * | |
| Generalized Extreme Value ** | −1.54 ± 11.1 | >0.251 | |
| Standard Normal | 0.00 ± 11.2 | <0.0002 |
| Reference | Beta | SND | |
|---|---|---|---|
| TCP1 | 77.0 Gy, 83.2% | 84.0 Gy, 86.3% | 84.0 Gy, 86.6% |
| TCP2A | 80.0 Gy, 81.2% | 87.0 Gy, 85.2% | 87.0 Gy, 85.8% |
| TCP2B | 85.0 Gy, 76.5% | 92.0 Gy, 82.1% | 92.0 Gy, 82.5% |
| TCP2C | 86.0 Gy, 79.5% | 92.0 Gy, 85.1% | 91.0 Gy, 85.7% |
| Reference TCP | Control | Beta | SND | ||
|---|---|---|---|---|---|
| Treatment Failure Rate (%) | Treatment Failure Rate (%) | σ Away from Control | Treatment Failure Rate (%) | σ Away from Control | |
| TCP1 | 8.10 ± 0.05 | 8.41 ± 0.06 | 7.03 | 8.25 ± 0.05 | 3.40 |
| TCP2A | 10.45 ± 0.05 | 11.0 ± 0.05 | 11.0 | 10.7 ± 0.06 | 5.00 |
| TCP2B | 16.6 ± 0.07 | 17.6 ± 0.07 | 14.3 | 17.0 ± 0.06 | 5.71 |
| TCP2C | 16.1 ± 0.06 | 17.9 ± 0.08 | 35.7 | 17.0 ± 0.07 | 17.8 |
| Beta and SND | |
|---|---|
| TCP1 | <0.001 |
| TCP2A | <0.001 |
| TCP2B | <0.001 |
| TCP2C | <0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Washington, B.; Cheek, D.; Fabian, D.; Kudrimoti, M.; Pokhrel, D.; Wang, C.; Thayer-Freeman, C.; Luo, W. Effects of Interfraction Dose Variations of Target and Organs at Risk on Clinical Outcomes in High Dose Rate Brachytherapy for Cervical Cancer. Cancers 2023, 15, 4862. https://doi.org/10.3390/cancers15194862
Washington B, Cheek D, Fabian D, Kudrimoti M, Pokhrel D, Wang C, Thayer-Freeman C, Luo W. Effects of Interfraction Dose Variations of Target and Organs at Risk on Clinical Outcomes in High Dose Rate Brachytherapy for Cervical Cancer. Cancers. 2023; 15(19):4862. https://doi.org/10.3390/cancers15194862
Chicago/Turabian StyleWashington, Brien, Dennis Cheek, Denise Fabian, Mahesh Kudrimoti, Damodar Pokhrel, Chi Wang, Cameron Thayer-Freeman, and Wei Luo. 2023. "Effects of Interfraction Dose Variations of Target and Organs at Risk on Clinical Outcomes in High Dose Rate Brachytherapy for Cervical Cancer" Cancers 15, no. 19: 4862. https://doi.org/10.3390/cancers15194862
APA StyleWashington, B., Cheek, D., Fabian, D., Kudrimoti, M., Pokhrel, D., Wang, C., Thayer-Freeman, C., & Luo, W. (2023). Effects of Interfraction Dose Variations of Target and Organs at Risk on Clinical Outcomes in High Dose Rate Brachytherapy for Cervical Cancer. Cancers, 15(19), 4862. https://doi.org/10.3390/cancers15194862






