Does Cancer Biology Rely on Parrondo’s Principles?
Abstract
Simple Summary
Abstract
1. Introduction
2. The Origins of the Increased Epigenetic and Transcriptional Heterogeneity in Cancer
3. Parrondo’s Paradox in Cancer?
3.1. Are Both Stability and Instability Losing Strategies for Malignant Cells?
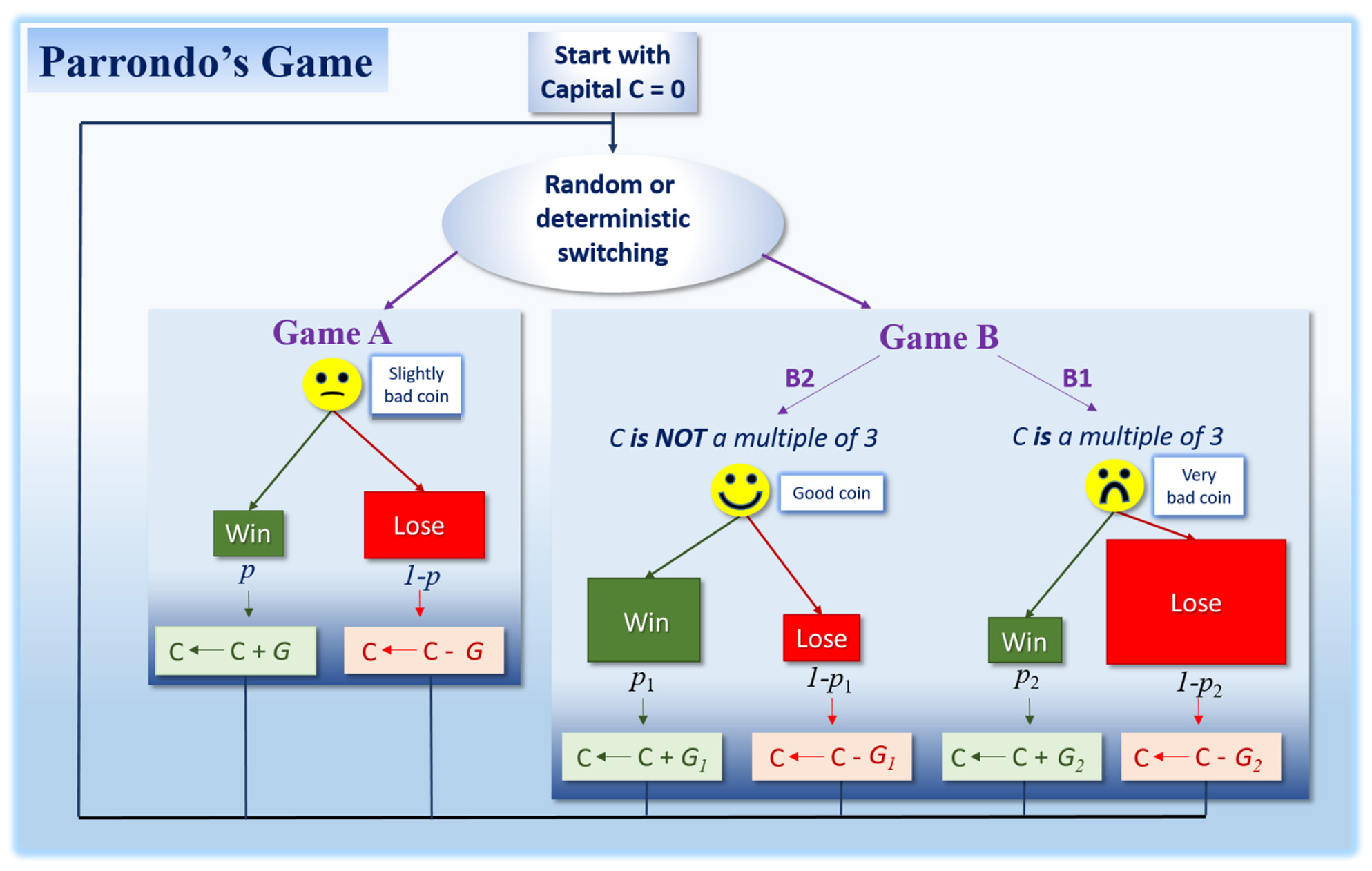
3.2. Why Should Cell Populations with High Instability/Stochasticity Be Needed for Long Term Survival and Proliferation?
3.3. Dormancy: A Losing Strategy in Parrondo’s Dynamics?
3.4. Is the Metastatic Behavior a Strategy within Parrondo’s Paradox?
4. Therapeutic Implications
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boumahdi, S.; de Sauvage, F.J. The great escape: Tumour cell plasticity in resistance to targeted therapy. Nat. Rev. Drug Discov. 2020, 19, 39–56. [Google Scholar] [CrossRef]
- Bell, C.C.; Gilan, O. Principles and mechanisms of non-genetic resistance in cancer. Br. J. Cancer 2020, 122, 465–472. [Google Scholar] [CrossRef]
- Salgia, R.; Kulkarni, P. The Genetic/Non-genetic Duality of Drug ‘Resistance’ in Cancer. Trends Cancer 2018, 4, 110–118. [Google Scholar] [CrossRef]
- LaFave, L.M.; Kartha, V.K.; Ma, S.; Meli, K.; Del Priore, I.; Lareau, C.; Naranjo, S.; Westcott, P.M.K.; Duarte, F.M.; Sankar, V.; et al. Epigenomic State Transitions Characterize Tumor Progression in Mouse Lung Adenocarcinoma. Cancer Cell 2020, 38, 212–228.e213. [Google Scholar] [CrossRef]
- Marjanovic, N.D.; Hofree, M.; Chan, J.E.; Canner, D.; Wu, K.; Trakala, M.; Hartmann, G.G.; Smith, O.C.; Kim, J.Y.; Evans, K.V.; et al. Emergence of a High-Plasticity Cell State during Lung Cancer Evolution. Cancer Cell 2020, 38, 229–246.e213. [Google Scholar] [CrossRef] [PubMed]
- Pastore, A.; Gaiti, F.; Lu, S.X.; Brand, R.M.; Kulm, S.; Chaligne, R.; Gu, H.; Huang, K.Y.; Stamenova, E.K.; Beguelin, W.; et al. Corrupted coordination of epigenetic modifications leads to diverging chromatin states and transcriptional heterogeneity in CLL. Nat. Commun. 2019, 10, 1874. [Google Scholar] [CrossRef]
- Hinohara, K.; Wu, H.J.; Vigneau, S.; McDonald, T.O.; Igarashi, K.J.; Yamamoto, K.N.; Madsen, T.; Fassl, A.; Egri, S.B.; Papanastasiou, M.; et al. KDM5 Histone Demethylase Activity Links Cellular Transcriptomic Heterogeneity to Therapeutic Resistance. Cancer Cell 2018, 34, 939–953.e939. [Google Scholar] [CrossRef] [PubMed]
- Ackermann, M. A functional perspective on phenotypic heterogeneity in microorganisms. Nat. Rev. Microbiol. 2015, 13, 497–508. [Google Scholar] [CrossRef] [PubMed]
- Capp, J.P.; Thomas, F. A Similar Speciation Process Relying on Cellular Stochasticity in Microbial and Cancer Cell Populations. iScience 2020, 23, 101531. [Google Scholar] [CrossRef]
- Fraser, D.; Kaern, M. A chance at survival: Gene expression noise and phenotypic diversification strategies. Mol. Microbiol. 2009, 71, 1333–1340. [Google Scholar] [CrossRef]
- Gupta, P.B.; Fillmore, C.M.; Jiang, G.; Shapira, S.D.; Tao, K.; Kuperwasser, C.; Lander, E.S. Stochastic state transitions give rise to phenotypic equilibrium in populations of cancer cells. Cell 2011, 146, 633–644. [Google Scholar] [CrossRef]
- Huang, S.; Ernberg, I.; Kauffman, S. Cancer attractors: A systems view of tumors from a gene network dynamics and developmental perspective. Semin. Cell Dev. Biol. 2009, 20, 869–876. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Wennborg, A.; Aurell, E.; Dekel, E.; Zou, J.Z.; Xu, Y.; Huang, S.; Ernberg, I. Dynamics inside the cancer cell attractor reveal cell heterogeneity, limits of stability, and escape. Proc. Natl. Acad. Sci. USA 2016, 113, 2672–2677. [Google Scholar] [CrossRef]
- Waddington, C.H. The Strategy of the Genes; A Discussion of Some Aspects of Theoretical Biology; Allen & Unwin: London, UK, 1957; 262p. [Google Scholar]
- Goldberg, A.D.; Allis, C.D.; Bernstein, E. Epigenetics: A landscape takes shape. Cell 2007, 128, 635–638. [Google Scholar] [CrossRef]
- Stergachis, A.B.; Neph, S.; Reynolds, A.; Humbert, R.; Miller, B.; Paige, S.L.; Vernot, B.; Cheng, J.B.; Thurman, R.E.; Sandstrom, R.; et al. Developmental fate and cellular maturity encoded in human regulatory DNA landscapes. Cell 2013, 154, 888–903. [Google Scholar] [CrossRef] [PubMed]
- Jenkinson, G.; Pujadas, E.; Goutsias, J.; Feinberg, A.P. Potential energy landscapes identify the information-theoretic nature of the epigenome. Nat. Genet. 2017, 49, 719–729. [Google Scholar] [CrossRef] [PubMed]
- Amir el, A.D.; Davis, K.L.; Tadmor, M.D.; Simonds, E.F.; Levine, J.H.; Bendall, S.C.; Shenfeld, D.K.; Krishnaswamy, S.; Nolan, G.P.; Pe’er, D. viSNE enables visualization of high dimensional single-cell data and reveals phenotypic heterogeneity of leukemia. Nat. Biotechnol. 2013, 31, 545–552. [Google Scholar] [CrossRef]
- Lawson, D.A.; Kessenbrock, K.; Davis, R.T.; Pervolarakis, N.; Werb, Z. Tumour heterogeneity and metastasis at single-cell resolution. Nat. Cell Biol. 2018, 20, 1349–1360. [Google Scholar] [CrossRef]
- Xiong, S.; Feng, Y.; Cheng, L. Cellular Reprogramming as a Therapeutic Target in Cancer. Trends Cell Biol. 2019, 29, 623–634. [Google Scholar] [CrossRef]
- Udyavar, A.R.; Wooten, D.J.; Hoeksema, M.; Bansal, M.; Califano, A.; Estrada, L.; Schnell, S.; Irish, J.M.; Massion, P.P.; Quaranta, V. Novel Hybrid Phenotype Revealed in Small Cell Lung Cancer by a Transcription Factor Network Model That Can Explain Tumor Heterogeneity. Cancer Res. 2017, 77, 1063–1074. [Google Scholar] [CrossRef]
- Jolly, M.K.; Huang, B.; Lu, M.; Mani, S.A.; Levine, H.; Ben-Jacob, E. Towards elucidating the connection between epithelial-mesenchymal transitions and stemness. J. R. Soc. Interface 2014, 11, 20140962. [Google Scholar] [CrossRef]
- Dongre, A.; Weinberg, R.A. New insights into the mechanisms of epithelial-mesenchymal transition and implications for cancer. Nat. Rev. Mol. Cell Biol. 2019, 20, 69–84. [Google Scholar] [CrossRef] [PubMed]
- Rios, A.C.; Capaldo, B.D.; Vaillant, F.; Pal, B.; van Ineveld, R.; Dawson, C.A.; Chen, Y.; Nolan, E.; Fu, N.Y.; Group, D.; et al. Intraclonal Plasticity in Mammary Tumors Revealed through Large-Scale Single-Cell Resolution 3D Imaging. Cancer Cell 2019, 35, 618–632.e616. [Google Scholar] [CrossRef] [PubMed]
- Capp, J.P.; Laforge, B. A Darwinian and Physical Look at Stem Cell Biology Helps Understanding the Role of Stochasticity in Development. Front. Cell Dev. Biol. 2020, 8, 659. [Google Scholar] [CrossRef]
- Capp, J.P. Tissue disruption increases stochastic gene expression thus producing tumors: Cancer initiation without driver mutation. Int. J. Cancer 2017, 140, 2408–2413. [Google Scholar] [CrossRef] [PubMed]
- Capp, J.P.; Bataille, R. Multiple Myeloma as a Bone Disease? The Tissue Disruption-Induced Cell Stochasticity (TiDiS) Theory. Cancers 2020, 12, 2158. [Google Scholar] [CrossRef]
- Capp, J.P.; Thomas, F. Tissue-disruption-induced cellular stochasticity and epigenetic drift: Common origins of aging and cancer? Bioessays 2021, 43, e2000140. [Google Scholar] [CrossRef]
- Shaffer, S.M.; Dunagin, M.C.; Torborg, S.R.; Torre, E.A.; Emert, B.; Krepler, C.; Beqiri, M.; Sproesser, K.; Brafford, P.A.; Xiao, M.; et al. Rare cell variability and drug-induced reprogramming as a mode of cancer drug resistance. Nature 2017, 546, 431–435. [Google Scholar] [CrossRef]
- Shaffer, S.M.; Emert, B.L.; Reyes Hueros, R.A.; Cote, C.; Harmange, G.; Schaff, D.L.; Sizemore, A.E.; Gupte, R.; Torre, E.; Singh, A.; et al. Memory Sequencing Reveals Heritable Single-Cell Gene Expression Programs Associated with Distinct Cellular Behaviors. Cell 2020, 182, 947–959.e917. [Google Scholar] [CrossRef]
- Magee, J.A.; Piskounova, E.; Morrison, S.J. Cancer stem cells: Impact, heterogeneity, and uncertainty. Cancer Cell 2012, 21, 283–296. [Google Scholar] [CrossRef]
- Harmer, G.P.; Abbott, D. Losing strategies can win by Parrondo’s paradox. Nature 1999, 402, 864. [Google Scholar] [CrossRef]
- Harmer, G.P.; Abbott, D.; Taylor, P.G.; Parrondo, J.M. Brownian ratchets and Parrondo’s games. Chaos 2001, 11, 705–714. [Google Scholar] [CrossRef] [PubMed]
- Shu, J.J.; Wang, Q.W. Beyond Parrondo’s paradox. Sci. Rep. 2014, 4, 4244. [Google Scholar] [CrossRef] [PubMed]
- Lai, J.W.; Cheong, K.H. Parrondo’s paradox from classical to quantum: A review. Nonlinear Dyn. 2020, 100, 849–861. [Google Scholar] [CrossRef]
- Parrondo, J.M.; Harmer, G.P.; Abbott, D. New paradoxical games based on brownian ratchets. Phys. Rev. Lett. 2000, 85, 5226–5229. [Google Scholar] [CrossRef] [PubMed]
- Arena, P.; Fazzino, S.; Fortuna, L.; Maniscalco, P. Game theory and non-linear dynamics: The Parrondo Paradox case study. Chaos Solit. Fract. 2003, 17, 545–555. [Google Scholar] [CrossRef]
- Ye, Y.; Wang, L.; Xie, N. Parrondo’s games based on complex networks and the paradoxical effect. PLoS ONE 2013, 8, e67924. [Google Scholar] [CrossRef]
- Harmer, G.P.; Abbott, D.; Taylor, P.G. The paradox of Parrondo’s games. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2000, 456, 247–259. [Google Scholar] [CrossRef]
- Amengual, P.; Allison, A.; Toral, R.; Abbott, D. Discrete–time ratchets, the Fokker–Planck equation and Parrondo’s paradox. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 460, 2269–2284. [Google Scholar] [CrossRef]
- Abbott, D. Asymmetry and disorder: A decade of Parrondo’s paradox. Fluct. Noise Lett. 2010, 09, 129–156. [Google Scholar] [CrossRef]
- Allison, A.; Abbott, D. Control systems with stochastic feedback. Chaos 2001, 11, 715–724. [Google Scholar] [CrossRef]
- Almeida, J.; Peralta-Salas, D.; Romera, M. Can two chaotic systems give rise to order? Physica D 2005, 200, 124–132. [Google Scholar] [CrossRef]
- Boyarsky, A.; Góra, P.; Islam, M.S. Randomly chosen chaotic maps can give rise to nearly ordered behavior. Physica D 2005, 210, 284–294. [Google Scholar] [CrossRef]
- Fulai, W. Improvement and empirical research on chaos control by theory of “chaos + chaos = order”. Chaos 2012, 22, 043145. [Google Scholar] [CrossRef]
- Danca, M.F.; Lai, D. Parrondo’s game model to find numerically stable attraactors of a tumor growth model. Int. J. Bifurcat Chaos 2012, 22, 1250258. [Google Scholar] [CrossRef]
- Danca, M.F.; Romera, M.; Pastor, G.; Montoya, F. Finding attractors of continuous-time systems by parameter switching. Nonlinear Dyn. 2012, 67, 2317–2342. [Google Scholar] [CrossRef]
- Cheong, K.H.; Koh, J.M.; Jones, M.C. Paradoxical Survival: Examining the Parrondo Effect across Biology. Bioessays 2019, 41, e1900027. [Google Scholar] [CrossRef] [PubMed]
- Reed, F.A. Two-locus epistasis with sexually antagonistic selection: A genetic Parrondo’s paradox. Genetics 2007, 176, 1923–1929. [Google Scholar] [CrossRef][Green Version]
- Wolf, D.M.; Vazirani, V.V.; Arkin, A.P. Diversity in times of adversity: Probabilistic strategies in microbial survival games. J. Theor. Biol. 2005, 234, 227–253. [Google Scholar] [CrossRef]
- Kussell, E.; Leibler, S. Phenotypic diversity, population growth, and information in fluctuating environments. Science 2005, 309, 2075–2078. [Google Scholar] [CrossRef]
- Acar, M.; Mettetal, J.T.; van Oudenaarden, A. Stochastic switching as a survival strategy in fluctuating environments. Nat. Genet. 2008, 40, 471–475. [Google Scholar] [CrossRef] [PubMed]
- Cheong, K.H.; Tan, Z.X.; Xie, N.G.; Jones, M.C. A Paradoxical Evolutionary Mechanism in Stochastically Switching Environments. Sci. Rep. 2016, 6, 34889. [Google Scholar] [CrossRef]
- Jansen, V.A.; Yoshimura, J. Populations can persist in an environment consisting of sink habitats only. Proc. Natl. Acad. Sci. USA 1998, 95, 3696–3698. [Google Scholar] [CrossRef] [PubMed]
- Tan, Z.X.; Cheong, K.H. Nomadic-colonial life strategies enable paradoxical survival and growth despite habitat destruction. Elife 2017, 6. [Google Scholar] [CrossRef]
- Cheong, K.H.; Tan, Z.X.; Ling, Y.H. A time-based switching scheme for nomadic-colonial alternation under noisy conditions. Commun. Nonlinear Sci. Numer. Simul. 2018, 60, 107–114. [Google Scholar] [CrossRef]
- Koh, J.M.; Xie, N.; Cheong, K.H. Nomadic-colonial switching with stochastic noise: Subsidence-recovery cycles and long-term growth. Nonlinear Dyn. 2018, 94, 1467–1477. [Google Scholar] [CrossRef]
- Tarnita, C.E.; Washburne, A.; Martinez-Garcia, R.; Sgro, A.E.; Levin, S.A. Fitness tradeoffs between spores and nonaggregating cells can explain the coexistence of diverse genotypes in cellular slime molds. Proc. Natl. Acad. Sci. USA 2015, 112, 2776–2781. [Google Scholar] [CrossRef] [PubMed]
- Nelson, P.; Masel, J. Intercellular competition and the inevitability of multicellular aging. Proc. Natl. Acad. Sci. USA 2017, 114, 12982–12987. [Google Scholar] [CrossRef]
- Cheong, K.H.; Koh, J.M.; Jones, M.C. Multicellular survival as a consequence of Parrondo’s paradox. Proc. Natl. Acad. Sci. USA 2018, 115, E5258–E5259. [Google Scholar] [CrossRef]
- Bindra, R.S.; Glazer, P.M. Genetic instability and the tumor microenvironment: Towards the concept of microenvironment-induced mutagenesis. Mutat. Res. 2005, 569, 75–85. [Google Scholar] [CrossRef]
- Sonugur, F.G.; Akbulut, H. The Role of Tumor Microenvironment in Genomic Instability of Malignant Tumors. Front. Genet. 2019, 10, 1063. [Google Scholar] [CrossRef]
- Ammerpohl, O.; Hattermann, K.; Held-Feindt, J.; Röcken, C.; Schäfer, H.; Schem, C.; Schewe, D.; Schulenburg, H.; Sebens, S.; Synowitz, M.; et al. Chapter 20-Dormancy: An Evolutionary Key Phenomenon in Cancer Developmenta. In Ecology and Evolution of Cancer; Ujvari, B., Roche, B., Thomas, F., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 235–242. [Google Scholar] [CrossRef]
- Almog, N. Molecular mechanisms underlying tumor dormancy. Cancer Lett. 2010, 294, 139–146. [Google Scholar] [CrossRef] [PubMed]
- Paez, D.; Labonte, M.J.; Bohanes, P.; Zhang, W.; Benhanim, L.; Ning, Y.; Wakatsuki, T.; Loupakis, F.; Lenz, H.J. Cancer dormancy: A model of early dissemination and late cancer recurrence. Clin. Cancer Res. 2012, 18, 645–653. [Google Scholar] [CrossRef]
- West-Eberhard, M.J. Phenotypic Plasticity and the Origins of Diversity. Annu. Rev. Ecol. Syst. 1989, 20, 249–278. [Google Scholar] [CrossRef]
- Arnal, A.; Ujvari, B.; Crespi, B.; Gatenby, R.A.; Tissot, T.; Vittecoq, M.; Ewald, P.W.; Casali, A.; Ducasse, H.; Jacqueline, C.; et al. Evolutionary perspective of cancer: Myth, metaphors, and reality. Evol. Appl. 2015, 8, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Childs, D.Z.; Metcalf, C.J.; Rees, M. Evolutionary bet-hedging in the real world: Empirical evidence and challenges revealed by plants. Proc. Biol. Sci. 2010, 277, 3055–3064. [Google Scholar] [CrossRef]
- Dillekas, H.; Rogers, M.S.; Straume, O. Are 90% of deaths from cancer caused by metastases? Cancer Med. 2019, 8, 5574–5576. [Google Scholar] [CrossRef]
- Lloyd, M.C.; Gatenby, R.A.; Brown, J.S. Chapter 11-Ecology of the Metastatic Process. In Ecology and Evolution of Cancer; Ujvari, B., Roche, B., Thomas, F., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 153–165. [Google Scholar] [CrossRef]
- Tissot, T.; Massol, F.; Ujvari, B.; Alix-Panabieres, C.; Loeuille, N.; Thomas, F. Metastasis and the evolution of dispersal. Proc. Biol. Sci. 2019, 286, 20192186. [Google Scholar] [CrossRef]
- Luzzi, K.J.; MacDonald, I.C.; Schmidt, E.E.; Kerkvliet, N.; Morris, V.L.; Chambers, A.F.; Groom, A.C. Multistep nature of metastatic inefficiency: Dormancy of solitary cells after successful extravasation and limited survival of early micrometastases. Am. J. Pathol. 1998, 153, 865–873. [Google Scholar] [CrossRef]
- Chambers, A.F.; Groom, A.C.; MacDonald, I.C. Dissemination and growth of cancer cells in metastatic sites. Nat. Rev. Cancer 2002, 2, 563–572. [Google Scholar] [CrossRef]
- Mehlen, P.; Puisieux, A. Metastasis: A question of life or death. Nat. Rev. Cancer 2006, 6, 449–458. [Google Scholar] [CrossRef]
- Ganesh, K.; Massague, J. Targeting metastatic cancer. Nat. Med. 2021, 27, 34–44. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.M.; Wilson, W.R. Exploiting tumour hypoxia in cancer treatment. Nat. Rev. Cancer 2004, 4, 437–447. [Google Scholar] [CrossRef] [PubMed]
- Gatenby, R.A.; Gillies, R.J. Why do cancers have high aerobic glycolysis? Nat. Rev. Cancer 2004, 4, 891–899. [Google Scholar] [CrossRef]
- Richards, C.H.; Mohammed, Z.; Qayyum, T.; Horgan, P.G.; McMillan, D.C. The prognostic value of histological tumor necrosis in solid organ malignant disease: A systematic review. Future Oncol. 2011, 7, 1223–1235. [Google Scholar] [CrossRef]
- Caruso, R.; Parisi, A.; Bonanno, A.; Paparo, D.; Quattrocchi, E.; Branca, G.; Scardigno, M.; Fedele, F. Histologic coagulative tumour necrosis as a prognostic indicator of aggressiveness in renal, lung, thyroid and colorectal carcinomas: A brief review. Oncol. Lett. 2012, 3, 16–18. [Google Scholar] [CrossRef]
- Makki, J. Diversity of Breast Carcinoma: Histological Subtypes and Clinical Relevance. Clin. Med. Insights Pathol. 2015, 8, 23–31. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Jin, Y.; Yang, W.; Zhang, L.; Jin, X.; Liu, X.; He, Y.; Li, X. Necroptosis in cancer: An angel or a demon? Tumour Biol. 2017, 39, 1010428317711539. [Google Scholar] [CrossRef] [PubMed]
- Jiao, D.; Cai, Z.; Choksi, S.; Ma, D.; Choe, M.; Kwon, H.J.; Baik, J.Y.; Rowan, B.G.; Liu, C.; Liu, Z.G. Necroptosis of tumor cells leads to tumor necrosis and promotes tumor metastasis. Cell Res. 2018, 28, 868–870. [Google Scholar] [CrossRef]
- Liu, Z.G.; Jiao, D. Necroptosis, tumor necrosis and tumorigenesis. Cell Stress 2020, 4, 1–8. [Google Scholar] [CrossRef]
- Della Torre, L.; Nebbioso, A.; Stunnenberg, H.G.; Martens, J.H.A.; Carafa, V.; Altucci, L. The Role of Necroptosis: Biological Relevance and Its Involvement in Cancer. Cancers 2021, 13, 684. [Google Scholar] [CrossRef]
- Gatenby, R.A.; Gawlinski, E.T.; Gmitro, A.F.; Kaylor, B.; Gillies, R.J. Acid-mediated tumor invasion: A multidisciplinary study. Cancer Res. 2006, 66, 5216–5223. [Google Scholar] [CrossRef] [PubMed]
- Donato, C.; Kunz, L.; Castro-Giner, F.; Paasinen-Sohns, A.; Strittmatter, K.; Szczerba, B.M.; Scherrer, R.; Di Maggio, N.; Heusermann, W.; Biehlmaier, O.; et al. Hypoxia Triggers the Intravasation of Clustered Circulating Tumor Cells. Cell Rep. 2020, 32, 108105. [Google Scholar] [CrossRef] [PubMed]
- Ujvari, B.; Roche, B.; Thomas, F. Ecology and Evolution of Cancer; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Gatenby, R.; Brown, J. The Evolution and Ecology of Resistance in Cancer Therapy. Cold Spring Harb Perspect Med. 2018, 8. [Google Scholar] [CrossRef]
- Gatenby, R.A.; Silva, A.S.; Gillies, R.J.; Frieden, B.R. Adaptive therapy. Cancer Res. 2009, 69, 4894–4903. [Google Scholar] [CrossRef] [PubMed]
- Kam, Y.; Das, T.; Tian, H.; Foroutan, P.; Ruiz, E.; Martinez, G.; Minton, S.; Gillies, R.J.; Gatenby, R.A. Sweat but no gain: Inhibiting proliferation of multidrug resistant cancer cells with “ersatzdroges”. Int. J. Cancer 2015, 136, E188–E196. [Google Scholar] [CrossRef] [PubMed]
- Gatenby, R.A.; Artzy-Randrup, Y.; Epstein, T.; Reed, D.R.; Brown, J.S. Eradicating Metastatic Cancer and the Eco-Evolutionary Dynamics of Anthropocene Extinctions. Cancer Res. 2020, 80, 613–623. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capp, J.-P.; Nedelcu, A.M.; Dujon, A.M.; Roche, B.; Catania, F.; Ujvari, B.; Alix-Panabières, C.; Thomas, F. Does Cancer Biology Rely on Parrondo’s Principles? Cancers 2021, 13, 2197. https://doi.org/10.3390/cancers13092197
Capp J-P, Nedelcu AM, Dujon AM, Roche B, Catania F, Ujvari B, Alix-Panabières C, Thomas F. Does Cancer Biology Rely on Parrondo’s Principles? Cancers. 2021; 13(9):2197. https://doi.org/10.3390/cancers13092197
Chicago/Turabian StyleCapp, Jean-Pascal, Aurora M Nedelcu, Antoine M Dujon, Benjamin Roche, Francesco Catania, Beata Ujvari, Catherine Alix-Panabières, and Frédéric Thomas. 2021. "Does Cancer Biology Rely on Parrondo’s Principles?" Cancers 13, no. 9: 2197. https://doi.org/10.3390/cancers13092197
APA StyleCapp, J.-P., Nedelcu, A. M., Dujon, A. M., Roche, B., Catania, F., Ujvari, B., Alix-Panabières, C., & Thomas, F. (2021). Does Cancer Biology Rely on Parrondo’s Principles? Cancers, 13(9), 2197. https://doi.org/10.3390/cancers13092197









