Effects of Process Parameters on Material Removal in Vibration-Assisted Polishing of Micro-Optic Mold
Abstract
1. Introduction
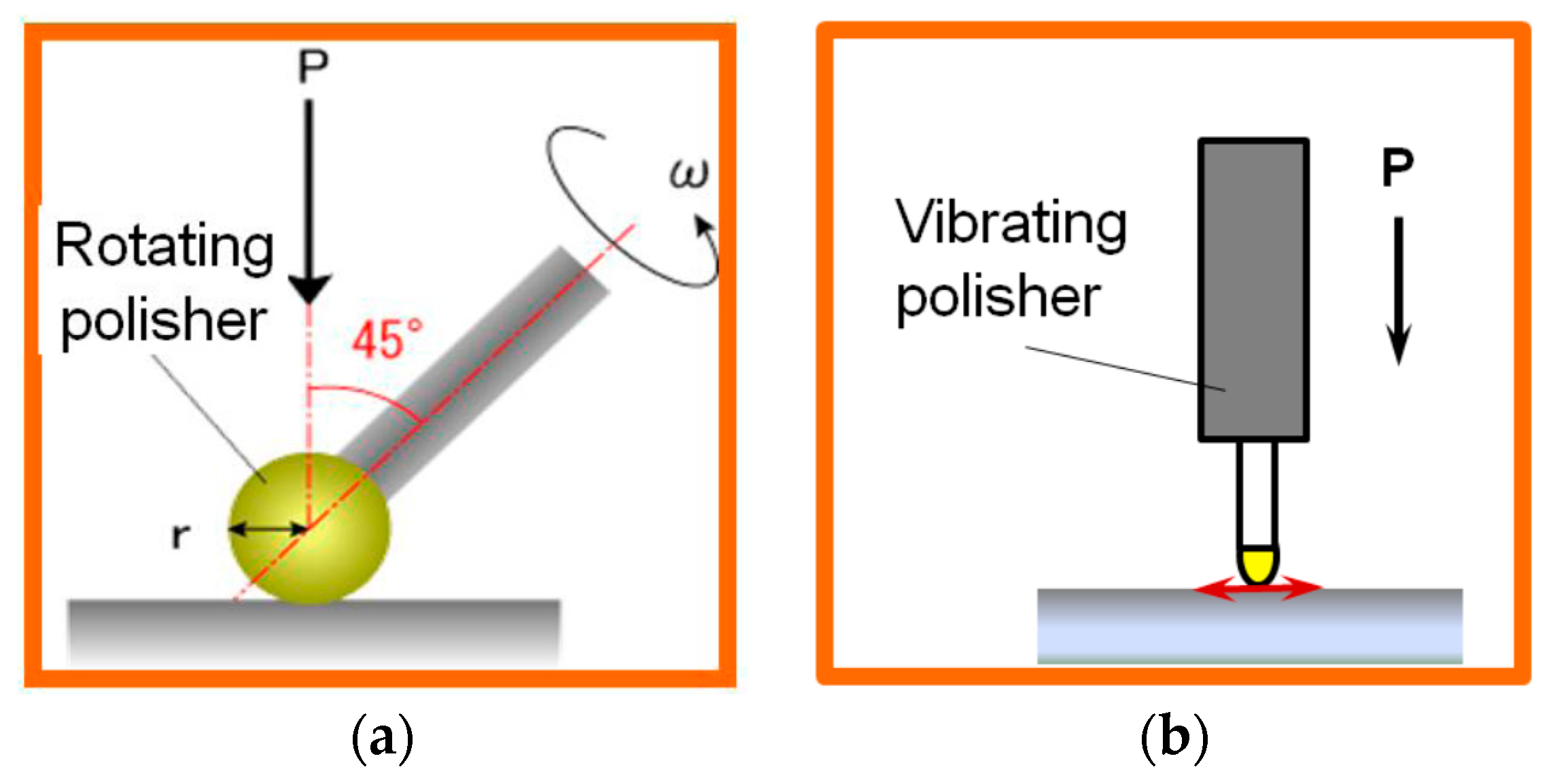
2. Experimental Setup and Conditions
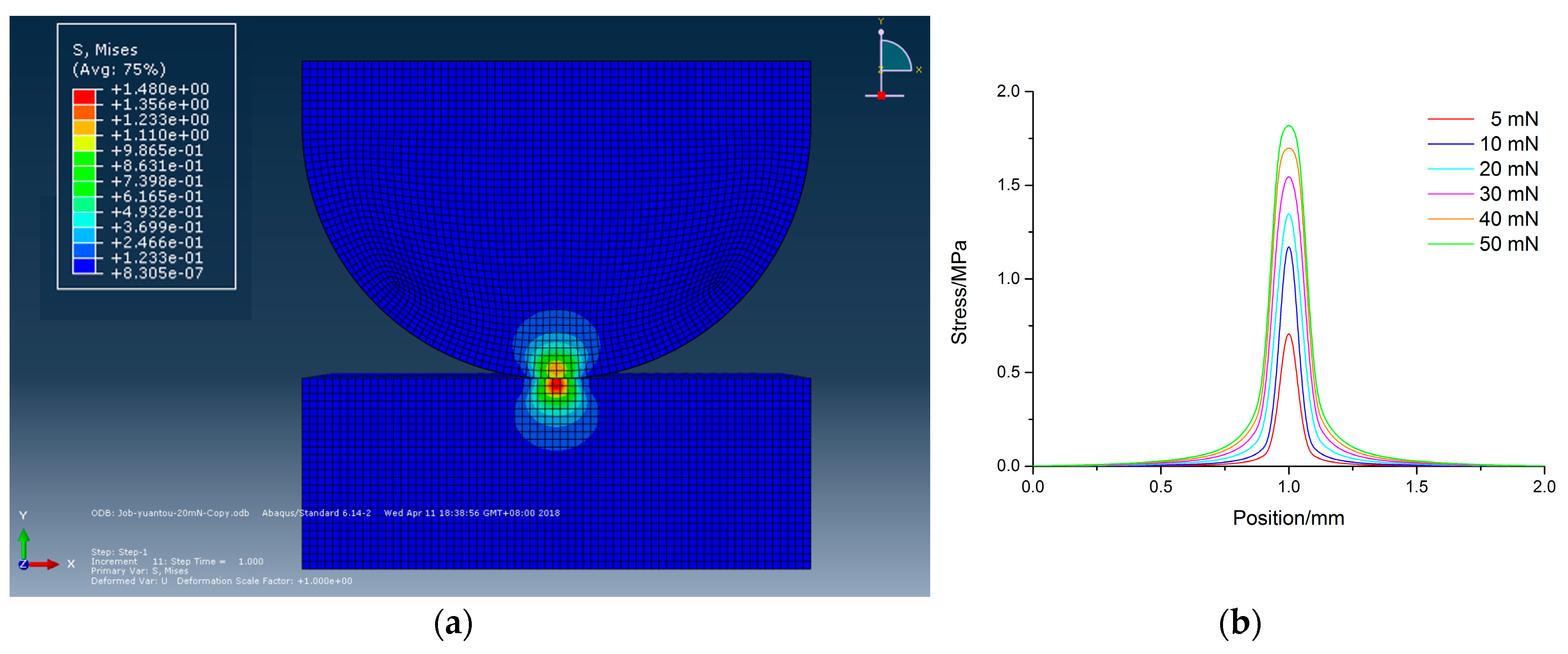
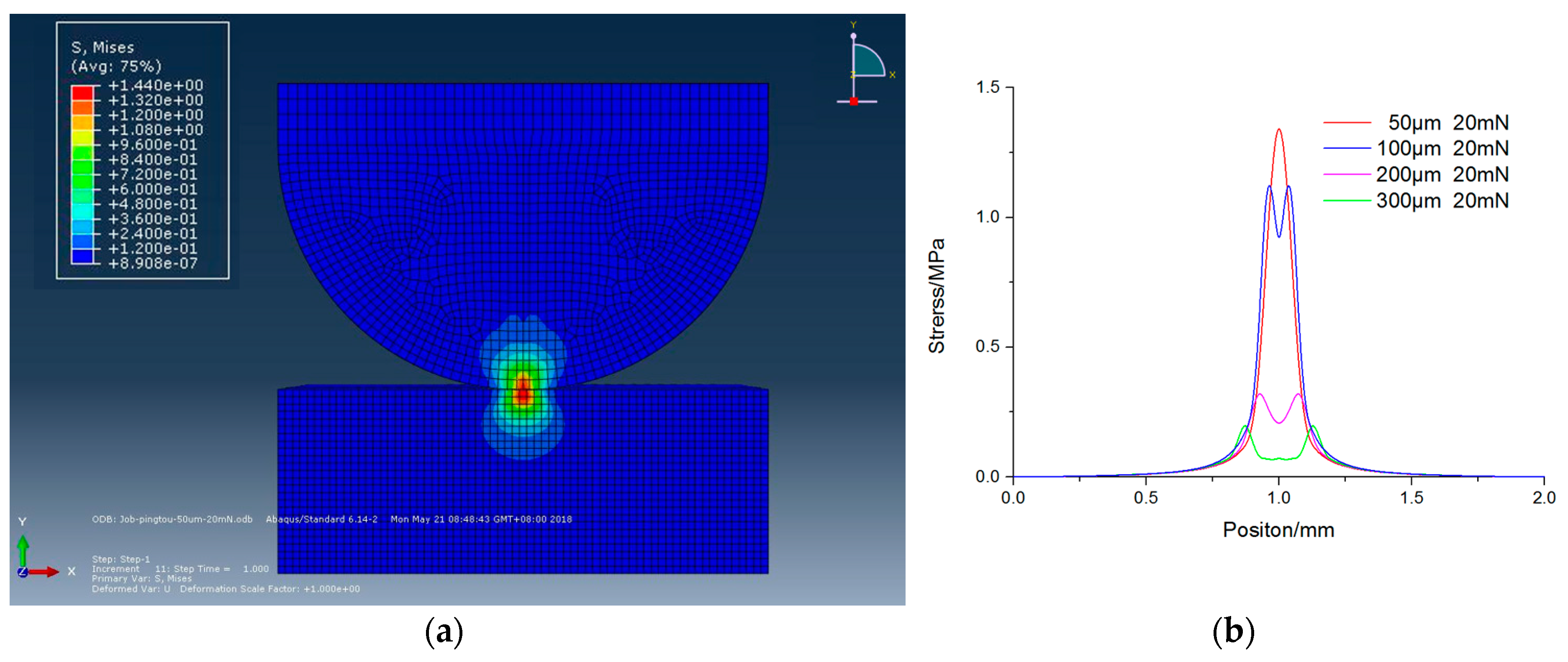
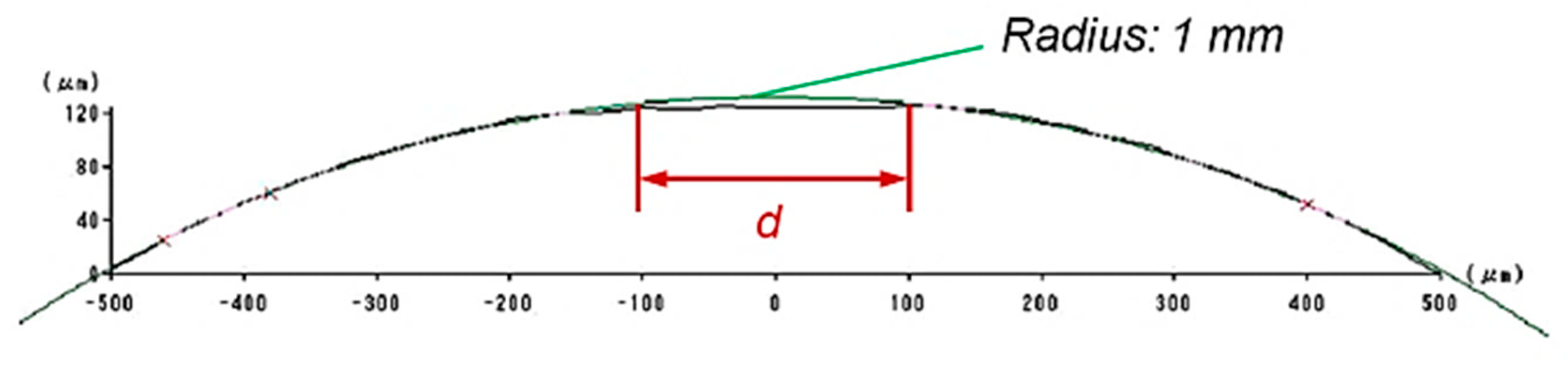
3. Analysis of Pressure and Tool Wear Effects
4. Results and Discussions
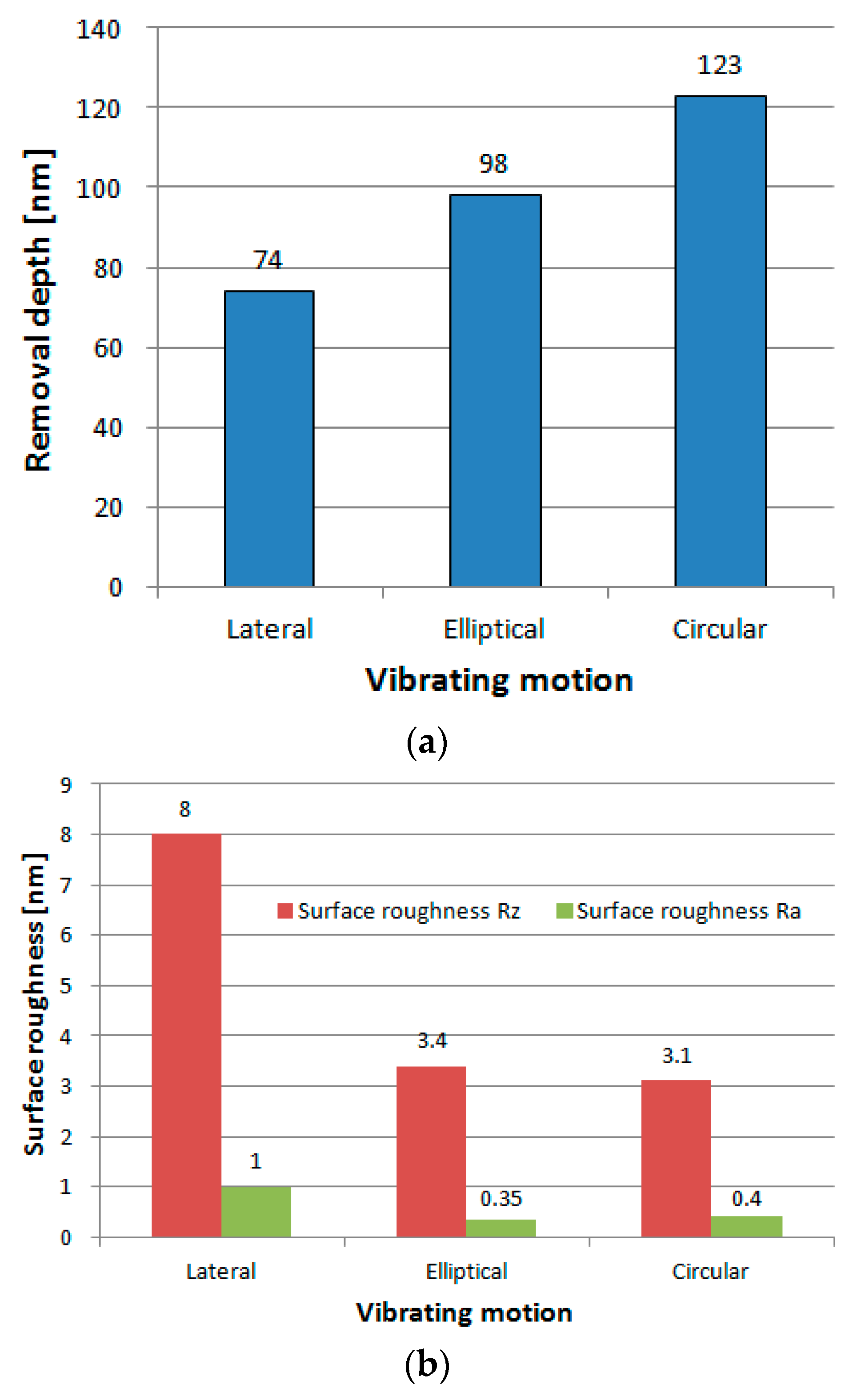
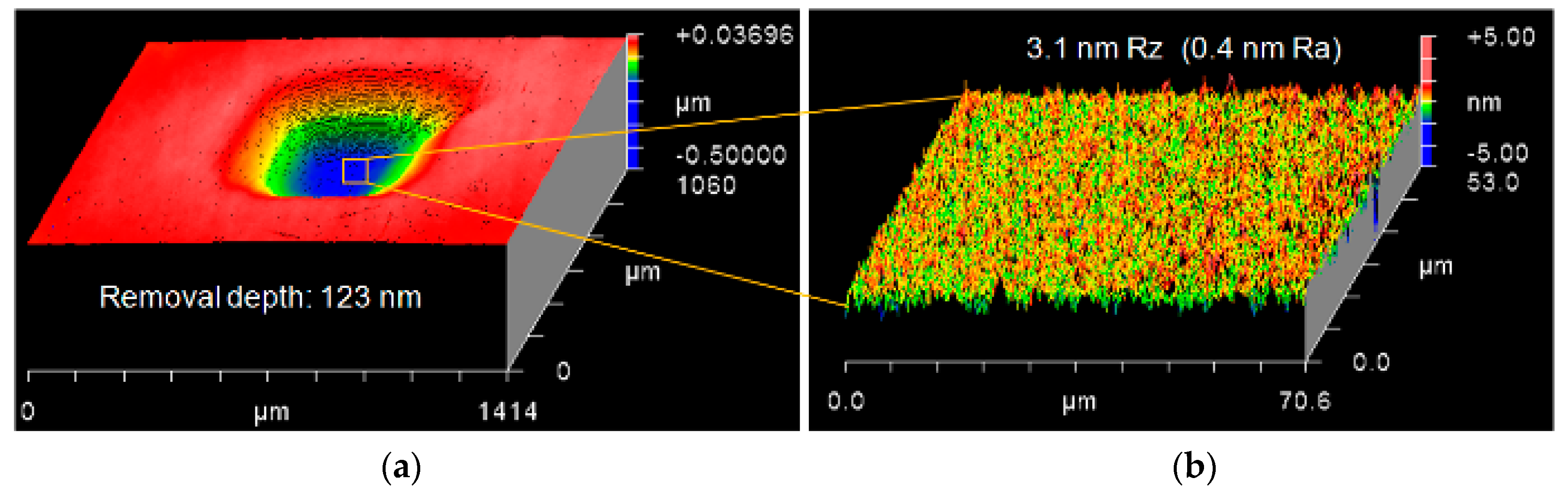
4.1. Effect of Vibrating Motion
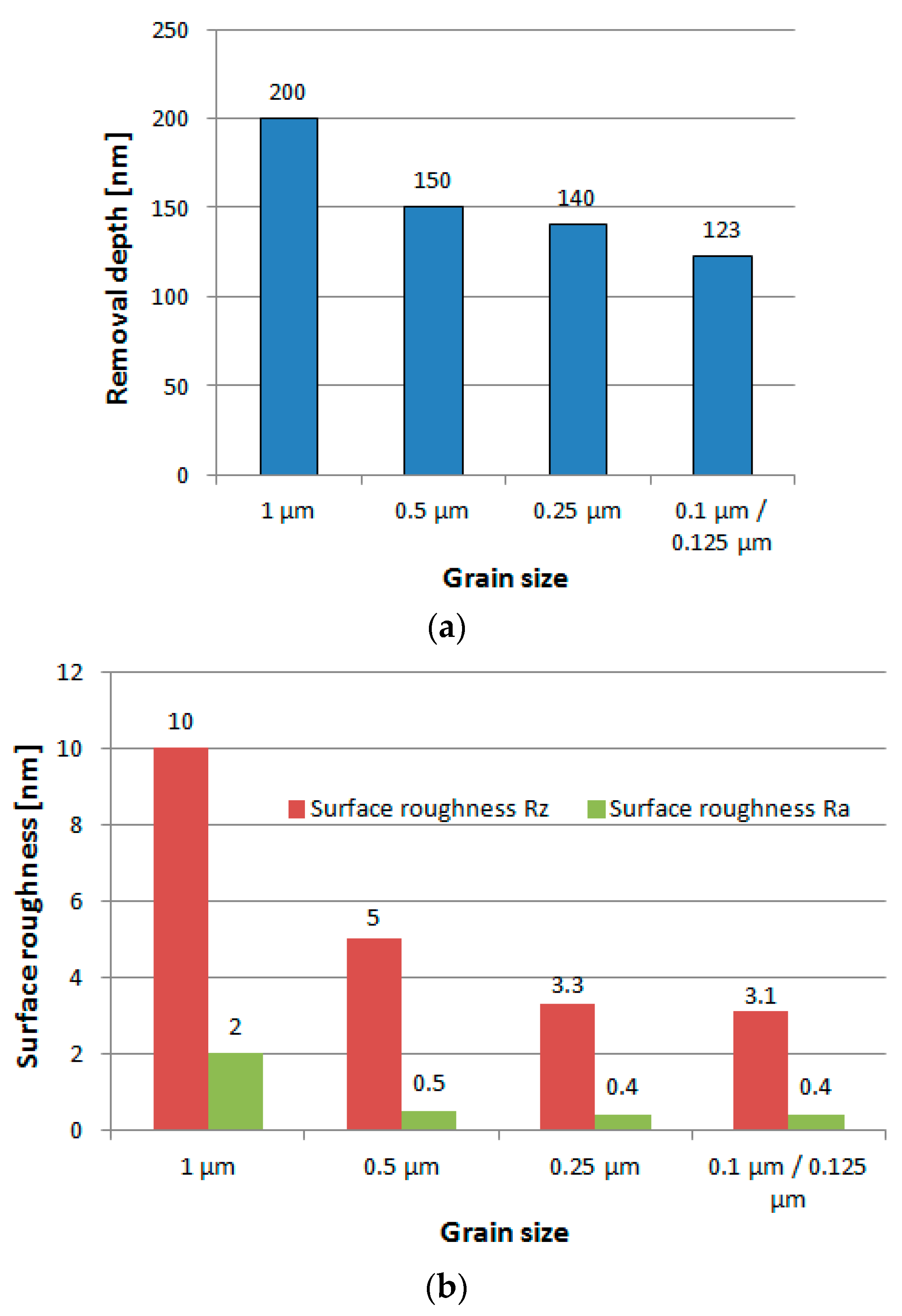
4.2. Effect of Abrasives
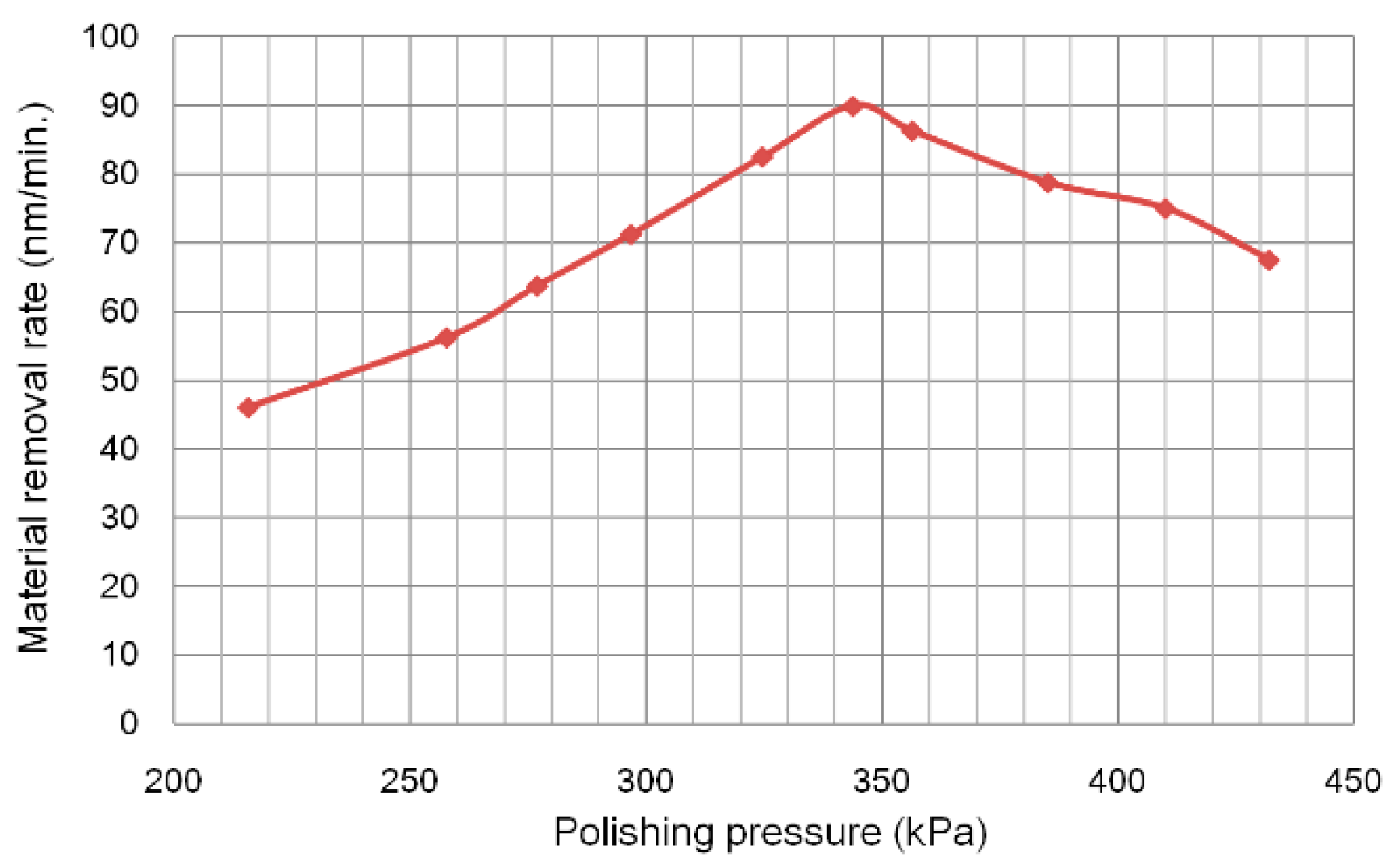
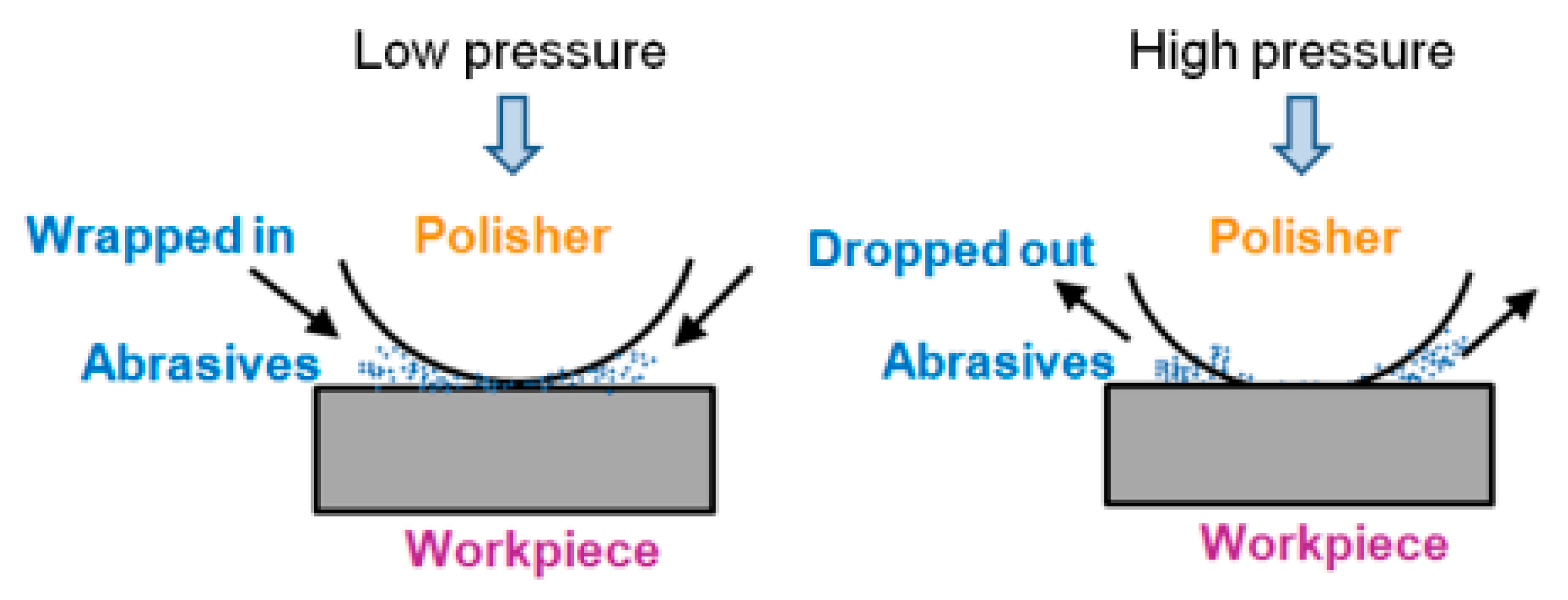
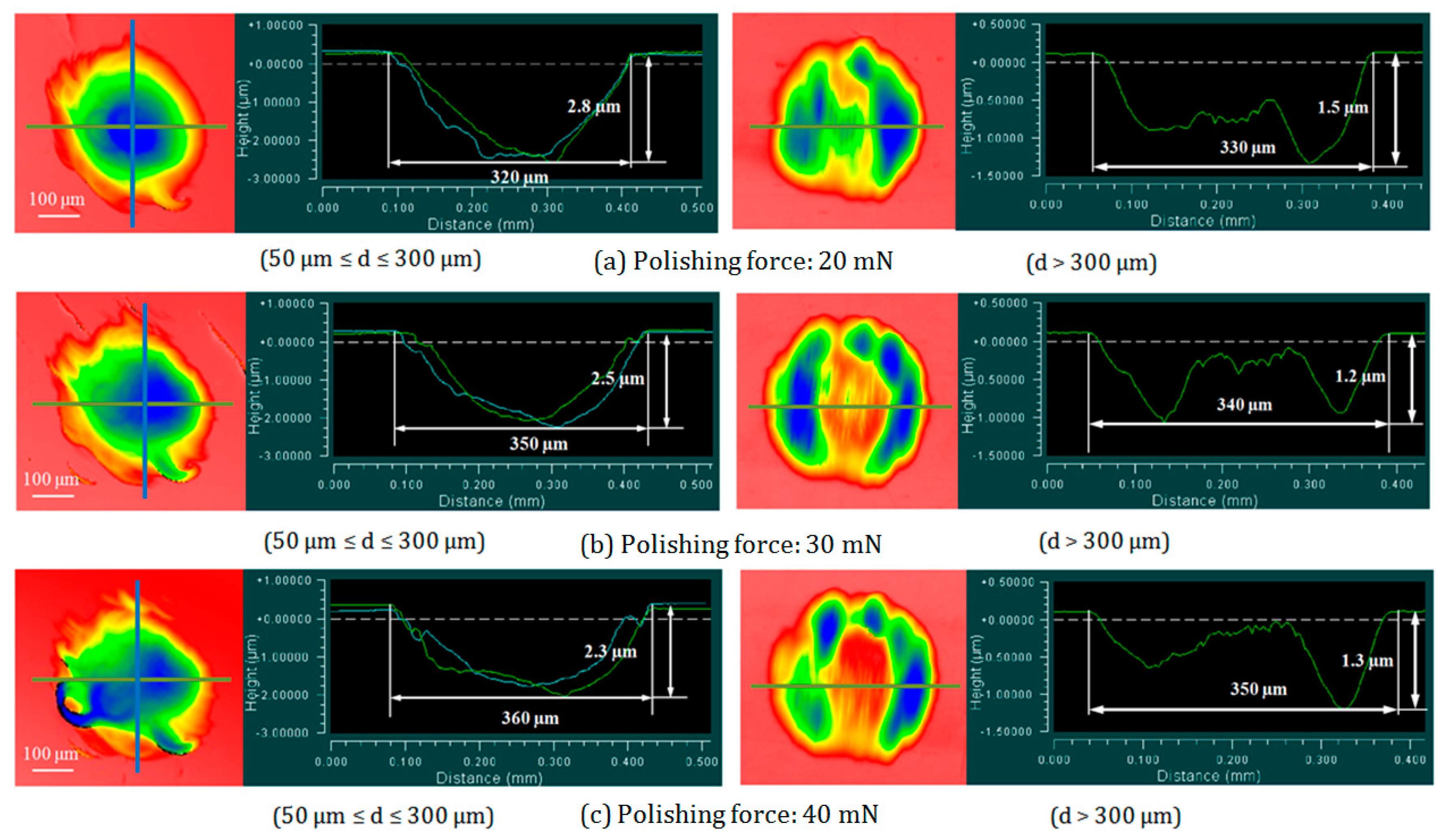
4.3. Effect of Pressure Conditions
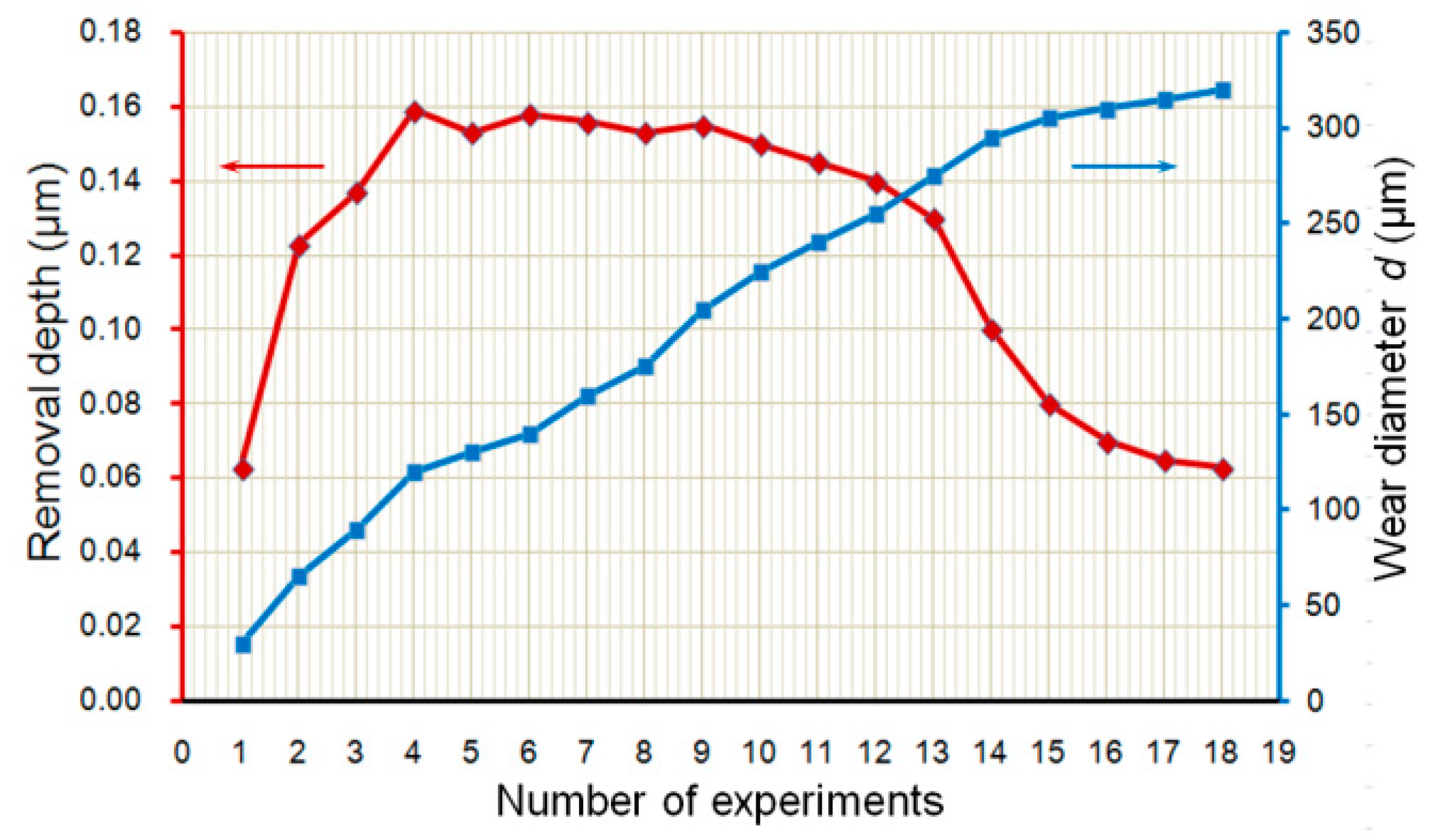
4.4. Effect of Tool Wear
5. Conclusions
- (1)
- 2D vibrating motion created a better surface roughness with higher removal efficiency than 1D vibration motion. The smaller the grain size of the diamond slurry, the better the surface roughness, but the MRR was reduced.
- (2)
- MRR increased when the polishing pressure was under 345 kPa. However, when the polishing pressure exceeded 345 kPa, MRR decreased gradually with the increase of polishing pressure.
- (3)
- MRR was greatly affected by the wear of the polisher when wear diameter on polisher’s head exceeded 300 μm.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brass, M.; Enoch, J.M.; van Stryland, E.W.; Wolfe, W.L. (Eds.) Handbook of Optics (Volume III): Vision and Vision Optics; McGraw Hill: New York, NY, USA, 2010; ISBN 0071498915/97800714. [Google Scholar]
- Fang, F.Z.; Zhang, X.D.; Weckenmann, A.; Zhang, G.X.; Evans, C. Manufacturing and measurement of freeform optics. CIRP Ann. 2013, 62, 823–846. [Google Scholar] [CrossRef]
- Yi, A.; Jain, A. Compression molding of aspherical glass lenses—A combined experimental and numerical analysis. J. Am. Ceram. Soc. 2005, 88, 579–586. [Google Scholar] [CrossRef]
- Yan, J.; Zhou, T.; Yoshihara, N.; Kuriyagawa, T. Shape transferability and microscopic deformation of molding dies in aspherical glass lens molding press. JMTR 2009, 1, 85–102. [Google Scholar]
- Suzuki, H.; Moriwaki, T.; Yamamoto, Y.; Goto, Y. Precision Cutting of Aspherical Ceramic Molds with Micro PCD Milling Tool. CIRP Ann.-Manuf. Technol. 2007, 56, 131–134. [Google Scholar] [CrossRef]
- Huang, H.; Chen, W.K.; Kuriyagawa, T. Profile error compensation approaches for parallel nanogrinding of aspherical mould inserts. Int. J. Mach. Tools Manuf. 2007, 47, 2237–2245. [Google Scholar] [CrossRef]
- Suzuki, H.; Okada, M.; Fujii, K.; Matsui, S.; Yamagata, Y. Development of micro milling tool made of single crystalline diamond for ceramic cutting. CIRP Ann.-Manuf. Technol. 2013, 62, 59–62. [Google Scholar] [CrossRef]
- Chen, F.J.; Yin, S.H.; Huang, H.; Ohmori, H.; Wang, Y.; Fan, Y.F.; Zhu, Y.J. Profile error compensation in ultra-precision grinding of aspheric surfaces with on-machine measurement. Int. J. Mach. Tools Manuf. 2010, 50, 480–486. [Google Scholar] [CrossRef]
- Kordonski, W.; Jacobs, S. Magnetorheological finishing. Int. J. Mod. Phys. B 1996, 10, 2837–2848. [Google Scholar] [CrossRef]
- Fähnle, W.; van Brug, H.; Frankena, H.J. Fluid jet polishing of optical surfaces. Appl. Opt. 1998, 37, 6771–6773. [Google Scholar] [CrossRef] [PubMed]
- Walker, D.D.; Brooks, D.; King, A.; Freeman, R.; Morton, R.; McCavana, G.; Kim, S.W. The ‘Precessions’ tooling for polishing and figuring flat, spherical and aspheric surfaces. Opt. Express 2003, 11, 958–964. [Google Scholar] [CrossRef] [PubMed]
- Walker, D.D.; Freeman, R.; Morton, R.; McCavana, G.; Beaucamp, A. Use of the ‘Precessions’TM process for prepolishing and correcting 2D & 2½D form. Opt. Express 2006, 14, 11787–11795. [Google Scholar] [PubMed]
- Beaucamp, A.; Namba, Y.; Inasaki, I.; Freeman, R. Finishing of optical molds to λ/20 by automated corrective polishing. CIRP Ann.-Manuf. Technol. 2011, 60, 375–378. [Google Scholar] [CrossRef]
- Brehl, D.E.; Dow, T.A. Review of vibration-assisted machining. Precis. Eng. 2008, 32, 153–172. [Google Scholar] [CrossRef]
- Kumar, M.N.; Subbu, S.K.; Krishna, P.V.; Venugopal, A. Vibration assisted conventional and advanced machining: A review. Procedia Eng. 2014, 97, 1577–1586. [Google Scholar] [CrossRef]
- Li, Z.; Jin, G.; Fang, F.; Gong, H.; Jia, H. Ultrasonically Assisted Single Point Diamond Turning of Optical Mold of Tungsten Carbide. Micromachines 2018, 9, 77. [Google Scholar] [CrossRef]
- Suzuki, H.; Moriwaki, T.; Okino, T.; Ando, Y. Development of Ultrasonic Vibration Assisted Polishing Machine for Micro Aspheric Die and Mold. CIRP Ann.-Manuf. Technol. 2006, 55, 385–388. [Google Scholar] [CrossRef]
- Suzuki, H.; Hamada, S.; Okino, T.; Kondo, M.; Yamagata, Y.; Higuchi, T. Ultraprecision finishing of micro-aspheric surface by ultrasonic two-axis vibration assisted polishing. CIRP Ann. 2010, 59, 347–350. [Google Scholar] [CrossRef]
- Guo, J.; Morita, S.; Hara, M.; Yamagata, Y.; Higuchi, T. Ultra-precision finishing of micro-aspheric mold using a magnetostrictive vibrating polisher. CIRP Ann.-Manuf. Technol. 2012, 61, 371–374. [Google Scholar] [CrossRef]
- Guo, J.; Suzuki, H.; Higuchi, T. Development of micro polishing system using magnetostrictive vibrating polisher. Precis. Eng. 2013, 37, 81–87. [Google Scholar] [CrossRef]
- Evans, C.J.; Paul, E.; Dornfeld, D.; Lucca, D.A.; Byrne, G.; Tricard, M.; Klocke, F.; Dambon, O.; Mullany, B.A. Material Removal Mechanisms in Lapping and Polishing. CIRP Ann.-Manuf. Technol. 2003, 52, 611–633. [Google Scholar] [CrossRef]
- Komanduri, R.; Lucca, D.A.; Tani, Y. Technological Advances in Fine Abrasive Process. CIRP Ann. 1997, 46, 545–596. [Google Scholar] [CrossRef]
- Brinksmeier, E.; Riemer, O.; Gessenharter, A. Finishing of structured surfaces by abrasive polishing. Precis. Eng. 2006, 30, 325–336. [Google Scholar] [CrossRef]
- Guo, J.; Suzuki, H.; Morita, S.; Yamagata, Y.; Higuchi, T. A real-time polishing force control system for ultra-precision finishing of micro-optics. Precis. Eng. 2013, 37, 787–792. [Google Scholar] [CrossRef]
- Preston, F.W. The theory and design of plate glass polishing machines. J. Glass Technol. 1927, 11, 214–256. [Google Scholar]
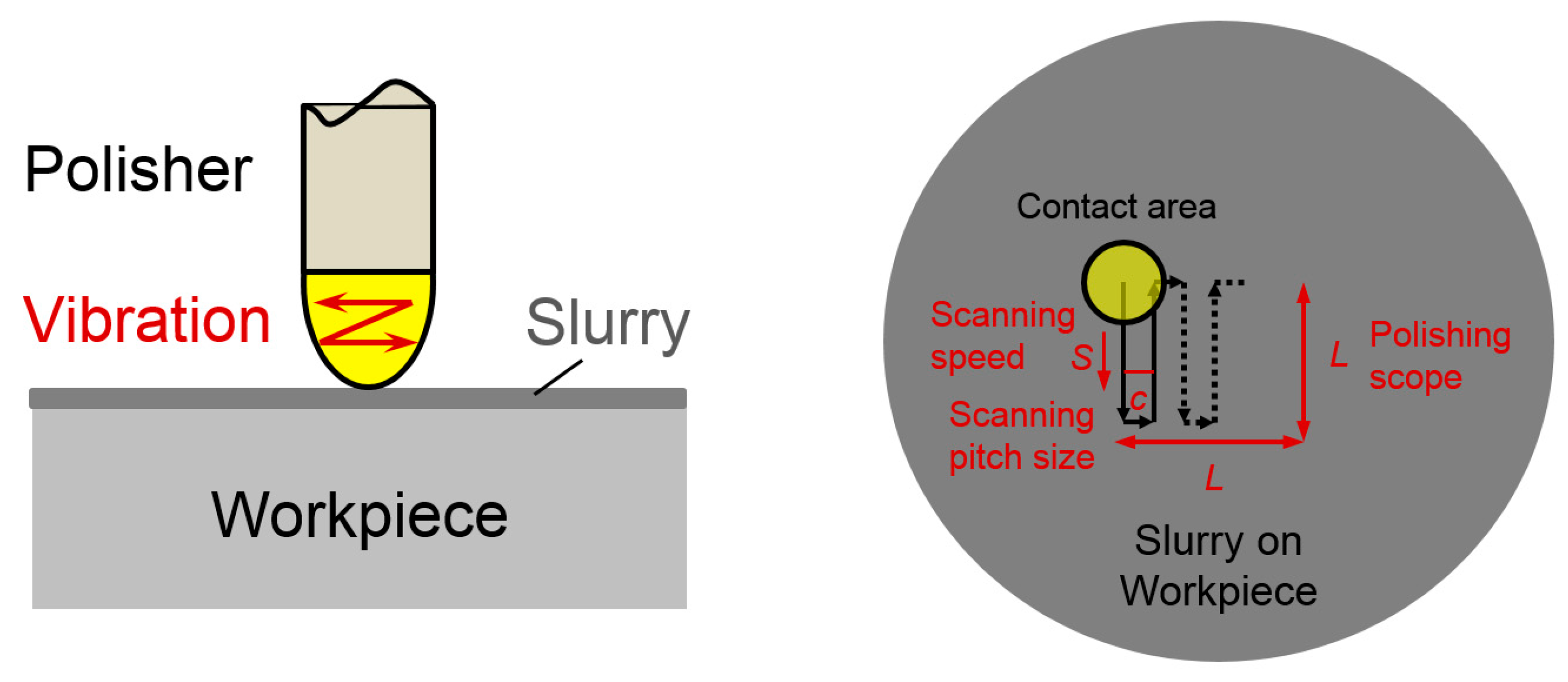



| Workpiece Material | Tungsten Carbide |
|---|---|
| Polisher head Radius Hardness | Polyurethane 1 mm IRHD 90 |
| Abrasive Grain size Density | Diamond slurry 0.1 μm/0.125 μm/0.25μm/0.5 μm/1 μm 1 wt % |
| Polishing force | W = 5–50 mN (Increment: 5 mN) |
| Vibrating motion | Lateral (λ = 43 μm) Circular (r = 30 μm) Elliptical (a = 40 μm, b = 16 μm) |
| Frequency | 9.2 kHz |
| Polishing scope Pitch size Scanning speed | 400 μm × 400 μm 20 μm 3.5 mm/min |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Suzuki, H. Effects of Process Parameters on Material Removal in Vibration-Assisted Polishing of Micro-Optic Mold. Micromachines 2018, 9, 349. https://doi.org/10.3390/mi9070349
Guo J, Suzuki H. Effects of Process Parameters on Material Removal in Vibration-Assisted Polishing of Micro-Optic Mold. Micromachines. 2018; 9(7):349. https://doi.org/10.3390/mi9070349
Chicago/Turabian StyleGuo, Jiang, and Hirofumi Suzuki. 2018. "Effects of Process Parameters on Material Removal in Vibration-Assisted Polishing of Micro-Optic Mold" Micromachines 9, no. 7: 349. https://doi.org/10.3390/mi9070349
APA StyleGuo, J., & Suzuki, H. (2018). Effects of Process Parameters on Material Removal in Vibration-Assisted Polishing of Micro-Optic Mold. Micromachines, 9(7), 349. https://doi.org/10.3390/mi9070349






