Numerical and Experimental Analyses of Three-Dimensional Unsteady Flow around a Micro-Pillar Subjected to Rotational Vibration
Abstract
1. Introduction
2. Numerical Procedures
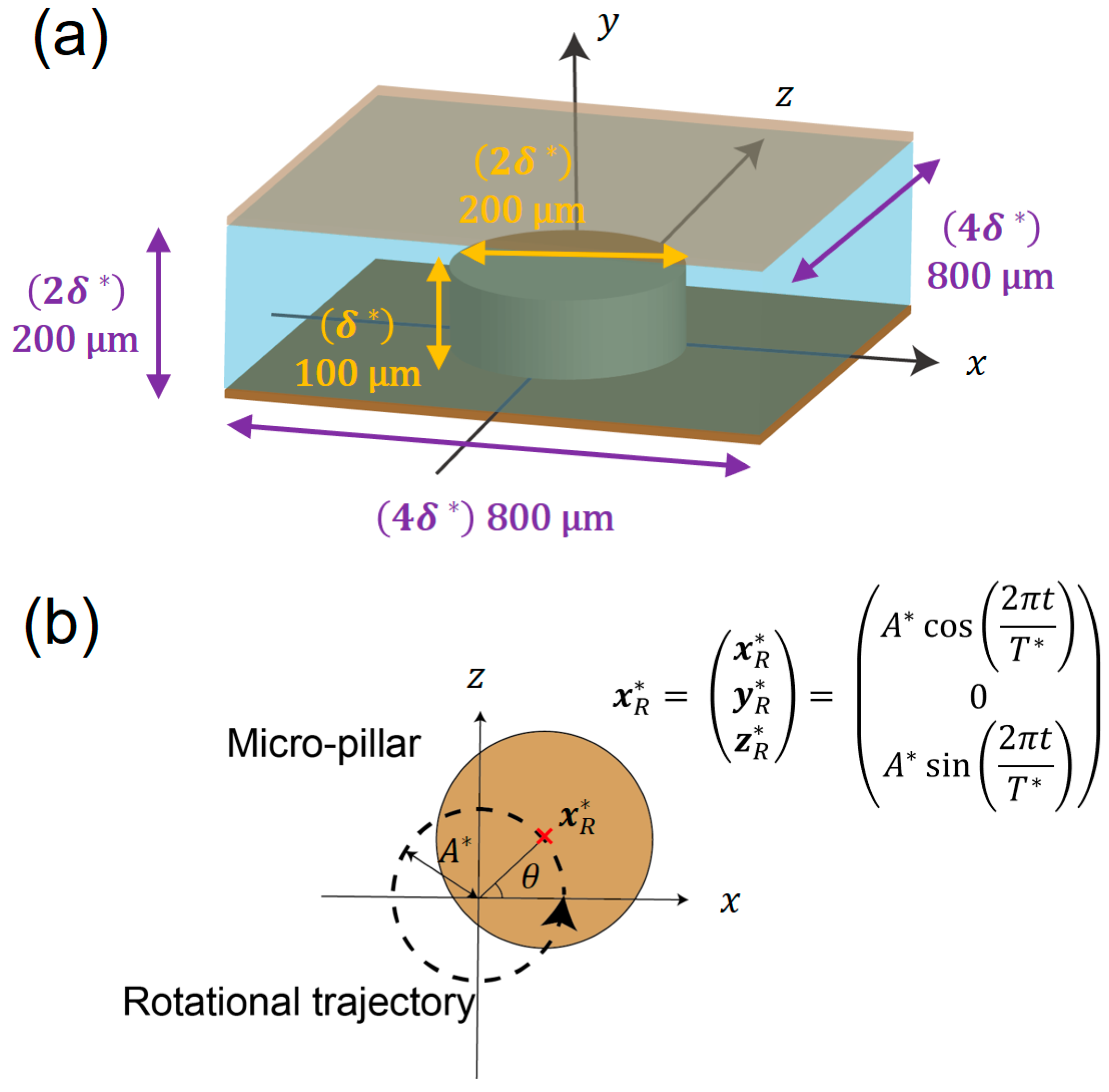
2.1. Computational Domain and Governing Equations
2.2. Volume Penalization Method
2.3. Numerical Methods and Conditions
2.4. Derivation of Steady Streaming Flow (Time-Averaged Velocity Field)
3. Experimental Procedure
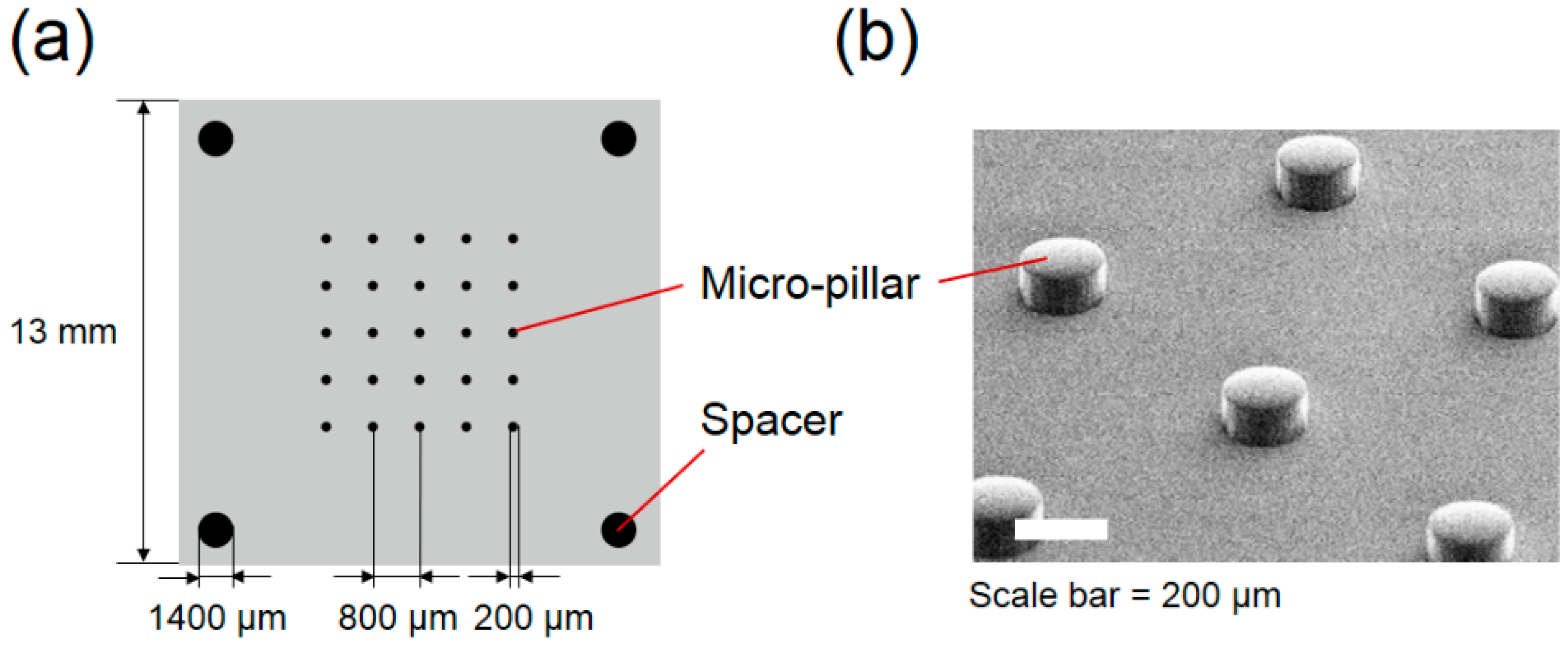
3.1. Fabrication of Micro-Pillar Array
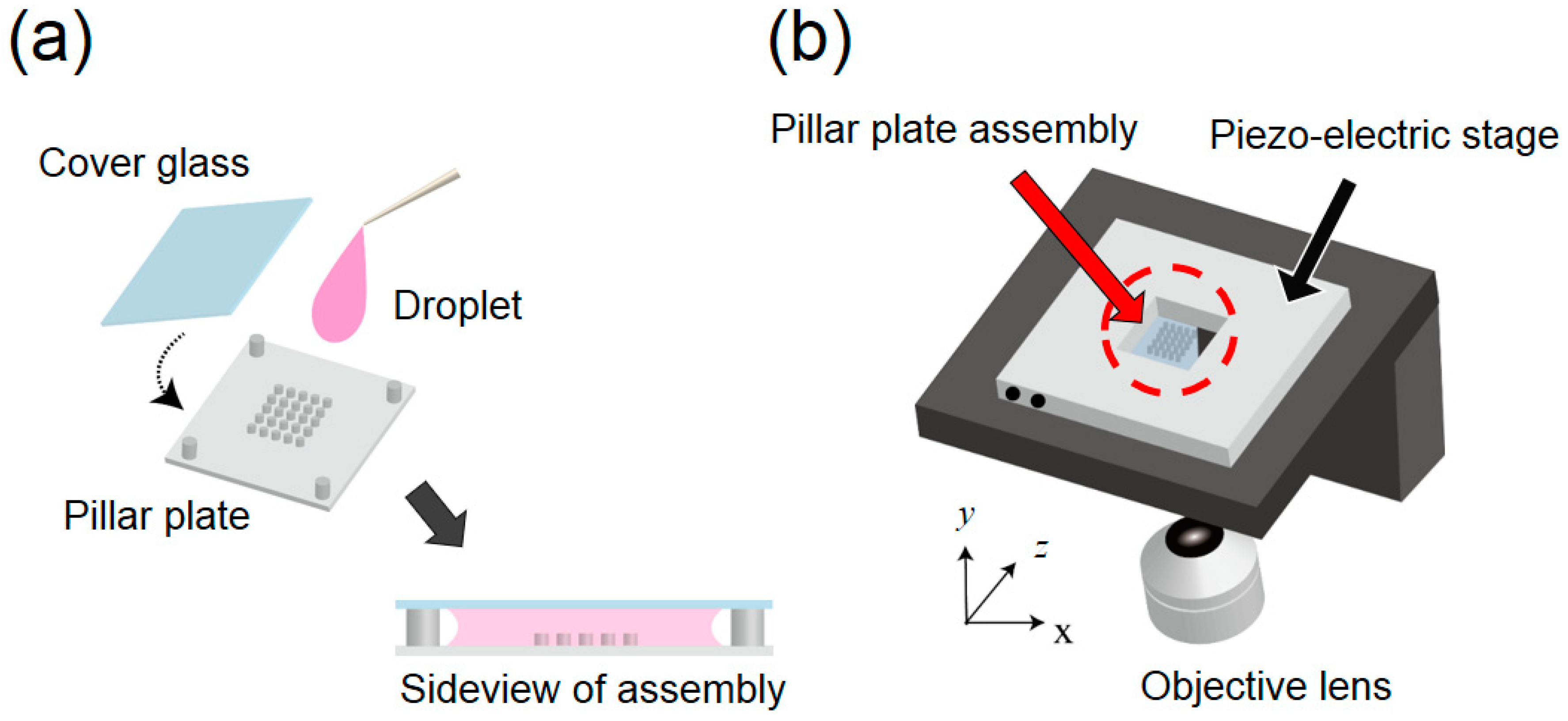
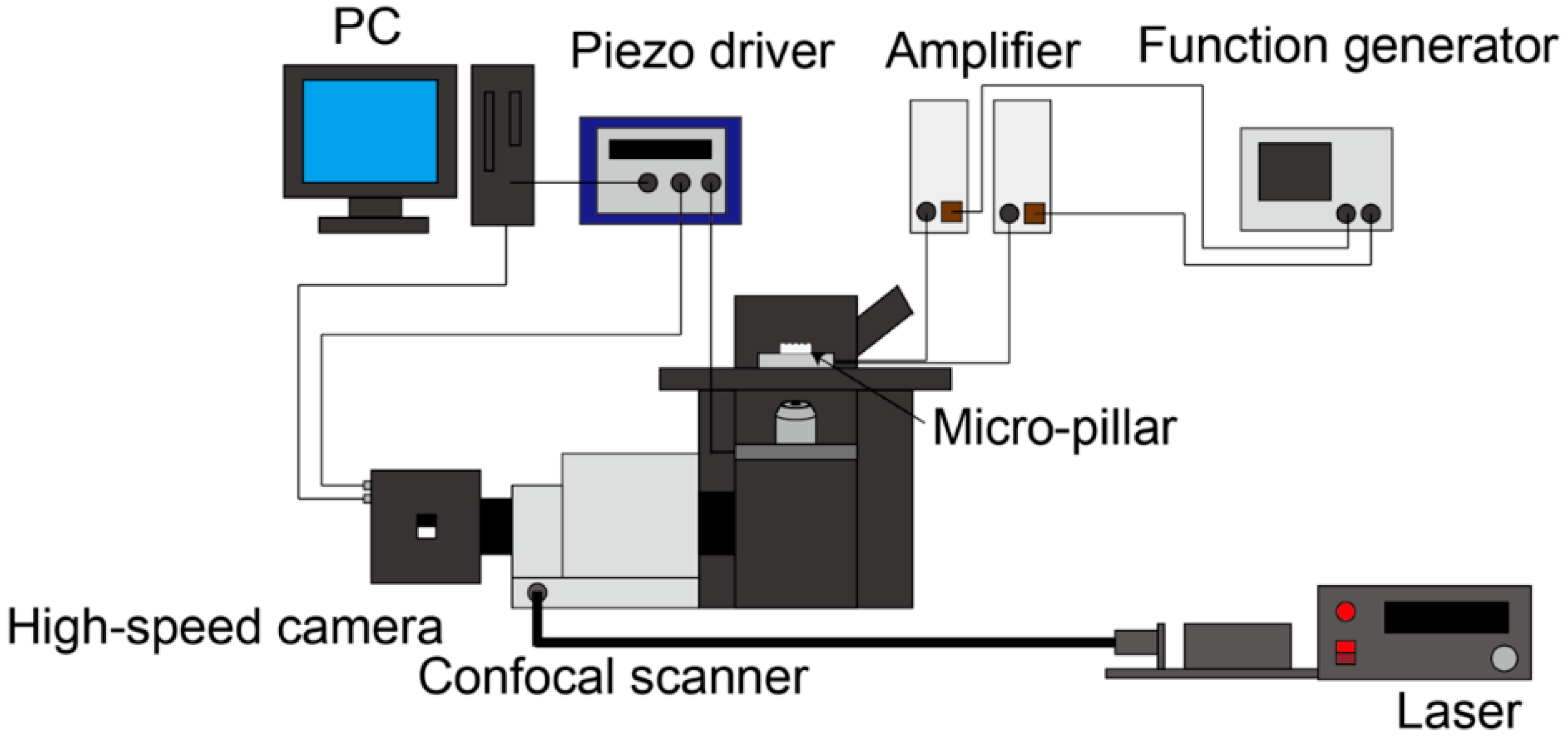
3.2. Experimental Setup and Conditions
3.3. PIV System
3.4. PIV Analysis
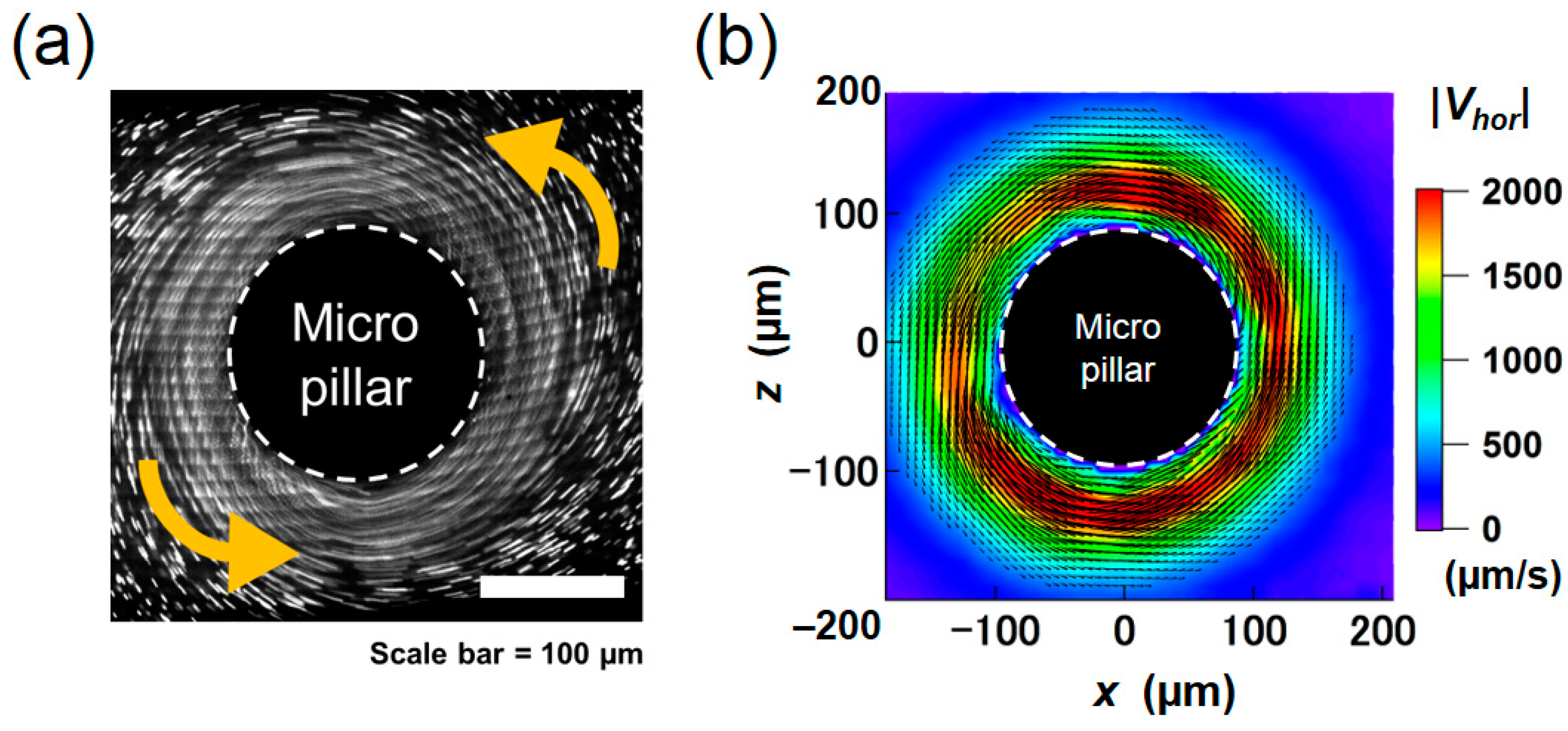
3.5. Horizontal Visualization
4. Numerical Results
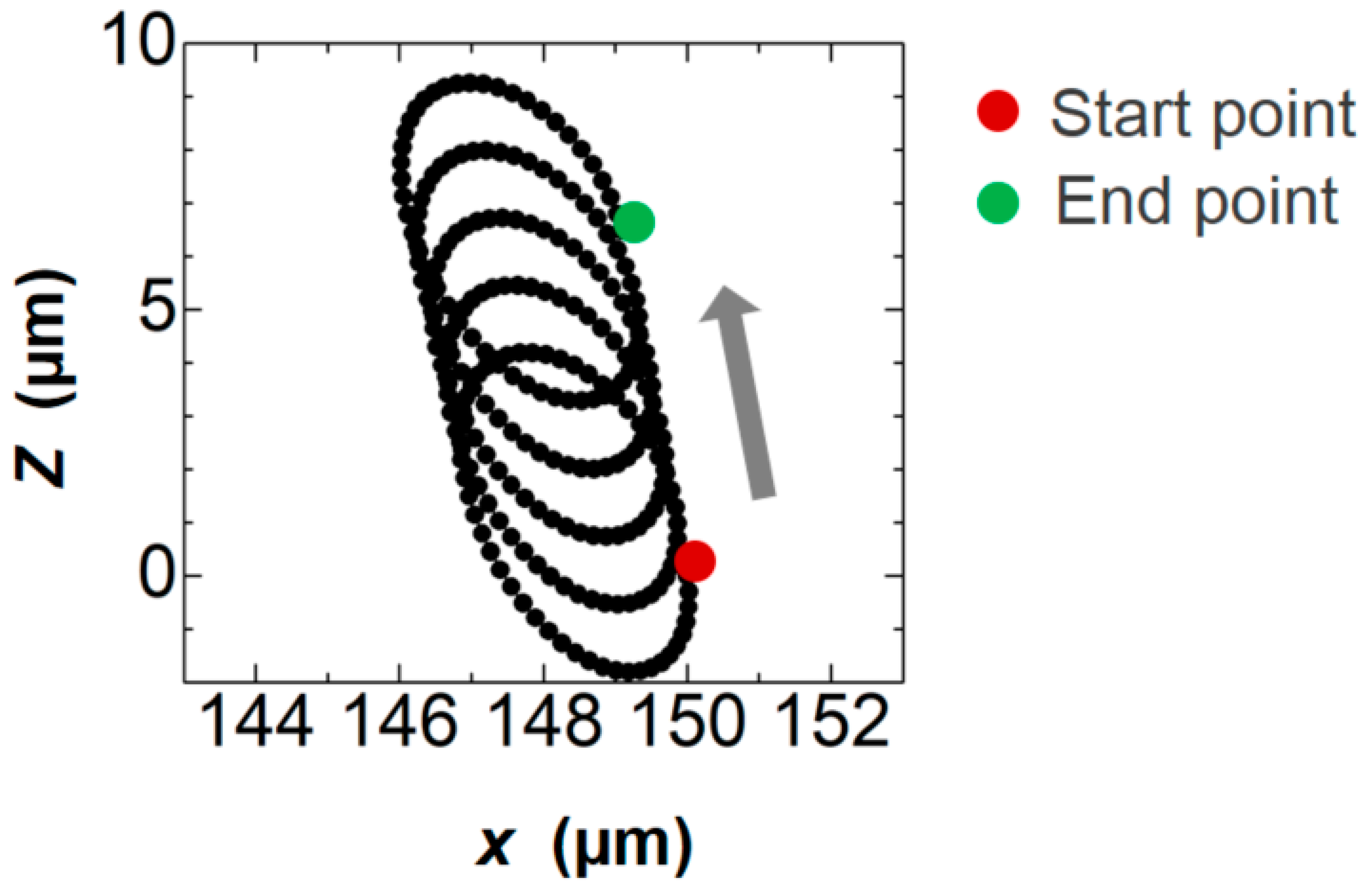
4.1. Instantaneous Velocity Field
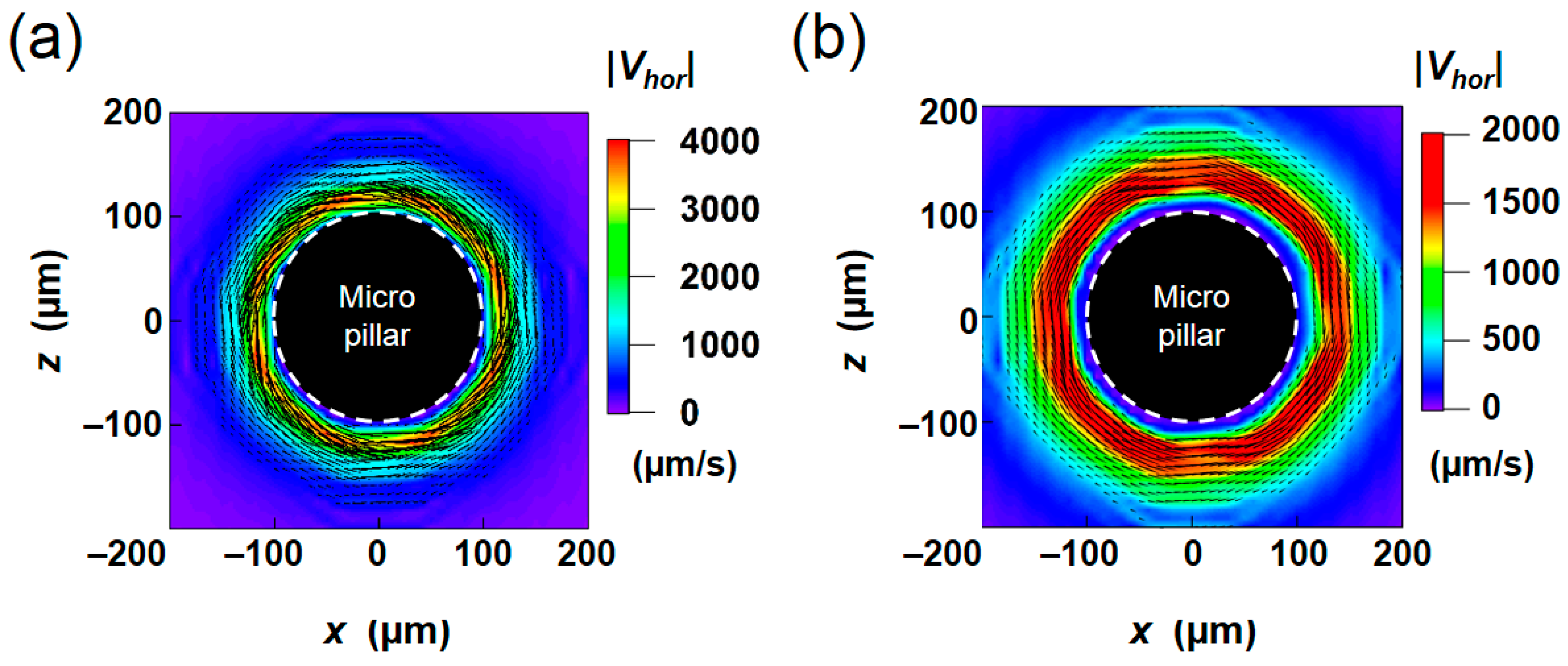
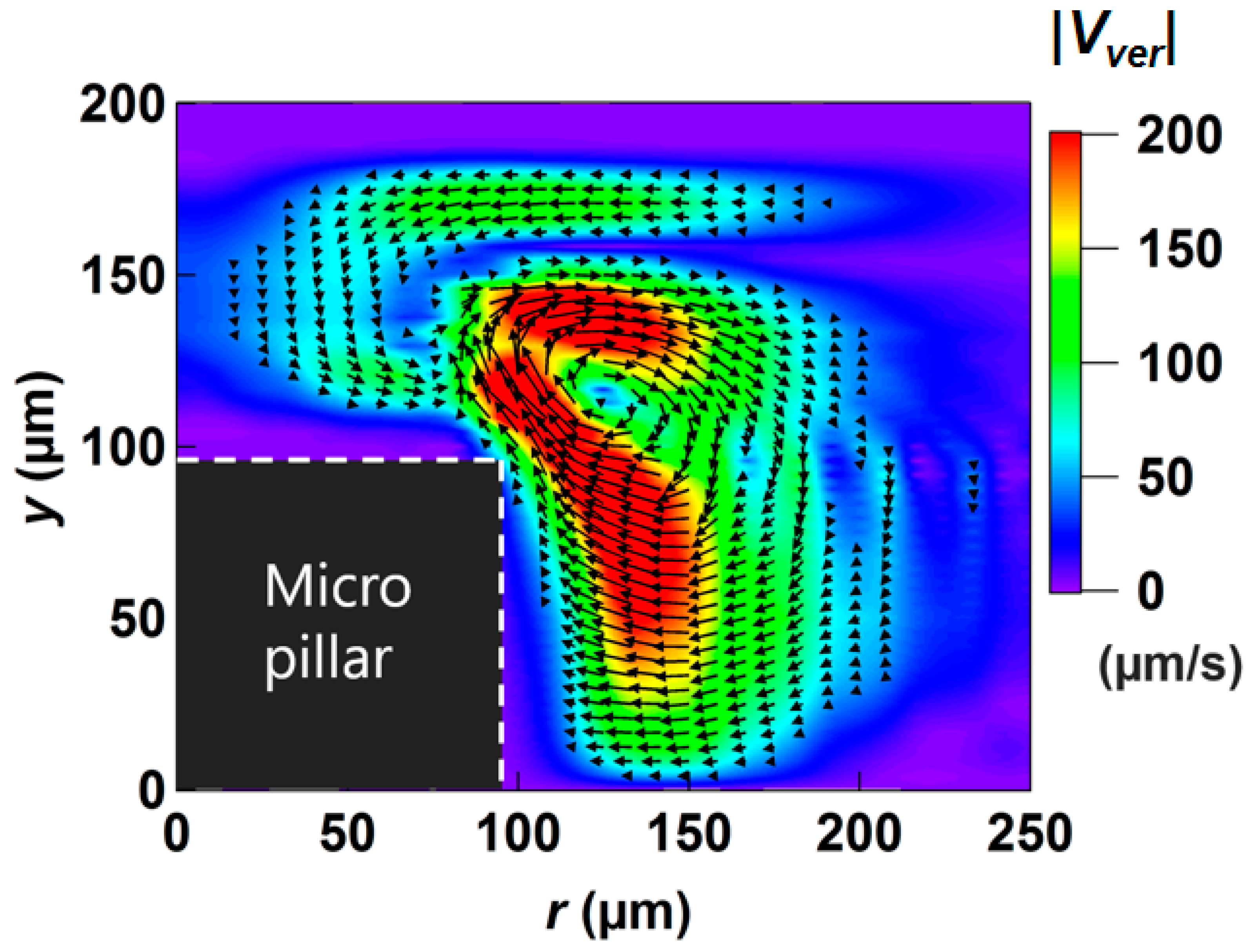
4.2. Time-Averaged Flow Field
5. Comparison with experimental results
5.1. Results of PIV Measurement
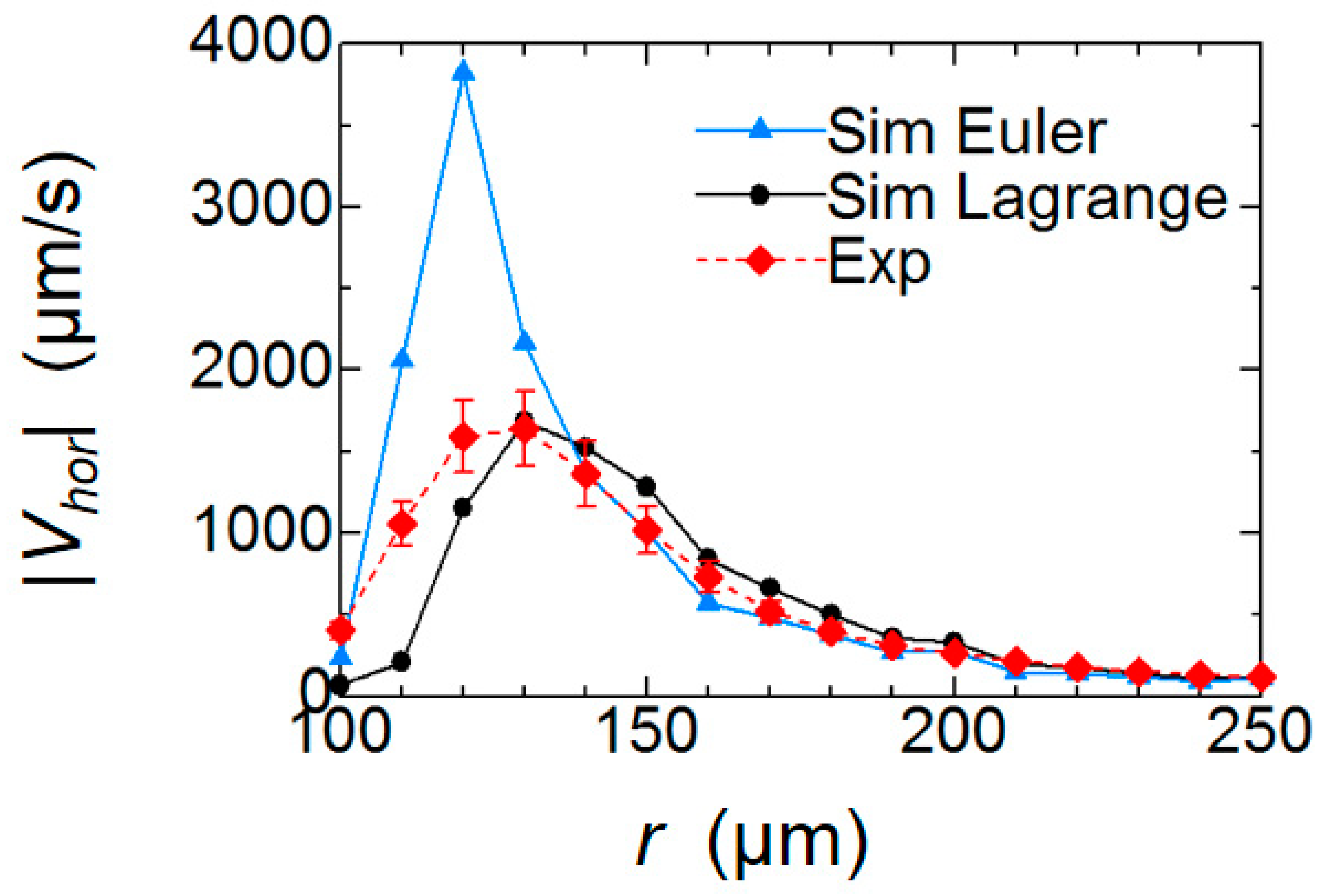
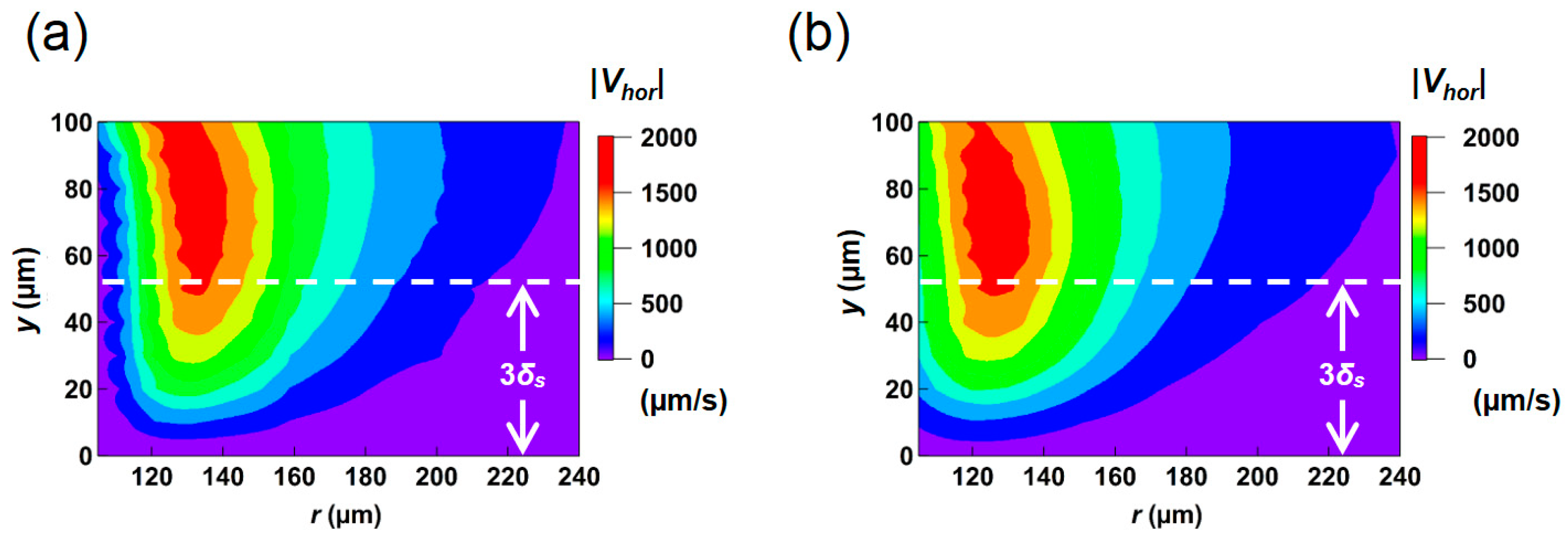
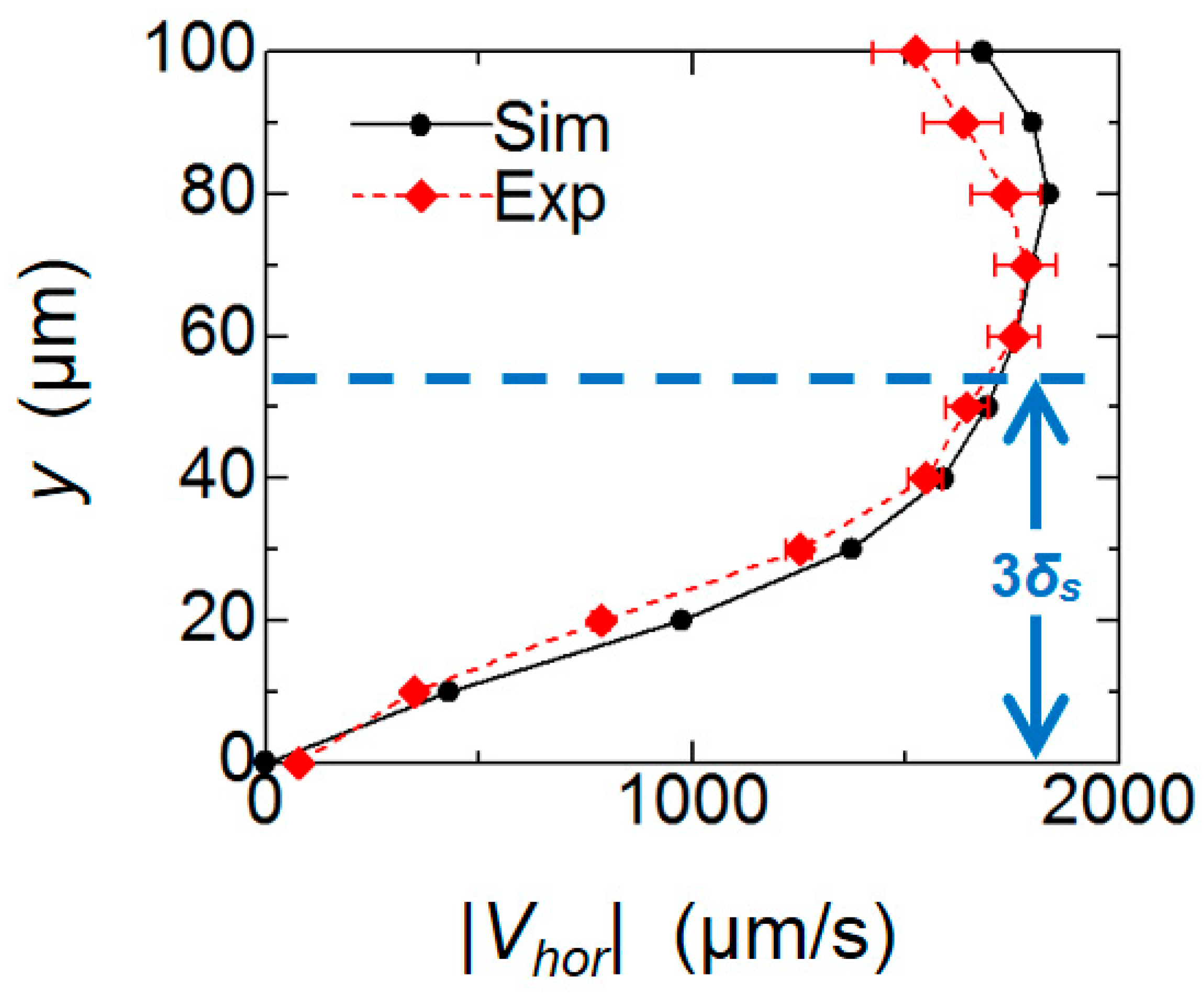
5.2. Comparison of Radial Velocity Profile
5.3. Comparison of Normal Velocity Profile
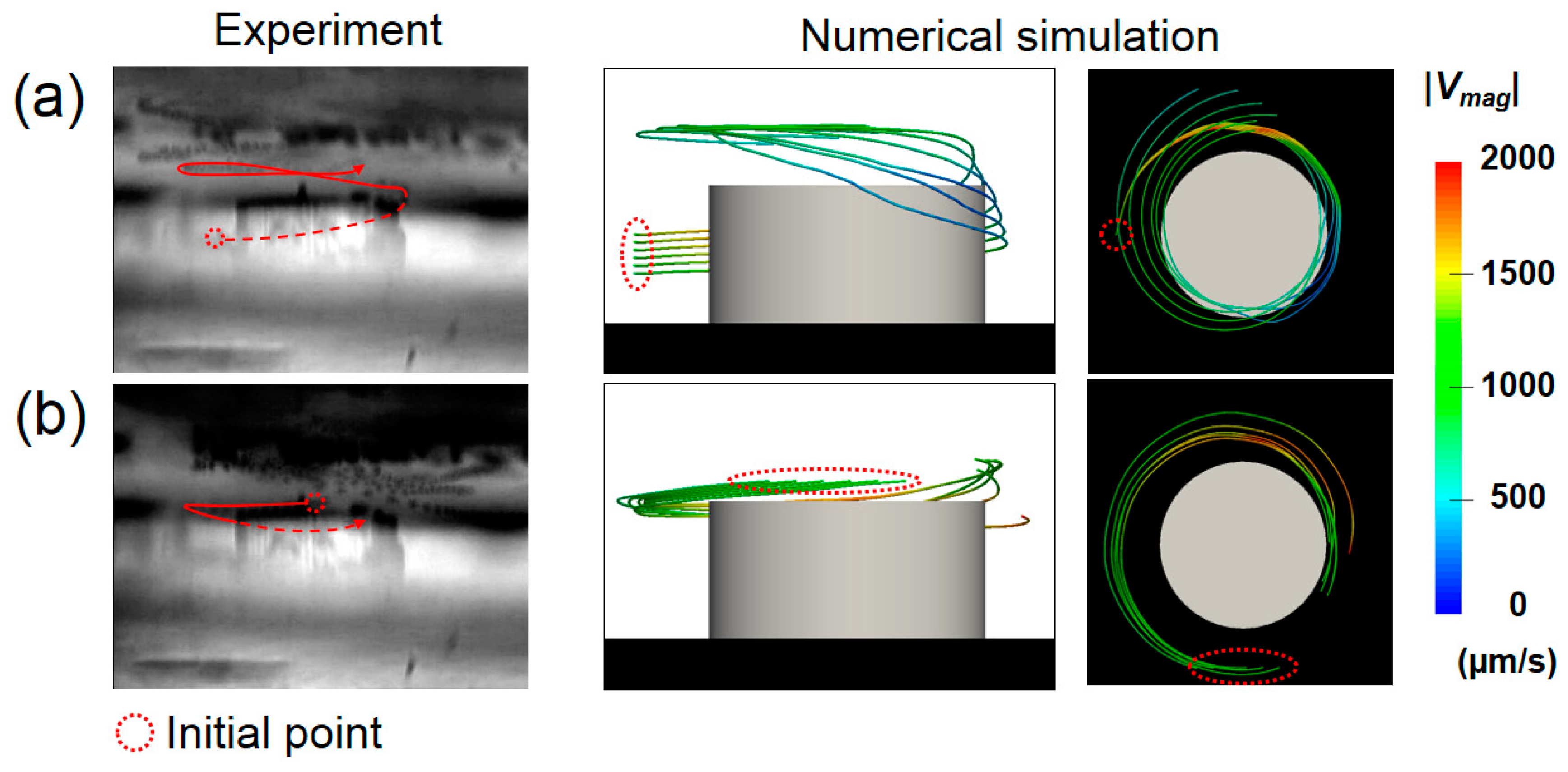
5.4. Three-Dimensionality of the Flow
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wiklund, M.; Green, R.; Ohlin, M. Acoustofluidics 14: Applications of acoustic streaming in microfluidic devices. Lab Chip 2012, 12, 2438–2451. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.; Yazdi, S.; Ardekani, A.M. Hydrodynamic mechanisms of cell and particle trapping in microfluidics. Biomicrofluidics 2013, 7, 021501. [Google Scholar] [CrossRef] [PubMed]
- Hagiwara, M.; Kawahara, T.; Arai, F. Local streamline generation by mechanical oscillation in a microfluidic chip for noncontact cell manipulations. Appl. Phys. Lett. 2012, 101, 074102. [Google Scholar] [CrossRef]
- Huang, P.H.; Xie, Y.L.; Ahmed, D.; Rufo, J.; Nama, N.; Chen, Y.C.; Chan, C.Y.; Huang, T.J. An acoustofluidic micromixer based on oscillating sidewall sharp-edges. Lab Chip 2013, 13, 3847–3852. [Google Scholar] [CrossRef] [PubMed]
- Ohlin, M.; Christakou, A.E.; Frisk, T.; Onfelt, B.; Wiklund, M. Influence of acoustic streaming on ultrasonic particle manipulation in a 100-well ring-transducer microplate. J. Micromech. Microeng. 2013, 23, 035008. [Google Scholar] [CrossRef]
- Huang, P.H.; Nama, N.; Mao, Z.M.; Li, P.; Rufo, J.; Chen, Y.C.; Xie, Y.L.; Wei, C.H.; Wang, L.; Huang, T.J. A reliable and programmable acoustofluidic pump powered by oscillating sharp-edge structures. Lab Chip 2014, 14, 4319–4323. [Google Scholar] [CrossRef] [PubMed]
- Hayakawa, T.; Akita, Y.; Arai, F. Parallel trapping of single motile cells based on vibration-induced flow. Microfluid. Nanofluid. 2018, 22, 42. [Google Scholar] [CrossRef]
- Hayakawa, T.; Sakuma, S.; Arai, F. On-chip 3D rotation of oocyte based on a vibration-induced local whirling flow. Microsyst. Nanoeng. 2015, 1, 15001. [Google Scholar] [CrossRef]
- Hayakawa, T.; Sakuma, S.; Fukuhara, T.; Yokoyama, Y.; Arai, F. A Single Cell Extraction Chip Using Vibration-Induced Whirling Flow and a Thermo-Responsive Gel Pattern. Micromachines 2014, 5, 681–696. [Google Scholar] [CrossRef]
- Ahmed, D.; Ozcelik, A.; Bojanala, N.; Nama, N.; Upadhyay, A.; Chen, Y.; Hanna-Rose, W.; Huang, T.J. Rotational manipulation of single cells and organisms using acoustic waves. Nat. Commun. 2016, 7, 11085. [Google Scholar] [CrossRef]
- Ozcelik, A.; Nama, N.; Huang, P.H.; Kaynak, M.; McReynolds, M.R.; Hanna-Rose, W.; Huang, T.J. Acoustofluidic Rotational Manipulation of Cells and Organisms Using Oscillating Solid Structures. Small 2016, 12, 5120–5125. [Google Scholar] [CrossRef] [PubMed]
- Kim, E.; Kojima, M.; Xiaoming, L.; Hattori, T.; Kamiyama, K.; Mae, Y.; Arai, T. Analysis of rotational flow generated by circular motion of an end effector for 3D micromanipulation. ROBOMECH J. 2017, 4, 5. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory, 8th ed.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Amin, N.; Riley, N. Streaming from a Sphere Due to a Pulsating Source. J. Fluid Mech. 1990, 210, 459–473. [Google Scholar] [CrossRef]
- Riley, N. Steady streaming. Annu. Rev. Fluid Mech. 2001, 33, 43–65. [Google Scholar] [CrossRef]
- Lieu, V.H.; House, T.A.; Schwartz, D.T. Hydrodynamic Tweezers: Impact of Design Geometry on Flow and Microparticle Trapping. Anal. Chem. 2012, 84, 1963–1968. [Google Scholar] [CrossRef] [PubMed]
- House, T.A.; Lieu, V.H.; Schwartz, D.T. A model for inertial particle trapping locations in hydrodynamic tweezers arrays. J. Micromech. Microeng. 2014, 24, 045019. [Google Scholar] [CrossRef]
- Nama, N.; Huang, P.H.; Huang, T.J.; Costanzo, F. Investigation of acoustic streaming patterns around oscillating sharp edges. Lab Chip 2014, 14, 2824–2836. [Google Scholar] [CrossRef] [PubMed]
- Nama, N.; Huang, P.H.; Huang, T.J.; Costanzo, F. Investigation of micromixing by acoustically oscillated sharp-edges. Biomicrofluidics 2016, 10, 024124. [Google Scholar] [CrossRef]
- Nama, N.; Huang, T.J.; Costanzo, F. Acoustic streaming: an arbitrary Lagrangian-Eulerian perspective. J. Fluid Mech. 2017, 825, 600–630. [Google Scholar] [CrossRef]
- Lutz, B.R.; Chen, J.; Schwartz, D.T. Microscopic steady streaming eddies created around short cylinders in a channel: Flow visualization and Stokes layer scaling. Phys. Fluids 2005, 17, 023601. [Google Scholar] [CrossRef]
- Amit, R.; Abadi, A.; Kosa, G. Characterization of steady streaming for a particle manipulation system. Biomed. Microdevices 2016, 18. [Google Scholar] [CrossRef] [PubMed]
- Rallabandi, B.; Marin, A.; Rossi, M.; Kahler, C.J.; Hilgenfeldt, S. Three-dimensional streaming flow in confined geometries. J. Fluid Mech. 2015, 777, 408–429. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Kasagi, N. Dissimilar control of momentum and heat transfer in a fully developed turbulent channel flow. J. Fluid Mech. 2011, 683, 57–93. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts Propagating with Curvature-Dependent Speed—Algorithms Based on Hamilton-Jacobi Formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Kolomenskiy, D.; Schneider, K. A Fourier spectral method for the Navier-Stokes equations with volume penalization for moving solid obstacles. J. Comput. Phys. 2009, 228, 5687–5709. [Google Scholar] [CrossRef]
- Suzuki, T.; Hasegawa, Y. Estimation of turbulent channel flow at Reτ =100 based on the wall measurement using a simple sequential approach. J. Fluid Mech. 2017, 830, 760–796. [Google Scholar] [CrossRef]
- Suzuki, H.; Ho, C.M.; Kasagi, N. A chaotic mixer for magnetic bead-based micro cell sorter. J. Microelectromech. Syst. 2004, 13, 779–790. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaneko, K.; Osawa, T.; Kametani, Y.; Hayakawa, T.; Hasegawa, Y.; Suzuki, H. Numerical and Experimental Analyses of Three-Dimensional Unsteady Flow around a Micro-Pillar Subjected to Rotational Vibration. Micromachines 2018, 9, 668. https://doi.org/10.3390/mi9120668
Kaneko K, Osawa T, Kametani Y, Hayakawa T, Hasegawa Y, Suzuki H. Numerical and Experimental Analyses of Three-Dimensional Unsteady Flow around a Micro-Pillar Subjected to Rotational Vibration. Micromachines. 2018; 9(12):668. https://doi.org/10.3390/mi9120668
Chicago/Turabian StyleKaneko, Kanji, Takayuki Osawa, Yukinori Kametani, Takeshi Hayakawa, Yosuke Hasegawa, and Hiroaki Suzuki. 2018. "Numerical and Experimental Analyses of Three-Dimensional Unsteady Flow around a Micro-Pillar Subjected to Rotational Vibration" Micromachines 9, no. 12: 668. https://doi.org/10.3390/mi9120668
APA StyleKaneko, K., Osawa, T., Kametani, Y., Hayakawa, T., Hasegawa, Y., & Suzuki, H. (2018). Numerical and Experimental Analyses of Three-Dimensional Unsteady Flow around a Micro-Pillar Subjected to Rotational Vibration. Micromachines, 9(12), 668. https://doi.org/10.3390/mi9120668





