Electrode Cooling Effect on Out-Of-Phase Electrothermal Streaming in Rotating Electric Fields
Abstract
1. Introduction
2. Materials and Methods
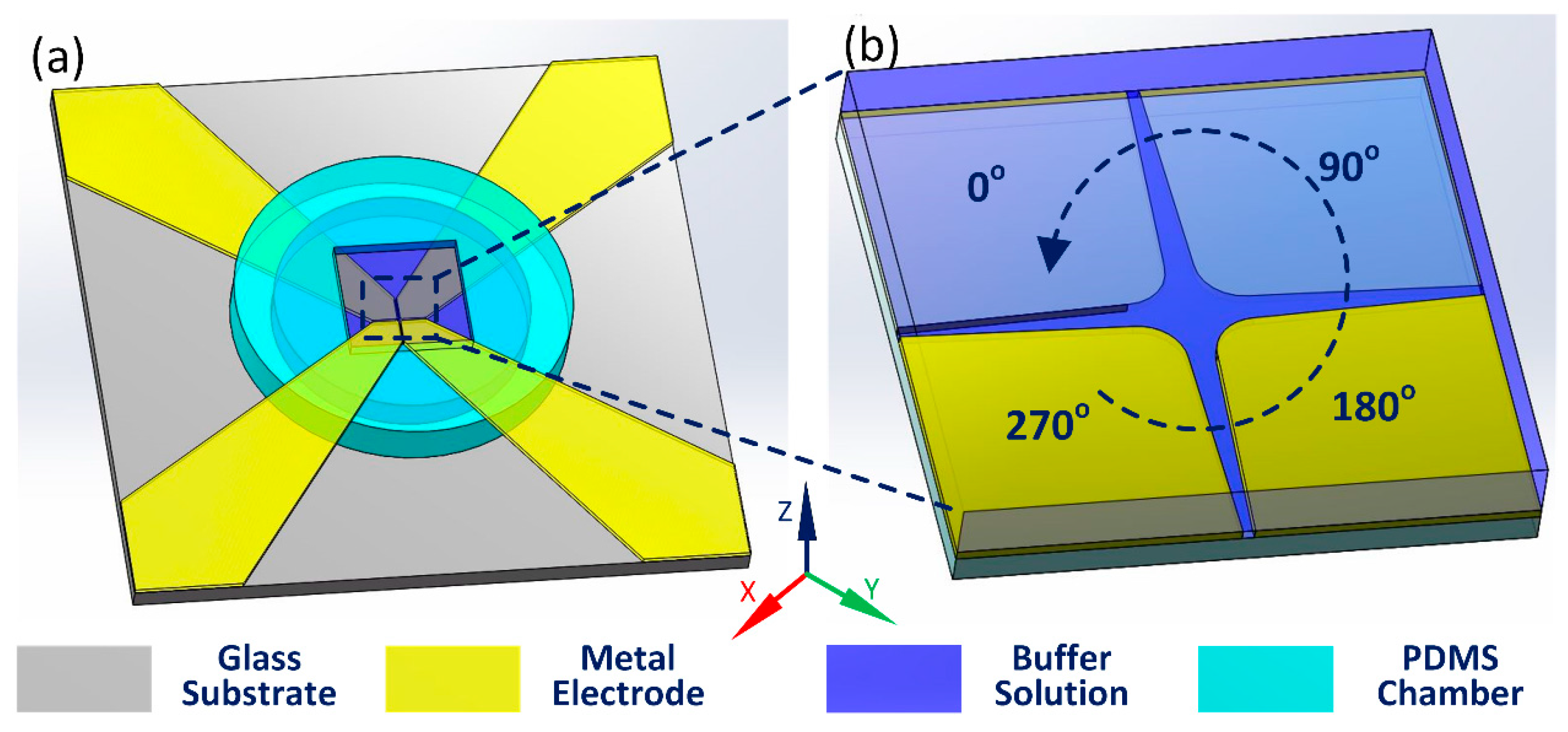
2.1. Basic Design of the Circulating Electrode Structure
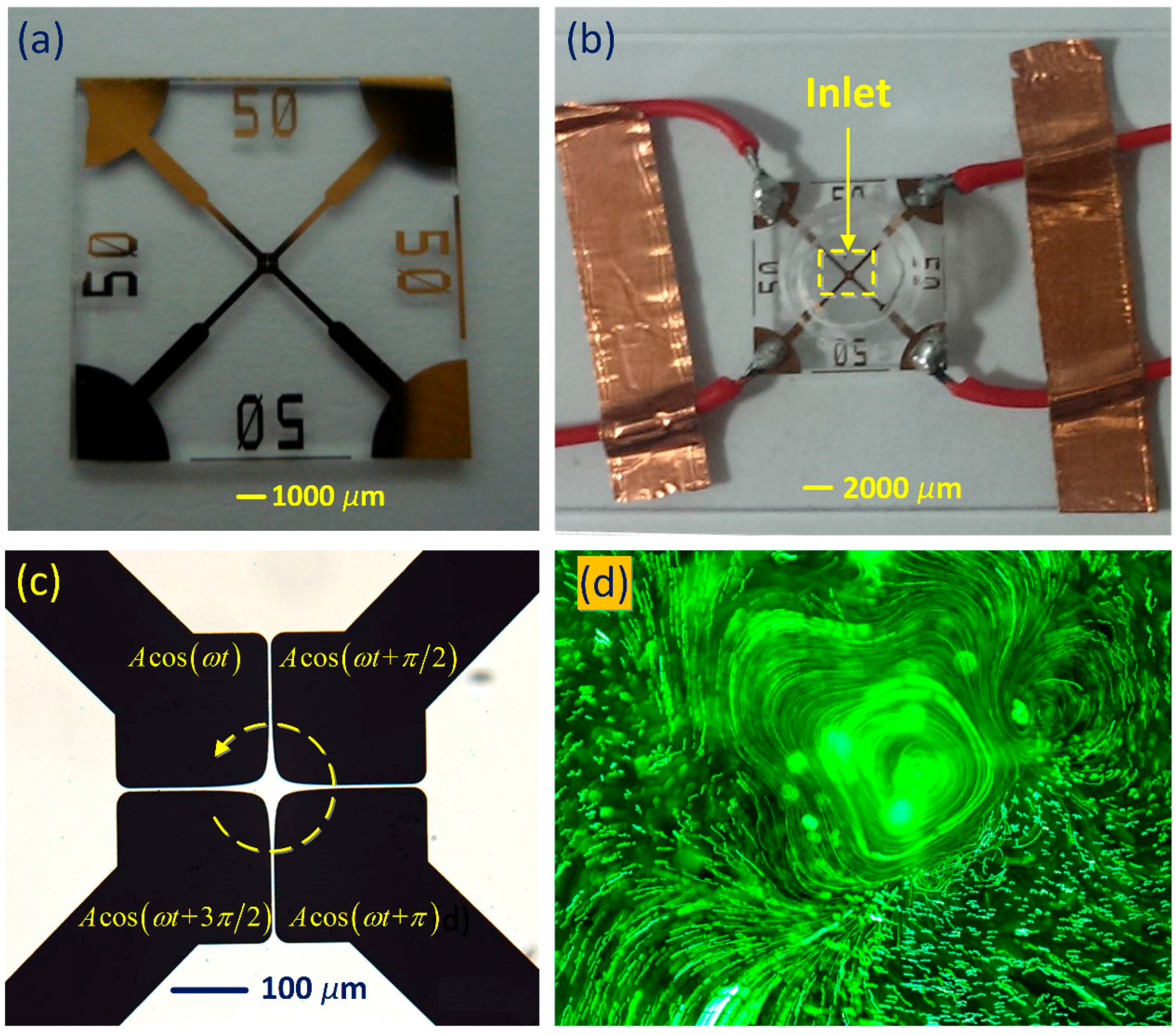
2.2. Chip Fabrication
2.3. Sample Preparation and Experimental Setup
2.4. Flow Components of Electrothermal Streaming in Rotating Electric Fields
2.5. Computational Model
3. Results and Discussion
3.1. Experimental Observation of ROT-ETF Fluid Motion
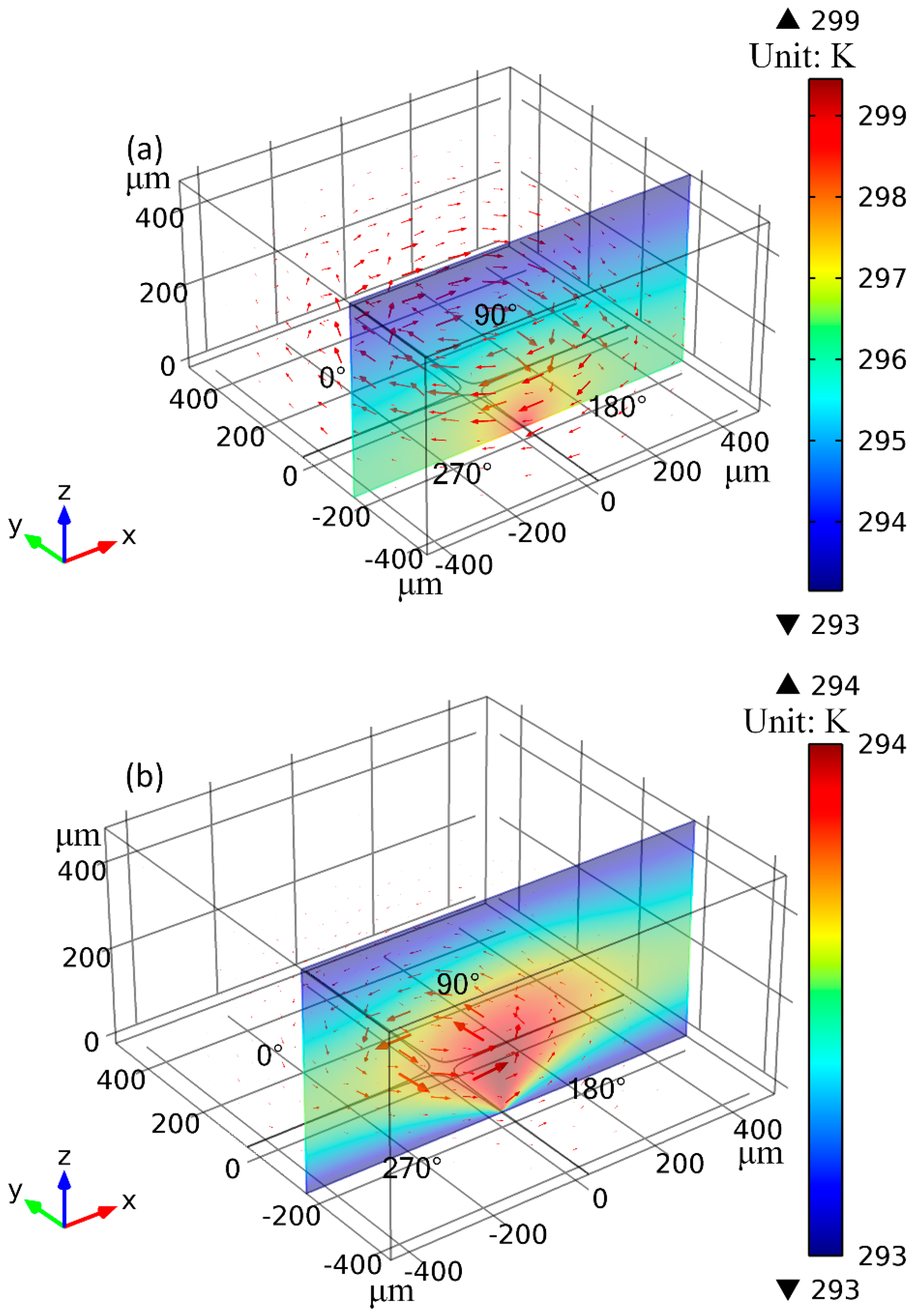
3.2. Electrode Cooling Effect on Rotating Direction of Induction Whirlpool
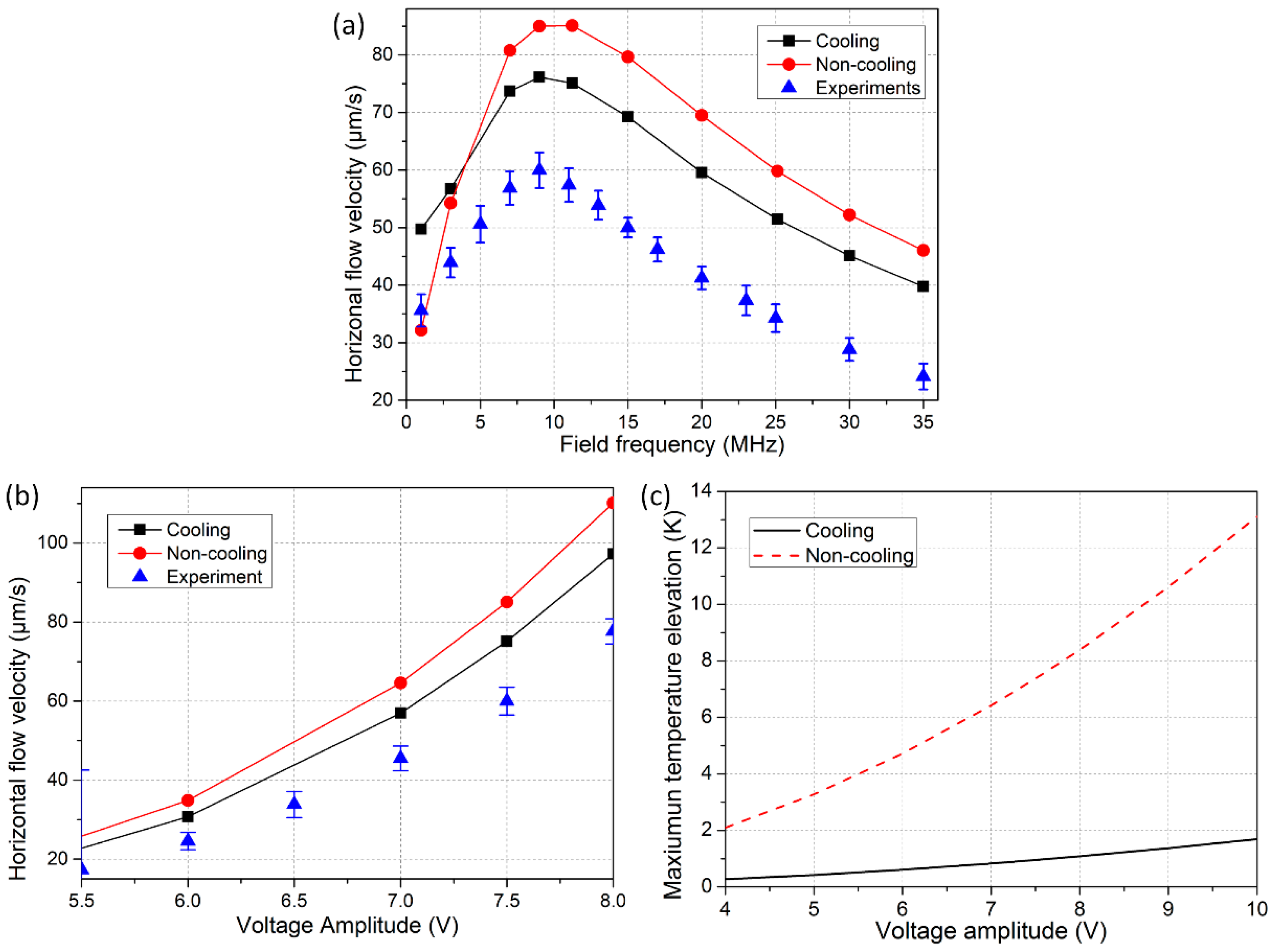
3.3. Comparison between Theory and Experiment
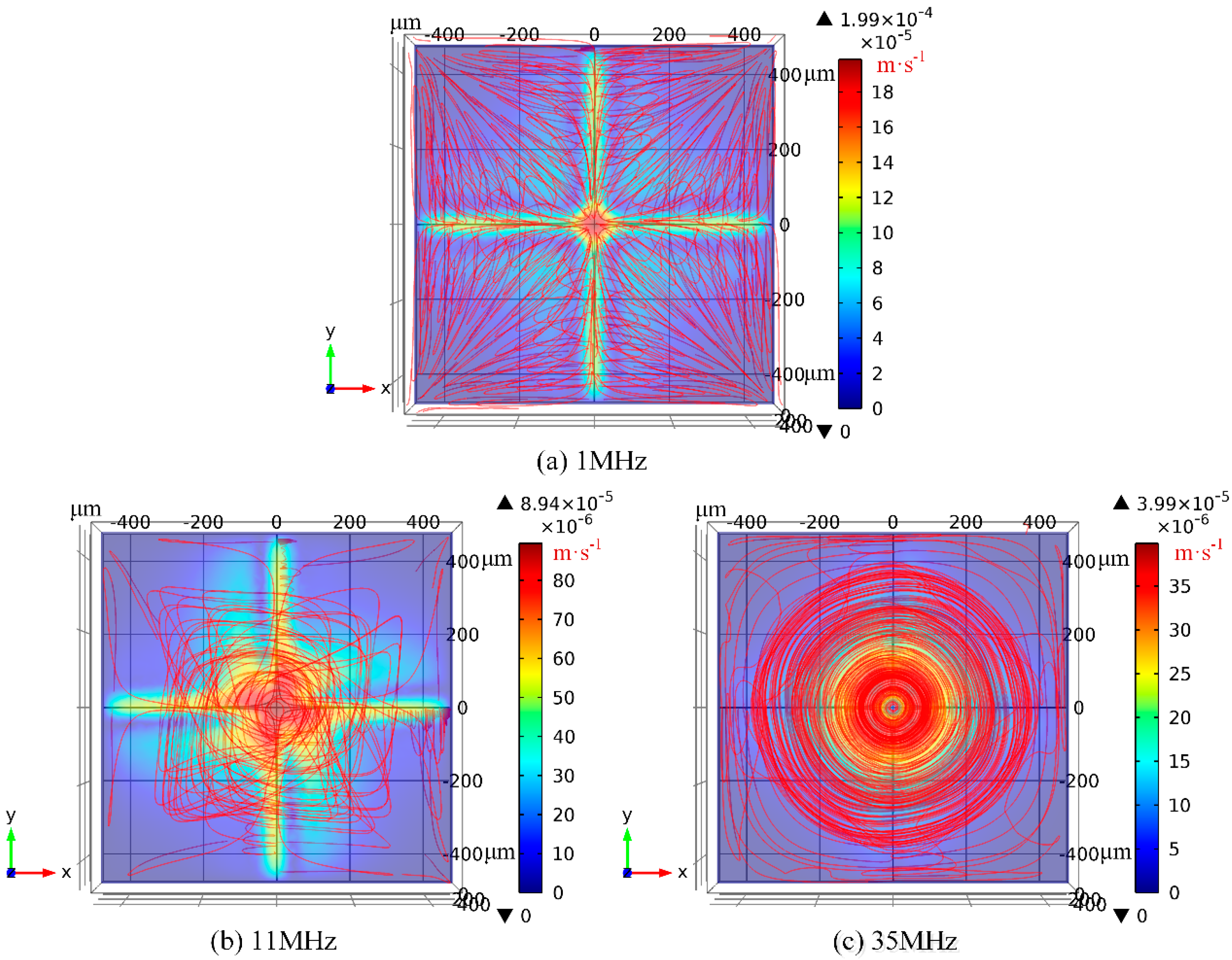
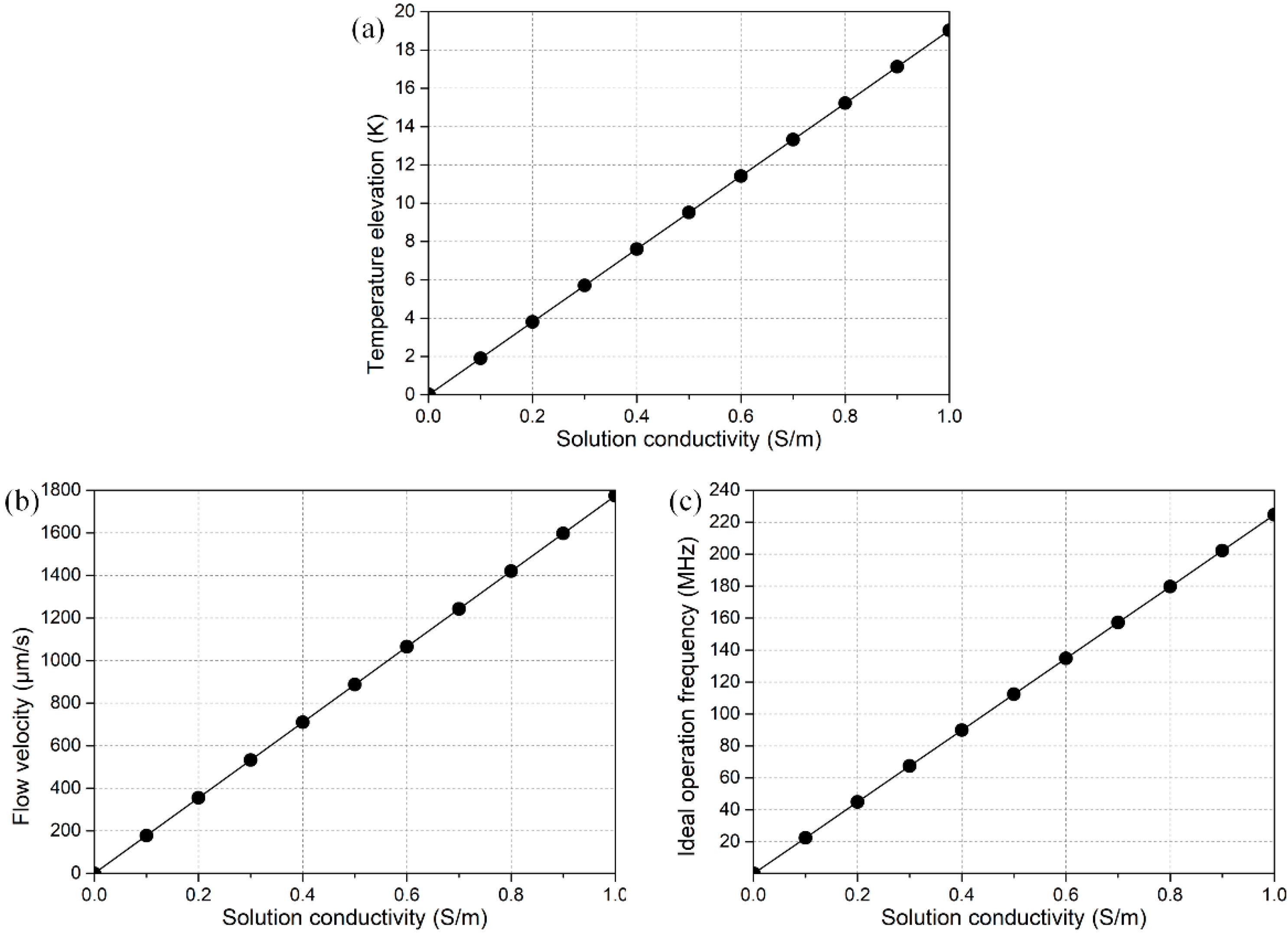
3.4. Numerical Prediction on the Effect of Electrical Conductivity
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hu, G.; Li, D. Multiscale phenomena in microfluidics and nanofluidics. Chem. Eng. Sci. 2007, 62, 3443–3454. [Google Scholar] [CrossRef]
- Pethig, R. Review article—Dielectrophoresis: Status of the theory, technology, and applications. Biomicrofluidics 2010, 4, 022811. [Google Scholar] [CrossRef] [PubMed]
- Dittrich, P.S.; Tachikawa, K.; Manz, A. Micro total analysis systems. Latest advancements and trends. Anal. Chem. 2006, 78, 3887–3908. [Google Scholar] [CrossRef] [PubMed]
- Laser, D.; Santiago, J. A review of micropumps. J. Micromech. Microeng. 2004, 14, R35. [Google Scholar] [CrossRef]
- Jones, T.B.; Jones, T.B. Electromechanics of Particles; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Morgan, H.; Green, N.G. Ac Electrokinetics: Colloids and Nanoparticles; Research Studies Press: Taunton, UK, 2003. [Google Scholar]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, C. Advances in electrokinetics and their applications in micro/nano fluidics. Microfluid. Nanofluid. 2012, 13, 179–203. [Google Scholar] [CrossRef]
- Jia, Y.; Ren, Y.; Liu, W.; Hou, L.; Tao, Y.; Hu, Q.; Jiang, H. Electrocoalescence of paired droplets encapsulated in double-emulsion drops. Lab Chip 2016, 16, 4313–4318. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Liu, J.; Liu, W.; Lang, Q.; Tao, Y.; Hu, Q.; Hou, L.; Jiang, H. Scaled particle focusing in a microfluidic device with asymmetric electrodes utilizing induced-charge electroosmosis. Lab Chip 2016, 16, 2803–2812. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Liu, W.; Liu, J.; Tao, Y.; Guo, Y.; Jiang, H. Particle rotational trapping on a floating electrode by rotating induced-charge electroosmosis. Biomicrofluidics 2016, 10, 054103. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; Ren, Y.; Liu, W.; Wu, Y.; Jia, Y.; Lang, Q.; Jiang, H. Enhanced particle trapping performance of induced charge electroosmosis. Electrophoresis 2016. [Google Scholar] [CrossRef] [PubMed]
- Ristenpart, W.; Aksay, I.; Saville, D. Electrohydrodynamic flow around a colloidal particle near an electrode with an oscillating potential. J. Fluid Mech. 2007, 575, 83–109. [Google Scholar] [CrossRef]
- García-Sánchez, P.; Ramos, A.; González, A.; Green, N.G.; Morgan, H. Flow reversal in traveling-wave electrokinetics: An analysis of forces due to ionic concentration gradients. Langmuir 2009, 25, 4988–4997. [Google Scholar] [CrossRef] [PubMed]
- García-Sánchez, P.; Ramos, A.; Green, N.; Morgan, H. Traveling-wave electrokinetic micropumps: Velocity, electrical current, and impedance measurements. Langmuir 2008, 24, 9361–9369. [Google Scholar] [CrossRef] [PubMed]
- Pretorius, V.; Hopkins, B.J.; Schieke, J. Electro-osmosis: A new concept for high-speed liquid chromatography. J. Chromatogr. A 1974, 99, 23–30. [Google Scholar] [CrossRef]
- Green, N.G.; Ramos, A.; González, A.; Morgan, H.; Castellanos, A. Fluid flow induced by nonuniform ac electric fields in electrolytes on microelectrodes. I. Experimental measurements. Phys. Rev. E 2000, 61, 4011. [Google Scholar] [CrossRef]
- Green, N.G.; Ramos, A.; Gonzalez, A.; Castellanos, A.; Morgan, H. Electrothermally induced fluid flow on microelectrodes. J. Electrost. 2001, 53, 71–87. [Google Scholar] [CrossRef]
- Stubbe, M.; Gimsa, J. A short review on ac electro-thermal micropumps based on smeared structural polarizations in the presence of a temperature gradient. Colloids Surf. Physicochem. Eng. Asp. 2011, 376, 97–101. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Kilic, M.S.; Storey, B.D.; Ajdari, A. Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solutions. Adv. Colloid Interface Sci. 2009, 152, 48–88. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.L.; Yang, C. Ac field induced-charge electroosmosis over leaky dielectric blocks embedded in a microchannel. Electrophoresis 2011, 32, 629–637. [Google Scholar] [CrossRef] [PubMed]
- Xuan, X.; Xu, B.; Sinton, D.; Li, D. Electroosmotic flow with joule heating effects. Lab Chip 2004, 4, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Bazant, M.Z.; Squires, T.M. Induced-charge electrokinetic phenomena. Curr. Opin. Colloid Interface Sci. 2010, 15, 203–213. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Squires, T.M. Induced-charge electrokinetic phenomena: Theory and microfluidic applications. Phys. Rev. Lett. 2004, 92, 066101. [Google Scholar] [CrossRef] [PubMed]
- Squires, T.M.; Bazant, M.Z. Induced-charge electro-osmosis. J. Fluid Mech. 2004, 509, 217–252. [Google Scholar] [CrossRef]
- Gimsa, J.; Stubbe, M.; Gimsa, U. A short tutorial contribution to impedance and ac-electrokinetic characterization and manipulation of cells and media: Are electric methods more versatile than acoustic and laser methods? J. Electr. Bioimpedance 2014, 5, 74–91. [Google Scholar] [CrossRef]
- Stubbe, M.; Holtappels, M.; Gimsa, J. A new working principle for ac electro-hydrodynamic on-chip micro-pumps. J. Phys. D Appl. Phys. 2007, 40, 6850. [Google Scholar] [CrossRef]
- Gimsa, J.; Eppmann, P.; Prüger, B. Introducing phase analysis light scattering for dielectric characterization: Measurement of traveling-wave pumping. Biophys. J. 1997, 73, 3309. [Google Scholar] [CrossRef]
- Fuhr, G.; Hagedorn, R.; Müller, T.; Benecke, W.; Wagner, B. Microfabricated electrohydrodynamic (EHD) pumps for liquids of higher conductivity. J. Microelectromech. Syst. 1992, 1, 141–146. [Google Scholar] [CrossRef]
- Iverson, B.D.; Cremaschi, L.; Garimella, S.V. Effects of discrete-electrode configuration on traveling-wave electrohydrodynamic pumping. Microfluid. Nanofluid. 2009, 6, 221–230. [Google Scholar] [CrossRef]
- Iverson, B.D.; Garimella, S.V. Experimental characterization of induction electrohydrodynamics for integrated microchannel pumping. J. Micromech. Microeng. 2009, 19, 055015. [Google Scholar] [CrossRef]
- Li, Y.; Ren, Y.; Liu, W.; Chen, X.; Tao, Y.; Jiang, H. On controlling the flow behavior driven by induction electrohydrodynamics in microfluidic channels. Electrophoresis 2017, 38, 983–995. [Google Scholar] [CrossRef] [PubMed]
- Green, N.G.; Ramos, A.; González, A.; Castellanos, A.; Morgan, H. Electric field induced fluid flow on microelectrodes: The effect of illumination. J. Phys. D Appl. Phys. 2000, 33, L13. [Google Scholar] [CrossRef]
- Liu, W.; Ren, Y.; Shao, J.; Jiang, H.; Ding, Y. A theoretical and numerical investigation of travelling wave induction microfluidic pumping in a temperature gradient. J. Phys. D Appl. Phys. 2014, 47, 075501. [Google Scholar] [CrossRef]
- Gunda, N.S.K.; Bhattacharjee, S.; Mitra, S.K. Study on the use of dielectrophoresis and electrothermal forces to produce on-chip micromixers and microconcentrators. Biomicrofluidics 2012, 6, 034118. [Google Scholar] [CrossRef] [PubMed]
- Lian, M.; Islam, N.; Wu, J. Ac electrothermal manipulation of conductive fluids and particles for lab-chip applications. IET Nanobiotechnol. 2007, 1, 36–43. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Koklu, M.; BeskoK, A. Particle trapping in high-conductivity media with electrothermally enhanced negative dielectrophoresis. Anal. Chem. 2009, 81, 2303–2310. [Google Scholar] [CrossRef] [PubMed]
- Melcher, J.R.; Firebaugh, M.S. Traveling-wave bulk electroconvection induced across a temperature gradient. Phys. Fluids 1967, 10, 1178–1185. [Google Scholar] [CrossRef]
- Ren, Y.K.; Morganti, D.; Jiang, H.Y.; Ramos, A.; Morgan, H. Electrorotation of metallic microspheres. Langmuir 2011, 27, 2128–2131. [Google Scholar] [CrossRef] [PubMed]
- García-Sánchez, P.; Ren, Y.; Arcenegui, J.J.; Morgan, H.; Ramos, A. Alternating current electrokinetic properties of gold-coated microspheres. Langmuir 2012, 28, 13861–13870. [Google Scholar] [CrossRef] [PubMed]
- González, A.; Ramos, A.; Morgan, H.; Green, N.G.; Castellanos, A. Electrothermal flows generated by alternating and rotating electric fields in microsystems. J. Fluid Mech. 2006, 564, 415–433. [Google Scholar] [CrossRef]
- Perch-Nielsen, I.R.; Green, N.G.; Wolff, A. Numerical simulation of travelling wave induced electrothermal fluid flow. J. Phys. D Appl. Phys. 2004, 37, 2323. [Google Scholar] [CrossRef]
- Matsumoto, M.; Dasari, R.R.; Ji, W.; Feriante, C.H.; Parker, T.C.; Marder, S.R.; Dichtel, W.R. Rapid, low temperature formation of imine-linked cofs catalyzed by metal triflates. J. Am. Chem. Soc. 2017, 139, 4999–5002. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Li, D.; Zhang, L.; Li, J.; Wang, E. Monodisperse mesoporous superparamagnetic single-crystal magnetite nanoparticles for drug delivery. Biomaterials 2009, 30, 1881. [Google Scholar] [CrossRef] [PubMed]
- Yoon, S.K.; Song, J.Y.; Lee, G.M. Effect of low culture temperature on specific productivity, transcription level, and heterogeneity of erythropoietin in chinese hamster ovary cells. Biotechnol. Bioeng. 2003, 82, 289–298. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Shao, J.; Ren, Y.; Wu, Y.; Wang, C.; Ding, H.; Jiang, H.; Ding, Y. Effects of discrete-electrode arrangement on traveling-wave electroosmotic pumping. J. Micromech. Microeng. 2016, 26, 095003. [Google Scholar] [CrossRef]
- Felten, M.; Geggier, P.; Jäger, M.; Duschl, C. Controlling electrohydrodynamic pumping in microchannels through defined temperature fields. Phys. Fluids 2006, 18, 051707. [Google Scholar] [CrossRef]
- Seyed-Yagoobi, J.; Chato, J.; Crowley, J.; Krein, P. Induction electrohydrodynamic pump in a vertical configuration: Part 1—Theory. J. Heat Transf. 1989, 111, 664–669. [Google Scholar] [CrossRef]
- Schmidt, S.; Latz, A. Numerical simulation of traveling wave-induced electroconvection. Microfluid. Nanofluid. 2012, 13, 421–428. [Google Scholar] [CrossRef]
- Loire, S.; Kauffmann, P.; Mezić, I.; Meinhart, C. A theoretical and experimental study of ac electrothermal flows. J. Phys. D Appl. Phys. 2012, 45, 185301. [Google Scholar] [CrossRef]


| Symbol | Implication | Value or Unit |
|---|---|---|
| Electrostatic potential field | [V] | |
| E | Electric field vector | [V/m] |
| T | Temperature field | [K] |
| p | Hydrostatic pressure field | [Pa] |
| u | Flow velocity vector | [m/s] |
| ρf | Volumetric free charge distribution | [C/m3] |
| ρb | Volumetric bound charge distribution | [C/m3] |
| fET | Electrothermal body force | [N/m3] |
| ΔT | Temperature elevation within the bulk fluid | [K] |
| Liquid permittivity | 7.08 × 10−10 [F/m] | |
| Electrolyte conductivity | 0.05 [S/m] | |
| fc1 | Charge relaxation frequency | = 11 [MHz] |
| τ | Charge relaxation time | = 1.42 × 10−8 [s] |
| fc2 | Characteristic crossover frequency of SWET | = 24.6 [MHz] |
| f | Field frequency | 1~35 [MHz] |
| ω | Angular field frequency | 2πf |
| d | Nearest distance between oppositely polarized electrodes | 50 [μm] |
| A | AC voltage amplitude | [V] |
| E0 | Electric field magnitude | 2A/d |
| T0 | Temperature of reference | 293.15 [K] |
| kwater | Thermal conductivity of water | 0.6 [W·m−1·K−1] |
| kPDMS | Thermal conductivity of PDMS lid | 0.2 [W·m−1·K−1] |
| kglass | Thermal conductivity of glass substrate | 1 [W·m−1·K−1] |
| kSi | Thermal conductivity of silicon material | 140 [W·m−1·K−1] |
| kAu | Thermal conductivity of gold electrodes | 340 [W·m−1·K−1] |
| η | Dynamic viscosity of water | 0.001 [Pa·s] |
| H | Thickness of the fluid layer | 500 [μm] |
| HSub | Thickness of glass substrate | 500 [μm] |
| HLid | Thickness of PDMS lid | 100 [μm] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Ren, Y.; Tao, Y.; Chen, X.; Wu, Q. Electrode Cooling Effect on Out-Of-Phase Electrothermal Streaming in Rotating Electric Fields. Micromachines 2017, 8, 327. https://doi.org/10.3390/mi8110327
Liu W, Ren Y, Tao Y, Chen X, Wu Q. Electrode Cooling Effect on Out-Of-Phase Electrothermal Streaming in Rotating Electric Fields. Micromachines. 2017; 8(11):327. https://doi.org/10.3390/mi8110327
Chicago/Turabian StyleLiu, Weiyu, Yukun Ren, Ye Tao, Xiaoming Chen, and Qisheng Wu. 2017. "Electrode Cooling Effect on Out-Of-Phase Electrothermal Streaming in Rotating Electric Fields" Micromachines 8, no. 11: 327. https://doi.org/10.3390/mi8110327
APA StyleLiu, W., Ren, Y., Tao, Y., Chen, X., & Wu, Q. (2017). Electrode Cooling Effect on Out-Of-Phase Electrothermal Streaming in Rotating Electric Fields. Micromachines, 8(11), 327. https://doi.org/10.3390/mi8110327







