Electrostatic Comb-Drive Actuator with High In-Plane Translational Velocity
Abstract
:1. Introduction
2. Actuator Design
- (1)
- Atmospheric pressure for compatibility with the micro-optical benches and lab-on-chip microsystems.
- (2)
- Actuation with direct current (DC) voltage of 100–150 V and alternating current (AC) voltage less than 10 V.
- (3)
- Maximum stress in flexure beams is less than 1% of the material’s Young’s modulus to avoid fracture [27].
- (4)
- Compatibility with optical MEMS technology with in-plane optical axis, for instance with DRIE of silicon-on-insulator (SOI) wafers.
Figure of Merit
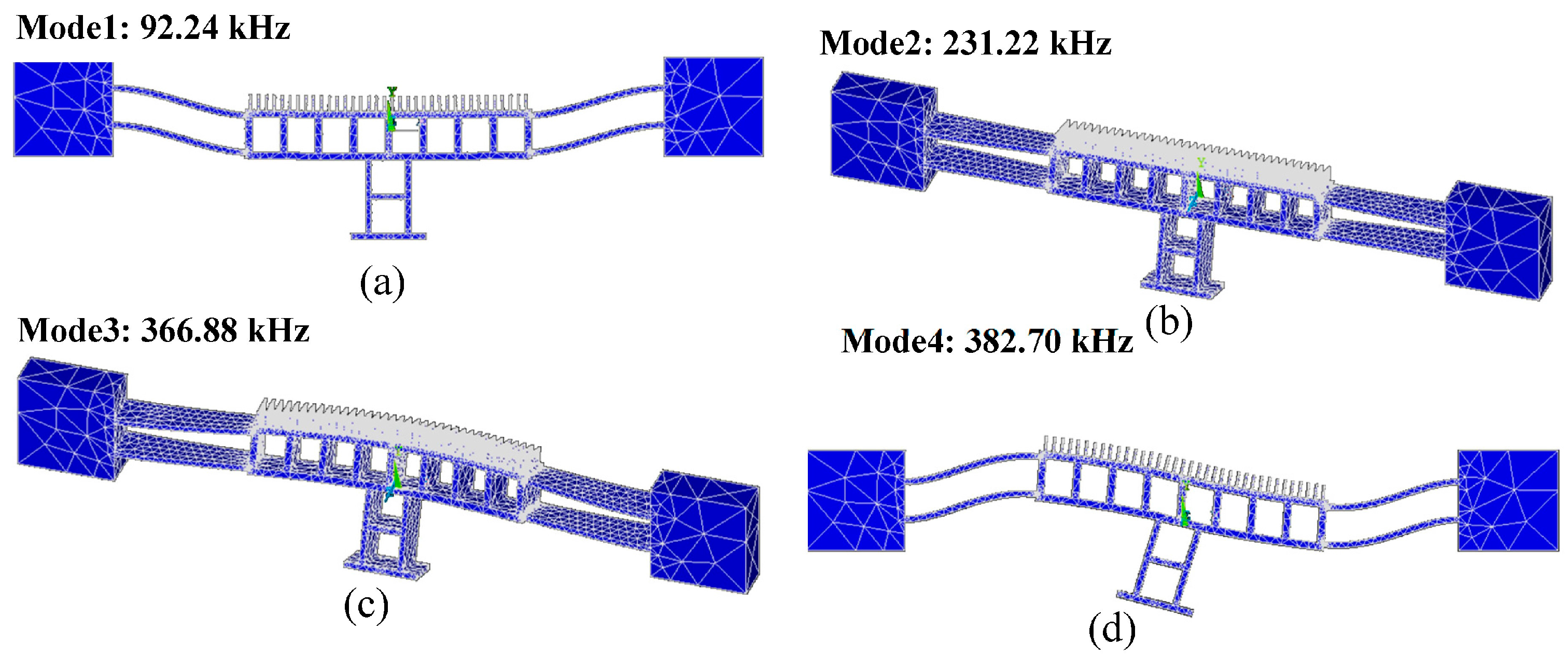
3. Finite Element Analysis
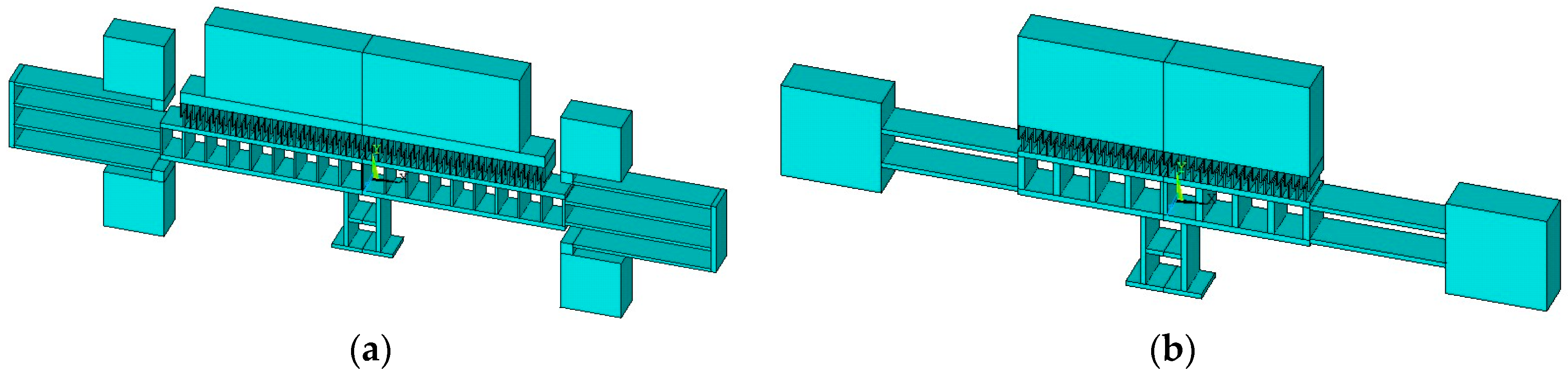
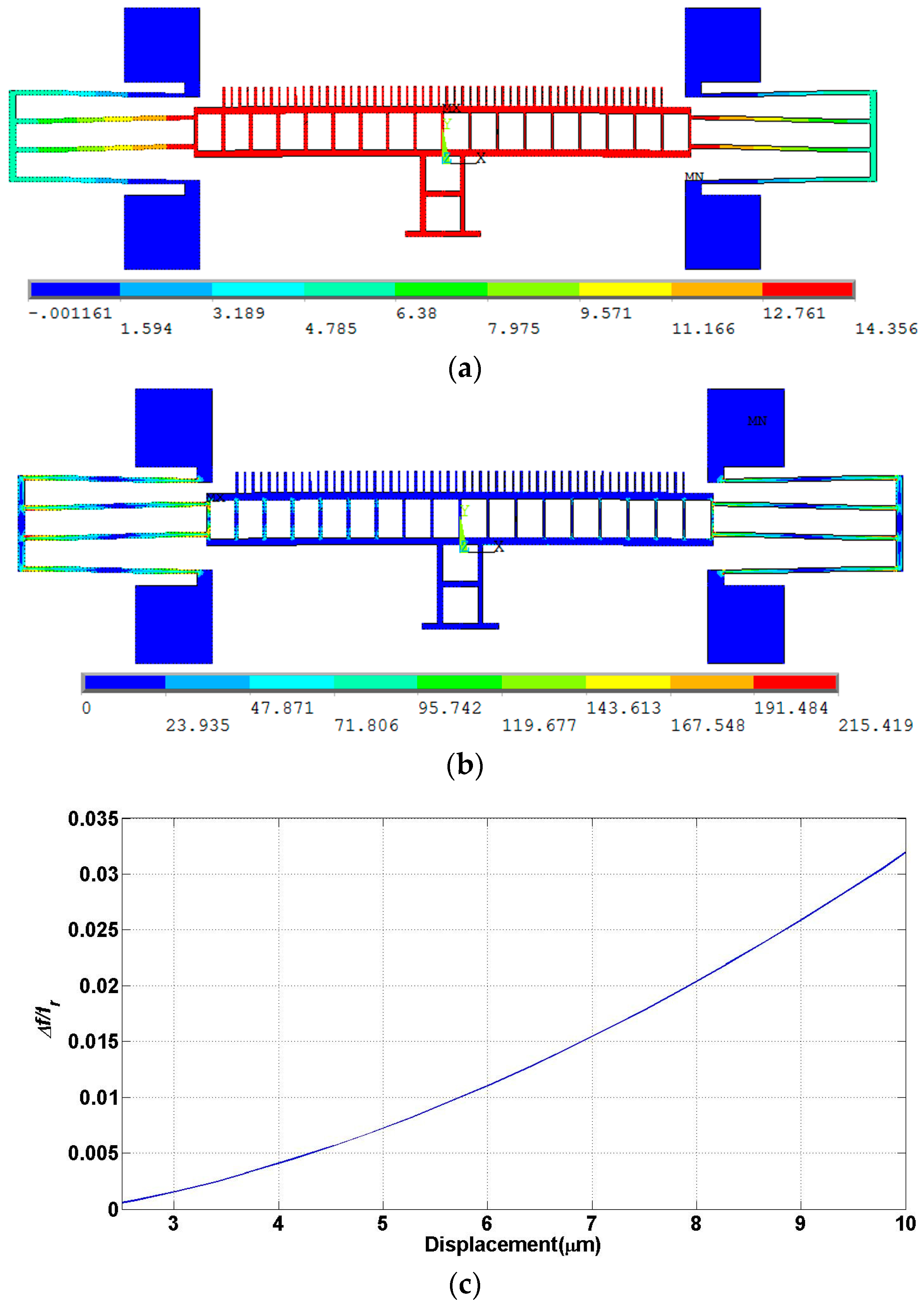
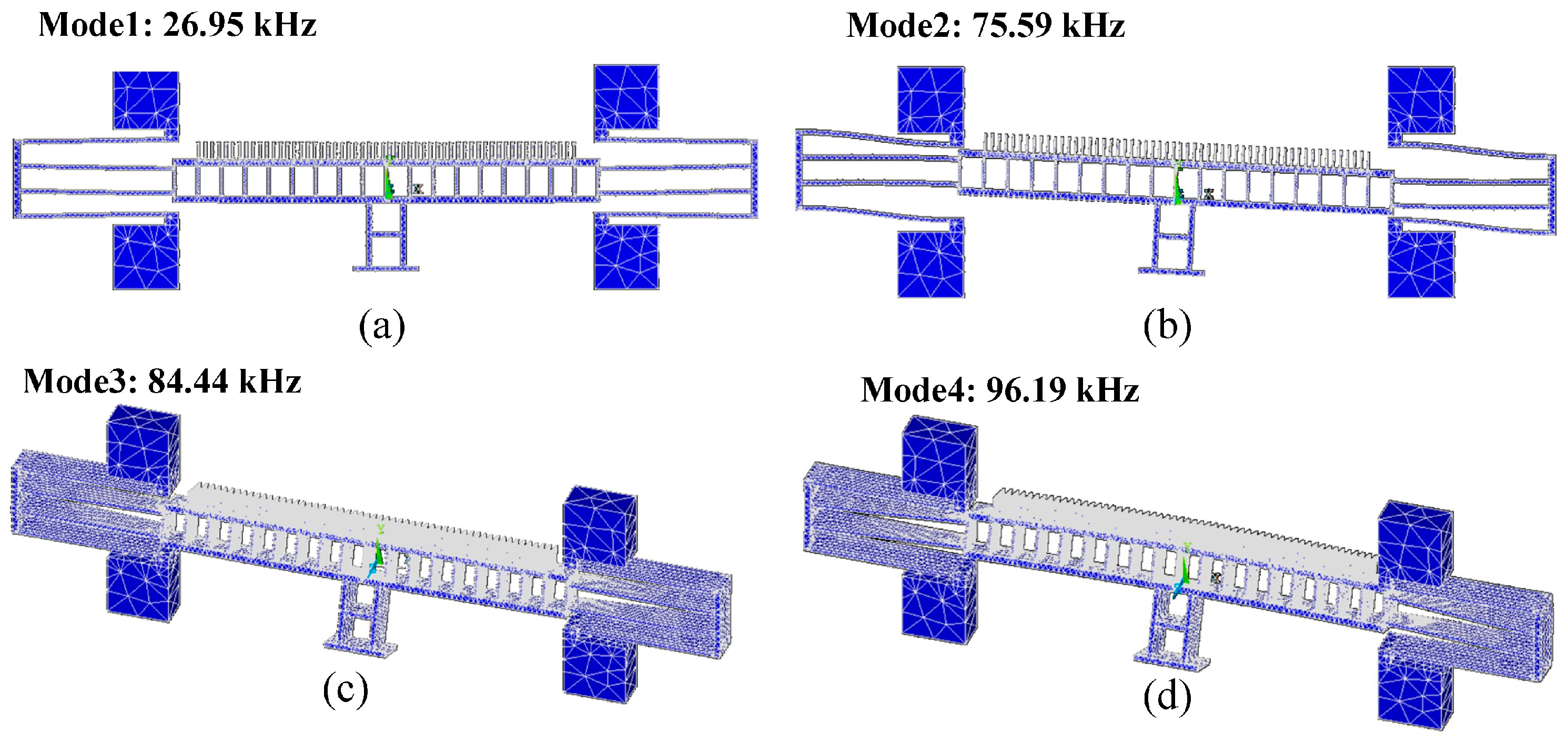
3.1. Design A
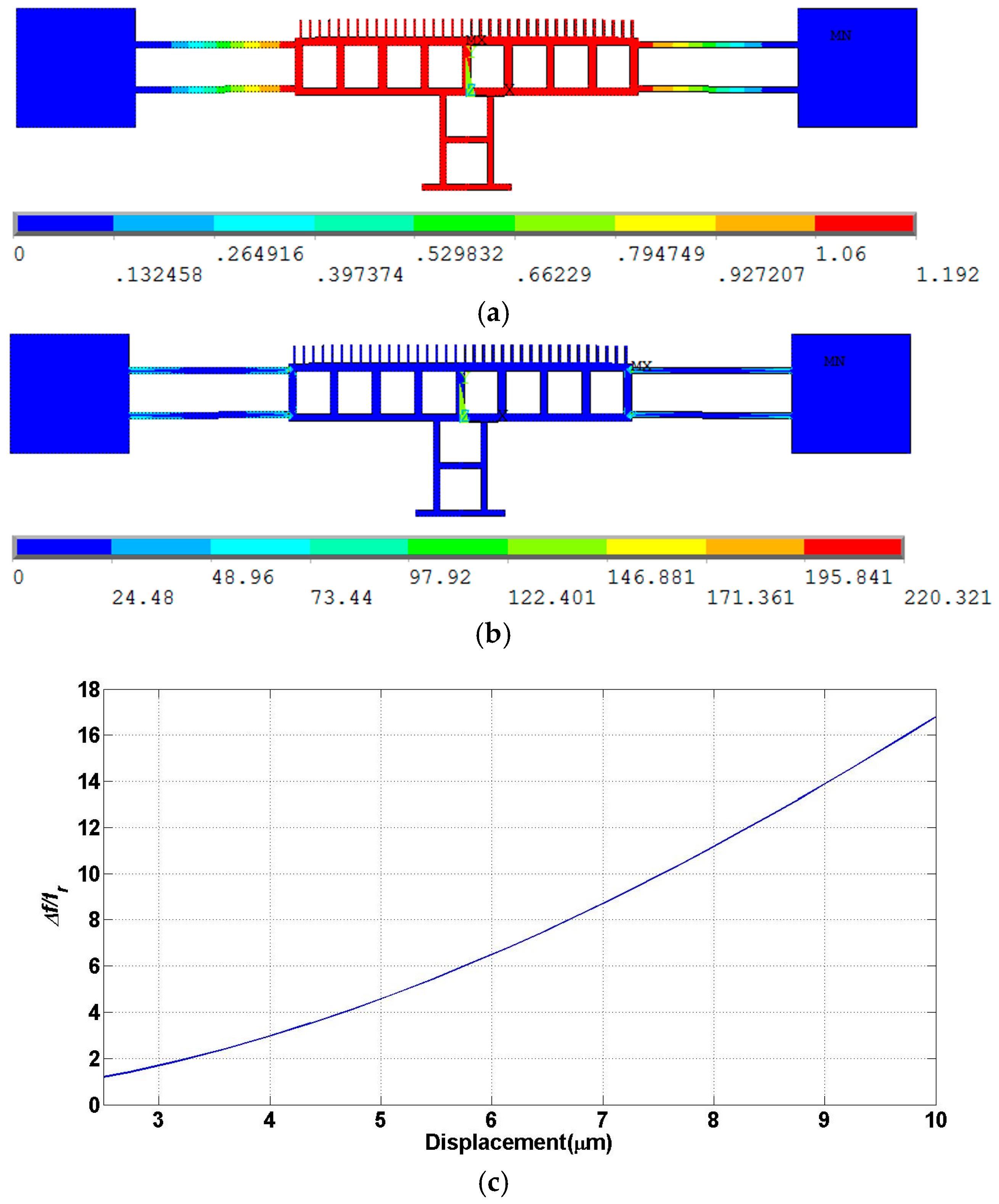
3.2. Design B
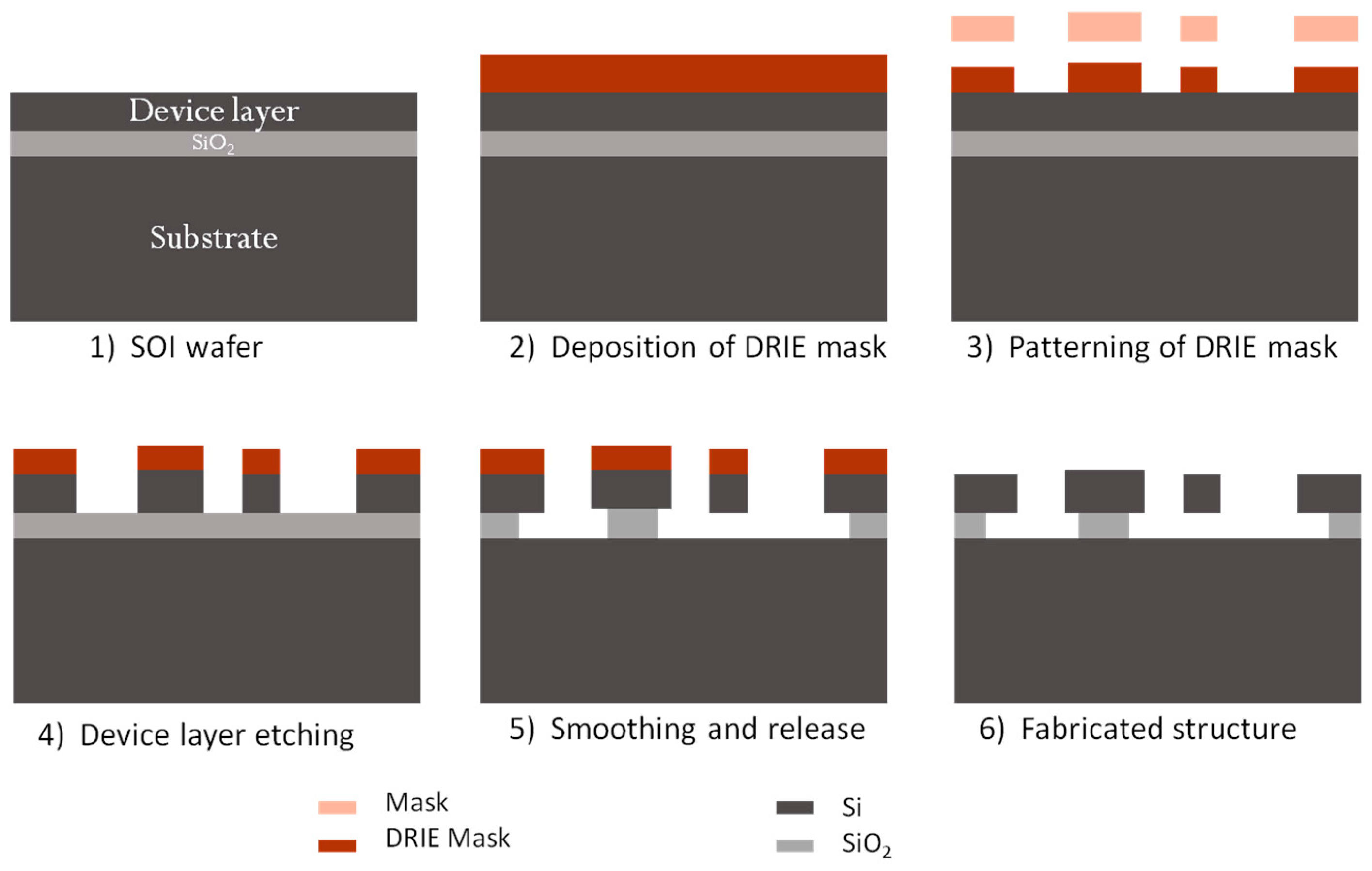
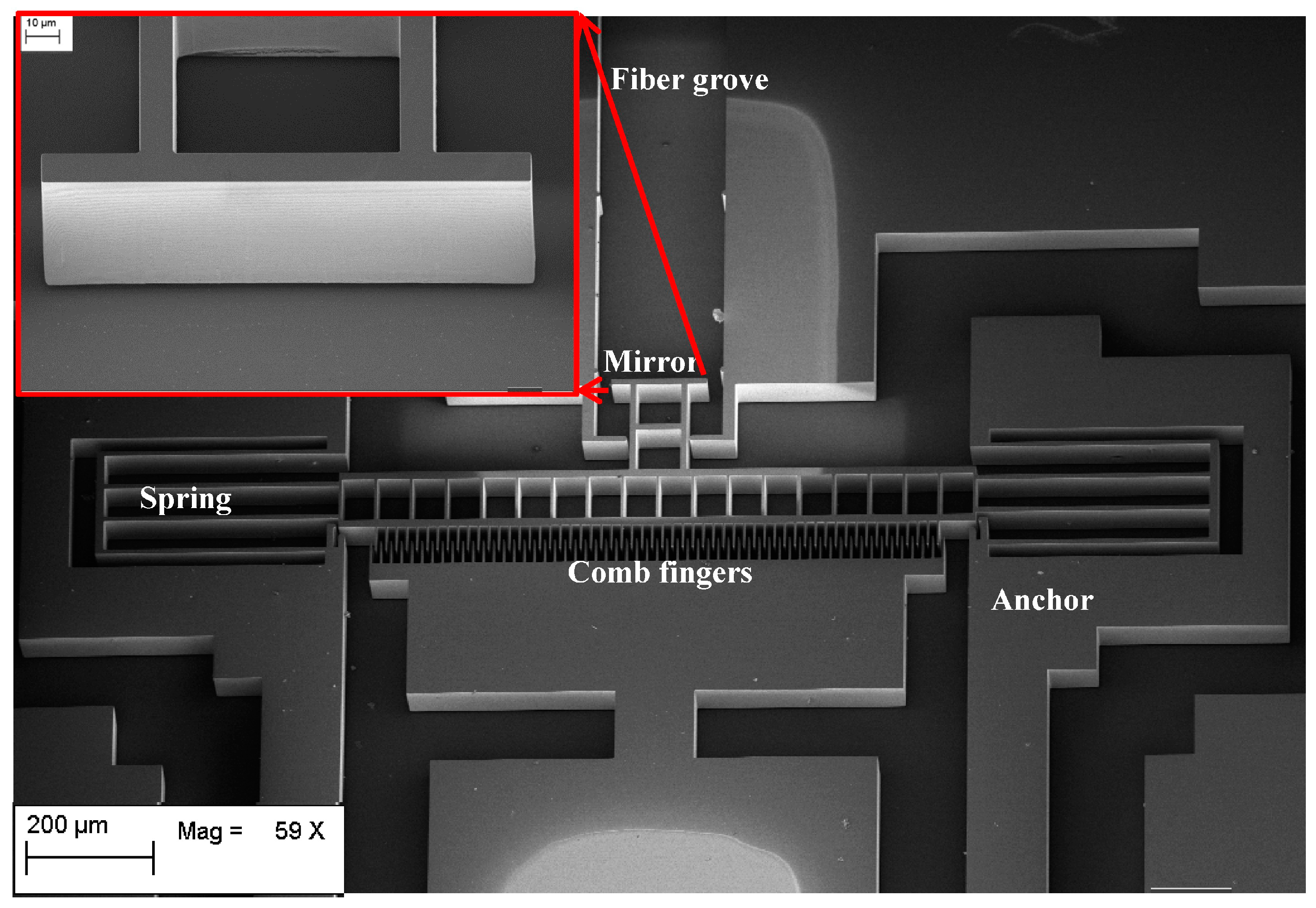
4. Device Fabrication
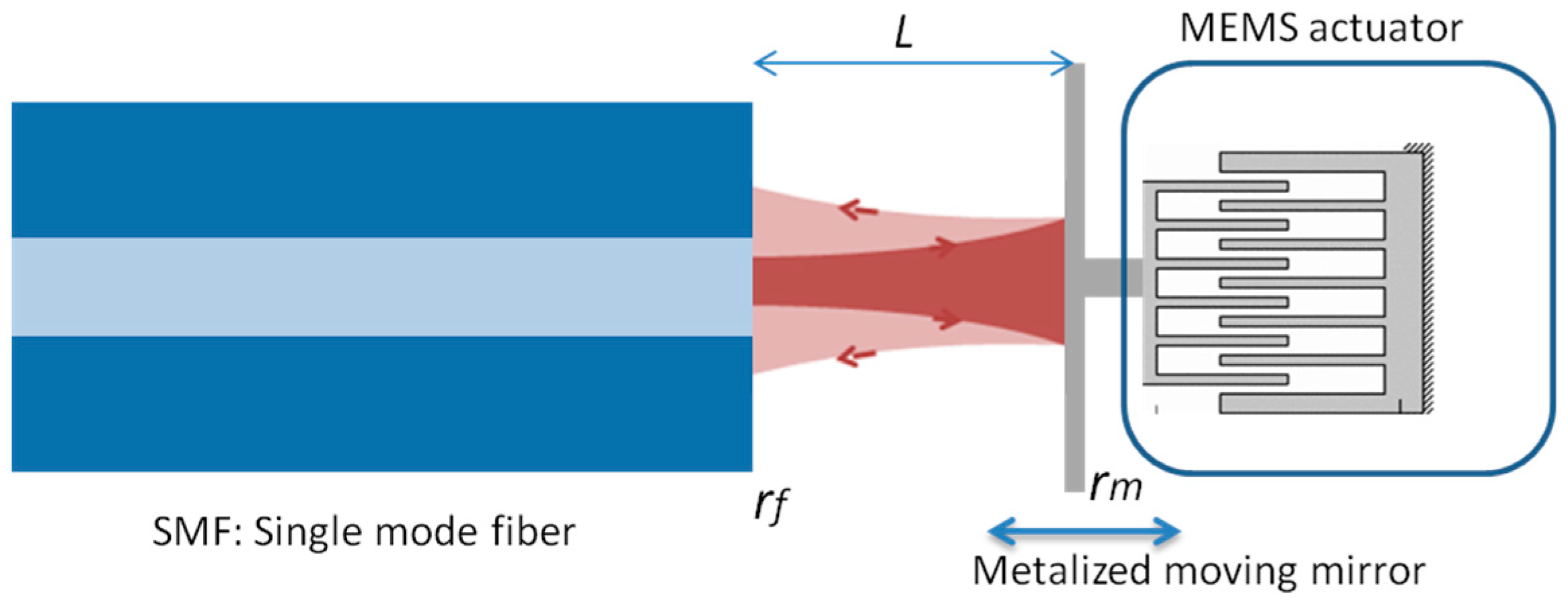
5. Opto-Mechanical Characterization Method
5.1. Analysis of the Characterization Method
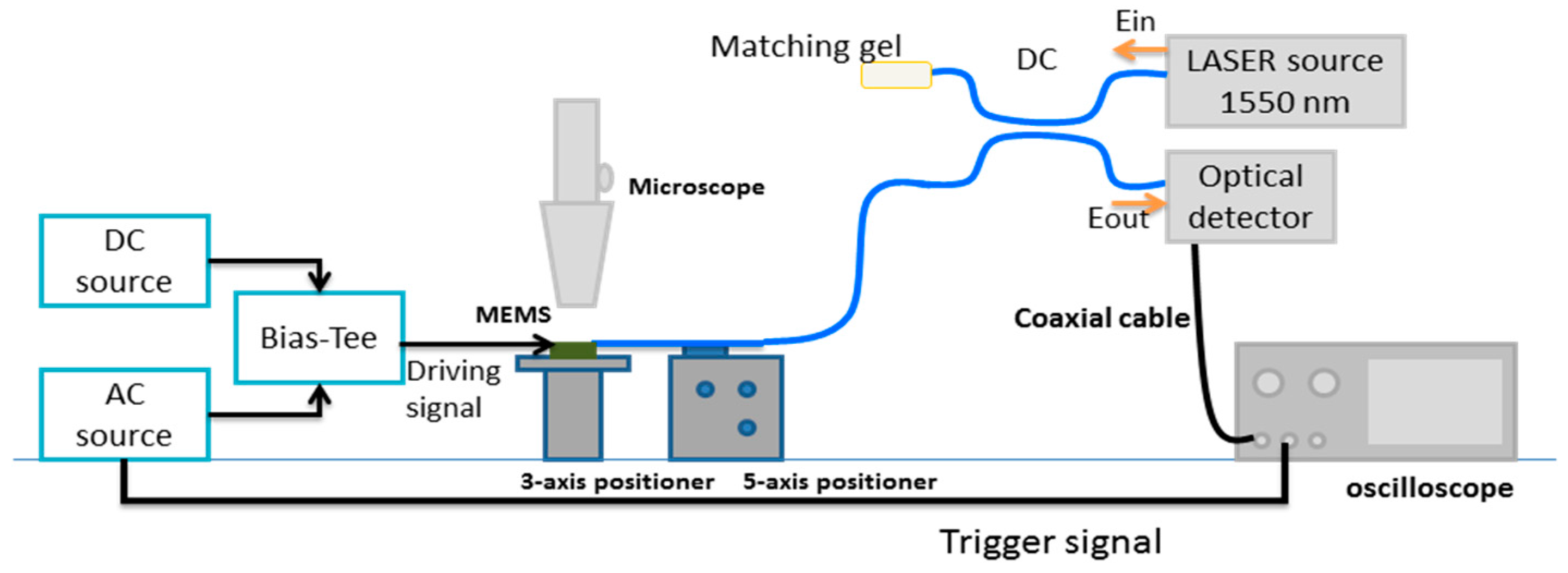
5.2. Characterization Setup
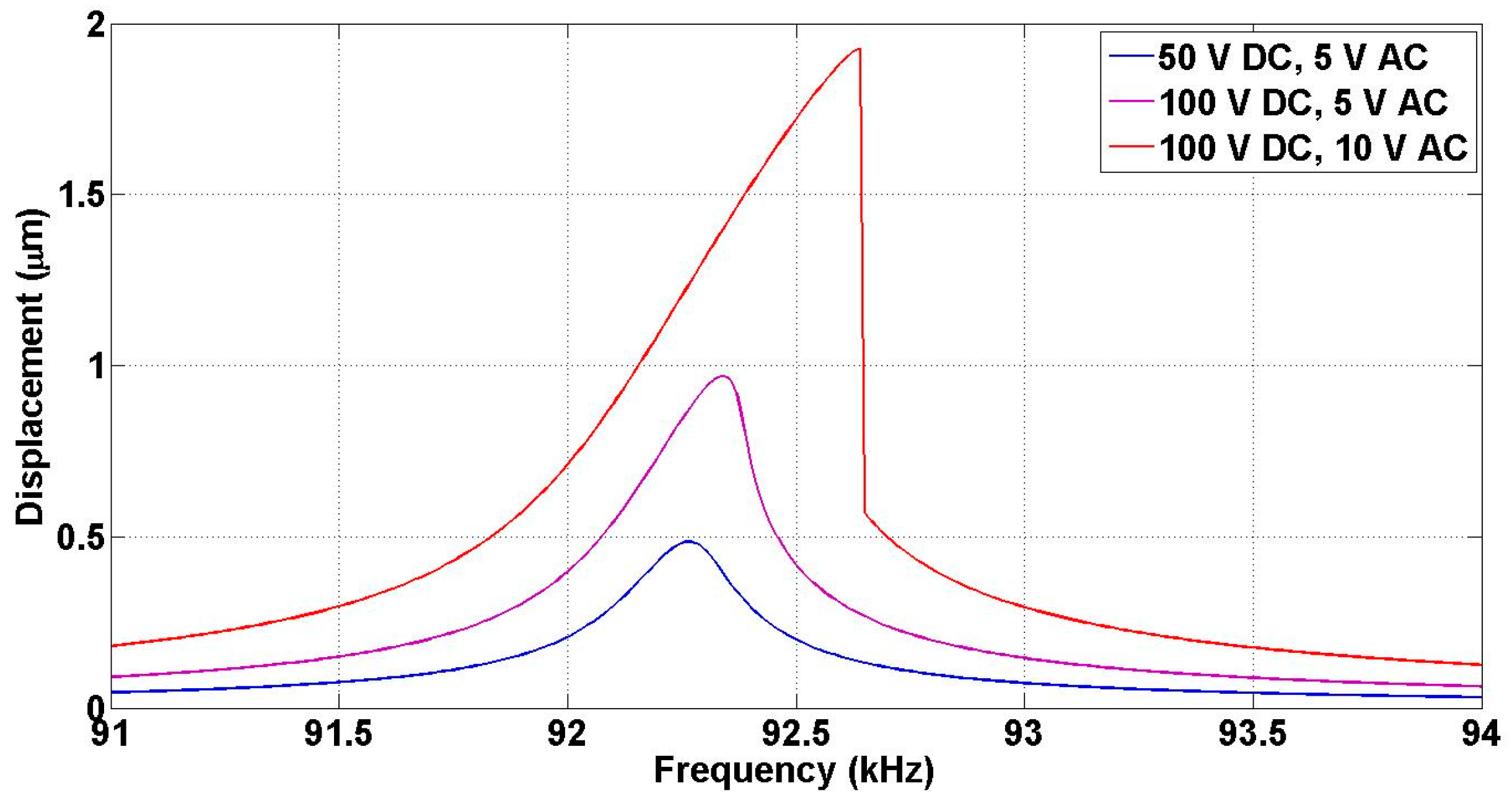
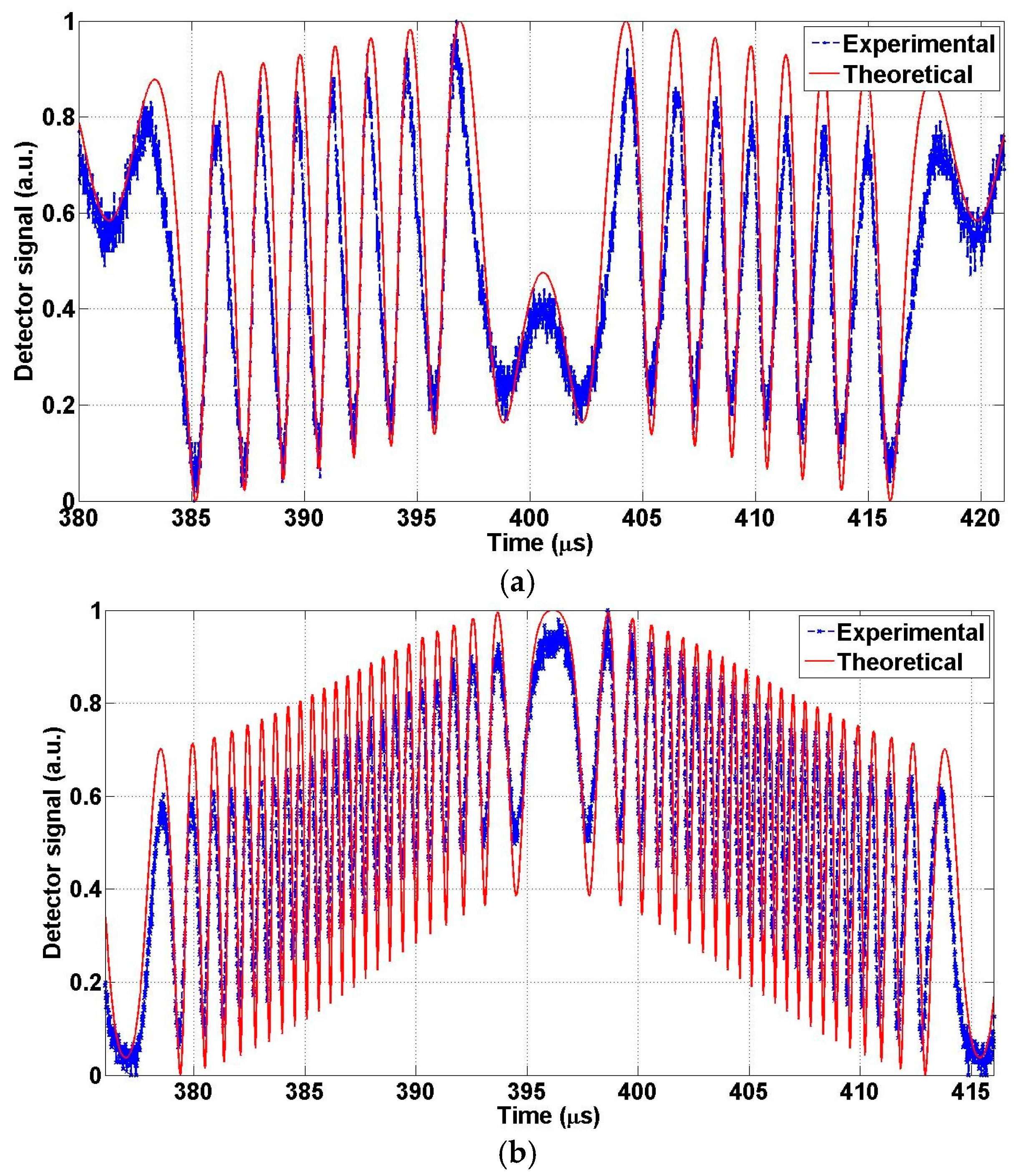
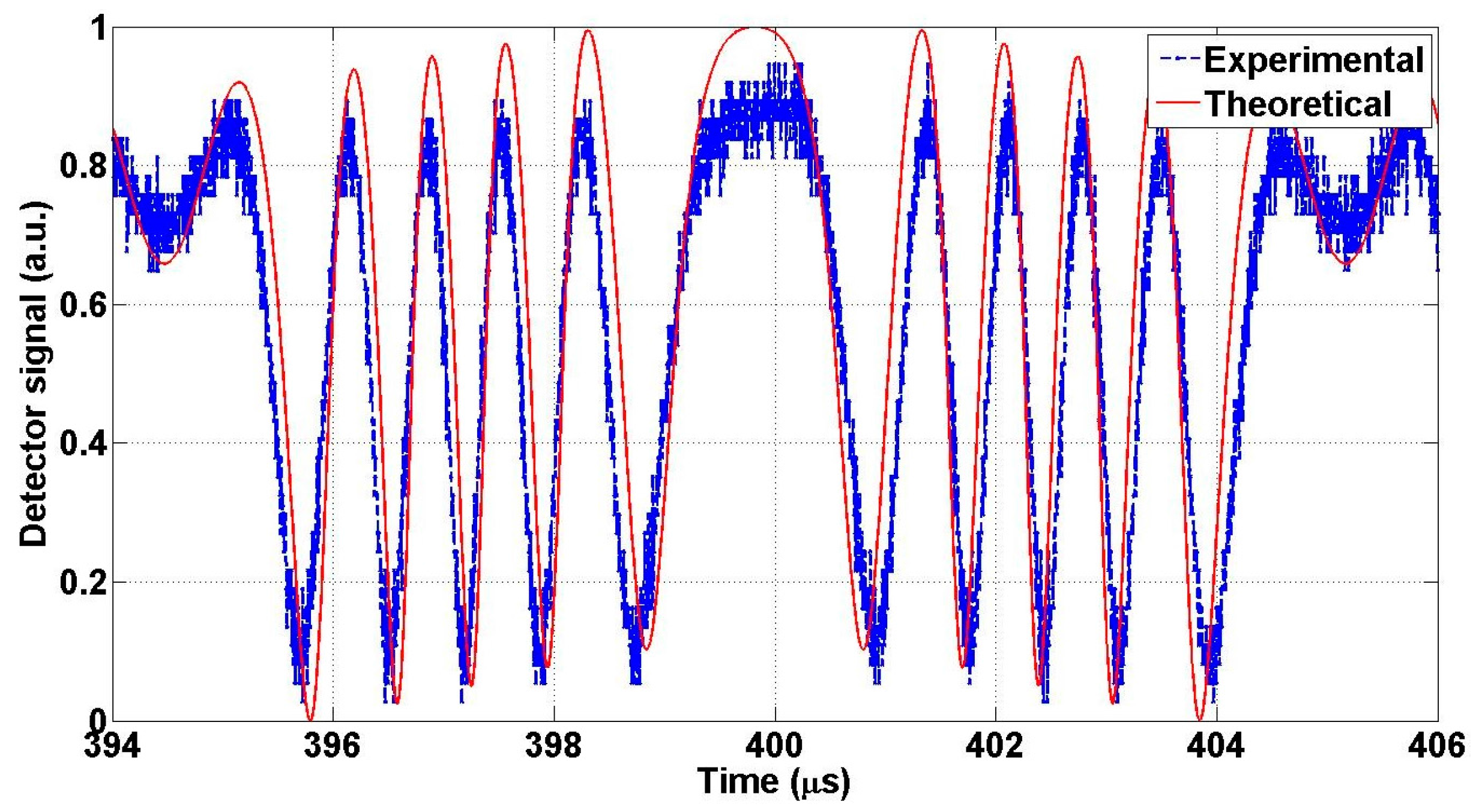
6. Experimental Results
6.1. Mirror Travel Range
6.2. Frequency Response
7. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| MEMS | Microelectromechanical system |
| SOI | Silicon-on-insulator |
| DRIE | Deep reactive ion etching |
| BOX | Buried oxide |
| FEA | Finite element analysis |
| FTR | Full travel range |
| SEM | Scanning electron microscope |
| FP | Fabry–Perot |
| SMF | Single-mode fiber |
References
- Sabry, Y.M.; Khalil, D.; Bourouina, T. Monolithic silicon micromachined free-space optical interferometers on chip. Laser Photonics Rev. 2015, 9, 1–24. [Google Scholar] [CrossRef]
- Sabry, Y.M.; Khalil, D.; Saadany, B.; Bourouina, T. Integrated wide-angle scanner based on translating a curved mirror of a cylindrical shape. Opt. Express 2013, 21, 13906–13916. [Google Scholar] [CrossRef] [PubMed]
- Omran, H.; Sabry, Y.M.; Sadek, M.; Hassan, K.; Shalaby, M.Y.; Khalil, D. Deeply-Etched Optical MEMS Tunable Filter for Swept Laser Source Applications. IEEE Photonics Technol. Lett. 2014, 26, 37–39. [Google Scholar] [CrossRef]
- Omran, H.; Medhat, M.; Saadany, B.; Khalil, D. Fully integrated Mach-Zhender MEMS interferometer with two complementary outputs. IEEE J. Quantum Electron. 2012, 48, 244–251. [Google Scholar] [CrossRef]
- Syms, R.R.A. Long-travel electrothermally driven resonant cantilever microactuators. J. Micromech. Microeng. 2002, 12, 211–218. [Google Scholar] [CrossRef]
- Lantz, M.A.; Rothuizen, H.E.; Drechsler, U.; Haeberle, W.; Despont, M. A vibration resistant nanopositioner for mobile parallel-probe storage applications. J. Microelectromech. Syst. 2007, 16, 130–139. [Google Scholar] [CrossRef]
- Gao, P.; Yao, K.; Tang, X.; He, X.; Shannigrahi, S.; Lou, Y.; Zhang, J.; Okada, K. A piezoelectric micro-actuator with a three-dimensional structure and its micro-fabrication. Sens. Actuators A Phys. 2006, 130, 491–496. [Google Scholar] [CrossRef]
- Bell, D.J.; Lu, J.; Fleck, N.A.; Spearing, S.M. MEMS actuators and sensors: Observations on their performance and selection for purpose. J. Micromech. Microeng. 2005, 15, S153. [Google Scholar] [CrossRef]
- Sabry, Y.M.; Khalil, D.; Saadany, B.; Bourouina, T. In-plane external fiber Fabry–Perot cavity comprising silicon micromachined concave mirror. J. Micro/Nanolith. MEMS MOEMS 2013, 13, 011110. [Google Scholar] [CrossRef]
- Gaber, N.; Sabry, Y.M.; Marty, F.; Bourouina, T. Optofluidic Fabry-Pérot micro-cavities comprising curved surfaces for homogeneous liquid refractometry—Design, simulation, and experimental performance assessment. Micromachines 2016, 7, 62. [Google Scholar] [CrossRef]
- Grade, J.D.; Jerman, H.; Kenny, T.W. Design of large deflection electrostatic actuator. J. Microelectromech. Syst. 2003, 12, 335–343. [Google Scholar] [CrossRef]
- Jeong, K.-H.; Lee, L.P. A novel microfabrication of a self-aligned vertical comb drive on a single SOI wafer for optical MEMS applications. J. Micromech. Microeng. 2005, 15, 277–281. [Google Scholar] [CrossRef]
- Zou, J.; Liu, C.; Schutt-Ainé, J.; Chen, J.; Kang, S.-M. Development of a Wide-Tuning-Range Two-Parallel-Plate Tunable Capacitor for Integrated Wireless Communication Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001; pp. 403–406. [Google Scholar]
- Linzon, Y.; Ilic, B.; Lulinsky, S.; Krylov, S. Efficient parametric excitation of silicon-on-insulator microcantilever beams by fringing electrostatic fields. J. Appl. Phys. 2013, 113, 16. [Google Scholar] [CrossRef]
- Felder, J.; Lee, E.; DeVoe, D.L. Large vertical displacement electrostatic zipper microstage actuators. J. Microelectromech. Syst. 2015, 24, 896–903. [Google Scholar] [CrossRef]
- Sasaki, M.; Bono, F.; Hane, K. Large-displacement micro-XY-stage with paired moving plates Japan. J. Appl. Phys. 2008, 47, 3226–3231. [Google Scholar] [CrossRef]
- Kota, S.; Joo, J.; Li, Z.; Rodgers, S.M.; Sniegowski, J. Design of compliant mechanisms: Applications to MEMS. Analog Integr. Circuits Signal Process. 2001, 29, 7–15. [Google Scholar] [CrossRef]
- Olfatnia, M.; Cui, L.; Chopra, P.; Awtar, S. Large range dual-axis micro-stage driven by electrostatic comb-drive actuators. J. Micromech. Microeng. 2013, 23, 105008. [Google Scholar] [CrossRef]
- Indermuhle, P.F.; Jaecklin, V.P.; Brugger, J.; Linder, C.; Derooij, N.F.; Binggeli, M. AFM imaging with an XY-micropositioner with integrated tip. Sens. Actuators A Phys. 1995, 47, 562–565. [Google Scholar] [CrossRef]
- Zhang, W.; Baskaran, R.; Turner, K.L. Effect of cubic nonlinearity on auto-parametrically amplified resonant MEMS mass sensor. Sens. Actuators A Phys. 2002, 102, 139–150. [Google Scholar] [CrossRef]
- Laszczyk, K.; Bargiel, S.; Gorecki, C.; Krezel, J.; Dziuban, P.; Kujawinskab, M.; Callet, D.; Frank, S. A two directional electrostatic comb-drive XY micro-stage for MOEMS applications. Sens. Actuators A Phys. 2010, 163, 255–265. [Google Scholar] [CrossRef]
- Kwon, H.N.; Lee, J.-H.; Takahashi, K.; Toshiyoshi, H. MicroXY stages with spider-leg actuators for two-dimensional optical scanning. Sens. Actuators A Phys. 2006, 130, 468–477. [Google Scholar] [CrossRef]
- Mukhopadhyay, D.; Dong, J.; Pengwang, E.; Ferreira, P. A SOI-MEMS-based 3-DOF planar parallel-kinematics nanopositioning stage. Sens. Actuators A Phys. 2008, 147, 340–351. [Google Scholar] [CrossRef]
- Chang, C.-M.; Wang, S.-Y.; Chen, R.; Yeh, A.; Hou, M.T. A comb-drive actuator driven by capacitively-coupled-power. Sensors 2012, 12, 10881–10889. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.; Qi, M.; Wu, X.; Wang, P.; Pu, J.; Lin, L. Electrostatic cantilever resonators under a double-sided pull–pull drive scheme. J. Micromech. Microeng. 2014, 24, 035004. [Google Scholar] [CrossRef]
- Kim, C.H.; Jeong, H.M.; Jeon, J.U.; Kim, Y.K. Silicon micro XY-stage with a large area shuttle and no-etching holes for SPM-based data storage. J. Microelectromech. Syst. 2003, 12, 470–478. [Google Scholar]
- Fedder, G.K. Simulation of Microelectromechanical Systems. Ph.D. Thesis, University of California, Berkeley, CA, USA, September 1994. [Google Scholar]
- Bao, M. Analysis and Design Principles of MEMS Devices, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Sabry, Y.M.; Eltagoury, Y.M.; Shebl, A.; Soliman, M.; Khalil, D. Fiber-coupled Fabry-Pérot notch filter combining in-plane axis, high speed MEMS tunability and large etching depth. Proc. SPIE 2015, 93750, 93750U. [Google Scholar]
- Piersol, A.G.; Paez, T.L. Harri’s Shock and Vibration Handbook, 6th ed.; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Bhushan, B. Springer Handbook of Nanotechnology, 3rd ed.; Springer-Verlag GmbH: Berlin, Germany, 2010. [Google Scholar]
- Ville, K. MEMS material. Available online: http://www.kaajakari.net/~ville/research/tutorials/tutorials.shtml (accessed on 5 October 2016).
- Lawrence, E.M.; Speller, E.S.; Yu, D. MEMS characterization using Laser Doppler Vibrometry. Proc. SPIE 2003, 4980, 51–62. [Google Scholar]
- Serio, B.; Hunsinger, J.-J.; Cretin, B. Stroboscopic illumination and synchronous imaging for the characterization of MEMS vibrations. Proc. SPIE 2004, 5458, 257–264. [Google Scholar]
- Lodi, V.A.; Merlo, S.; Norgia, M. Measurements on a micromachined silicon gyroscope by feedback interferometry. IEEE/ASME Trans. Mechatron. 2001, 6, 1–6. [Google Scholar] [CrossRef]
- Lodi, V.A.; Merlo, S.; Norgia, M. Comparison of capacitive and feedback-interferometric measurements on MEMS. J. Microelectromech. Syst. 2001, 10, 327–335. [Google Scholar] [CrossRef]
- Sabry, Y.M.; Eltagoury, Y.M.; Shebl, A.; Soliman, M.; Sadek, M.; Khalil, D. In-plane deeply-etched optical MEMS notch filter with high-speed tunability. J. Opt. 2015, 17, 125703. [Google Scholar] [CrossRef]
- Sabry, Y.; Medhat, M.; Saadany, B.; Safwat, A.M.E.; Khalil, D. Optical Characterization Technique for MEMS Comb-Drive Resonators. In Proceedings of the IEEE/LEOS International Conference on Optical MEMS and Nanophotonics, Clearwater, FL, USA, 17–20 August 2009; pp. 127–128.
- Kilic, O.; Digonnet, M.J.; Kino, G.S.; Solgaard, O. spectral response in fiber Fabry–Perot interferometers. J. Lightw. Technol. 2009, 27, 5648–5656. [Google Scholar] [CrossRef]


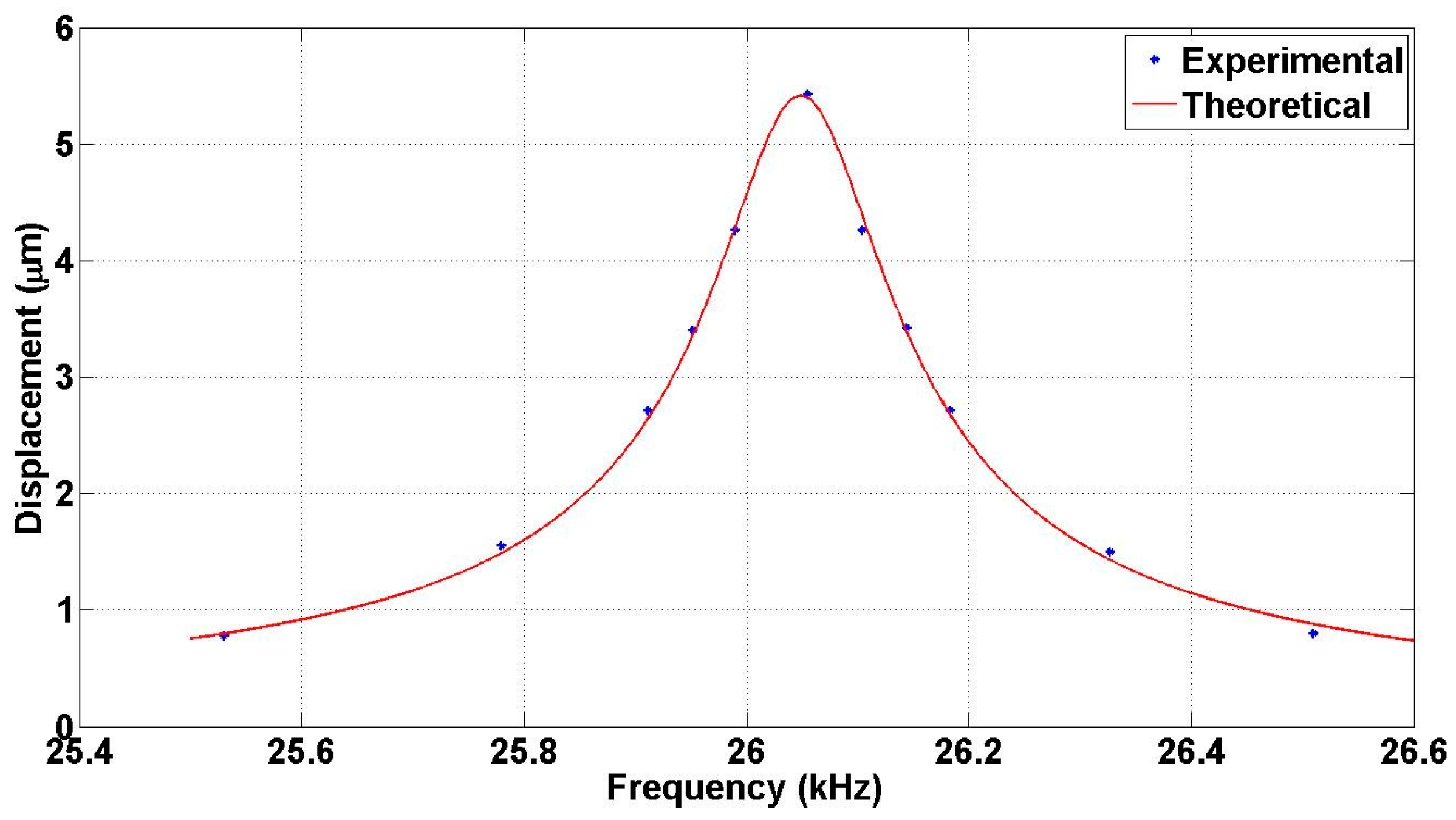
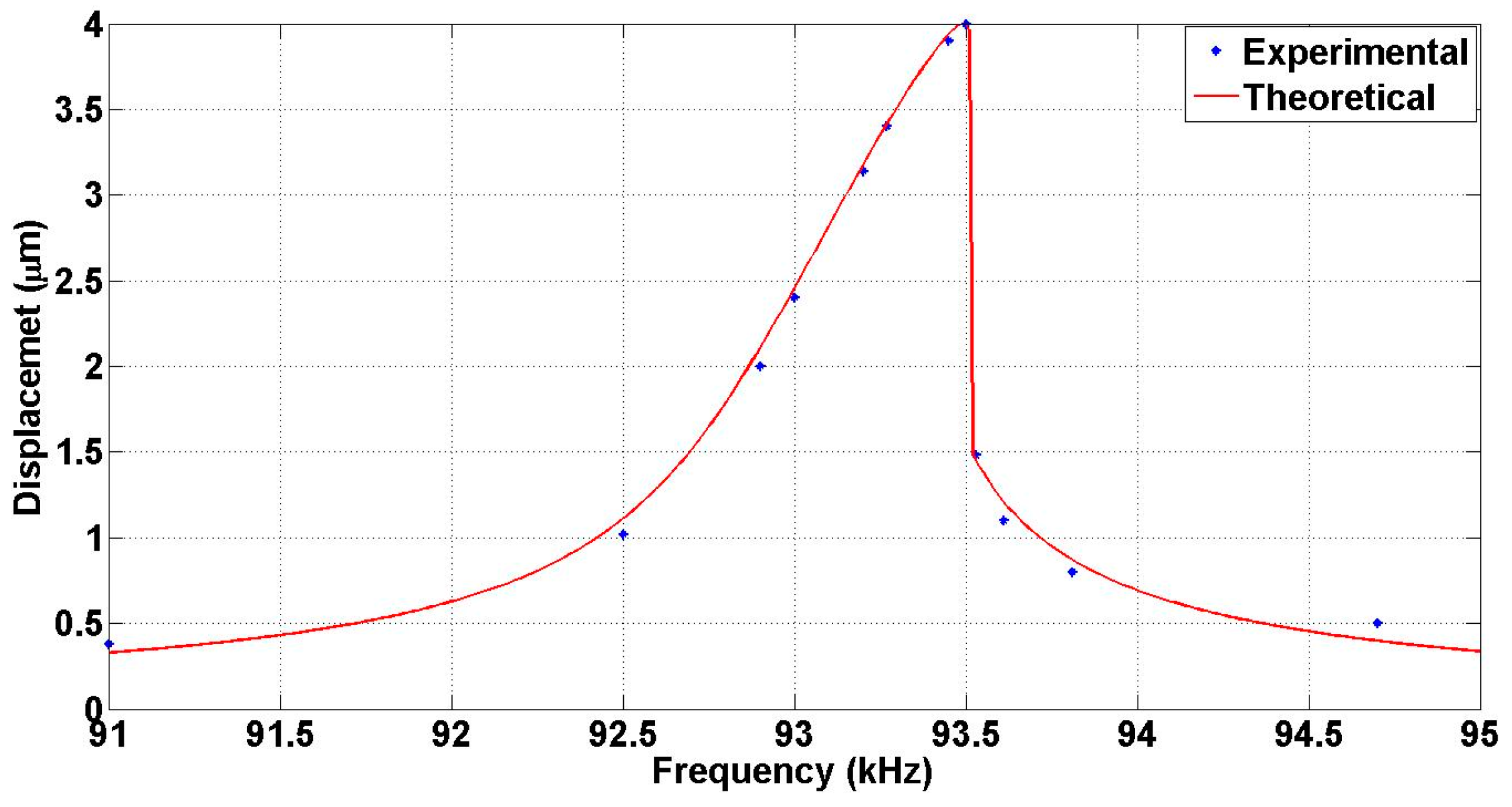
| Peak Travel Range (µm) | Resonance Frequency | Figure of Merit (µm·kHz) | Peak Translation Velocity (m/s) | References |
|---|---|---|---|---|
| 9.06 | 26.055 kHz | 236.06 | 1.48 | Current work |
| 2 | 93.5 kHz | 187 | 1.18 | |
| 180 | 769 Hz | 138.42 | 0.87 | [11] |
| 115 | 690 Hz | 79.35 | 0.5 | [16] |
| 20 | 3.8 kHz | 76 | 0.48 | [17] |
| 200 | 329 Hz | 65.8 | 0.41 | [2] |
| 112.5 | 400 Hz | 45 | 0.28 | [18] |
| 3 | 10 kHz | 30 | 0.19 | [19] |
| 1 | 26.48 kHz | 26.48 | 0.17 | [20] |
| 37 | 550 Hz | 20.35 | 0.13 | [21] |
| 55 | 280 Hz | 15.4 | 0.1 | [22] |
| 18 | 465 Hz | 8.37 | 0.05 | [23] |
| 14 | 577 Hz | 8.08 | 0.05 | [24] |
| 183.5 | 30 Hz | 5.50 | 0.03 | [25] |
| 18 | 164 Hz | 2.95 | 0.02 | [26] |
| Physical Dimension | Value |
|---|---|
| Device thickness | 80 µm |
| Young’s modules | 169 × 103 µN/µm2 |
| Number of moving fingers | 56 |
| Spring beams width | 8 µm |
| Spring beams length | 360 µm |
| Spring truss width | 13 µm |
| Finger length | 40 µm |
| Finger width | 3 µm |
| Air gap between moving and fixed finger | 5 µm |
| Anchors | 150 µm × 150 µm |
| Physical Dimension | Value |
|---|---|
| Device thickness | 80 µm |
| Number of moving fingers | 36 |
| Beams width | 10 µm |
| Beams length | 270 µm |
| Truss width | 13 µm |
| Finger length | 30 µm |
| Finger width | 3 µm |
| Air gap between moving and fixed finger | 5 µm |
| Anchors | 150 µm × 150 µm |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eltagoury, Y.M.; Soliman, M.; Sabry, Y.M.; Alotaibi, M.J.; Khalil, D. Electrostatic Comb-Drive Actuator with High In-Plane Translational Velocity. Micromachines 2016, 7, 188. https://doi.org/10.3390/mi7100188
Eltagoury YM, Soliman M, Sabry YM, Alotaibi MJ, Khalil D. Electrostatic Comb-Drive Actuator with High In-Plane Translational Velocity. Micromachines. 2016; 7(10):188. https://doi.org/10.3390/mi7100188
Chicago/Turabian StyleEltagoury, Yomna M., Mostafa Soliman, Yasser M. Sabry, Mohammed J. Alotaibi, and Diaa Khalil. 2016. "Electrostatic Comb-Drive Actuator with High In-Plane Translational Velocity" Micromachines 7, no. 10: 188. https://doi.org/10.3390/mi7100188
APA StyleEltagoury, Y. M., Soliman, M., Sabry, Y. M., Alotaibi, M. J., & Khalil, D. (2016). Electrostatic Comb-Drive Actuator with High In-Plane Translational Velocity. Micromachines, 7(10), 188. https://doi.org/10.3390/mi7100188








