A Monolithic Micro-Tensile Tester for Investigating Silicon Dioxide Polymorph Micromechanics, Fabricated and Operated Using a Femtosecond Laser
Abstract
:1. Introduction
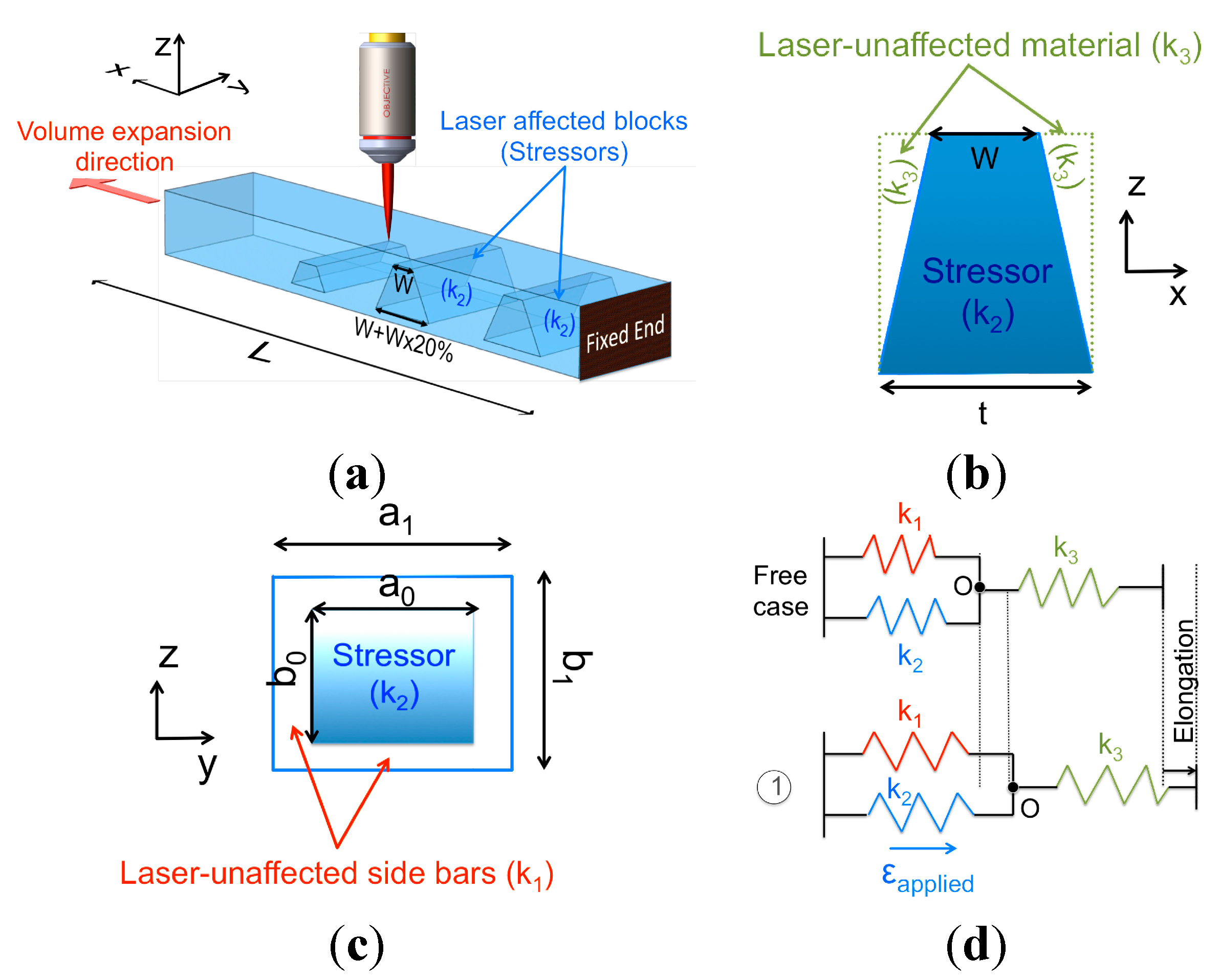
2. Microtensile Tester Design and Working Principle
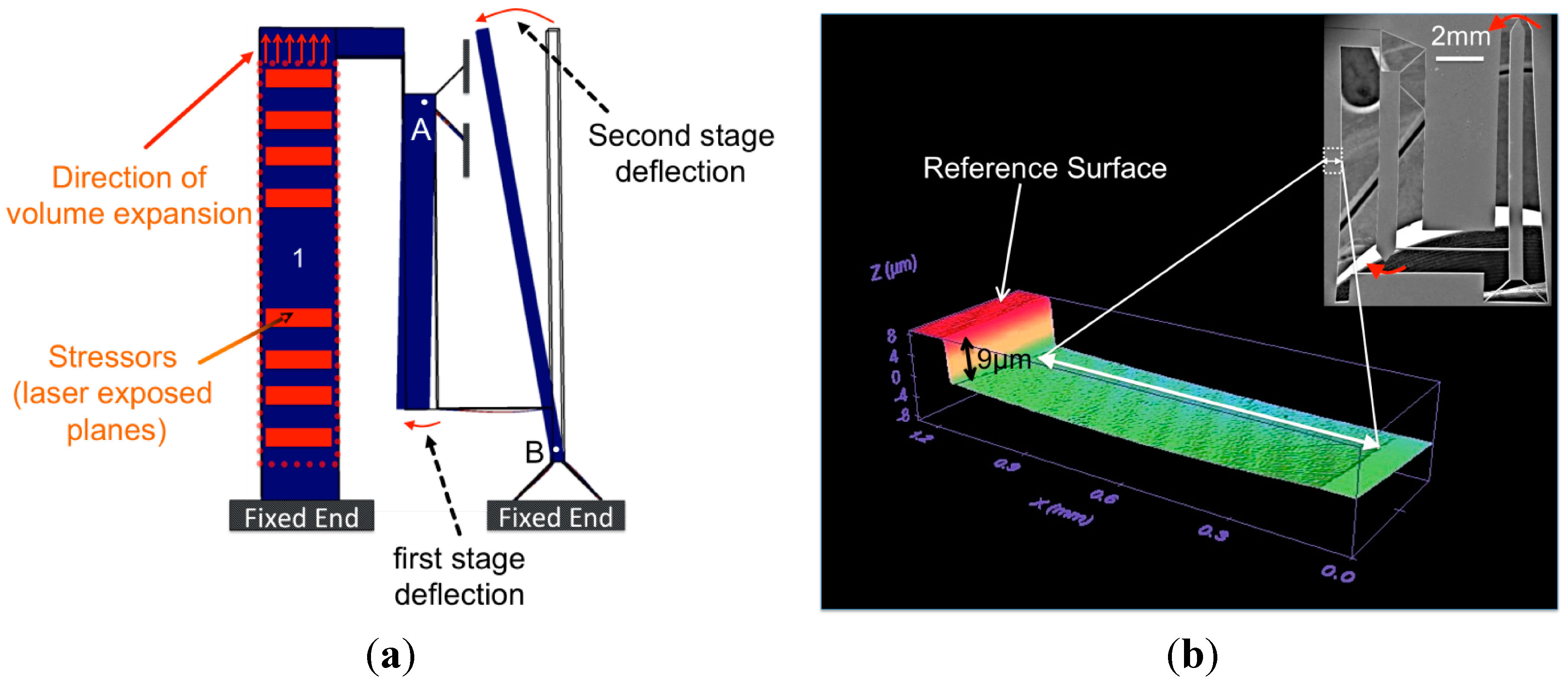
2.1. Working Principle
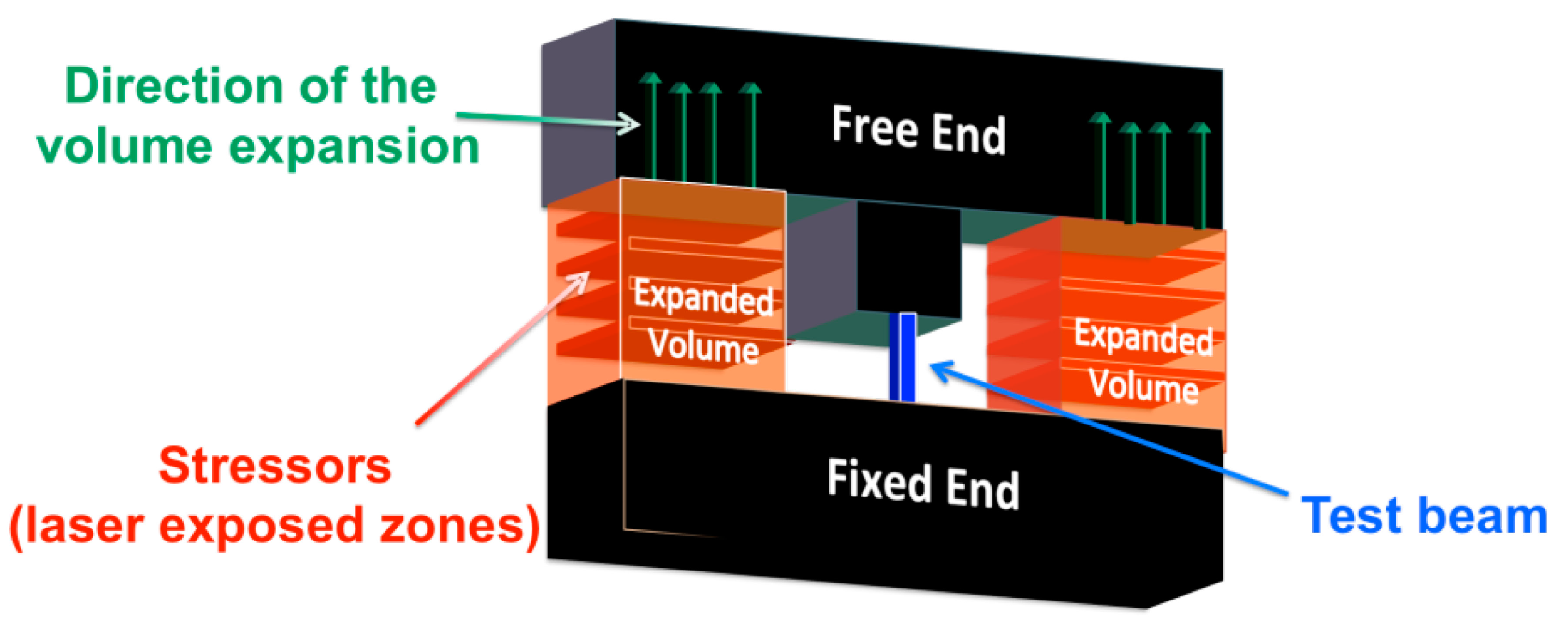
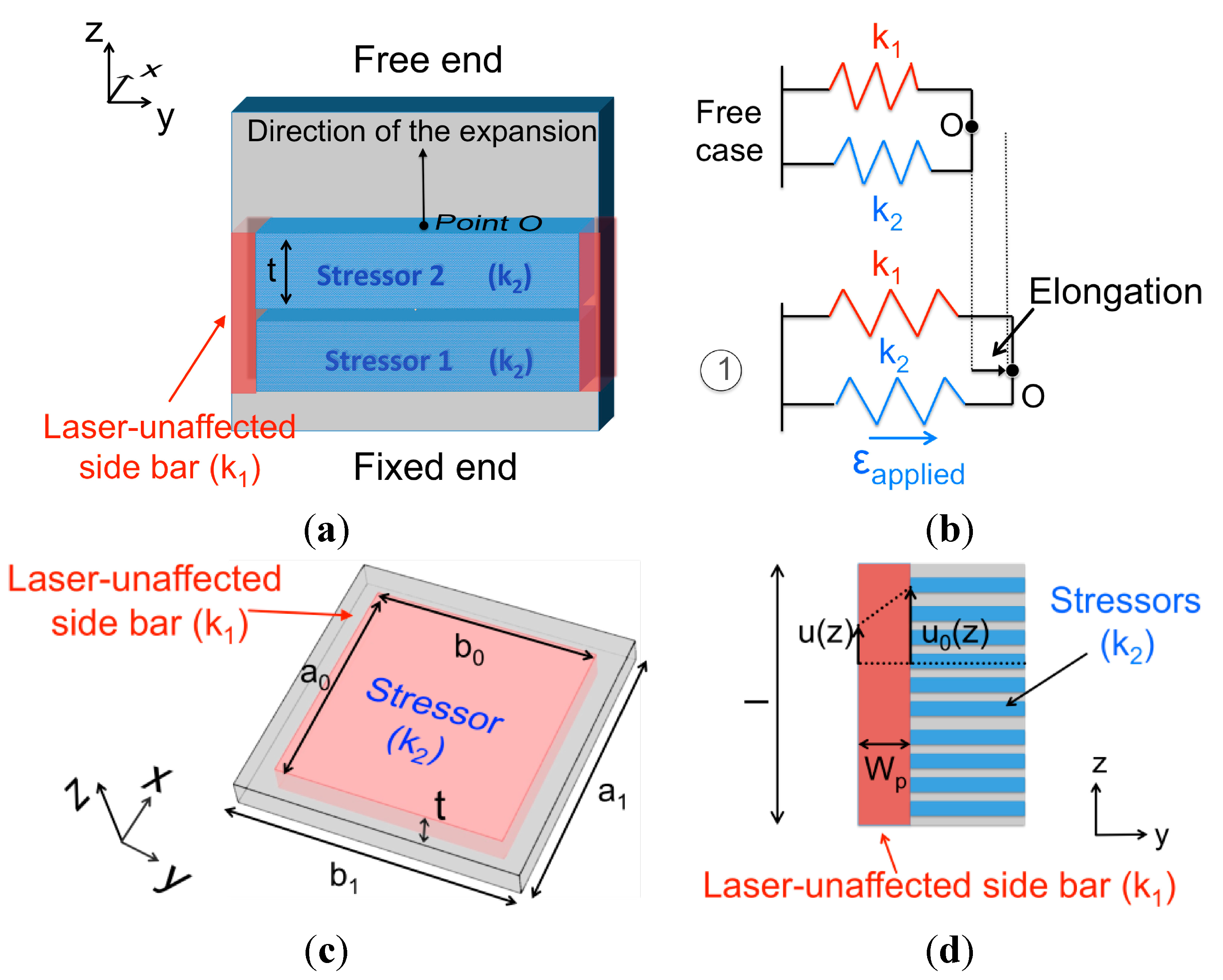
2.2. Test Beam Dimensioning
2.3. Loading Cell
2.4. Lever Amplification Mechanism
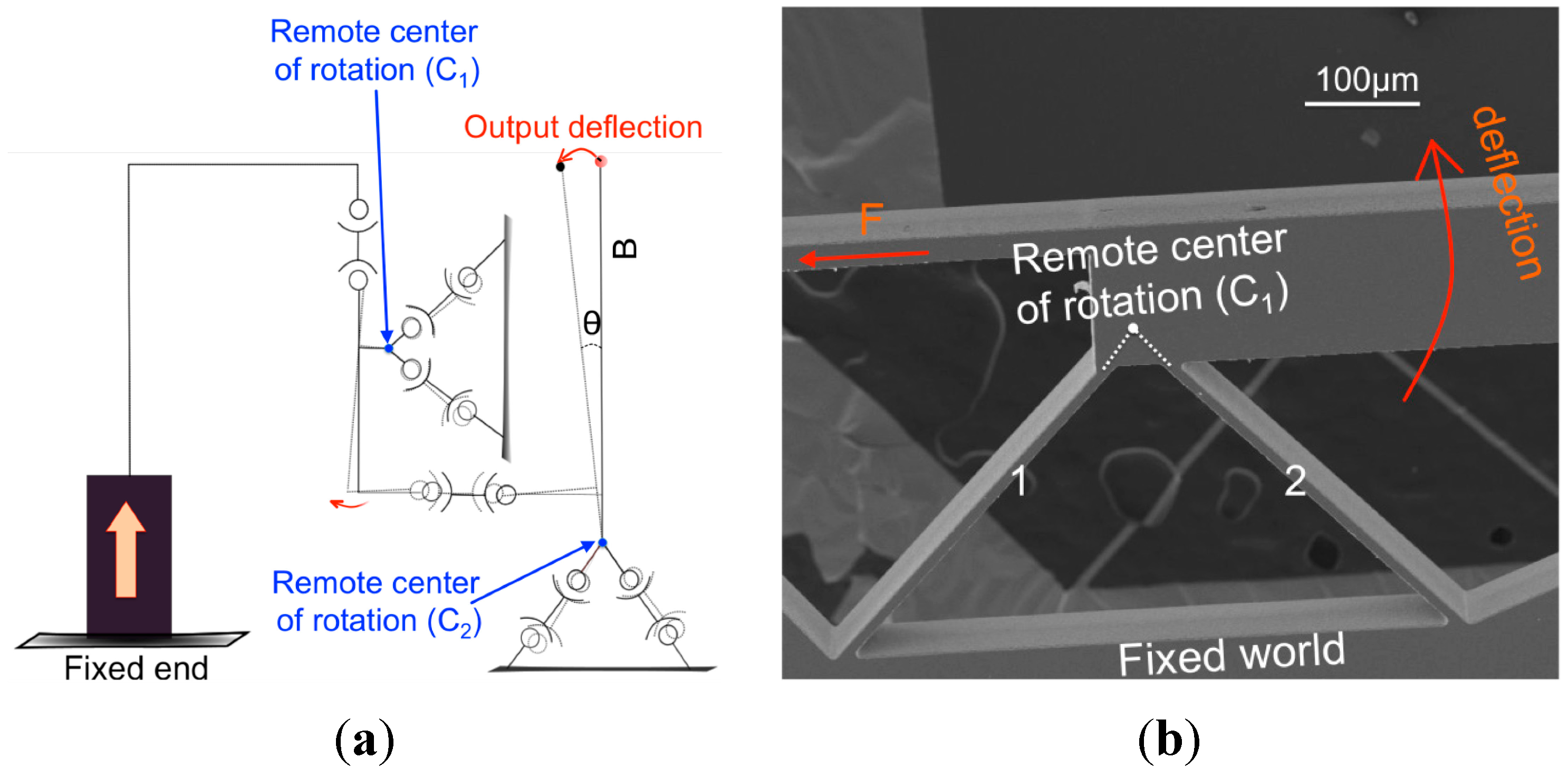
2.5. Mechanical Guidance
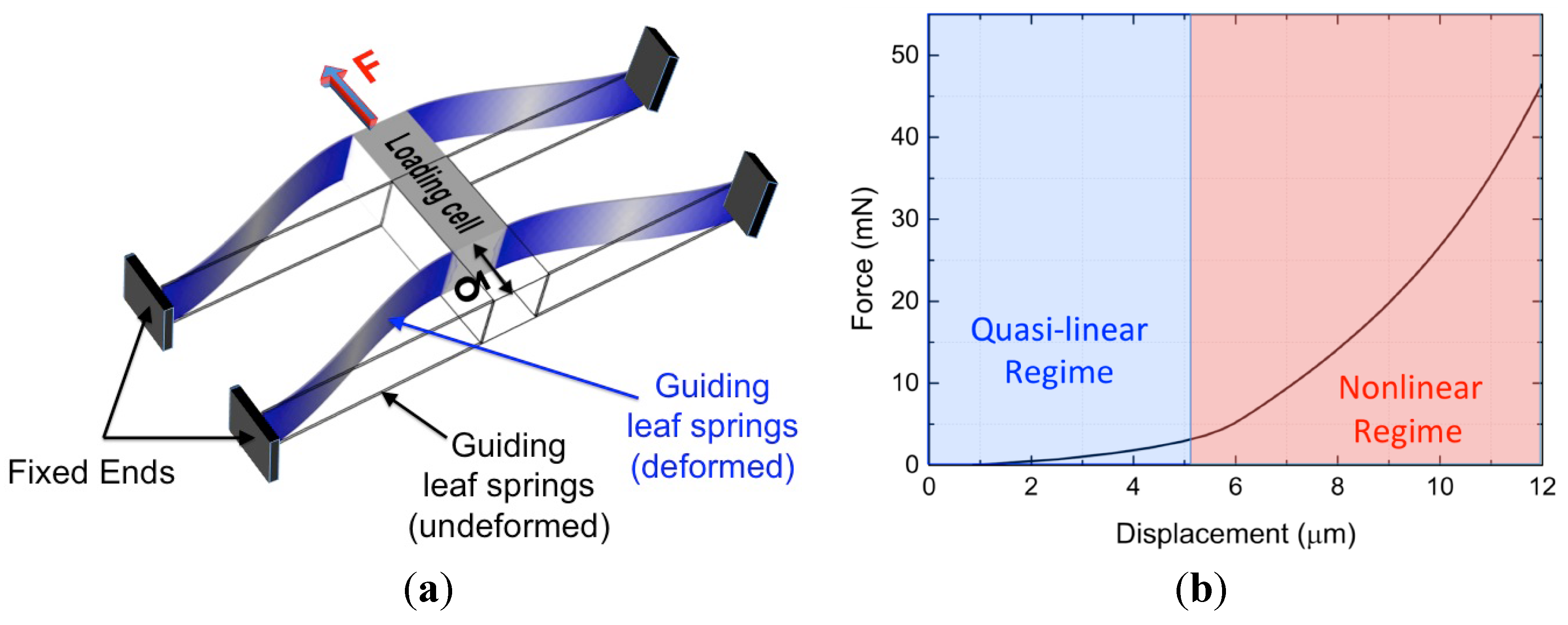
3. Experimental Results
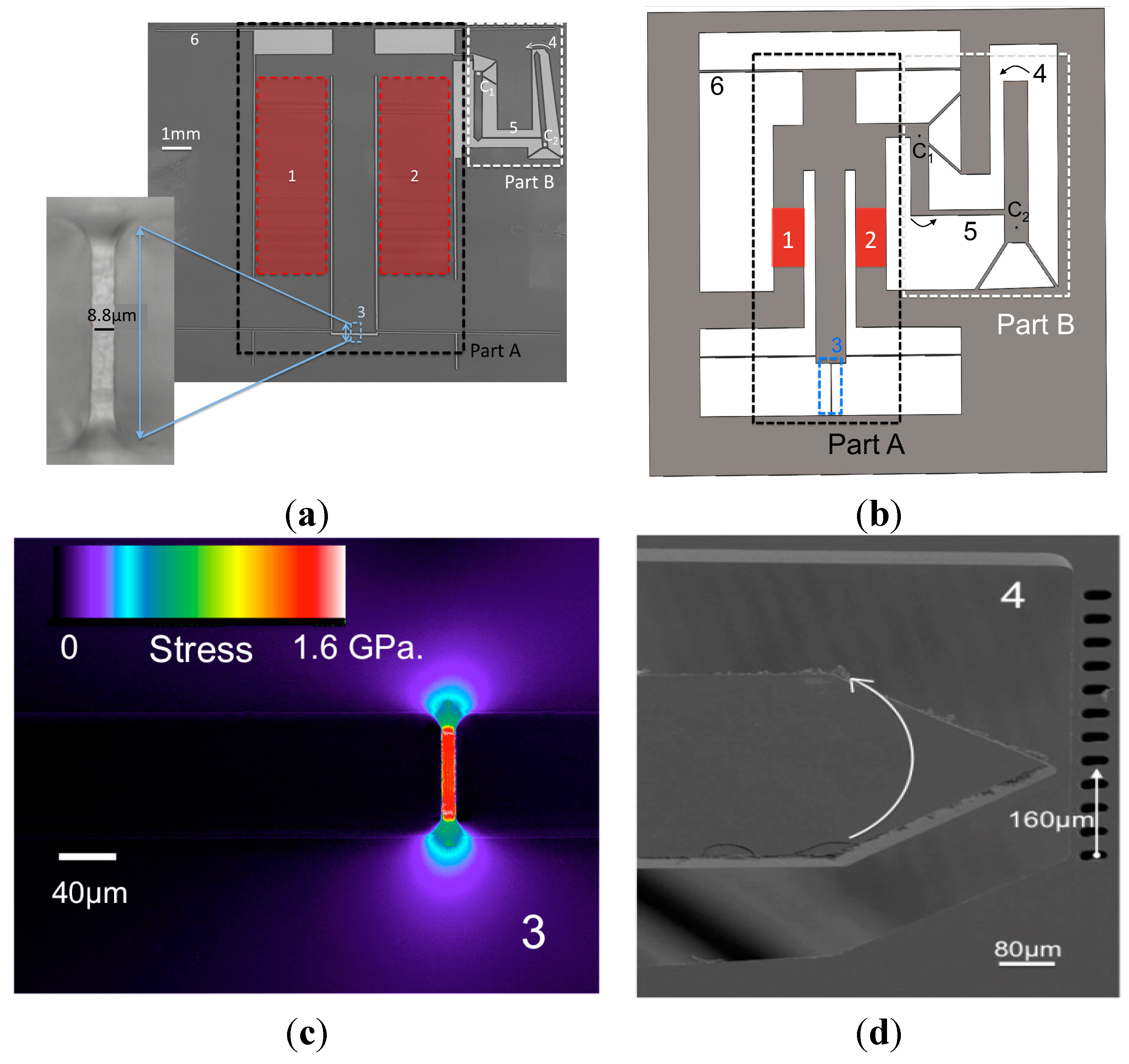
3.1. Manufacturing
3.2. Stressors Model Validation and Optimization
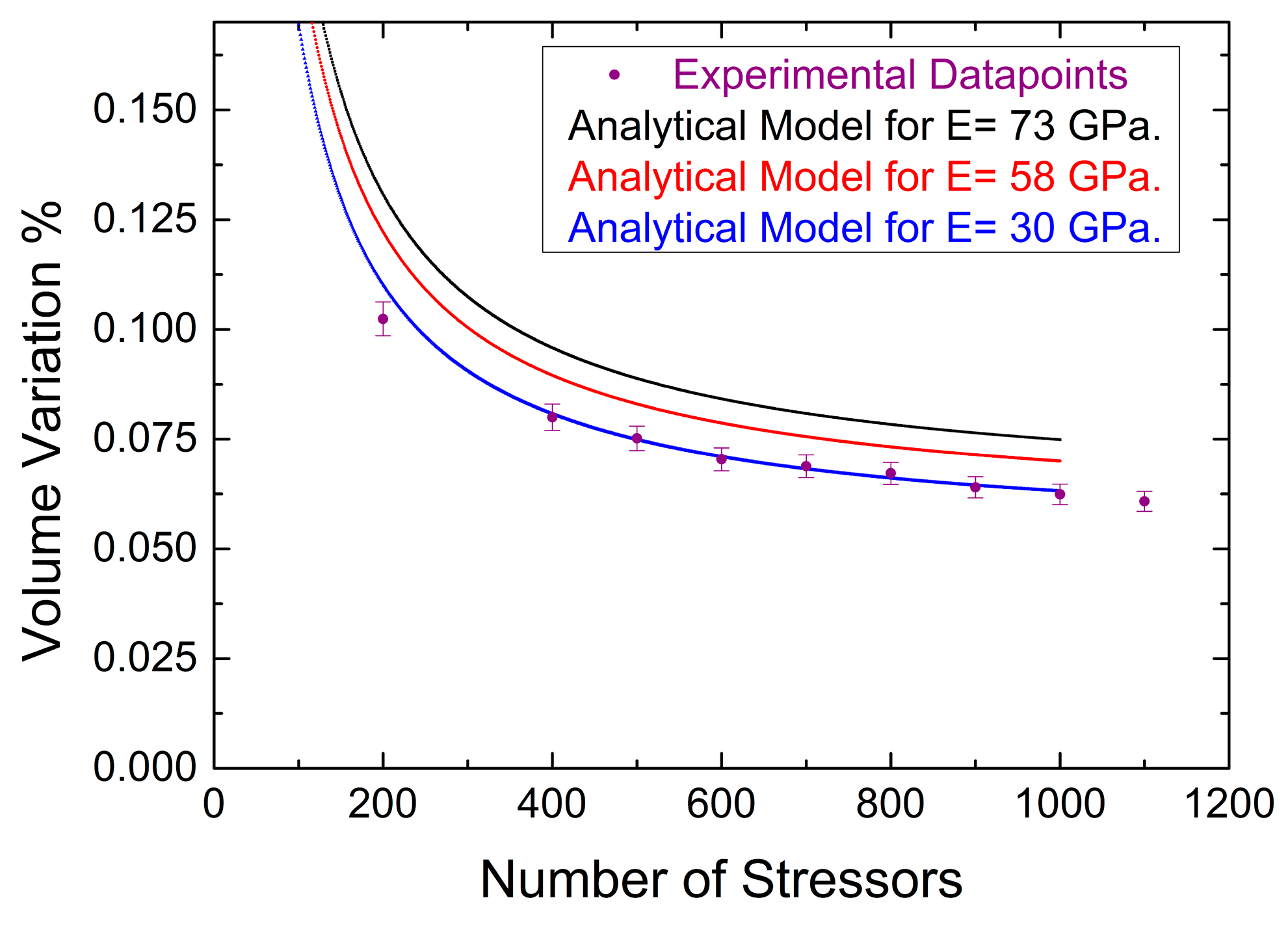
| Elastic Modulus of Laser-Affected Zones for Different Porosity Parameters | Eporous (GPa) |
|---|---|
| p = 0.40 | 41.1 |
| p = 0.45 | 37.8 |
| p = 0.50 | 34.0 |

| For Given Exposure Conditions (NA), Pulse Energy + Writing Speed | Tip Deflection (μm) | Mean Value of the Volume Variation % | ||
|---|---|---|---|---|
| Loading case 1 | 42.0 | 41.5 | 42.0 | 0.0011 |
| Loading case 2 | 53.0 | 52.5 | 53.0 | 0.0009 |
3.3. Third-Harmonics Generation (THG) as an In Situ Metrology Tool
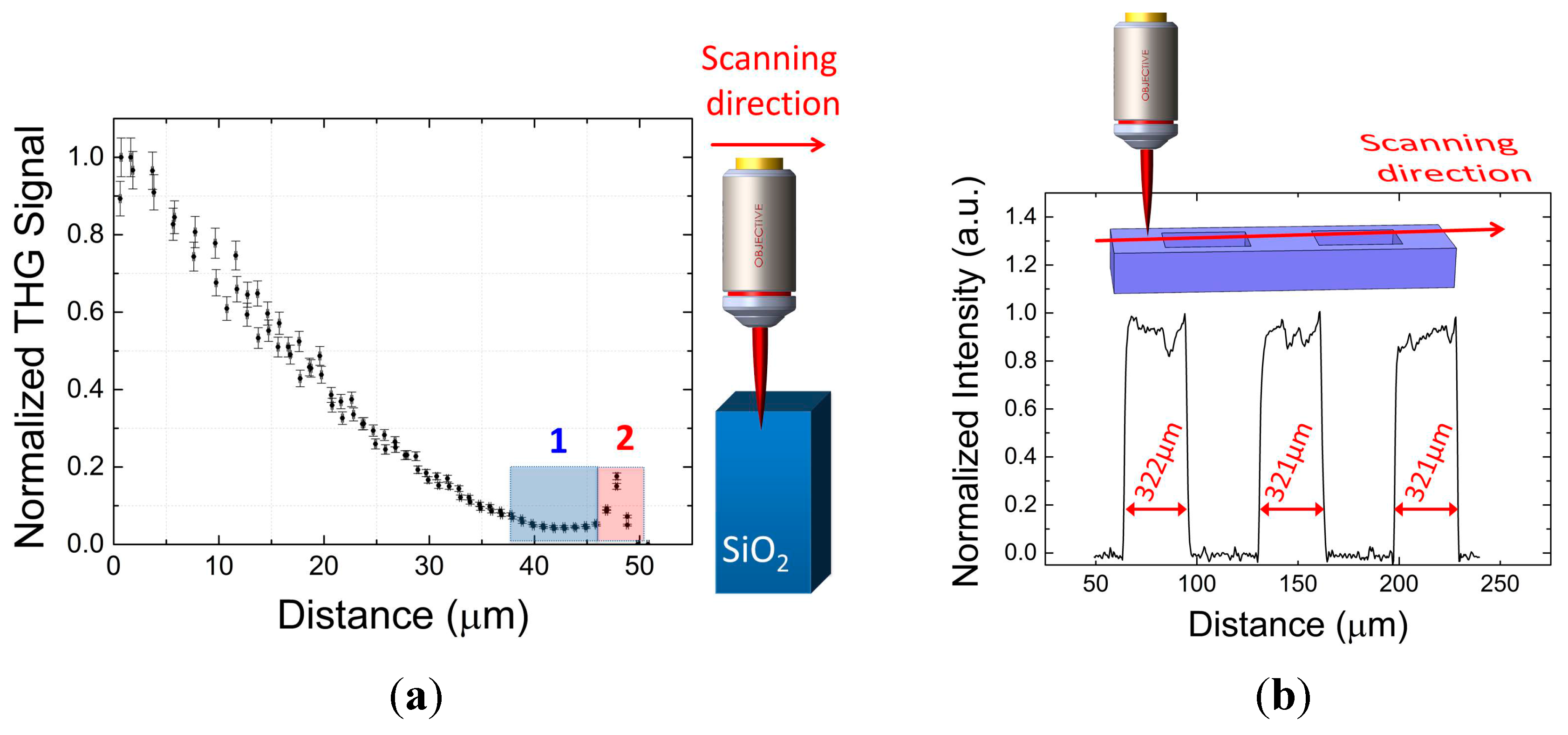
3.4. Stress Monitoring through Photoelasticity
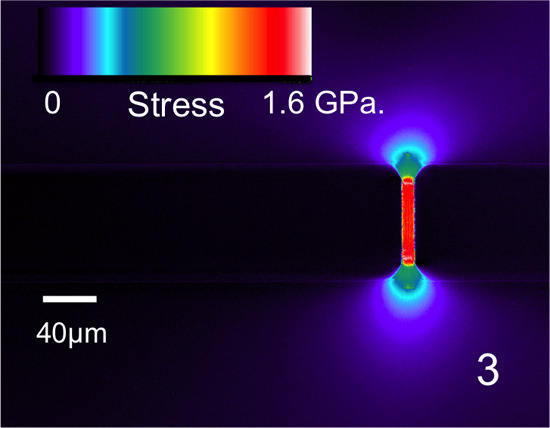
3.5. Example of Stress Measurements on a Silica Micro-Beam
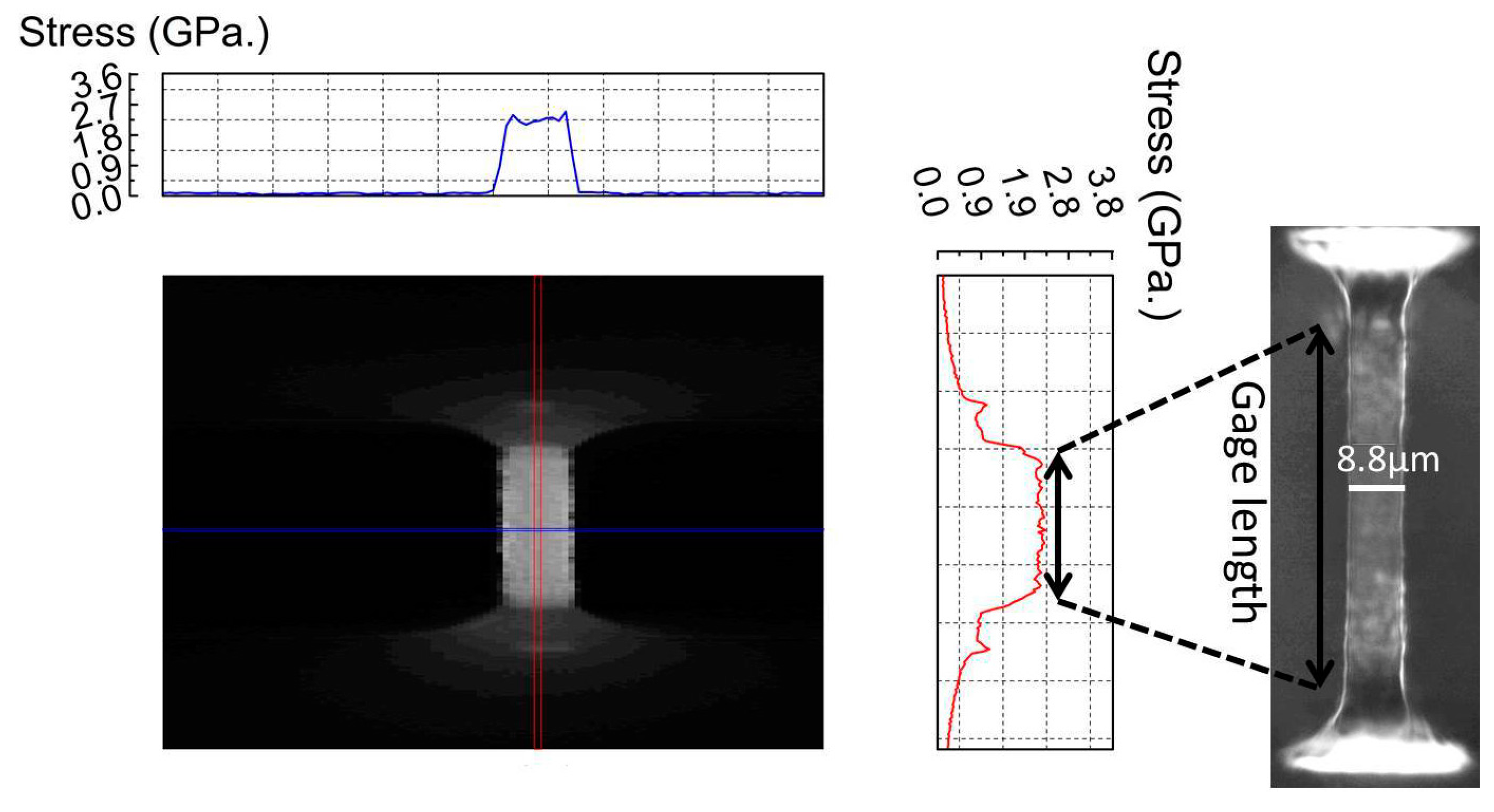
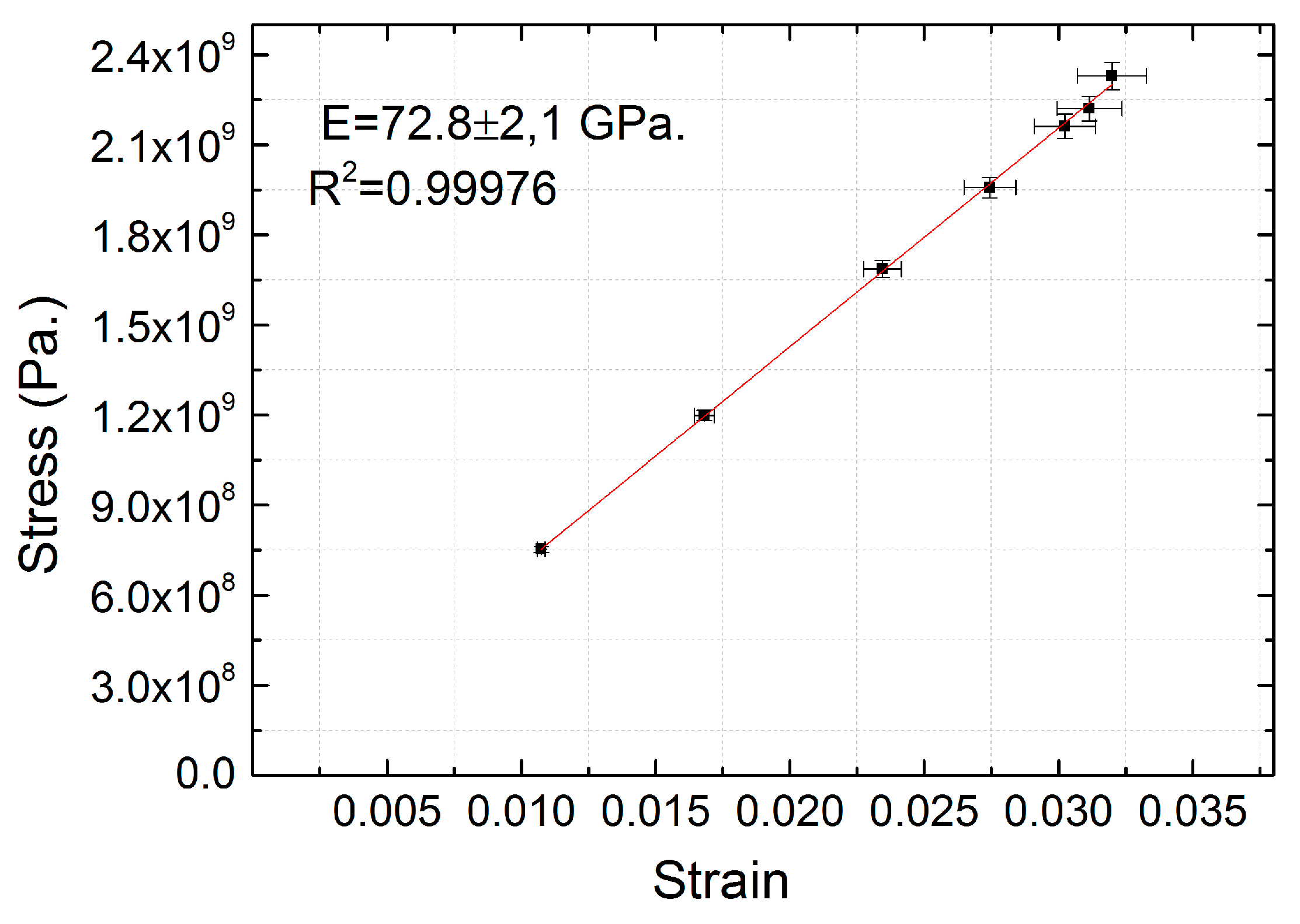
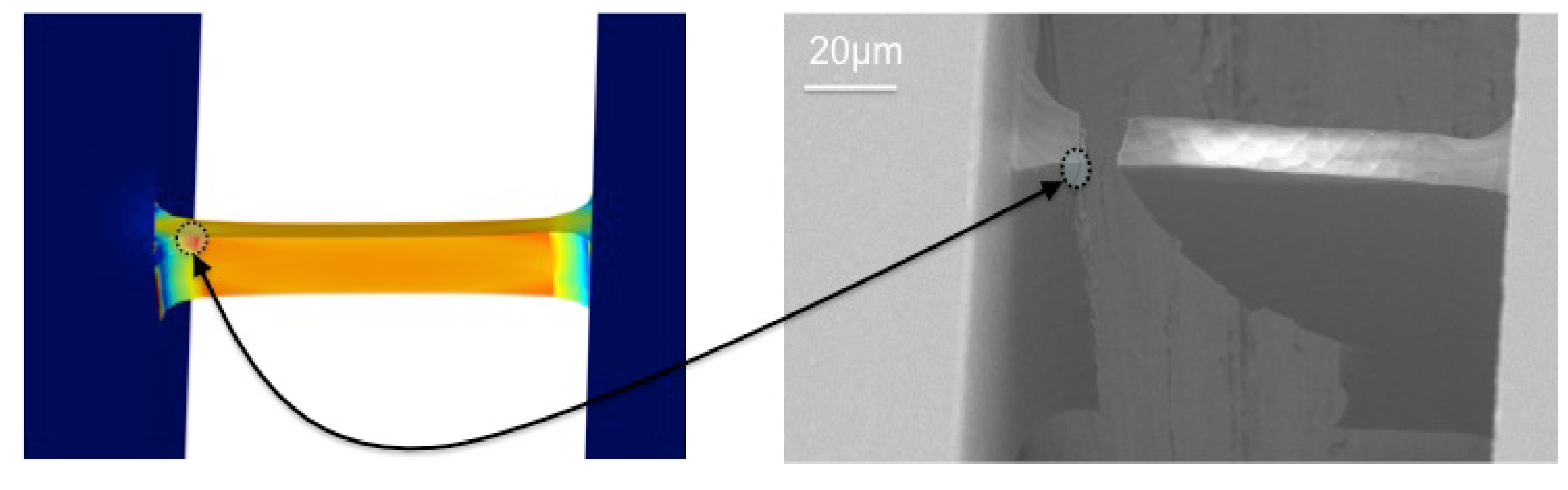
3.6. Error Analysis for the Experimental Technique
4. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
Derivation of the Shear-Lag Model
References
- Nix, D.W. Exploiting new opportunities in materials research by remembering and applying old lessons. MRS Bull. 2009, 34, 82–91. [Google Scholar] [CrossRef]
- Nix, D.W. Mechanical properties of thin films. Metall. Trans. A 1989, 20, 2217–2245. [Google Scholar] [CrossRef]
- Greer, J.R.; Oliver, W.C.; Nix, D.W. Size dependence of mechanical properties of gold at the micron scale in the absence of strain gradients. Acta Mater. 2005, 53, 1821–1830. [Google Scholar] [CrossRef]
- Srikar, V.T.; Spearing, S.M. A critical review of microscale mechanical testing methods used in the design of microelectromechanical systems. Expe. Mech. 2003, 43, 238–247. [Google Scholar] [CrossRef]
- Hemker, K.J.; Sharpe, W.N. Microscale characterization of mechanical properties. Annu. Rev. Mater. Res. 2007, 37, 93–126. [Google Scholar] [CrossRef]
- Vlassak, J.J.; Nix, W.D. A new bulge test technique for the determination of young’s modulus and poisson’s ratio of thin films. J. Mater. Res. 1992, 7, 3242–3249. [Google Scholar] [CrossRef]
- Hémel, A.; Jacques, A.; Schenk, T.; Ferry, O.; Kruml, T. Investigation of mechanical properties of gold thin films using a bulge test technique. J. Phys. Conf. Ser. 2010, 240, 012163. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Schuh, C.A. Nanoindentation studies of materials. Mater. Today 2006, 9, 32–40. [Google Scholar] [CrossRef]
- Haque, M.A.; Saif, M.T. Microscale materials testing using mems actuators. J. Microelectromech. Syst. 2001, 10, 146–152. [Google Scholar] [CrossRef]
- Haque, M.A.; Saif, M.T. A review of mems-based microscale and nanoscale tensile and bending testing. Expe. Mech. 2003, 43, 248–255. [Google Scholar] [CrossRef]
- Liu, R.; Wang, H.; Li, X.; Ding, G.; Yang, C.A. Micro-tensile method for measuring mechanical properties of mems materials. J. Micromech. Microeng. 2008, 18, 065002. [Google Scholar] [CrossRef]
- Chasiotis, I.; Knauss, W.G. A New microtensile tester for the study of mems materials with the aid of atomic force microscopy. Expe. Mech. 2002, 42, 51–57. [Google Scholar] [CrossRef]
- Petersen, K.E. Dynamic micromechanics on silicon: Techniques and advantages. IEEE Trans. Electron Dev. 1978, 66, 1241–1250. [Google Scholar] [CrossRef]
- Petersen, K.E.; Guarnieri, C.R. Young’s modulus measurements of thin films using micromechanics. J. Appl. Phys. 1979, 50, 6761–6766. [Google Scholar] [CrossRef]
- Timoshenko, S.; Young, D.H.; Weaver, W. Vibration Problems in Engineering; John Wiley and Sons: New York, NY, USA, 1974. [Google Scholar]
- Osterberg, P.M.; Senturia, S.D. M-test: A test chip for MEMS material property measurements using electrostatically actuated test structures. J. Microelectro. Syst. 1997, 6, 107–117. [Google Scholar] [CrossRef]
- Gregoriou, V.G.; Brairman, M.S. Vibrational Spectroscopy of Biological and Polymeric Materials; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Tsoukleri, G.; Parthenios, J.; Papagelis, K.; Jalil, R.; Ferrari, A.; Geim, A.; Novoselov, K.; Galiotis, C. Subjecting a graphine monolayer to tension and compression. Small 2009, 5, 2397–2402. [Google Scholar] [CrossRef] [PubMed]
- Charitidis, C.A.; Dragatogiannis, D.A. Finite element analysis, stress–strain distribution and size effects rise during nanoindentation of welded aluminum alloy. Int. J. Struct. Integr. 2013, 4, 78–90. [Google Scholar]
- Tabor, D. The Hardness of Metals; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Stathis, J.H. Reliability Limits for the gate insulator in CMOS technology. IBM J. Res. Dev. 2002, 46, 265–286. [Google Scholar] [CrossRef]
- Strege, M.; Lagu, A. Separation of DNA restriction fragments by capillary electrophoresis using coated fused silica capillaries. Anal. Chem. 1991, 63, 1233–1236. [Google Scholar] [CrossRef] [PubMed]
- Marshall, G.D.; Ams, M.; Withford, M.J. Direct laser written waveguide-bragg gratings in bulk fused silica. Opt. Lett. 2006, 31, 2690–2691. [Google Scholar] [CrossRef] [PubMed]
- Schaap, A.; Rohrlack, T.; Bellouard, Y. Optical classification of algae species with a glass lab-on-a-chip. Lab Chip 2012, 12, 1527–1532. [Google Scholar] [CrossRef] [PubMed]
- Kurkjian, C.R.; Albarino, R.V.; Krause, J.T.; Vazirani, H.N.; DiMarcello, F.V.; Torza, S.; Schonhorn, H. Strength of 0.04–50-m lengths of coated fused silica fibers. Appl. Phys. Lett. 1976, 28, 588–590. [Google Scholar] [CrossRef]
- Jayatilaka, A.S.; Trustrum, K. Statistical approach to brittle fracture. J. Mater. Sci. 1977, 12, 1426–1430. [Google Scholar] [CrossRef]
- Griffith, A.A. The phenomena of rupture and flow in solids. Phil. Trans. R. Soc. Lond. A 1921, 221, 163–198. [Google Scholar] [CrossRef]
- Marsh, D.M. Plastic flow and fracture of glass. Proc. R. Soc. Lond. A 1964, 282, 33–43. [Google Scholar] [CrossRef]
- Rountree, C.L.; Kalia, R.K.; Lidorikis, E.; Nakaro, A.; van Brutzel, L.; Vashishta, P. Atomistic aspects of crack propagation in brittle materials Multimillion atom molecular dynamics simulations. Annu. Rev. Mater. Res. 2002, 32, 377–400. [Google Scholar] [CrossRef]
- Kalia, R.K.; Nakano, A.; Vashishta, P.; Rountree, C.L.; van Brutzel, L.; Ogata, S. Multiresolution atomistic simulations of dynamic fracture in nanostructured ceramics and glasses. Int. J. Fract. 2003, 121, 71–79. [Google Scholar] [CrossRef]
- Custers, J.F.H. Plastic deformation of glass during scratching. Nature 1949, 164, 627–627. [Google Scholar] [CrossRef]
- Célarié, F.; Prades, S.; Bonamy, D.; Ferrero, L.; Bouchaud, E.; Guillot, C.; Marlière, C. Glass breaks like metal, but at the nanometer scale. Phys. Rev. Lett. 2003, 90, 075504. [Google Scholar] [CrossRef] [PubMed]
- Bellouard, Y. On the Bending Strength of Fused Silica Flexures Fabricated by Ultrafast Lasers [Invited]. Opt. Mater. Express 2011, 1, 816–831. [Google Scholar] [CrossRef]
- Bellouard, Y.; Said, A.; Dugan, M.; Bado, P. Fabrication of high-aspect ratio, micro-fluidic channels and tunnels using femtosecond laser pulses and chemical etching. Opt. Express 2004, 12, 2120–2129. [Google Scholar] [CrossRef] [PubMed]
- Gattass, R.R.; Mazur, E. Femtosecond laser micromachining in transparent materials. Nat. Photonics 2008, 2, 219–225. [Google Scholar] [CrossRef]
- Marcinkevičius, A.; Juodkazis, S.; Watanabe, M.; Miwa, M.; Matsuo, S.; Misawa, S.; Nishii, J. Femtosecond laser-assisted three-dimensional microfabrication in silica. Opt. Lett. 2001, 26, 277–279. [Google Scholar] [CrossRef]
- Bellouard, Y. Femtosecond laser-based production of 3D micro- and nano- devices in transparent substrate: A step toward system-materials. In Proceedings of SPIE, San Francisco, CA, USA, 8–9 September 2015.
- Yang, T.; Bellouard, Y. A three-dimentional monolithic dielectrophoretic actuator, fabricated by femtosecond laser and chemical etching. J. Micromech. Microeng. 2015, in press. [Google Scholar] [CrossRef]
- Kiyama, S.; Matsuo, S.; Hashimoto, S.; Morihira, Y. Examination of etching agent and etching mechanism on femotosecond laser microfabrication of channels inside vitreous silica substrates. J. Phys. Chem. C 2009, 113, 11560–11566. [Google Scholar] [CrossRef]
- Champion, A.; Bellouard, Y. Direct volume variation measurements in fused silica specimens exposed to femtosecond laser. Opt. Mater. Express 2012, 2, 789–798. [Google Scholar] [CrossRef]
- Barad, Y.; Eisenberg, H.; Horowitz, M.; Silberberg, Y. Nonlinear scanning laser microscopy by third harmonic generation. Appl. Phys. Lett. 1997, 70, 922–924. [Google Scholar] [CrossRef]
- Squier, J.A.; Müller, M. Third-harmonic generation imaging of laser-induced breakdown in glass. Appl. Opt. 1999, 38, 5789–5794. [Google Scholar] [CrossRef] [PubMed]
- Marshall, G.D.; Jesacher, A.; Thayil, A.; Withford, M.J.; Booth, M. Three-dimensional imaging of direct-written photonic structures. Opt. Lett. 2011, 36, 695–697. [Google Scholar] [CrossRef] [PubMed]
- Tsang, T. Optical third-harmonic generation at interfaces. Phys. Rev. A 1995, 52, 4116–4125. [Google Scholar] [CrossRef] [PubMed]
- Schins, J.M.; Schrama, T.; Squier, J.; Brakenhoff, G.J.; Müller, M. Determination of material properties by use of third-harmonic generation microscopy. J. Opt. Soc. Am. B 2002, 19, 1627–1634. [Google Scholar] [CrossRef]
- Schaffer, C.B.; der Au, J.A.; Mazur, E.; Squier, J.A. Micromachining and material change characterization using femtosecond laser oscillators. In Proceedings of SPIE, San Jose, CA, USA, 20 January 2002.
- Oron, D.; Yelin, D.; Tal, E.; Raz, S.; Fachima, R.; Silberberga, Y. Depth-resolved structural imaging by third-harmonic generation microscopy. J. Struct. Biol. 2004, 147, 3–11. [Google Scholar] [CrossRef]
- Bhardwaj, V.R.; Simova, E.; Rajeev, P.P.; Hnatovsky, C.; Taylor, R.S.; Rayner, D.M.; Corkum, P.B. Optically produced arrays of planar nanostructures inside fused silica. Phys. Rev. Lett. 2006, 96, 057404. [Google Scholar] [CrossRef] [PubMed]
- Shimotsuma, Y.; Kazansky, P.G.; Qiu, J.; Hirao, K. Self-organized nanogratings in glass irradiated by ultrashort light pulses. Phys. Rev. Lett. 2003, 91, 247405. [Google Scholar] [CrossRef] [PubMed]
- Clyne, T.W. A simple development of the shear lag theory appropriate for composites with a relatively small modulus mismatch. Mater. Sci. Eng. A 1989, 122, 183–192. [Google Scholar] [CrossRef]
- Nairn, J.A. On the use of shear-lag methods for analysis of stress transfer in unidirectional composites. Mech. Mater. 1997, 26, 63–80. [Google Scholar] [CrossRef]
- Kotha, S.P.; Kotha, S.; Guzelsu, N. A shear-lag model to account for interaction effects between inclusions in composites reinforced with rectangular platelets. Compos. Sci. Technol. 2000, 60, 2147–2158. [Google Scholar] [CrossRef]
- Sears, J.E. A symmetrically opening optical slit. J. Sci. Instrum. 1933, 10, 376–377. [Google Scholar]
- Smith, S.T. Flexures: Elements of Elastic Mechanisms; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Bellouard, Y. Microrobotics: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Howell, L.L. Compliant Mechanisms; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Henein, S. Conception des structures articulées à guidages flexibles de haute précision. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, June 2000. [Google Scholar]
- Canning, J.; Lancry, M.; Cook, K.; Weickman, A.; Brisset, F.; Poumellec, B. Anatomy of a femtosecond laser processed silica waveguide [invited]. Opt. Mater. Express 2011, 1, 998–1008. [Google Scholar] [CrossRef]
- Lancry, M.; Poumellec, B.; Canning, J.; Cook, K.; Poulin, J.C.; Brisset, F. Ultrafast nanoporous silica formation driven by femtosecond laser irradiation: In the heart of nanogratings. Laser Phononics Rev. 2013, 7, 953–962. [Google Scholar] [CrossRef]
- Bricchi, E.; Klappauf, B.G.; Kazansky, P.G. Form birefringence and negative index change created by femtosecond direct writing in transparent materials. Opt. Lett. 2004, 29, 119–121. [Google Scholar] [CrossRef] [PubMed]
- Phani, K.K.; Niyogi, S.K. Young’s modulus of porous brittle solids. J. Mater. Sci. 1987, 22, 257–263. [Google Scholar] [CrossRef]
- Kovacik, J. Correlation between the Young’s modulus and porosity in porous materials. J. Mater. Sci. Lett. 1999, 18, 1007–1010. [Google Scholar] [CrossRef]
- Wagh, A.S.; Poeppel, R.B.; Singh, J.P. Open pore description of mechanical properties of ceramics. J. Mater. Sci. 1991, 26, 3862–3868. [Google Scholar] [CrossRef]
- Stoney, G.G. The tension of metallic films deposited by electrolysis. Proc. R. Soc. Lond. A 1909, 82, 172–175. [Google Scholar] [CrossRef]
- Sun, Q.; Jiang, H.; Liu, Y.; Zhou, Y.; Yang, H.; Gong, Q. Effect of spherical aberration on the propagation of a tightly focused femtosecond laser pulse inside fused silica. J. Opt. A Pure Appl. Opt. 2005, 7, 655–659. [Google Scholar] [CrossRef]
- Shen, Y.R. The Principles of Nonlinear Optics; Wiley-Interscience: New York, NY, USA, 1984. [Google Scholar]
- Vasudevan, T.N.; Krishnan, R.S. Dispersion of the stress-optic coefficient in glasses. J. Phys. D: Appl. Phys. 1972, 5, 2283–2287. [Google Scholar] [CrossRef]
- Bellouard, Y.; Colomb, T.; Depeursinge, C.; Dugan, M.; Said, A.A.; Bado, P. Nanoindentation and birefringence measurements on fused silica specimen exposed to low-energy femtosecond Pulses. Opt. Express 2006, 14, 8360–8366. [Google Scholar] [CrossRef] [PubMed]
- Bansal, N.; Doremus, R.H. Handbook of Glass Properties; Academic Press: Orlando, FL, USA, 1986. [Google Scholar]
- Gabauer, W. The Determination of Uncertainties in Tensile Testing; Voest-Alpine Stahl Linz GmbH: Linz, Austria, 2000. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Athanasiou, C.-E.; Bellouard, Y. A Monolithic Micro-Tensile Tester for Investigating Silicon Dioxide Polymorph Micromechanics, Fabricated and Operated Using a Femtosecond Laser. Micromachines 2015, 6, 1365-1386. https://doi.org/10.3390/mi6091365
Athanasiou C-E, Bellouard Y. A Monolithic Micro-Tensile Tester for Investigating Silicon Dioxide Polymorph Micromechanics, Fabricated and Operated Using a Femtosecond Laser. Micromachines. 2015; 6(9):1365-1386. https://doi.org/10.3390/mi6091365
Chicago/Turabian StyleAthanasiou, Christos-Edward, and Yves Bellouard. 2015. "A Monolithic Micro-Tensile Tester for Investigating Silicon Dioxide Polymorph Micromechanics, Fabricated and Operated Using a Femtosecond Laser" Micromachines 6, no. 9: 1365-1386. https://doi.org/10.3390/mi6091365
APA StyleAthanasiou, C.-E., & Bellouard, Y. (2015). A Monolithic Micro-Tensile Tester for Investigating Silicon Dioxide Polymorph Micromechanics, Fabricated and Operated Using a Femtosecond Laser. Micromachines, 6(9), 1365-1386. https://doi.org/10.3390/mi6091365