1. Introduction
A plasmonic particle inserted in a transparent material can enhance the effect of laser radiation. The particle absorbs incident radiation and is heated, causing the elevation of the temperature of adjacent material layers. This effect has been considered in numerous papers (for references, see the recent reviews [
1,
2]). Heating could be provided by irradiation of the materials containing plasmonic particles using sufficiently long laser pulses or continuous waveform (CW) lasers. In this case, the stationary distribution of temperature around the particle is established [
3]. Heating of gold nanoparticles within the tumor is considered as a way to kill cancer cells [
4]. Heating of metal nanoparticles in water can cause the water to boil. The work in [
5] considers the melting of the polymer mediated by laser-irradiated metal particles. It is recognized [
5] that the CW irradiation of a separate nanoparticle cannot provide a significant temperature elevation of the surrounding material, whereas the cumulative effect provided by a great number of compactly-situated particles can be dramatic.
The effect of femtosecond laser pulses on the plasmonic particles in a transparent material is reviewed in [
2]. Here, a significant heating effect can be provided even by a separate particle.
It should be noted that in both cases of long and short pulse irradiation, the effect of electron emission from the laser-irradiated particle into the surrounding medium could occur. This effect is considered in detail in [
1]. It is shown that in the case of long or CW laser irradiation, the electron emission is noticeable for relatively small-sized particles with diameters of about several nanometers.
With femtosecond pulses, the breakdown of the surrounding material is provoked by the laser field enhancement near the plasmonic particles. Here, the effect of electron emission from the metal particle can promote additional seed electrons for the breakdown. This effect provides bubbling of water in a biological tissue, optoporation and transfection of a cell membrane [
2].
The effect of the plasmonic particles due to laser heating, field enhancement and electron transfer on some photocatalytic chemical reactions is considered in, e.g., [
6] and a recent review [
7].
The effect of the plasmonic particles on the surrounding medium is of particular interest concerning the so-called photo-induced nanocomposites [
8,
9,
10]. Here, the nanoparticles are produced by UV irradiation of the matrix containing dissolved precursor molecules that typically include atoms of a noble metal. After the UV-mediated reduction of those molecules, the extracted metal atoms form an oversaturated solid solution; then, the plasmonic particles appear as nuclei of the new phase [
11]. Thus, these nanocomposites are products of the light-material interaction. However, taking into account the ability of the metal nanoparticles to enhance the effect of light, the further irradiation of the formed nanocomposites can provide a further modification of the material, resulting in the alteration of the material properties in a rather sophisticated manner.
The enhanced laser light can modify the properties of the matrix in the vicinity of the nanoparticle, either directly or through specially introduced molecules that serve as initiators of the subsequent transformations.
In [
12], photo-induced isomerization in an azobenzene-dye polymer is used for the sub-diffraction imaging of the optical near-field around the plasmonic nanoparticles on the surface of a polymer film irradiated by the laser light.
In this article, we consider a photochemical reaction initiated by the two-photon absorption of light near the plasmonic nanoparticle within the matrix. We also consider the material heating caused by this absorption in comparison with the heating by the light directly absorbed by the particle and analyze the distribution of the product of a thermally-activated chemical reaction just near the metal nanoparticle irradiated by the laser pulse.
This study aims at developing the laser-induced production of 3D nanoplasmonic systems where the formation of photo-induced nanocomposites is only the first step.
2. The Near-Field Effects
Let us consider the irradiation of a metal spherical nanoparticle in a transparent matrix by a series of ultrashort pulses from the laser operated in the visible, near-IR or near-UV ranges (see
Figure 1).
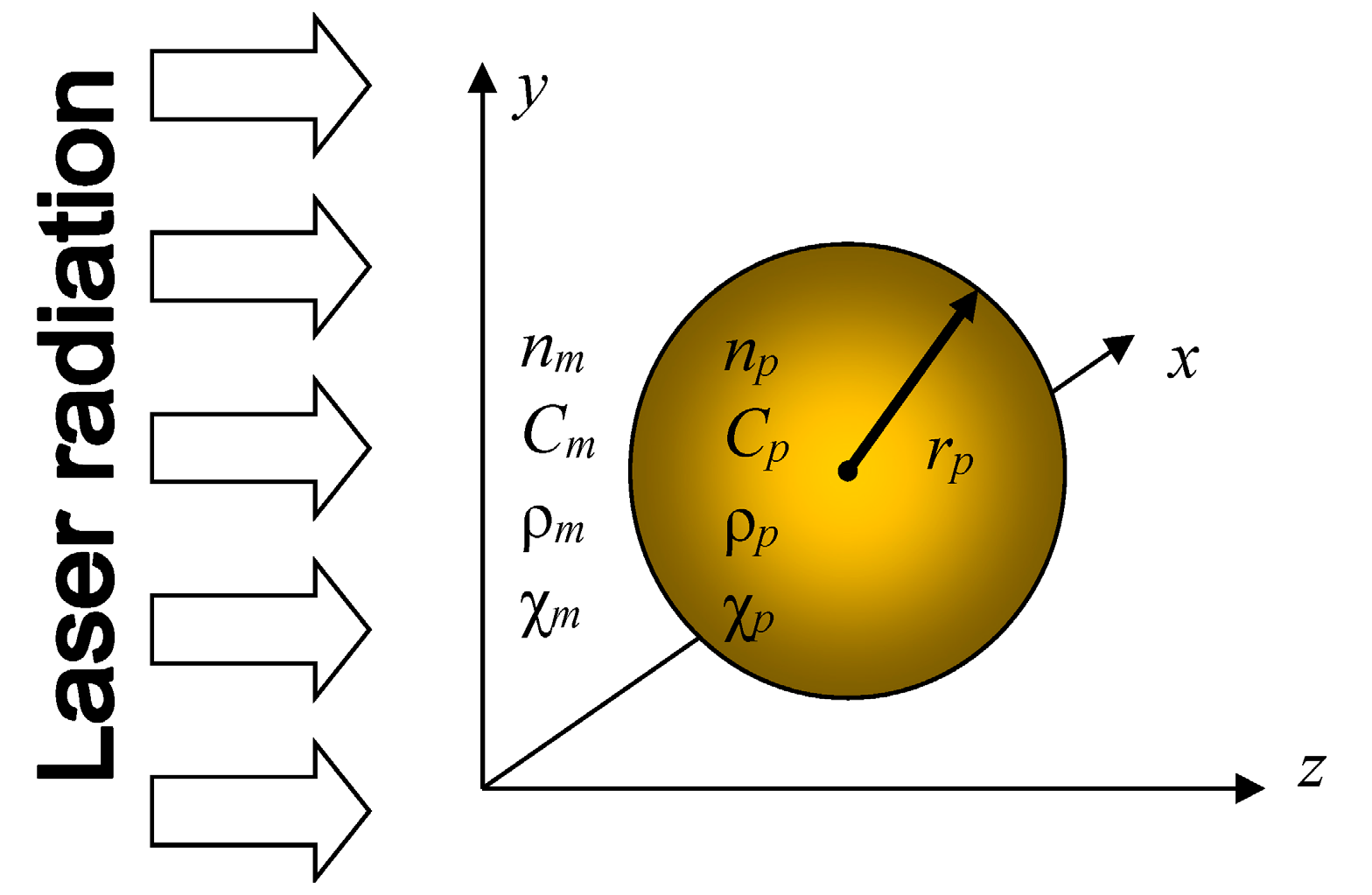
Figure 1.
The modeling setup. A spherical gold nanoparticle of radius
rp is irradiated by femtosecond laser pulses at the central wavelength λ. The complex refractive index of the particle, its specific heat, density and heat diffusivity are
np,
Cp, ρ
p and χ
p, respectively. The corresponding properties of the matrix are denoted by
nm,
Cm, ρ
m and χ
m. For a complete list of notations, see in
Appendix A1.
Figure 1.
The modeling setup. A spherical gold nanoparticle of radius
rp is irradiated by femtosecond laser pulses at the central wavelength λ. The complex refractive index of the particle, its specific heat, density and heat diffusivity are
np,
Cp, ρ
p and χ
p, respectively. The corresponding properties of the matrix are denoted by
nm,
Cm, ρ
m and χ
m. For a complete list of notations, see in
Appendix A1.
The laser light is significantly enhanced in the near-field domain. We consider a simple photochemical reaction promoted by the two-photon absorption by species X within the matrix. Species X can either belong to the matrix base being, e.g., chromophore groups within the polymer chains or being some dopant molecules dissolved in the matrix.
Assume that the particle radius rp is on the order of 10 nm and the pulse length τpulse lies in a range of 10 fs to 1 ps. We approximate the incident laser radiation as a quasi-monochromatic wave at the central wavelength λ.
The evolution of the number density
of species
X is described by the equation:
Here,
I is the local laser field intensity, σ
X(2) is two-photon absorption cross-section of
X,
is the photon energy and η is the quantum yield. The solution of Equation (1) reads:
where
NX0 is the initial concentration of
X. The fraction
v = (
NX0 −
NX)/
NX0 of reacted species
X is further referred to as the conversion.
In the vicinity of a nanoparticle, the incident field can be approximated as a quasi-monochromatic plane wave with the intensity
Iinc =
I0f(
t), where
I0 is the peak incident intensity and function
f(
t) is of a unity amplitude. If the dispersion on the particle size-scale is neglected, then the actual function
can be calculated by means of Mie theory [
13]:
Here,
is the enhancement of the electric field squared calculated near the metal nanoparticle irradiated by a plane monochromatic wave. Thus, Equation (2) can be evaluated as:
where
Npulse is the number of laser pulses applied.
The distribution of
can be calculated by means of different near-field Mie codes; some of them can be found here [
14]. The linear absorption of the matrix is assumed to be negligible at the laser wavelength, and the refractive index of the polymer is
nm. The complex refractive index of the metal particle is
np =
np' +
inp".
In
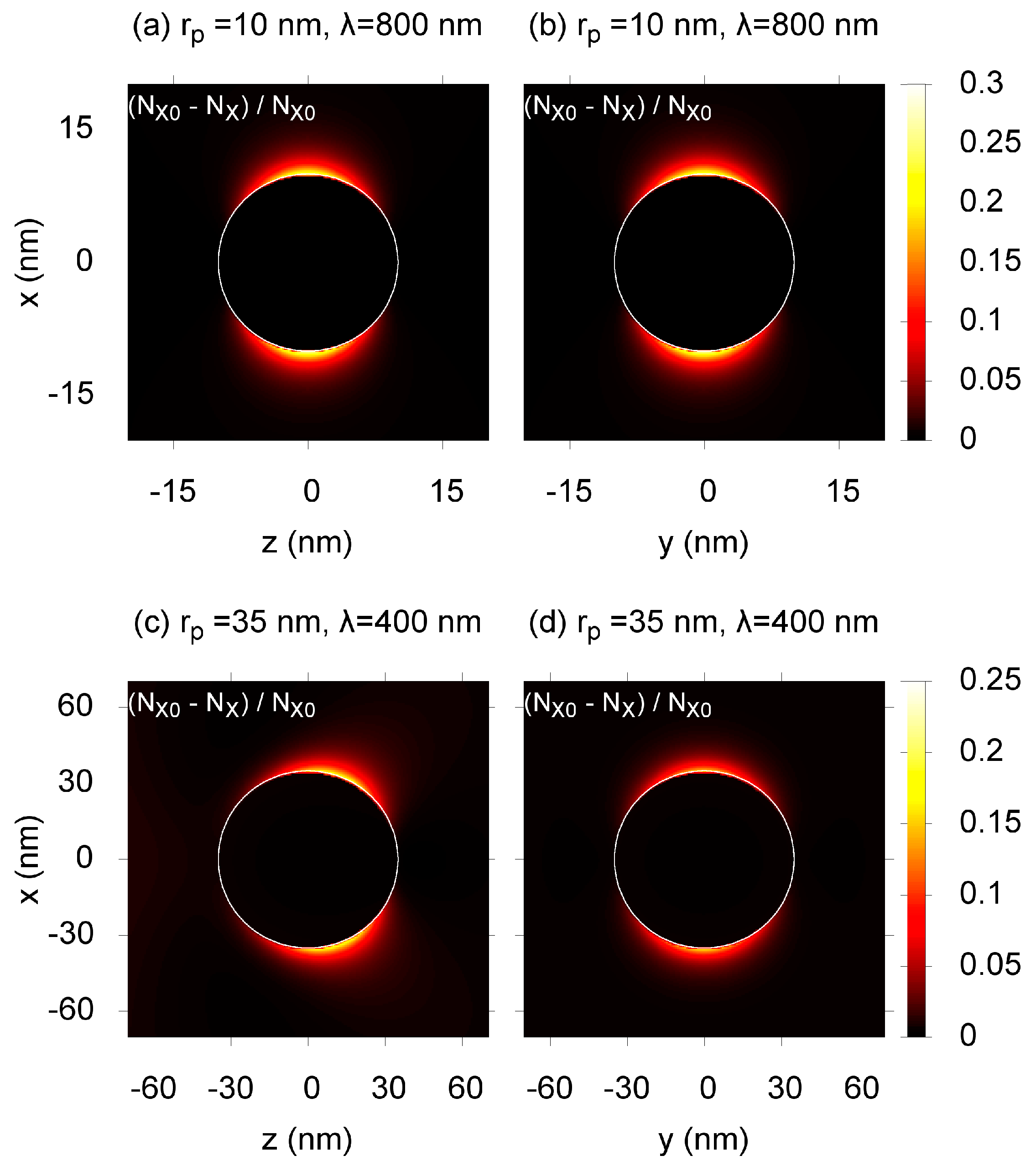
Figure 2, we plot typical spatial distributions of the conversion after a series of laser pulses. The case where
rp = 10 nm and λ = 800 nm is presented in
Figure 2a,b. Here, two field maxima are formed near the sphere opposite each other, following the dipole approximation. The locations of the maxima are directed by the incident wave polarization and, thus, are the same for all irradiated nanoparticles within the matrix. This gives an opportunity to induce anisotropy into laser-irradiated domains of the material. The results for
rp = 35 nm and λ = 400 nm are presented in
Figure 2c,d. Here, the dipole approximation is not applicable, because the thickness of the skin-layer becomes smaller than the diameter of the particle. Thus, the higher-order spherical modes become important, resulting in the shift of the maxima towards the direction of the incident wave propagation. The photochemical reaction in this case results not only in laser-induced anisotropy, but also in the laser-induced loss of the center of symmetry. This is important for the applications in nonlinear optics, in particular for the second harmonic generation. It is notable that such a modification can be performed using reasonable irradiation regimes and materials without an outstanding two-photon sensitivity (see
Figure 2 caption). This allows for possible applications of commercially available materials and lasers for a single-step modification of large volumes of about 1 cm
3.
Thermo-sensitive rather than photo-sensitive additives can also be employed. Thermal alteration processes can also be locally induced due to laser irradiation of nanoparticles. In what follows, we consider two main possibilities to heat a transparent matrix near the nanoparticle: either to do it directly via multi-photon absorption or to heat the particle and rely on the heat diffusion. We calculate the temperature rise in the particle and in the surrounding polymer provided by a single laser pulse.
Once an ultra-short laser pulse is absorbed by the gold nanoparticle, the electron subsystem is excited. The electron energy is transferred to the lattice during the electron-phonon coupling time on the order of τ
e–ph = 1–3 ps [
2]. This is the period during which the particle is effectively heated, even if the actual laser pulse length is shorter. The temperature diffusion time over the particle is τ
diffus =
rp2χ
p−1, where χ
p is the heat diffusion coefficient, which is on the order of 1 cm
2/s for many metals, including gold and silver. For
rp = 10 nm, the value τ
diffus = 1 ps, which is on the order of τ
e–ph.
Figure 2.
The conversion of species
X near the gold nanoparticle (indicated by a white circle) irradiated by
Npulse = 10
5 laser pulses of length τ
pulse = 100 fs. The two-photon absorption cross-section is σ
X(2) = 10 GM (1 GM = 10
−50 cm
4·s). The quantum yield is η = 0.8, and the incident wave is linearly polarized along the
x and propagates toward the
z direction. For (
a) and (
b):
rp = 10 nm, λ = 800 nm; the complex refractive index of gold is
np = 0.15 + 4.91
i [
15], the refractive index of polymethyl methacrylate (PMMA) is
nm = 1.484 [
16]; the incident beam intensity is
I0 = 5 × 10
8 W/cm
2. For (
c) and (
d):
rp = 35 nm, λ = 400 nm,
np = 1.47 + 1.954
i [
15],
nm = 1.503 [
16],
I0 = 2 × 10
9W/cm
2.
Figure 2.
The conversion of species
X near the gold nanoparticle (indicated by a white circle) irradiated by
Npulse = 10
5 laser pulses of length τ
pulse = 100 fs. The two-photon absorption cross-section is σ
X(2) = 10 GM (1 GM = 10
−50 cm
4·s). The quantum yield is η = 0.8, and the incident wave is linearly polarized along the
x and propagates toward the
z direction. For (
a) and (
b):
rp = 10 nm, λ = 800 nm; the complex refractive index of gold is
np = 0.15 + 4.91
i [
15], the refractive index of polymethyl methacrylate (PMMA) is
nm = 1.484 [
16]; the incident beam intensity is
I0 = 5 × 10
8 W/cm
2. For (
c) and (
d):
rp = 35 nm, λ = 400 nm,
np = 1.47 + 1.954
i [
15],
nm = 1.503 [
16],
I0 = 2 × 10
9W/cm
2.
The temperature rise over the particle can be considered uniform if the radius of the particle is well below the thickness of the skin-layer or after the irradiation period t >> τdiffus and t >> τe–ph.
The heating and thermalization can be considered adiabatic over the time period τ
adiab if the fraction of heat that leaks from the particle to the matrix during this period can be neglected. The heat penetration depth from the particle into the matrix by the moment
t can be evaluated as
. Provided Δ
Tp is the temperature rise of the particle due to the laser pulse, the amount of heat transferred to the matrix is evaluated as
. The amount of heat transferred to the particle is
Qp ≈
Cpρ
pΔ
Tp·4π
rp3/3. The ratio is:
where
Cp and
Cm are the specific heat capacities; ρ
p and ρ
m are the densities. Subscripts “
p” and “
m” denote the particle and the matrix, respectively. It is seen in Equation (5) that
Qm/
Qp << 1 if:
The ratio of volume-specific heat capacities can be considered Cpρp/Cmρm ~ 1 for gold particles in a polymer matrix; thus, τadiab ≈ rp2χm−1. The thermal diffusivity of the polymer, χm, is on the order of 10−3 cm2/s. Thus, for a 10-nm particle, τadiab ~ 100 ps.
It is seen that due to χ
m << χ
p, the heat transfer from the particle to the matrix may be neglected during the time period needed to equalize the temperature inside the particle. The different time scales allow the solution of the problems of the particle heating and the heat diffusion from the particle to the matrix separately. Namely, the laser irradiation causes the uniform temperature rise in the particle by:
which is the starting condition for the calculations of the heat diffusion within the matrix. Such calculations will be performed in the next section of the paper. In Equation (7),
Vp is the volume of the particle and
is the heat power density, which is given by:
Laser field intensity inside the particle can be calculated by employing the Mie solution again:
Finally,
where
means averaging over the volume of the particle and
is the incident fluence. In the case of Rayleigh scattering, for the small particles, Equation (10) transforms [
17] to:
where ε' and ε" are the real and imaginary parts of ε =
np2/
nm2.
The multi-photon heating of the matrix directly due to the field maxima near the particles can be treated in a similar way. The temperature rise in the matrix after the electron-phonon thermalization is calculated as:
where:
is the heat power density due to the two-photon absorption in the matrix. In Equation (13),
Nm is the number density of chromophores in the matrix and η
T is the quantum yield. Taking
I(
r,
t) outside the particle from Equation (3), one can evaluate the temperature rise in the matrix as:
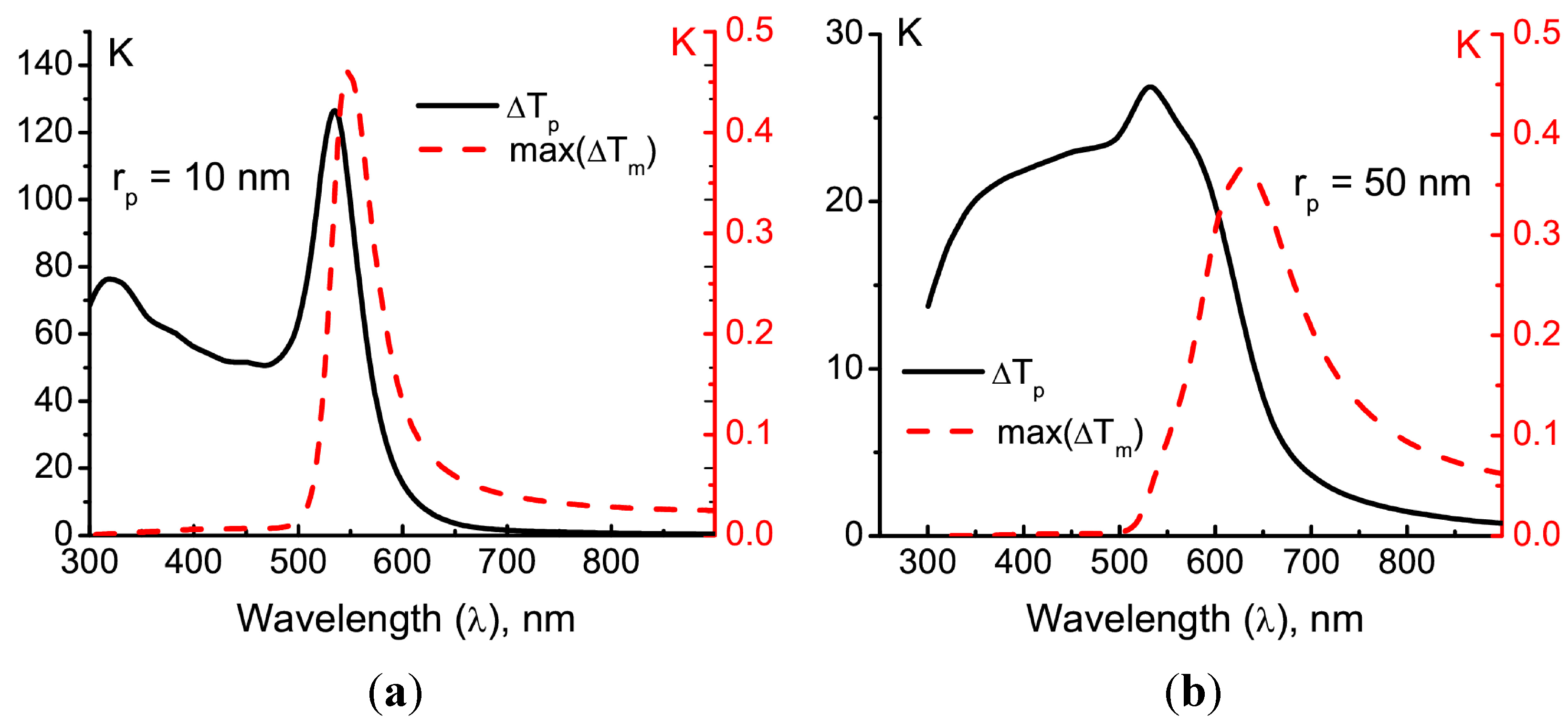
The dependencies of both the temperature rise Δ
Tp in the particle and the maximal temperature rise max(Δ
Tm) in the matrix due to two-photon absorption exhibit a pronounced plasmonic resonance, as is shown in
Figure 3.
Figure 3.
Temperature rise in the particle (black solid lines, left axis) and the temperature rise in the matrix due to the two-photon absorption (red dashed lines, right axis) after irradiation by a single laser pulse of duration τ
pulse = 100 fs. The particle radius is either 10 nm (
a) or 50 nm (
b). The incident laser fluence is
F0 = 2 × 10
−4 J/cm
2, which corresponds to the maximum field intensity
I0 = 2 × 10
9 W/cm
2. The incident polarization is circular. The volume-specific heat values for the particle and the matrix are
Cpρ
p = 2.5 J·cm
−3K
−1 and
Cmρ
m = 1.7 J·cm
−3K
−1, respectively. The dependencies of
np(λ) and
nm(λ) for gold and PMMA are taken from [
15,
16], respectively. For the two-photon absorption, σ
m(2) = 100 GM,
Nm = 6 × 10
20 cm
−3 and η
T = 1 are employed.
Figure 3.
Temperature rise in the particle (black solid lines, left axis) and the temperature rise in the matrix due to the two-photon absorption (red dashed lines, right axis) after irradiation by a single laser pulse of duration τ
pulse = 100 fs. The particle radius is either 10 nm (
a) or 50 nm (
b). The incident laser fluence is
F0 = 2 × 10
−4 J/cm
2, which corresponds to the maximum field intensity
I0 = 2 × 10
9 W/cm
2. The incident polarization is circular. The volume-specific heat values for the particle and the matrix are
Cpρ
p = 2.5 J·cm
−3K
−1 and
Cmρ
m = 1.7 J·cm
−3K
−1, respectively. The dependencies of
np(λ) and
nm(λ) for gold and PMMA are taken from [
15,
16], respectively. For the two-photon absorption, σ
m(2) = 100 GM,
Nm = 6 × 10
20 cm
−3 and η
T = 1 are employed.
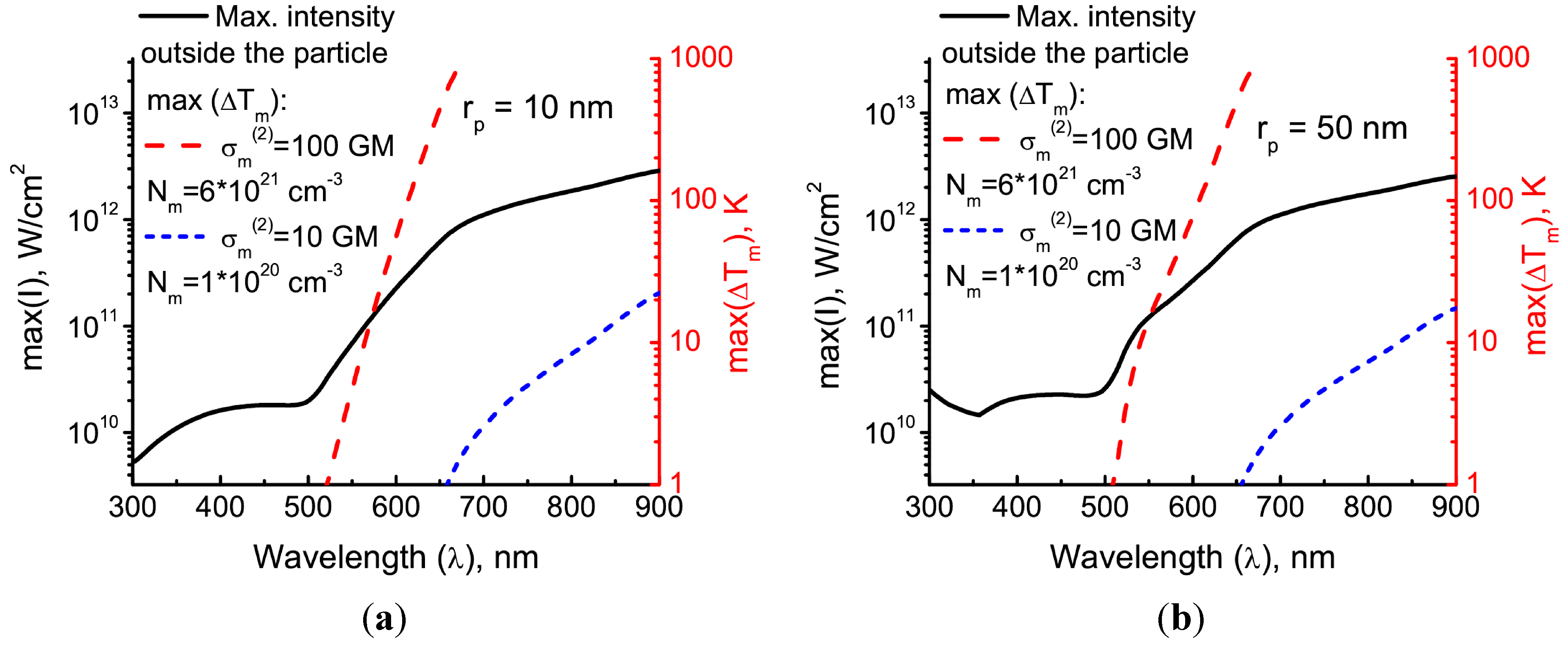
Now, we can compare the contributions of either of the heating mechanisms for typical experimental cases. For that, using Equation (10), we find the incident field intensity needed to achieve a certain temperature rise in the particle (e.g., ΔTp = 100 K). Then, we calculate the maximum temperature rise max(ΔTm) in the matrix for that intensity. Additionally, we calculate the maximum field intensity that is reached near the particle.
Figure 4 shows the calculation results for two different matrices. The first one has an unrealistically high two-photon sensitivity, σ
m(2) = 100 GM, and the number density of chromophores
Nm = 6 × 10
21 cm
−3 nearly matches the typical number density of monomer chains in the polymer. The other has realistic parameters: σ
m(2) = 10 GM and
Nm = 1 × 10
20 cm
−3. It is seen that direct heating of the matrix due to the two-photon absorption becomes advantageous in the longer wavelength part of the visible and near-IR spectrum. However, the field intensity reached near the particle in order to provide a temperature rise comparable to the one in the particle is above 10
11 W/cm
2 even in the case where the two-photon absorption is overestimated. This intensity is even higher for realistic matrices, overcoming the optical breakdown level.
For the small enough particles (see
Figure 4a), the irradiation at wavelengths shorter than the plasmonic resonance (530 nm) causes significant heating of the particle without reaching the breakdown level of intensities near the particle. In this case, direct heating of the matrix due to the multi-photon absorption can also be neglected. This case will be analyzed in the next section of the paper. For the longer wavelengths, the optical breakdown must be taken into account [
2].
Figure 4.
The maximum temperature rise (dashed lines, right axis) and maximum field intensity (black solid lines, left axis) outside the particle reached when the temperature of the particle is raised by 100 K due to irradiation by a circularly-polarized single laser pulse of duration τ
pulse = 100 fs. The particle radius is either 10 nm (
a) or 50 nm (
b). The volume-specific heat values for the particle and the matrix are
Cpρ
p = 2.5 J·cm
−3K
−1 and
Cmρ
m = 1.7 J·cm
−3K
−1, respectively. The dependencies of
np(λ) and
nm(λ) for gold and PMMA are taken from [
15,
16], respectively. The quantum yield η
T = 1.
Figure 4.
The maximum temperature rise (dashed lines, right axis) and maximum field intensity (black solid lines, left axis) outside the particle reached when the temperature of the particle is raised by 100 K due to irradiation by a circularly-polarized single laser pulse of duration τ
pulse = 100 fs. The particle radius is either 10 nm (
a) or 50 nm (
b). The volume-specific heat values for the particle and the matrix are
Cpρ
p = 2.5 J·cm
−3K
−1 and
Cmρ
m = 1.7 J·cm
−3K
−1, respectively. The dependencies of
np(λ) and
nm(λ) for gold and PMMA are taken from [
15,
16], respectively. The quantum yield η
T = 1.
3. The Particle Heating Effect
Below, we consider the effect of heat diffusion from the metal nanoparticle uniformly heated by an ultrashort laser pulse. We consider the thermal destruction of some dopant X by a simple, thermally-activated chemical reaction promoted by the temperature elevation resulting from the heat flow from the particle. These molecules are dissolved within the matrix with the starting number density NX0.
The heat diffusion problem is formulated as follows:
Here, Tr is the “room” temperature (the initial temperature of the surrounding matter or a thermostat), ΔTp is the initial particle temperature increment after the pulse (above the room temperature), rp is the radius of the particle, χm is the heat diffusivity of the matrix and r is the radial coordinate. Here, we introduce the dimensionless parameter β = (3Cmρm)/(Cpρp) (for gold nanoparticles in PMMA matrix, we have β = 1.821) and use the dimensionless variables: p = (β2/rp2)χmt is the dimensionless time and R = r/rp is the dimensionless coordinate (normalized by the nanoparticle radius). We suppose that only a small amount of dopant molecules are converted due to a single pulse. This allows us to neglect the effect of reaction enthalpy on the heat propagation process.
The way of solving Equation (15) is the Laplace transform. The result is given in [
18]:
This expression can be rewritten via a special function.
We assume the Arrhenius law for the reaction rate:
where
TA is the activation temperature and
A is the reaction constant. We calculate the part of reacted molecules after one laser pulse. We suppose that this part is much less than unity, so that
NX under the integral can be considered as a constant.
Expression (17) represents the fraction of the destroyed species in a pulse. After
Npulse pulses, the conversion
ν reads:
According to (16), we have the distribution of temperature in the matrix in the form T(R, p) = Tr + ΔTpg(R, p), where g(R, p) is the normalized function, so that g(R = 1, p = 0) = 1.
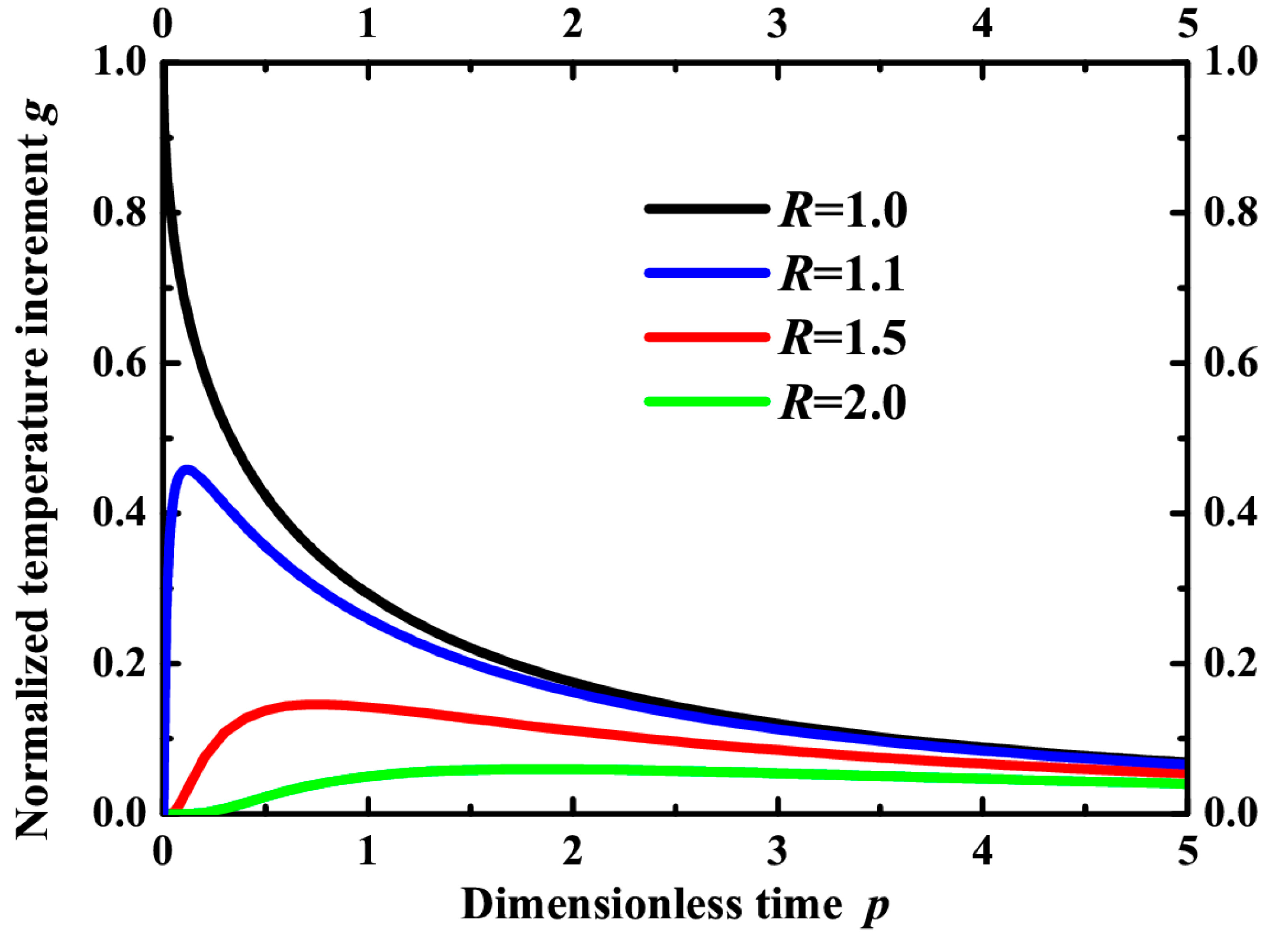
Figure 5 shows the time dependence of temperature at different points in the vicinity of the particle. It is seen that the temperature increases rather fast to its maximum and then slowly returns to the initial value. Another situation is on the surface of the particle where the temperature decreases just after the pulse. The most important contribution to the reaction yield occurs during the time interval when the temperature value is close to its maximum.
Figure 5.
Evolution of normalized temperature g as a function of dimensionless time p in different points of the polymer matrix surrounding a gold nanoparticle: R = 1 (black line), R = 1.1 (blue line), R = 1.5 (red line) and R = 2 (green line).
Figure 5.
Evolution of normalized temperature g as a function of dimensionless time p in different points of the polymer matrix surrounding a gold nanoparticle: R = 1 (black line), R = 1.1 (blue line), R = 1.5 (red line) and R = 2 (green line).
On the surface of the particle, the highest temperature is in the beginning of the process. That is why we can use an approximation for temperature dependence on time on the surface for times close to zero. This approximation follows from Equation (16):
In the problem of the estimation of the integral
G, we have large parameter
TA/(
Tr + Δ
Tp). It allows one to use the saddle-point method. Here, we can approximately calculate the integral
G (see Equation (17)):
This result is in good agreement with numerical calculations (
Figure 6).
Having a simple formula, such as Equation (19), for the integral
G, we can estimate the realistic conversion of dopant molecules, which can be provided by the particle heating just near the particle surface. We can reach a repetition rate of up to 10
3 pulses per second. Each pulse raises the nanoparticle temperature to Δ
Tp. It was mentioned above that for small particles, Δ
Tp can be calculated using Equation (11). The laser pulse at the plasmon resonance wavelength (λ = 530 nm) with the fluence
F0 = 10
−4 J/cm
2 increases the temperature up to about 100 K. This value of fluence is available from commercial lasers and makes it possible to irradiate simultaneously an area of about 1 cm
2. Thus, for our estimates, we will use Δ
Tp ~ 100 K. It should be noted that when energetic femtosecond laser pulses are employed for large-volume processing, the beam power may be significantly higher than the critical value for self-focusing. However, the considered intensities (not higher than 10
9 W/cm
2) are not sufficient to provide filamentation within a sample of reasonable thickness. Indeed, for the filamentation development, the retardation integral
should be larger than unity. Here,
l is the distance at which filamentation starts to develop and
n2 is the nonlinear refractive index. With the typical value
n2 ≈ 10
−14 cm
2/W and the intensity
I ≈ 10
9 W/cm
2,
B = 1 will be reached at
l ≈ 1.5 cm. This is an estimate for the possible thickness of the sample. Moreover, our studies [
10,
19] show that the presence of the plasmonic nanoparticles within the polymer matrix provides a significant negative input in the nonlinear refractive index, which essentially hinders the filamentation.
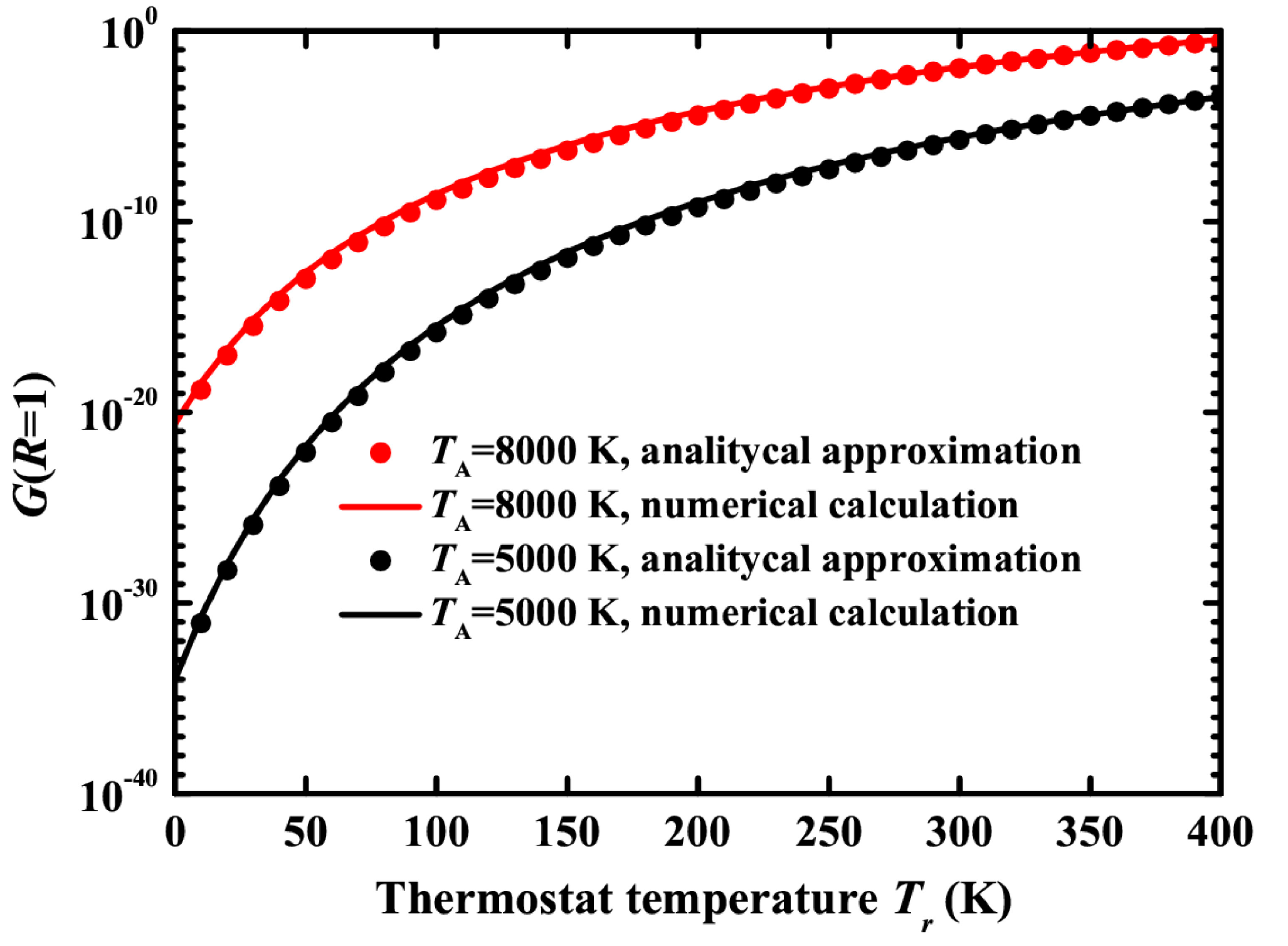
Figure 6.
The integral G(R = 1) as a function of thermostat temperature for TA = 8000 K (black color) and TA = 5000 K (red color). The points show numerical calculations using Equation (16), and the line shows the approximation by Equation (19). The radius of a gold nanoparticle is rp = 20 nm.
Figure 6.
The integral G(R = 1) as a function of thermostat temperature for TA = 8000 K (black color) and TA = 5000 K (red color). The points show numerical calculations using Equation (16), and the line shows the approximation by Equation (19). The radius of a gold nanoparticle is rp = 20 nm.
We assume the room temperature value to be about 300 K. However, it should be noted that we can control it by using a thermostat. The reaction constant
A is supposed to be less than 10
13 s
−1. An activation temperature range
TA less than 12,000 K is typical of precursor molecules (see, for example, [
20,
21,
22,
23]). The typical heat diffusivity of polymers is χ
m ~ 10
−3 cm
2/s. The radius
rp of a nanoparticle is about 20 nm. The number of pulses
Npulse can be up to 10
6 for a few minutes. Thus, the conversion near the particle surface, according to Equations (18) and (19), is:
Irradiation by a large number of pulses results in overall heating of the sample. It depends on many factors, including the repetition rate, the beam radius, the sample thickness, cooling conditions on the surface,
etc. The effect of the overall heating on
G could be understood from its dependence on
Tr (see Equation (19) and
Figure 6). The complete analysis of this phenomenon is beyond the scope of this paper.
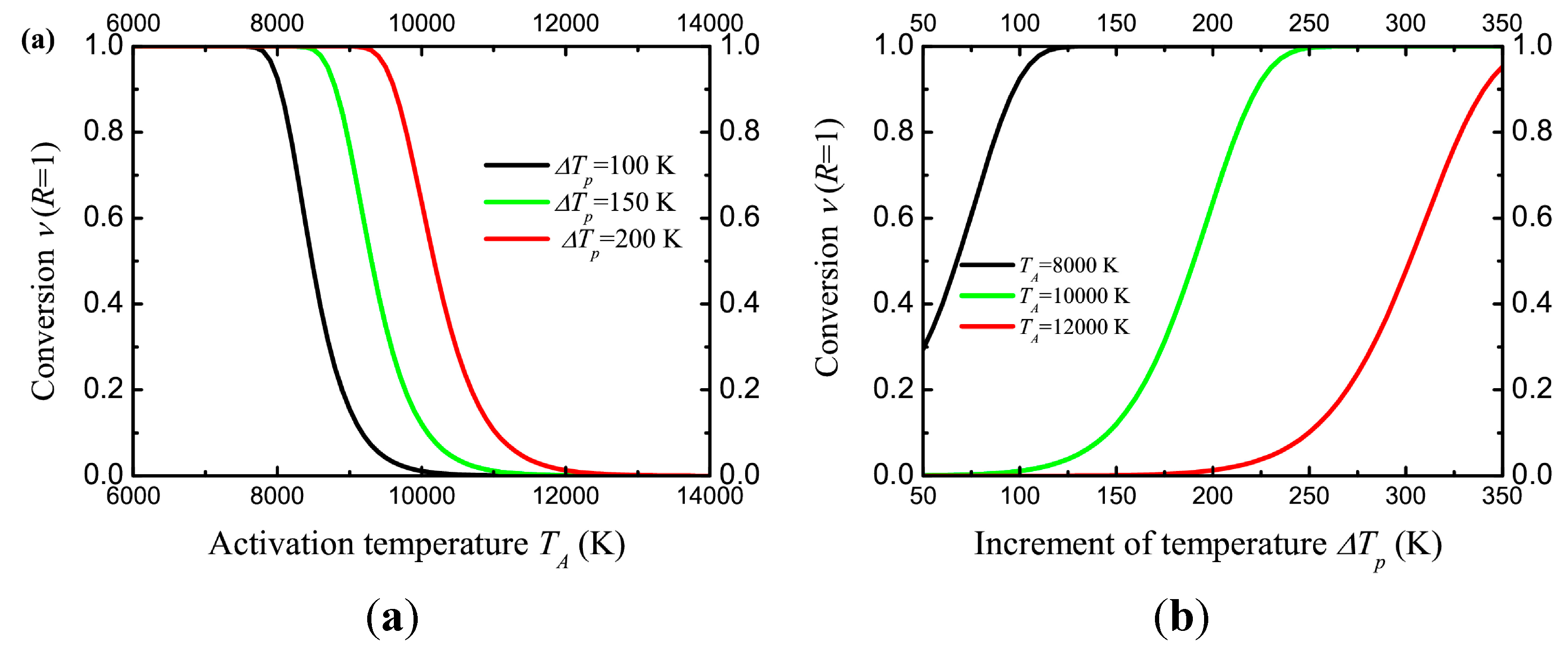
It can be noted (
Figure 7) that for
TA = 10,000 K, the increase in temperature by 100 K is not enough for the reaction.
ΔTp = 150 K will transform about 10% of the dopant molecules, and
ΔTp = 200 K is much more efficient. On the other hand, a large increase in temperature is not desirable, since it can lead to damage of the polymer matrix.
Figure 7.
(a) The conversion in the polymer matrix on the surface of a gold nanoparticle (radius rp = 20 nm) as a function of activation temperature, for different temperature increment ΔTp. (b) The conversion in the polymer matrix on the surface of a gold nanoparticle (radius rp = 20 nm) as a function of temperature increment ΔTp, for different activation temperature TA. The thermostat temperature Tr = 300 K. The number of pulses Npulse = 106. The curves are calculated using Equation (20).
Figure 7.
(a) The conversion in the polymer matrix on the surface of a gold nanoparticle (radius rp = 20 nm) as a function of activation temperature, for different temperature increment ΔTp. (b) The conversion in the polymer matrix on the surface of a gold nanoparticle (radius rp = 20 nm) as a function of temperature increment ΔTp, for different activation temperature TA. The thermostat temperature Tr = 300 K. The number of pulses Npulse = 106. The curves are calculated using Equation (20).
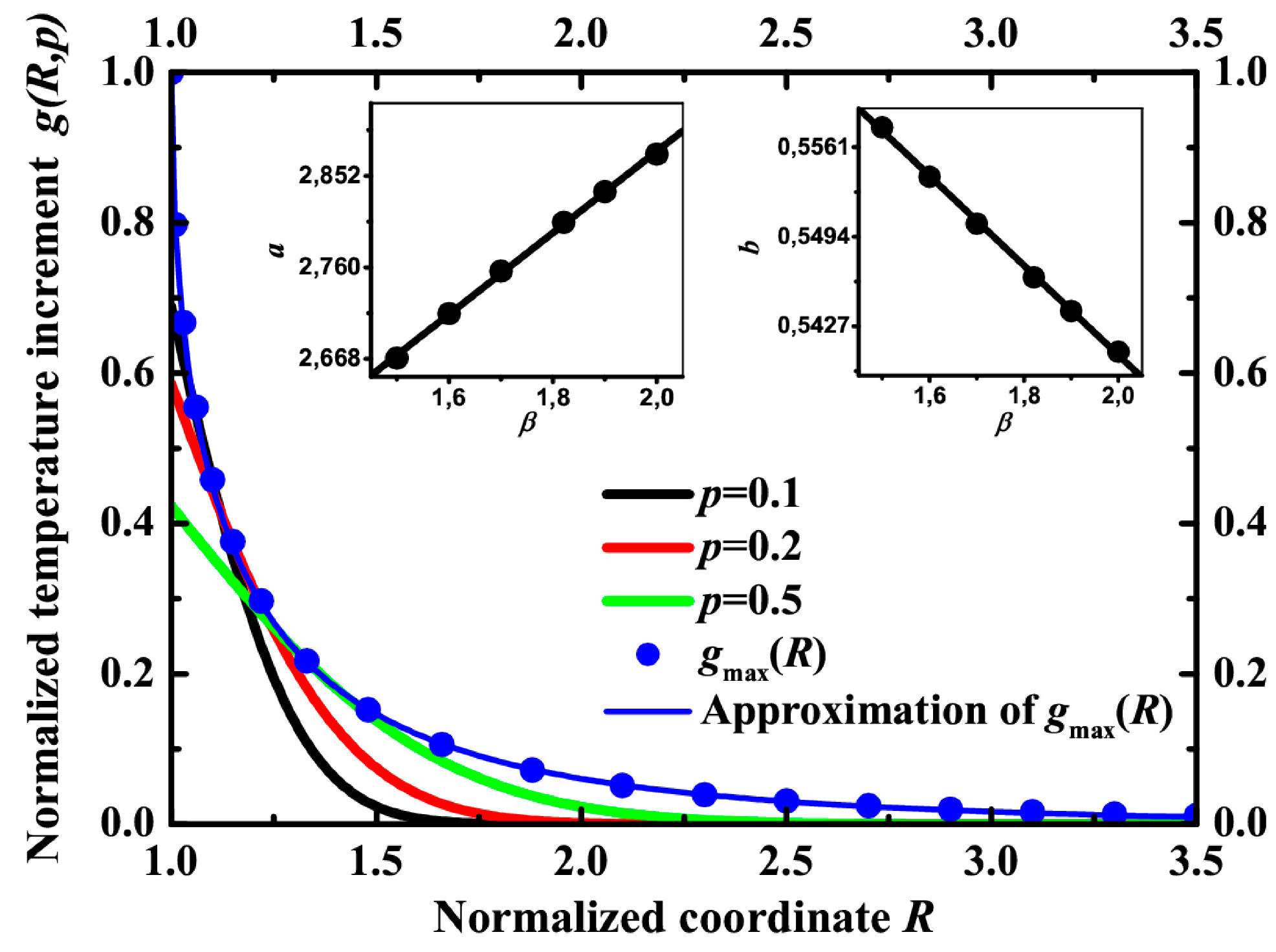
It has been mentioned above that the maximum temperature at the point is a very important characteristic of the process. It determines the highest rate of reaction.
Figure 8 represents spatial distributions of normalized temperature increment
g in different moments of time and the envelope of these distributions. The maximum temperature increment can be approximated by the formula
gmax(
R) = exp(−
a(
R − 1)
b).
This form of temperature confinement was described in [
24] for a gold nanoparticle in water with another parameter β. For most of the materials, however, β is of the order of unity. This is the only parameter in the system. The distribution of temperature depends on β. The parameters
a and
b in the approximation of the maximum temperature can be linearly fitted as functions of β (see inset in
Figure 8).
Figure 9 represents the result of the calculation of
G(
R), introduced above. For a nonzero room temperature, this integral diverges. In fact, at room temperature, the rate of reaction is negligibly small. Since we calculate the laser heating effect, we subtract this background. The resulting expression is:
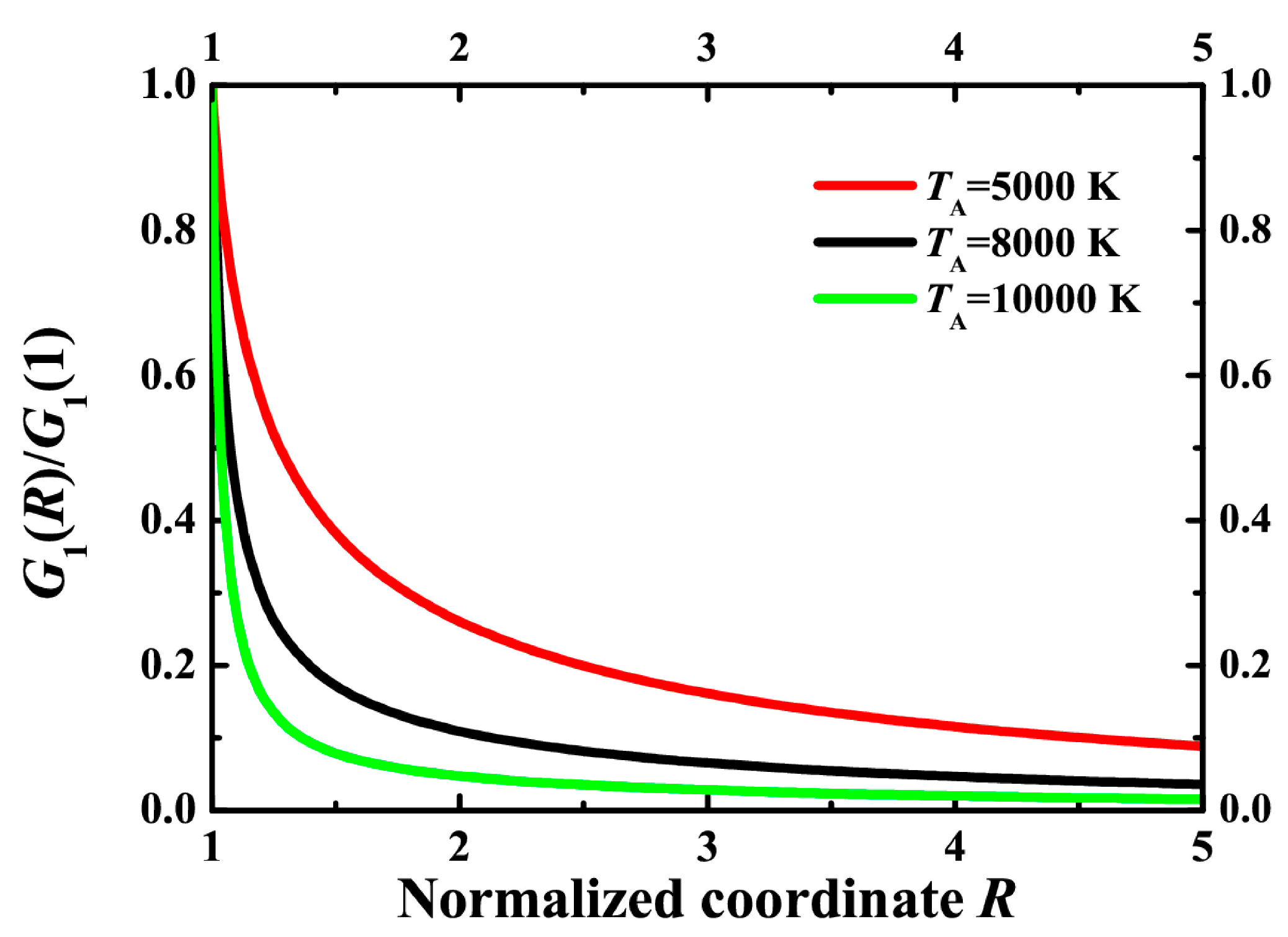
In order to compare the volume of reaction, we calculate the normalized distribution G1(R)/G1(R = 1). It is seen that a higher activation energy leads to a smaller volume of reaction. It is seen that the thermally-activated reaction can be effective enough at the very surface of the heated particle. However, the reaction domain is highly localized just near the particle, thus preventing the conversion of a large net amount of molecules. In order to convert remote molecules that are initially located at more significant distances from the plasmonic particles than the particle radius, one should use nonlocal effects, which are beyond the scope of this paper.
Figure 8.
The distribution of normalized temperature g vs. normalized coordinate R at different moments of time: p = 0.1 (black line), p = 0.2 (red line), p = 0.5 (green line). Blue dots demonstrate the spatial distribution of the maximum temperature. The blue line is its approximation by gmax(R) = exp(−a(R − 1)b). Inset: parameters a and b vs. coefficient β and their linear approximation by a = 2.06 + 0.41β and b = 0.61 − 0.034β.
Figure 8.
The distribution of normalized temperature g vs. normalized coordinate R at different moments of time: p = 0.1 (black line), p = 0.2 (red line), p = 0.5 (green line). Blue dots demonstrate the spatial distribution of the maximum temperature. The blue line is its approximation by gmax(R) = exp(−a(R − 1)b). Inset: parameters a and b vs. coefficient β and their linear approximation by a = 2.06 + 0.41β and b = 0.61 − 0.034β.
Figure 9.
Normalized number of reacted molecules G1(R)/G1 (R = 1) according to Equation (21) for ΔTp = 100 K, Tr = 300 K, TA = 10,000 K (green line), TA = 8000 K (black line) and TA = 5000 K (red line).
Figure 9.
Normalized number of reacted molecules G1(R)/G1 (R = 1) according to Equation (21) for ΔTp = 100 K, Tr = 300 K, TA = 10,000 K (green line), TA = 8000 K (black line) and TA = 5000 K (red line).
4. Conclusions
We consider the opportunities provided by plasmonic nanoparticles inserted into the bulk of transparent media to modify the material by means of the laser light irradiation.
This is of particular importance for photo-induced nanocomposites. Here, the plasmonic nanoparticles are formed due to laser irradiation of the initially homogeneous material containing precursor molecules by a self-organization process. This process significantly changes the optical property of the medium. The further micro-modification of the material employing previously-formed plasmonic nanoparticles can be considered as the next-step laser alteration of the material properties.
As an example, we discuss a photochemical reaction in the vicinity of the plasmonic nanoparticle initiated by the laser radiation in the near-field domain due to nonlinear absorption. We show that the spatial distribution of the products of such a reaction changes the symmetry of the material, resulting in the appearance of anisotropy in the initially isotropic material or even in the loss of the center of symmetry.
The latter is important for the optical nonlinearity. Photo-induced nanocomposites are highly optically nonlinear (see, e.g., [
10]). First of all, this is true for the cubic nonlinearity described by the third-order susceptibility [
19]. The second-order susceptibility responsible for the second harmonic generation is zero in the center-symmetric media. The loss of the center of symmetry of the composites due to a photochemical reaction in the near-field of the plasmonic nanoparticles permits one to observe optical nonlinear phenomena of the second order in such materials [
25]. Such a modification can be performed using reasonable irradiation regimes with an intensity of about 10
9 W/cm
2 and materials with a not outstanding two-photon sensitivity. This allows for possible applications of commercially available materials and lasers for a single-step modification of large volumes of about 1 cm
3.
It is shown that it is possible to significantly heat small plasmonic nanoparticles by an ultrashort laser pulse without causing optical breakdown in the near field. In this case, the direct material heating by the nonlinear absorption in the vicinity of the particle can be neglected as compared with the heating of the particle itself.
We considered a thermally-activated reaction of the first order initiated in the medium by the femtosecond pulse heating of a plasmonic particle. We analyzed a spherically symmetric solution of the corresponding heat diffusion equation and determined the fraction of reacted molecules (conversion) at the surface of a metal sphere and within the domain surrounding the nanoparticle. We present an analytical formula for the conversion at the very surface and a numerical solution for the conversion distribution within the material bulk. Our estimation shows that a conversion of about unity can be obtained by defocused femtosecond pulses of the mJ energy level for a reasonable number of pulses if the activation energy of the thermally-activated reaction is close to 1 eV or smaller.
It should be noted that the thermoactivated reaction could mean either the thermodestruction of the matrix or the transformation (destruction) of the inserted dopants. An activation energy of about 1 eV is typical of the precursor molecules. Thus, this reaction could start the processes of further complicated changes in the material localized near the plasmonic particles.