Dynamics of Microvalve Operations in Integrated Microfluidics
Abstract
:1. Introduction
2. Methods
2.1. Fabrication
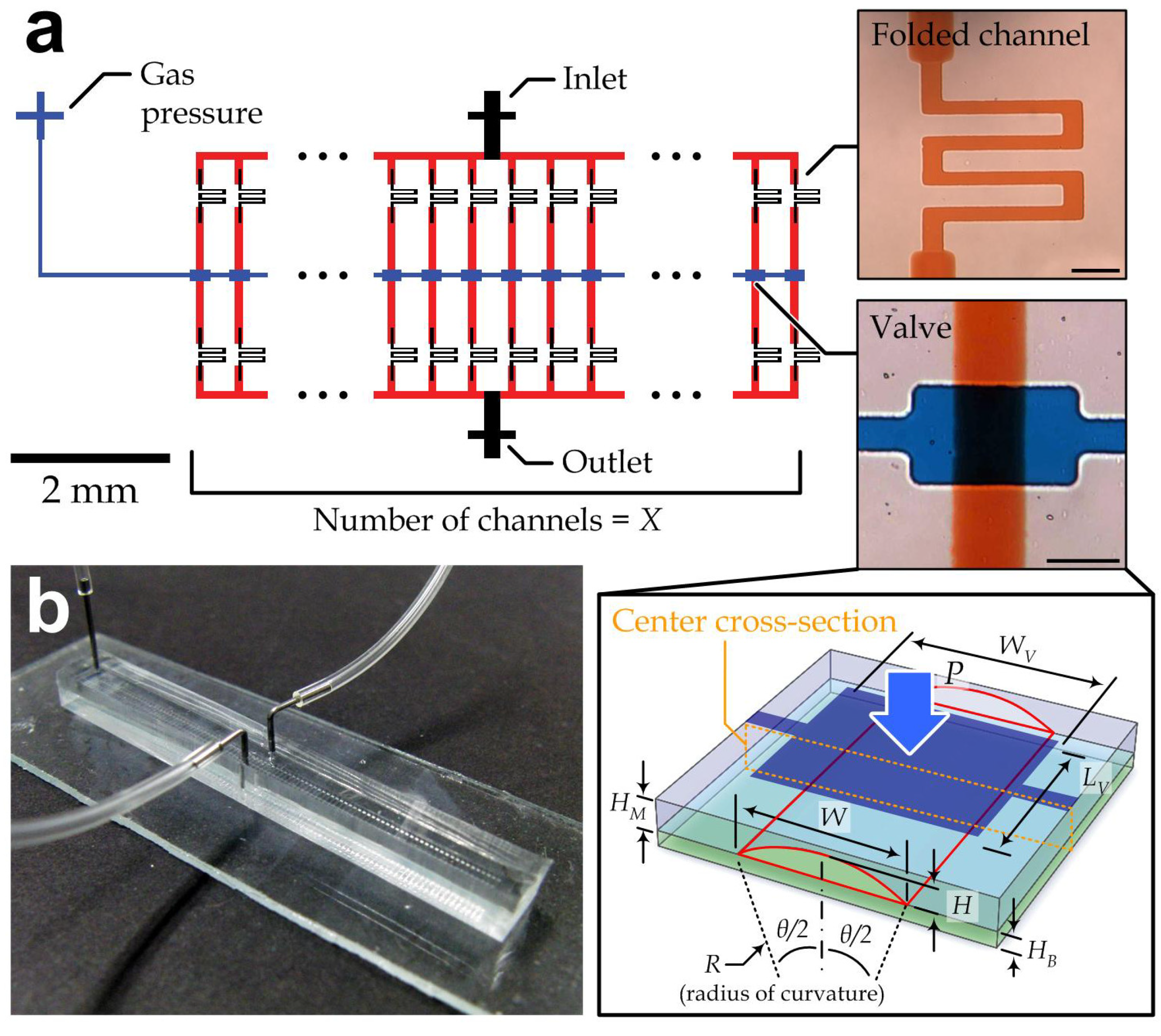
2.2. Measurement of Valve Responses
2.3. Membrane Deformation Simulation
2.4. Simulation of Lumped Circuit Models for Multiple-Valve Devices
2.5. Statistics
3. Results and Discussion
3.1. Device Configuration
3.2. Individual Membrane Deformation

3.3. Dynamics of Individual Microvalves
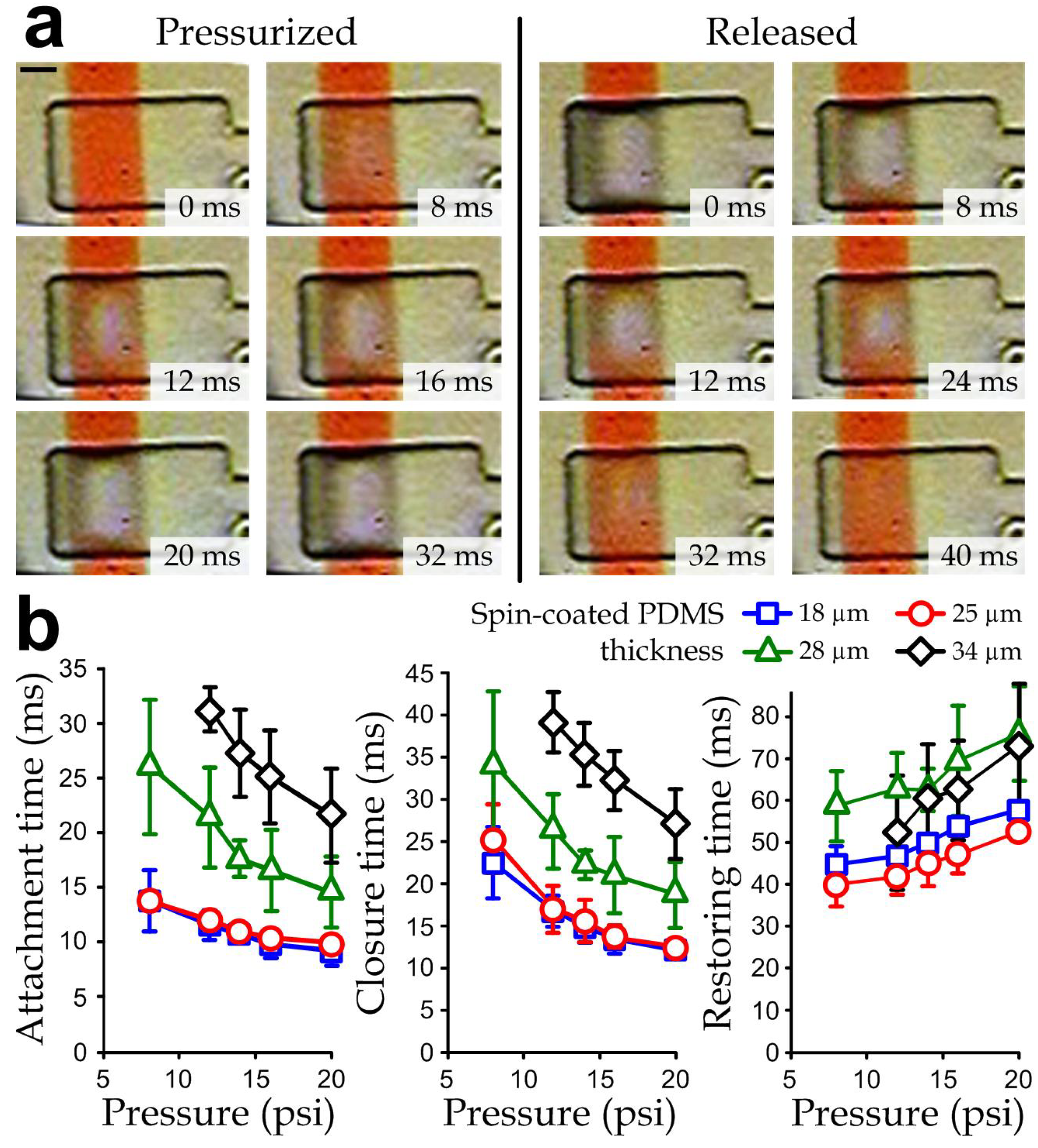
3.4. Dynamics of Multiple-Valve Operations
3.5. Lumped Modeling for Prediction of Valve Dynamics
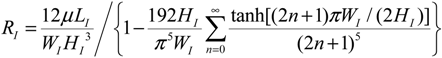
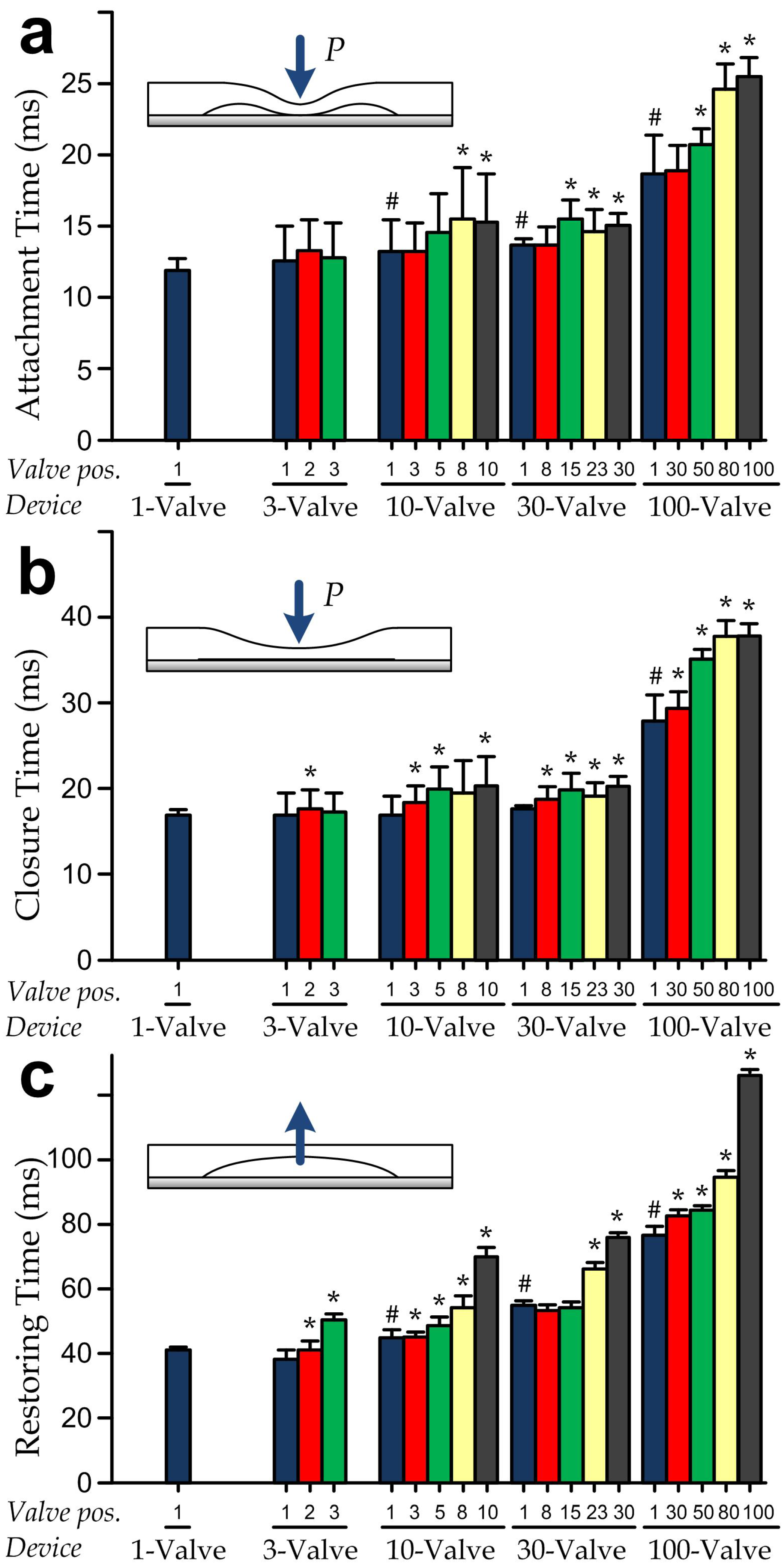

4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef]
- Ho, C.-M.; Tai, Y.-C. Micro-electro-mechanical-systems (MEMS) and fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 579–612. [Google Scholar] [CrossRef]
- Unger, M.A.; Chou, H.-P.; Thorsen, T.; Scherer, A.; Quake, S.R. Monolithic microfabricated valves and pumps by multilayer soft lithography. Science 2000, 288, 113–116. [Google Scholar] [CrossRef]
- Hong, J.W.; Studer, V.; Hang, G.; Anderson, W.F.; Quake, S.R. A nanoliter-scale nucleic acid processor with parallel architecture. Nat. Biotechnol. 2004, 22, 435–439. [Google Scholar] [CrossRef]
- Stroock, A.D.; Dertinger, S.K.; Ajdari, A.; Mezic, I.; Stone, H.A.; Whitesides, G.M. Chaotic mixer for microchannels. Science 2002, 295, 647–651. [Google Scholar] [CrossRef]
- Fu, A.Y.; Chou, H.P.; Spence, C.; Arnold, F.H.; Quake, S.R. An integrated microfabricated cell sorter. Anal. Chem. 2002, 74, 2451–2457. [Google Scholar] [CrossRef]
- Wu, J.; Cao, W.; Wen, W.; Chang, D.C.; Sheng, P. Polydimethylsiloxane microfluidic chip with integrated microheater and thermal sensor. Biomicrofluidics 2009, 3, 012005. [Google Scholar] [CrossRef]
- Melin, J.; Quake, S.R. Microfluidic large-scale integration: The evolution of design rules for biological automation. Annu. Rev. Biophys. Biomol. Struct. 2007, 36, 213–231. [Google Scholar] [CrossRef]
- Smith, C. Tools for drug discovery: Tools of the trade. Nature 2007, 446, 219–222. [Google Scholar] [CrossRef]
- Lau, B.T.; Baitz, C.A.; Dong, X.P.; Hansen, C.L. A complete microfluidic screening platform for rational protein crystallization. J. Am. Chem. Soc. 2007, 129, 454–455. [Google Scholar] [CrossRef]
- Paik, S.-J.; Byun, S.; Lim, J.-M.; Park, Y.; Lee, A.; Chung, S.; Chang, J.; Chun, K.; Cho, D.D. In-plane single-crystal-silicon microneedles for minimally invasive microfluid systems. Sens. Actuators A 2004, 114, 276–284. [Google Scholar] [CrossRef]
- Hadd, A.G.; Jacobson, S.C.; Ramsey, J.M. Microfluidic assays of acetylcholinesterase inhibitors. Anal. Chem. 1999, 71, 5206–5212. [Google Scholar] [CrossRef]
- Harrison, D.J. Micromachining a miniaturized capillary electrophoresis-base. Science 1993, 261, 895–895. [Google Scholar]
- Li, P.C.H.; Harrison, D.J. Transport, manipulation, and reaction of biological cells on-chip using electrokinetic effects. Anal. Chem. 1997, 69, 1564–1568. [Google Scholar] [CrossRef]
- Hadd, A.G.; Raymond, D.E.; Halliwell, J.W.; Jacobson, S.C.; Ramsey, J.M. Microchip device for performing enzyme assays. Anal. Chem. 1997, 69, 3407–3412. [Google Scholar] [CrossRef]
- Lagally, E.T.; Medintz, I.; Mathies, R.A. Single-molecule DNA amplification and analysis in an integrated microfluidic device. Anal. Chem. 2001, 73, 565–570. [Google Scholar] [CrossRef]
- Wang, J.; Ibáñez, A.; Chatrathi, M.P.; Escarpa, A. Electrochemical enzyme immunoassays on microchip platforms. Anal. Chem. 2001, 73, 5323–5327. [Google Scholar] [CrossRef]
- Zeng, Y.; Novak, R.; Shuga, J.; Smith, M.T.; Mathies, R.A. High-performance single cell genetic analysis using microfluidic emulsion generator arrays. Anal. Chem. 2010, 82, 3183–3190. [Google Scholar] [CrossRef]
- Hung, P.J.; Lee, P.J.; Sabounchi, P.; Lin, R.; Lee, L.P. Continuous perfusion microfluidic cell culture array for high-throughput cell-based assays. Biotechnol. Bioeng. 2005, 89, 1–8. [Google Scholar] [CrossRef]
- Fu, A.Y.; Spence, C.; Scherer, A.; Arnold, F.H.; Quake, S.R. A microfabricated fluorescence-activated cell sorter. Nat. Biotechnol. 1999, 17, 1109–1111. [Google Scholar] [CrossRef]
- Kim, M.S.; Ju, H.Y.; Park, J.-K. A microfluidic platform for 3-dimensional cell culture and cell-based assays. Biomed. Microdevices 2007, 9, 25–34. [Google Scholar] [CrossRef]
- Tian, J.; Gong, H.; Sheng, N.; Zhou, X.; Gulari, E.; Gao, X.; Church, G. Accurate multiplex gene synthesis from programmable DNA microchips. Nature 2004, 432, 1050–1054. [Google Scholar] [CrossRef]
- Gomez-Sjoberg, R.; Leyrat, A.A.; Pirone, D.M.; Chen, C.S.; Quake, S.R. Versatile, fully automated, microfluidic cell culture system. Anal. Chem. 2007, 79, 8557–8563. [Google Scholar] [CrossRef]
- Lam, R.H.; Kim, M.C.; Thorsen, T. Culturing aerobic and anaerobic bacteria and mammalian cells with a microfluidic differential oxygenator. Anal. Chem. 2009, 81, 5918–5924. [Google Scholar] [CrossRef]
- Thorsen, T.; Maerkl, S.J.; Quake, S.R. Microfluidic large-scale integration. Science 2002, 298, 580–584. [Google Scholar] [CrossRef]
- Ottesen, E.A.; Hong, J.W.; Quake, S.R.; Leadbetter, J.R. Microfluidic digital PCR enables multigene analysis of individual environmental bacteria. Science 2006, 314, 1464–1467. [Google Scholar] [CrossRef]
- Marcus, J.S.; Anderson, W.F.; Quake, S.R. Microfluidic single-cell mRNA isolation and analysis. Anal. Chem. 2006, 78, 3084–3089. [Google Scholar] [CrossRef]
- Ben-Ari, Y.; Glick, Y.; Kipper, S.; Schwartz, N.; Barbiro-Michaely, E.; Gerber, D. Microfluidic large scale integration of viral-host interaction analysis. Lab Chip 2013, 13, 2202–2209. [Google Scholar] [CrossRef]
- Hosokawa, K.; Maeda, R. A pneumatically-actuated three-way microvalve fabricated with polydimethylsiloxane using the membrane transfer technique. J. Micromech. Microeng. 2000, 10, 415. [Google Scholar] [CrossRef]
- Kartalov, E.P.; Scherer, A.; Quake, S.R.; Taylor, C.R.; Anderson, W.F. Experimentally validated quantitative linear model for the device physics of elastomeric microfluidic valves. J. Appl. Phys. 2007, 101, 64505. [Google Scholar] [CrossRef]
- Goulpeau, J.; Trouchet, D.; Ajdari, A.; Tabeling, P. Experimental study and modeling of polydimethylsiloxane peristaltic micropumps. J. Appl. Phys. 2005, 98. [Google Scholar] [CrossRef]
- Hou-Pu, C.; Unger, M.A.; Quake, S.R. A microfabricated rotary pump. Biomed. Microdevices 2001, 3, 323–323. [Google Scholar] [CrossRef]
- El-Ali, J.; Sorger, P.K.; Jensen, K.F. Cells on chips. Nature 2006, 442, 403–411. [Google Scholar] [CrossRef]
- Bourouina, T.; Grandchamp, J.-P. Modeling micropumps with electrical equivalent networks. J. Micromech. Microeng. 1996, 6, 398. [Google Scholar] [CrossRef]
- Zeng, Y.; Azizi, F.; Mastrangelo, C. Behavioral Modeling of Solute Tracking in Microfluidics. In Proceedings of the IEEE Behavioral Modeling and Simulation Workshop 2009, San José, CA, USA, 17–18 September 2009; pp. 1–6.
- Chen, L.; Azizi, F.; Mastrangelo, C.H. Generation of dynamic chemical signals with microfluidic C-DACs. Lab Chip 2007, 7, 850–855. [Google Scholar] [CrossRef]
- Azizi, F.; Mastrangelo, C.H. Generation of dynamic chemical signals with pulse code modulators. Lab Chip 2008, 8, 907–912. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, Y.; Chen, L.; Mastrangelo, C.H. Fourier microfluidics. Lab Chip 2008, 8, 779–785. [Google Scholar] [CrossRef]
- Hong, L.; Pan, T. Three-dimensional surface microfluidics enabled by spatiotemporal control of elastic fluidic interface. Lab Chip 2010, 10, 3271–3276. [Google Scholar] [CrossRef]
- Studer, V.; Hang, G.; Pandolfi, A.; Ortiz, M.; French Anderson, W.; Quake, S.R. Scaling properties of a low-actuation pressure microfluidic valve. J. Appl. Phys. 2004, 95, 393–398. [Google Scholar] [CrossRef]
- Pandolfi, A.; Ortiz, M. Numerical Analysis of Elastomeric Fluidic Microvalves. Sens. Lett. 2008, 6, 43–48. [Google Scholar] [CrossRef] [Green Version]
- Basar, Y.; Ding, Y. Shear deformation models for large-strain shell analysis. Int. J. Solids Struct. 1997, 34, 1687–1708. [Google Scholar] [CrossRef]
- Khanafer, K.; Duprey, A.; Schlicht, M.; Berguer, R. Effects of strain rate, mixing ratio, and stress-strain definition on the mechanical behavior of the polydimethylsiloxane (PDMS) material as related to its biological applications. Biomed. Microdevices 2009, 11, 503–508. [Google Scholar] [CrossRef]
- Xia, Y.; Kim, E.; Zhao, X.-M.; Rogers, J.A.; Prentiss, M.; Whitesides, G.M. Complex optical surfaces formed by replica molding against elastomeric masters. Science 1996, 273, 347–349. [Google Scholar]
- Joekar-Niasar, V.; Schotting, R.; Leijnse, A. Analytical solution of electrohydrodynamic flow and transport in rectangular channels: Inclusion of double layer effects. Comput. Geosci. 2013, 17, 497–513. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lau, A.T.H.; Yip, H.M.; Ng, K.C.C.; Cui, X.; Lam, R.H.W. Dynamics of Microvalve Operations in Integrated Microfluidics. Micromachines 2014, 5, 50-65. https://doi.org/10.3390/mi5010050
Lau ATH, Yip HM, Ng KCC, Cui X, Lam RHW. Dynamics of Microvalve Operations in Integrated Microfluidics. Micromachines. 2014; 5(1):50-65. https://doi.org/10.3390/mi5010050
Chicago/Turabian StyleLau, Alan T. H., Hon Ming Yip, Kathy C. C. Ng, Xin Cui, and Raymond H. W. Lam. 2014. "Dynamics of Microvalve Operations in Integrated Microfluidics" Micromachines 5, no. 1: 50-65. https://doi.org/10.3390/mi5010050
APA StyleLau, A. T. H., Yip, H. M., Ng, K. C. C., Cui, X., & Lam, R. H. W. (2014). Dynamics of Microvalve Operations in Integrated Microfluidics. Micromachines, 5(1), 50-65. https://doi.org/10.3390/mi5010050





