Enhancing Confidence and Interpretability of a CNN-Based Wafer Defect Classification Model Using Temperature Scaling and LIME
Abstract
1. Introduction
2. Automated Wafer Defect Classification Model and Grad-CAM
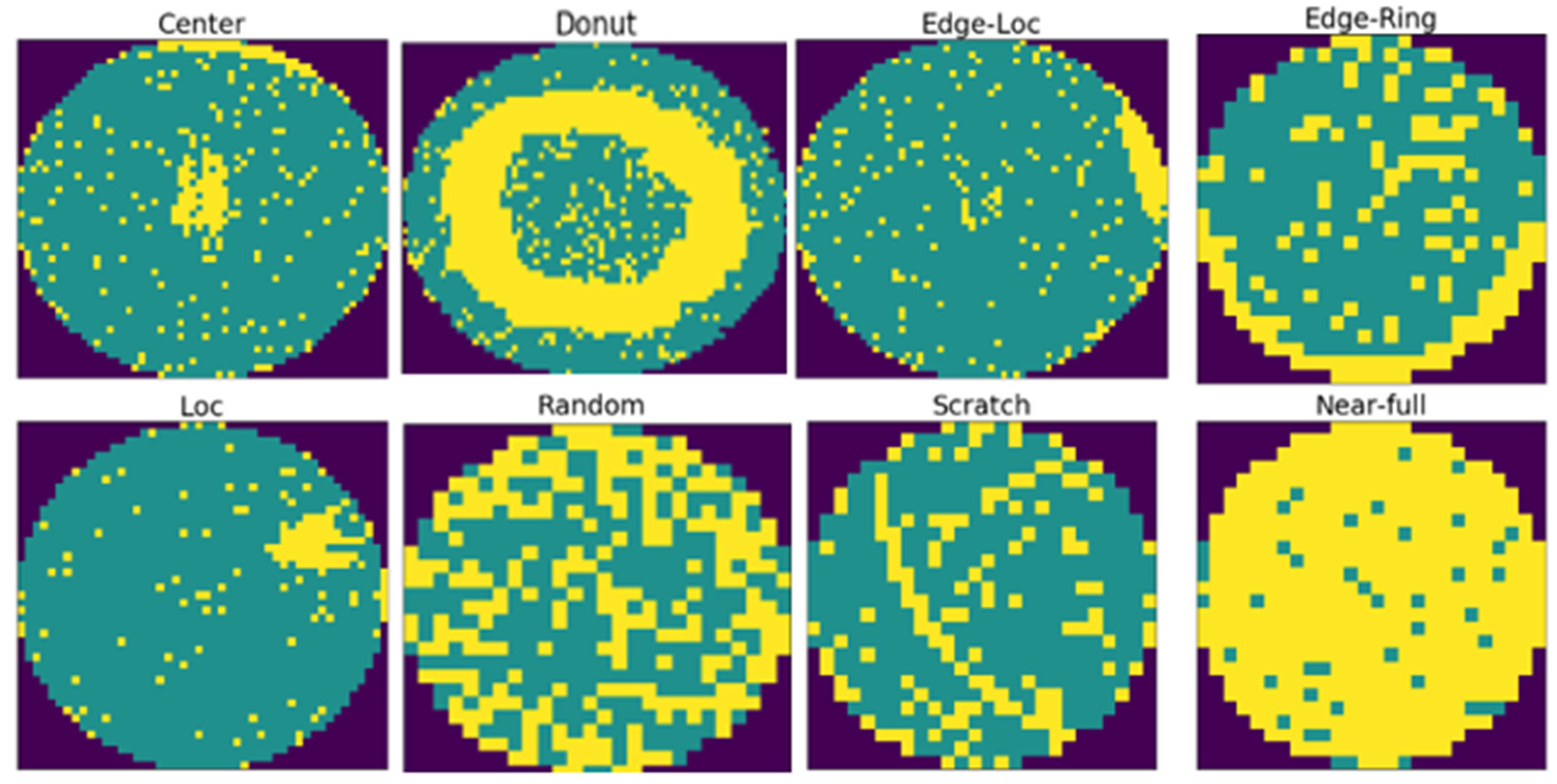
2.1. WM-811K Dataset and Overall Architecture
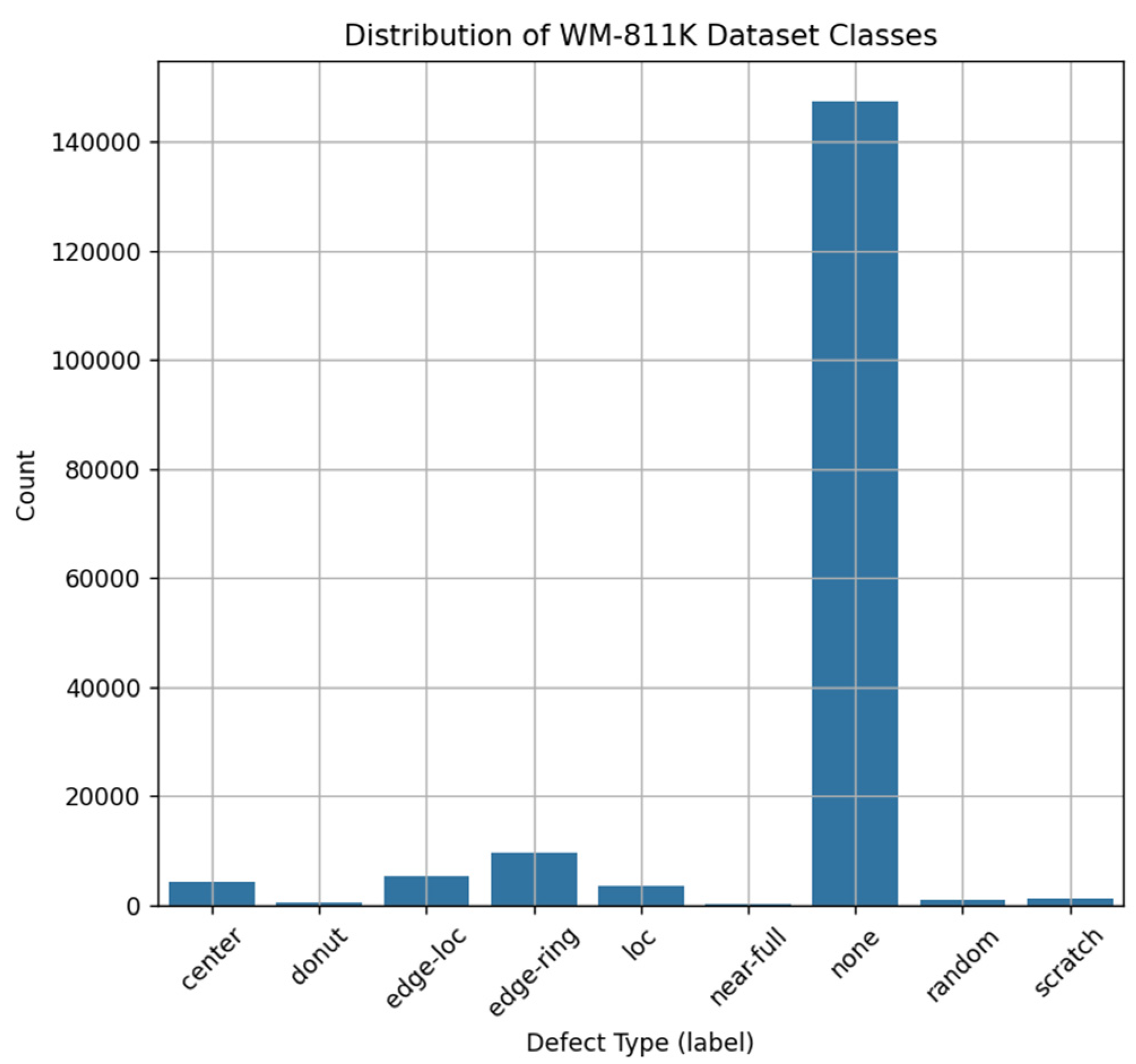
2.2. Data Preprocessing and Class Balancing
2.3. Implementation of the CNN-Based Classification Model
2.4. Implementation of the Grad-CAM-Based Visual Explanation Module
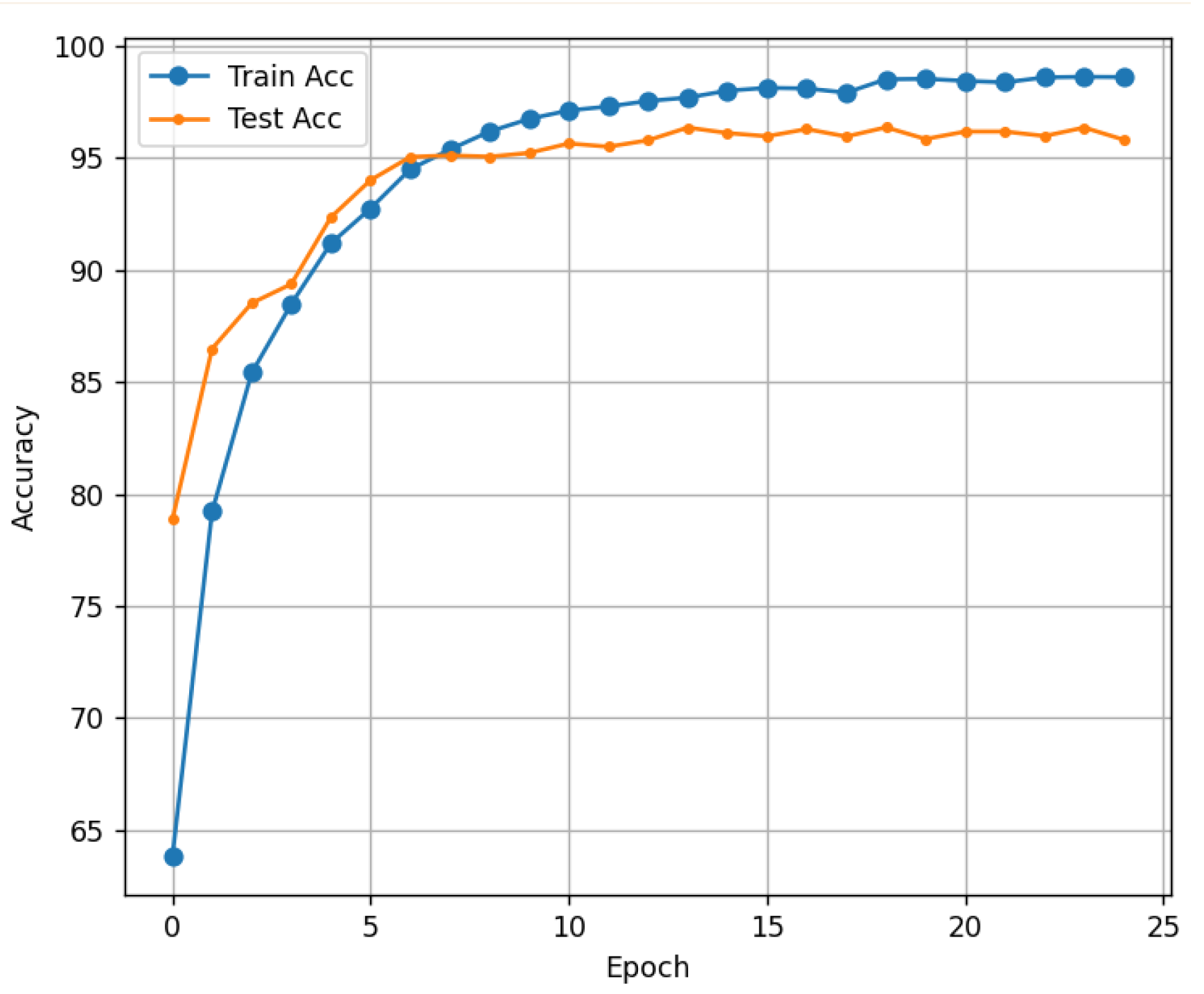
2.5. Training Configuration and Performance Evaluation
2.6. Comparative Analysis with State-of-the-Art Architectures
2.7. Expected Calibration Error and Maximum Calibration Error
2.8. Analysis of the Effects Before and After Calibration
3. Model Interpretation Using LIME
3.1. LIME Overview
3.2. LIME Overview
3.3. Results and Interpretation
3.4. Complementary Use of LIME and Grad-CAM
3.5. Synergistic Integration of Grad-CAM and LIME for Model Interpretability
4. Evaluation of Model Accuracy and Confidence Calibration Performance
4.1. Verification of the Effectiveness of the Proposed Method
4.2. Performance Evaluation Metrics
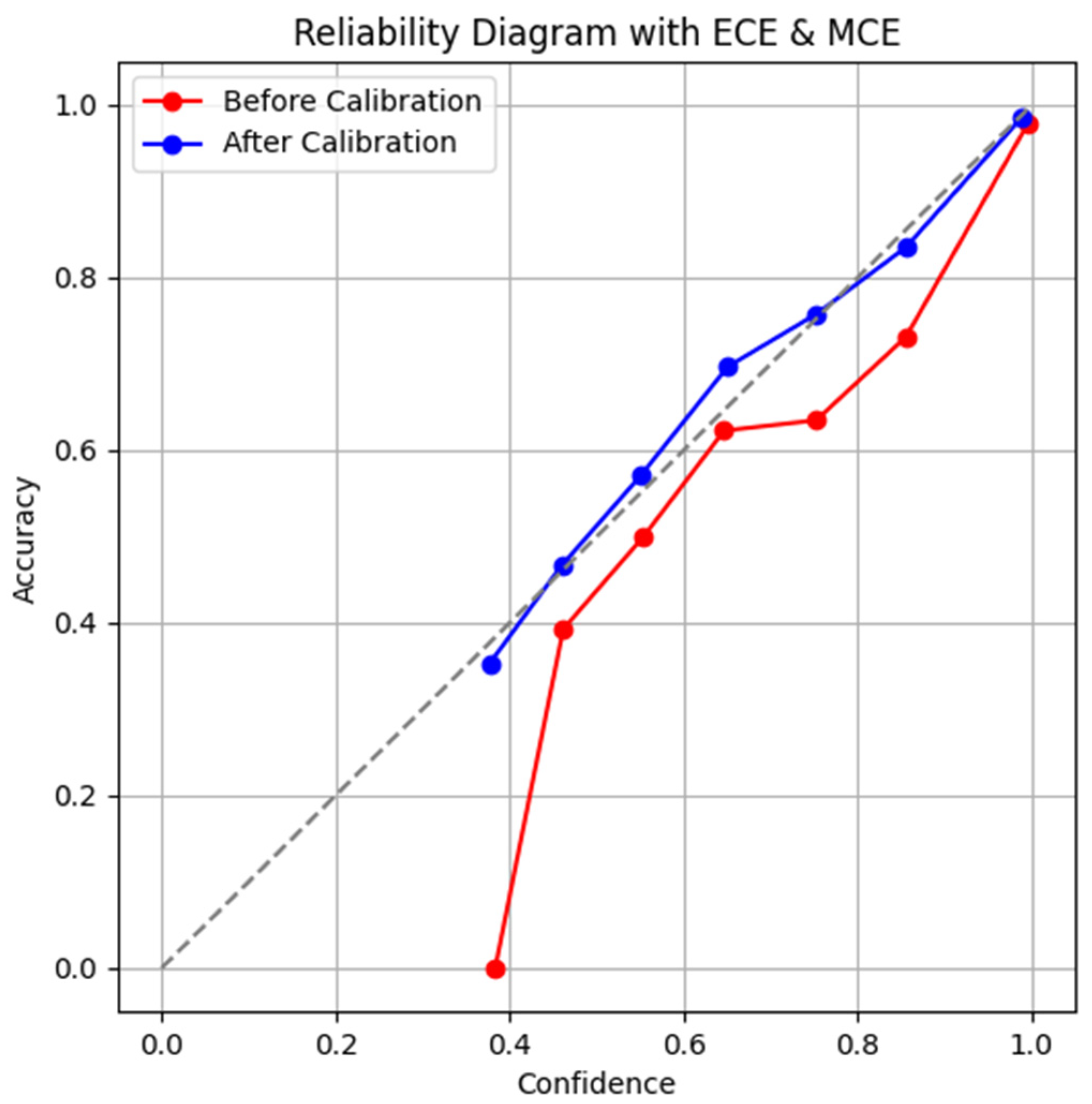
4.3. Confidence Calibration Results
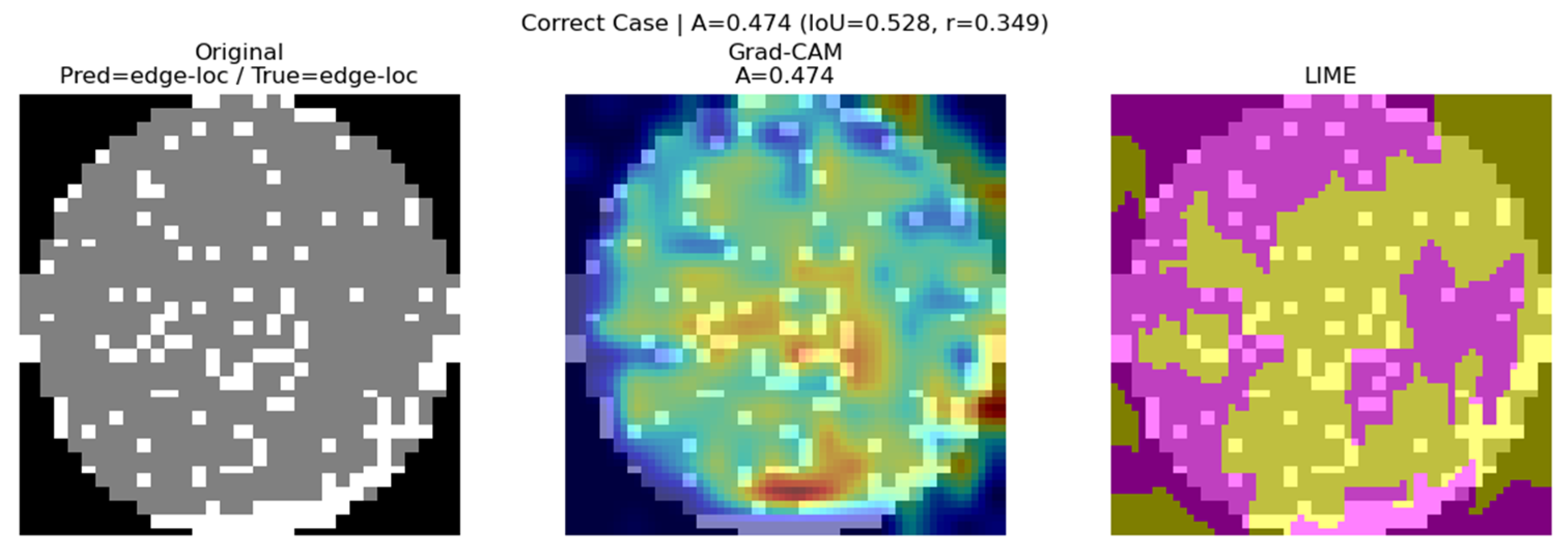
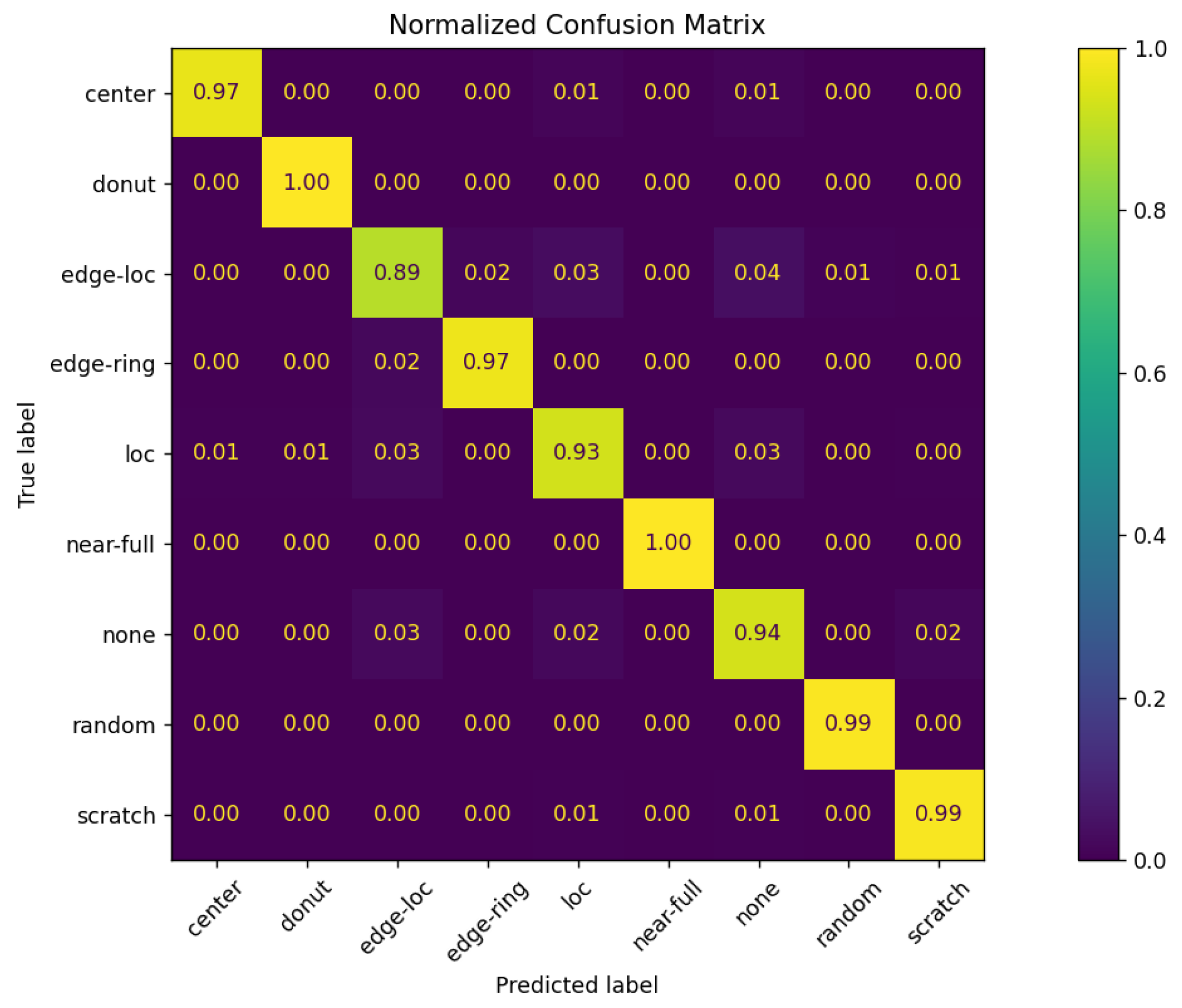
4.4. Visual Interpretation Results (Grad-CAM and LIME)
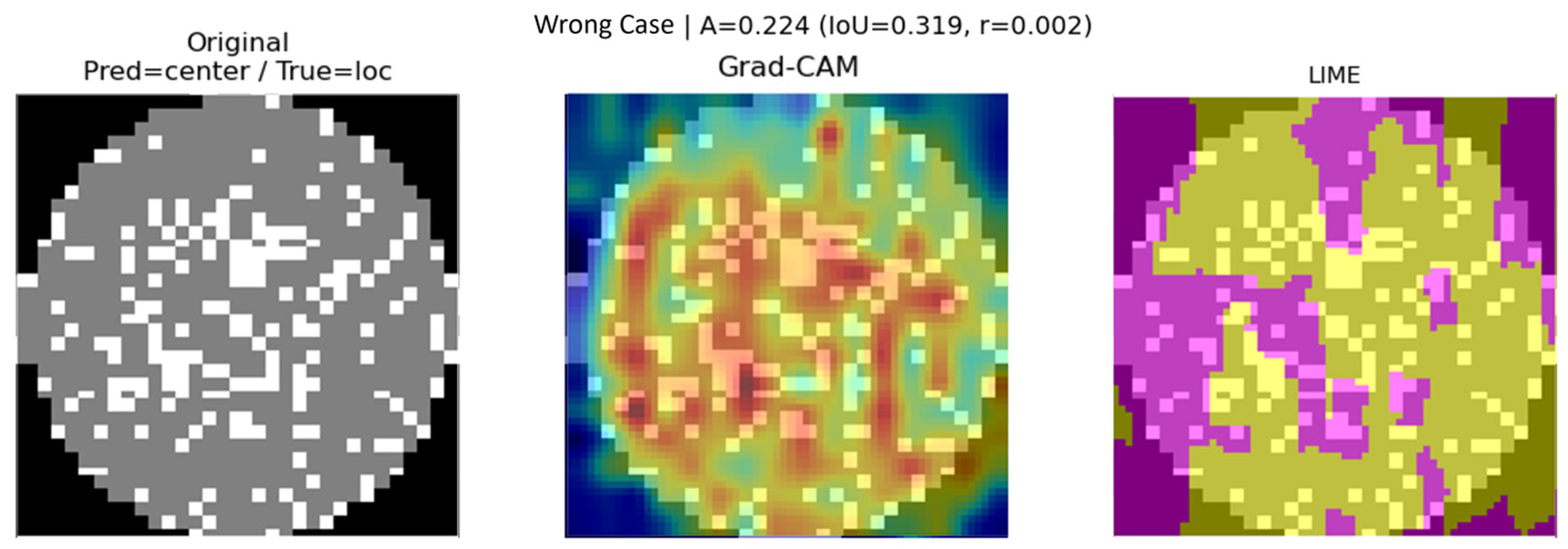
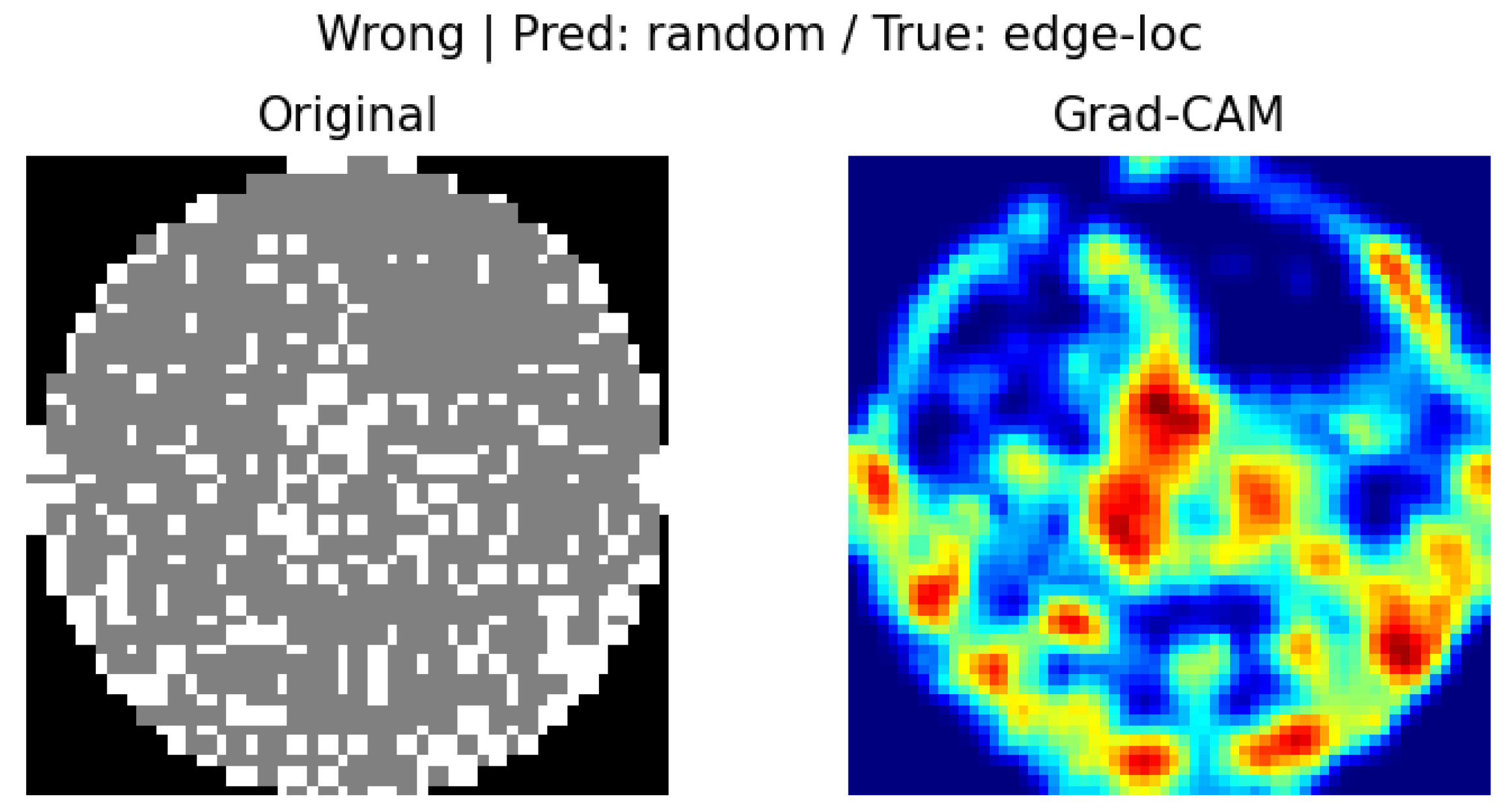
4.5. In-Depth Analysis of Misclassification Cases
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, H.-S.; Cho, H.-C. Wafer Map Defect Analysis Based on EfficientNetV2 using Grad-CAM. Trans. Korean Inst. Electr. Eng. 2023, 72, 553–558. [Google Scholar] [CrossRef]
- Hwang, S.J. Detecting New Defect Patterns in Wafer Bin Maps with Deep Active Learning Model. Master’s Thesis, Department of Industrial Management Engineering, Korea University, Seoul, Republic of Korea, 2023. [Google Scholar] [CrossRef]
- Park, I.; Kim, J. Semiconductor Wafer Bin Map Defect Pattern Classification based on Transfer Learning Considering Data Class Imbalance. J. Korea Acad. Coop. Soc. 2024, 25, 637–643. [Google Scholar] [CrossRef]
- Shin, W. Wafer Defect Pattern Classification Based on Mixup and Self-Supervised Learning. Ph.D. Dissertation, Department of Industrial Management Engineering, Korea University, Seoul, Republic of Korea, 2023. [Google Scholar] [CrossRef]
- RO, H.R.; Kwak, S.Y. Wafer defect classification using DCGAN and CNN model. In Proceedings of the ICCC2024 International Conference on Convergence Content, Danang, Vietnam, 17–19 September 2024; Volume 22, pp. 403–404. [Google Scholar]
- Sung, D.S.; Kim, H.S. An Study on Identification of the Causing Factors for Defected Wafer Using CNN: Focusing on Semi-conductor In-line Process. Commer. Educ. Res. 2022, 36, 71–91. [Google Scholar] [CrossRef]
- Park, J.; Kim, J.; Kim, H.; Mo, K.; Kang, P. Wafer Map-based Defect Detection Using Convolutional Neural Networks. J. Korean Inst. Ind. Eng. 2018, 44, 249–258. [Google Scholar] [CrossRef]
- Buda, M.; Maki, A.; Mazurowski, M.A. A systematic study of the class imbalance problem in convolutional neural networks. Neural Netw. 2018, 106, 249–259. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Jia, M.; Lin, T.; Song, Y.; Belongie, S. Class-Balanced Loss Based on Effective Number of Samples. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–19 June 2019; pp. 9260–9269. [Google Scholar] [CrossRef]
- Zhang, N.; Mahmoud, W.H. Semiconductor Wafer Map Defect Classification Using Convolutional Neural Networks on Imbalanced Classes. In Proceedings of the 2025 17th International Conference on Advanced Computational Intelligence (ICACI), Bath, UK, 7–13 July 2025; pp. 54–62. [Google Scholar]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef]
- Omeiza, D.; Speakman, S.; Cintas, C.; Weldermariam, K. Smooth Grad-CAM++: An Enhanced Inference Level Visualization Technique for Deep Convolutional Neural Network Models. arXiv 2019, arXiv:1908.01224. [Google Scholar]
- Saqlain, M.; Abbas, Q.; Lee, J.Y. A Deep Convolutional Neural Network for Wafer Defect Identification on an Imbalanced Dataset in Semiconductor Manufacturing Processes. IEEE Trans. Semicond. Manuf. 2020, 33, 436–444. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Pleva, M.; Hládek, D.; Lee, C.-W.; Su, M.-H. Ensemble Learning for Wafer Defect Pattern Classification in the Semiconductor Industry. IEEE Access 2025, 13, 155714–155728. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual explanations from deep networks via gradient-based localization. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Why Should I Trust You? Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’16), San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar] [CrossRef]
- Chattopadhay, A.; Sarkar, A.; Howlader, P.; Balasubramanian, V.N. Grad-cam++: Generalized gradient-based visual explanations for deep convolutional networks. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 839–847. [Google Scholar]
- Balanya, S.A.; Maroñas, J.; Ramos, D. Adaptive temperature scaling for Robust calibration of deep neural networks. Neural Comput. Appl. 2024, 36, 8073–8095. [Google Scholar] [CrossRef]
- Niculescu-Mizil, A.; Caruana, R. Predicting good probabilities with supervised learning. In Proceedings of the 22nd International Conference on Machine Learning, Ithaca, NY, USA, 7 August 2005; pp. 625–632. [Google Scholar]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On calibration of modern neural networks. In Proceedings of the 34th International Conference on Machine Learning Mach. Learn (ICML), Sydney, NSW, Australia, 6–11 July 2017; Volume 70, pp. 1321–1330. [Google Scholar]
- Kumar, A. Verified uncertainty calibration. In Proceedings of the 33rd International Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8 December 2019; pp. 3792–3803. [Google Scholar]
- Chen, W.; Li, Y.; Zhang, Y. Deep Networks under Block-level Supervision for Pixel-level Cloud Detection in Multi-spectral Satellite Imagery. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September 2020–2 October 2020; pp. 1612–1615. [Google Scholar] [CrossRef]
- Garreau, D.; von Luxburg, U. Explaining the Explainer: A First Theoretical Analysis of LIME. arXiv 2020, arXiv:2001.03447. [Google Scholar] [CrossRef]
- Islam, M.M.M. Improved Wafer Defect Pattern Classification in Semiconductor Manufacturing Using Deep Learning and Explainable AI. In Artificial Intelligence for Smart Manufacturing and Industry X.0; Springer: Berlin/Heidelberg, Germany, 2025; pp. 147–164. [Google Scholar] [CrossRef]
- Chien, J.-C.; Wu, M.-T.; Lee, J.-D. Inspection and Classification of Semiconductor Wafer Surface Defects Using CNN Deep Learning Networks. Appl. Sci. 2020, 10, 5340. [Google Scholar] [CrossRef]
- Deng, G.; Wang, H. Efficient Mixed-Type Wafer Defect Pattern Recognition Based on Light-Weight Neural Network. Micromachines 2024, 15, 836. [Google Scholar] [CrossRef] [PubMed]








| Architecture | Accuracy (%) | Parameters (M) | Inference Time (ms) |
|---|---|---|---|
| CNN | 98.7 | 2.192 | 0.067 |
| ResNet | 98.91 | 11.2 | 0.285 |
| EfficientNet | 98.15 | 5.3 | 0.120 |
| MobileNet | 95.01 | 3.216 | 0.156 |
| Metric | Correct Classification | Wrong Classification | Low Consensus |
|---|---|---|---|
| IoU | 0.528 | 0.319 | 0.284 |
| Correlation Coefficient | 0.349 | 0.002 | 0.145 |
| Agreement Score A | 0.474 | 0.224 | 0.243 |
| Model Configuration | Accuracy | ECE |
|---|---|---|
| Baseline | 93.93% | 0.0358 |
| Baseline + Weighted Loss | 97.8% | 0.073 |
| Baseline + Weighted Loss + Temperature Scaling | 97.8% | 0.021 |
| Metric | Before Calibration | After Calibration |
|---|---|---|
| ECE | 0.073 | 0.021 |
| MCE | 0.209 | 0.068 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Ju, Y.; Lim, J.; Hong, S.; Baek, S.-W.; Lee, J. Enhancing Confidence and Interpretability of a CNN-Based Wafer Defect Classification Model Using Temperature Scaling and LIME. Micromachines 2025, 16, 1057. https://doi.org/10.3390/mi16091057
Lee J, Ju Y, Lim J, Hong S, Baek S-W, Lee J. Enhancing Confidence and Interpretability of a CNN-Based Wafer Defect Classification Model Using Temperature Scaling and LIME. Micromachines. 2025; 16(9):1057. https://doi.org/10.3390/mi16091057
Chicago/Turabian StyleLee, Jieun, Yeonwoo Ju, Junho Lim, Sungmin Hong, Soo-Whang Baek, and Jonghwan Lee. 2025. "Enhancing Confidence and Interpretability of a CNN-Based Wafer Defect Classification Model Using Temperature Scaling and LIME" Micromachines 16, no. 9: 1057. https://doi.org/10.3390/mi16091057
APA StyleLee, J., Ju, Y., Lim, J., Hong, S., Baek, S.-W., & Lee, J. (2025). Enhancing Confidence and Interpretability of a CNN-Based Wafer Defect Classification Model Using Temperature Scaling and LIME. Micromachines, 16(9), 1057. https://doi.org/10.3390/mi16091057





