A Novel Motion Platform Based on Dual Driving Feet Linear Ultrasonic Motor
Abstract
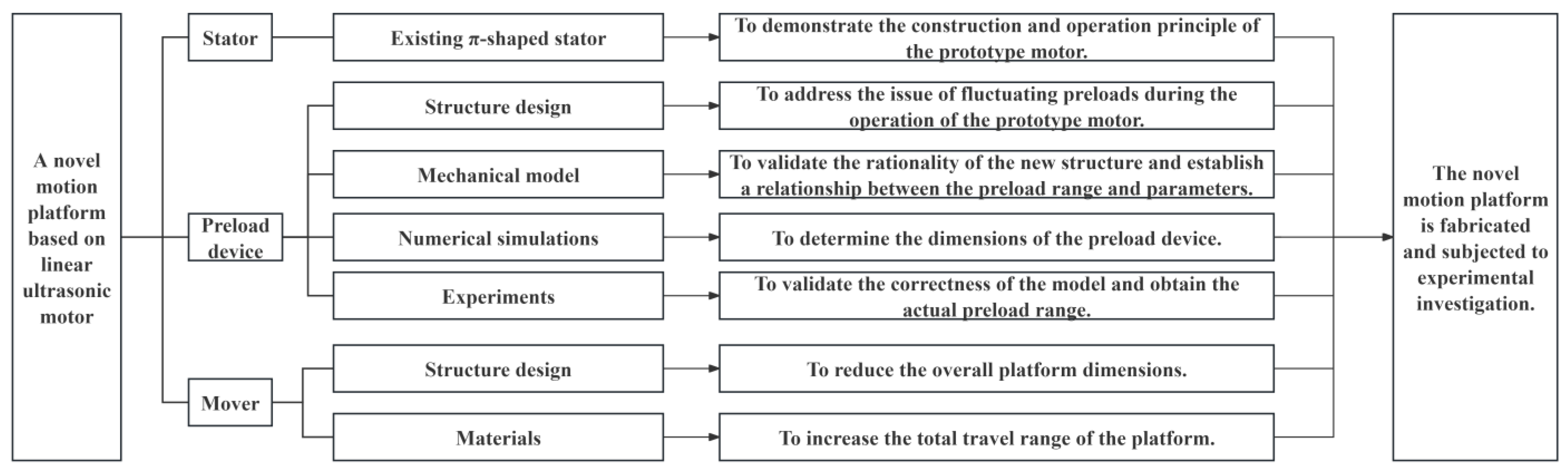
1. Introduction
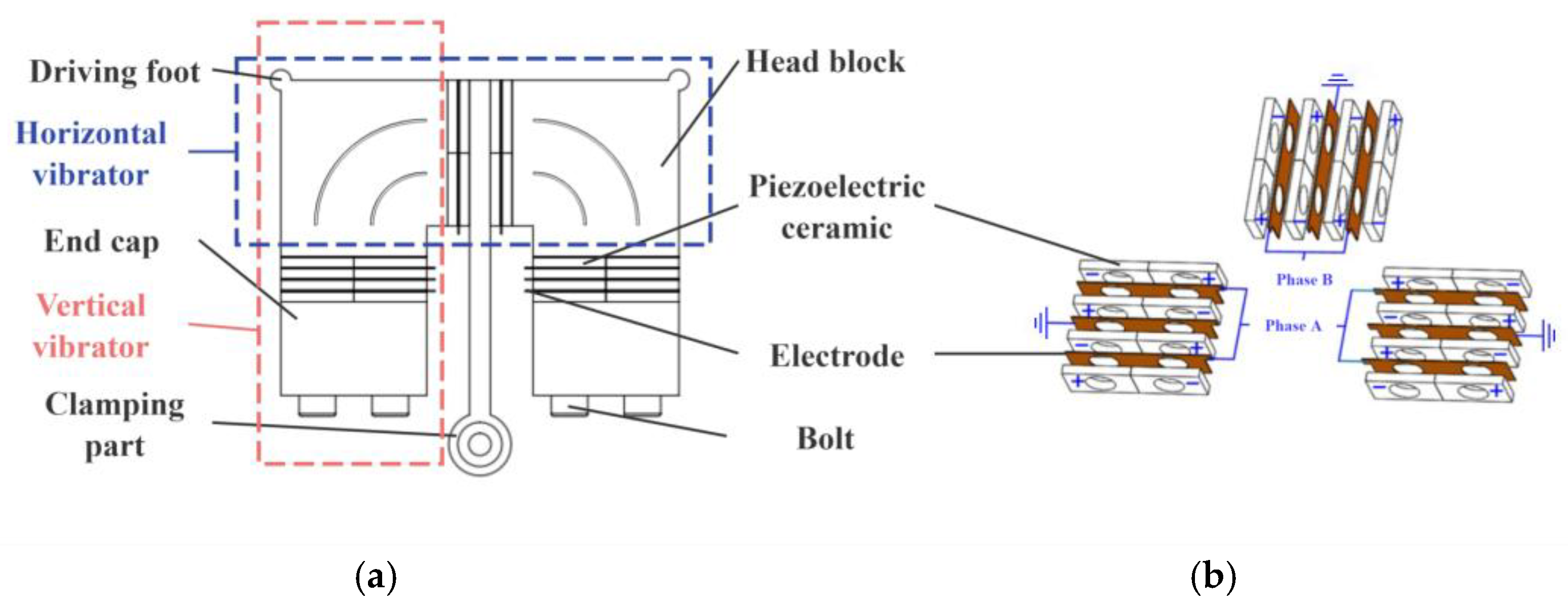
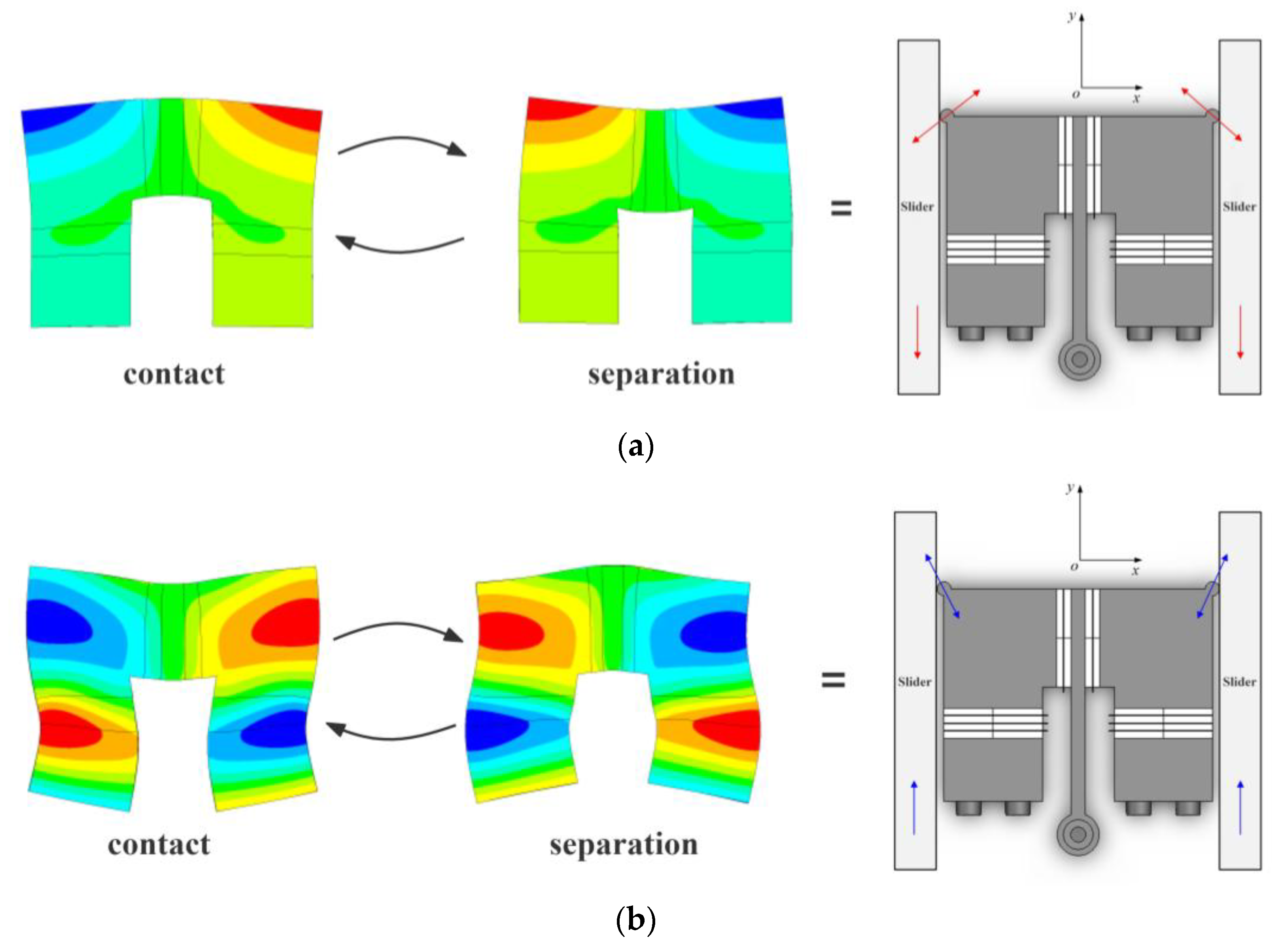
2. Structure and Principle of the Platform
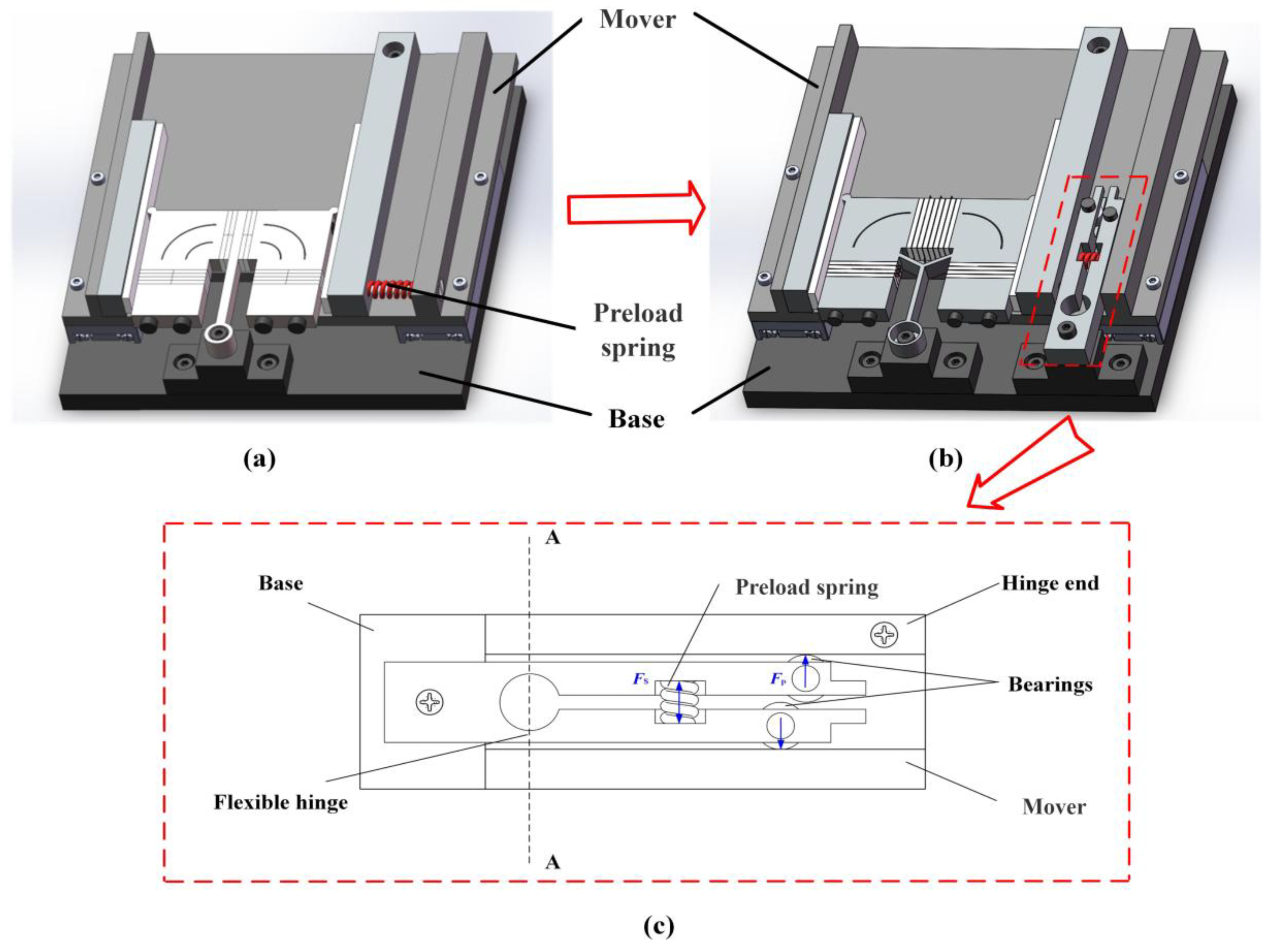
3. Design of Preload Device
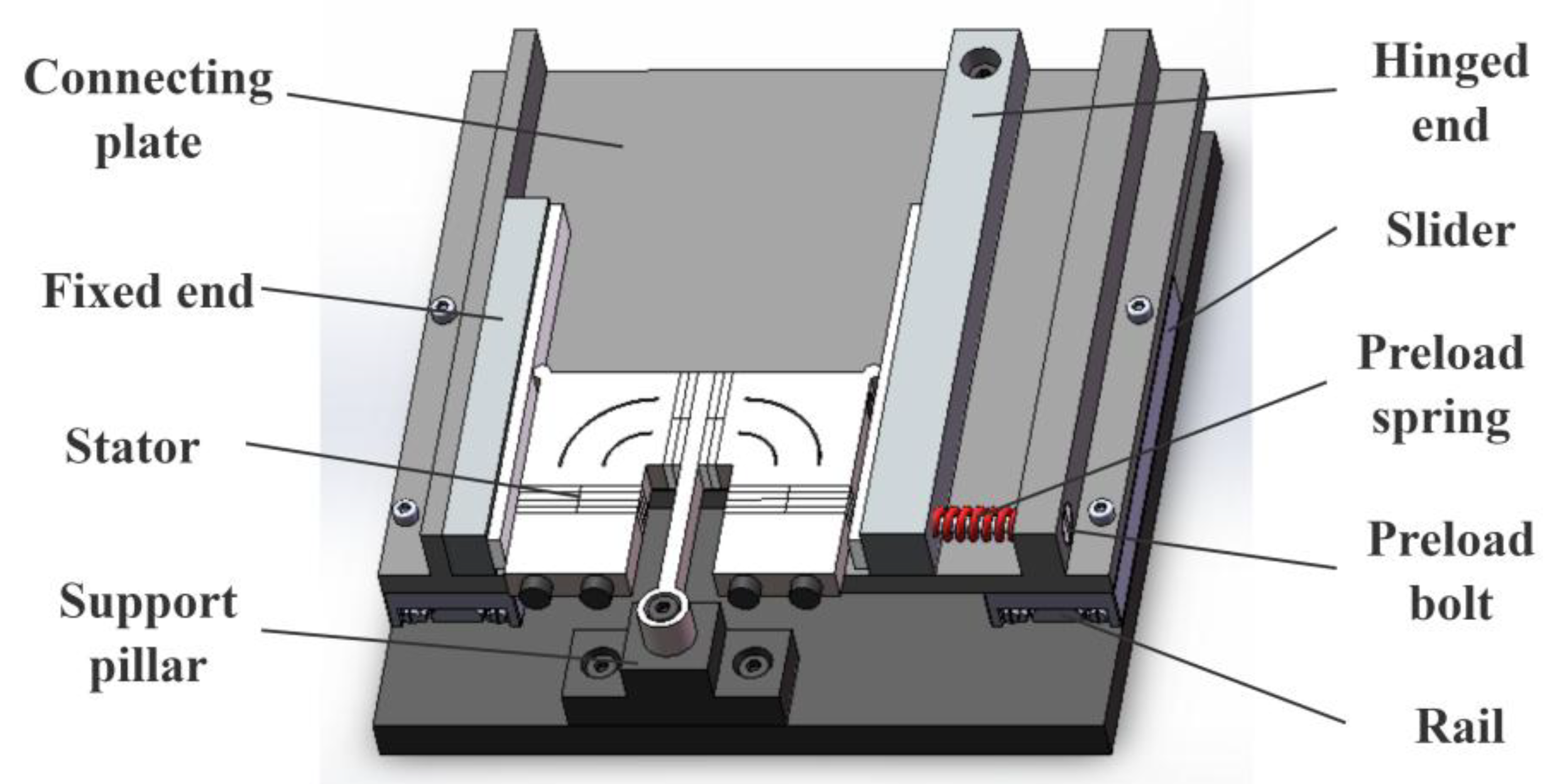
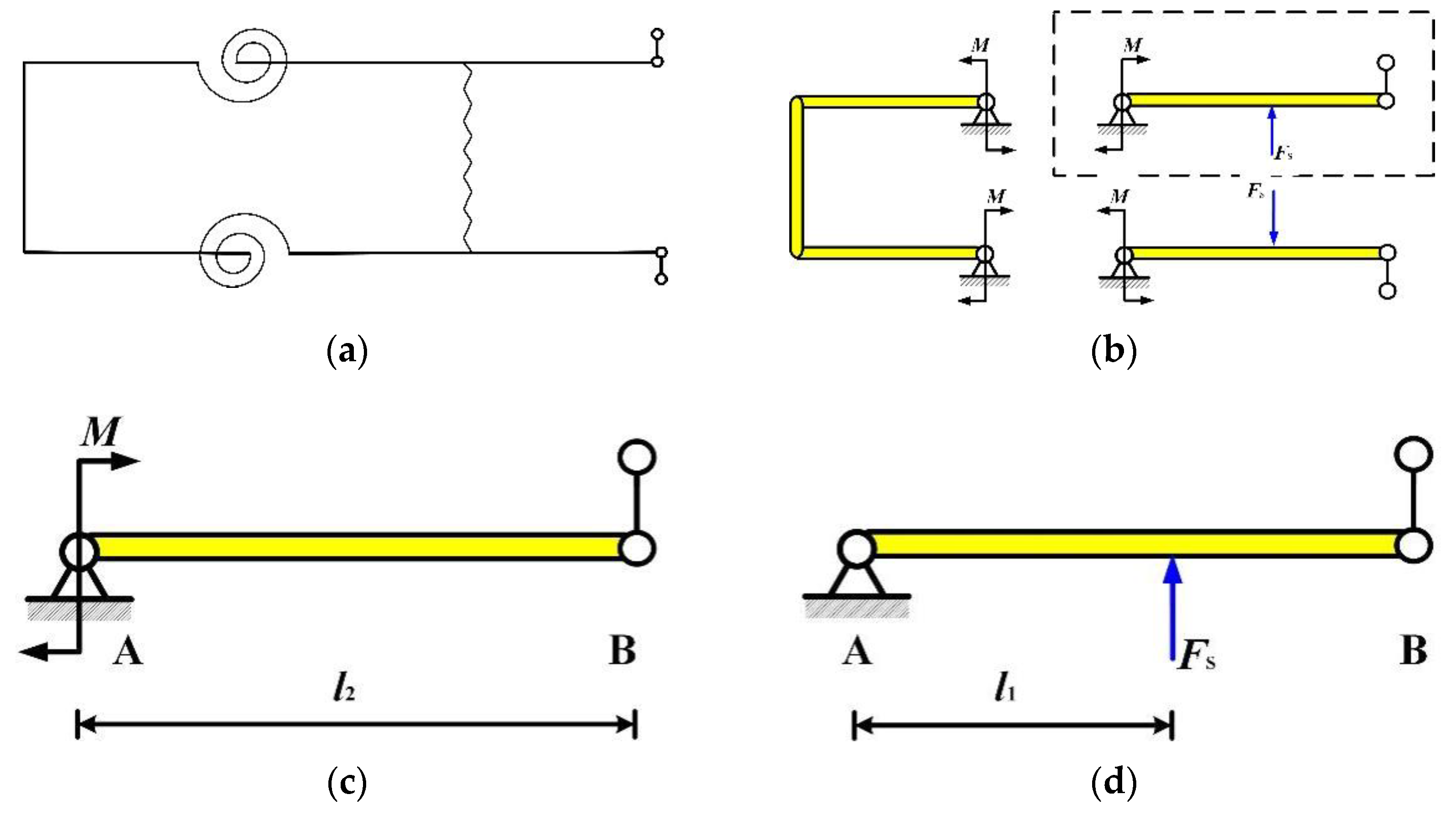
3.1. Structure and Principle of Preload Device
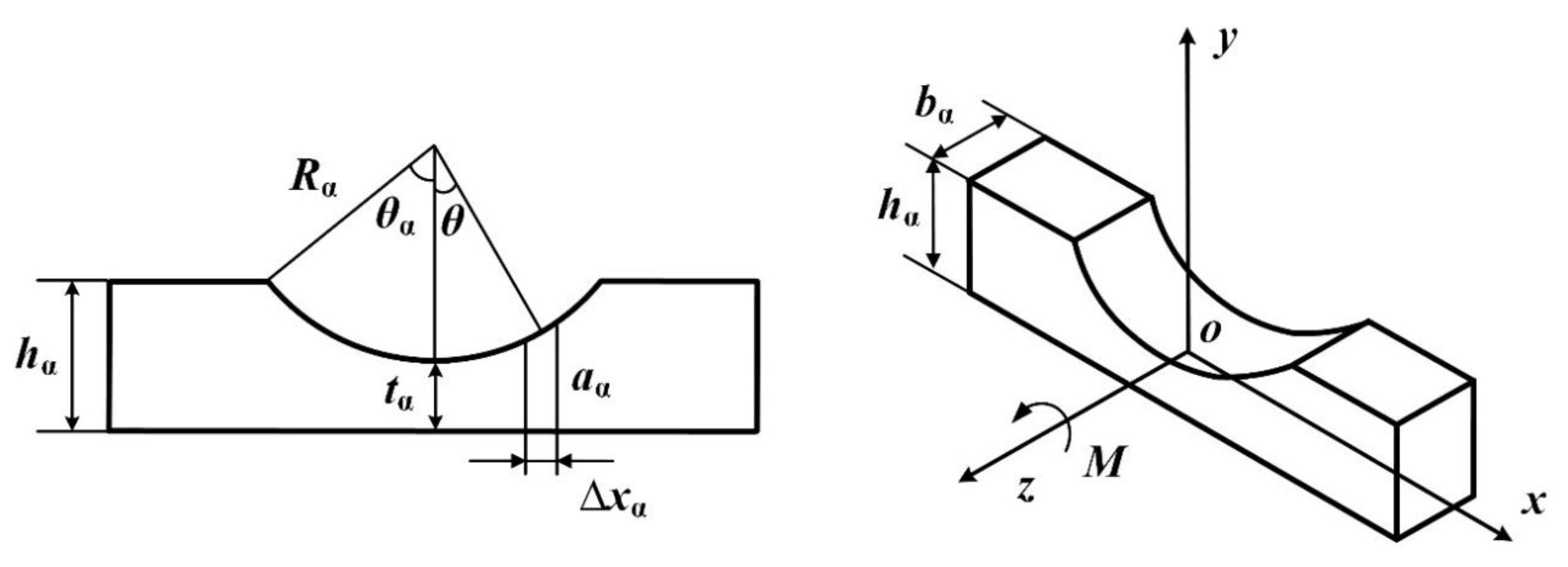
3.2. Model and Dimension of Preload Device
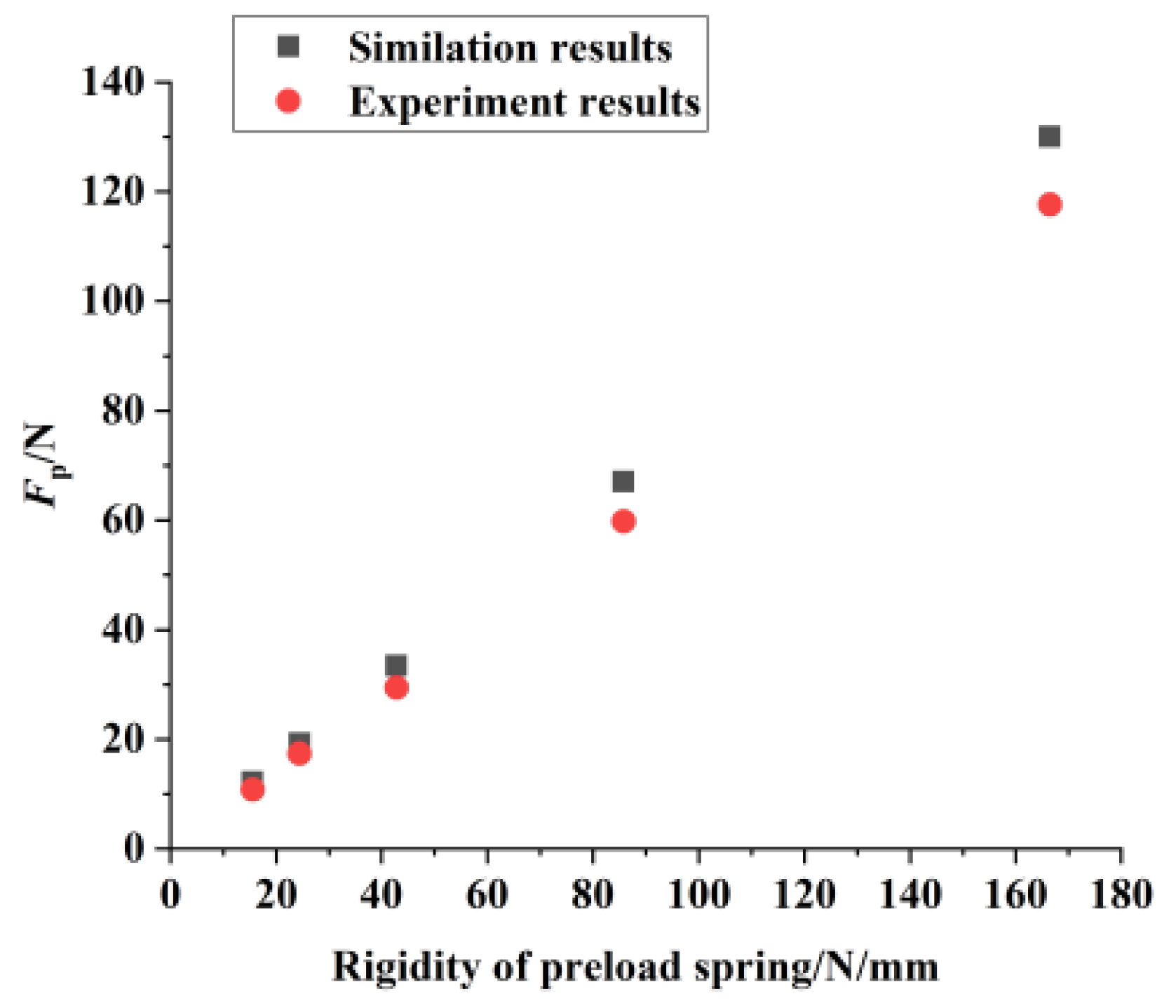
3.3. Experiments on Preload Device
4. Novel Motion Platform
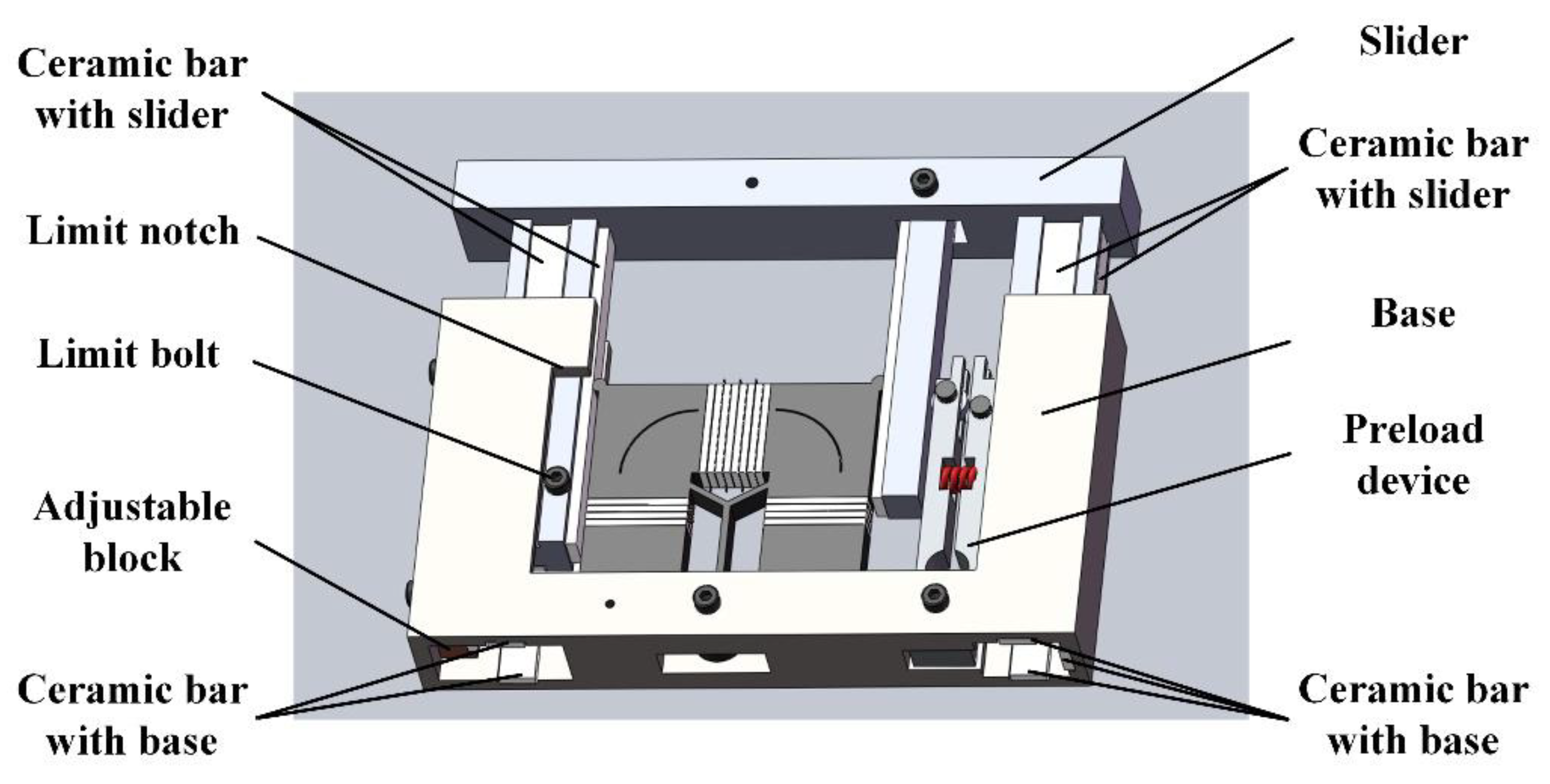
4.1. Structure of Motion Platform
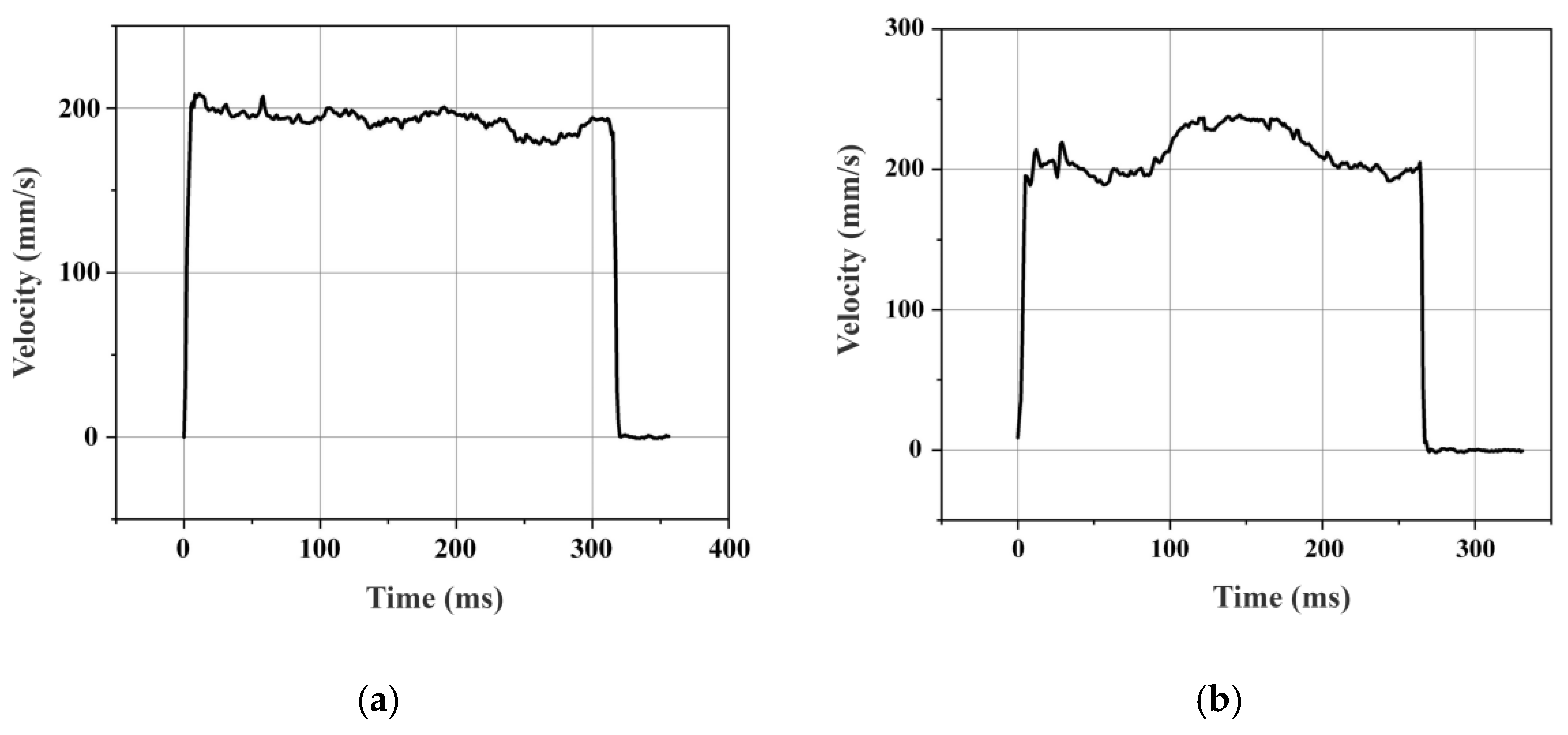
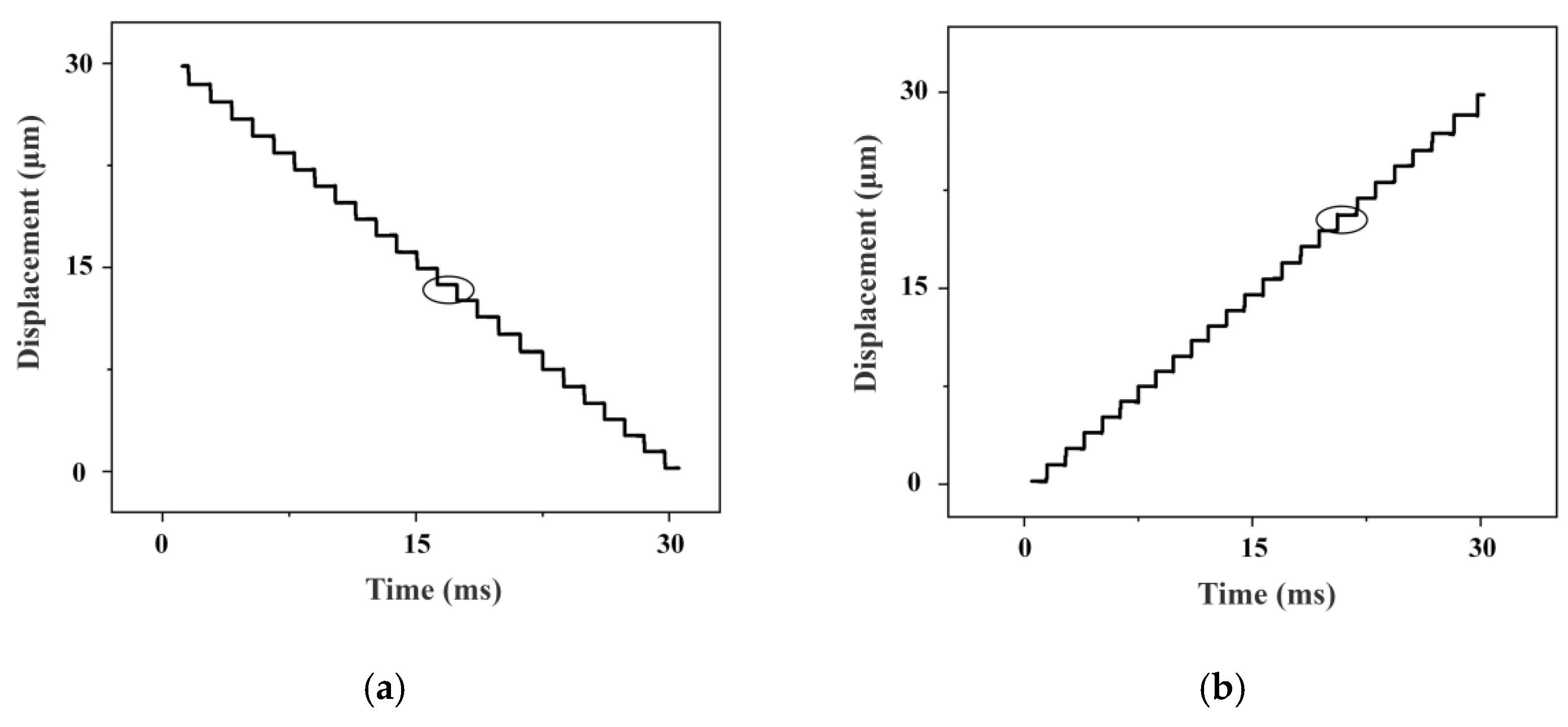
4.2. Experiments on Motion Platform
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, P.; Chen, W.; Deng, J.; Zhang, S.; Zhang, J.; Liu, Y. A critical review of piezoelectric ultrasonic transducers for ultrasonic-assisted precision machining. Ultrasonics 2023, 135, 18. [Google Scholar] [CrossRef] [PubMed]
- Ghafarian, M.; Shirinzadeh, B.; Al-Jodah, A.; Das, T.K.; Wei, W.; Tian, Y.; Zhang, D. An XYZ micromanipulator for precise positioning applications. J. Micro-Bio Robot. 2020, 16, 53–63. [Google Scholar] [CrossRef]
- Bansevicius, R.; Mazeika, D.; Jurenas, V.; Kulvietis, G.; Drukteiniene, A.; Wallaschek, J. Multi-DOF Ultrasonic Actuators for Laser Beam Positioning. Shock Vib. 2019, 2019, 4919505. [Google Scholar] [CrossRef]
- Wang, R.; Wu, H.; Wang, H.; Zhang, X. Design and stiffness modeling of a four-degree-of-freedom nanopositioning stage based on six-branched-chain compliant parallel mechanisms. Rev. Sci. Instrum. 2020, 91, 065002. [Google Scholar] [CrossRef]
- Zhao, C. Ultrasonic Motors: Technologies and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Watson, B.; Friend, J.; Yeo, L. Piezoelectric ultrasonic micro/milli-scale actuators. Sens. Actuators A Phys. 2009, 152, 219–233. [Google Scholar] [CrossRef]
- Tian, X.; Liu, Y.; Deng, J.; Wang, L.; Chen, W. A review on piezoelectric ultrasonic motors for the past decade: Classification, operating principle, performance, and future work perspectives. Sens. Actuators A Phys. 2020, 306, 111971. [Google Scholar] [CrossRef]
- Mohith, S.; Upadhya, A.R.; Navin, K.P.; Kulkarni, S.M.; Rao, M. Recent trends in piezoelectric actuators for precision motion and their applications: A review. Smart Mater. Struct. 2020, 30, 013002. [Google Scholar] [CrossRef]
- Zhu, W.L.; Zhu, Z.; Shi, Y.; Wang, X.; Guan, K.; Ju, B.-F. Design, modeling, analysis and testing of a novel piezo-actuated XY compliant mechanism for large workspace nano-positioning. Smart Mater. Struct. 2016, 25, 115033. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.; Morita, T. Stepping piezoelectric actuators with large working stroke for nano-positioning systems: A review. Sens. Actuators A Phys. 2019, 292, 39–51. [Google Scholar] [CrossRef]
- Liu, Z.; Fu, Q.; Yang, P.; Dong, Z.; Zhang, L.; Yao, Z. Design and performance evaluation of a miniature I-shaped linear ultrasonic motor with two vibrators. Ultrasonics 2023, 131, 106965. [Google Scholar] [CrossRef]
- Ma, X.; Liu, J.; Deng, J.; Liu, Q.; Liu, Y. A Rotary Traveling Wave Ultrasonic Motor With Four Groups of Nested PZT Ceramics: Design and Performance Evaluation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 1462–1469. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Liu, Y.; Deng, J.; Chen, W.; Li, K. Design Philosophy for Ultrasonic Motors Using the Bending Hybrid Modes. Sens. Actuators A Phys. 2021, 331 (Suppl. S1), 113029. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J.A.; Jin, J.M.; Yang, L.; Wu, S.-W.; Zhou, C.C. Theoretical modeling, verification, and application study on a novel bending-bending coupled piezoelectric ultrasonic transducer. Mech. Syst. Signal Process. 2022, 168, 108644. [Google Scholar] [CrossRef]
- Jian, Y.; Liu, Z.; He, J.; Zhou, W.; Liang, H. Development of a Plate Linear Ultrasonic Motor Using the Power Flow Method. Micromachines 2024, 15, 1016. [Google Scholar] [CrossRef]
- Kuribayashi Kurosawa, M.; Kodaira, O.; Tsuchitoi, Y.; Higuchi, T. Transducer for high speed and large thrust ultrasonic linear motor using two sandwich-type vibrators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1998, 45, 1188–1195. [Google Scholar] [CrossRef]
- Li, X.; Yao, Z. Analytical modeling and experimental validation of a V-shape piezoelectric ultrasonic transducer. Smart Mater. Struct. 2016, 25, 075026. [Google Scholar] [CrossRef]
- Asumi, K.; Fukunaga, R.; Fujimura, T.; Kurosawa, M.K. High speed, high resolution ultrasonic linear motor using V-shape two bolt-clamped Langevin-type transducers. Acoust. Sci. Technol. 2009, 30, 180–186. [Google Scholar] [CrossRef]
- Asumi, K.; Fukunaga, R.; Fujimura, T.; Kurosawa, M.K. Miniaturization of a V-Shape Transducer Ultrasonic Motor. Jpn. J. Appl. Phys. 2009, 48, 07GM02. [Google Scholar] [CrossRef]
- Jeong, S.S.; Park, T.G.; Kim, M.H.; Song, T.-K. Characteristics of a V-type ultrasonic rotary motor. Curr. Appl. Phys. 2011, 11, S364–S367. [Google Scholar] [CrossRef]
- Zhang, H.; Dong, S.X.; Zhang, S.Y.; Wang, T.-H.; Zhang, Z.-N.; Fan, L. Ultrasonic micro-motor using miniature piezoelectric tube with diameter of 1.0 mm. Ultrasonics 2006, 44, e603–e606. [Google Scholar] [CrossRef]
- Takano, M.; Takimoto, M.; Nakamura, K. Electrode design of multilayered piezoelectric transducers for longitudinal-bending ultrasonic actuators. Acoust. Sci. Technol. 2011, 32, 100–108. [Google Scholar] [CrossRef][Green Version]
- Xin, X.; Gao, X.; Wu, J.; Li, Z.; Chu, Z.; Dong, S. A ring-shaped, linear piezoelectric ultrasonic motor operating in E01 mode. Appl. Phys. Lett. 2020, 116, 152902. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Y.; Jin, D.; Zhou, M. A Review of Single-Cell Pose Adjustment and Puncture. Adv. Intell. Syst. 2022, 4, 2200096. [Google Scholar] [CrossRef]
- Masuda, N.; Izuhara, S.; Mashimo, T. Miniature camera module with a hollow linear ultrasonic motor-based focus feature. Sens. Actuators A Phys. 2023, 354, 114248. [Google Scholar] [CrossRef]
- Tu, Y.; Peng, F.; Wilson, D.A. Motion Manipulation of Micro- and Nanomotors. Adv. Mater. 2017, 29, 1701970. [Google Scholar] [CrossRef]
- Zhu, Z.; To, S.; Ehmann, K.F.; Zhou, X. Design, analysis, and realization of a novel piezoelectrically actuated rotary spatial vibration system for micro-/nanomachining. IEEE/ASME Trans. Mechatron. 2017, 22, 1227–1237. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Sun, W.; Wang, K.; Yang, Z.; Liang, T.; Huang, H. A compact 2-DOF piezo-driven positioning stage designed by using the parasitic motion of flexure hinge mechanism. Smart Mater. Struct. 2020, 29, 015022. [Google Scholar] [CrossRef]
- Li, J.; Liu, H.; Zhao, H. A Compact 2-DOF Piezoelectric-Driven Platform Based on “Z-Shaped” Flexure Hinges. Micromachines 2017, 8, 245. [Google Scholar] [CrossRef]
- Jian, Y.; Yao, Z.; Liu, Z.; Zhang, B. A novel Π -type linear ultrasonic motor driven by a single mode. Rev. Sci. Instrum. 2018, 89, 125010. [Google Scholar] [CrossRef]
- Jian, Y.; Yao, Z.; Silberschmidt, V.V. Linear Ultrasonic Motor for Absolute Gravimeter. Ultrasonics 2017, 77, 88–94. [Google Scholar] [CrossRef]
- Lobontiu, N.; Garcia, E. Analytical model of displacement amplification and stiffness optimization for a class of flexure-based compliant mechanisms. Comput. Struct. 2003, 81, 2797–2810. [Google Scholar] [CrossRef]
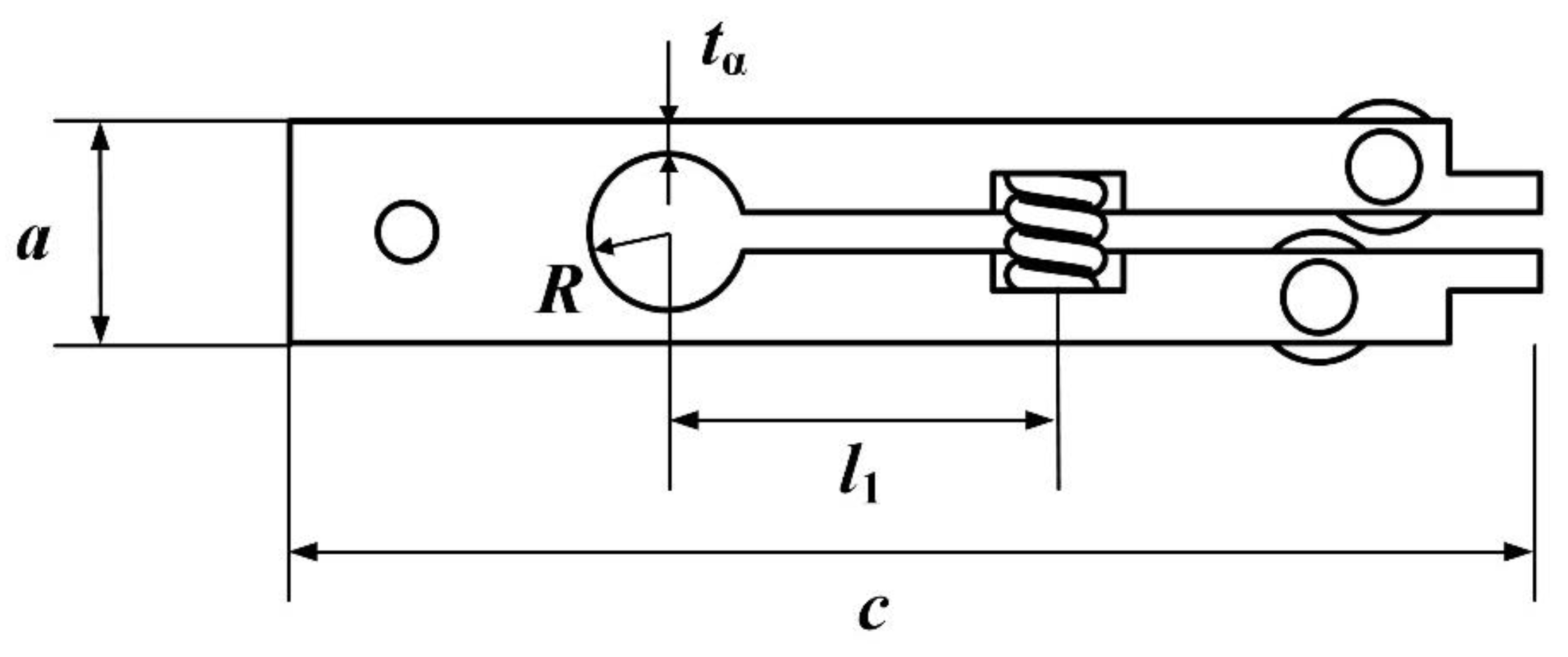



| Parameters | a | b | c | l1 | R | tα |
|---|---|---|---|---|---|---|
| Values | 17 | 10 | 96 | 30 | 6 | 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jian, Y.; Liu, Z.; Yao, P.; Zhou, W.; He, J.; Liang, H. A Novel Motion Platform Based on Dual Driving Feet Linear Ultrasonic Motor. Micromachines 2025, 16, 1039. https://doi.org/10.3390/mi16091039
Jian Y, Liu Z, Yao P, Zhou W, He J, Liang H. A Novel Motion Platform Based on Dual Driving Feet Linear Ultrasonic Motor. Micromachines. 2025; 16(9):1039. https://doi.org/10.3390/mi16091039
Chicago/Turabian StyleJian, Yue, Zhen Liu, Ping Yao, Wenjie Zhou, Junfeng He, and Huazhuo Liang. 2025. "A Novel Motion Platform Based on Dual Driving Feet Linear Ultrasonic Motor" Micromachines 16, no. 9: 1039. https://doi.org/10.3390/mi16091039
APA StyleJian, Y., Liu, Z., Yao, P., Zhou, W., He, J., & Liang, H. (2025). A Novel Motion Platform Based on Dual Driving Feet Linear Ultrasonic Motor. Micromachines, 16(9), 1039. https://doi.org/10.3390/mi16091039






