Integrated Additive Manufacturing of TGV Interconnects and High-Frequency Circuits via Bipolar-Controlled EHD Jetting
Abstract
1. Introduction
2. Methods
2.1. EHD Filling and Printing Scheme
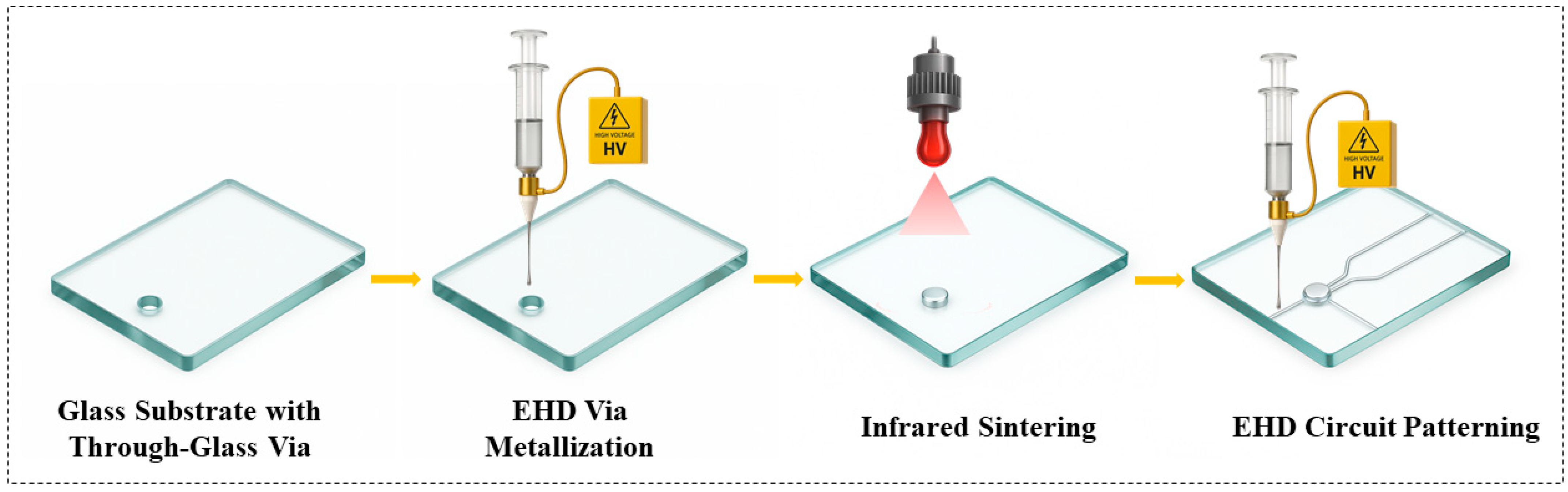
2.2. Process Workflow
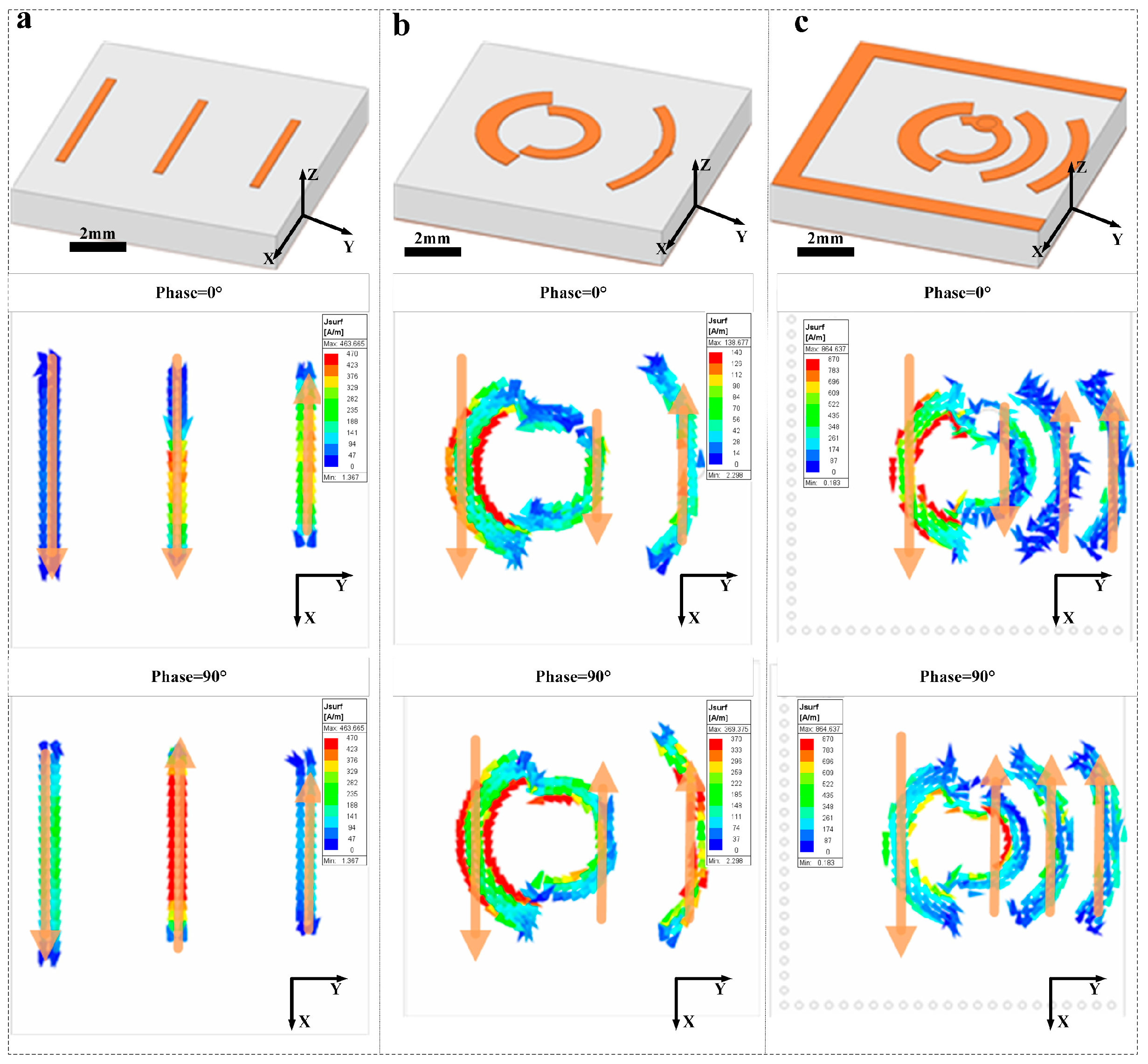
2.3. SIW Antenna Design Methodology
3. Results and Discussion
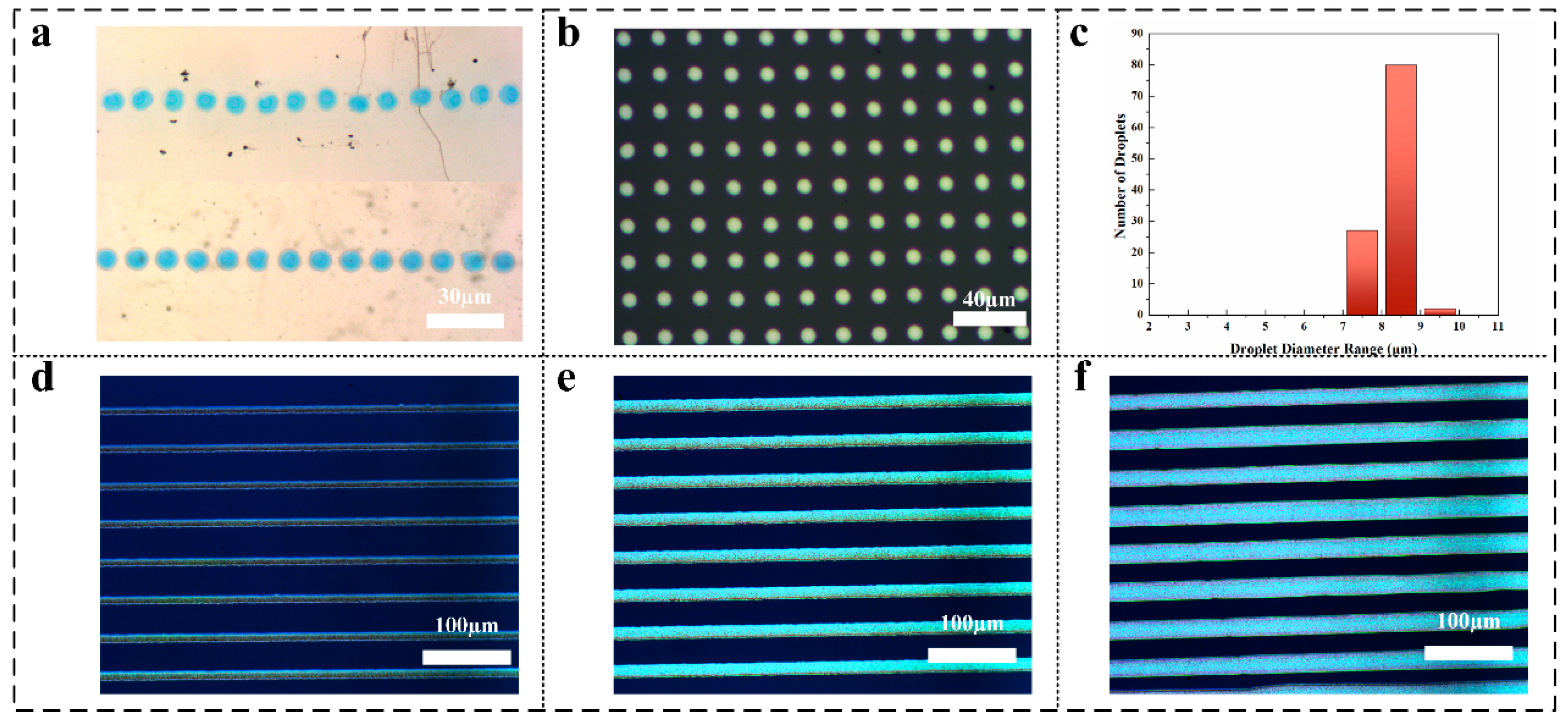
3.1. TGV Filling Performance Optimization
3.2. EHD Drop-on-Demand Printing with PWM Control
3.3. Printed Antenna and Performance Validation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Taylor, G.I. Disintegration of water drops in an electric field. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1964, 280, 383–397. [Google Scholar]
- Melcher, J.R.; Taylor, G.I. Electrohydrodynamics: A review of the role of interfacial shear stresses. Annu. Rev. Fluid Mech. 1969, 1, 111–146. [Google Scholar] [CrossRef]
- Taylor, G.I. Electrically driven jets. Proc. R. Soc. Lond. A Math. Phys. Sci. 1969, 313, 453–475. [Google Scholar]
- An, S.; Lee, M.W.; Kim, N.Y.; Lee, C.; Al-Deyab, S.S.; James, S.C.; Yoon, S.S. Effect of viscosity, electrical conductivity, and surface tension on direct-current-pulsed drop-on-demand electrohydrodynamic printing frequency. Appl. Phys. Lett. 2014, 105, 214102. [Google Scholar] [CrossRef]
- Kim, S.H.; Kang, H.; Kang, K.; Lee, S.H.; Cho, K.H.; Hwang, J.Y. Effect of meniscus damping ratio on drop-on-demand electrohydrodynamic jetting. Appl. Sci. 2018, 8, 164. [Google Scholar] [CrossRef]
- Yin, Z.; Wang, D.; Guo, Y.; Zhao, Z.; Li, L.; Chen, W.; Duan, Y. Electrohydrodynamic printing for high resolution patterning of flexible electronics toward industrial applications. InfoMat 2024, 6, e12505. [Google Scholar] [CrossRef]
- Mkhize, N.; Bhaskaran, H. Electrohydrodynamic jet printing: Introductory concepts and considerations. Small Sci. 2022, 2, 2100073. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, G.; Zhang, J.; Song, D.; Guo, C.; Zhou, W.; Fu, Z.; Zhu, X.; Wang, F.; Duan, Y.; et al. Advanced multi-nozzle electrohydrodynamic printing: Mechanism, processing, and diverse applications at micro/nano-scale. Int. J. Extrem. Manuf. 2024, 7, 012008. [Google Scholar] [CrossRef]
- Jiang, Y.; Ye, D.; Li, A.; Zhang, B.; Han, W.; Niu, X.; Zeng, M.; Guo, L.; Zhang, G.; Yin, Z.; et al. Transient charge-driven 3D conformal printing via pulsed-plasma impingement. Proc. Natl. Acad. Sci. USA 2024, 121, e2402135121. [Google Scholar] [CrossRef]
- Chaloun, T.; Brandl, S.; Ambrosius, N.; Kröhnert, K.; Maune, H.; Waldschmidt, C. RF glass technology is going mainstream: Review and future applications. IEEE J. Microw. 2023, 3, 783–799. [Google Scholar] [CrossRef]
- Hu, P.F.; Leung, K.W.; Luk, K.M.; Pan, Y.M.; Zheng, S.Y. Diversity glass antennas for tri-band WiFi applications. Engineering 2023, 23, 157–169. [Google Scholar] [CrossRef]
- Jang, D.; Kong, N.K.; Choo, H. Design of an on-glass 5G monopole antenna for a vehicle window glass. IEEE Access 2021, 9, 152749–152755. [Google Scholar] [CrossRef]
- Su, Y.; Yu, D.; Ruan, W.; Jia, N. Development of compact millimeter-wave antenna by stacking of five glass wafers with through glass vias. IEEE Electron Device Lett. 2022, 43, 934–937. [Google Scholar] [CrossRef]
- Morimoto, Y.; Shiu, S.; Huang, I.W.; Fest, E.; Ye, G.; Zhu, J. Optically transparent antenna for smart glasses. IEEE Open J. Antennas Propag. 2023, 4, 159–167. [Google Scholar] [CrossRef]
- Hussain, H.; Khalil, S.M.; Cho, D.H.; Byun, D. Void-less metallization of high aspect ratio through glass via using electrohydrodynamic drop-on-demand printing. J. Manuf. Process. 2024, 131, 2029–2036. [Google Scholar] [CrossRef]
- Gong, H.; Huang, J.; Wang, J.; Liang, C.; Guo, W.; Cao, R. Characterization of electrohydrodynamic drop-on-demand injection of viscoelastic fluids in pulsed voltage. J. Manuf. Process. 2023, 94, 255–265. [Google Scholar] [CrossRef]
- Gong, H.; Huang, J.; Zhang, J.; Cao, Y.; Wang, J.; Zhao, P.; Liang, C.; Bai, D. Generation of neutral droplets via waveform optimization for stable electrohydrodynamic drop-on-demand printing. J. Manuf. Process. 2024, 112, 103–111. [Google Scholar] [CrossRef]
- Guan, Y.; Wu, S.; Wang, M.; Tian, Y.; Yu, C.; Lai, W.; Huang, Y. Numerical investigation of high-frequency pulsating electrohydrodynamic jet at low electric Bond numbers. Phys. Fluids 2022, 34, 012001. [Google Scholar] [CrossRef]
- Bajpai, V.K.; Mishra, D.K.; Dixit, P. Fabrication of Through-glass Vias (TGV) based 3D microstructures in glass substrate by a lithography-free process for MEMS applications. Appl. Surf. Sci. 2022, 584, 152494. [Google Scholar] [CrossRef]
- Yang, F.; Wang, Q.; Lee, J.; Song, Y.; Hwang, I.; Yoon, S.; Yoo, B. Silicon dioxide (SiO2) solid blocking layer on through-glass via surface for efficient highly selective copper filling. Surf. Interfaces 2024, 55, 105431. [Google Scholar] [CrossRef]
- Sung, M.; Lee, Y.; Lee, M.; Jeon, Y.; Lim, T.; Kim, Y.G.; Kim, J.J. Polyethylene glycol-based single organic additive for through silicon via filling and its structural modification effect. J. Electrochem. Soc. 2021, 168, 012506. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, J.; Lei, Z.; Mou, Y.; Chen, M. Computational and experiments exploration of convection on Cu filling characteristics of multiple aspect-ratio micro through-holes. Electrochim. Acta 2022, 416, 140218. [Google Scholar] [CrossRef]
- Li, Y.; Bian, J.; Ji, M.; Wang, Y.; Gu, W. A Through Glass Via (TGV) metallization strategy based on Electrohydrodynamic printing. J. Phys. Conf. Series. 2025, 2954, 012065. [Google Scholar] [CrossRef]
- Lin, Y. Two-phase electro-hydrodynamic flow modeling by a conservative level set model. Electrophoresis 2013, 34, 736–744. [Google Scholar] [CrossRef] [PubMed]
- Cadiou, S.; Courtois, M.; Carin, M.; Berckmans, W. 3D heat transfer, fluid flow and electromagnetic model for cold metal transfer wire arc additive manufacturing (Cmt-Waam). Addit. Manuf. 2020, 36, 101541. [Google Scholar] [CrossRef]
- Liu, H.; Wu, H.; Yang, D.; Chen, J.; Wang, J. A study of the temperature effect on the spray characteristics in the cone-jet mode of electrohydrodynamic atomization (EHDA) with viscous liquids. Phys. Fluids 2023, 35, 043338. [Google Scholar] [CrossRef]
- Xiao, S.; Zheng, C.; Li, M.; Xiong, J.; Wang, B.Z. Varactor-loaded pattern reconfigurable array for wide-angle scanning with low gain fluctuation. IEEE Trans. Antennas Propag. 2015, 63, 2364–2369. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, D.; Huang, J.; Gong, H.; Wang, J.; Pu, Y.; Zhang, J.; Sun, P.; Zhu, Z.; Li, P.; Wang, H.; et al. Integrated Additive Manufacturing of TGV Interconnects and High-Frequency Circuits via Bipolar-Controlled EHD Jetting. Micromachines 2025, 16, 907. https://doi.org/10.3390/mi16080907
Bai D, Huang J, Gong H, Wang J, Pu Y, Zhang J, Sun P, Zhu Z, Li P, Wang H, et al. Integrated Additive Manufacturing of TGV Interconnects and High-Frequency Circuits via Bipolar-Controlled EHD Jetting. Micromachines. 2025; 16(8):907. https://doi.org/10.3390/mi16080907
Chicago/Turabian StyleBai, Dongqiao, Jin Huang, Hongxiao Gong, Jianjun Wang, Yunna Pu, Jiaying Zhang, Peng Sun, Zihan Zhu, Pan Li, Huagui Wang, and et al. 2025. "Integrated Additive Manufacturing of TGV Interconnects and High-Frequency Circuits via Bipolar-Controlled EHD Jetting" Micromachines 16, no. 8: 907. https://doi.org/10.3390/mi16080907
APA StyleBai, D., Huang, J., Gong, H., Wang, J., Pu, Y., Zhang, J., Sun, P., Zhu, Z., Li, P., Wang, H., Zhao, P., & Liang, C. (2025). Integrated Additive Manufacturing of TGV Interconnects and High-Frequency Circuits via Bipolar-Controlled EHD Jetting. Micromachines, 16(8), 907. https://doi.org/10.3390/mi16080907





