Investigation and Application of Key Alignment Parameters for Overlay Accuracy in 3D Structures
Abstract
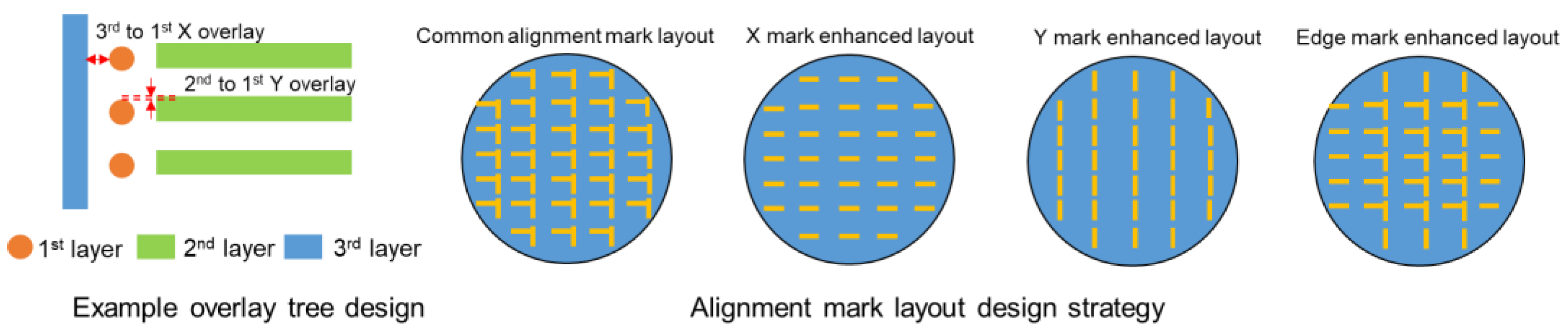
1. Introduction
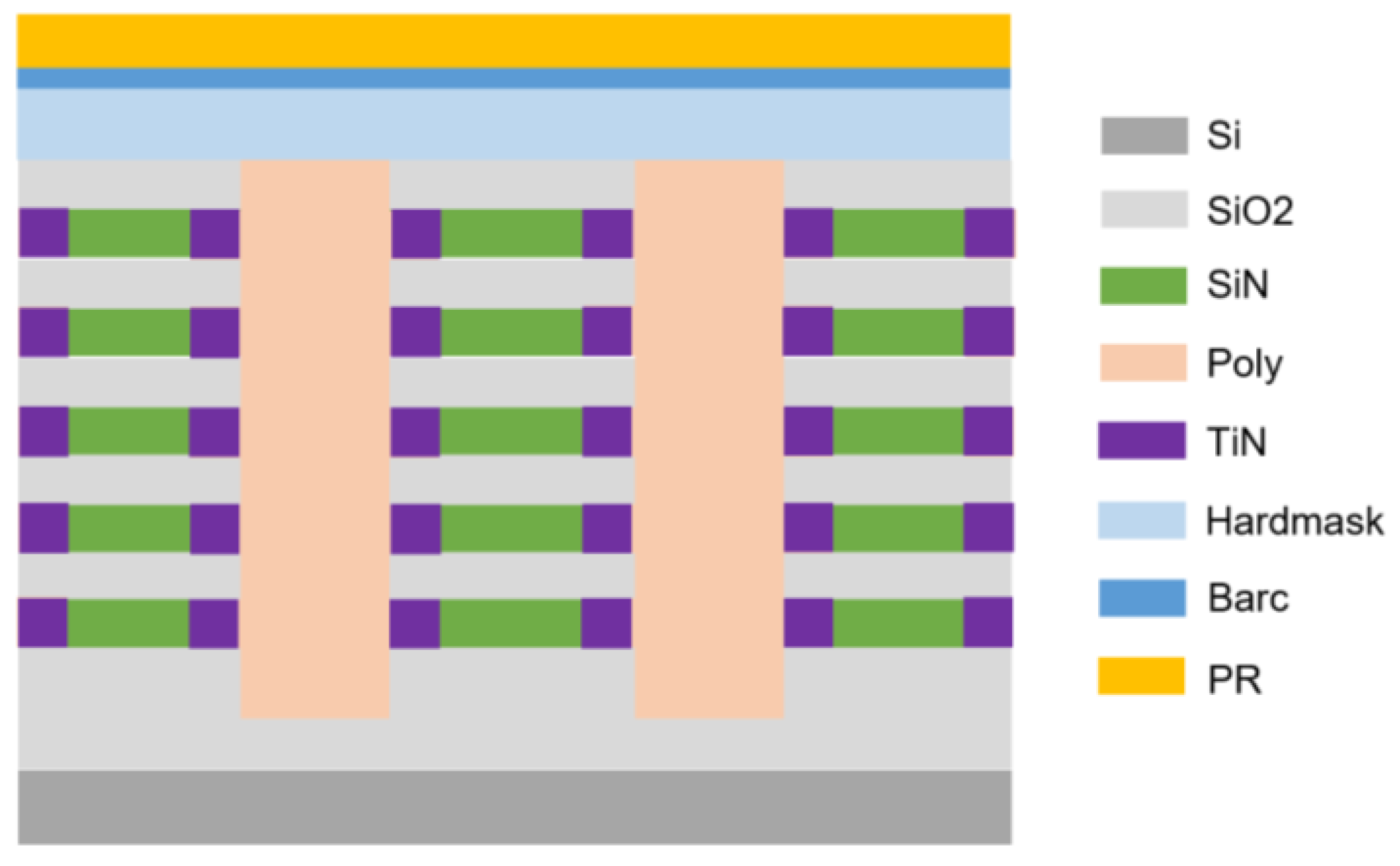
2. Experimental Design
3. Experimental Results
3.1. Polarization Selection
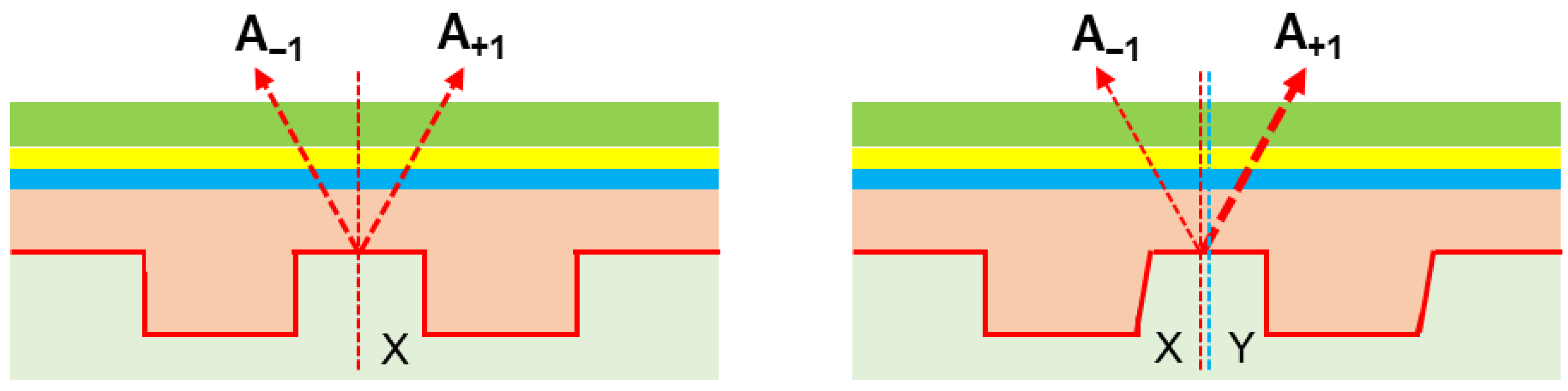
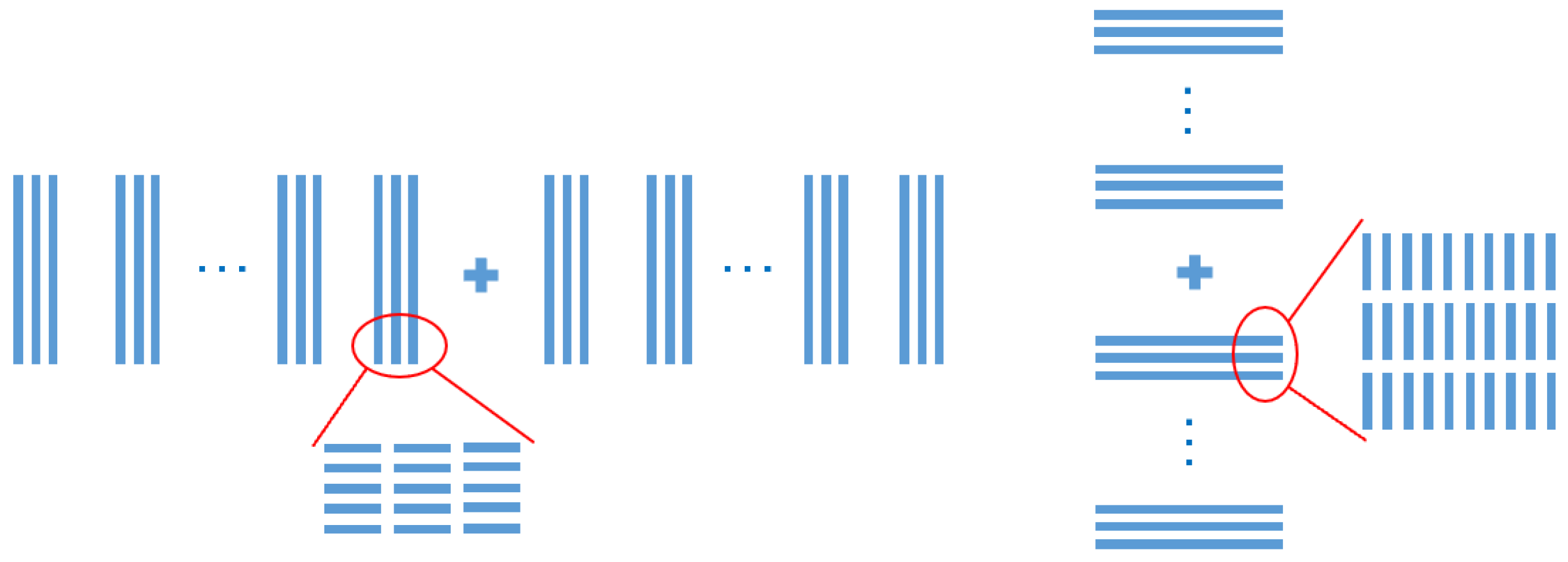
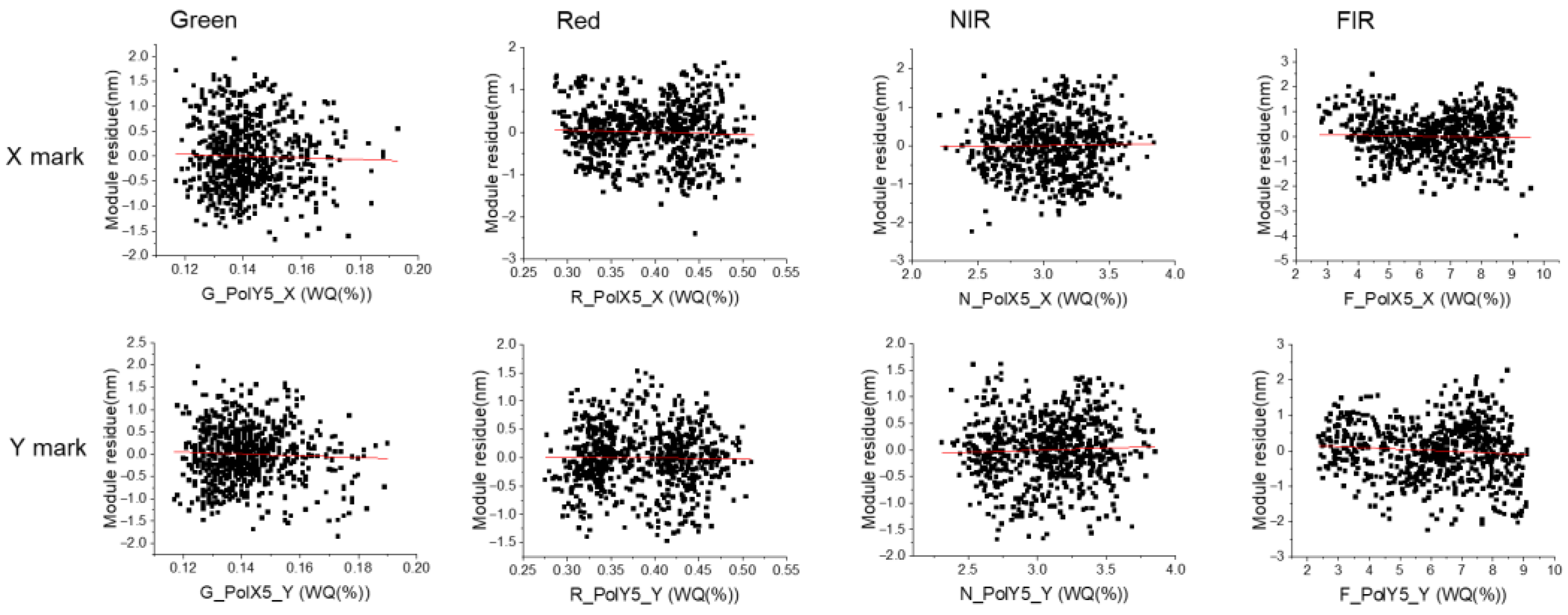
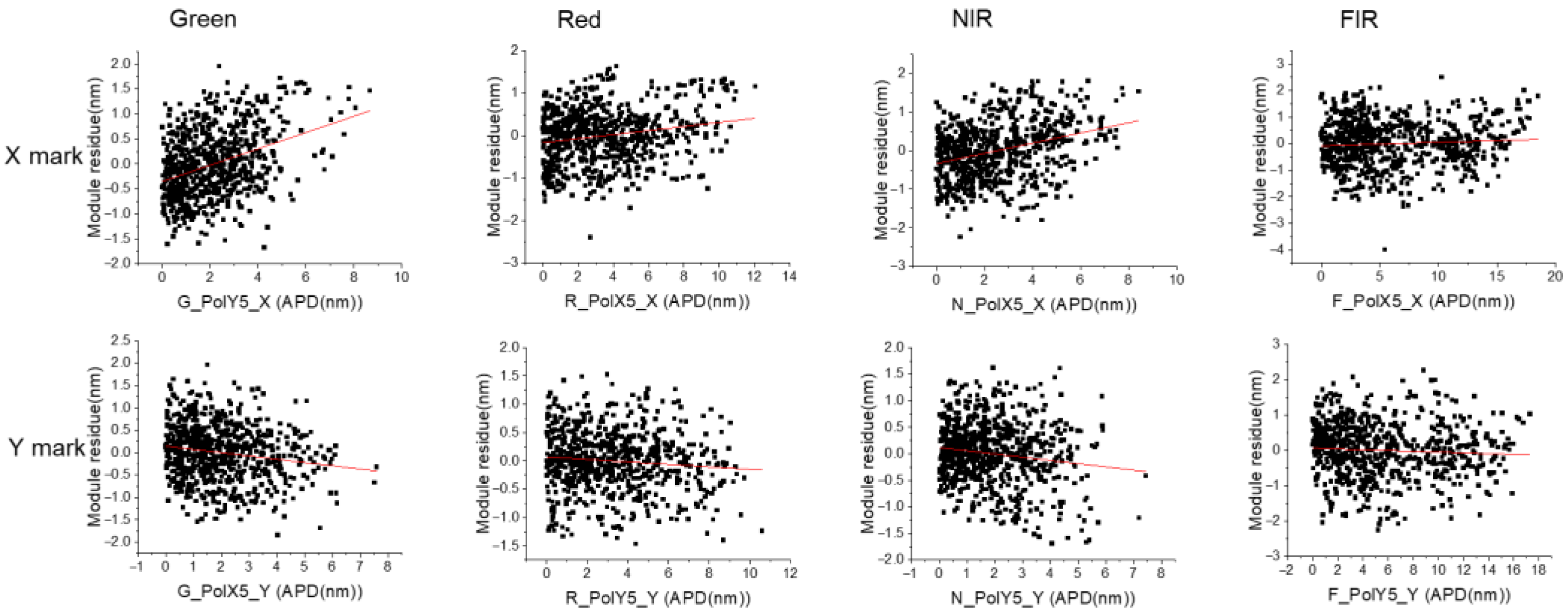
3.2. Alignment Key Parameter Analysis
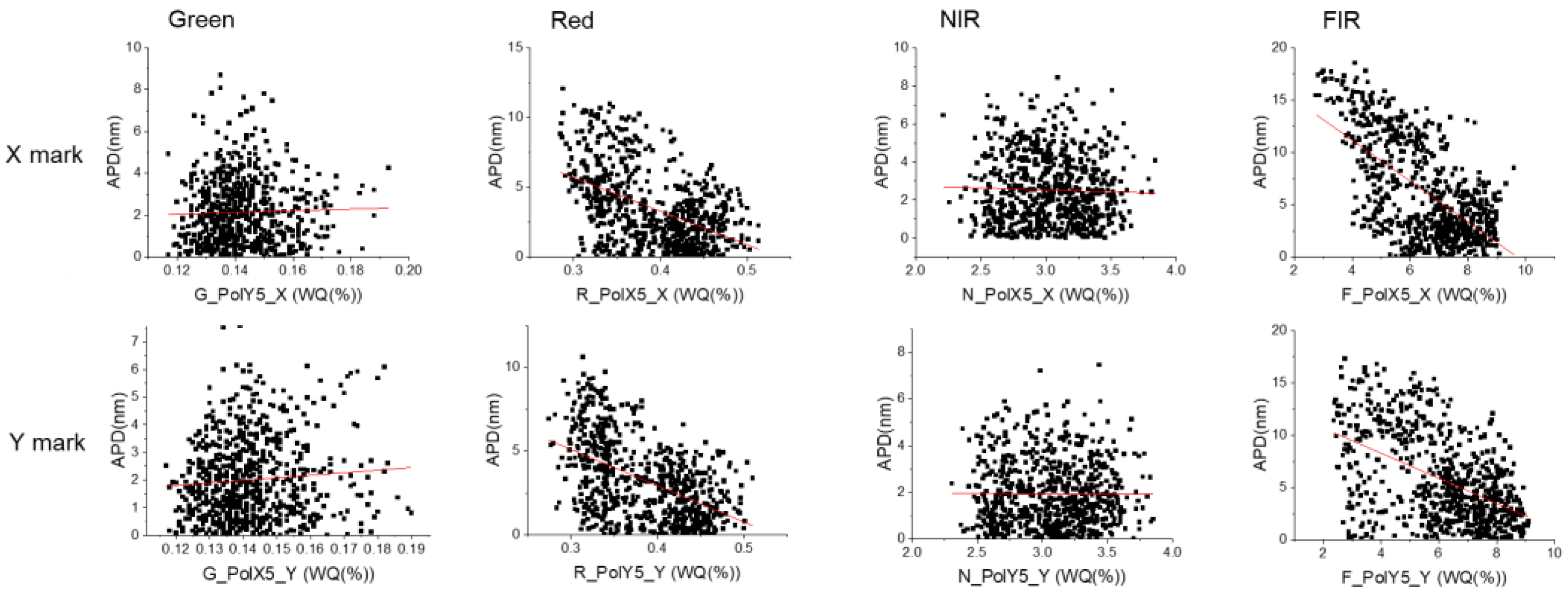
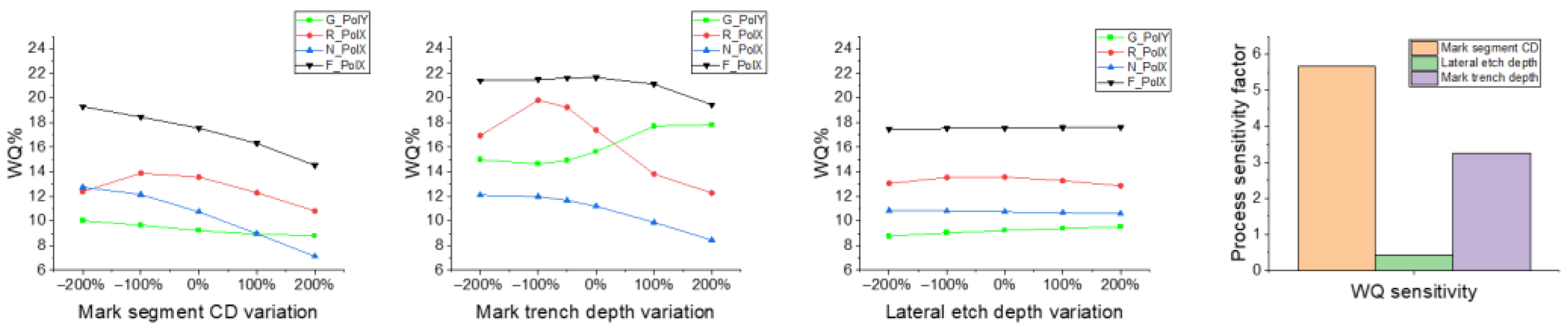
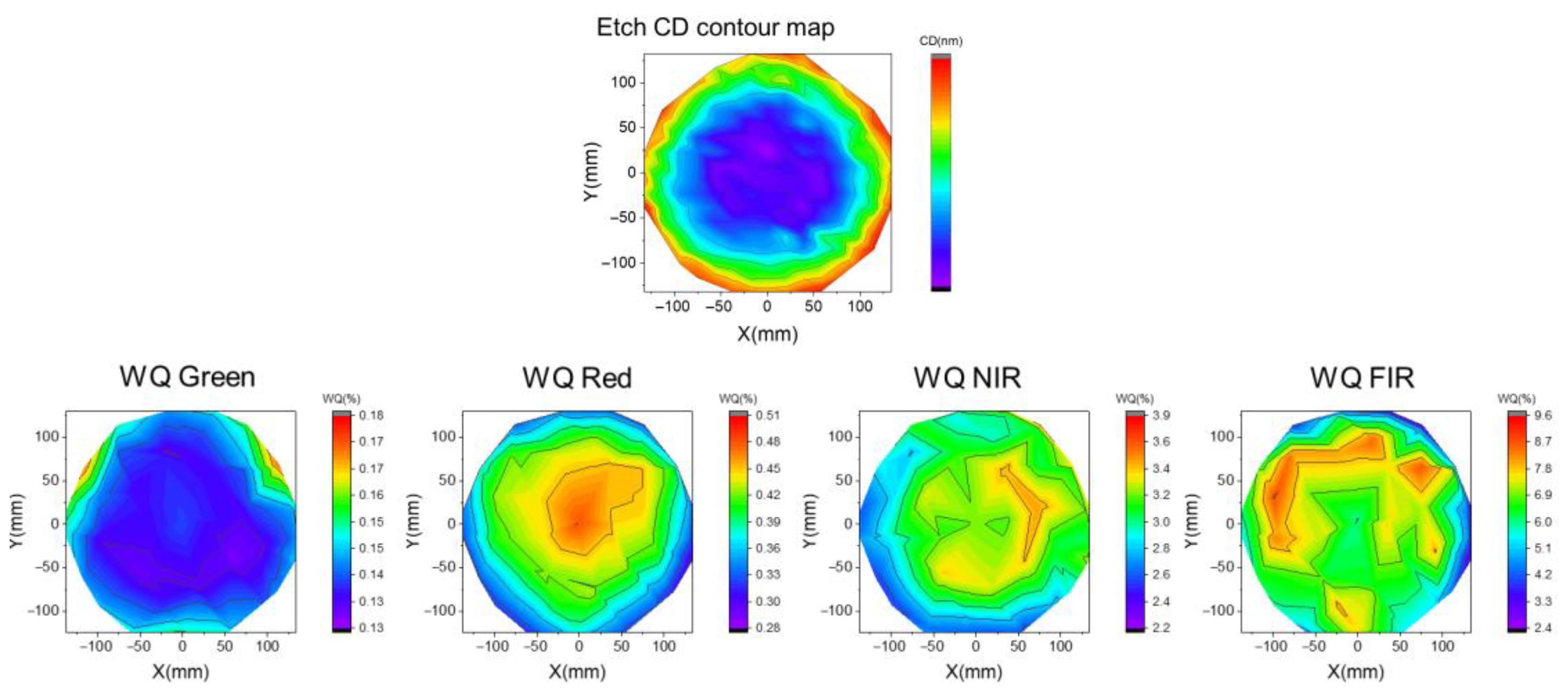
3.3. WQ Impact Factors
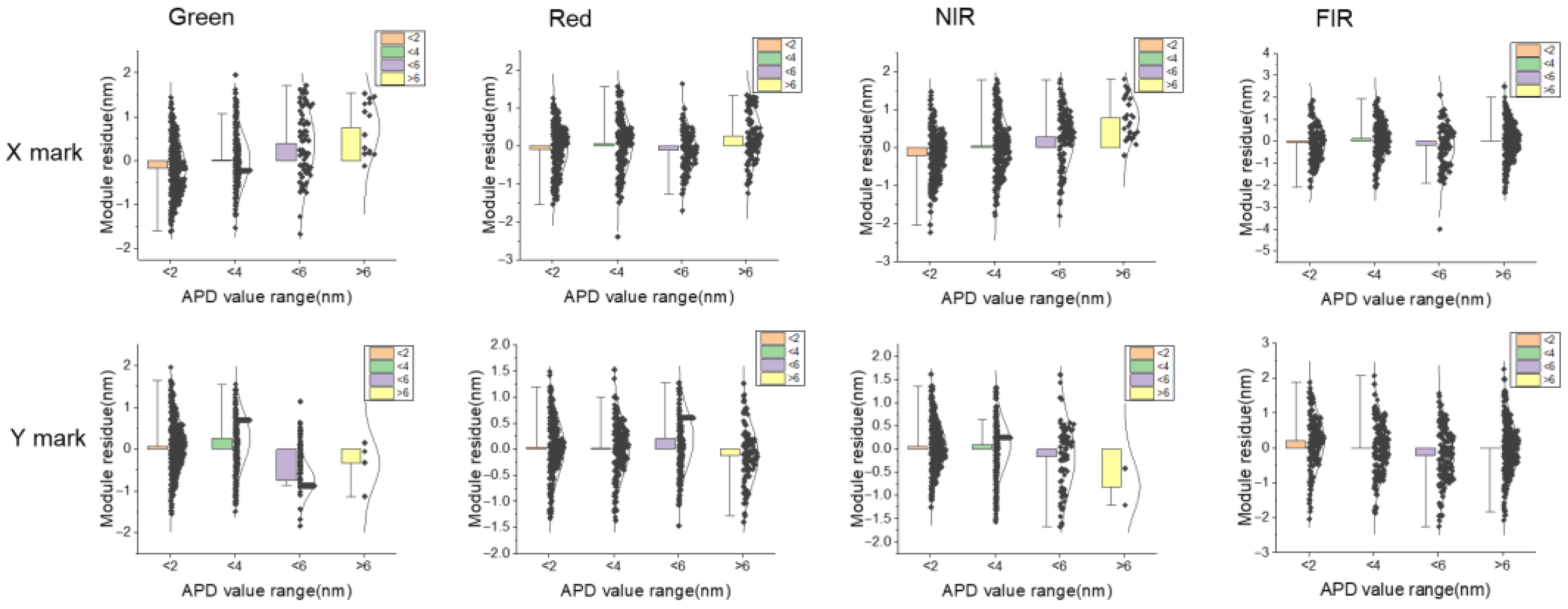
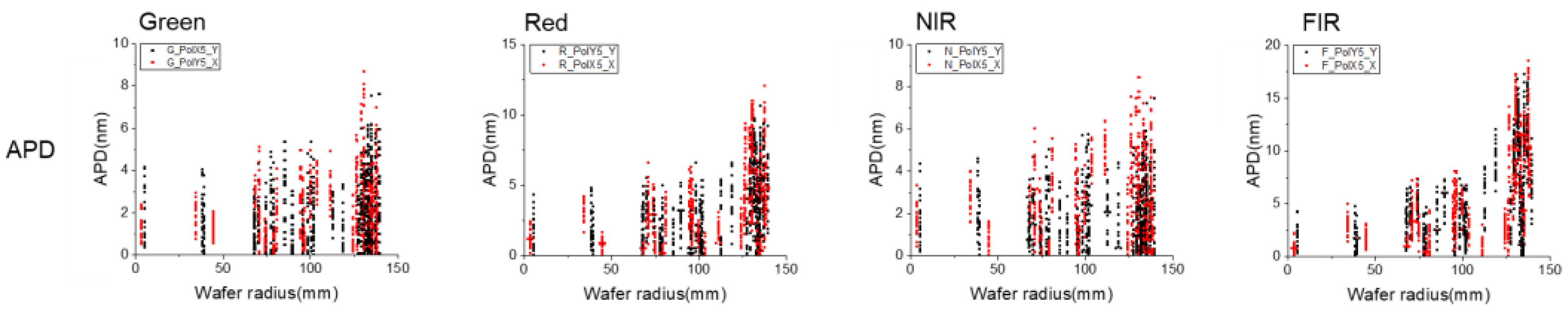
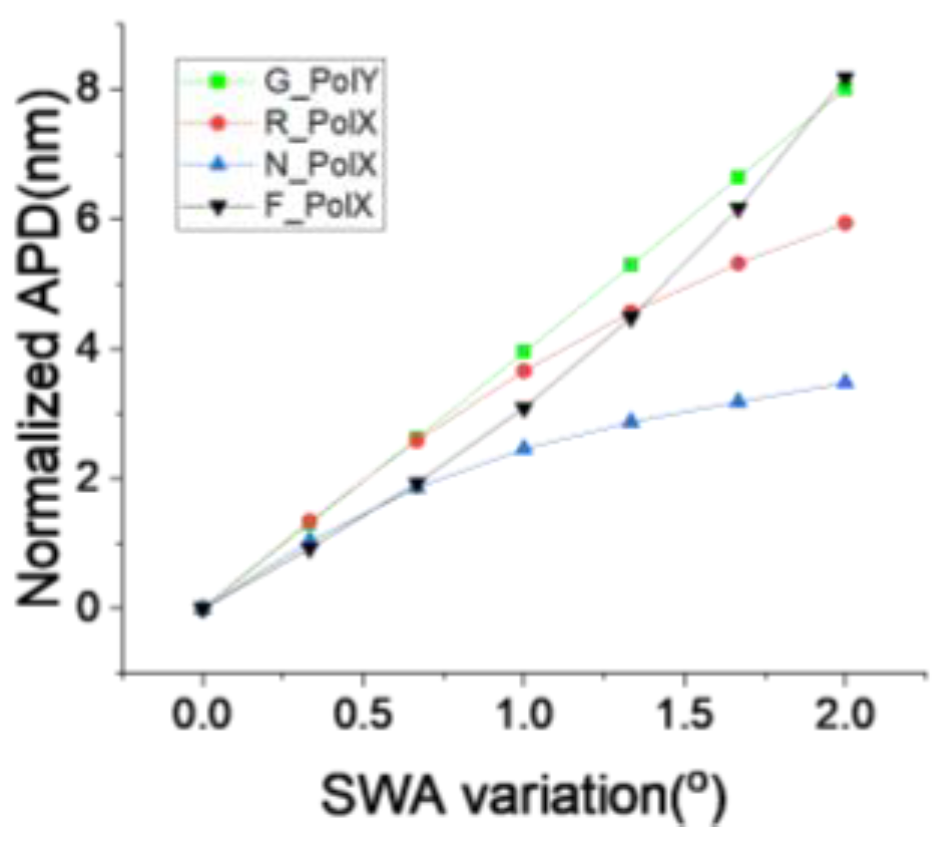
3.4. APD Improvement Investigation
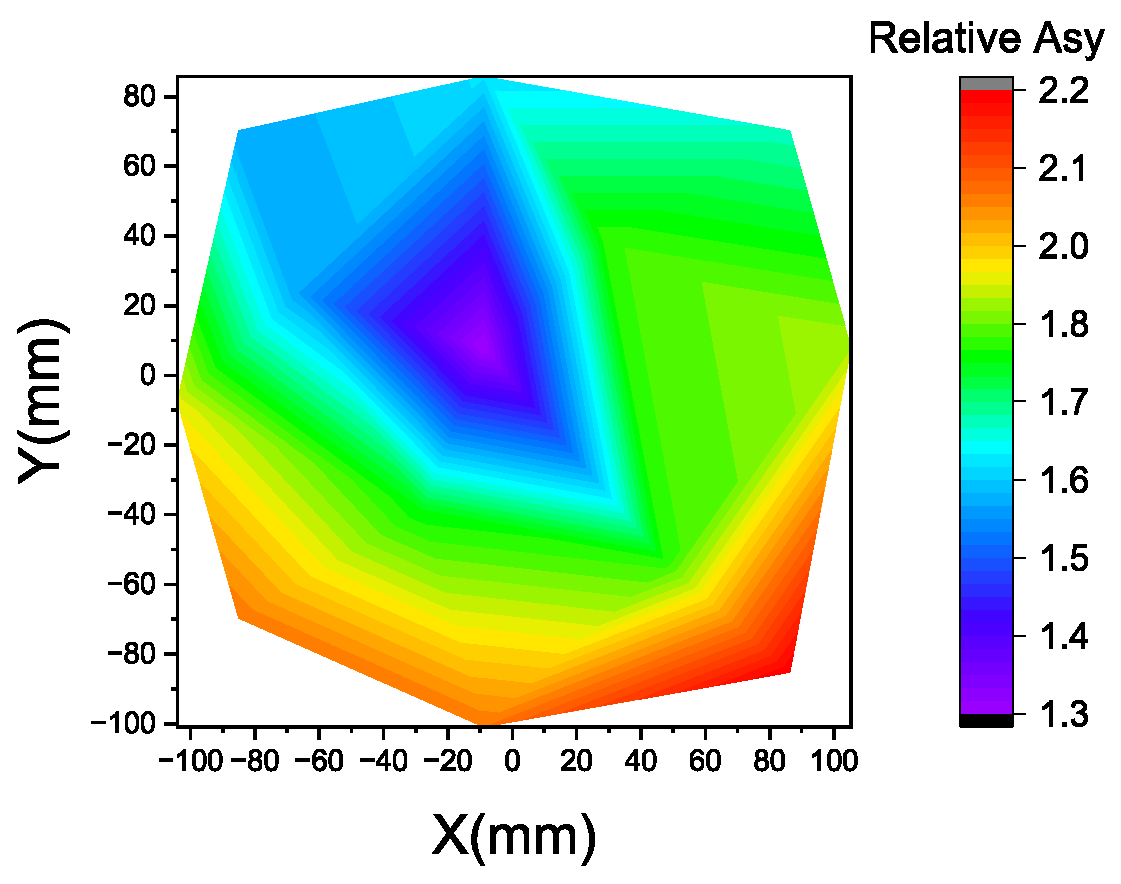
4. Discussion of Applications of Key Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wei, Y.Y. Advanced Lithography Theory and Application of Very Large Scale Integrated Circuits; Science Press: Beijing, China, 2016; pp. 311–313. [Google Scholar]
- Shin, J.; Kang, H.; Choi, S.; Woo, S.; Kim, H.; Lee, S.; Lee, J.; Kang, C.-J. Study of process contributions to total overlay error budget for sub-60-nm memory devices. J. Vac. Sci. Technol. B Microelectron. Process. Phenom. 2007, 25, 2444–2446. [Google Scholar] [CrossRef]
- Zhou, G.Y.; Qi, Y.J.; Li, L. Robustness Analysis Method and Simulation Research of Alignment Mark. Acta Opt. Sin. 2023, 43, 1113002. [Google Scholar]
- Li, D.; Zhang, S.; Chen, C.-H.; Zhang, Y.; Huang, A.; Xu, D.; Wang, Y.; Shi, Z.; Wang, S.-L.; Tsao, S.-T.; et al. Robust alignment mark design for DRAM using a holistic computational approach. In Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 26–27 February 2019; 109610Z. pp. 1–3. [Google Scholar]
- Blanco Carballo, V.M.; Canga, E.; Jehoul, C.; Moussa, A.; Tamaddon, A.H.; Tabery, C.; Gunjala, G.; Menchtchikov, B.; Zacca, V.G.; Lalbahadoersing, S.; et al. Alignment and Overlay through Opaque Metal Layers. In Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 26 February–2 March 2023; 124960I. pp. 2–3. [Google Scholar]
- Menchtchikov, B.; Socha, R.; Zheng, C.; Raghunathan, S.; Aarts, I.; Shome, K.; Lee, J.; de Ruiter, C.; Rijpstra, M.; Megens, H.; et al. Reduction in overlay error from mark asymmetry using simulation, ORION, and alignment models. In Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 27 February–1 March 2018; 105870C. p. 1. [Google Scholar]
- Boris, M.; Robert, S.; Sudharshanan, R.; Irina, L.; Hielke, S.; Patrick, T.; Paul, T.; Philippe, L.; Christiane, J. Computational Scanner Wafer Mark Alignment. In Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 28 February–2 March 2017; 101471C. pp. 1–9. [Google Scholar]
- Cho, H.; Chung, N.-Y.; Kim, J.; Kim, S.; Uh, S.; Kim, I.; Platt, J.; Menchtchikov, B.; Gu, N.; Rehman, S.U.; et al. Characterization of grating asymmetries through multicolor EUV alignment simulation: Process incoming analysis. In Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 24–27 February 2025; 134240P. pp. 1–6. [Google Scholar]
- Qiu, J.; Yang, G.; Li, J. Development and Challenges of Lithographical Alignment Technologies. Acta Opt. Sin. 2023, 43, 1900001. [Google Scholar]
- den Boef, A.J. Optical metrology of semiconductor wafers in lithography. In Proceedings of the International Conference on Optics in Precision Engineering and Nanotechnology, Singapore, 9–11 April 2013; 876907. p. 4. [Google Scholar]
- van Haren, R.; Calado, V.; van Dijk, L.; Hermans, J.; Kumar, K.; Yamashita, F. Wafer edge overlay control solution for N7 and beyond. In Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 26–28 February 2018; 105890D. p. 4. [Google Scholar]
- Cui, Y.; So, A.; Louks, S. Fine tune W-CMP process with alignment mark selection for optimal metal layer overlay and yield benefits. In Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 23–26 February 2004; pp. 1–3. [Google Scholar]
- Zhou, Y.; Zhou, G.; Jiang, M.; Yao, M.; Tian, E.; Song, G.; Cheng, X.; Wang, C.; Shi, J. Investigation of lateral etch impact to the segmented alignment marks. In Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 24–27 February 2025; 134263S. pp. 1–6. [Google Scholar]
- van Haren, R.; Otten, R.; Singh, S.; Singh, A.; van Dijk, L.; Owen, D.; Anberg, D.; Mileham, J.; Gu, Y.; Hermans, J. Intra-field stress impact on global wafer deformation. In Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 25–28 February 2019; 109591I. p. 2. [Google Scholar]
- Jeon, B.; Pal, S.; Mehta, S.; Lokesh, S.; Jiang, Y.T.; Li, C.; Yelverton, M.; Wei, Y. High order wafer alignment for 20nm node logic process. In Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 25–28 February 2013; 868110. p. 2. [Google Scholar]
- Zhou, G.; Qi, Y.; Yao, M.; Li, L.; Jiang, M.; Shi, J. Simulation study on the robustness of polar mark for incident light polarization states. In Proceedings of the Workshop on Advanced Patterning Solutions (IWAPS), Lishui, China, 26–27 October 2023; pp. 1–3. [Google Scholar]





| Incident Light | Wavelength | Polarization (Orion) | Polarization (SMASH) |
|---|---|---|---|
| Green | 532 nm | X/Y | Y |
| Red | 633 nm | X/Y | X |
| Near infrared (NIR) | 780 nm | X/Y | Y |
| Far infrared (FIR) | 852 nm | X/Y | X |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, M.; Yao, M.; Song, G.; Zhou, Y.; Su, J.; Qi, Y.; Shi, J. Investigation and Application of Key Alignment Parameters for Overlay Accuracy in 3D Structures. Micromachines 2025, 16, 876. https://doi.org/10.3390/mi16080876
Jiang M, Yao M, Song G, Zhou Y, Su J, Qi Y, Shi J. Investigation and Application of Key Alignment Parameters for Overlay Accuracy in 3D Structures. Micromachines. 2025; 16(8):876. https://doi.org/10.3390/mi16080876
Chicago/Turabian StyleJiang, Miao, Mingyi Yao, Ganlin Song, Yuxing Zhou, Jiani Su, Yuejing Qi, and Jiangliu Shi. 2025. "Investigation and Application of Key Alignment Parameters for Overlay Accuracy in 3D Structures" Micromachines 16, no. 8: 876. https://doi.org/10.3390/mi16080876
APA StyleJiang, M., Yao, M., Song, G., Zhou, Y., Su, J., Qi, Y., & Shi, J. (2025). Investigation and Application of Key Alignment Parameters for Overlay Accuracy in 3D Structures. Micromachines, 16(8), 876. https://doi.org/10.3390/mi16080876






