Optical Full Adder Based on Integrated Diffractive Neural Network
Abstract
1. Introduction
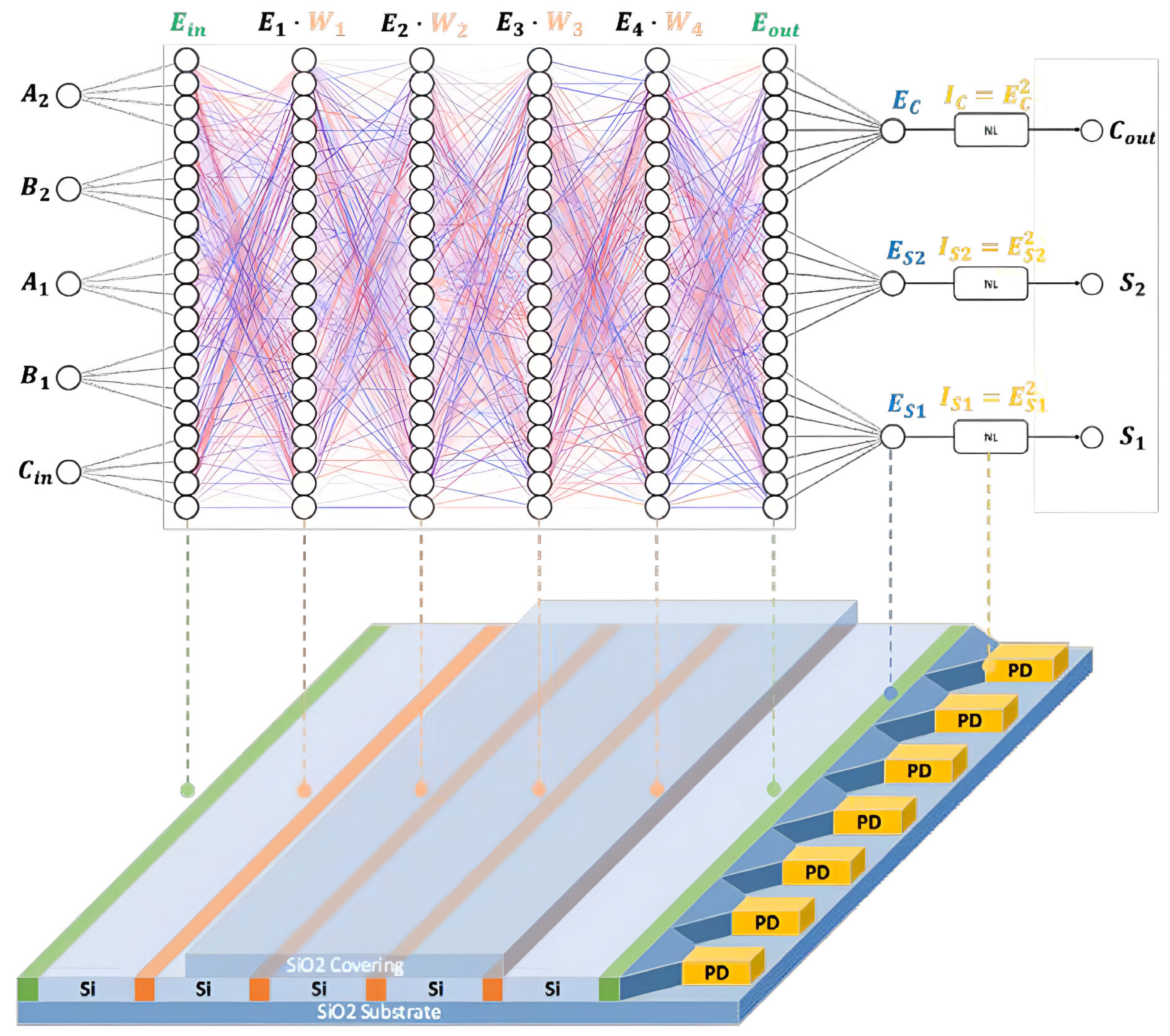
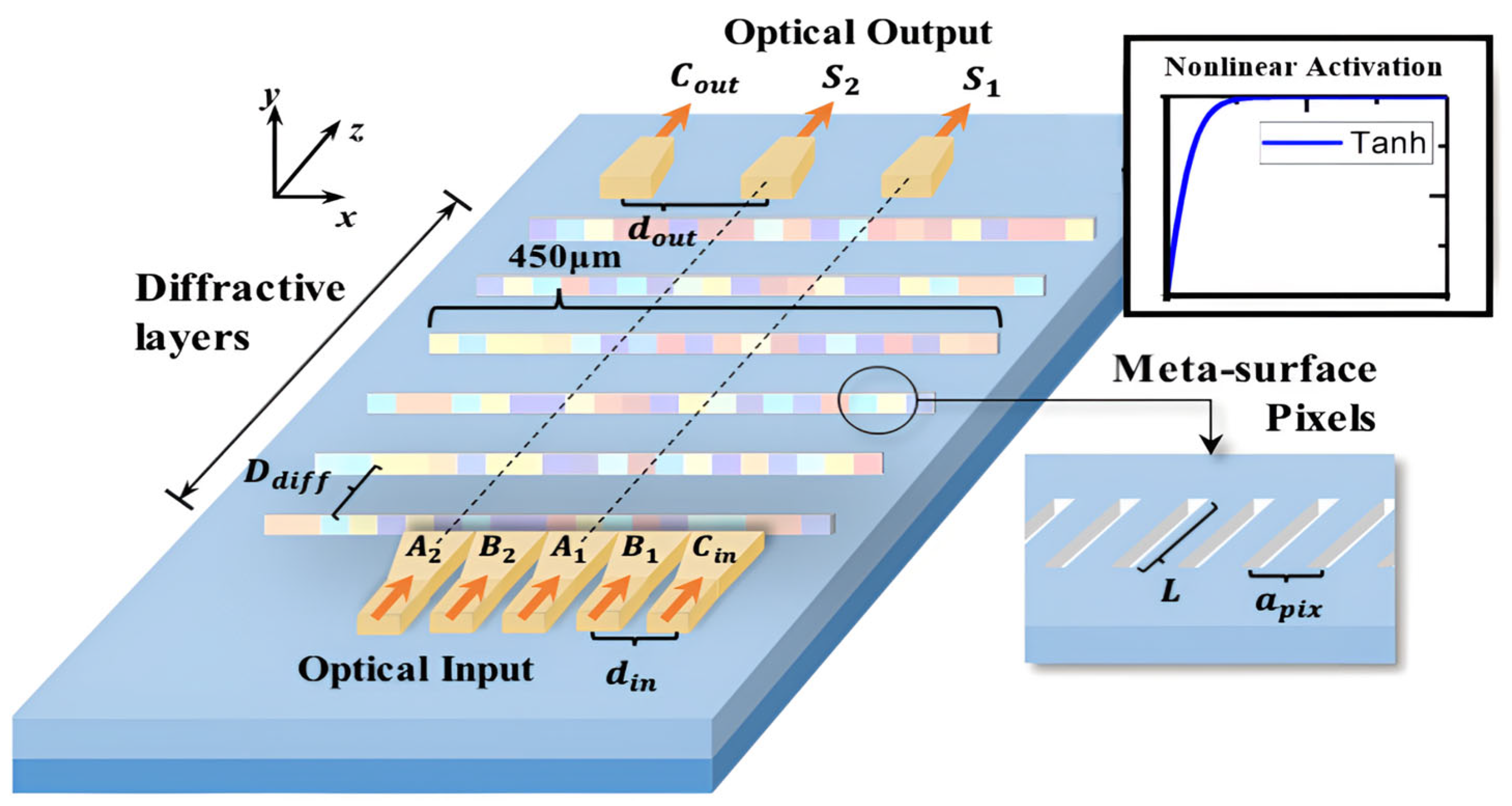
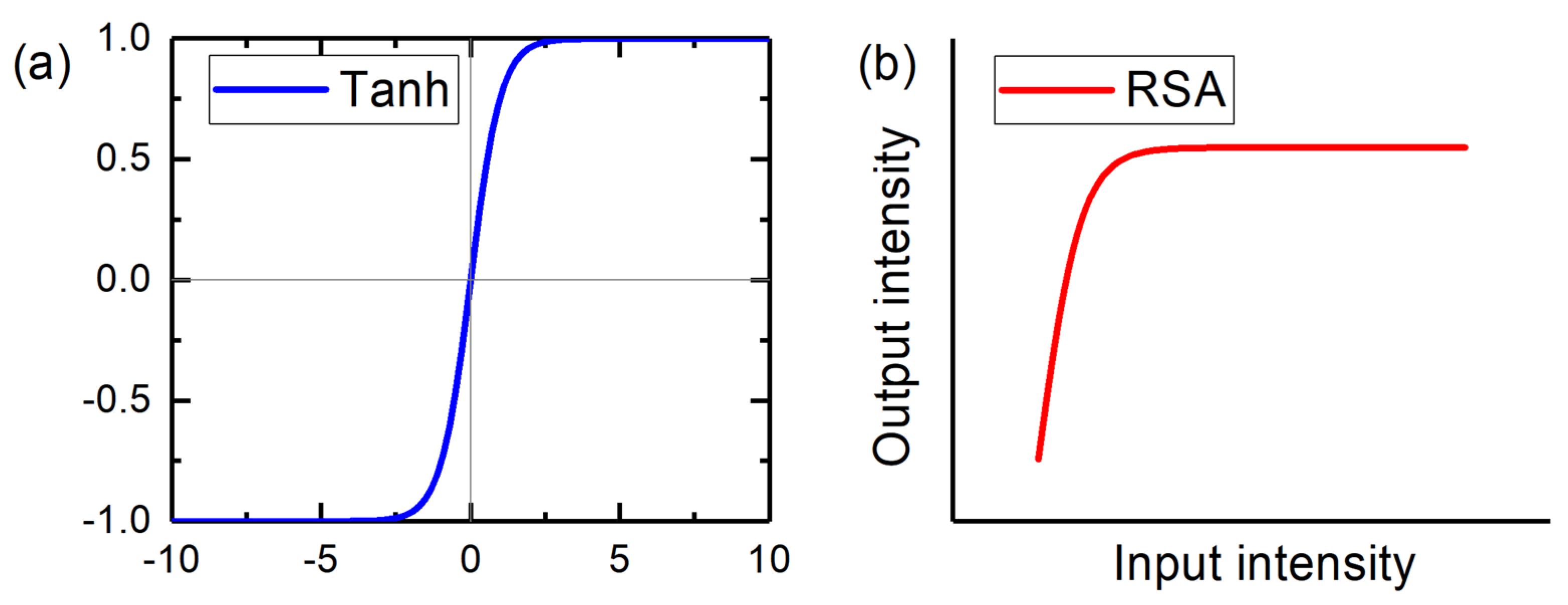
2. Architecture of the D2NN Optical Full Adder
3. Results
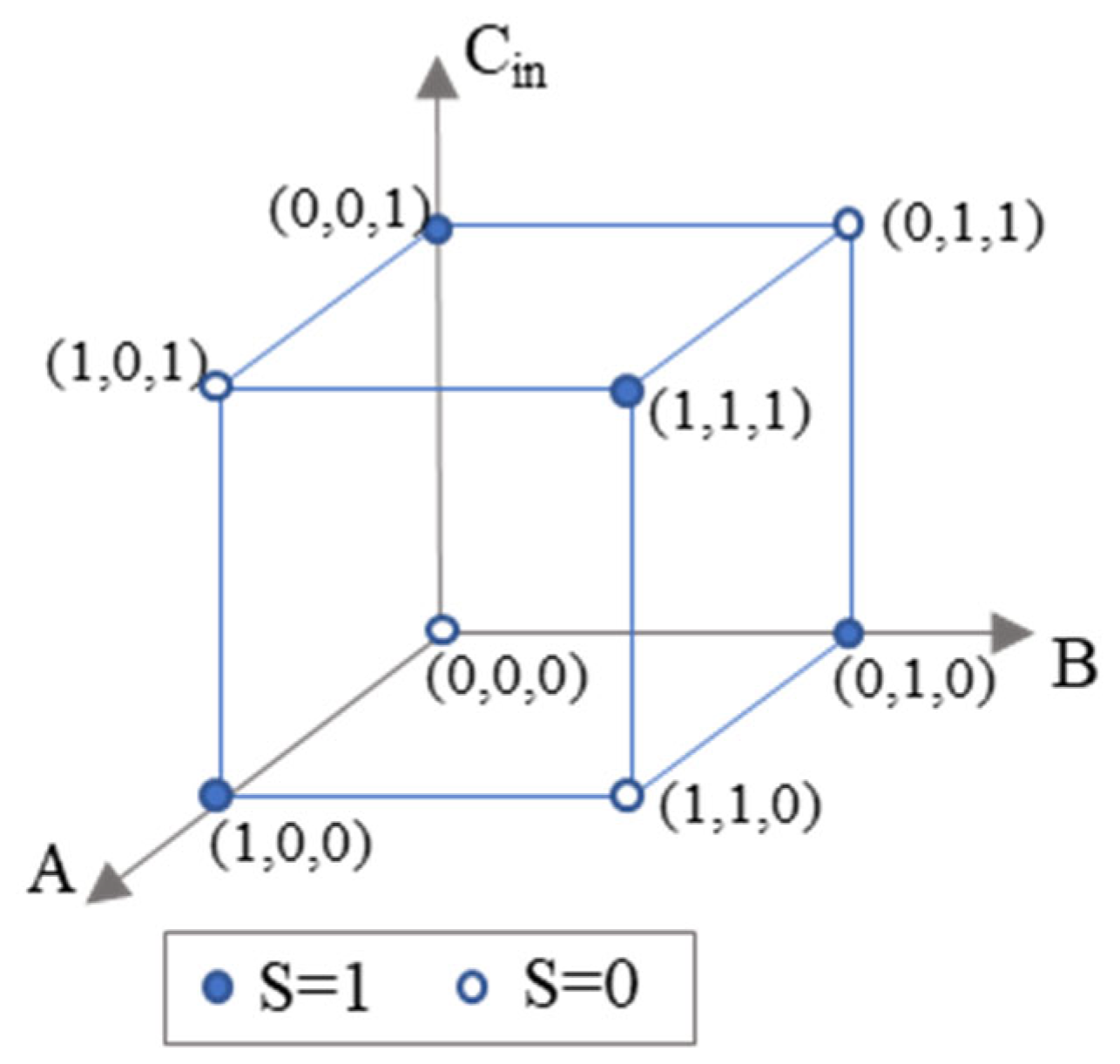
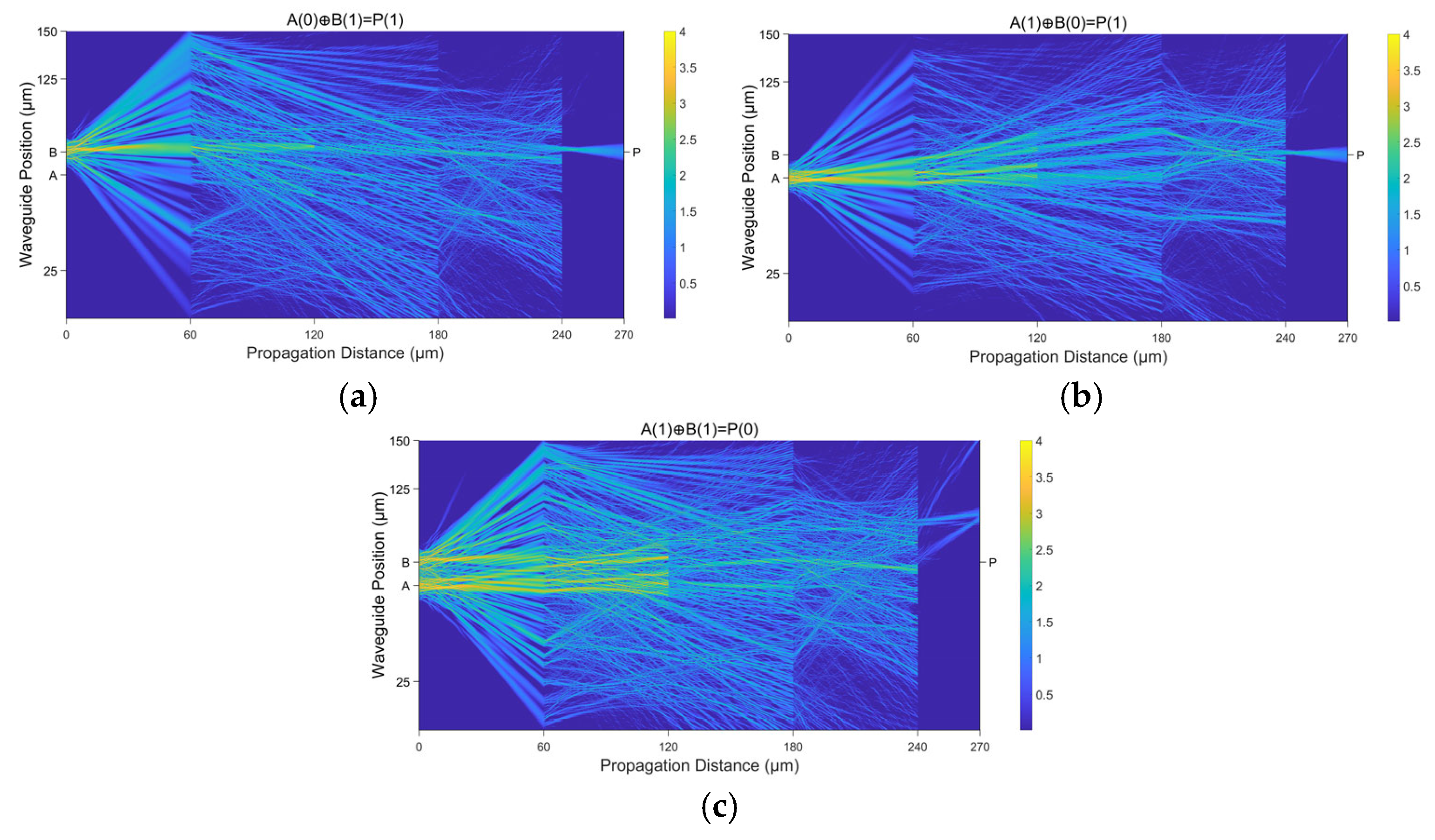
3.1. A Demonstration of the Fundamental XOR Function
3.2. Training of the 4-Bit Full Adder
3.3. Realization of the 4-Bit Full Adder
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Leiserson, C.E.; Thompson, N.C.; Emer, J.S.; Kuszmaul, B.C.; Lampson, B.W.; Sanchez, D.; Schardl, T.B. There’s plenty of room at the Top: What will drive computer performance after Moore’s law? Science 2020, 368, eaam9744. [Google Scholar] [CrossRef]
- Kotb, A.; Zoiros, K.E.; Guo, C. All-optical logic gates using E-shaped silicon waveguides at 1.55 μm. J. Appl. Phys. 2023, 133, 173101. [Google Scholar] [CrossRef]
- Corbin, A.; Shen, J.-T. Ultrafast reconfigurable optical logic gates using a nonlinear metallodielectric grating. Opt. Lett. 2021, 46, 2782–2785. [Google Scholar] [CrossRef] [PubMed]
- Rao, D.G.S.; Swarnakar, S.; Palacharla, V.; Raju, K.S.R.; Kumar, S. Design of all-optical AND, OR, and XOR logic gates using photonic crystals for switching applications. Photonic Netw. Commun. 2021, 41, 109–118. [Google Scholar] [CrossRef]
- Abdulnabi, S.H.; Abbas, M.N. Design an All-Optical Combinational Logic Circuits Based on Nano-Ring Insulator-Metal-Insulator Plasmonic Waveguides. Photonics 2019, 6, 30. [Google Scholar] [CrossRef]
- Cheraghi, F.; Soroosh, M.; Akbarizadeh, G. An ultra-compact all optical full adder based on nonlinear photonic crystal resonant cavities. Superlattices Microstruct. 2018, 113, 359–365. [Google Scholar] [CrossRef]
- Stabile, R.; Calabretta, N.; Shi, B. Large-Scale Photonic Integrated Cross-Connects for Optical Communication and Computation. In Proceedings of the 2020 Optical Fiber Communications Conference and Exposition (OFC 2020), San Diego, CA, USA, 8–12 March 2020. [Google Scholar]
- Chen, X.; Huo, L.; Zhao, Z.X.; Zhuang, L.; Lou, C.Y. Study on 100-Gb/s reconfigurable all-optical logic gates using a single semiconductor optical amplifier. Opt. Express 2016, 24, 30245–30253. [Google Scholar] [CrossRef]
- Dong, W.C.; Huang, Z.Y.; Hou, J.; Santos, R.; Zhang, X.L. Integrated all-optical programmable logic array based on semiconductor optical amplifiers. Opt. Lett. 2018, 43, 2150–2153. [Google Scholar] [CrossRef]
- Alipour-Banaei, H.; Serajmohammadi, S.; Mehdizadeh, F. All optical NAND gate based on nonlinear photonic crystal ring resonators. Optik 2017, 130, 1214–1221. [Google Scholar] [CrossRef]
- Sang, Y.; Wu, X.; Raja, S.S.; Wang, C.Y.; Li, H.; Ding, Y. Broadband Multifunctional Plasmonic Logic Gates. Adv. Opt. Mater. 2018, 6, 1701368. [Google Scholar] [CrossRef]
- Szilagyi, L.; Pliva, J.; Henker, R.; Schoeniger, D.; Turkiewicz, J.P.; Ellinger, F. A 53-Gbit/s Optical Receiver Frontend With 0.65 pJ/bit in 28-nm Bulk-CMOS. IEEE J. Solid-State Circuits 2019, 54, 845–855. [Google Scholar] [CrossRef]
- Shen, Y.; Harris, N.C.; Skirlo, S.; Prabhu, M.; Baehr-Jones, T.; Hochberg, M. Deep learning with coherent nanophotonic circuits. Nat. Photonics 2017, 11, 441–446. [Google Scholar] [CrossRef]
- Feldmann, J.; Youngblood, N.; Wright, C.D.; Bhaskaran, H.; Pernice, W.H.P. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 2019, 569, 208–214. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Rivenson, Y.; Yardimci, N.T.; Veli, M.; Luo, Y.; Jarrahi, M.; Ozcan, A. All-optical machine learning using diffractive deep neural networks. Science 2018, 361, 1004–1008. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.Q.; Dai, Q.H. Artificial intelligence accelerated by light. Nature 2021, 589, 25–26. [Google Scholar] [CrossRef]
- Zhang, Q.M.; Yu, H.Y.; Barbiero, M.; Wang, B.K.; Gu, M. Artificial neural networks enabled by nanophotonics. Light-Sci. Appl. 2019, 8, 42. [Google Scholar] [CrossRef]
- Qian, C.; Lin, X.; Lin, X.; Xu, J.; Sun, Y.; Li, E. Performing optical logic operations by a diffractive neural network. Light-Sci. Appl. 2020, 9, 59. [Google Scholar] [CrossRef]
- Jiao, S.M.; Liu, J.W.; Zhang, L.W.; Yu, F.H.; Zuo, G.M.; Zhang, J. All-optical logic gate computing for high-speed parallel information processing. Opto-Electron. Sci. 2022, 1, 220010. [Google Scholar] [CrossRef]
- Wang, Z.; Li, T.; Soman, A.; Mao, D.; Kananen, T.; Gu, T. On-chip wavefront shaping with dielectric metasurface. Nat. Commun. 2019, 10, 3547. [Google Scholar] [CrossRef]
- Machol, J.L.; Wise, F.W.; Patel, R.C.; Tanner, D.B. Vibronic quantum beats in PbS microcrystallites. Phys. Rev. B 1993, 48, 2819. [Google Scholar] [CrossRef]
- Martucci, A.; Fick, J.; Schell, J.; Battaglin, G.; Guglielmi, M. Microstructural and nonlinear optical properties of silica-titania sol-gel film doped with PbS quantum dots. J. Appl. Phys. 1999, 86, 79. [Google Scholar] [CrossRef]
- Lu, S.W.; Sohling, U.; Mennig, M.; Schmidt, H. Nonlinear optical properties of lead sulfide nanocrystals in polymeric coatings. Nanotechnology 2002, 13, 669–673. [Google Scholar] [CrossRef]
- Gao, M.; Yang, Y.; Yang, B.; Bian, F.; Shen, J. Synthesis of PbS nanoparticles in polymer matrices. J. Chem. Soc. Chem. Commun. 1994, 24, 2779–2780. [Google Scholar] [CrossRef]
- Moreels, I.; Lambert, K.; Smeets, D.; De Muynck, D.; Nollet, T.; Martins, J.C. Size-dependent optical properties of colloidal PbS quantum dots. ACS Nano 2009, 3, 3023–3030. [Google Scholar] [CrossRef] [PubMed]
- Georgitzikis, E.; Malinowski, P.E.; Li, Y.; Maes, J.; Hagelsieb, L.M.; Guerrieri, S. Integration of PbS Quantum Dot Photodiodes on Silicon for NIR Imaging. IEEE Sens. J. 2020, 20, 6841–6848. [Google Scholar] [CrossRef]
- Rarick, H.; Choi, M.; Saxena, A.; Manna, A.; Sharp, D.; Nguyen, H.; Cossairt, B.; Majumdar, A. Integration of Colloidal PbS Quantum Dots with Silicon Nanophotonics. In Proceedings of the 2023 Conference on Lasers and Electro-Optics (CLEO 2023), Technical Digest Series, San Jose, CA, USA, 7–12 May 2023. [Google Scholar]
- Mourgias-Alexandris, G.; Tsakyridis, A.; Passalis, N.; Tefas, A.; Vyrsokinos, K.; Pleros, N. An all-optical neuron with sigmoid activation function. Opt. Express 2019, 27, 9620–9630. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Harris, N.C.; Englund, D.; Soljacic, M. Deep Learning with Coherent Nanophotonic Circuits. In Proceedings of the Fifth Berkeley Symposium on Energy Efficient Electronic Systems & Steep Transistors Workshop, Berkeley, CA, USA, 19–20 October 2017. [Google Scholar]
- Tait, A.N.; Ferreira de Lima, T.; Nahmias, M.A.; Miller, H.B.; Peng, H.T.; Shastri, B.J.; Prucnal, P.R. Silicon Photonic Modulator Neuron. Phys. Rev. Appl. 2019, 11, 064043. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, C.; Chen, S.; Du, J.; Tang, P.; Jiang, G.; Zhang, H.; Wen, S.; Tang, D. Large energy, wavelength widely tunable, topological insulator Q-switched Erbium-doped fiber laser. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 315. [Google Scholar]
- Yang, Z.; Tan, W.; Zhang, T.; Chen, C.; Wang, Z.; Mao, Y.; Ma, C.; Lin, Q.; Bi, W.; Yu, F.; et al. MXene-based broadband ultrafast nonlinear activator for optical computing. Adv. Opt. Mater. 2022, 10, 2200714. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Q.; Sui, X.; Chen, Q.; Gu, G.; Wang, L.; Li, S. Research progress in optical neural networks: Theory, applications and developments. PhotoniX 2021, 2, 5. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, C.; Wang, Y.; Li, G.; Zheng, J.; Liu, Y.; Wang, C.; Wang, Y.; Guo, Y.; Fan, J.; Du, Q.; et al. Optical Full Adder Based on Integrated Diffractive Neural Network. Micromachines 2025, 16, 681. https://doi.org/10.3390/mi16060681
Deng C, Wang Y, Li G, Zheng J, Liu Y, Wang C, Wang Y, Guo Y, Fan J, Du Q, et al. Optical Full Adder Based on Integrated Diffractive Neural Network. Micromachines. 2025; 16(6):681. https://doi.org/10.3390/mi16060681
Chicago/Turabian StyleDeng, Chenchen, Yilong Wang, Guangpu Li, Jiyuan Zheng, Yu Liu, Chao Wang, Yuyan Wang, Yuchen Guo, Jingtao Fan, Qingyang Du, and et al. 2025. "Optical Full Adder Based on Integrated Diffractive Neural Network" Micromachines 16, no. 6: 681. https://doi.org/10.3390/mi16060681
APA StyleDeng, C., Wang, Y., Li, G., Zheng, J., Liu, Y., Wang, C., Wang, Y., Guo, Y., Fan, J., Du, Q., & Yu, S. (2025). Optical Full Adder Based on Integrated Diffractive Neural Network. Micromachines, 16(6), 681. https://doi.org/10.3390/mi16060681





