Optimization of Gas-Liquid Sulfonation in Cross-Shaped Microchannels for α-Olefin Sulfonate Synthesis
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals
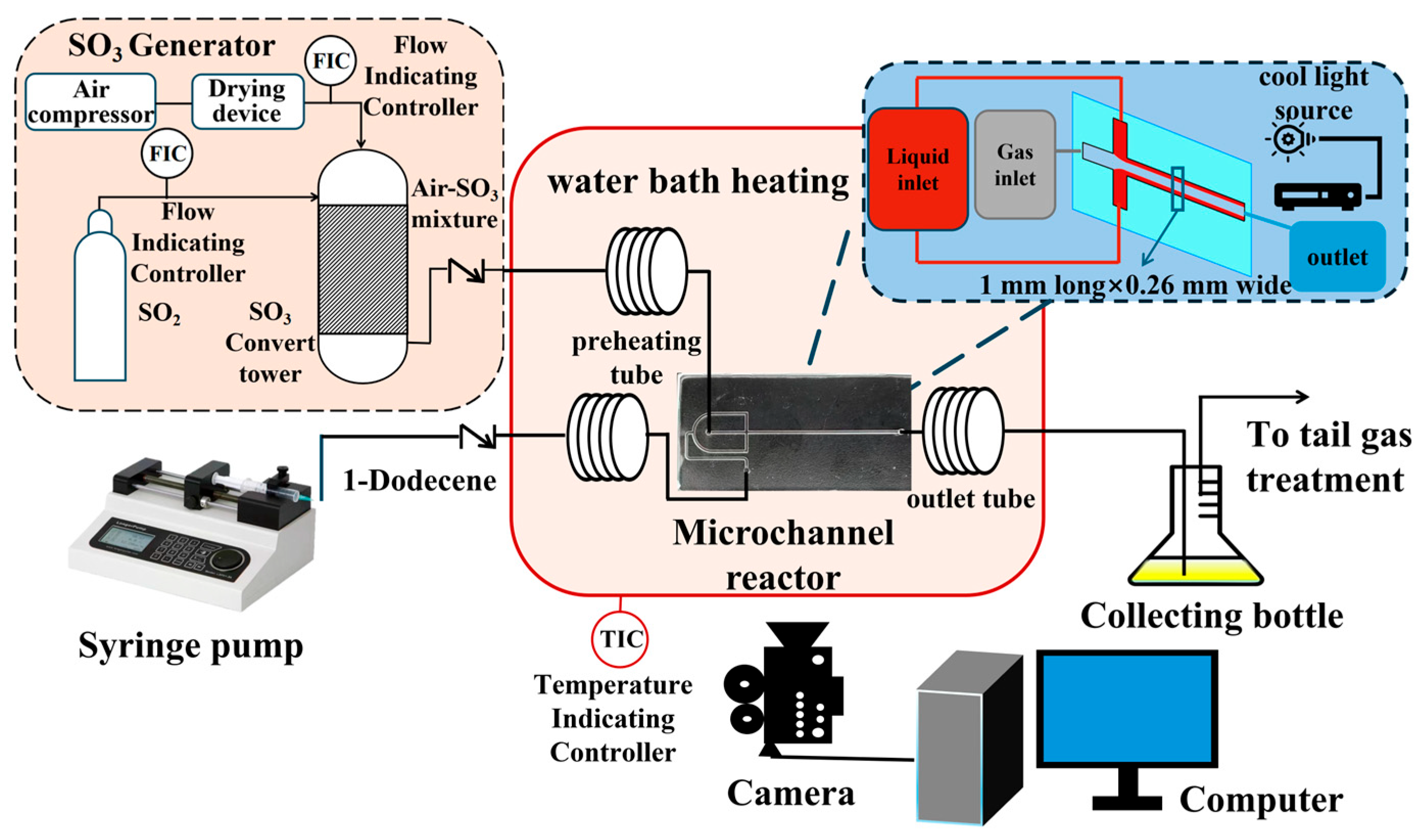
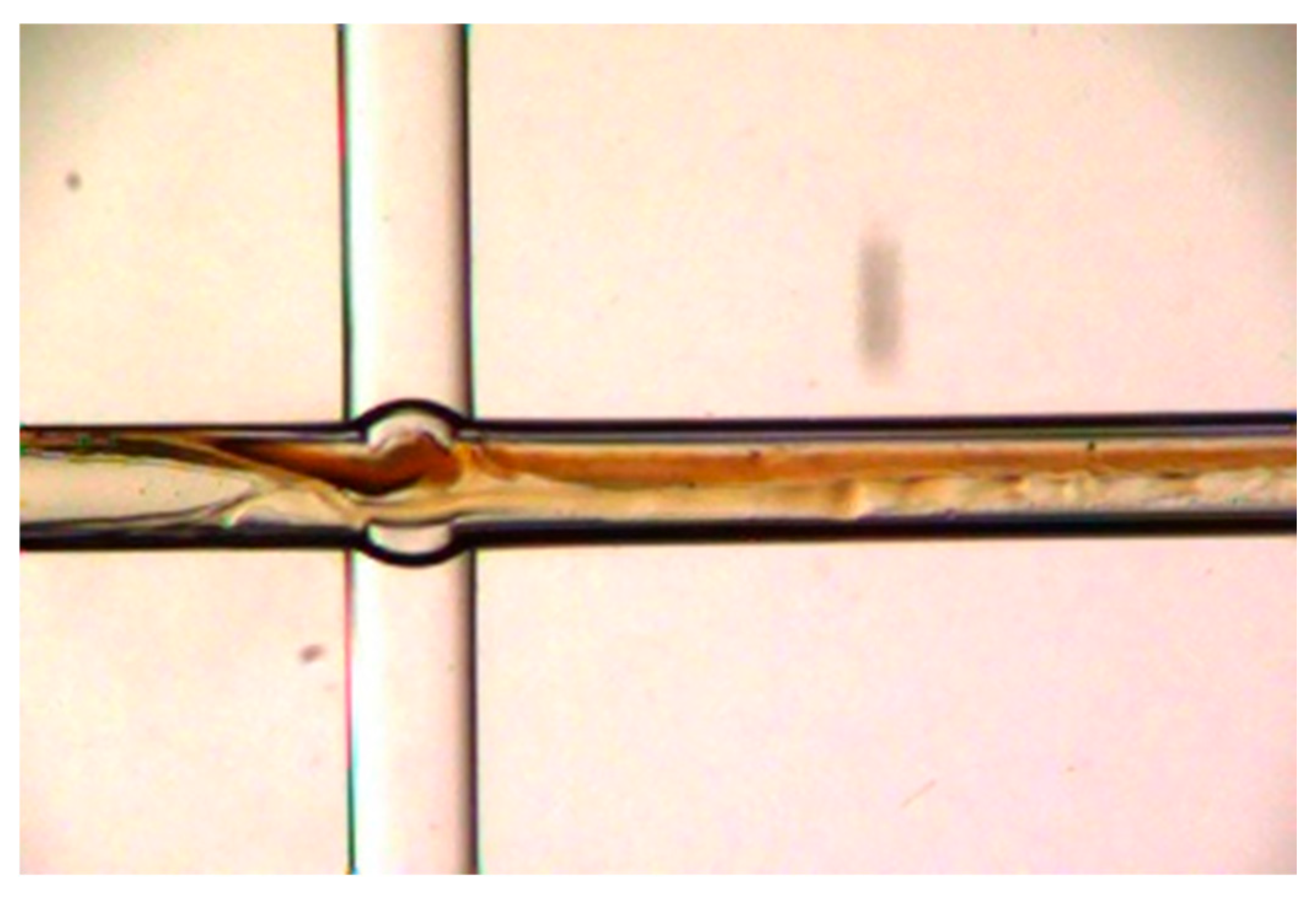
2.2. Synthesis of AOS in the Microchannel Reactor
2.3. Product Analysis Methods
2.4. Box-Behnken Response Surface Experimental Design
3. Results and Discussion
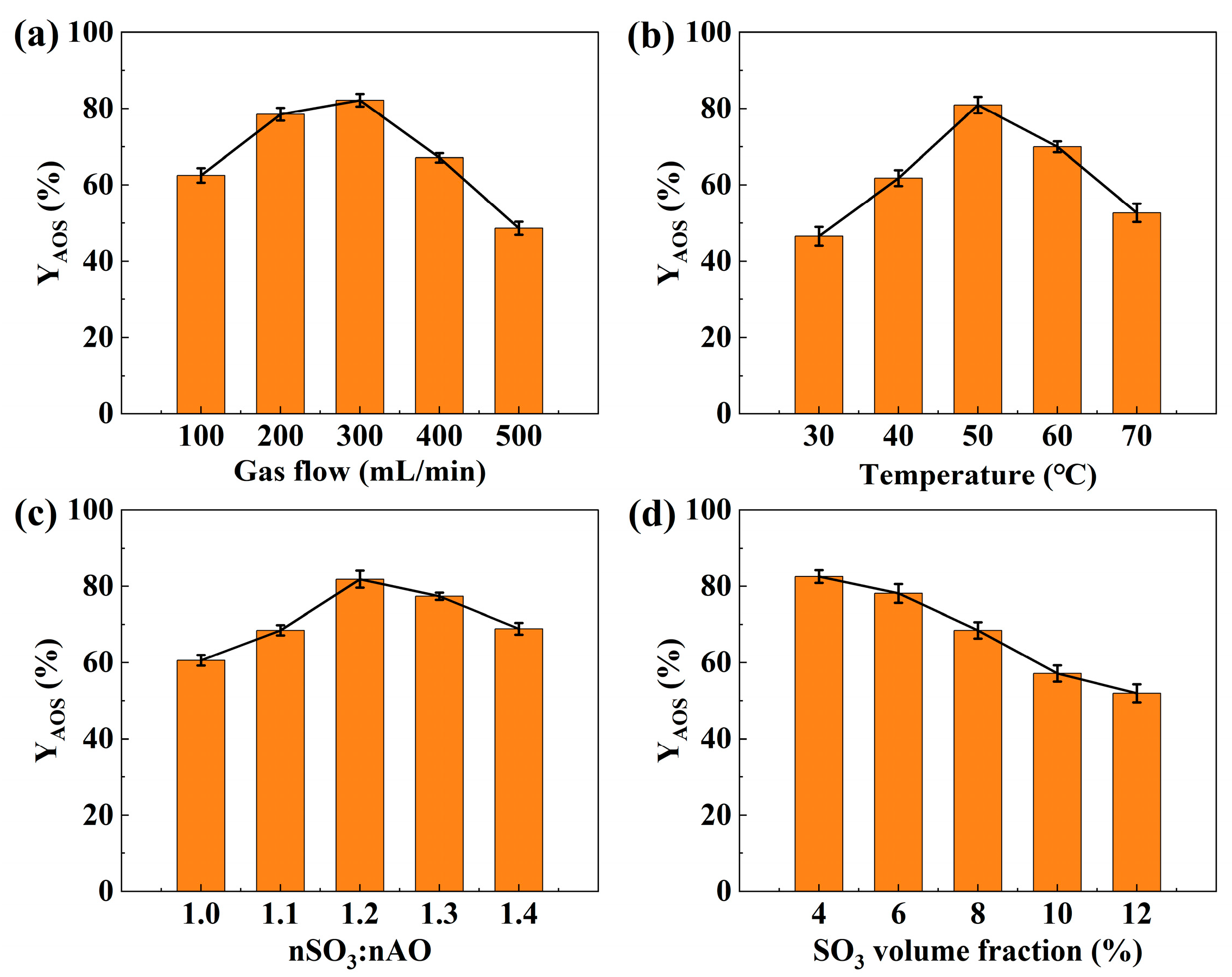
3.1. Single-Factor Experimental Analysis
3.1.1. Effect of Gas-Phase Flow Rate
3.1.2. Effect of Reaction Temperature
3.1.3. Effect of SO3/AO Molar Ratio
3.1.4. Effect of SO3 Volume Fraction
3.2. BBD Response Surface Experiment Analysis
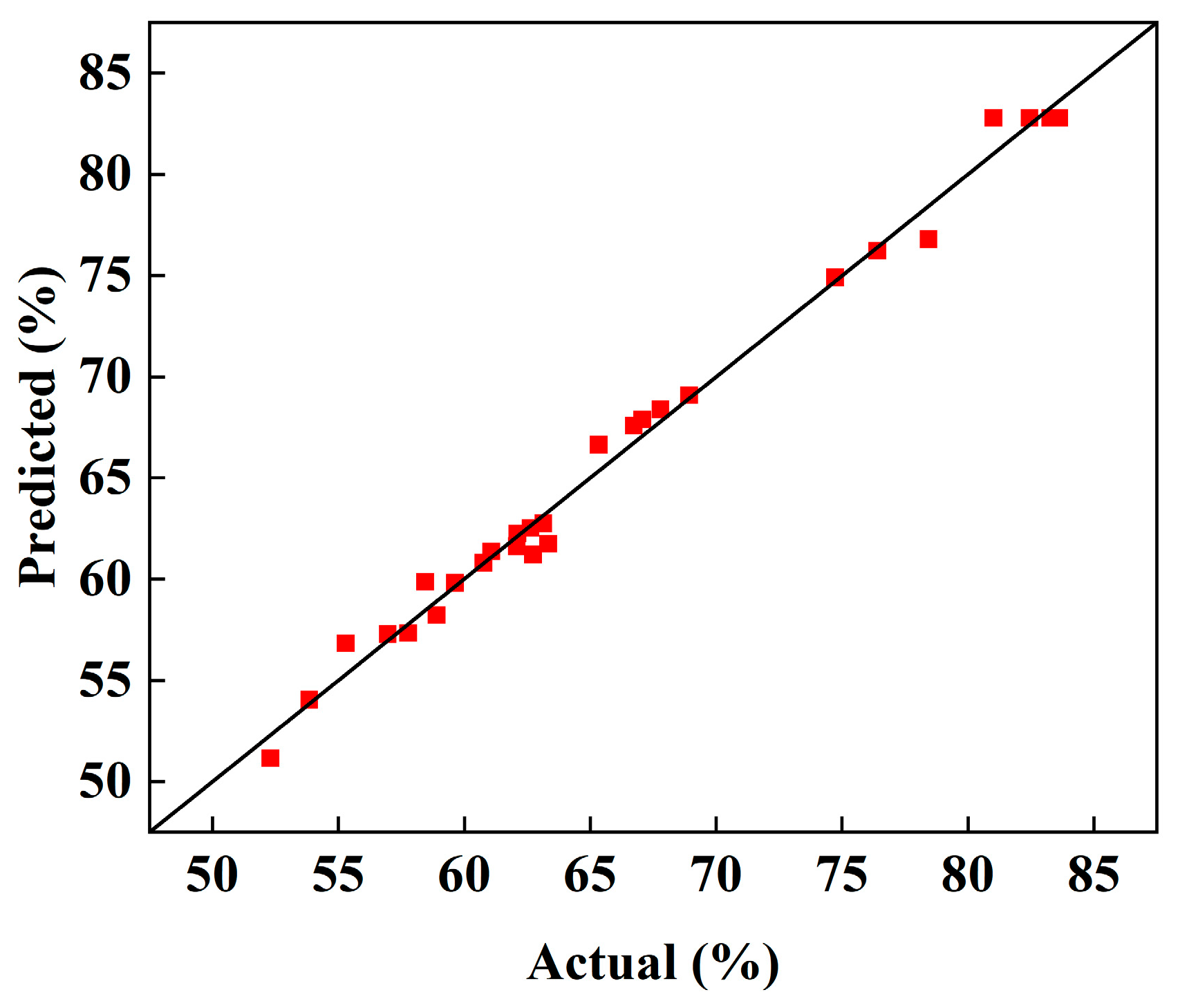
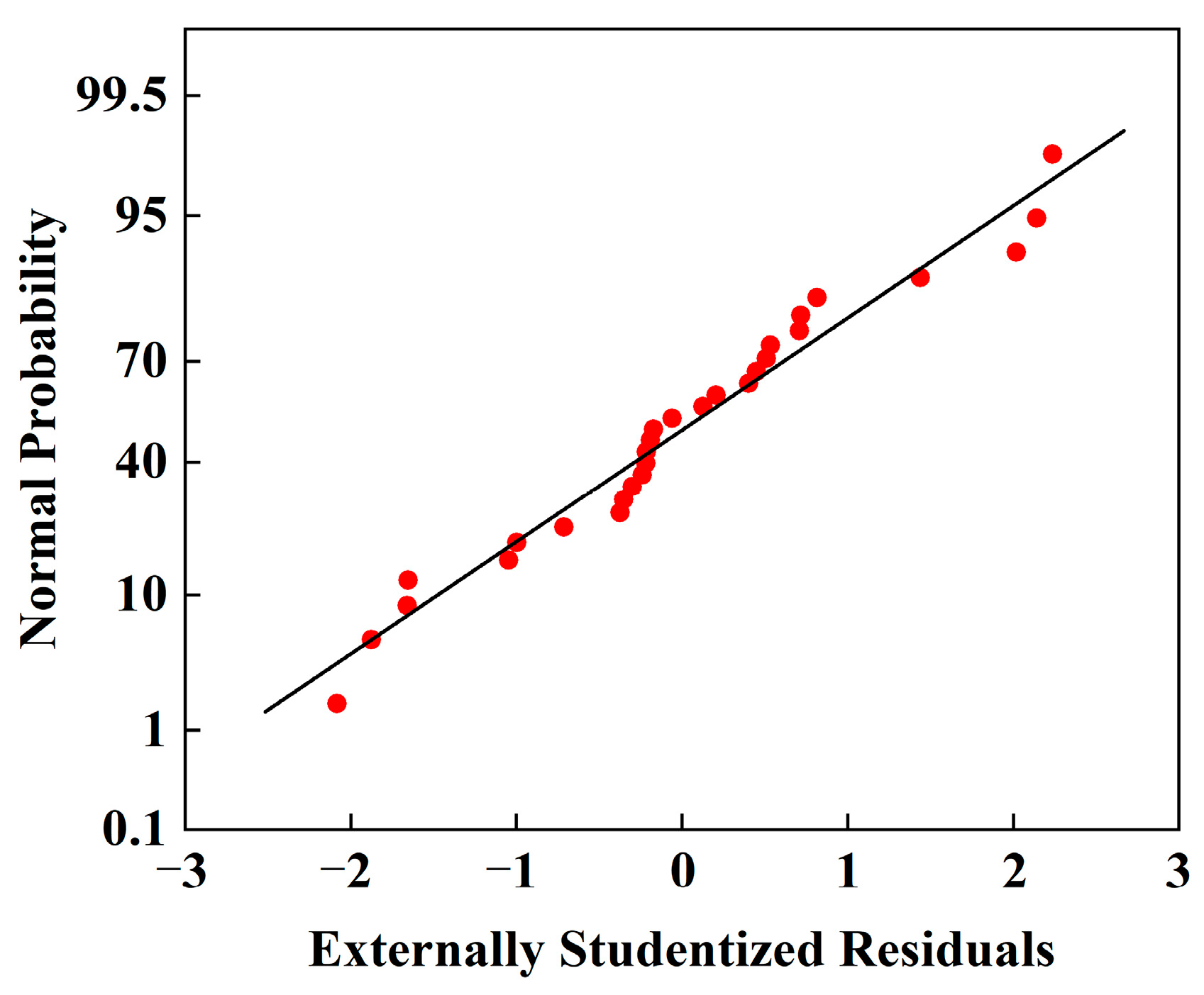
3.2.1. Model Construction and Fitting
3.2.2. Response Surface Analysis
3.2.3. Experimental Validation of Optimized Conditions
3.3. Multi-Objective Optimization of Process Parameters Using NSGA-II and Entropy-Weighted TOPSIS
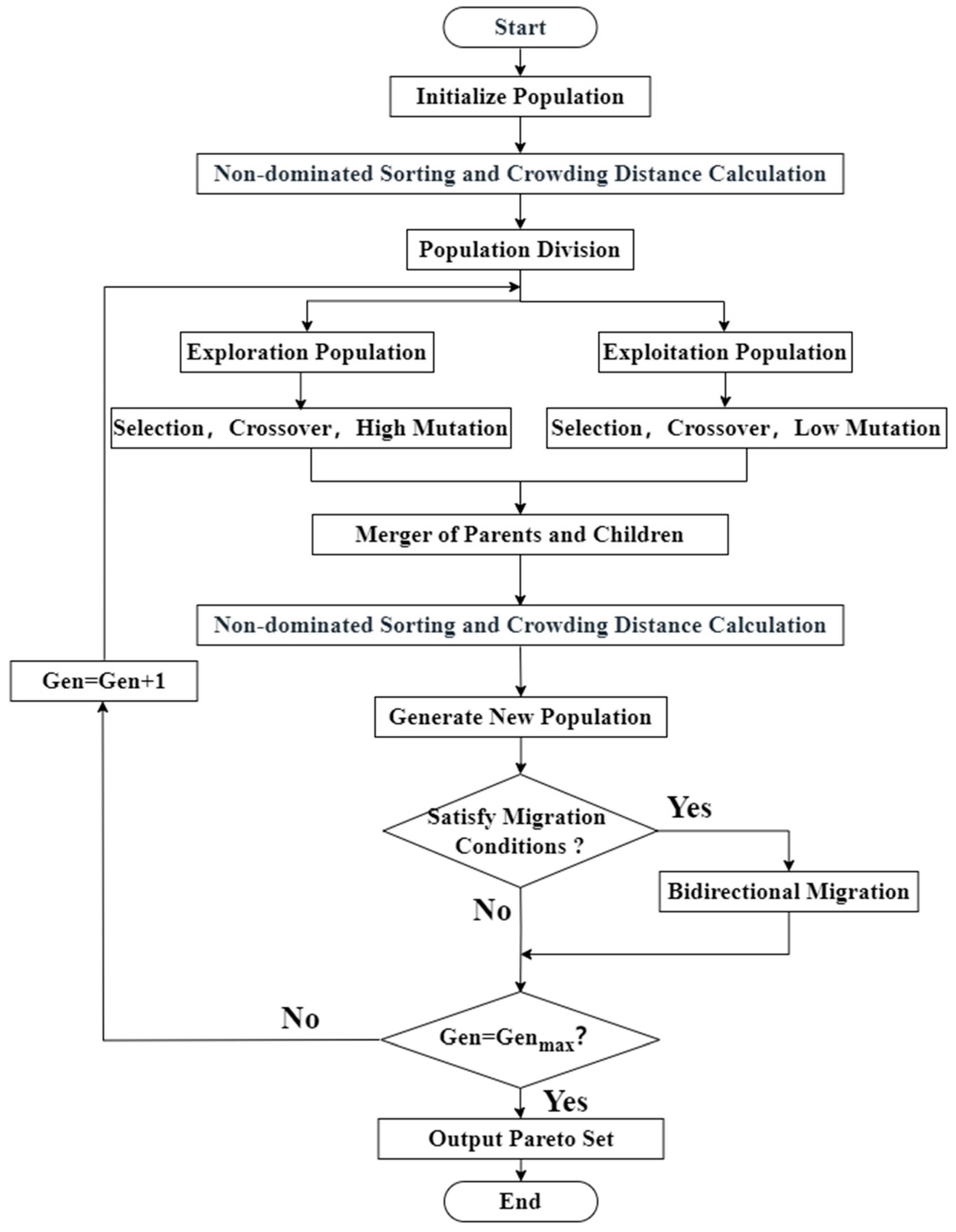
3.3.1. Multi-Objective Optimization of AOS Synthesis Using a Dual-Population NSGA-II and Entropy-Weighted TOPSIS
3.3.2. Objective Function
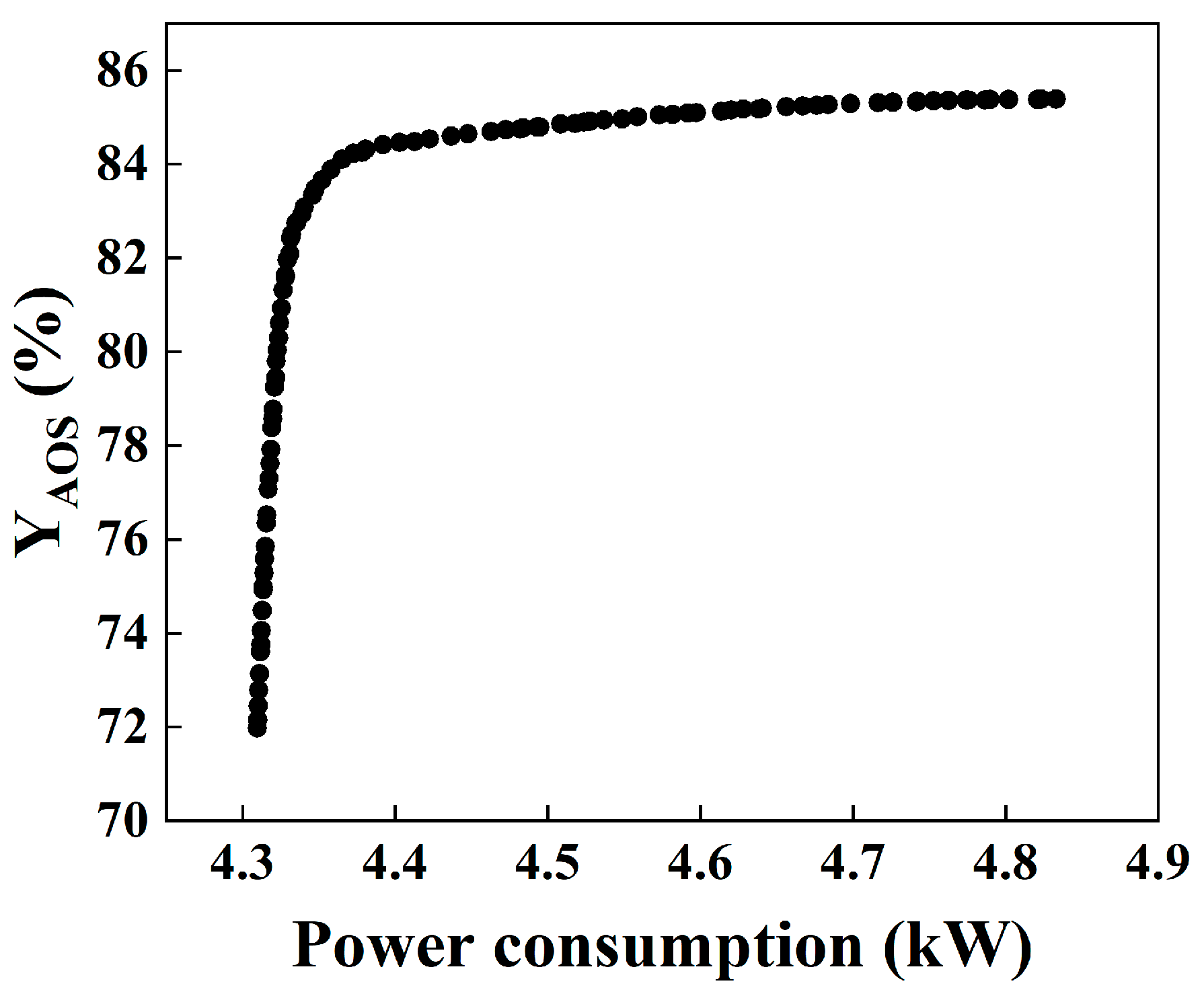
3.3.3. Optimization and Decision Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lin, J.; Chang, W. Evaluation of Foaming Chemical Composition and Performance of Commonly Used Detergents. Acad. J. Sci. Technol. 2023, 7, 243–247. [Google Scholar] [CrossRef]
- Farajzadeh, R.; Krastev, R.; Zitha, P.L.J. Foam Films Stabilized with Alpha Olefin Sulfonate (AOS). Colloids Surf. Physicochem. Eng. Asp. 2008, 324, 35–40. [Google Scholar] [CrossRef]
- Chakraborty, D.; Chukwuka, A.V.; Podder, S.; Sharma, P.; Bhowmick, S.; Mistri, T.K.; Saha, N.C. Effects of α-Olefin Sulfonate (AOS) on Tubifex Tubifex: Toxicodynamic-Toxicokinetic Inferences from the General Unified Threshold (GUTS) Model, Biomarker Responses and Molecular Docking Predictions. Ecotoxicology 2024, 33, 905–920. [Google Scholar] [CrossRef]
- Hu, J.; Fu, M.; Zhou, Y.; Wu, F.; Li, M. Experimental Study on SiO2 Nanoparticles-Assisted Alpha-Olefin Sulfonate Sodium (AOS) and Hydrolyzed Polyacrylamide (HPAM) Synergistically Enhanced Oil Recovery. Energies 2023, 16, 7523. [Google Scholar] [CrossRef]
- Verma, A.; Chauhan, G.; Ojha, K. Characterization of α-Olefin Sulfonate Foam in Presence of Cosurfactants: Stability, Foamability and Drainage Kinetic Study. J. Mol. Liq. 2018, 264, 458–469. [Google Scholar] [CrossRef]
- Yorke, K.; Potanin, A.; Jogun, S.; Morgan, A.; Shen, H.; Amin, S. High-Performance Sulphate-Free Cleansers: Surface Activity, Foaming and Rheology. Int. J. Cosmet. Sci. 2021, 43, 636–652. [Google Scholar] [CrossRef]
- Berger, P.D.; Lee, C.H. New Anionic Alkylaryl Surfactants Based on Olefin Sulfonic Acids. J. Surfactants Deterg. 2002, 5, 39–43. [Google Scholar] [CrossRef]
- Geng, Y.; Ling, S.; Huang, J.; Xu, J. Multiphase Microfluidics: Fundamentals, Fabrication, and Functions. Small 2020, 16, 1906357. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, J.; Ni, L.; Jiang, J.; Yu, Y.; Pan, Y. Continuous-Flow Synthesis of Methyl Sulfone with Microchannel Reactors: A Safer and Efficient Production Strategy. Org. Process Res. Dev. 2023, 27, 1445–1454. [Google Scholar] [CrossRef]
- Chruściel, A.; Hreczuch, W. Kinetic Modelling and Improvement of the Ageing Step of Industrial Alkylbenzene Sulfonation Process. Chem. Eng. Process.-Process Intensif. 2022, 181, 109143. [Google Scholar] [CrossRef]
- Liu, L.; Liang, J.; Jiang, J.; Ni, L. Investigating the Inherent Safety Designs of Typical Exothermic Reaction Processes. J. Loss Prev. Process Ind. 2022, 76, 104586. [Google Scholar] [CrossRef]
- Wang, Y.-Y.; Zhang, D.-F.; Zhang, H.-R.; Liu, W.-J.; Chen, Z.-Q.; Jiang, J.-C.; Ni, L. Process Optimization and Thermal Hazard Study for the Preparation of TBPB by a Two–Step Reaction. Sustainability 2024, 16, 8568. [Google Scholar] [CrossRef]
- Ovchinnikova, E.V.; Vernikovskaya, N.V.; Gribovskii, A.G.; Chumachenko, V.A. Multichannel Microreactors for Highly Exothermic Catalytic Process: The Influence of Thermal Conductivity of Reactor Material and of Transport Phenomena inside the Channels on the Process Efficiency. Chem. Eng. J. 2021, 409, 128046. [Google Scholar] [CrossRef]
- Engelbrecht, N.; Everson, R.C.; Bessarabov, D.; Kolb, G. Microchannel Reactor Heat-Exchangers: A Review of Design Strategies for the Effective Thermal Coupling of Gas Phase Reactions. Chem. Eng. Process.-Process Intensif. 2020, 157, 108164. [Google Scholar] [CrossRef]
- Fuentes, I.; Mmbaga, J.P.; Hayes, R.E.; Gracia, F. Potential of Microreactors for Heat Transfer Efficient CO2 Methanation. Chem. Eng. Sci. 2023, 280, 119047. [Google Scholar] [CrossRef]
- Widianto, A.Y.; Lorenza, V.; Clarisa, C.; Valentino, R.; Elfa, C.; Sapei, L. Mass Transfer Phenomena of Partially Miscible Liquids under Liquid-Liquid Slug Flow in a Circular Microchannel. Chem. Eng. Res. Des. 2024, 205, 57–66. [Google Scholar] [CrossRef]
- Xue, X.; Xie, C.; Qian, G.; Qiu, M.; Jiang, R.; Pasha, M.; Shang, M.; Su, Y. Control over Selectivity for Demethylation in Dolutegravir Synthesis in Microreactors: Kinetics and Mechanisms. Chem. Eng. Sci. 2024, 284, 119453. [Google Scholar] [CrossRef]
- Zhan, W.; Wang, J.; He, C.; Jiang, B.; Zhu, C.; Ma, Y.; Fu, T. Kinetics of Glyoxal Oxidation by Nitric Acid in a Capillary Microreactor. Chem. Eng. Sci. 2023, 276, 118813. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, S.; Meng, W.; Yuan, H.; Ma, W.; Sun, X.; Xu, J.; Tan, B.; Li, P. Continuous Sulfonation of Hexadecylbenzene in a Microreactor. Green Process. Synth. 2021, 10, 219–229. [Google Scholar] [CrossRef]
- Geng, Y.; Huang, J.; Tan, B.; Xu, Y.; Li, P.; Xu, J. Efficient Synthesis of Dodecylbenzene Sulfonic Acid in Microreaction Systems. Chem. Eng. Process.-Process Intensif. 2020, 149, 107858. [Google Scholar] [CrossRef]
- Yuan, M.; Feng, H.; Zhang, W.; Zheng, J.; Zhang, K.; Kong, X.; Han, N.; Dong, J. Gas-Liquid Sulfonation in T-Shaped Microchannel for DBSA Synthesis and Process Optimization with Response Surface Method. Chem. Eng. Process.-Process Intensif. 2022, 174, 108890. [Google Scholar] [CrossRef]
- Xu, N.; Yu, J.; Zhang, L.; Ma, X.; Zhang, Z.; Zhang, W.; Zhang, Y.; Fang, J. Study on Gas–Liquid Sulfonation Reaction under Annular Flow Pattern in Micro-Reactor: Mechanism, Model and Process Optimization. Chem. Eng. J. 2024, 498, 155611. [Google Scholar] [CrossRef]
- Ma, H.; Li, P.; Huang, A.; Zhao, W.; Zhang, X. The Kinetics Study on Sulfonation Reaction of Continuous Microfluidic Synthesis of 1-Tetradecene. Chem. Eng. Sci. 2024, 290, 119883. [Google Scholar] [CrossRef]
- Xu, Y.; Li, P.; Ma, H.; Huang, A.; Zhao, W.; Zhao, X. Multistep Cascade Continuous Flow Synthesis of AOS Based on Microreactor. Chem. Eng. Process.-Process Intensif. 2023, 192, 109505. [Google Scholar] [CrossRef]
- Huang, W.; Xiang, D. Optimal Design Framework and Techno-Economic-Environmental Assessment for Efficient Solvent Recovery Separation of Ethyl Acetate and Methanol. Sep. Purif. Technol. 2021, 260, 118210. [Google Scholar] [CrossRef]
- Qin, Y.; Huang, W.; Wang, Z.; Wang, C.; Wang, C.; Zhang, M.; Wu, S.; Wang, G.; Zhao, F. 1,2-Dichloroethane Causes Anxiety and Cognitive Dysfunction in Mice by Disturbing GABA Metabolism and Inhibiting the cAMP-PKA-CREB Signaling Pathway. Ecotoxicol. Environ. Saf. 2024, 279, 116464. [Google Scholar] [CrossRef]
- Yao, C.; Zhao, Y.; Ma, H.; Liu, Y.; Zhao, Q.; Chen, G. Two-Phase Flow and Mass Transfer in Microchannels: A Review from Local Mechanism to Global Models. Chem. Eng. Sci. 2021, 229, 116017. [Google Scholar] [CrossRef]
- Sobieszuk, P.; Pohorecki, R.; Cygański, P.; Grzelka, J. Determination of the Interfacial Area and Mass Transfer Coefficients in the Taylor Gas–Liquid Flow in a Microchannel. Chem. Eng. Sci. 2011, 66, 6048–6056. [Google Scholar] [CrossRef]
- Shrouf, F.; Ordieres-Meré, J.; García-Sánchez, A.; Ortega-Mier, M. Optimizing the Production Scheduling of a Single Machine to Minimize Total Energy Consumption Costs. J. Clean. Prod. 2014, 67, 197–207. [Google Scholar] [CrossRef]
- Asghar, I.; Sarkar, B.; Kim, S. Economic Analysis of an Integrated Production–Inventory System under Stochastic Production Capacity and Energy Consumption. Energies 2019, 12, 3179. [Google Scholar] [CrossRef]
- Khan, A.M.; Liang, L.; Mia, M.; Gupta, M.K.; Wei, Z.; Jamil, M.; Ning, H. Development of Process Performance Simulator (PPS) and Parametric Optimization for Sustainable Machining Considering Carbon Emission, Cost and Energy Aspects. Renew. Sustain. Energy Rev. 2021, 139, 110738. [Google Scholar] [CrossRef]
- Cui, Y.; Geng, Z.; Zhu, Q.; Han, Y. Review: Multi-Objective Optimization Methods and Application in Energy Saving. Energy 2017, 125, 681–704. [Google Scholar] [CrossRef]
- Sharma, S.; Kumar, V. A Comprehensive Review on Multi-Objective Optimization Techniques: Past, Present and Future. Arch. Comput. Methods Eng. 2022, 29, 5605–5633. [Google Scholar] [CrossRef]
- Alexandrova, A.A.; Koledin, S.N. Optimal Temperature Calculation for Multicriteria Optimization of the Hydrogenation of Polycyclic Aromatic Hydrocarbons by NSGA-II Method. Adv. Eng. Res. Rostov-Don 2024, 24, 109–118. [Google Scholar] [CrossRef]
- Verhellen, J. Graph-Based Molecular Pareto Optimisation. Chem. Sci. 2022, 13, 7526–7535. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A Fast Elitist Non-Dominated Sorting Genetic Algorithm for Multi-Objective Optimization: NSGA-II. In Parallel Problem Solving from Nature PPSN VI; Lecture Notes in Computer Science; Schoenauer, M., Deb, K., Rudolph, G., Yao, X., Lutton, E., Merelo, J.J., Schwefel, H.-P., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1917, pp. 849–858. ISBN 978-3-540-41056-0. [Google Scholar]
- Zheng, W.; Doerr, B. Mathematical Runtime Analysis for the Non-Dominated Sorting Genetic Algorithm II (NSGA-II). Artif. Intell. 2023, 325, 104016. [Google Scholar] [CrossRef]
- Senthil Kannan, V.; Lenin, K.; Navneethakrishnan, P. Machining Parameters Optimization in Laser Beam Machining for Micro Elliptical Profiles Using TOPSIS Method. Mater. Today Proc. 2020, 21, 727–730. [Google Scholar] [CrossRef]



| Chromatographic Conditions | Parameters |
|---|---|
| column | C18 column (250 × 4.6 × 5 μm) |
| mobile phase | methanol |
| detector | differential refractive index detector |
| flow rate (mL/min) | 1 |
| column temperature (°C) | 40 |
| feed volume (μL) | 15 |
| Variables | Units | Ranges |
|---|---|---|
| gas-phase flow rate | mL/min | 100, 200, 300, 400, 500 |
| reaction temperature | °C | 30, 40, 50, 60, 70 |
| SO3/α-olefin molar ratio | — | 1.0, 1.1, 1.2, 1.3, 1.4 |
| SO3 volume fraction | % | 4, 6, 8, 10, 12 |
| Variables | Units | Level | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| gas-phase flow rate | mL/min | 200 | 300 | 400 |
| reaction temperature | °C | 40 | 50 | 60 |
| SO3/AO molar ratio | — | 1.1 | 1.2 | 1.3 |
| SO3 volume fraction | % | 4 | 6 | 8 |
| No. | Factors | Response Value Y (%) | ||||
|---|---|---|---|---|---|---|
| A | B | C | D | Experimental Value | Predicted Value | |
| 1 | −1 | −1 | 0 | 0 | 67.61 | 68.11 |
| 2 | 1 | −1 | 0 | 0 | 58.4 | 57.57 |
| 3 | −1 | 1 | 0 | 0 | 71.23 | 71.61 |
| 4 | 1 | 1 | 0 | 0 | 63.27 | 62.32 |
| 5 | 0 | 0 | −1 | −1 | 71.84 | 72.45 |
| 6 | 0 | 0 | 1 | −1 | 80.9 | 80.79 |
| 7 | 0 | 0 | −1 | 1 | 68.13 | 67.79 |
| 8 | 0 | 0 | 1 | 1 | 68.83 | 67.77 |
| 9 | −1 | 0 | 0 | −1 | 82.93 | 81.12 |
| 10 | 1 | 0 | 0 | −1 | 66.57 | 66.46 |
| 11 | −1 | 0 | 0 | 1 | 67.64 | 67.53 |
| 12 | 1 | 0 | 0 | 1 | 60.79 | 62.37 |
| 13 | 0 | −1 | −1 | 0 | 64.4 | 64.59 |
| 14 | 0 | 1 | −1 | 0 | 68.23 | 66.71 |
| 15 | 0 | −1 | 1 | 0 | 65.45 | 66.75 |
| 16 | 0 | 1 | 1 | 0 | 73.29 | 72.88 |
| 17 | −1 | 0 | −1 | 0 | 67.57 | 68.29 |
| 18 | 1 | 0 | −1 | 0 | 60.13 | 60.48 |
| 19 | −1 | 0 | 1 | 0 | 74.22 | 74.55 |
| 20 | 1 | 0 | 1 | 0 | 62.58 | 62.54 |
| 21 | 0 | −1 | 0 | −1 | 73.26 | 73.06 |
| 22 | 0 | 1 | 0 | −1 | 77.43 | 77.06 |
| 23 | 0 | −1 | 0 | 1 | 65.04 | 64.09 |
| 24 | 0 | 1 | 0 | 1 | 67.46 | 68.34 |
| 25 | 0 | 0 | 0 | 0 | 79.01 | 80.39 |
| 26 | 0 | 0 | 0 | 0 | 81.13 | 80.39 |
| 27 | 0 | 0 | 0 | 0 | 80.77 | 80.39 |
| 28 | 0 | 0 | 0 | 0 | 79.94 | 80.39 |
| 29 | 0 | 0 | 0 | 0 | 81.12 | 80.39 |
| Source | Square Sum | Degrees of Freedom | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|
| model | 1408.16 | 14 | 100.58 | 63.9 | <0.0001 | significant |
| A | 294.62 | 1 | 294.62 | 187.19 | <0.0001 | significant |
| B | 51.05 | 1 | 51.05 | 32.43 | <0.0001 | significant |
| C | 51.96 | 1 | 51.96 | 33.01 | <0.0001 | significant |
| D | 234.44 | 1 | 234.44 | 148.95 | <0.0001 | significant |
| AB | 0.3906 | 1 | 0.3906 | 0.2482 | 0.6261 | |
| AC | 4.41 | 1 | 4.41 | 2.8 | 0.1163 | |
| AD | 22.61 | 1 | 22.61 | 14.37 | 0.002 | significant |
| BC | 4.02 | 1 | 4.02 | 2.55 | 0.1323 | |
| BD | 0.0156 | 1 | 0.0156 | 0.0099 | 0.922 | |
| CD | 17.47 | 1 | 17.47 | 11.1 | 0.0049 | significant |
| A2 | 455.46 | 1 | 455.46 | 289.37 | <0.0001 | significant |
| B2 | 328.21 | 1 | 328.21 | 208.52 | <0.0001 | significant |
| C2 | 199.85 | 1 | 199.85 | 126.97 | <0.0001 | significant |
| D2 | 45.36 | 1 | 45.36 | 28.82 | <0.0001 | significant |
| residual | 22.04 | 14 | 1.57 | |||
| lost proposal | 18.7 | 10 | 1.87 | 2.25 | 0.2263 | insignificant |
| pure error | 3.33 | 4 | 0.8329 | |||
| total deviation | 1430.2 | 28 |
| R2 | R2adj | R2pre | CV (%) | Signal-to-Noise Ratio |
|---|---|---|---|---|
| 0.9882 | 0.9763 | 0.9415 | 1.57 | 29.9645 |
| Gas-Phase Flow Rate (mL/min) | Reaction Temperature (°C) | SO3/AO Molar Ratio | SO3 Volume Fraction (%) | Active Substance Content (%) |
|---|---|---|---|---|
| 266 | 52 | 1.24 | 4.1 | 85.14 |
| Gas-Phase Flow Rate (mL/min) | Reaction Temperature (°C) | SO3/AO Molar Ratio | SO3 Volume Fraction (%) | Active Substance Content (%) | Power Consumption (kW) | Proximity to the Optimal Level |
|---|---|---|---|---|---|---|
| 228 | 52.22 | 1.27 | 4 | 81.31 | 4.365 | 0.898 |
| 227 | 51.36 | 1.27 | 4.1 | 80.61 | 4.358 | 0.897 |
| 229 | 51.24 | 1.25 | 4 | 81.42 | 4.372 | 0.895 |
| 227 | 51.26 | 1.28 | 4.2 | 80.66 | 4.352 | 0.892 |
| 225 | 51.24 | 1.26 | 4 | 80.73 | 4.352 | 0.892 |
| Type of Program | Gas-Phase Flow Rate (mL/min) | Reaction Temperature (°C) | SO3/AO Molar Ratio | SO3 Volume Fraction (%) | Active Substance Content (%) | Power Consumption (kW) |
|---|---|---|---|---|---|---|
| MOO | 228 | 52.22 | 1.27 | 4 | 81.31 | 4.365 |
| RSM | 266 | 52 | 1.24 | 4.1 | 85.14 | 4.893 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Mu, Y.; Qin, M.; Zhang, W.; Zhou, W. Optimization of Gas-Liquid Sulfonation in Cross-Shaped Microchannels for α-Olefin Sulfonate Synthesis. Micromachines 2025, 16, 638. https://doi.org/10.3390/mi16060638
Li Y, Mu Y, Qin M, Zhang W, Zhou W. Optimization of Gas-Liquid Sulfonation in Cross-Shaped Microchannels for α-Olefin Sulfonate Synthesis. Micromachines. 2025; 16(6):638. https://doi.org/10.3390/mi16060638
Chicago/Turabian StyleLi, Yao, Yingxin Mu, Muxuan Qin, Wei Zhang, and Wenjin Zhou. 2025. "Optimization of Gas-Liquid Sulfonation in Cross-Shaped Microchannels for α-Olefin Sulfonate Synthesis" Micromachines 16, no. 6: 638. https://doi.org/10.3390/mi16060638
APA StyleLi, Y., Mu, Y., Qin, M., Zhang, W., & Zhou, W. (2025). Optimization of Gas-Liquid Sulfonation in Cross-Shaped Microchannels for α-Olefin Sulfonate Synthesis. Micromachines, 16(6), 638. https://doi.org/10.3390/mi16060638






