Kinetostatic Modeling and Performance Analysis of Redundant-Actuated 4-PSS&S Compliant Parallel 3-DOF Micro-Rotation Mechanism
Abstract
1. Introduction
2. Description of Mechanism and Definition of Parameters
3. Kinetostatic Modeling and Verification
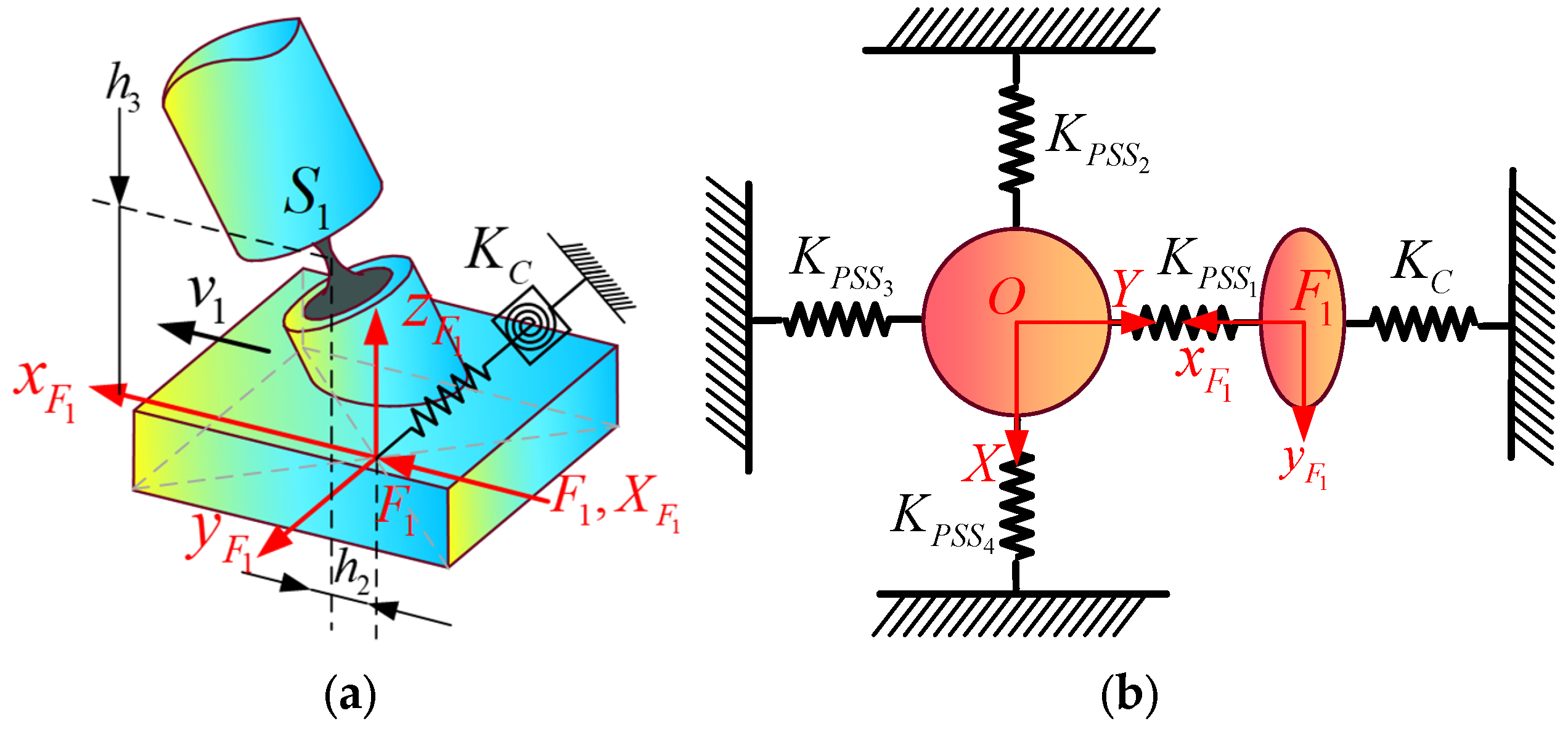
3.1. Compliance Modeling
3.1.1. Compliance Model of the Flexible Spherical Hinge and Its Coordinate Transformation
3.1.2. Compliance Modeling of Each Branch and the Overall Mechanism
3.2. Kinetostatic Modeling
3.2.1. Establishment of Input/Output Force–Displacement Model (F-D Model)
3.2.2. Establishment of Input/Output Displacement–Displacement Model (D-D Model)
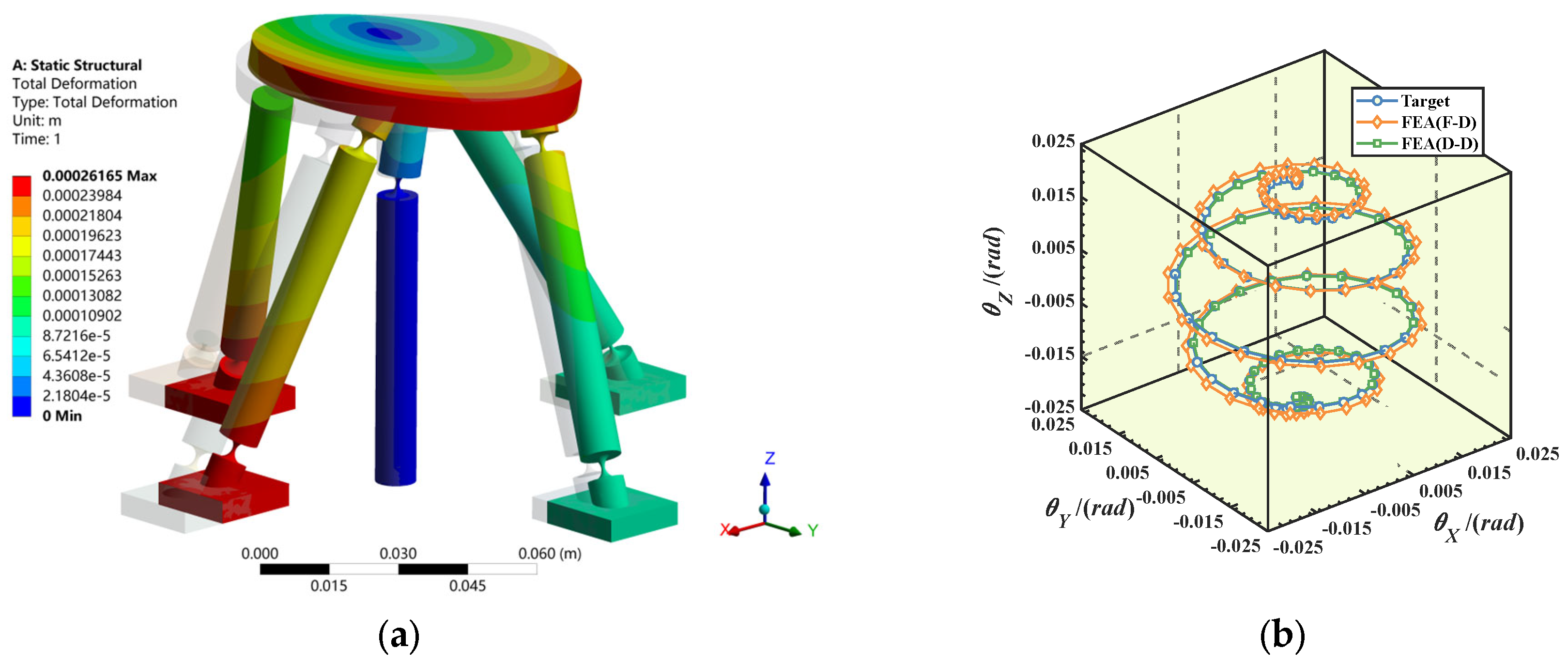
3.3. Example Verification
4. Comparative Analysis of Mechanism Performance
4.1. Comparative Analysis of Peak Actuating Force
4.2. Comparison of Output Stiffness
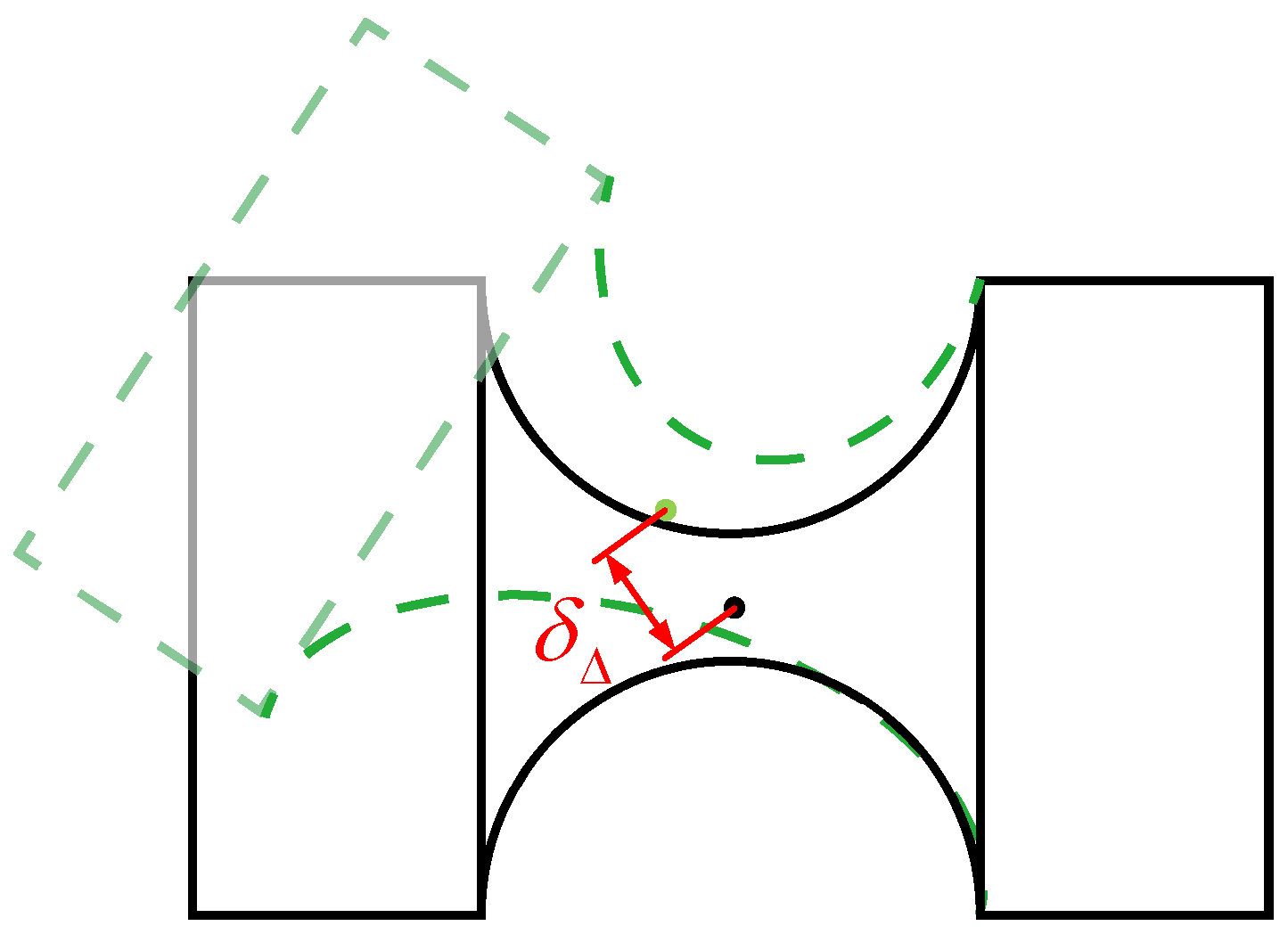
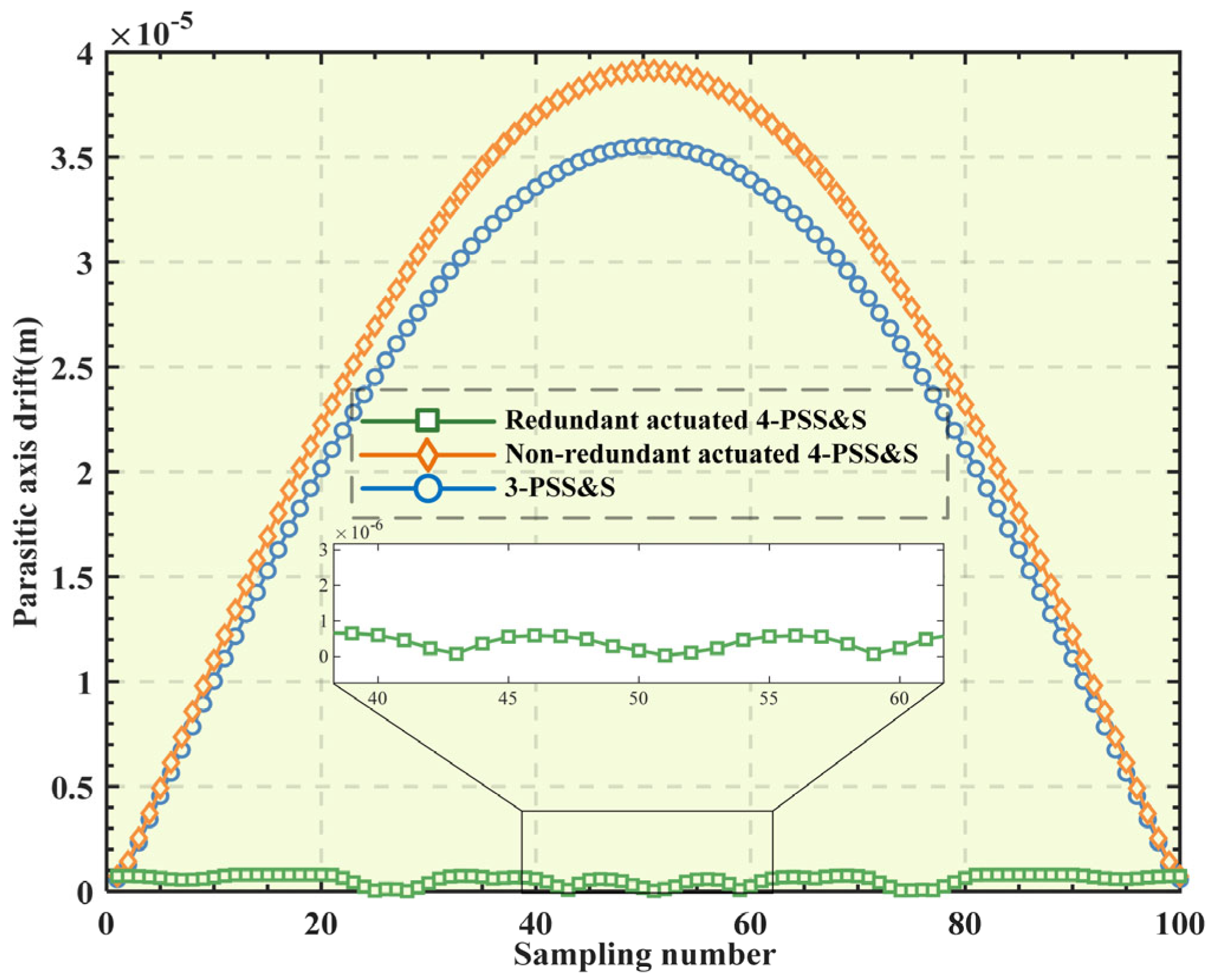
4.3. Comparative Analysis of Parasitic Axis Drift
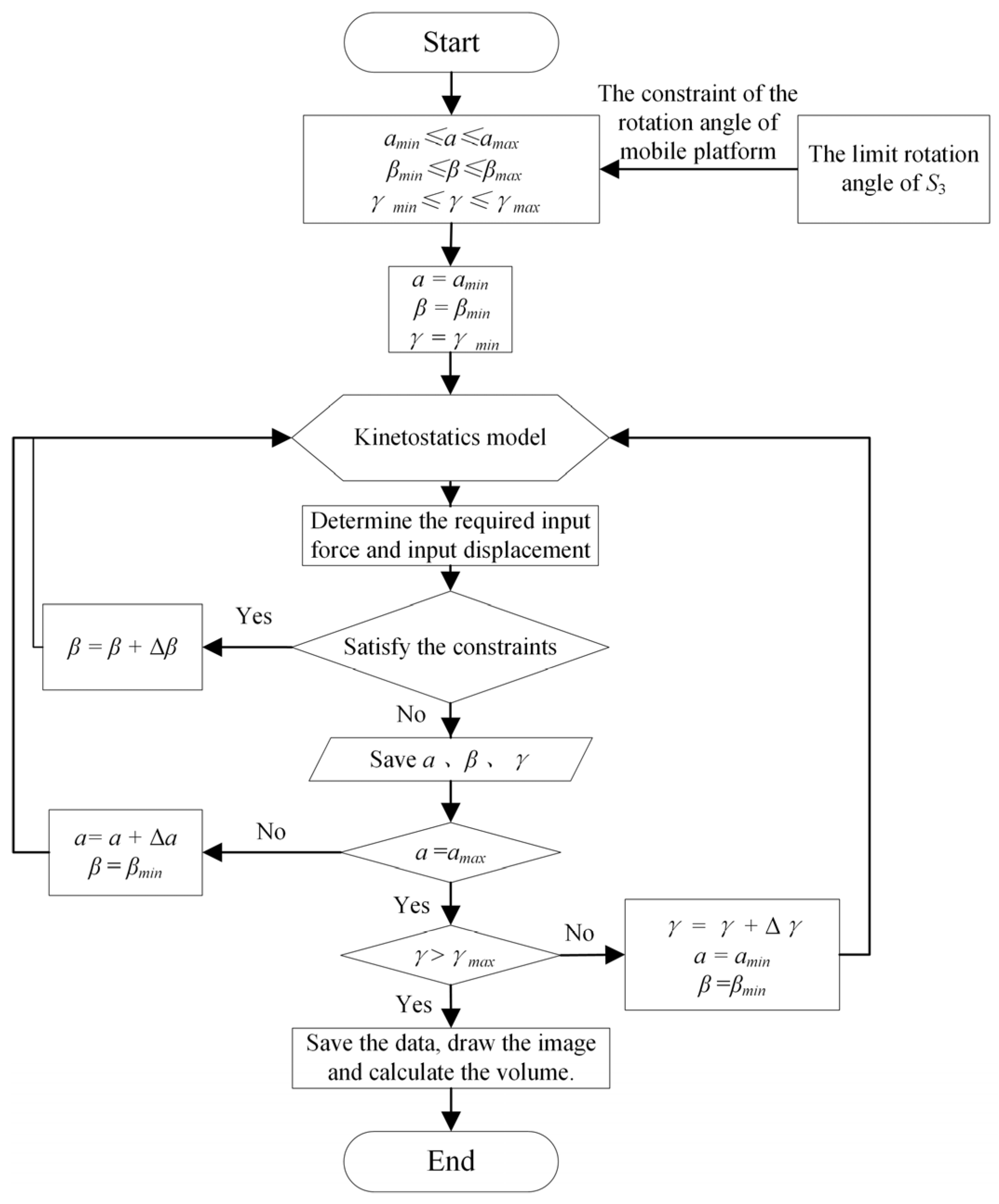
4.4. Analysis of Kinetostatic Workspace
5. Conclusions
- For the 4-PSS&S mechanism, redundant actuation combined with optimized actuating force distribution can effectively reduce the peak actuating force, with the maximum reduction rate reaching up to 50% and the average reduction amplitude being 40.95%. Compared with the 3-PSS&S mechanism, the reduction rate of the peak force of the redundant-actuated 4-PSS&S mechanism is slightly smaller, with an average reduction rate of 10.79% in general.
- Compared with the 3-PSS&S mechanism, the output stiffness of the 4-PSS&S mechanism increases by 26.68% in the θx and θy directions and by 33.31% in the θz direction, indicating that the addition of a redundant branch can significantly improve the output stiffness of the mechanism.
- Compared with the 3-PSS&S mechanism and the non-redundant-actuated 4-PSS&S mechanism, after the optimal distribution of the actuating force, the parasitic axis drift of the redundant-actuated 4-PSS&S mechanism at the restraining spherical hinge S3 is significantly reduced. This shows that the redundant-actuated 4-PSS&S mechanism has higher motion accuracy compared with the other two mechanisms.
- After the optimal distribution of the actuating force, the volume of the workspace of the redundant-actuated 4-PSS&S mechanism increases by 94.32% compared with that of the 3-PSS&S mechanism and by 372.89% compared with that of the non-redundant-actuated 4-PSS&S mechanism.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Ye, L.; Song, X. Magnetic alignment technology for wafer bonding. Microelectron. Int. 2024, 41, 32–40. [Google Scholar] [CrossRef]
- Okubo, T.; Harada, K.; Fujii, M. Hand-held Multi-DOF Robotic Forceps for Neurosurgery Designed for Dexterous Manipulation in Deep and Narrow Space. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Sydney, Australia, 24–27 July 2023. [Google Scholar]
- Cui, G.; Liu, J. Kinematic performance analysis of a cable-driven redundant-actuated parallel manipulator. Int. J. Robot. Autom. 2019, 34, 344–358. [Google Scholar] [CrossRef]
- Chai, X.; Ye, W. Elastostatic stiffness modeling and performance evaluation of a 2UPR-2PRU redundant-actuated parallel manipulator. Machines 2022, 10, 1219. [Google Scholar] [CrossRef]
- Han, M.; Che, J. Performance evaluation and dimensional optimization design of planar 6R redundant actuation parallel mechanism. Robotica 2024, 42, 1649–1675. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, L. Optimal design of loading device based on a redundant-actuated parallel manipulator. Mech. Mach. Theory 2022, 178, 105084. [Google Scholar] [CrossRef]
- Ren, J.; Shu, Y. Kinetostatic modeling and workspace analysis of redundant-actuated n-4R compliant parallel pointing mechanism. Micromachines 2025, 16, 478. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Li, Q. Analysis of compliance and kinetostatic of a novel class of n-4R compliant parallel micro pointing mechanism. Micromachines 2022, 13, 1014. [Google Scholar] [CrossRef] [PubMed]
- Arredondo-Soto, M.; Cuan-Urquizo, E. The compliant version of the 3-RRR spherical parallel mechanism known as “Agile-Eye”: Kinetostatic analysis and parasitic displacement evaluation. Mech. Mach. Theory 2023, 180, 105160. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, P. Kinetostatic analysis of a novel 6-DoF 3UPS parallel manipulator with multi-fingers. Mech. Mach. Theory 2014, 78, 36–50. [Google Scholar] [CrossRef]
- Ren, J.; Wu, H. Kinematic modeling of a novel 3-PSS/S flexible parallel micro-turntable: Accuracy comparison between pseudo-rigid-body model-based and compliance matrix method-based models. Iran. J. Sci. Technol.-Trans. Mech. Eng. 2023, 47, 2071–2088. [Google Scholar] [CrossRef]
- Arredondo-Soto, M.; Cuan-Urquizo, E. The compliance matrix method for the kinetostatic analysis of flexure-based compliant parallel mechanisms: Conventions and general force-displacement cases. Mech. Mach. Theory 2022, 168, 104583. [Google Scholar] [CrossRef]
- Kedzierski, O. Characterization of matrices satisfying the reverse order law for the Moore-Penrose pseudoinverse. Linear Multilinear Algebra 2025. [Google Scholar] [CrossRef]
- Yang, M.; Sun, M. Design of a redundant-actuated 4-PPR planar 3-DOF compliant nanopositioning stage. Precis. Eng. 2023, 82, 68–79. [Google Scholar] [CrossRef]
- Verotti, M.; Serafino, S. Position accuracy criteria for planar flexural hinges. Precis. Eng. 2023, 80, 82–94. [Google Scholar] [CrossRef]
- Zhou, Y.; Niu, J. A novel numerical approach for workspace determination of parallel mechanisms. J. Mech. Sci. Technol. 2017, 31, 3005–3015. [Google Scholar] [CrossRef]
- Saputra, V.B.; Ong, S.K. A swarm optimization approach for solving workspace determination of parallel manipulators. Robotica 2015, 33, 649–668. [Google Scholar] [CrossRef]


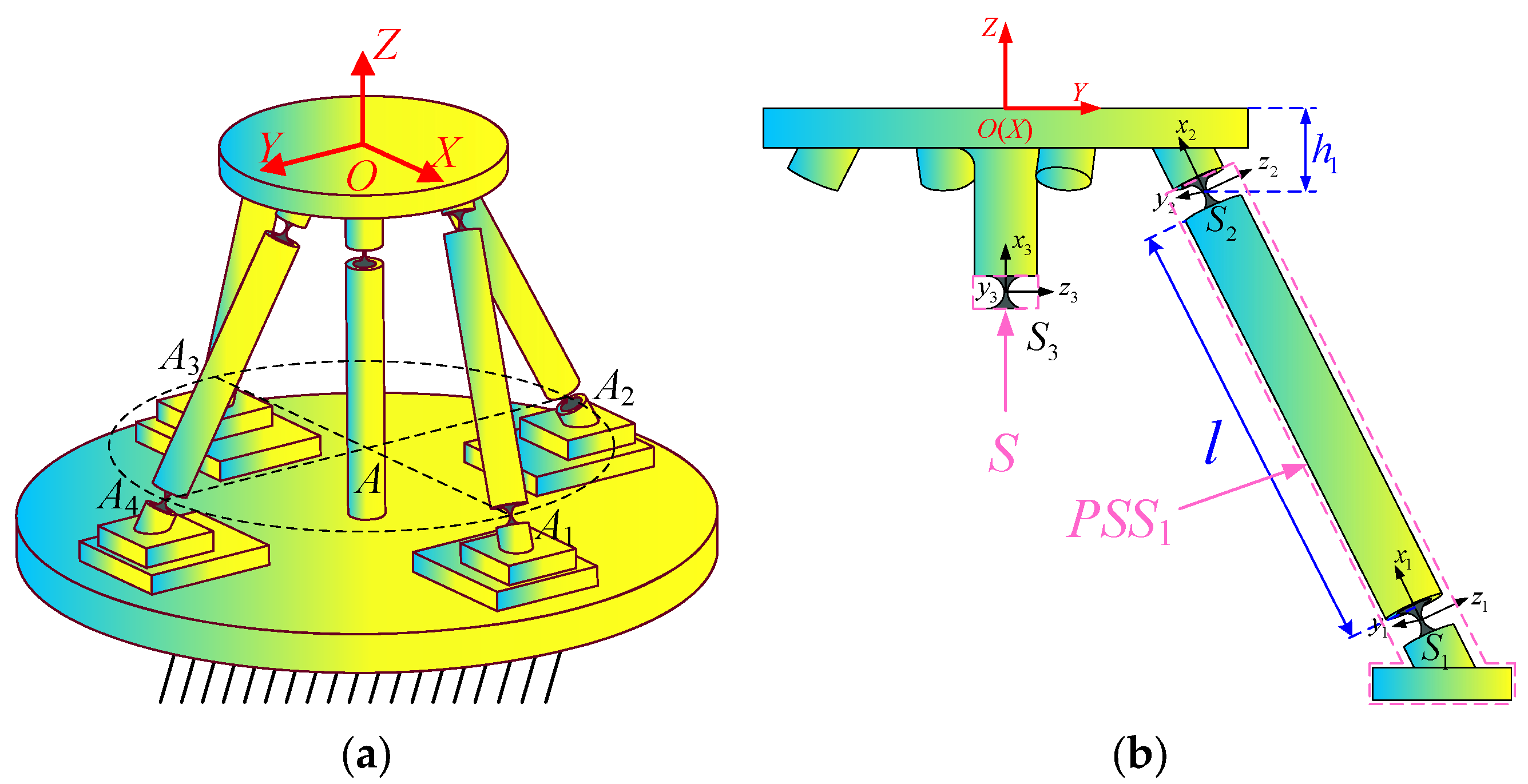






| Parameter | Value (mm) | Parameter | Value (mm) |
|---|---|---|---|
| r | 30 | r0 | 2.5 |
| R | 60 | tmin | 0.8 |
| h0 | 15 | h1 | 13 |
| h | 50 | h2 | 2 |
| l | 72.5 | h3 | 12 |
| Output Stiffness (N/rad) | 3-PSS&S | 4-PSS&S | Increase in Amplitude |
|---|---|---|---|
| θx(θy) | 2.353 × 104 | 2.981 × 104 | +26.68% |
| θz | 3.414 × 103 | 4.552 × 103 | +33.31% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Xiao, R.; Lu, Y. Kinetostatic Modeling and Performance Analysis of Redundant-Actuated 4-PSS&S Compliant Parallel 3-DOF Micro-Rotation Mechanism. Micromachines 2025, 16, 612. https://doi.org/10.3390/mi16060612
Ren J, Xiao R, Lu Y. Kinetostatic Modeling and Performance Analysis of Redundant-Actuated 4-PSS&S Compliant Parallel 3-DOF Micro-Rotation Mechanism. Micromachines. 2025; 16(6):612. https://doi.org/10.3390/mi16060612
Chicago/Turabian StyleRen, Jun, Ruihan Xiao, and Yahao Lu. 2025. "Kinetostatic Modeling and Performance Analysis of Redundant-Actuated 4-PSS&S Compliant Parallel 3-DOF Micro-Rotation Mechanism" Micromachines 16, no. 6: 612. https://doi.org/10.3390/mi16060612
APA StyleRen, J., Xiao, R., & Lu, Y. (2025). Kinetostatic Modeling and Performance Analysis of Redundant-Actuated 4-PSS&S Compliant Parallel 3-DOF Micro-Rotation Mechanism. Micromachines, 16(6), 612. https://doi.org/10.3390/mi16060612






