Study on the Driving Performance and Influencing Factors of Multi-Electrothermal Co-Actuation Devices Considering Application Environments
Abstract
1. Introduction
2. Overall Structure of Multi-Electrothermal Co-Actuation Device
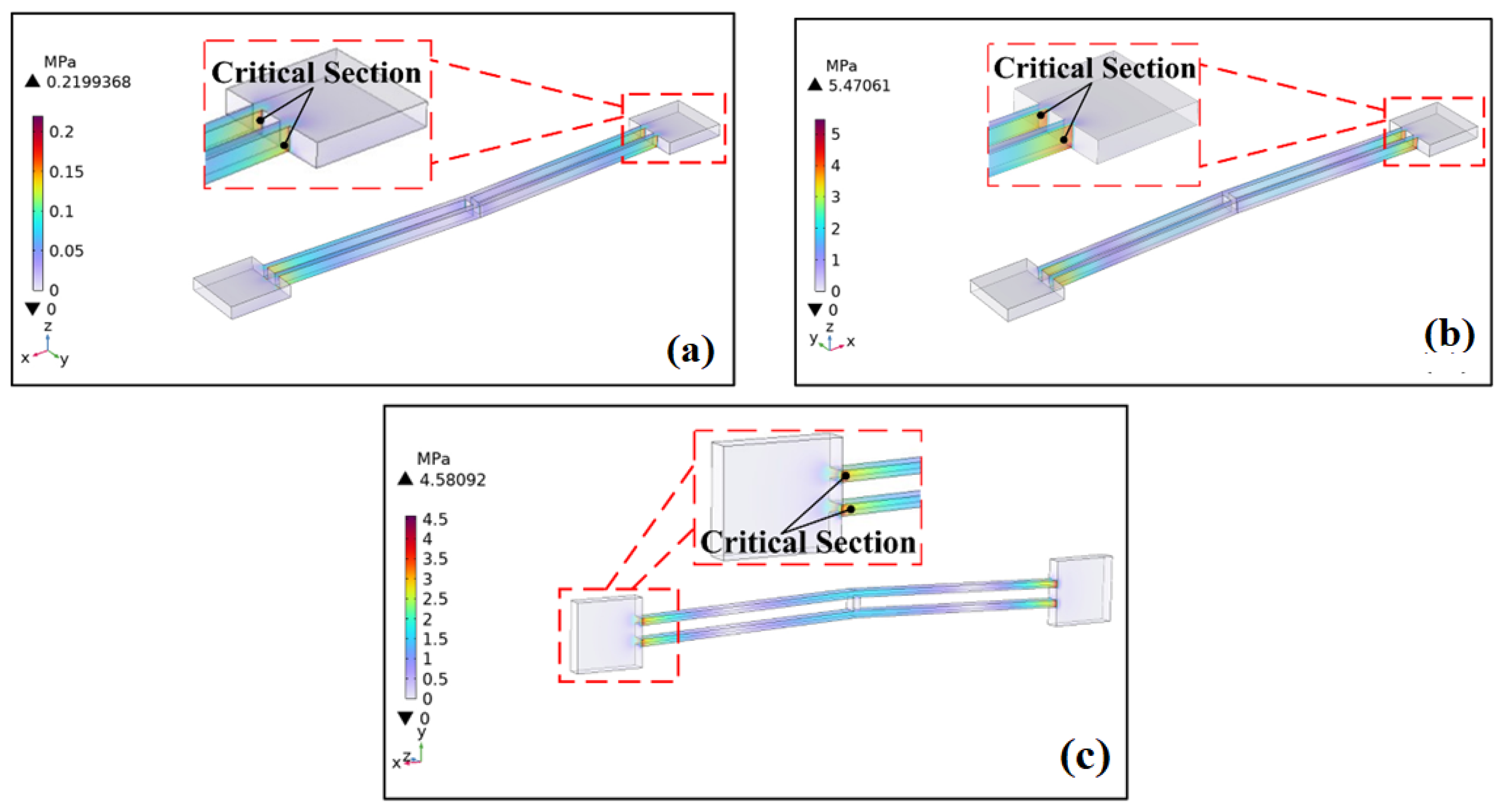
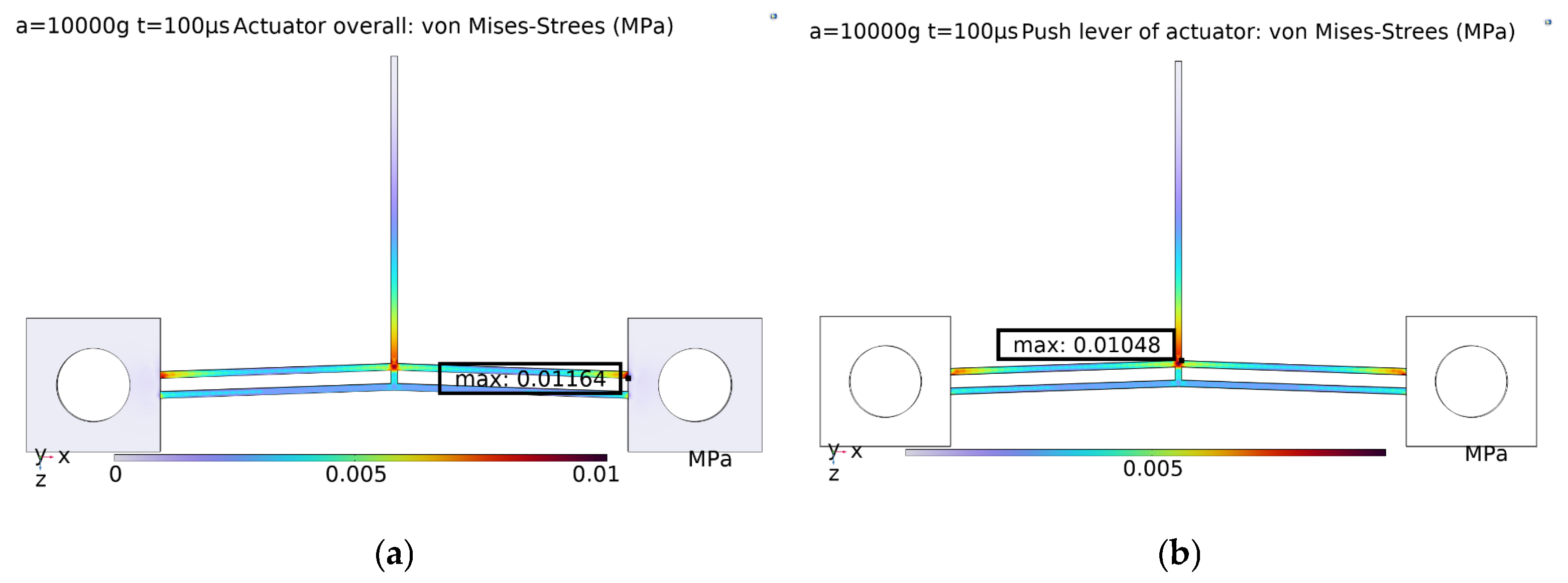
3. Analysis of High Overload Resistance Performance of the Multi-Electrothermal Co-Actuation Device
4. Simulation Analysis of Performance-Influencing Factors of the Multi-Electrothermal Co-Actuation Device
4.1. Structural Influencing Factors
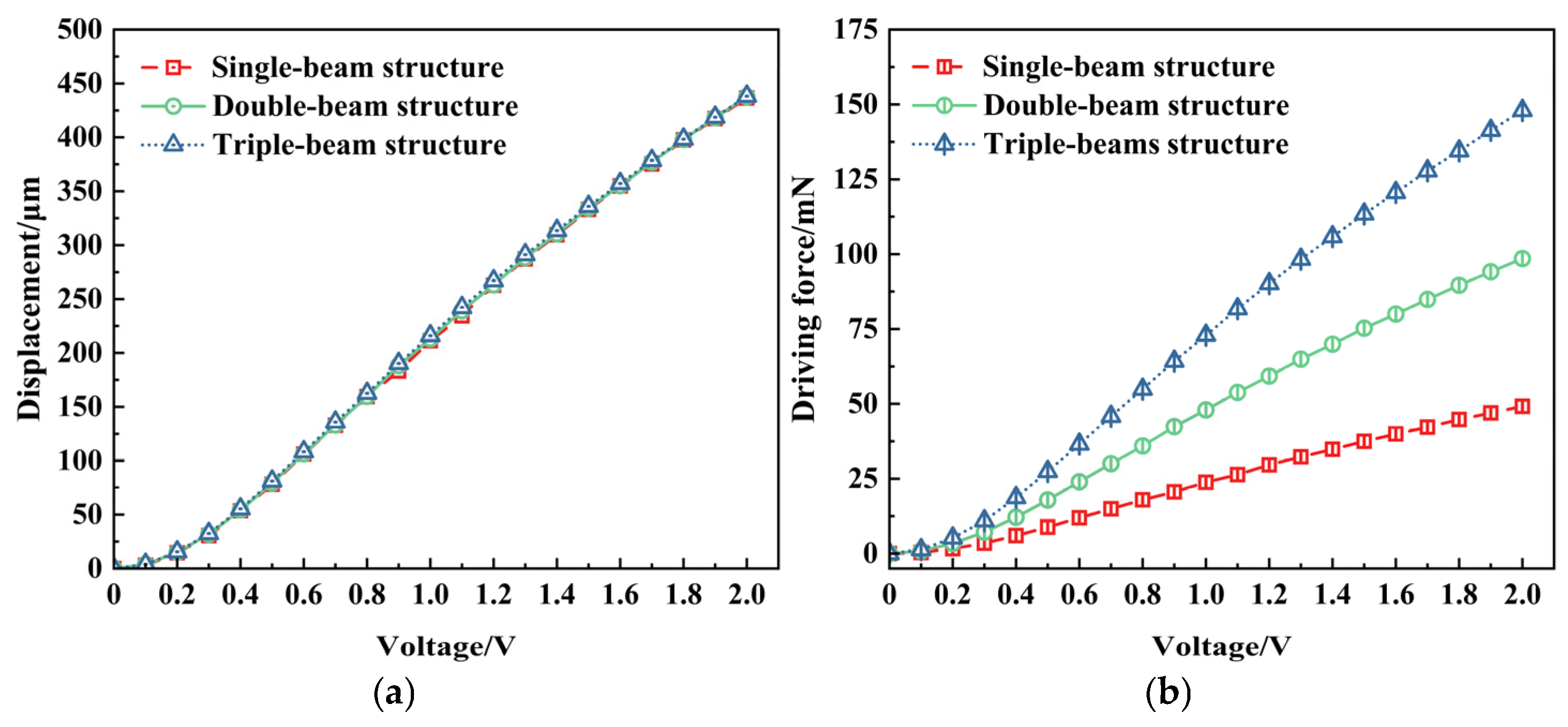
4.1.1. Number of the Actuating V-Beams
4.1.2. Air Gap
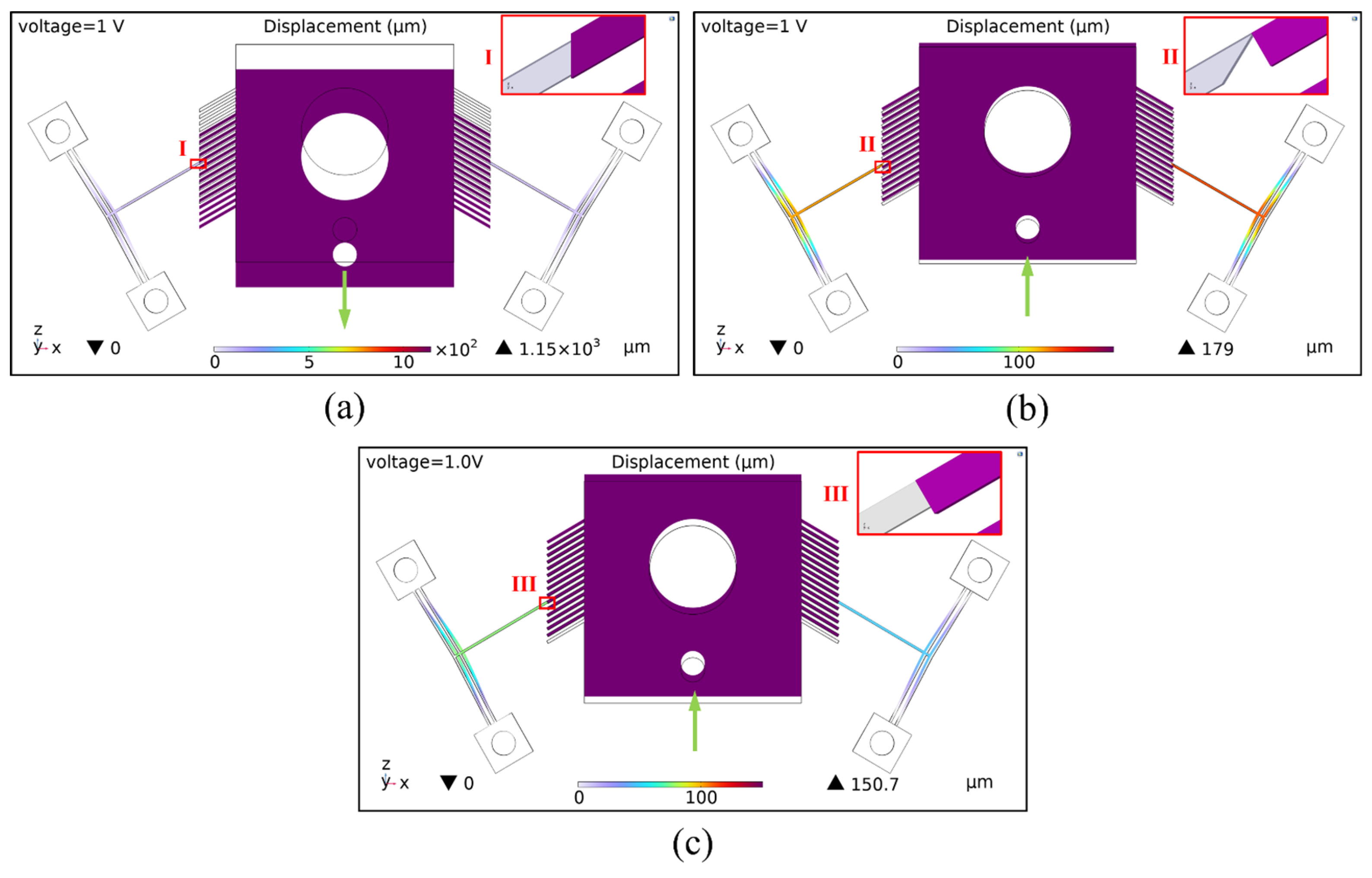
4.1.3. Type of Contact Surface
4.2. External Influencing Factors
4.2.1. External Load Force
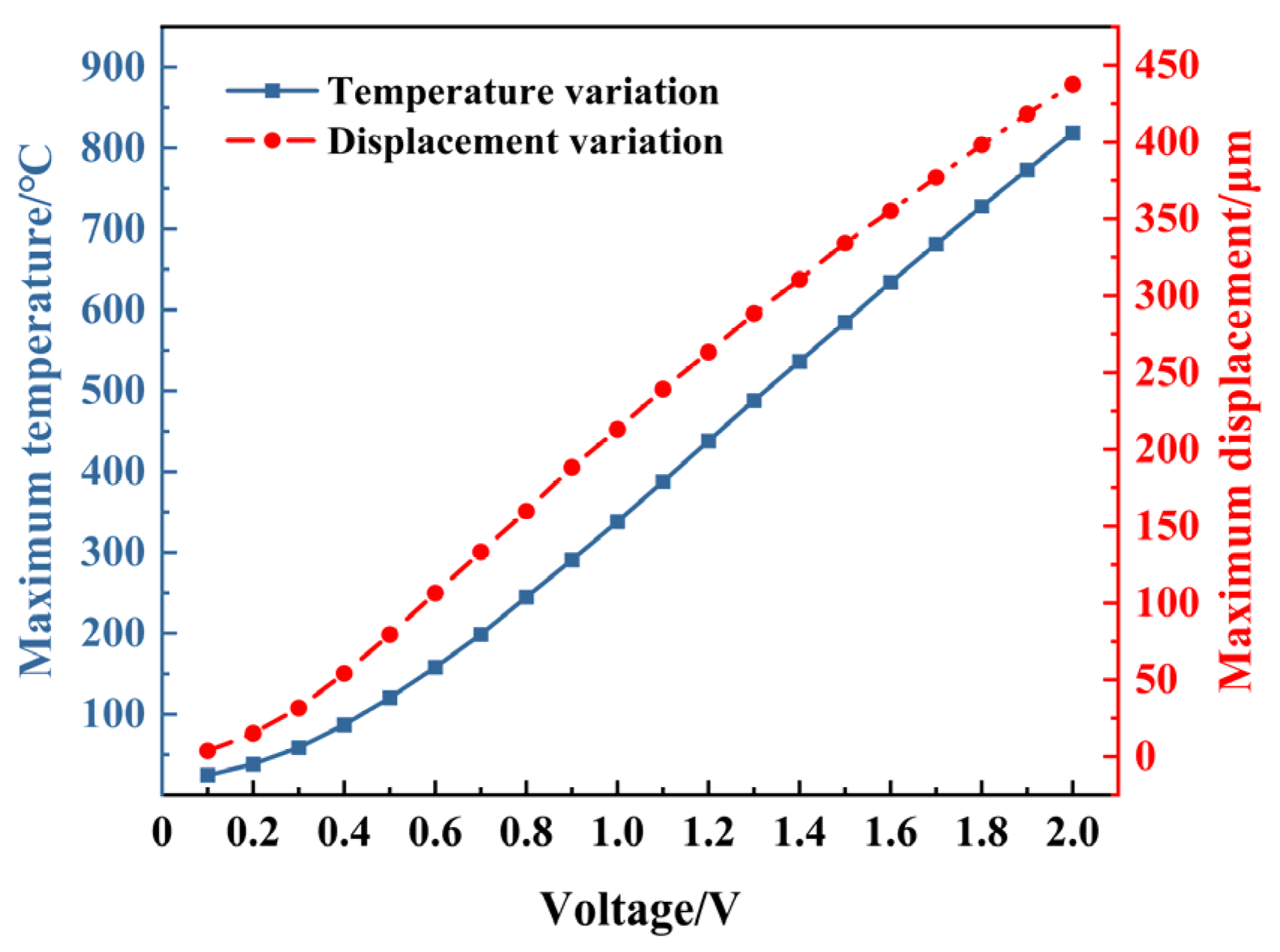
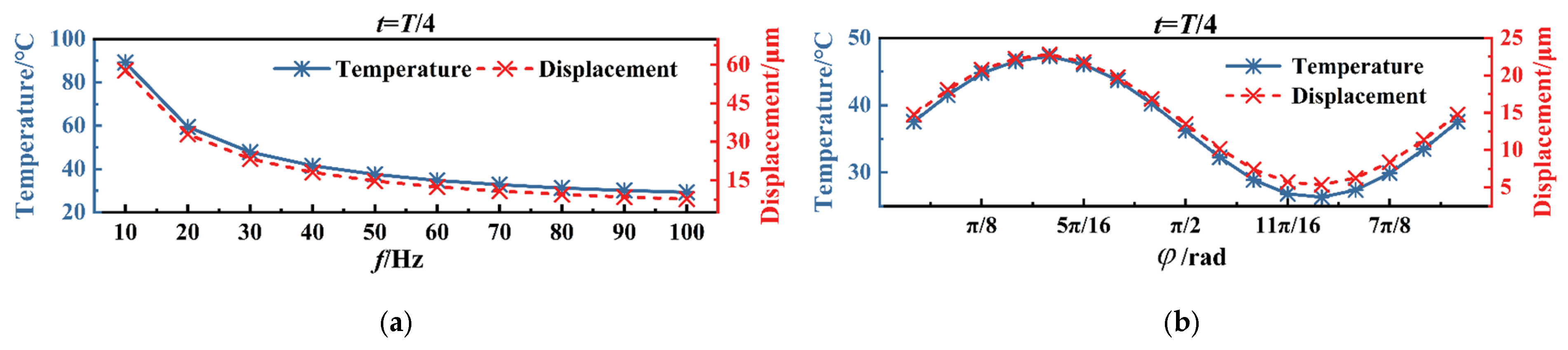
4.2.2. Periodic Voltage
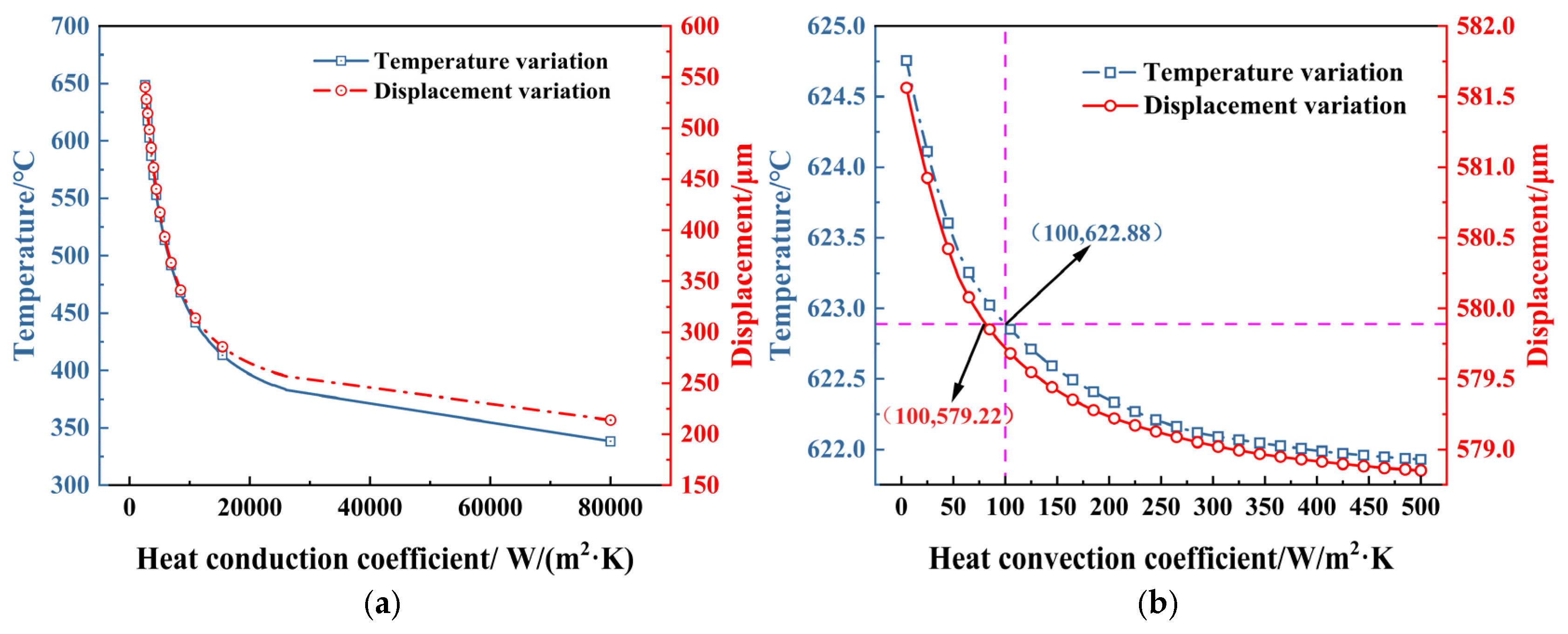
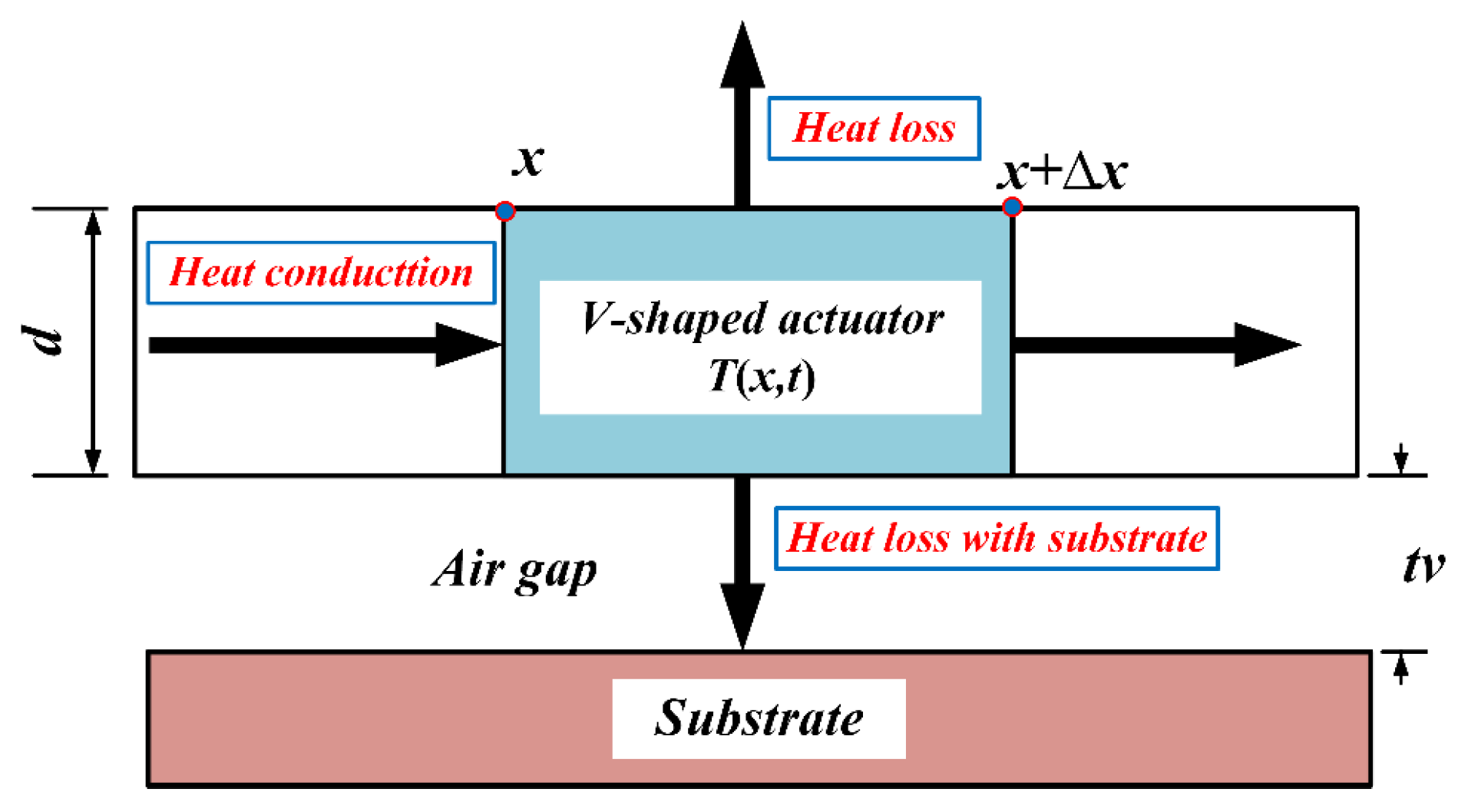
4.2.3. Heat Transfer
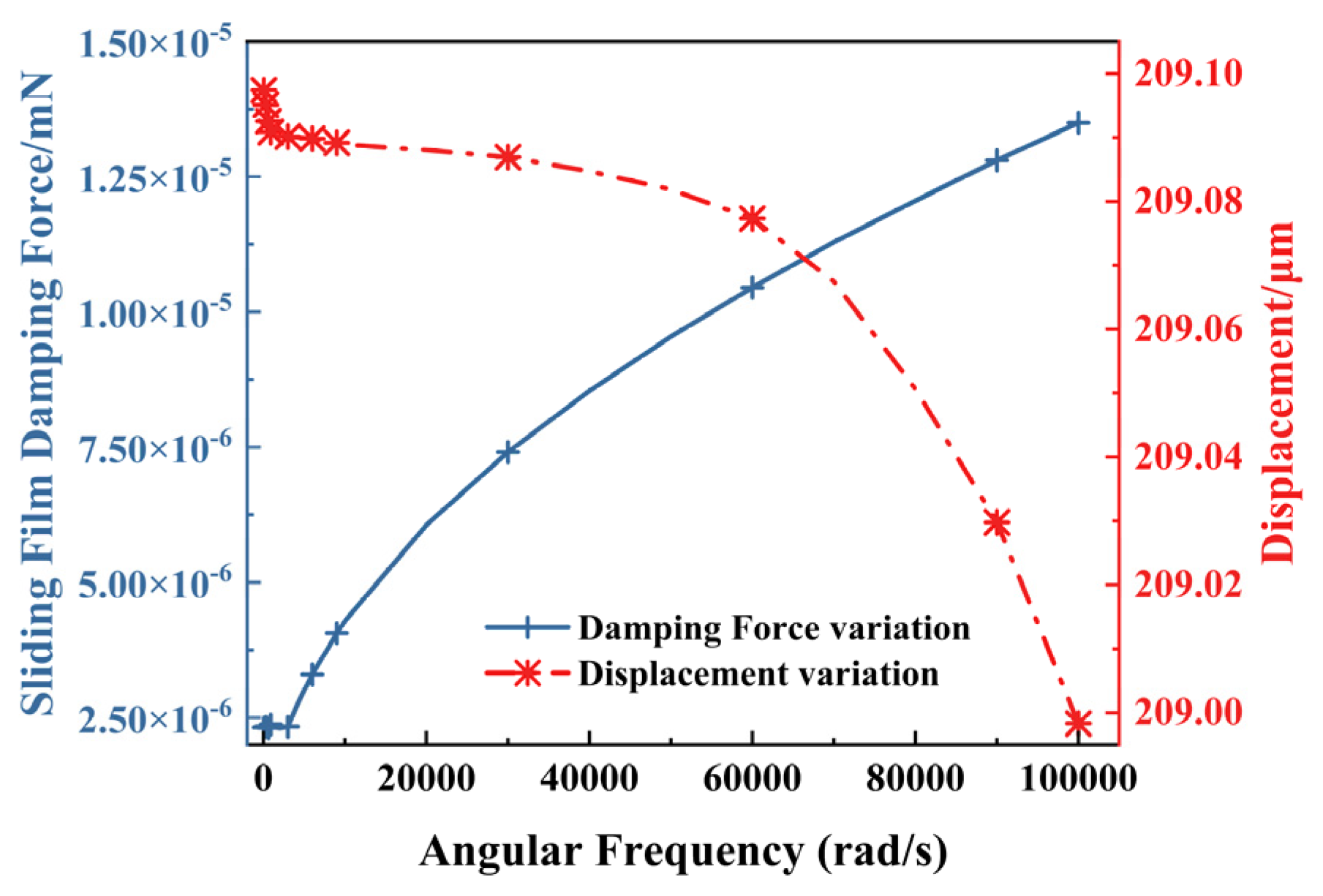
4.2.4. Gas Damping
5. Performance Experiments of the Multi-Electrothermal Co-Actuation Device
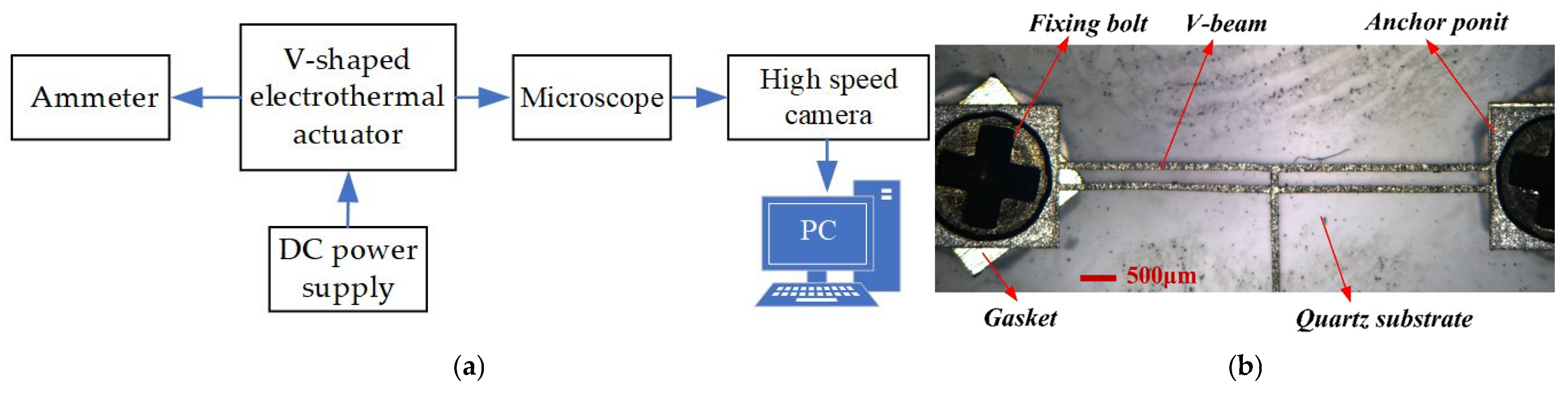
5.1. Experiments of Processing Technology Influence on the Actuator Performance
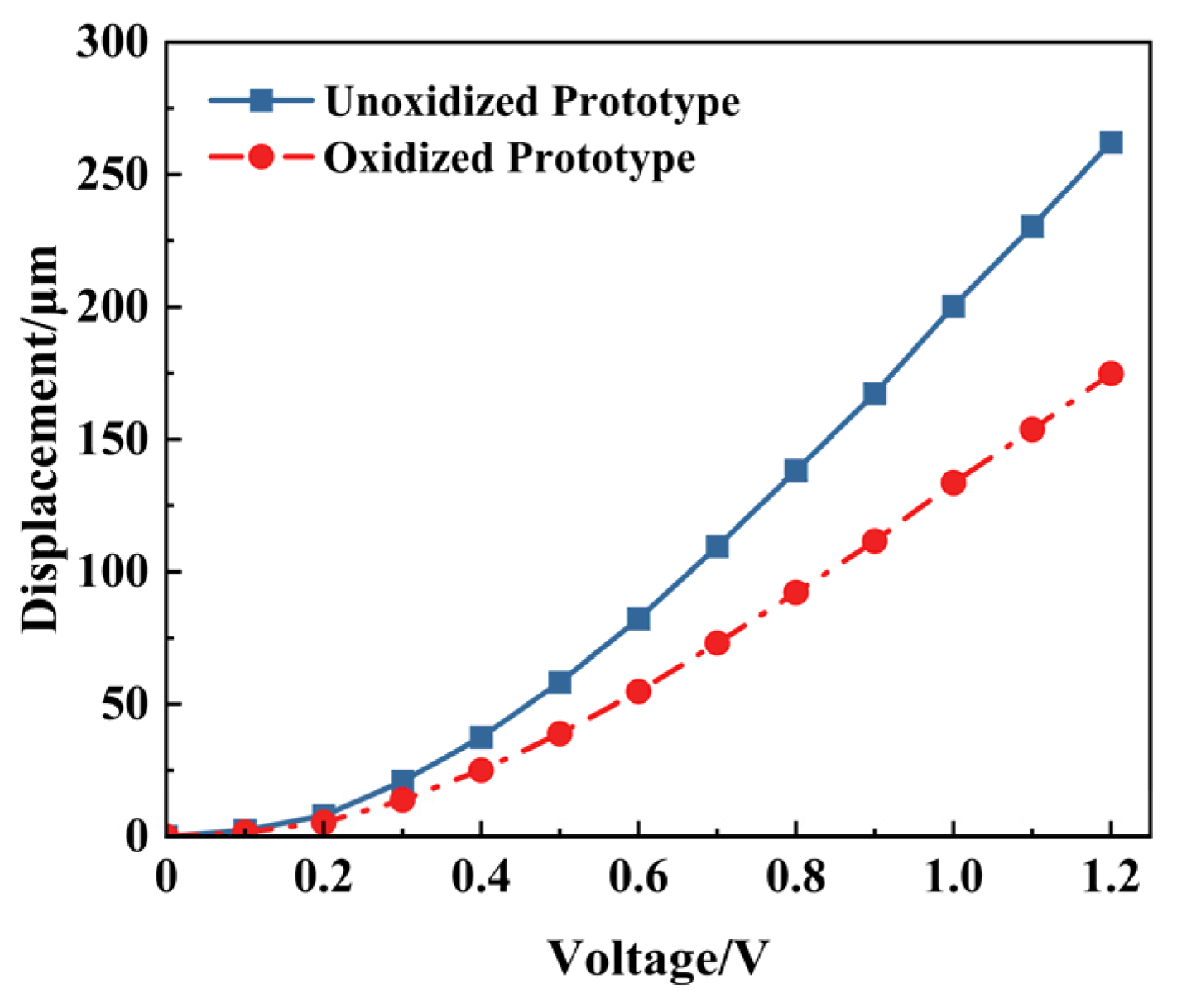
5.1.1. Influence of Material Characteristics Changes on Actuator Performance
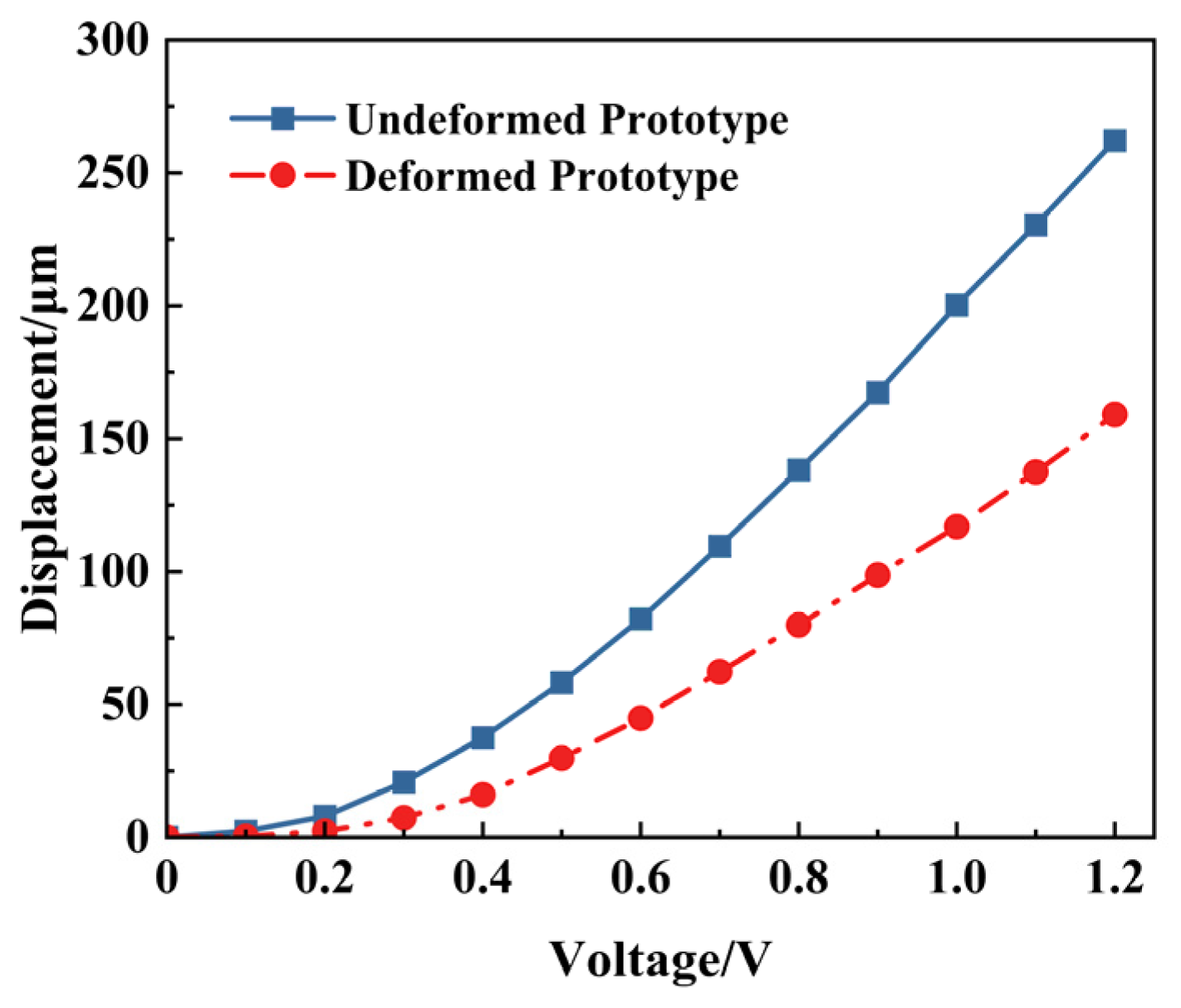
5.1.2. Influence of Deformation Caused by External Forces on Actuator Performance
5.2. Experiment of Contact Surface Type Influence on the Slider Output Performance
5.3. Experiment of High Overload Resistance Performance
5.3.1. Experiment Under Impact Load in Six Directions
5.3.2. Experiment Under Impact Load at an Angle of 30° to the y Direction
6. Conclusions
- Based on finite element simulation, the effects of influence factors such as the number of V-beams, air gaps, contact surface type, external load force, periodic voltage, heat transfer, and slip film damping on the multi-electrothermal co-actuation device’s performance are investigated. The simulation results indicate that adequately optimizing structural parameters and driving conditions can significantly enhance the device’s performance. In addition, the flameproof slider’s contact surface II structure provides the best output displacement performance.
- The multi-electrothermal co-actuation device has excellent high overload resistance performance. It maintains stable driving performance under high-impact load conditions, with only slight and recoverable deformation observed at the push lever, which meets the high overload resistance requirements of fuze applications.
- Temperature changes and external forces during the laser fabrication process will influence the actuator’s performance to different degrees. Experimental results show that changes in the material properties of the structural deformation lead to performance degradation, so strict control of influence factors in the fabrication process is necessary to ensure the stability of the driving performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ishihara, H.; Arai, F.; Fukuda, T. Micro mechatronics and microactuators. IEEE/ASME Trans. Mechatron. 1996, 1, 68–79. [Google Scholar] [CrossRef]
- Algoos, Y.; Lenz, W.B.; Khan, F.; Younis, M.I. An electrostatically actuated MEMS microgripper with high amplification for precision manipulation. Sens. Actuators A Phys. 2024, 378, 115800. [Google Scholar] [CrossRef]
- Duan, B.; Hu, H.; Lei, Y.; Chen, J. Design and experimental investigation of a novel stick-slip piezoelectric actuator based on V-shaped driving mechanism. Mechatronics 2023, 95, 103067. [Google Scholar] [CrossRef]
- Nah, S.K.; Zhong, Z.W. A microgripper using piezoelectric actuation for micro-object manipulation. Sens. Actuators A Phys. 2007, 133, 218–224. [Google Scholar] [CrossRef]
- Zhu, K.; Li, H.; Zhang, X.; Xu, T.; Li, S. A miniature electromagnetic linear actuator with 3D MEMS coil. IEEE Electron Device Lett. 2023, 44, 1732–1735. [Google Scholar] [CrossRef]
- Sciberras, T.; Demicoli, M.; Grech, I.; Mallia, B.; Mollicone, P.; Sammut, N. Coupled finite element-finite volume multi-physics analysis of MEMS electrothermal actuators. Micromachines 2021, 13, 8. [Google Scholar] [CrossRef]
- Potekhina, A.; Wang, C. Review of electrothermal actuators and applications. Actuators 2019, 8, 69. [Google Scholar] [CrossRef]
- Jackson, N.; Sridharan, A.; Anand, S.; Baker, M.; Okandan, M.; Muthuswamy, J. Long-term neural recordings using MEMS based moveable microelectrodes in the brain. Front. Neuroeng. 2010, 3, 1302. [Google Scholar] [CrossRef]
- Shen, Y.Y.; Song, R.C.; Tang, H.M.; Chen, Q.S.; Guan, P. The Dynamic Characteristics Research of MEMS V-Shaped SiO2/Al Electrothermal Actuator. Key Eng. Mater. 2015, 645, 963–967. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Hoang, K.T.; Pham, P.H. Larger displacement of silicon electrothermal V-shaped actuator using surface sputtering process. Microsyst. Technol. 2021, 27, 1985–1991. [Google Scholar] [CrossRef]
- Tecpoyotl-Torres, M.; Vargas-Chable, P.; Escobedo-Alatorre, J.; Cisneros-Villalobos, L.; Sarabia-Vergara, J. Z-Shaped Electrothermal Microgripper Based on Novel Asymmetric Actuator. Micromachines 2022, 13, 1460. [Google Scholar] [CrossRef] [PubMed]
- Vargas-Chable, P.; Tecpoyotl-Torres, M.; Vera-Dimas, G.; Grimalsky, V.; Mireles García, J., Jr. Novel Electrothermal Microgrippers Based on a Rotary Actuator System. Micromachines 2022, 13, 2189. [Google Scholar] [CrossRef]
- Ho, Y.N.; Michael, A.; Kwok, C.Y.; Pulikkaseril, C. Parallel in-plane electrothermal actuators. J. Microelectromech. Syst. 2024, 33, 305–307. [Google Scholar] [CrossRef]
- Ostrow, S.A.; Lake, R.A.; Lombardi, J.P.; Coutu, R.A.; Starman, L.A. Fabrication process comparison and dynamics evaluation of electrothermal actuators for a prototype MEMS safe and arming devices. Exp. Mech. 2012, 52, 1229–1238. [Google Scholar] [CrossRef]
- Li, X.; Zhao, Y.; Hu, T.; Bai, Y. Design of a high-speed electrothermal linear micromotor for microelectromechanical systems safety-and-arming devices. Micro Nano Lett. 2016, 11, 692–696. [Google Scholar] [CrossRef]
- Wang, D.; Lou, W.; Feng, Y.; Wang, F. Design, Fabrication and Analysis of Threshold-Value Judging Mechanism in MEMS Safety and Arming Device. Preprints 2017. [Google Scholar] [CrossRef]
- Hu, T.; Fang, K.; Zhang, Z.; Jiang, X.; Zhao, Y. Design and research on large displacement bidirectional MEMS stage with interlock mechanism. Sens. Actuators A Phys. 2018, 283, 26–33. [Google Scholar] [CrossRef]
- Tang, Y.; Guo, Z.; Ding, Y.; Wang, X. Design and Driving Characteristics of a Bidirectional Micro-Device Based on Multi-Electrothermal Co-Actuation. Micromachines 2025, 16, 487. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, Y.; Liu, X.; Zhang, X. Dynamic modelling and analysis of V-and Z-shaped electrothermal microactuators. Microsyst. Technol. 2017, 23, 3775–3789. [Google Scholar] [CrossRef]
- Qin, H.; Jiang, X. Low-g MEMS inertial switch with spiral spring for fuze. J. Terahertz Sci. Electron. Inf. Technol. 2024, 22, 459–466. [Google Scholar]
- Chen, W.; Cao, Y.; Kong, X.; Xie, H.; Xi, Z. Research of Anti-High Overload Performance of U and V- Shaped Micro Electrothermal Actuators. J. Shanghai Jiaotong Univ. 2024. [Google Scholar] [CrossRef]
- Gwinn, J.P.; Webb, R.L. Performance and testing of thermal interface materials. Microelectron. J. 2003, 34, 215–222. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, X.; Wang, X. Design and analysis of large displacement bidirectional device based on multi-electrothermal co-actuation. J. Phys. Conf. Ser. 2024, 2853, 012033. [Google Scholar] [CrossRef]
- Bityukov, V.K.; Khudak, Y.I.; Gusein-Zade, N.G. Analytical derivation of the Stefan–Boltzmann law for integral radiance from Planck’s law for spectral radiance. Bull. Lebedev Phys. Inst. 2018, 45, 46–50. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, W.; Wu, Q.; Yu, Y.; Liu, X.; Zhang, X. A comprehensive analytical model and experimental validation of Z-shaped electrothermal microactuators. In Recent Advances in Mechanism Design for Robotics, Proceedings of the 3rd IFToMM Symposium on Mechanism Design for Robotics, Aalborg, Denmark, 2–4 June 2015; Springer: Cham, Switzerland, 2015; pp. 177–187. [Google Scholar]
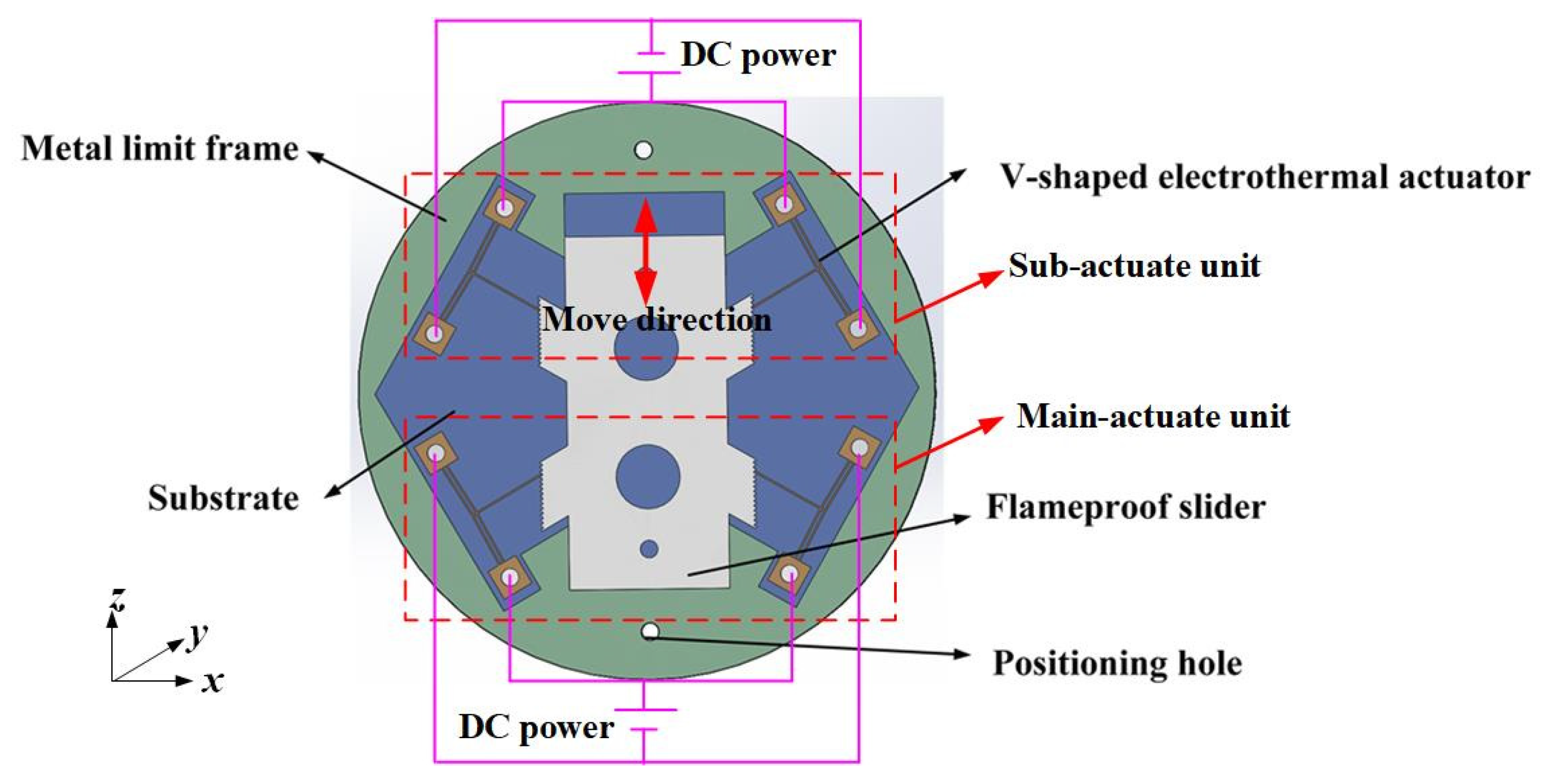











| Parameter Name | Parameters | Physical Unit | Specific Value |
|---|---|---|---|
| Length of the actuator | Lz | μm | 7000 |
| Thickness of the actuator | d | μm | 200 |
| Width of the actuator | a | μm | 100 |
| Tilt angle of the V beam | θ | ° | 2 |
| Length of the lever | Lp | μm | 5000 |
| Prototype | Direction | Amplitude/g | Pulse Width/μs | Break or Not |
|---|---|---|---|---|
| Prototype 1 | +x | 8600/10,600/9200 | 71.79/91.79/73.29 | Not |
| Prototype 2 | −x | 8400/9600/11,000 | 75.79/89.79/77.79 | Not |
| Prototype 3 | +y | 7200/9600/12,000 | 79.79/75.79/73.79 | Not |
| Prototype 4 | −y | 6400/10,600/9400 | 81.79/77.79/75.79 | Not |
| Prototype 5 | +z | 8600/10,600/12,200 | 77.79/89.79/81.79 | Not |
| Prototype 6 | −z | 7800/8400/12,600 | 71.79/71.79/75.79 | Not |
| Impact Load Number | Amplitude/g | Pulse Width/μs | Deformity or Not |
|---|---|---|---|
| Impact load 1 | 7800 | 71.79 | Not |
| Impact load 2 | 8600 | 75.79 | Not |
| Impact load 3 | 9200 | 73.29 | Not |
| Impact load 4 | 10,600 | 77.79 | Not |
| Impact load 5 | 11,000 | 77.79 | Not |
| Impact load 6 | 12,000 | 73.79 | Not |
| Impact load 7 | 12,200 | 69.79 | Not |
| Impact load 8 | 13,800 | 67.79 | A little |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Guo, Z.; Ding, Y.; Wang, X. Study on the Driving Performance and Influencing Factors of Multi-Electrothermal Co-Actuation Devices Considering Application Environments. Micromachines 2025, 16, 603. https://doi.org/10.3390/mi16060603
Tang Y, Guo Z, Ding Y, Wang X. Study on the Driving Performance and Influencing Factors of Multi-Electrothermal Co-Actuation Devices Considering Application Environments. Micromachines. 2025; 16(6):603. https://doi.org/10.3390/mi16060603
Chicago/Turabian StyleTang, Yujuan, Zihao Guo, Yujiao Ding, and Xinjie Wang. 2025. "Study on the Driving Performance and Influencing Factors of Multi-Electrothermal Co-Actuation Devices Considering Application Environments" Micromachines 16, no. 6: 603. https://doi.org/10.3390/mi16060603
APA StyleTang, Y., Guo, Z., Ding, Y., & Wang, X. (2025). Study on the Driving Performance and Influencing Factors of Multi-Electrothermal Co-Actuation Devices Considering Application Environments. Micromachines, 16(6), 603. https://doi.org/10.3390/mi16060603







