High-Resolution Thermometric Scheimpflug LiDAR for Surface Morphology and Temperature Mapping
Abstract
1. Introduction
2. Principle
2.1. Scheimpflug Principle
2.2. Upconversion Primary Thermometry
3. System and Calibration
3.1. System Setup
3.2. Sample Preparation
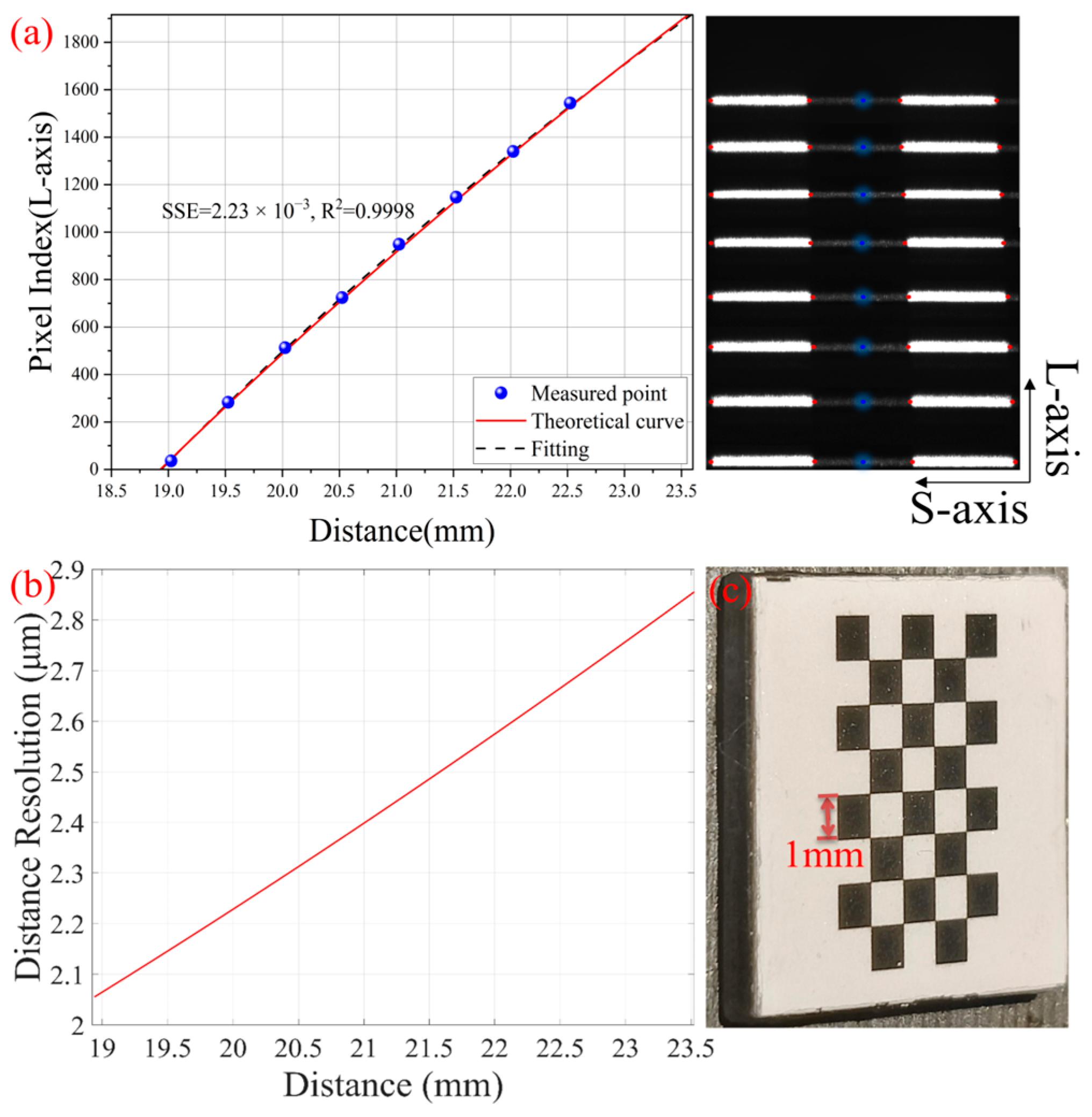
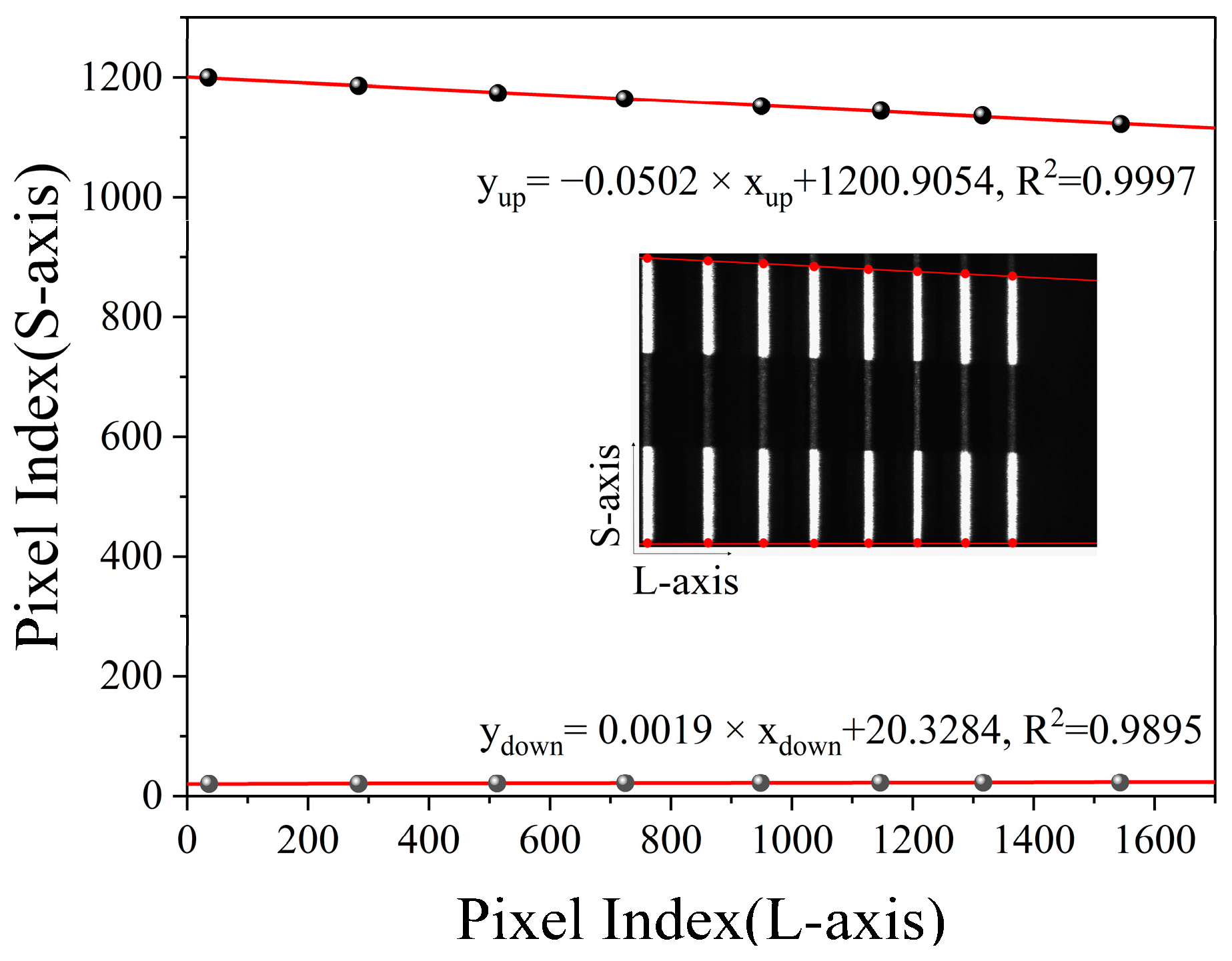
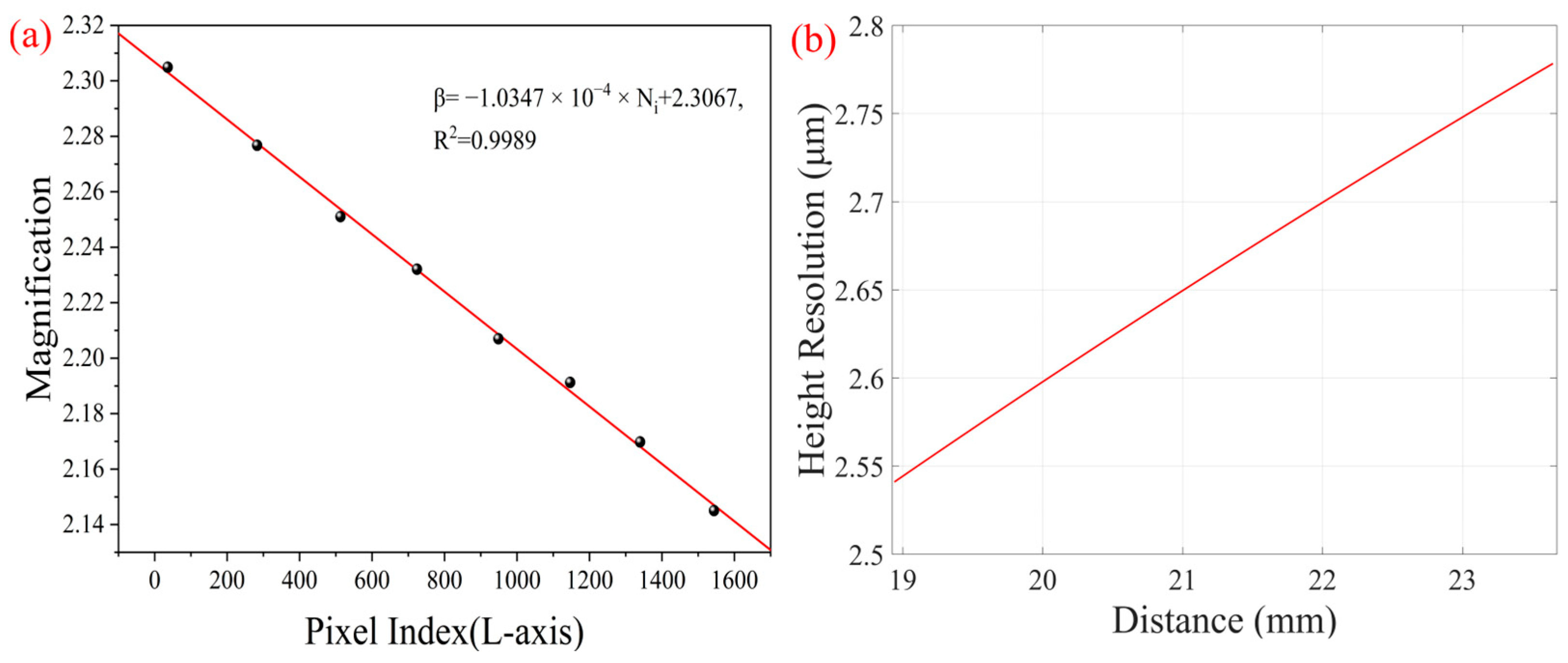
3.3. Distance and Height Calibration of Morphology Information Path
3.3.1. Morphology Depth Calibration (z-Axis)
3.3.2. Morphology Height Calibration (y-Axis)
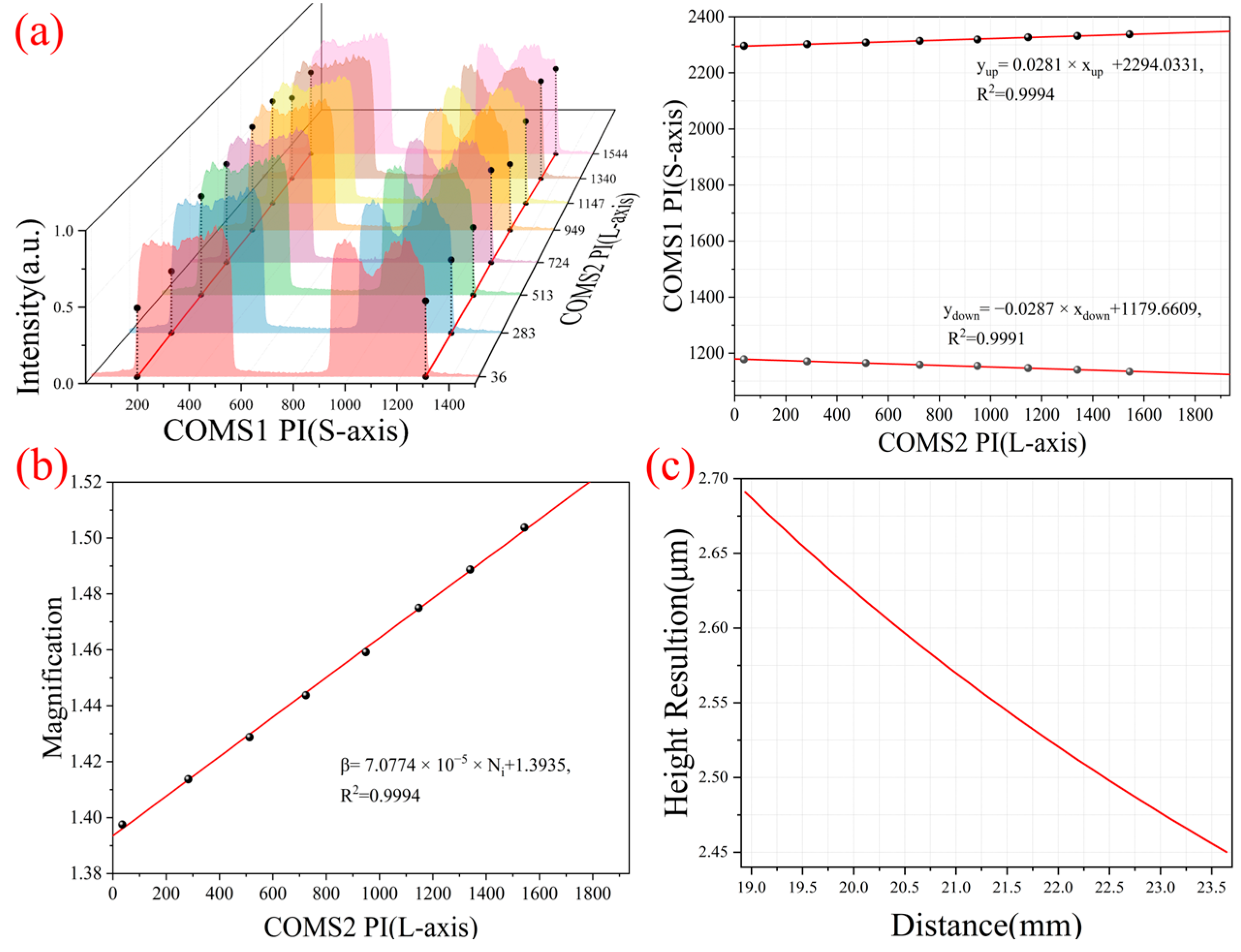
3.4. Height and Temperature Calibration of Fluorescence Spectrum Information Path
3.4.1. Height Calibration (y-Axis)
3.4.2. Spectral and Temperature Calibration (λ-Axis)
3.5. Data Fusion and Temperature Inversion
4. Results and Discussion
4.1. Verification of Morphology Reconstruction Capability
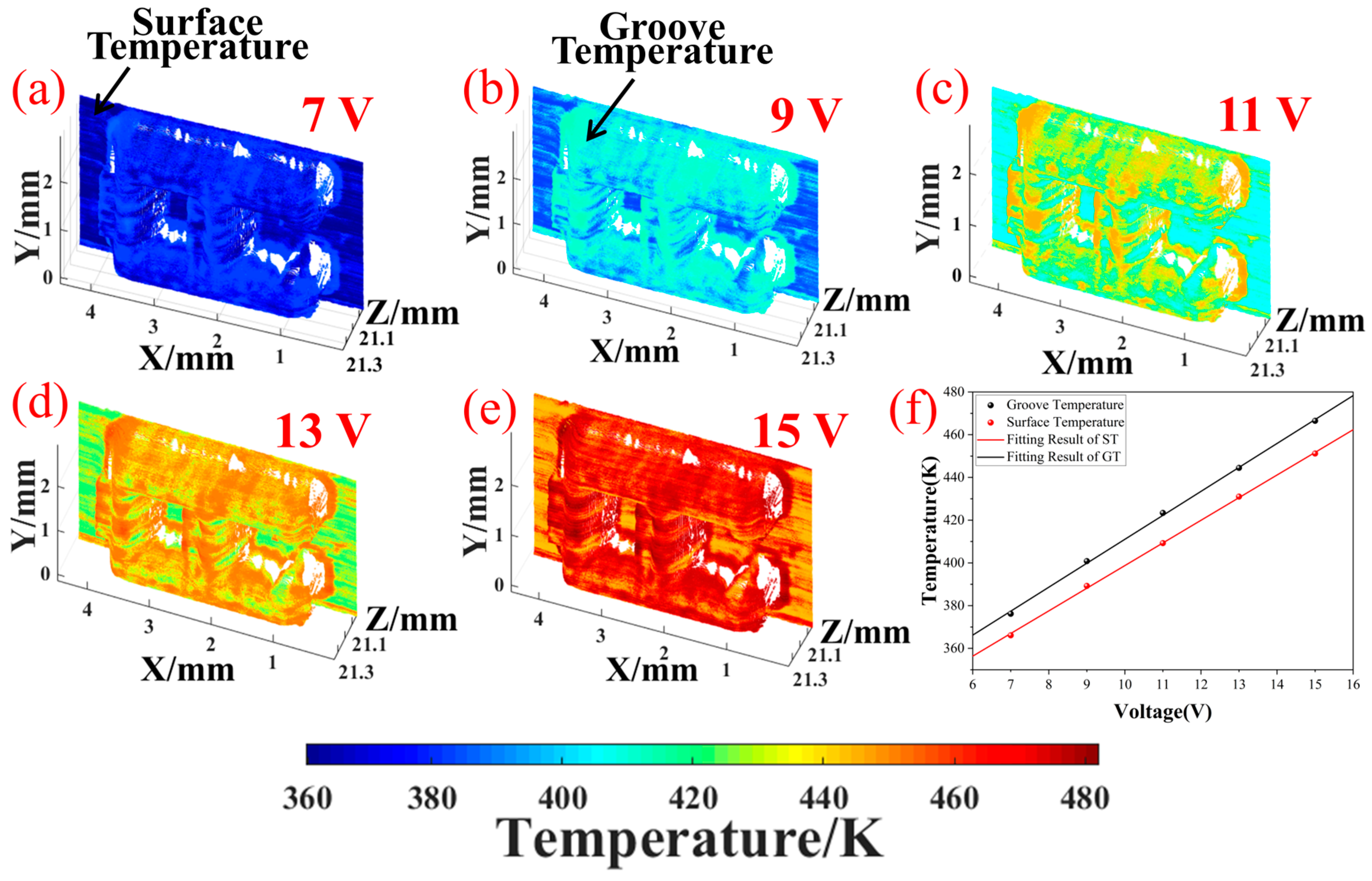
4.2. Temperature Recovery
| Techniques | Temperature Measurement Performance | 3D Morphology Recovery Performance | ||||
|---|---|---|---|---|---|---|
| Measurement Range | Temperature Resolution | Error | 2D Resolution | Depth Resolution | Depth of Field | |
| MMTL system | 373.15 K–508.15 K | 0.0131 K | <1 K | 2.8 μm | 2.1 μm | 4.6 mm |
| Commcial infrared systems (P20Max, HIKVISION, Hangzhou, China) | 373.15 K–623.15 K | 0.1 K | 1.2 K | 161.9 μm | - | 0.5143 mm |
| Other microscopic Scheimpflug LiDAR [51] | - | - | - | 3.8 μm | 3.8 μm | 3.5 mm |
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arai, T.; Nakamura, T.; Tanaka, S.; Demura, H.; Ogawa, Y.; Sakatani, N.; Horikawa, Y.; Senshu, H.; Fukuhara, T.; Okada, T. Thermal imaging performance of TIR onboard the Hayabusa2 spacecraft. Space Sci. Rev. 2017, 208, 239–254. [Google Scholar] [CrossRef]
- Leite, R.M.; Centeno, F.R. Effect of tank diameter on thermal behavior of gasoline and diesel storage tanks fires. J. Hazard. Mater. 2018, 342, 544–552. [Google Scholar] [CrossRef] [PubMed]
- Altet, J.; Claeys, W.; Dilhaire, S.; Rubio, A. Dynamic surface temperature measurements in ICs. Proc. IEEE 2006, 94, 1519–1533. [Google Scholar] [CrossRef]
- Pfefferkorn, F.; Rozzi, J.; Incropera, F.; Shin, Y. Surface temperature measurement in laser-assisted machining processes. Exp. Heat Transf. 1997, 10, 291–313. [Google Scholar] [CrossRef]
- Harzheim, A.; Könemann, F.; Gotsmann, B.; van der Zant, H.; Gehring, P. Single-Material Graphene Thermocouples. Adv. Funct. Mater. 2020, 30, 2000574. [Google Scholar] [CrossRef]
- Holmes, D.S.; Courts, S.S. Resolution and accuracy of cryogenic temperature measurements. Temp. Its Meas. Control Sci. Ind. 1992, 6, 1225–1230. [Google Scholar]
- Usamentiaga, R.; Venegas, P.; Guerediaga, J.; Vega, L.; Molleda, J.; Bulnes, F.G. Infrared thermography for temperature measurement and non-destructive testing. Sensors 2014, 14, 12305–12348. [Google Scholar] [CrossRef]
- Flora, F.; Boccaccio, M.; Fierro, G.; Meo, M. Real-time thermography system for composite welding: Undamaged baseline approach. Compos. Part B Eng. 2021, 215, 108740. [Google Scholar] [CrossRef]
- Wang, H.; Gong, D.; Cheng, G.; Jiang, J.; Wu, D.; Zhu, X.; Wu, S.; Ye, G.; Guo, L.; He, S. Detecting Temperature Anomaly at the Key Parts of Power Transmission and Transformation Equipment Using Infrared Imaging Based on SegFormer. Prog. Electromagn. Res. M 2023, 119, 117–128. [Google Scholar] [CrossRef]
- Avdelidis, N.; Moropoulou, A. Emissivity considerations in building thermography. Energy Build. 2003, 35, 663–667. [Google Scholar] [CrossRef]
- Du, W.; Addepalli, S.; Zhao, Y. The spatial resolution enhancement for a thermogram enabled by controlled subpixel movements. IEEE Trans. Instrum. Meas. 2019, 69, 3566–3575. [Google Scholar] [CrossRef]
- Streeter, R. High-Resolution Deep-Tissue Microwave Thermometry. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 2023. [Google Scholar]
- Abdali, A.; Abedi, A.; Masoumkhani, H.; Mazlumi, K.; Rabiee, A.; Guerrero, J.M. Magnetic-thermal analysis of distribution transformer: Validation via optical fiber sensors and thermography. Int. J. Electr. Power Energy Syst. 2023, 153, 109346. [Google Scholar] [CrossRef]
- Wang, Y.; Lei, L.; Ye, R.; Jia, G.; Hua, Y.; Deng, D.; Xu, S. Integrating Positive and Negative Thermal Quenching Effect for Ultrasensitive Ratiometric Temperature Sensing and Anti-counterfeiting. ACS Appl. Mater. Interfaces 2021, 13, 23951–23959. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Rui, J.; Song, H.; Yuan, Z.; Huang, X.; Liu, J.; Zhou, J.; Li, C.; Wang, H.; Wu, S.; et al. Antithermal Quenching Upconversion Luminescence via Suppressed Multiphonon Relaxation in Positive/Negative Thermal Expansion Core/Shell NaYF(4):Yb/Ho@ScF(3) Nanoparticles. J. Am. Chem. Soc. 2024, 146, 6530–6535. [Google Scholar] [CrossRef]
- Mi, C.; Zhou, J.; Wang, F.; Lin, G.; Jin, D. Ultrasensitive Ratiometric Nanothermometer with Large Dynamic Range and Photostability. Chem. Mater. 2019, 31, 9480–9487. [Google Scholar] [CrossRef]
- Ning, X.; Liu, N.; Liu, J.; Wu, Y.; Qian, J.; Zhang, W.; Gu, W. Temperature sensing and bioimaging realized in NaErF4:40%Tm@NaYF4 with extremely intense red upconversion and suitable R/G emission ratio. Opt. Mater. 2022, 131, 112659. [Google Scholar] [CrossRef]
- Lei, L.; Chen, D.; Li, C.; Huang, F.; Zhang, J.; Xu, S. Inverse thermal quenching effect in lanthanide-doped upconversion nanocrystals for anti-counterfeiting. J. Mater. Chem. C 2018, 6, 5427–5433. [Google Scholar] [CrossRef]
- Janjua, R.A.; Iqbal, O.; Ahmed, M.A.; Al-Kahtani, A.A.; Saeed, S.; Imran, M.; Wattoo, A.G. Homo-hetero/core-shell structure design strategy of NaYF(4) nanocrystals for superior upconversion luminescence. RSC Adv. 2021, 11, 20746–20751. [Google Scholar] [CrossRef]
- Wang, L.; Han, S.; Li, C.; Tu, D.; Chen, X. Lanthanide-doped inorganic nanoprobes for luminescent assays of biomarkers. Acc. Mater. Res. 2023, 4, 193–204. [Google Scholar] [CrossRef]
- Ryszczynska, S.; Trejgis, K.; Marciniak, Ł.; Grzyb, T. Upconverting SrF2: Er3+ nanoparticles for optical temperature sensors. ACS Appl. Nano Mater. 2021, 4, 10438–10448. [Google Scholar] [CrossRef]
- Cheng, Z.; Meng, M.; Wang, J.; Li, Z.; He, J.; Liang, H.; Qiao, X.; Liu, Y.; Ou, J. High-sensitivity NaYF(4):Yb(3+)/Ho(3+)/Tm(3+) phosphors for optical temperature sensing based on thermally coupled and non-thermally coupled energy levels. Nanoscale 2023, 15, 11179–11189. [Google Scholar] [CrossRef]
- Mei, L.; Ma, T.; Kong, Z.; Fei, R.; Cheng, Y.; Gong, Z. Comparison Studies Between the Pulsed Lidar Technique and the Scheimpflug Lidar Technique on a Near-Horizontal Measurement Path; SPIE: Bellingham, WA, USA, 2019. [Google Scholar]
- Chen, X.; Huang, X.; He, S. 4D hyperspectral surface topography measurement system based on the Scheimpflug principle and hyperspectral imaging. Appl. Opt. 2023, 62, 8855–8868. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Zhang, Y.; Mei, L. Fluorescence Scheimpflug LiDAR developed for the three-dimension profiling of plants. Opt. Express 2020, 28, 9269–9279. [Google Scholar] [CrossRef]
- Boateng, R.; Huzortey, A.A.; Gbogbo, Y.A.; Yamoa, A.s.-d.; Zoueu, J.T.; Brydegaard, M.; Anderson, B.; Månefjord, H. Remote Vegetation Diagnostics in Ghana with a Hyperspectral Fluorescence Lidar. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 7100607. [Google Scholar] [CrossRef]
- Zheng, K.; Lin, H.; Hong, X.; Che, H.; Ma, X.; Wei, X.; Mei, L. Development of a multispectral fluorescence LiDAR for point cloud segmentation of plants. Opt. Express 2023, 31, 18613–18629. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, A.; Borggren, J.; Xu, C.; Otxoterena, P.; Försth, M.; Leffler, T.; Bood, J. A compact Scheimpflug lidar imaging instrument for industrial diagnostics of flames. Meas. Sci. Technol. 2023, 34, 075901. [Google Scholar] [CrossRef]
- Malmqvist, E.; Brydegaard, M.; Alden, M.; Bood, J. Scheimpflug Lidar for combustion diagnostics. Opt. Express 2018, 26, 14842–14858. [Google Scholar] [CrossRef]
- Malmqvist, E.; Borggren, J.; Alden, M.; Bood, J. Lidar thermometry using two-line atomic fluorescence. Appl. Opt. 2019, 58, 1128–1133. [Google Scholar] [CrossRef]
- Duan, Z.; Yuan, Y.; Lu, J.C.; Wang, J.L.; Li, Y.; Svanberg, S.; Zhao, G.Y. Underwater spatially, spectrally, and temporally resolved optical monitoring of aquatic fauna. Opt. Express 2020, 28, 2600–2610. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, Y.; Yao, Q.; Ji, J.; Evans, J.; He, S. Inelastic hyperspectral Scheimpflug lidar for microalgae classification and quantification. Appl. Opt. 2021, 60, 4778–4786. [Google Scholar] [CrossRef]
- Gao, F.; Li, J.; Lin, H.; He, S. Oil pollution discrimination by an inelastic hyperspectral Scheimpflug lidar system. Opt. Express 2017, 25, 25515–25522. [Google Scholar] [CrossRef]
- Mei, L.; Brydegaard, M. Continuous-wave differential absorption lidar. Laser Photonics Rev. 2015, 9, 629–636. [Google Scholar] [CrossRef]
- Gao, F.; Lin, H.; Chen, K.; Chen, X.; He, S. Light-sheet based two-dimensional Scheimpflug lidar system for profile measurements. Opt. Express 2018, 26, 27179–27188. [Google Scholar] [CrossRef]
- Luo, L.; Chen, X.; Xu, Z.; Li, S.; Sun, Y.; He, S. A parameter-free calibration process for a Scheimpflug LIDAR for volumetric profiling. Prog. Electromagn. Res. 2020, 169, 117–127. [Google Scholar] [CrossRef]
- Martínez, E.D.; Brites, C.D.S.; Carlos, L.D.; García-Flores, A.F.; Urbano, R.R.; Rettori, C. Electrochromic Switch Devices Mixing Small- and Large-Sized Upconverting Nanocrystals. Adv. Funct. Mater. 2018, 29, 1807758. [Google Scholar] [CrossRef]
- Cho, J.; Gemperline, P.J.; Walker, D. Wavelength calibration method for a CCD detector and multichannel fiber-optic probes. Appl. Spectrosc. 1995, 49, 1841–1845. [Google Scholar] [CrossRef]
- Xu, Z.; Jiang, Y.; He, S. Multi-mode microscopic hyperspectral imager for the sensing of biological samples. Appl. Sci. 2020, 10, 4876. [Google Scholar] [CrossRef]
- Petit, S.; Xavier, P.; Godard, G.; Grisch, F. Improving the temperature uncertainty of Mg4 FGeO6: Mn4+ ratio-based phosphor thermometry by using a multi-objective optimization procedure. Appl. Phys. B 2022, 128, 57. [Google Scholar] [CrossRef]
- Wang, Q.; Liao, M.; Lin, Q.; Xiong, M.; Zhang, X.; Dong, H.; Lin, Z.; Wen, M.; Zhu, D.; Mu, Z.; et al. The design of dual-switch fluorescence intensity ratio thermometry with high sensitivity and thermochromism based on a combination strategy of intervalence charge transfer and up-conversion fluorescence thermal enhancement. Dalton Trans. 2021, 50, 9298–9309. [Google Scholar] [CrossRef]
- Niu, Y.; Wu, F.; Zhang, Q.; Teng, Y.; Huang, Y.; Yang, Z.; Mu, Z. Luminescence and thermometry sensing of Sr2InTaO6: Eu3+, Mn4+ phosphors in a wide temperature range. J. Lumin. 2024, 275, 120748. [Google Scholar] [CrossRef]
- Brites, C.; Millán, A.; Carlos, L. Lanthanides in Luminescent Thermometry; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Jones, E.M.C.; Jones, A.R.; Hoffmeister, K.N.G.; Winters, C. Advances in phosphor two-color ratio method thermography for full-field surface temperature measurements. Meas. Sci. Technol. 2022, 33, 085201. [Google Scholar] [CrossRef]
- He, R.; Fang, D.; Wang, P.; Zhang, X.; Zhang, R. Electrical properties of ZrB2–SiC ceramics with potential for heating element applications. Ceram. Int. 2014, 40, 9549–9553. [Google Scholar] [CrossRef]
- Winterton, R. Newton’s law of cooling. Contemp. Phys. 1999, 40, 205–212. [Google Scholar] [CrossRef]
- Setälä, O.E.; Prest, M.J.; Stefanov, K.D.; Jordan, D.; Soman, M.R.; Vähänissi, V.; Savin, H. CMOS Image Sensor for Broad Spectral Range with >90% Quantum Efficiency. Small 2023, 19, 2304001. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, H.; Li, Y.; Huo, J.; Deng, H.; Zhang, H. Method of 3D reconstruction of underwater concrete by laser line scanning. Opt. Lasers Eng. 2024, 183, 108468. [Google Scholar] [CrossRef]
- Meng, S.; Zhang, C.; Shi, Q.; Chen, Z.; Hu, W.; Lu, F. A Robust Infrared Small Target Detection Method Jointing Multiple Information and Noise Prediction: Algorithm and Benchmark. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5517117. [Google Scholar] [CrossRef]
- Zhou, G.; Zhou, X.; Li, W.; Zhao, D.; Song, B.; Xu, C.; Zhang, H.; Liu, Z.; Xu, J.; Lin, G.; et al. Development of a Lightweight Single-Band Bathymetric LiDAR. Remote Sens. 2022, 14, 5880. [Google Scholar] [CrossRef]
- Bian, Q.; Chen, X.; He, S. Line laser scanning microscopy based on the Scheimpflug principle for high-resolution topography restoration and quantitative measurement. Appl. Opt. 2023, 62, 5014–5022. [Google Scholar] [CrossRef]


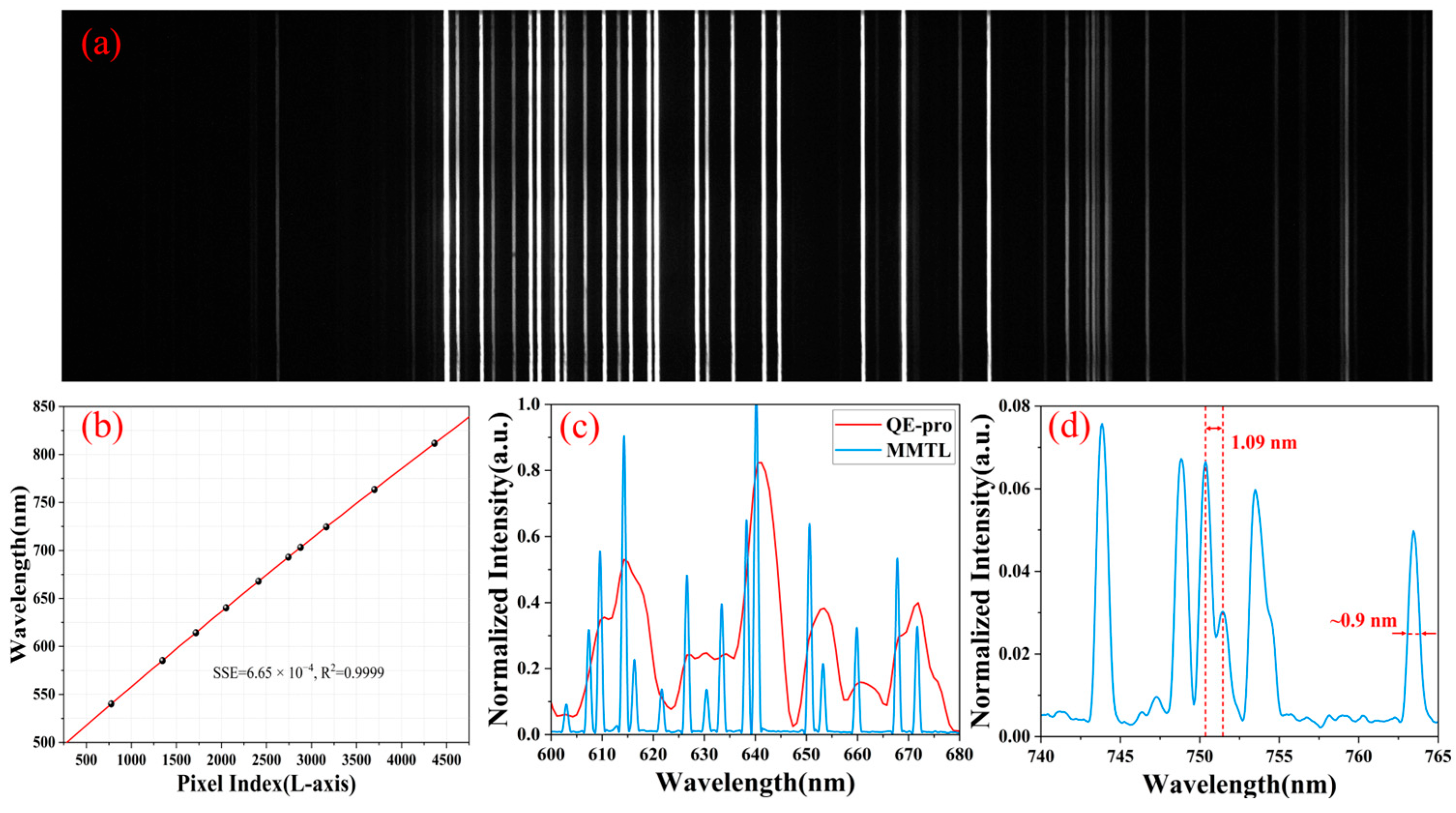
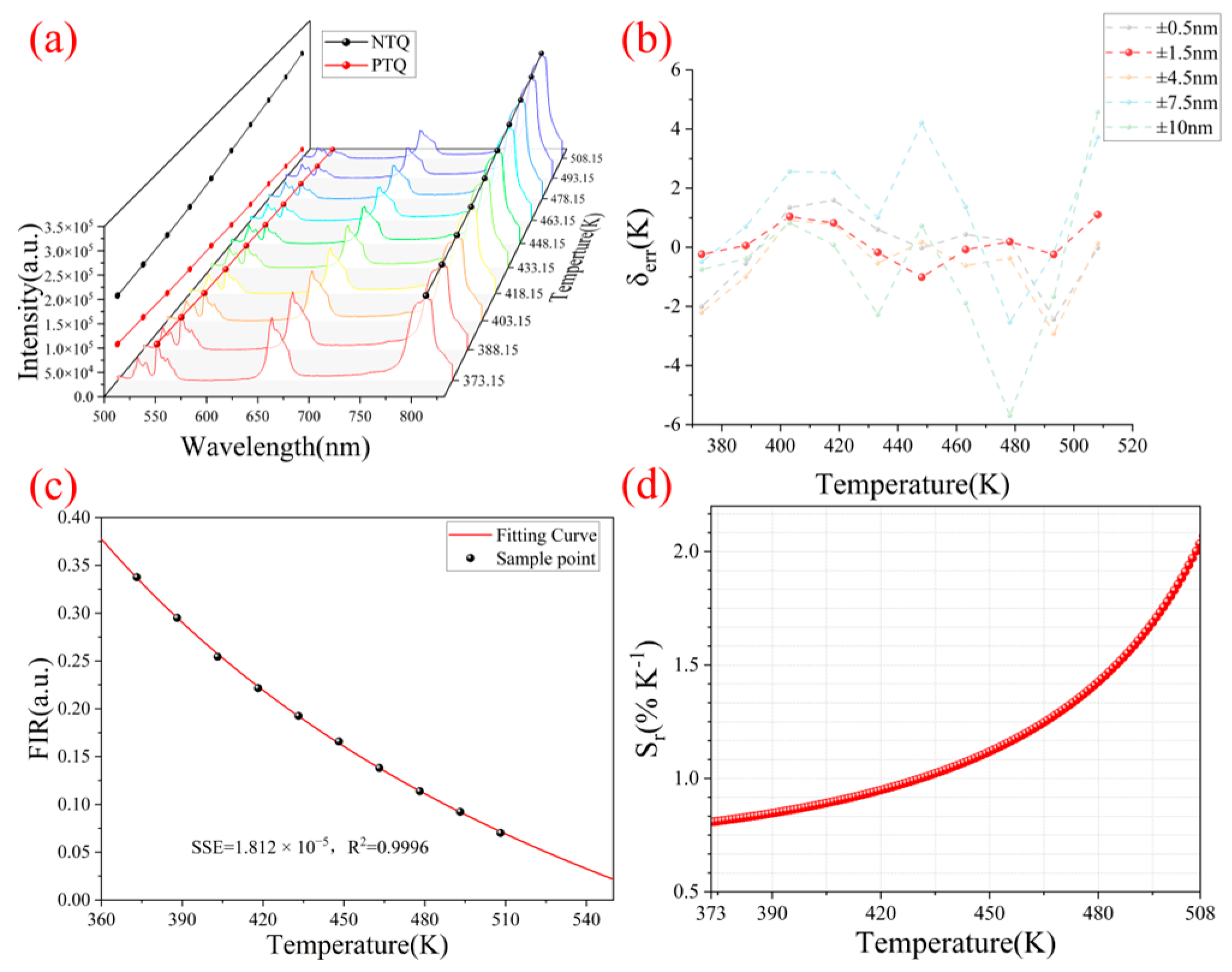
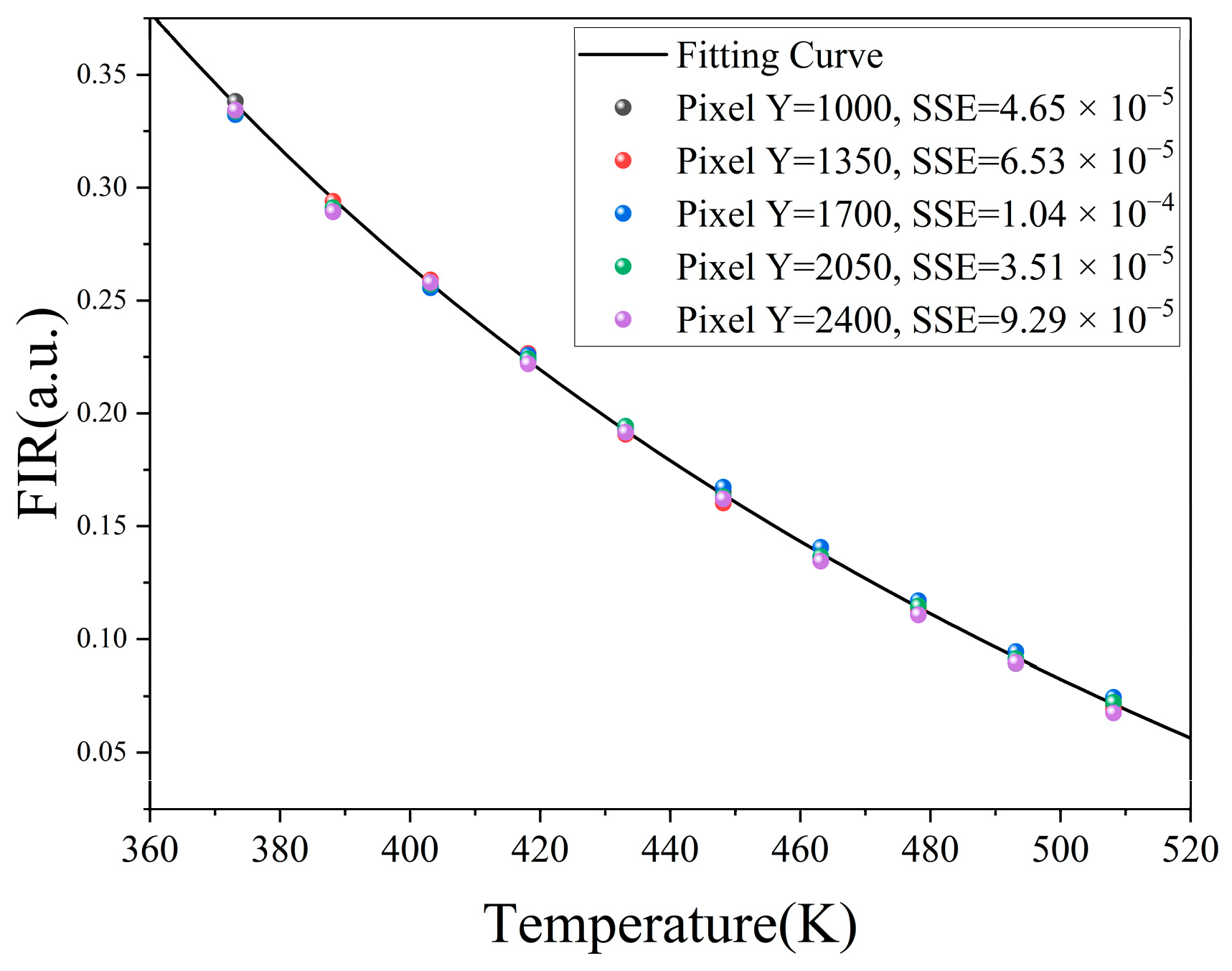

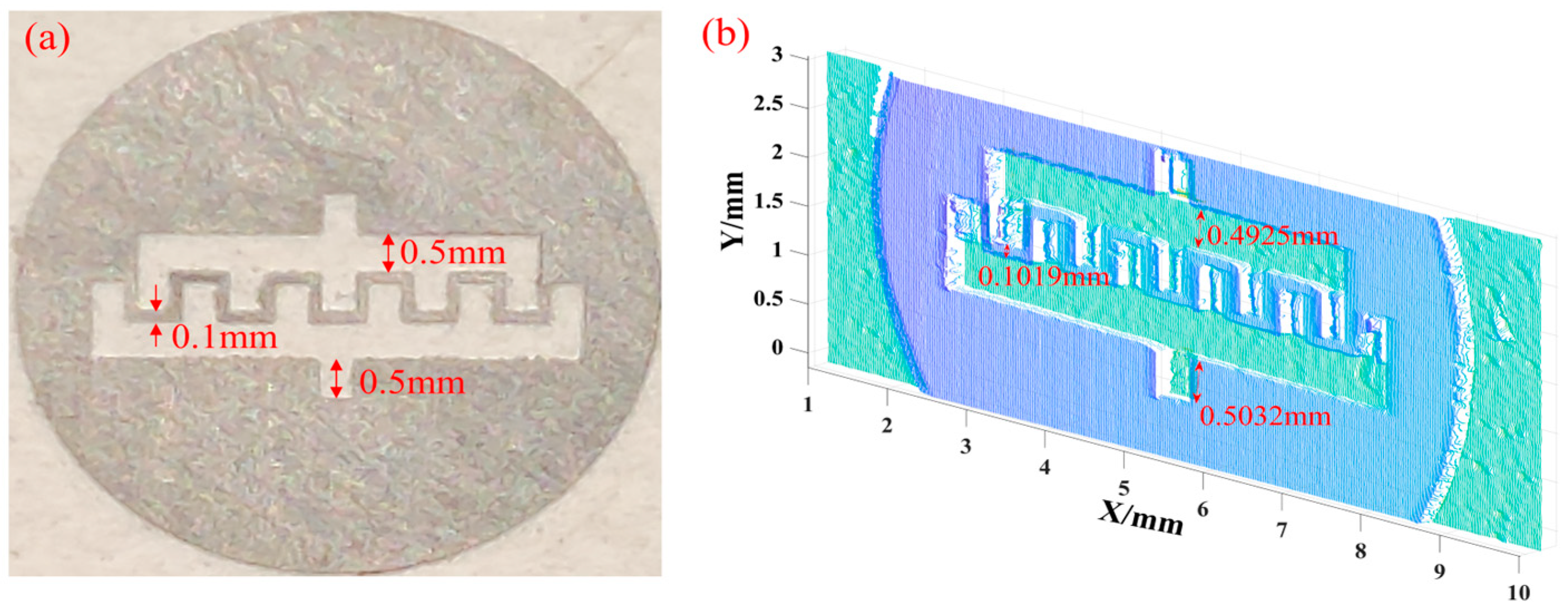




| Filter Group (nm) | Standard Deviation (K) |
|---|---|
| ±0.5 | 1.2976 |
| ±1.5 | 0.6651 |
| ±4.5 | 1.2244 |
| ±7.5 | 2.0531 |
| ±10 | 2.6384 |
| Point # | X/mm | Y/mm | Z/mm | T/K | Zreal/mm | Z Measurement Accuracy/mm |
|---|---|---|---|---|---|---|
| A | 1.467 | 2.732 | 21.262 | 376.19 | 21.26 | 0.002 |
| B | 1.787 | 2.724 | 21.265 | 400.81 | 0.005 | |
| C | 0.853 | 2.736 | 21.257 | 423.39 | 0.003 | |
| D | 3.040 | 2.736 | 21.259 | 444.46 | 0.001 | |
| E | 1.827 | 2.724 | 21.264 | 466.51 | 0.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Janjua, R.A.; He, S. High-Resolution Thermometric Scheimpflug LiDAR for Surface Morphology and Temperature Mapping. Micromachines 2025, 16, 590. https://doi.org/10.3390/mi16050590
Huang X, Janjua RA, He S. High-Resolution Thermometric Scheimpflug LiDAR for Surface Morphology and Temperature Mapping. Micromachines. 2025; 16(5):590. https://doi.org/10.3390/mi16050590
Chicago/Turabian StyleHuang, Xuhui, Raheel Ahmed Janjua, and Sailing He. 2025. "High-Resolution Thermometric Scheimpflug LiDAR for Surface Morphology and Temperature Mapping" Micromachines 16, no. 5: 590. https://doi.org/10.3390/mi16050590
APA StyleHuang, X., Janjua, R. A., & He, S. (2025). High-Resolution Thermometric Scheimpflug LiDAR for Surface Morphology and Temperature Mapping. Micromachines, 16(5), 590. https://doi.org/10.3390/mi16050590







