HE-BiDet: A Hardware Efficient Binary Neural Network Accelerator for Object Detection in SAR Images
Abstract
1. Introduction
2. Related Work and Contributions
- (1)
- We propose an ultra light-weight BNN model, namely HE-BiDet, to carry out the ship detection task on the SAR imagery with low computation complexity. Both activation and weights are represented by 1-bit data, significantly reducing computational and storage overhead. With extreme binary quantization, feature pyramid structure, and model capacity enhancement, our model achieves a detection accuracy comparable to State-of-the-Art floating point ship detection models, while reducing the model size by a factor up to 18.9×.
- (2)
- We design a low latency BNN inference accelerator for ship detection on SAR imagery. It utilizes four degrees of parallelism within the convolution inference calculation to achieve low detection latency. In addition, a novel on-chip data buffer and the corresponding data addressing algorithm are proposed to efficiently supply data to the computing array with high parallelism.
- (3)
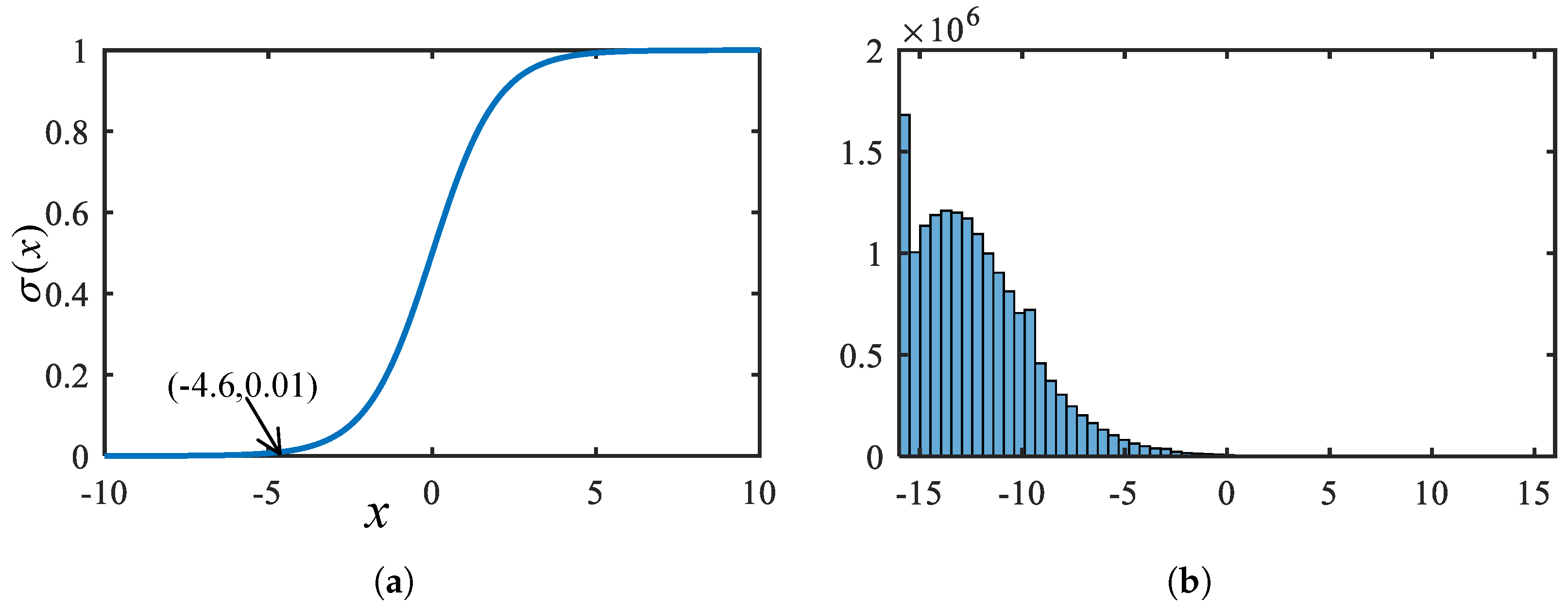
- We propose a “threshold first” post-processing unit to accelerate post-processing with low hardware consumption. This is based on our observation in the SSDD dataset that only 1.47% of the candidate boxes have confidence scores higher than the commonly used threshold of 0.01 [18]. Before confidence and coordinate decode, a parallel threshold hardware unit filters out redundant anchor boxes according to the raw data of the convolution output, which reduces the workload of subsequent operations. Therefore, subsequent decoding and NMS operations are performed with low latency even with low hardware consumption.
- (4)
- Our SAR image target detection system is validated on a platform using the XC7VX690T FPGA device. The design achieves an mAP of 92.7%, an FPS of 80.5, and a latency of ms on the SSDD data set. For the SAR-SHIP dataset, it achieves an mAP of 90.12%, an FPS of 189.3, and a latency of ms. Compared with State-of-the-Art ship detection works on SAR imagery, our work achieves up to 6.34 times latency reduction and 15.8 times DSP consumption reduction.
3. BNN-Based Ship Detection Model
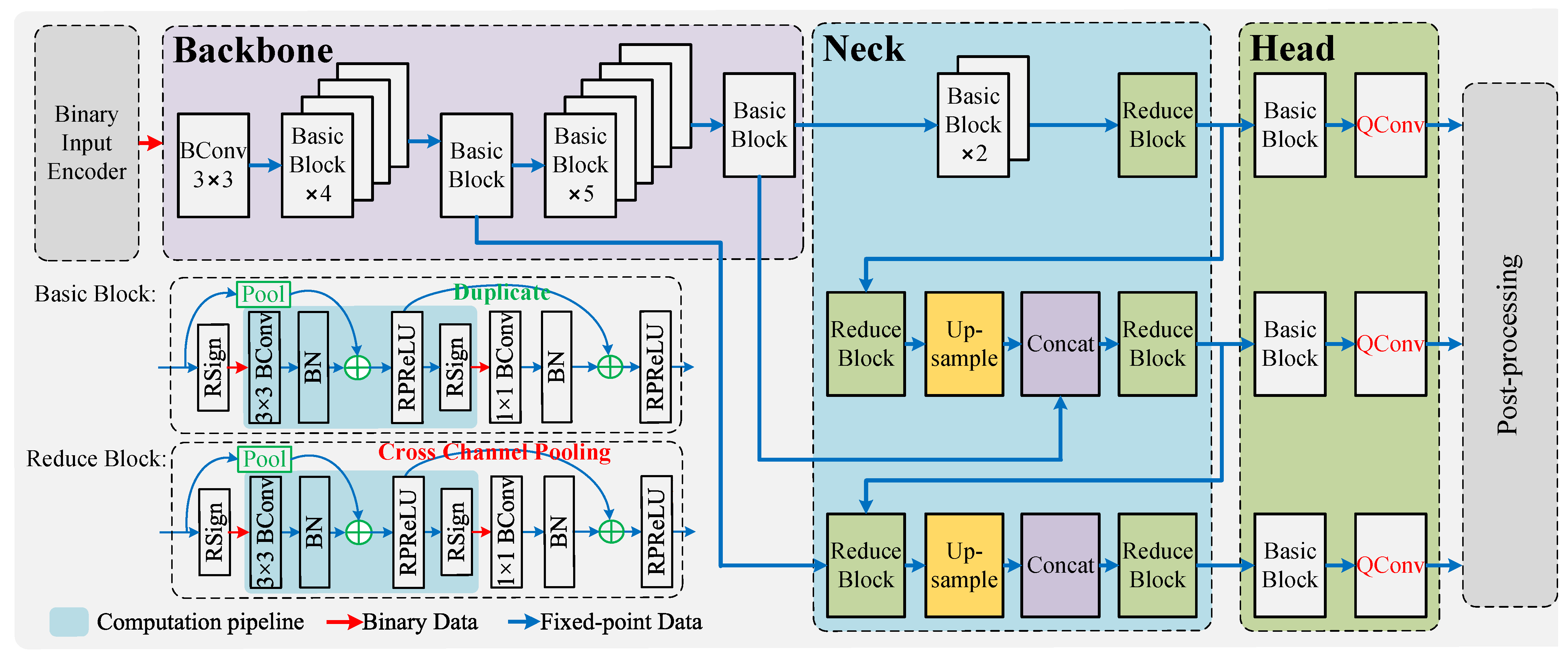
3.1. Network Structure Overview
3.2. Basic Block Design
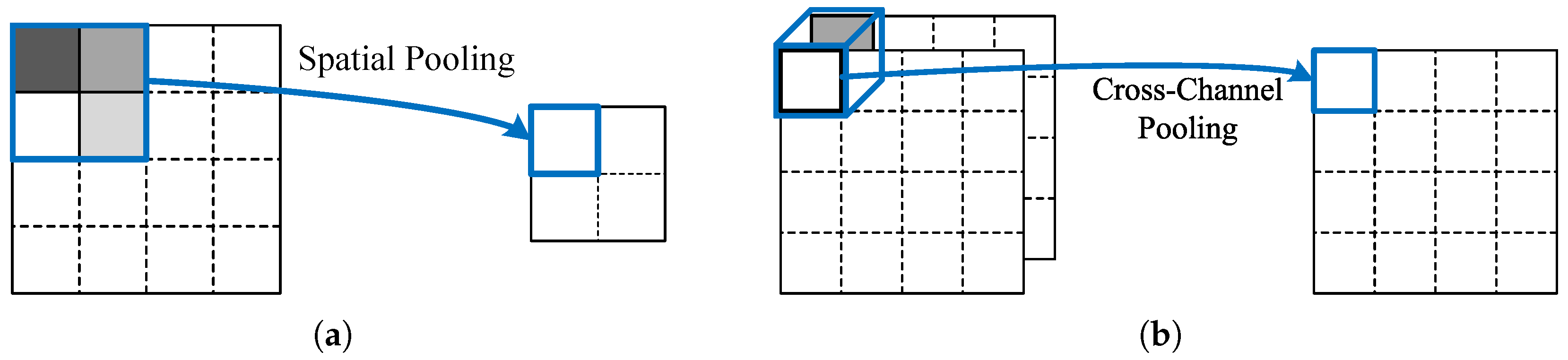
3.3. Cross-Channel Pooling
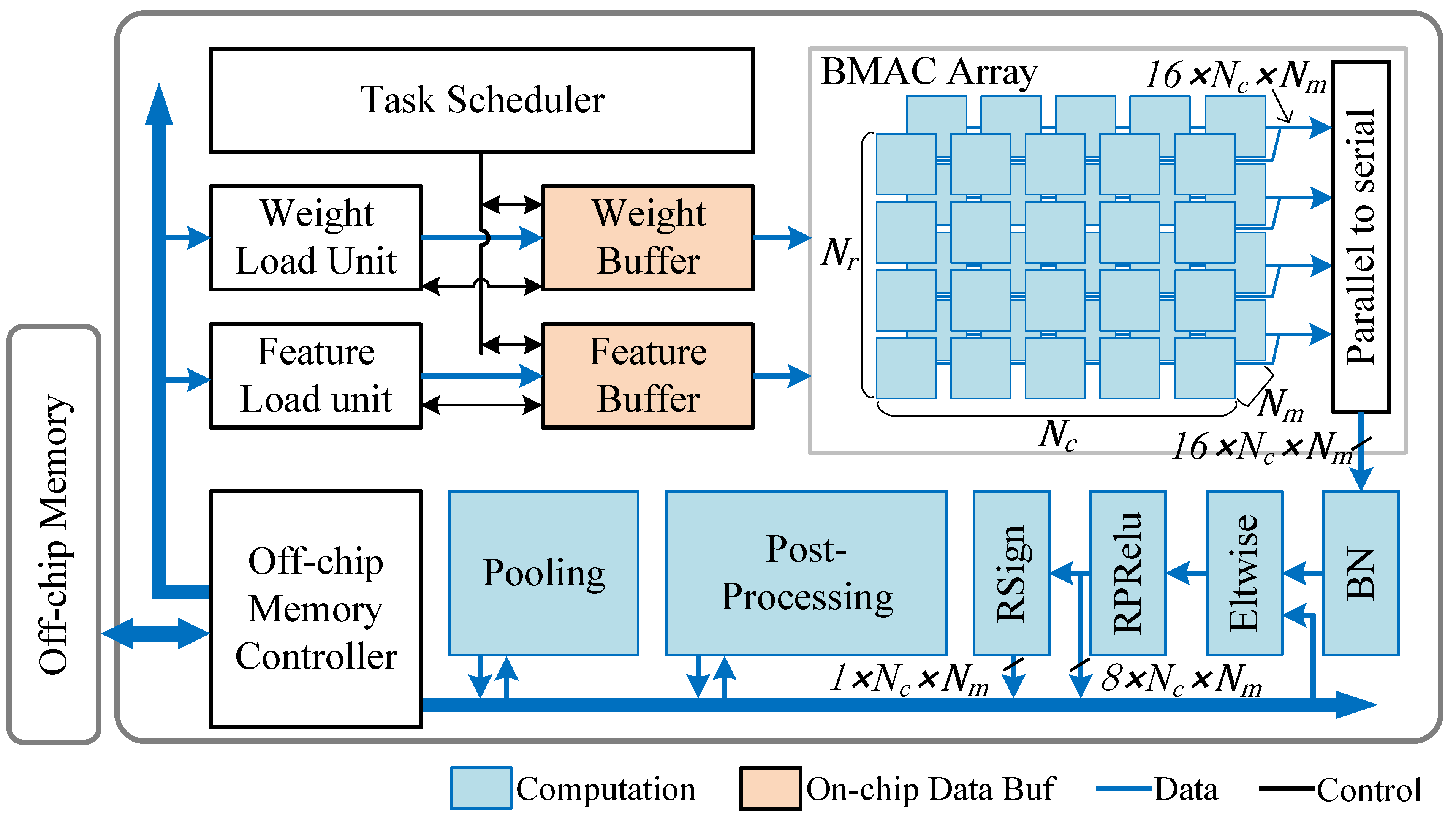
4. Hardware Accelerator Design
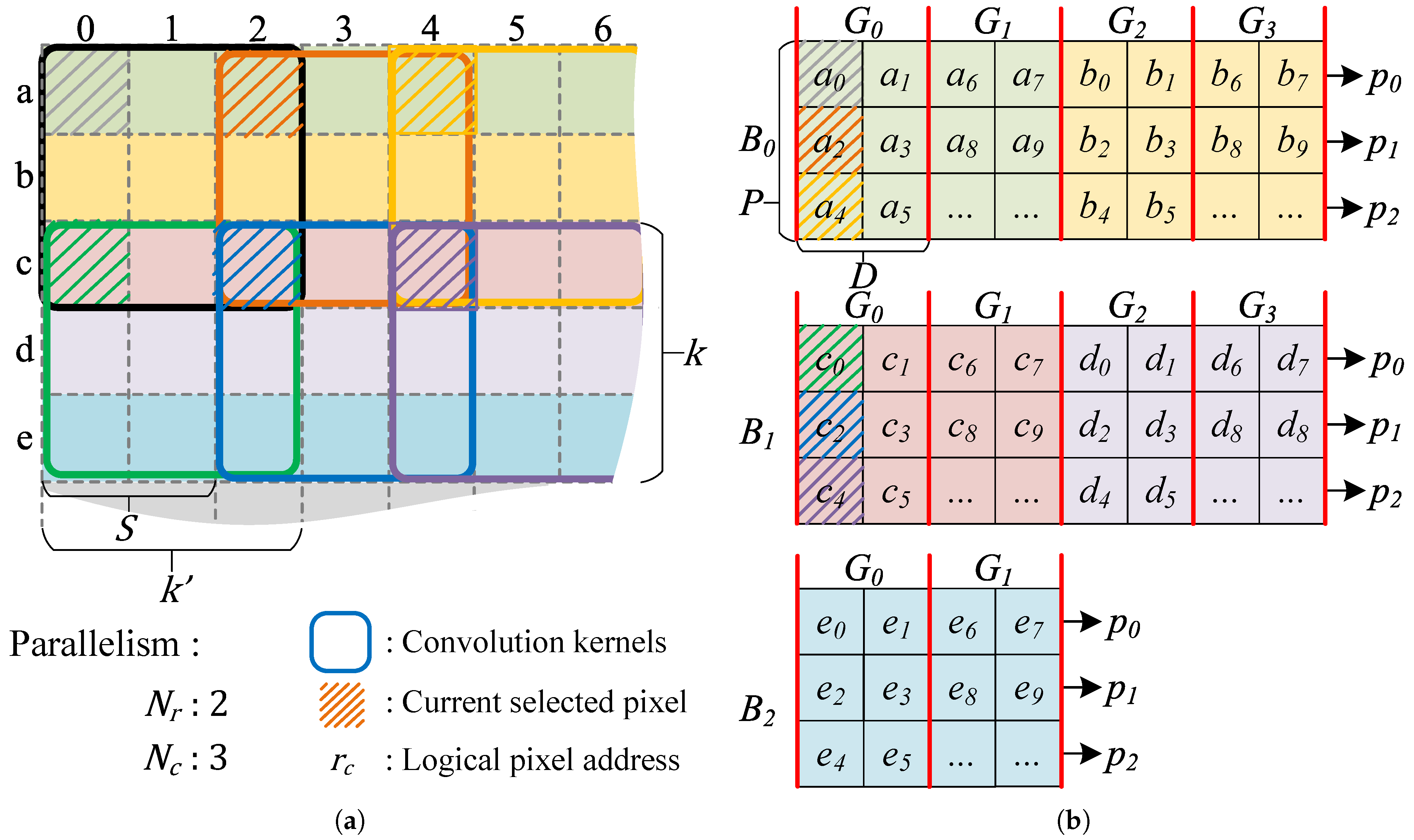
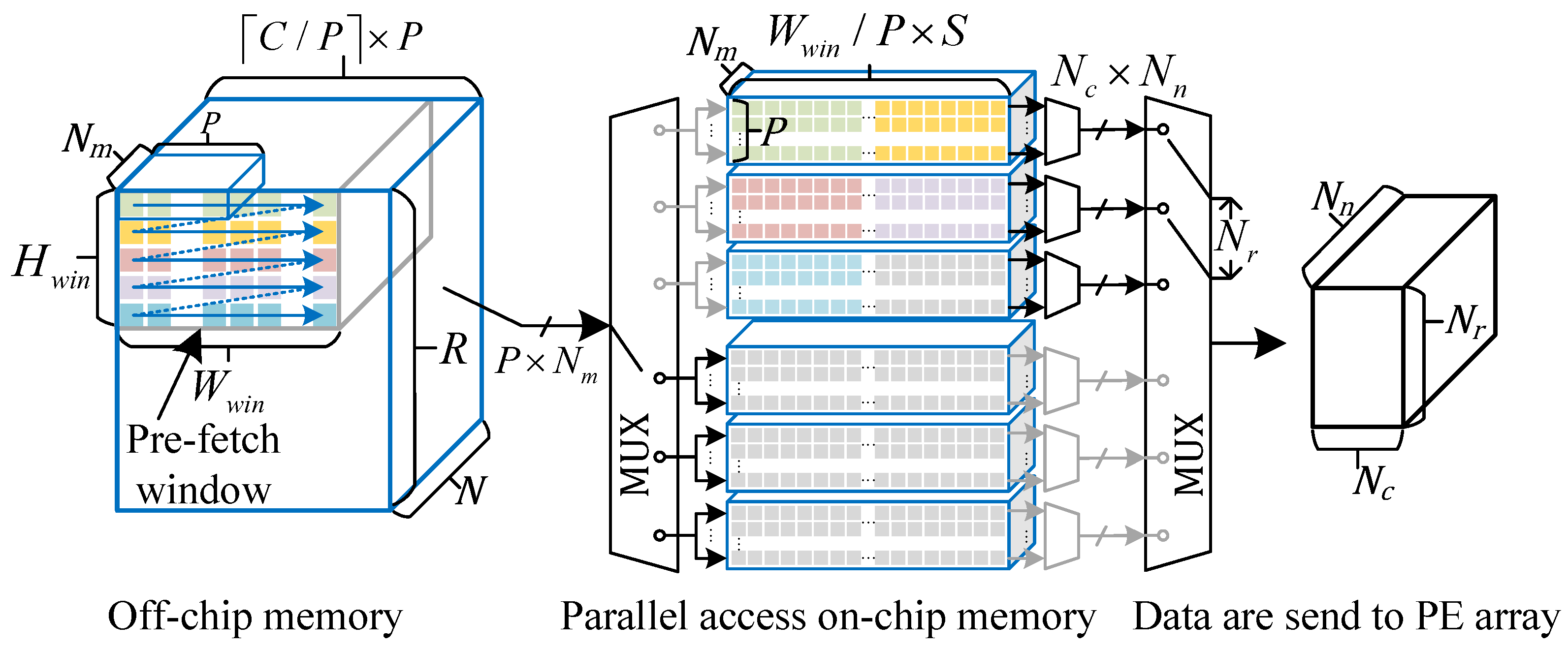
4.1. High Parallel Data Access System
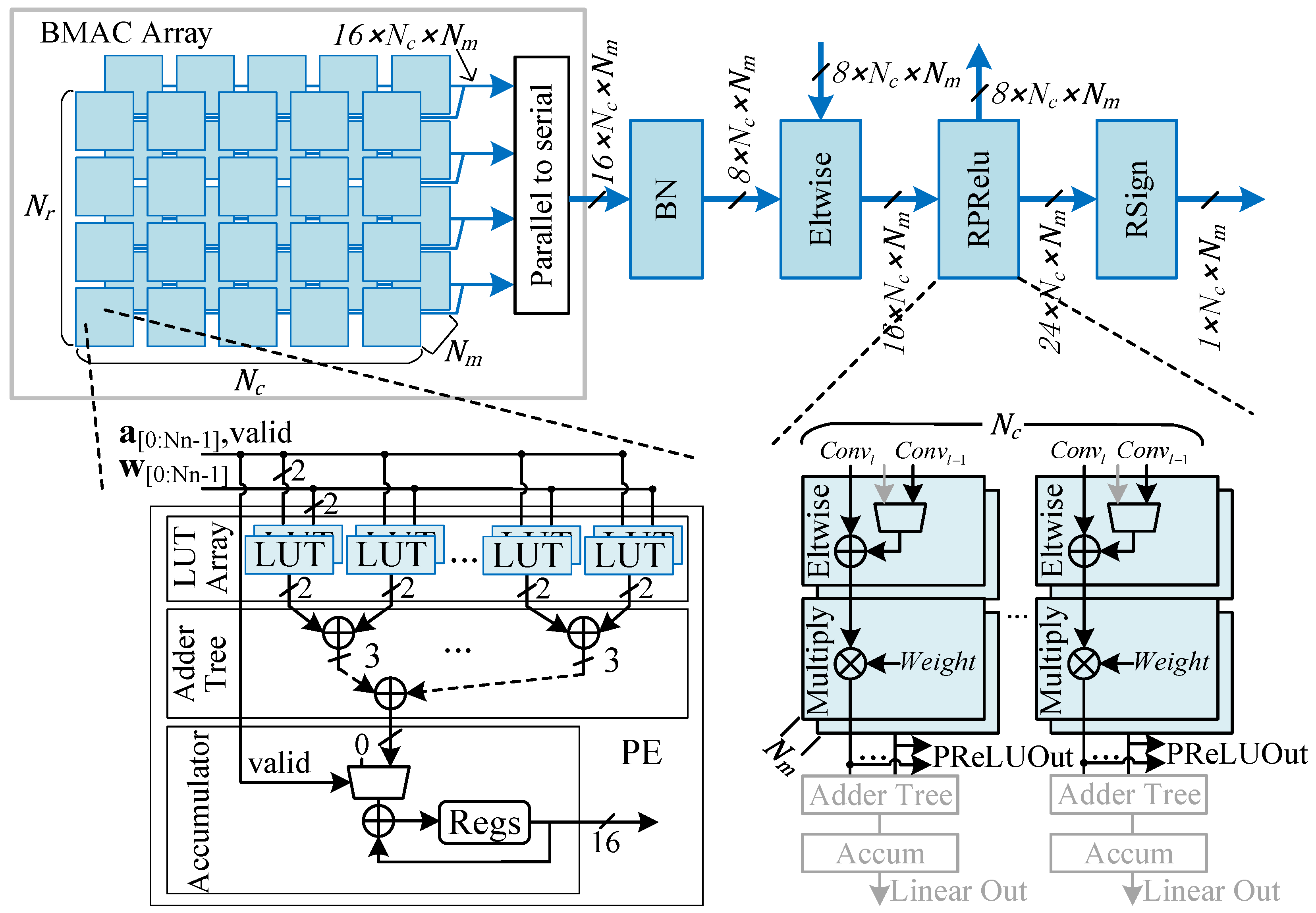
4.2. Computation Pipeline Design
4.3. Hardware Efficient Post-Processing Unit
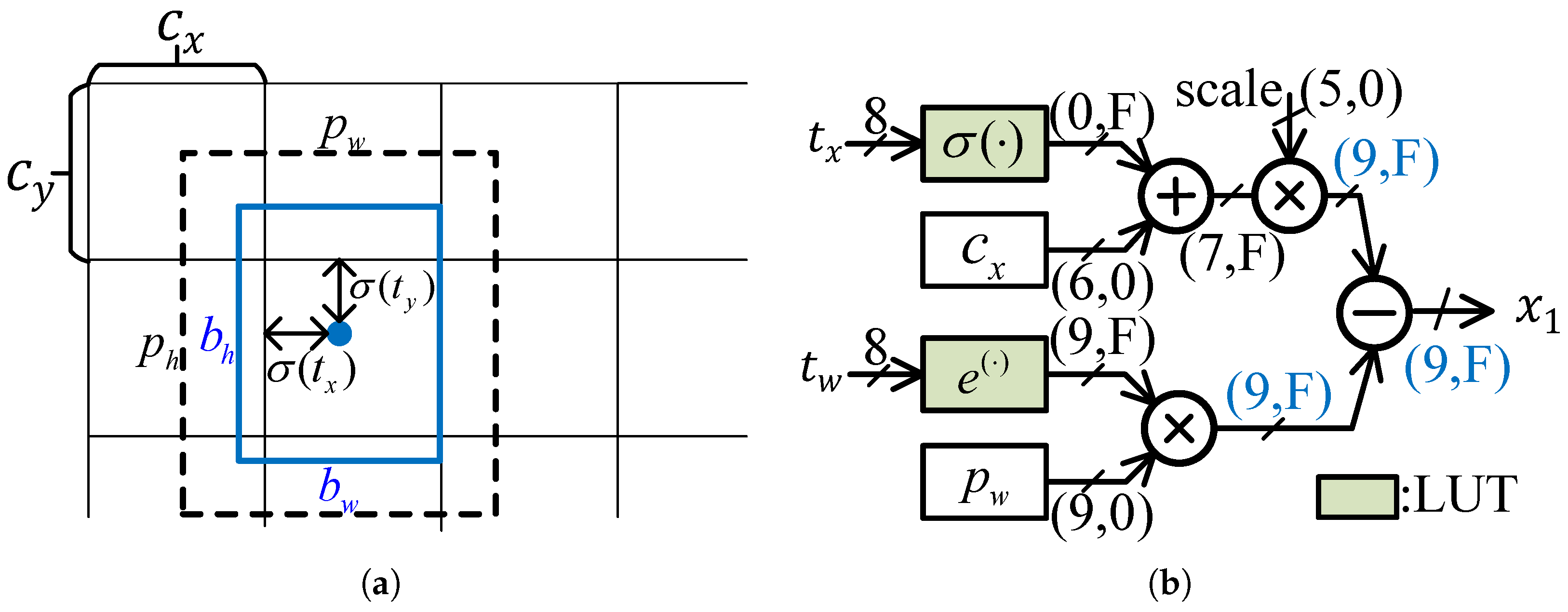
4.3.1. Coordinate Calculation
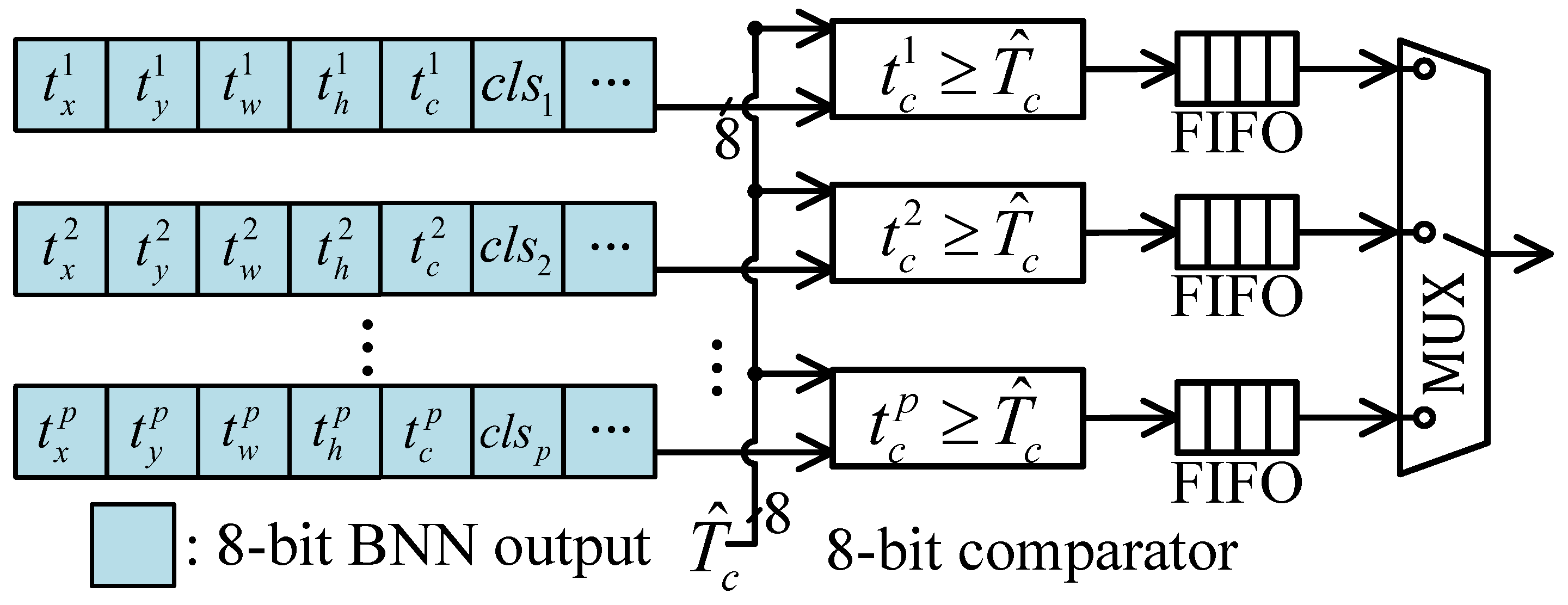
4.3.2. Sorting-Free NMS Unit
| Algorithm 1: NMS implementation |
 |
5. System Implementation and Performance Evaluation
5.1. Experimental Setup
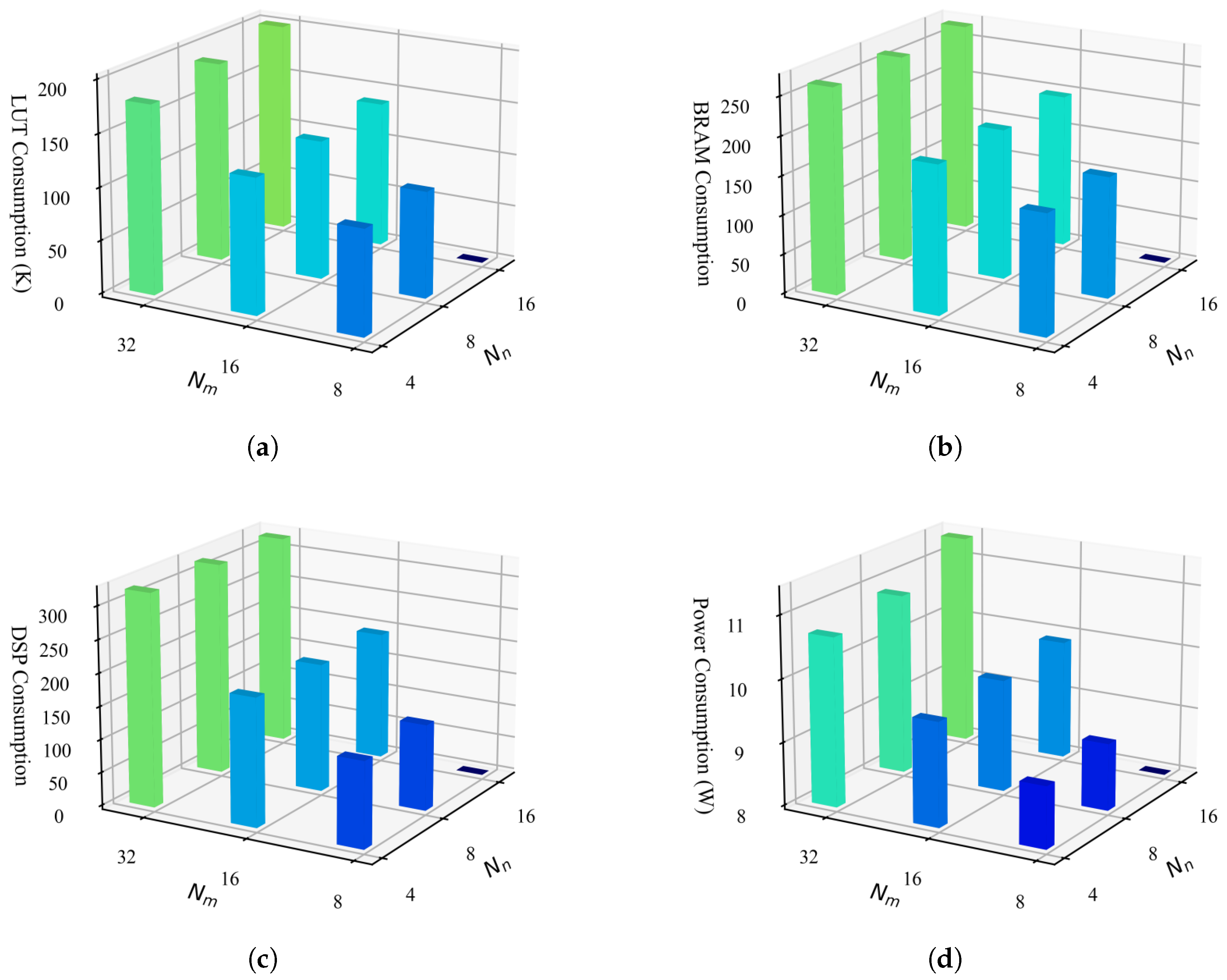
5.2. Resource and Power Evaluation
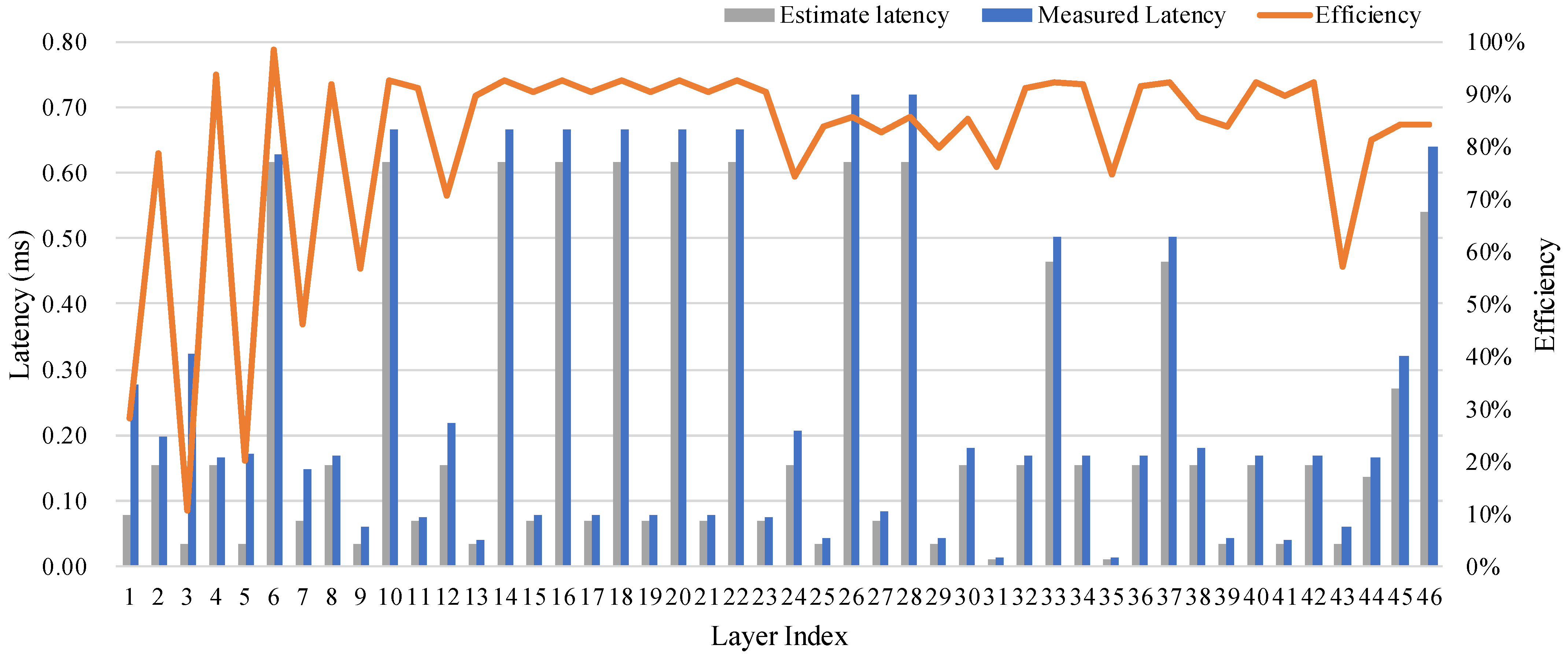
5.3. Performance Evaluation
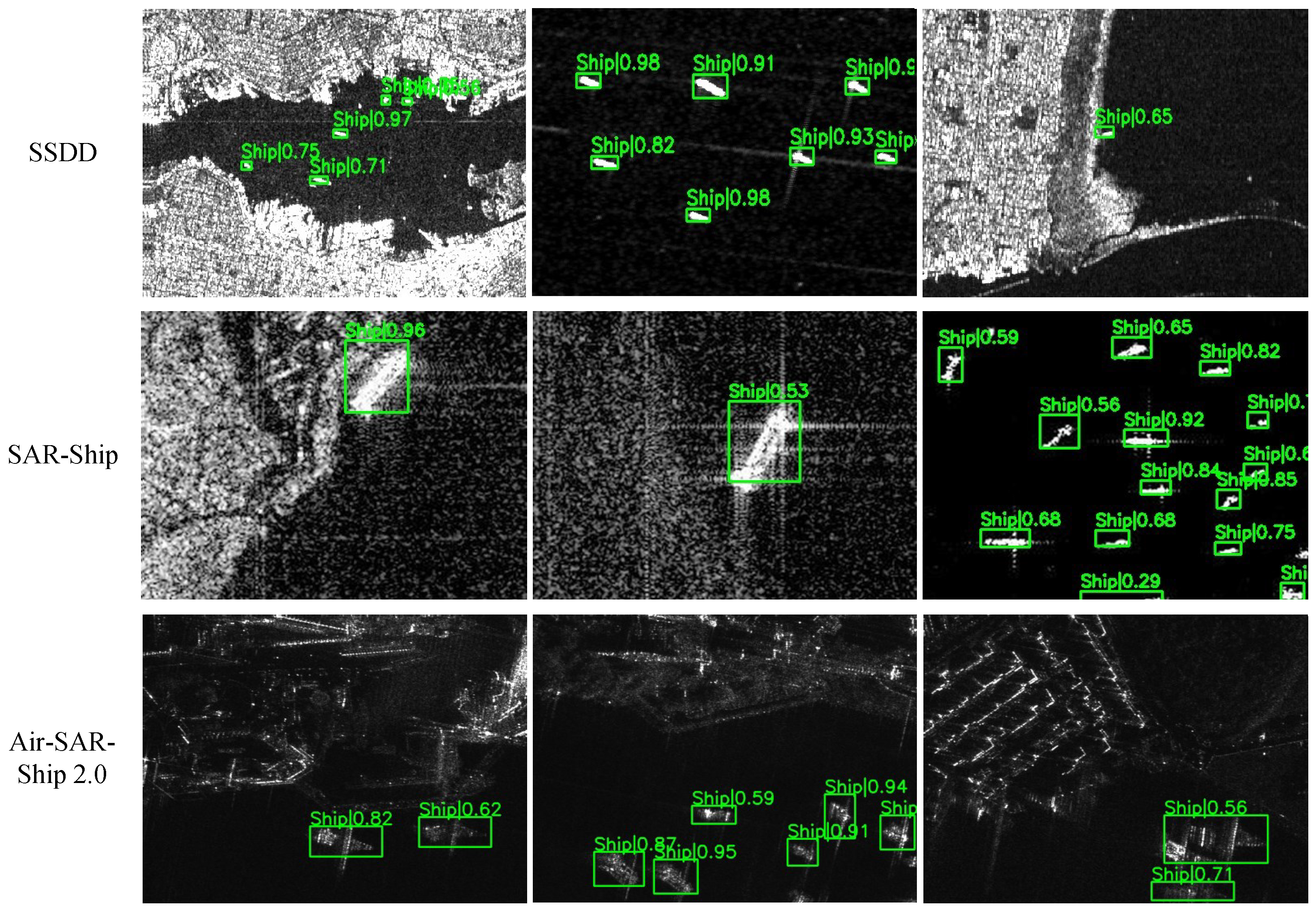
5.4. Comparison with State-of-the-Art Designs
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Network |
| SAR | Synthetic Aperture Radar |
| BN | Batch normalization |
| FPS | Frame Per Second |
| NMS | Non-Maximum Suppression |
| PReLU | Parametric rectified linear unit |
| Parallelism of BMAC array in row direction | |
| Parallelism of BMAC array in column direction | |
| Parallelism of BMAC array in channel direction | |
| Parallelism of within each PE | |
| Bank index of the on-chip buffer | |
| P | Port number of the on-chip buffer |
| Port index of the on-chip buffer | |
| S | Stride of the convolution neural network |
| K | Kernel size of the convolution neural network |
| Number of rows of the output feature map | |
| Number of columns of the output feature map | |
| M | Number of channels of the output feature map |
| N | Number of channels of the input feature map |
References
- Tello, M.; Lopez-Martinez, C.; Mallorqui, J. A novel algorithm for ship detection in SAR imagery based on the wavelet transform. IEEE Geosci. Remote Sens. Lett. 2005, 2, 201–205. [Google Scholar] [CrossRef]
- Crisp, D.J. The State-of-the-Art in Ship Detection in Synthetic Aperture Radar Imagery; Technical Report; Department of Defence: Canberra, Australia, 2004. [Google Scholar]
- Yang, X.; Zhang, X.; Wang, N.; Gao, X. A Robust One-Stage Detector for Multiscale Ship Detection With Complex Background in Massive SAR Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5217712. [Google Scholar] [CrossRef]
- Hu, Q.; Hu, S.; Liu, S. BANet: A balance attention network for anchor-free ship detection in SAR images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5222212. [Google Scholar] [CrossRef]
- Liu, N.; Cao, Z.; Cui, Z.; Pi, Y.; Dang, S. Multi-Scale Proposal Generation for Ship Detection in SAR Images. Remote Sens. 2019, 11, 526. [Google Scholar] [CrossRef]
- Wang, J.; Lin, Y.; Guo, J.; Zhuang, L. SSS-YOLO: Towards more accurate detection for small ships in SAR image. Remote Sens. Lett. 2021, 12, 93–102. [Google Scholar] [CrossRef]
- Liu, F.; Li, Y. SAR Remote Sensing Image Ship Detection Method NanoDet Based on Visual Saliency. J. Radars 2021, 10, 885. [Google Scholar]
- Yoshida, K.; Sageyama, R.; Miwa, S.; Yamaki, H.; Honda, H. Analyzing Performance and Power-Efficiency Variations among NVIDIA GPUs. In Proceedings of the 51st International Conference on Parallel Processing, Bordeaux, France, 29 August–1 September 2022; pp. 1–12. [Google Scholar] [CrossRef]
- Huang, X.; Xu, K.; Chen, J.; Wang, A.; Chen, S.; Li, H. Real-Time Processing of Ship Detection with SAR Image Based on FPGA. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 8954–8957. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Zhang, H.; Dong, Y.; Wei, S. A SAR Dataset of Ship Detection for Deep Learning under Complex Backgrounds. Remote Sens. 2019, 11, 765. [Google Scholar] [CrossRef]
- Yang, G.; Lei, J.; Xie, W.; Fang, Z.; Li, Y.; Wang, J.; Zhang, X. Algorithm/Hardware Codesign for Real-Time On-Satellite CNN-Based Ship Detection in SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Kim, M.; Oh, K.; Cho, Y.; Seo, H.; Nguyen, X.T.; Lee, H.J. A Low-Latency FPGA Accelerator for YOLOv3-Tiny With Flexible Layerwise Mapping and Dataflow. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 1158–1171. [Google Scholar] [CrossRef]
- Jiang, W.; Yu, H.; Ha, Y. A High-Throughput Full-Dataflow MobileNetv2 Accelerator on Edge FPGA. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2023, 42, 1532–1545. [Google Scholar] [CrossRef]
- Zhang, P.; Lo, E.; Lu, B. High Performance Depthwise and Pointwise Convolutions on Mobile Devices. Proc. AAAI Conf. Artif. Intell. 2020, 34, 6795–6802. [Google Scholar] [CrossRef]
- Wu, S.; Yang, H.; You, X.; Gong, R.; Liu, Y.; Luan, Z.; Qian, D. PRoof: A Comprehensive Hierarchical Profiling Framework for Deep Neural Networks with Roofline Analysis. In Proceedings of the 53rd International Conference on Parallel Processing, Gotland, Sweden, 12–15 August 2024; pp. 822–832. [Google Scholar] [CrossRef]
- Anupreetham, A.; Ibrahim, M.; Hall, M.; Boutros, A.; Kuzhively, A.; Mohanty, A.; Nurvitadhi, E.; Betz, V.; Cao, Y.; Seo, J.s. End-to-End FPGA-based Object Detection Using Pipelined CNN and Non-Maximum Suppression. In Proceedings of the 2021 31st International Conference on Field-Programmable Logic and Applications (FPL), Dresden, Germany, 30 August–3 September 2021; pp. 76–82. [Google Scholar] [CrossRef]
- Anupreetham, A.; Ibrahim, M.; Hall, M.; Boutros, A.; Kuzhively, A.; Mohanty, A.; Nurvitadhi, E.; Betz, V.; Cao, Y.; Seo, J.S. High Throughput FPGA-Based Object Detection via Algorithm-Hardware Co-Design. ACM Trans. Reconfigurable Technol. Syst. 2024, 17, 1–20. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Proceedings of the Computer Vision—ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, Switzerland, 2016; pp. 21–37. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, J. FracBNN: Accurate and FPGA-efficient binary neural networks with fractional activations. In Proceedings of the 2021 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Virtual, 28 February–2 March 2021; pp. 171–182. [Google Scholar]
- Liu, Z.; Shen, Z.; Savvides, M.; Cheng, K.T. Reactnet: Towards precise binary neural network with generalized activation functions. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XIV 16. Springer: Cham, Switzerland, 2020; pp. 143–159. [Google Scholar]
- Liu, L.; Shen, C.; Van Den Hengel, A. The treasure beneath convolutional layers: Cross-convolutional-layer pooling for image classification. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 4749–4757. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, Z.; Wu, X.; Chen, Y.; Zhao, J.; Hu, Y.; Liu, J. Pyramid Pixel Context Adaption Network for Medical Image Classification with Supervised Contrastive Learning. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 6802–6815. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, Z.; Lew, L. PokeBNN: A Binary Pursuit of Lightweight Accuracy. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 12465–12475. [Google Scholar] [CrossRef]
- Chen, T.W.; Yoshinaga, M.; Gao, H.; Tao, W.; Wen, D.; Liu, J.; Osa, K.; Kato, M. Condensation-Net: Memory-Efficient Network Architecture with Cross-Channel Pooling Layers and Virtual Feature Maps. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Long Beach, CA, USA, 16–20 June 2019; pp. 149–157. [Google Scholar] [CrossRef]
- Zhang, D.; Cen, R.; Pu, H.; Wan, R.; Wang, D. An FPGA-based binary neural network accelerator with enhanced hardware efficiency and data reuse. Microelectron. J. 2025, 156, 106556. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, A.; Mo, R.; Wang, D. End-to-end acceleration of the YOLO object detection framework on FPGA-only devices. Neural Comput. Appl. 2023, 36, 1067–1089. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, W.; Ma, Y.; Wang, Z. Efficient Hardware Post Processing of Anchor-Based Object Detection on FPGA. In Proceedings of the 2020 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Limassol, Cyprus, 6–8 July 2020; pp. 580–585. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Li, J.; Qu, C.; Shao, J. Ship detection in SAR images based on an improved Faster R-CNN. In Proceedings of the 2017 SAR in Big Data Era: Models, Methods and Applications, Beijing, China, 13–14 November 2017; IEEE: New York, NY, USA, 2017; pp. 1–6. [Google Scholar]
- Sun, X.; Wang, P.; Yan, Z.; Diao, W.; Lu, X.; Yang, Z.; Zhang, Y.; Xiang, D.; Yan, C.; Guo, J.; et al. Automated high-resolution earth observation image interpretation: Outcome of the 2020 Gaofen challenge. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8922–8940. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Li, Y.; Yao, B.; Peng, Y. FPGA-based Large-scale Remote Sensing Image ROI Extraction for On-orbit Ship Detection. In Proceedings of the 2022 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Ottawa, ON, Canada, 6–19 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Ma, X.; Ji, K.; Xiong, B.; Zhang, L.; Feng, S.; Kuang, G. Light-YOLOv4: An Edge-Device Oriented Target Detection Method for Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10808–10820. [Google Scholar] [CrossRef]

| LUTs (K) | DSP | BRAM (36k) | Latency (ms) @10,647 Boxes | |
|---|---|---|---|---|
| BNN Computation | 184.9 | 299 | 261.5 | 12.12 |
| Post Processing | 5.3 | 23 | 10 | 0.04 |
| Total | 190 | 322 | 271.5 | 12.17 |
| IGARSS2024 [9] | TGRS2022 [11] | I2MTC2022 [33] | Ours | Ours | Ours | |
|---|---|---|---|---|---|---|
| Model | YOLOv5 | YOLOv2 | Traditional | HE-BiDet | HE-BiDet | HE-BiDet |
| Model size (MB) | 114.2 | - | - | 6.03 | 6.03 | 6.03 |
| Dataset | SAR-SHIP | SSDD | - | SAR-SHIP | Air-SAR-SHIP | SSDD |
| Input Size | 256 × 256 | 416 × 416 | 1000 × 1024 | 256 × 256 | 416 × 416 | 416 × 416 |
| AP50 | 78.74 | 93.3 | 91.3 | 91.3 | 71.0 | 92.7 |
| Data width (W/A) | FP16 | 4/3-6 | 8 | 1/1 | 1/1 | 1/1 |
| FPGA Device | XCVU9P | XC7VX690T | XCKU115 | XC7VX690T | XC7VX690T | XC7VX690T |
| Technology (nm) | 16 | 16 | 16 | 28 | 28 | 28 |
| LUTs (K) | - | 196.9 | 77.1 | 190 | 190 | 190 |
| DSP | 5107 | 2496 | 120 | 322 | 322 | 322 |
| BRAM 36K | - | 319.5 | 970 | 271.5 | 271.5 | 271.5 |
| Frequency (MHz) | - | 250 | - | 180 | 180 | 180 |
| Batch Size | 1 | 50 | 1 | 1 | 1 | 1 |
| Latency (ms) | 68.9 | 76.68 | 16 | 5.2 | 12.4 | 12.4 |
| FPS | 25.9 | 636 | 62.5 | 189.3 | 80.5 | 80.5 |
| Throughput (GOP/S) | - | - | - | 3500.3 | 3929.7 | 3929.7 |
| On-chip Power (W) | - | - | - | 12.9 | 12.9 | 12.9 |
| Platform Power (W) | 36.8 | - | - | 18.3 | 18.3 | 18.3 |
| GOPs/W | - | - | - | 271.3 | 304.6 | 304.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Liang, Z.; Cen, R.; Yan, Z.; Wan, R.; Wang, D. HE-BiDet: A Hardware Efficient Binary Neural Network Accelerator for Object Detection in SAR Images. Micromachines 2025, 16, 549. https://doi.org/10.3390/mi16050549
Zhang D, Liang Z, Cen R, Yan Z, Wan R, Wang D. HE-BiDet: A Hardware Efficient Binary Neural Network Accelerator for Object Detection in SAR Images. Micromachines. 2025; 16(5):549. https://doi.org/10.3390/mi16050549
Chicago/Turabian StyleZhang, Dezheng, Zehan Liang, Rui Cen, Zhihong Yan, Rui Wan, and Dong Wang. 2025. "HE-BiDet: A Hardware Efficient Binary Neural Network Accelerator for Object Detection in SAR Images" Micromachines 16, no. 5: 549. https://doi.org/10.3390/mi16050549
APA StyleZhang, D., Liang, Z., Cen, R., Yan, Z., Wan, R., & Wang, D. (2025). HE-BiDet: A Hardware Efficient Binary Neural Network Accelerator for Object Detection in SAR Images. Micromachines, 16(5), 549. https://doi.org/10.3390/mi16050549





