Glass Microbubble Encapsulation for Improving the Lifetime of a Ferrofluid-Based Magnetometer
Abstract
1. Introduction
2. Fabrication and Experimental Setup
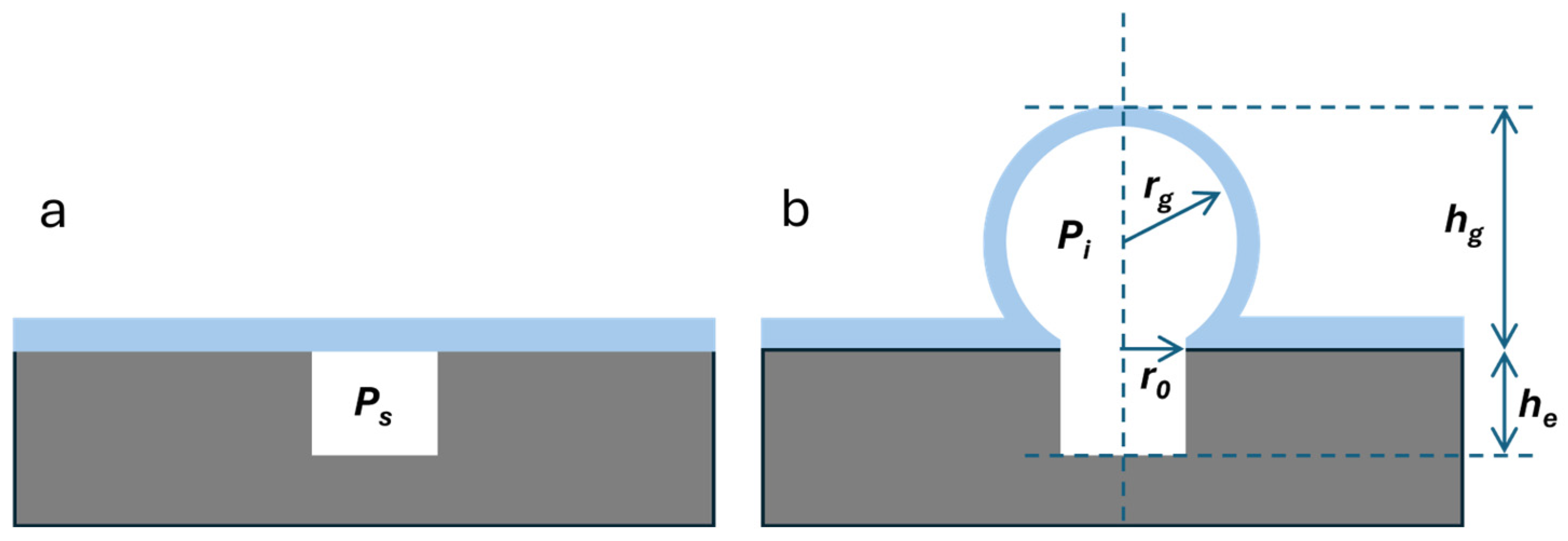
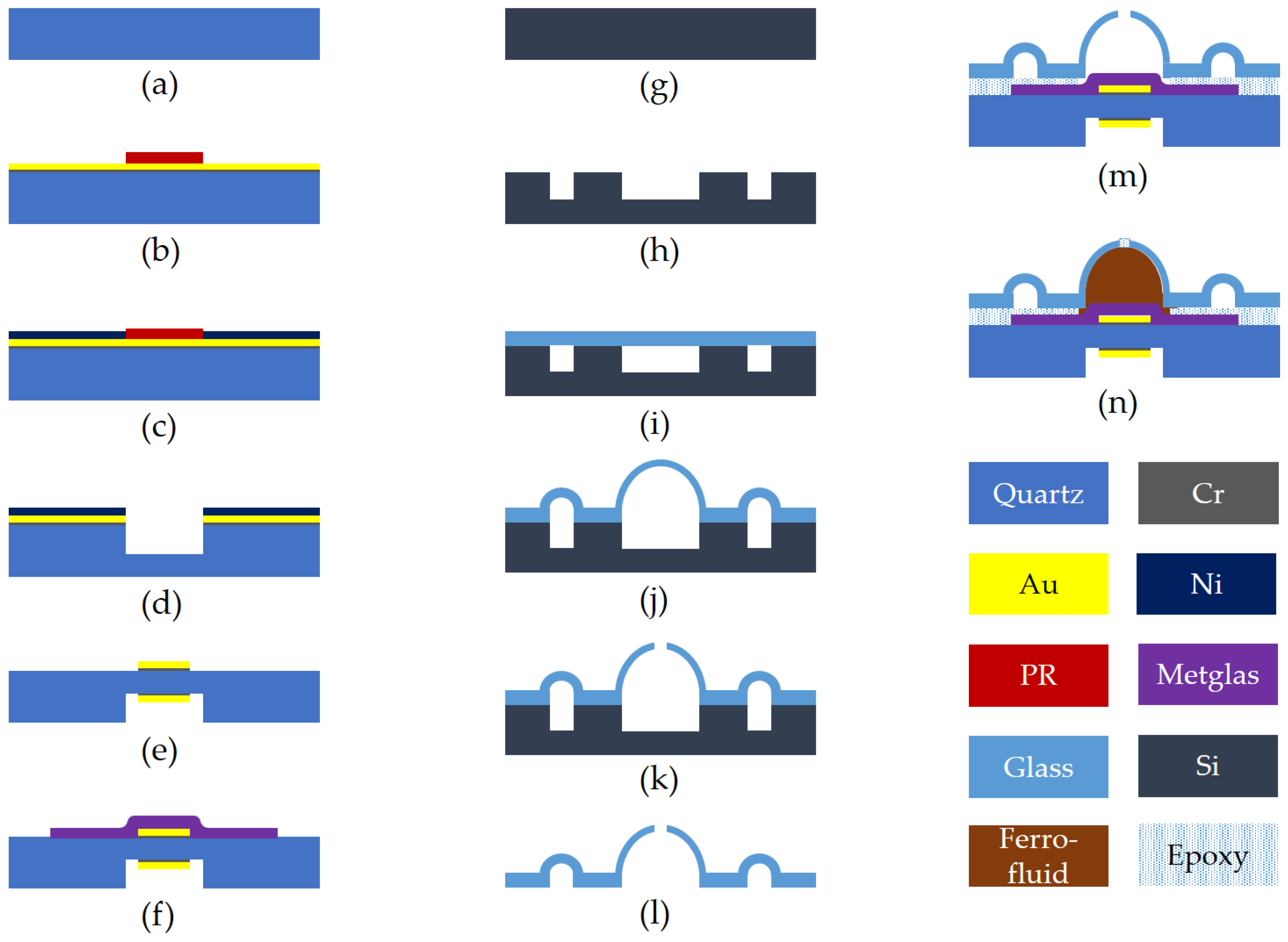
2.1. Quartz Resonator Chip
2.2. Glass Microbubble Chip
2.3. Ferrofluid Magnetometer Packaging
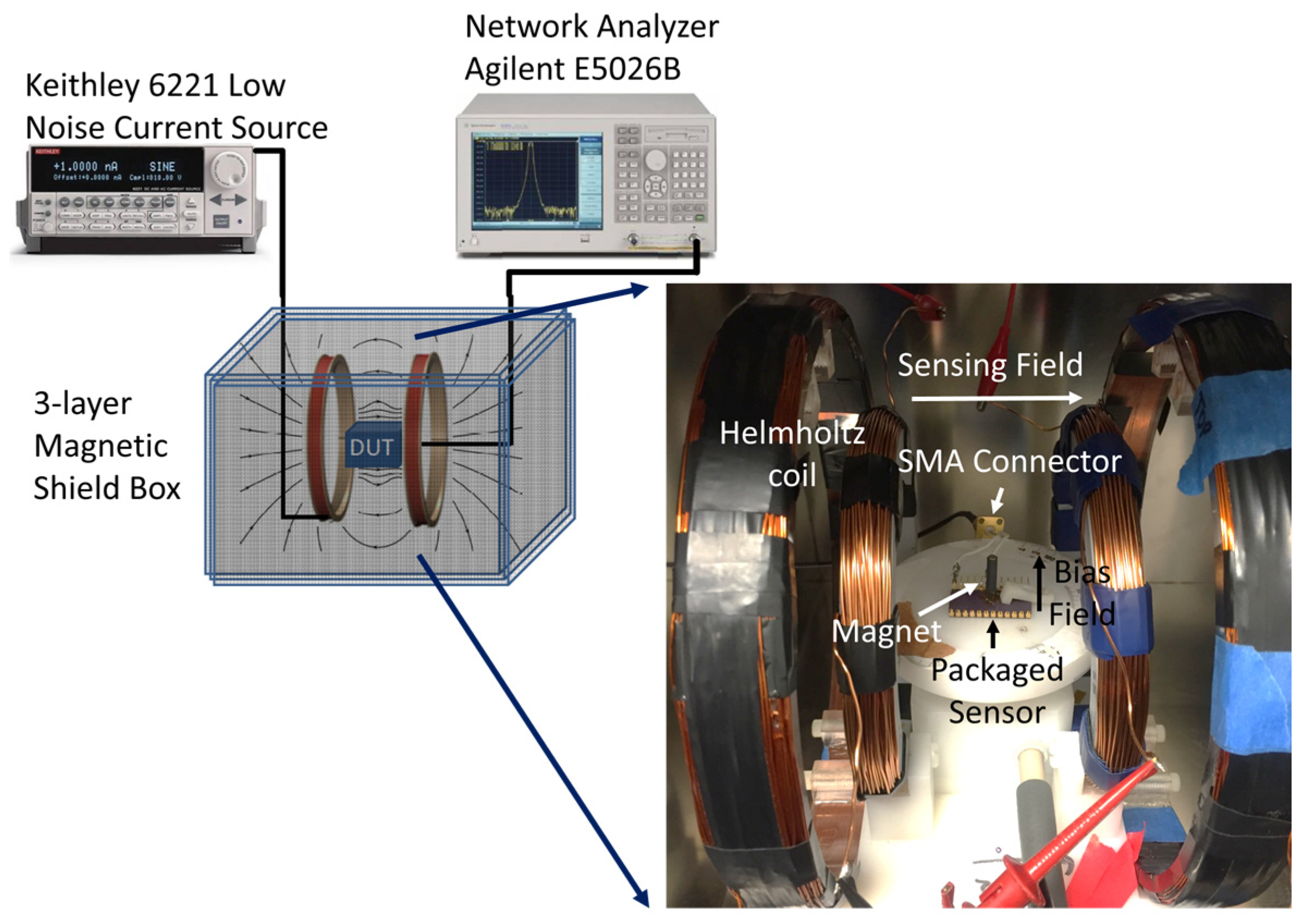
2.4. Experimental Setup
3. Results and Discussion
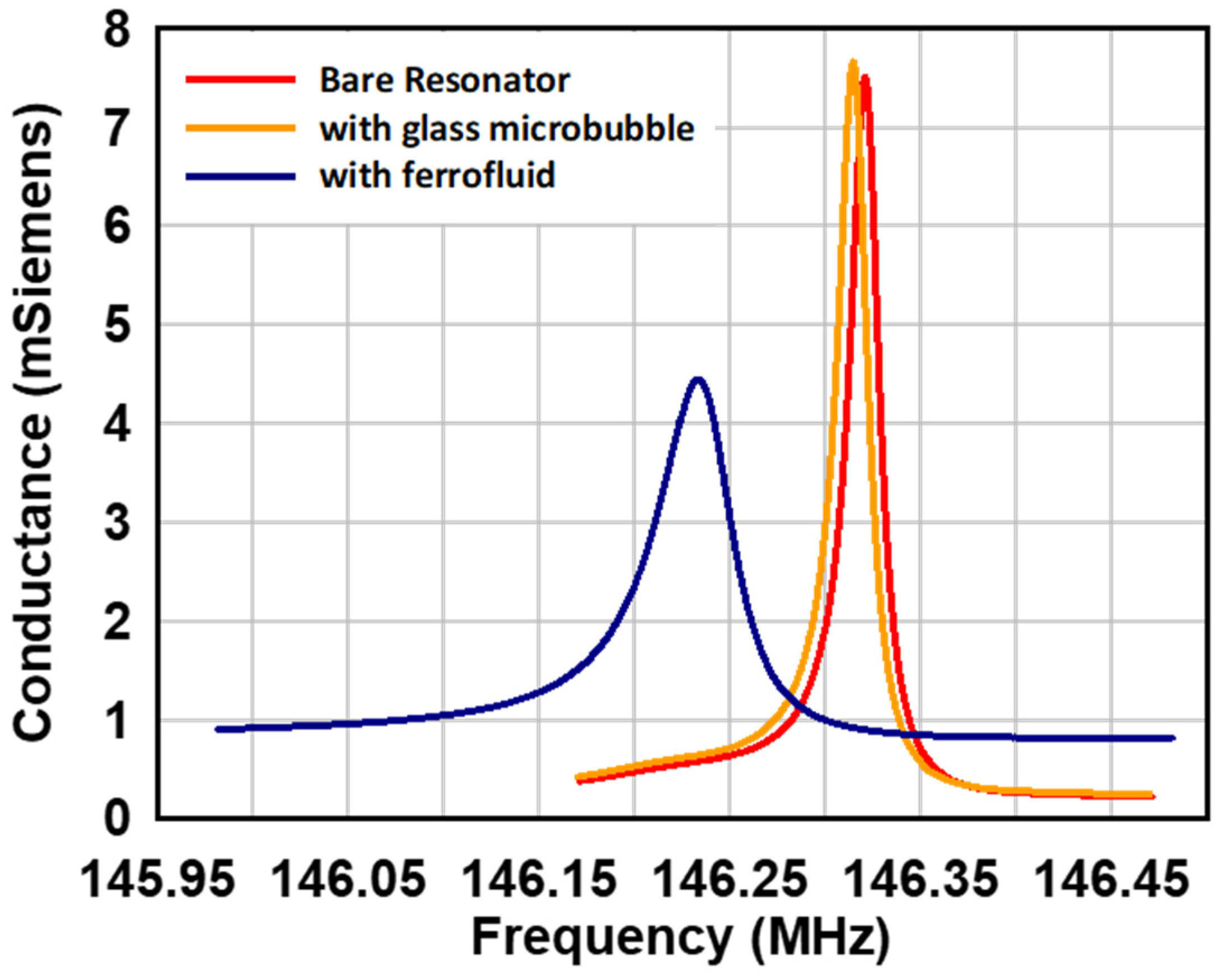
3.1. Characterization of Quartz Resonator
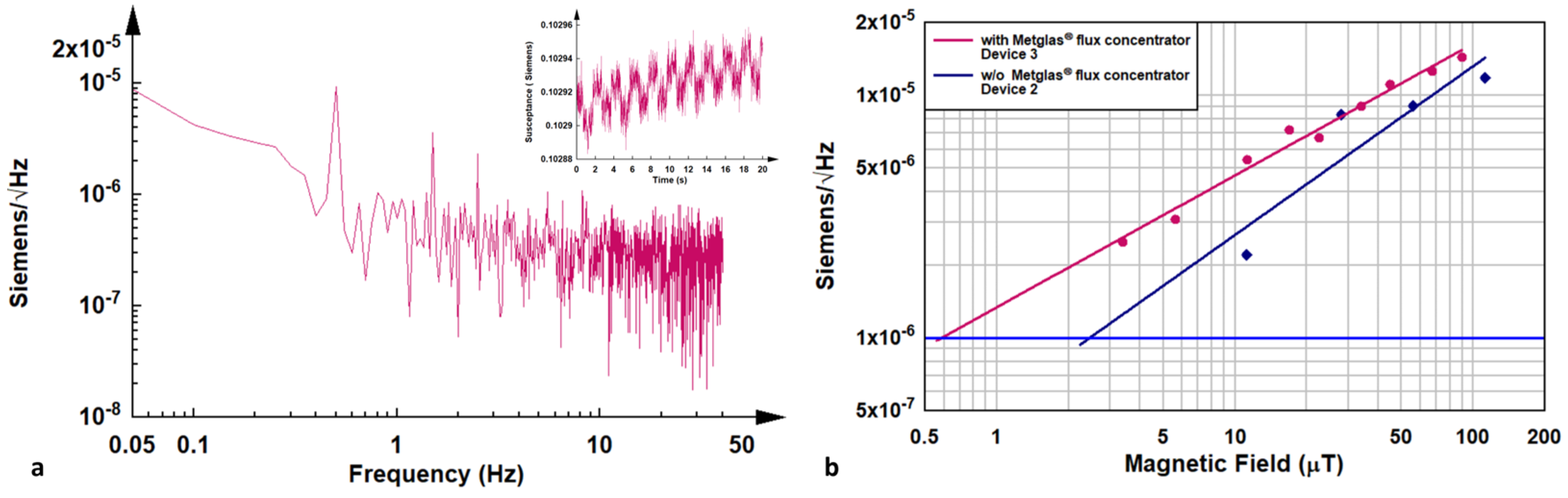
3.2. Response to Magnetic Field
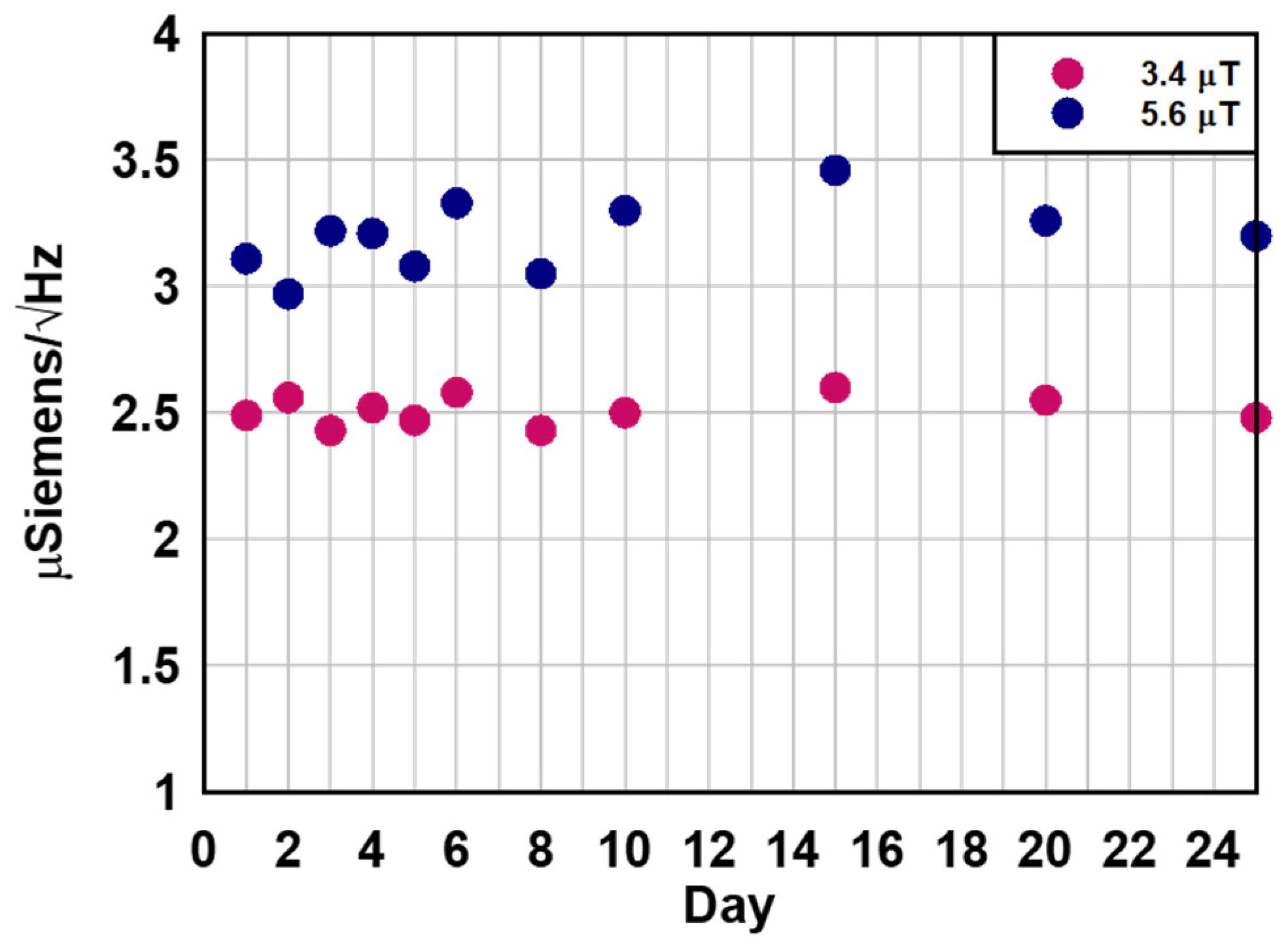
3.3. Lifetime of Packaged Device
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Darveaux, R.; Munukutla, L. Critical challenges in packaging MEMS devices. In Proceedings of the IEEE/SEMI Conference and Workshop on Advanced Semiconductor Manufacturing, Munich, Germany, 11–12 April 2005; pp. 210–216. [Google Scholar]
- Del Sarto, M. MEMS Package Design and Technology. In Silicon Sensors and Actuators: The Feynman Roadmap; Vigna, B., Ferrari, P., Villa, F.F., Lasalandra, E., Zerbini, S., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 833–859. [Google Scholar]
- Reichl, H.; Grosser, V. Overview and development trends in the field of MEMS packaging. Technical Digest. MEMS 2001. In Proceedings of the 14th IEEE International Conference on Micro Electro Mechanical Systems, Interlaken, Switzerland, 21–25 January 2001; Cat. No.01CH37090. pp. 1–5. [Google Scholar]
- Zhang, Y.; Tan, X.; Chen, W.; Zhang, G.; Liu, X. Study of MEMS packaging technology. In Proceedings of the 2005 6th International Conference on Electronic Packaging Technology, Shenzhen, China, 30 August–2 September 2005; pp. 1–4. [Google Scholar]
- Esashi, M. Wafer level packaging of MEMS. J. Micromech. Microeng. 2008, 18, 073001. [Google Scholar] [CrossRef]
- Hilton, A.; Temple, D.S. Wafer-Level Vacuum Packaging of Smart Sensors. Sensors 2016, 16, 1819. [Google Scholar] [CrossRef] [PubMed]
- Torunbalci, M.M.; Alper, S.E.; Akin, T. Advanced MEMS Process for Wafer Level Hermetic Encapsulation of MEMS Devices Using SOI Cap Wafers With Vertical Feedthroughs. J. Microelectromech. Syst. 2015, 24, 556–564. [Google Scholar] [CrossRef]
- Hata, H.; Nakaki, Y.; Inoue, H.; Kosasayama, Y.; Ohta, Y.; Fukumoto, H.; Seto, T.; Kama, K.; Takeda, M.; Kimata, M. Uncooled IRFPA with Chip Scale Vacuum Package; SPIE: Bellingham, DC, USA, 2006; pp. 602619-1–602619-10. [Google Scholar]
- Suni, T.; Henttinen, K.; Lipsanen, A.; Dekker, J.; Luoto, H.; Kulawski, M. Wafer Scale Packaging of MEMS by Using Plasma-Activated Wafer Bonding. J. Electrochem. Soc. 2006, 153, G78. [Google Scholar] [CrossRef]
- Knowles, K.M.; van Helvoort, A.T.J. Anodic bonding. Int. Mater. Rev. 2006, 51, 273–311. [Google Scholar] [CrossRef]
- Baum, M.; Chenping, J.; Haubold, M.; Wiemer, M.; Schneider, A.; Rank, H.; Trautmann, A.; Gessner, T. Eutectic wafer bonding for 3-D integration. In Proceedings of the 3rd Electronics System Integration Technology Conference ESTC, Berlin, Germany, 13–16 September 2010; pp. 1–6. [Google Scholar]
- Goyal, A.; Cheong, J.; Tadigadapa, S. Tin-based solder bonding for MEMS fabrication and packaging applications. J. Micromech. Microeng. 2004, 14, 819. [Google Scholar] [CrossRef]
- Knechtel, R. Glass frit bonding: An universal technology for wafer level encapsulation and packaging. Microsyst. Technol. 2005, 12, 63–68. [Google Scholar] [CrossRef]
- Sarvar, F.; Hutt, D.A.; Whalley, D.C. Application of adhesives in MEMS and MOEMS assembly: A review. In Proceedings of the 2nd International IEEE Conference on Polymers and Adhesives in Microelectronics and Photonics. POLYTRONIC 2002, Zalaegerszeg, Hungary, 23–26 June 2002; Conference Proceedings (Cat. No.02EX599). pp. 22–28. [Google Scholar]
- Zhang, C.; Cocking, A.; Freeman, E.; Liu, Z.; Tadigadapa, S. On-Chip Glass Microspherical Shell Whispering Gallery Mode Resonators. Sci. Rep. 2017, 7, 14965. [Google Scholar] [CrossRef]
- Eklund, E.J.; Shkel, A.M. Glass Blowing on a Wafer Level. J. Microelectromech. Syst. 2007, 16, 232–239. [Google Scholar] [CrossRef]
- Llandro, J.; Palfreyman, J.J.; Ionescu, A.; Barnes, C.H.W. Magnetic biosensor technologies for medical applications: A review. Med. Biol. Eng. Comput. 2010, 48, 977–998. [Google Scholar] [CrossRef]
- Drung, D.; Cantor, R.; Peters, M.; Scheer, H.J.; Koch, H. Low-noise high-speed dc superconducting quantum interference device magnetometer with simplified feedback electronics. Appl. Phys. Lett. 1990, 57, 406–408. [Google Scholar] [CrossRef]
- Savukov, I.M.; Romalis, M.V. NMR Detection with an Atomic Magnetometer. Phys. Rev. Lett. 2005, 94, 123001. [Google Scholar] [CrossRef]
- Shah, V.; Knappe, S.; Schwindt, P.D.D.; Kitching, J. Subpicotesla atomic magnetometry with a microfabricated vapour cell. Nat. Photonics 2007, 1, 649–652. [Google Scholar] [CrossRef]
- Li, F.; Misra, R.; Fang, Z.; Wu, Y.; Schiffer, P.; Zhang, Q.; Tadigadapa, S.A.; Datta, S. Magnetoelectric Flexural Gate Transistor with Nanotesla Sensitivity. J. Microelectromech. Syst. 2013, 22, 71–79. [Google Scholar] [CrossRef]
- Baibich, M.N.; Broto, J.M.; Fert, A.; Van Dau, F.N.; Petroff, F.; Etienne, P.; Creuzet, G.; Friederich, A.; Chazelas, J. Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices. Phys. Rev. Lett. 1988, 61, 2472–2475. [Google Scholar] [CrossRef]
- Fang, Z.; Lu, S.G.; Li, F.; Datta, S.; Zhang, Q.M.; El Tahchi, M. Enhancing the magnetoelectric response of Metglas/polyvinylidene fluoride laminates by exploiting the flux concentration effect. Appl. Phys. Lett. 2009, 95, 112903. [Google Scholar] [CrossRef]
- Hatipoglu, G.; Tadigadapa, S. Micromachined magnetoflexoelastic resonator based magnetometer. Appl. Phys. Lett. 2015, 107, 192406. [Google Scholar] [CrossRef]
- Hatipoglu, G.; Tadigadapa, S. Magnetoviscoelastic Ferrofluid-Based Magnetometer. J. Microelectromech. Syst. 2016, 25, 170–178. [Google Scholar] [CrossRef]
- Mendelev, V.S.; Ivanov, A.O. Ferrofluid aggregation in chains under the influence of a magnetic field. Phys. Rev. E 2004, 70, 051502. [Google Scholar] [CrossRef]
- Odenbach, S. Magnetoviscous and viscoelastic effects in ferrofluids. Int. J. Mod. Phys. B 2000, 14, 1615–1631. [Google Scholar] [CrossRef]
- Zhang, C.; Hatipoglu, G.; Tadigadapa, S. High-Speed Ultrasmooth Etching of Fused Silica Substrates in SF6, NF3, and H2O-Based Inductively Coupled Plasma Process. Microelectromech. Syst. J. 2015, 24, 922–930. [Google Scholar] [CrossRef]
- Dhivyaraja, K.; Gaddes, D.; Freeman, E.; Tadigadapa, S.; Panchagnula, M.V. Dynamical similarity and universality of drop size and velocity spectra in sprays. J. Fluid Mech. 2018, 860, 510–543. [Google Scholar] [CrossRef]
- Lapadatu, A.C.; Jakobsen, H. Chapter 30—Anodic Bonding. In Handbook of Silicon Based MEMS Materials and Technologies, 2nd ed.; Tilli, M., Motooka, T., Airaksinen, V.-M., Franssila, S., Paulasto-Kröckel, M., Lindroos, V., Eds.; William Andrew Publishing: Boston, MA, USA, 2015; pp. 599–610. [Google Scholar]
- Rogers, T.; Kowal, J. Selection of glass, anodic bonding conditions and material compatibility for silicon-glass capacitive sensors. Sens. Actuators A Phys. 1995, 46, 113–120. [Google Scholar] [CrossRef]
- Baier, V.; Schmidt, K.; Straube, B.; Horst, H. Anodic Bonding at Low Temperatures using Laser Microstructurable Li–Doped Glass. In Proceedings of the Fourth International Symposium on Semiconductor Wafer Bonding: Science, Technology, and Applications, Pennington, NJ, USA, 1997; The Electrochemical Society: Pennington, NJ, USA, 1998; p. 222. [Google Scholar]


| Device | f0 * | Q * | Q′ * | t * | Metglas Patterns | Bias Field * |
|---|---|---|---|---|---|---|
| 1 | 131.0 | 1500 | 440 | 12.7 | Yes | 5 |
| 2 | 146.3 | 7726 | 2753 | 11.4 | No | 10 |
| 3 | 122.6 | NA | 10779 | 13.6 | Yes | 3 |
| Device Number | Minimum Measured Magnetic Field (µT) | Minimum Predicted Magnetic Field (µT) | Modulation Frequency (Hz) |
|---|---|---|---|
| 1 | 200 | 15 | 0.01 |
| 2 | 11.2 | 2.4 | 0.5 |
| 3 | 3.4 | 0.6 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Tadigadapa, S. Glass Microbubble Encapsulation for Improving the Lifetime of a Ferrofluid-Based Magnetometer. Micromachines 2025, 16, 519. https://doi.org/10.3390/mi16050519
Zhang C, Tadigadapa S. Glass Microbubble Encapsulation for Improving the Lifetime of a Ferrofluid-Based Magnetometer. Micromachines. 2025; 16(5):519. https://doi.org/10.3390/mi16050519
Chicago/Turabian StyleZhang, Chenchen, and Srinivas Tadigadapa. 2025. "Glass Microbubble Encapsulation for Improving the Lifetime of a Ferrofluid-Based Magnetometer" Micromachines 16, no. 5: 519. https://doi.org/10.3390/mi16050519
APA StyleZhang, C., & Tadigadapa, S. (2025). Glass Microbubble Encapsulation for Improving the Lifetime of a Ferrofluid-Based Magnetometer. Micromachines, 16(5), 519. https://doi.org/10.3390/mi16050519






