Electro-Elastic Instability and Turbulence in Electro-osmotic Flows of Viscoelastic Fluids: Current Status and Future Directions
Abstract
1. Introduction
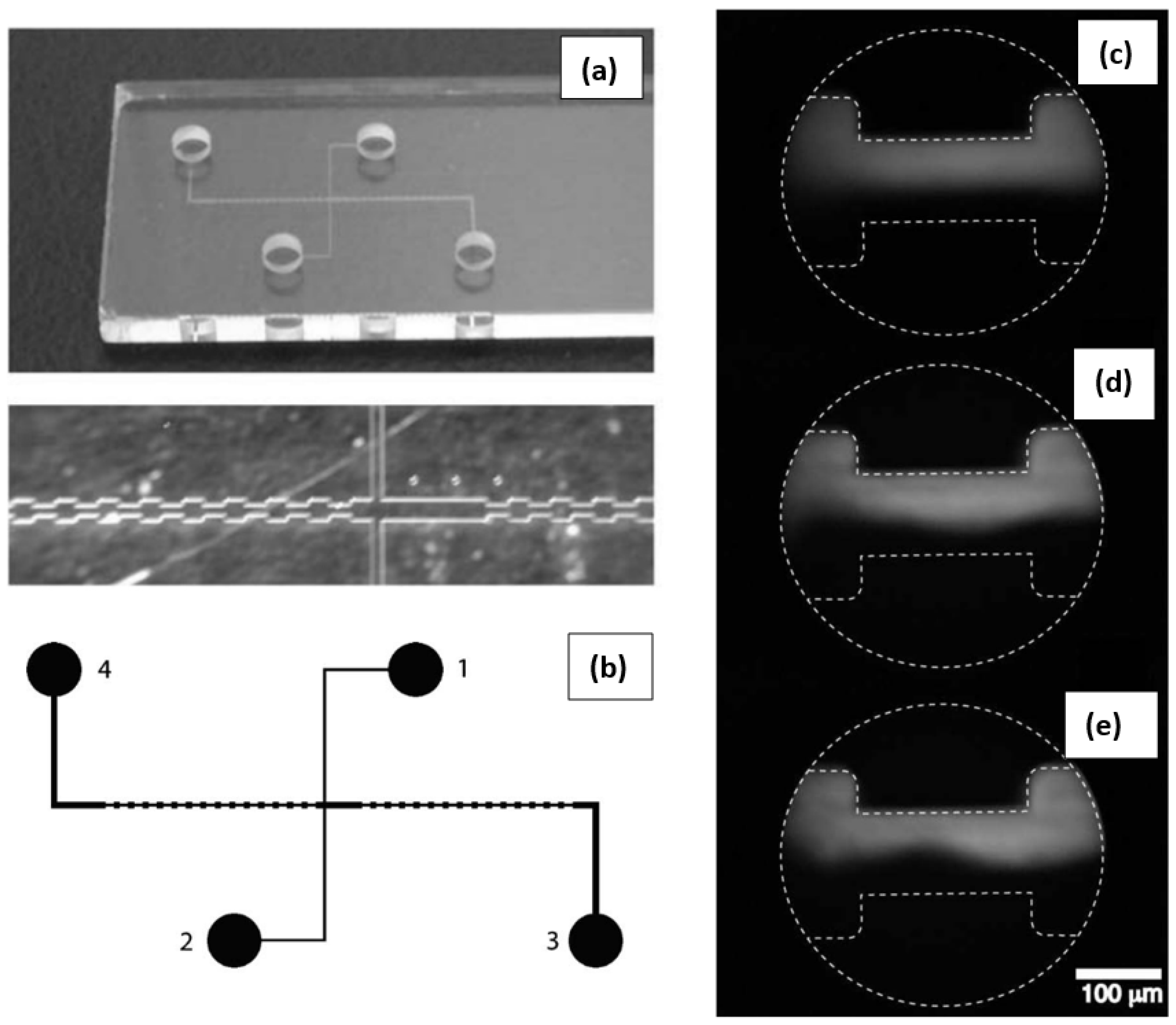
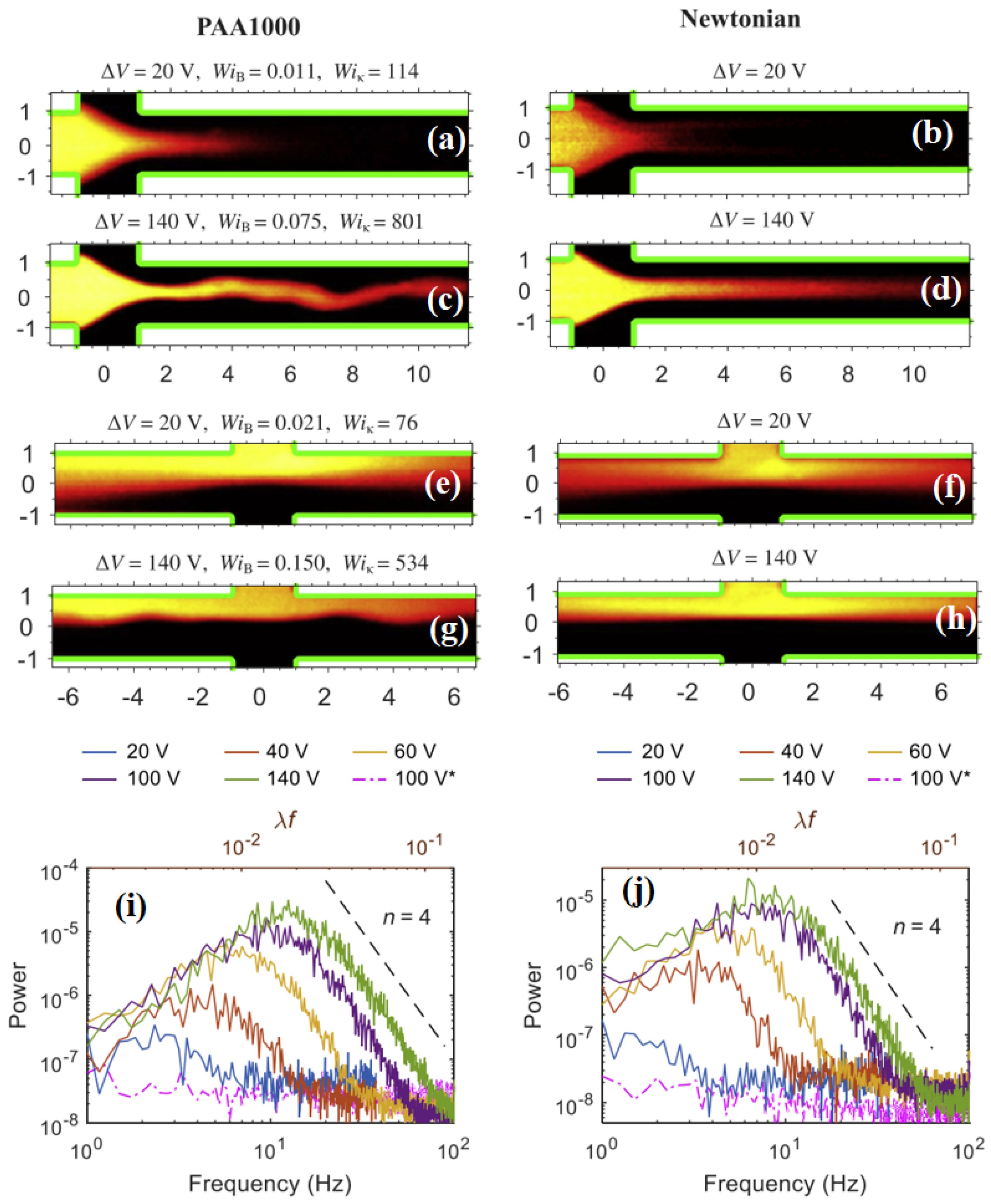
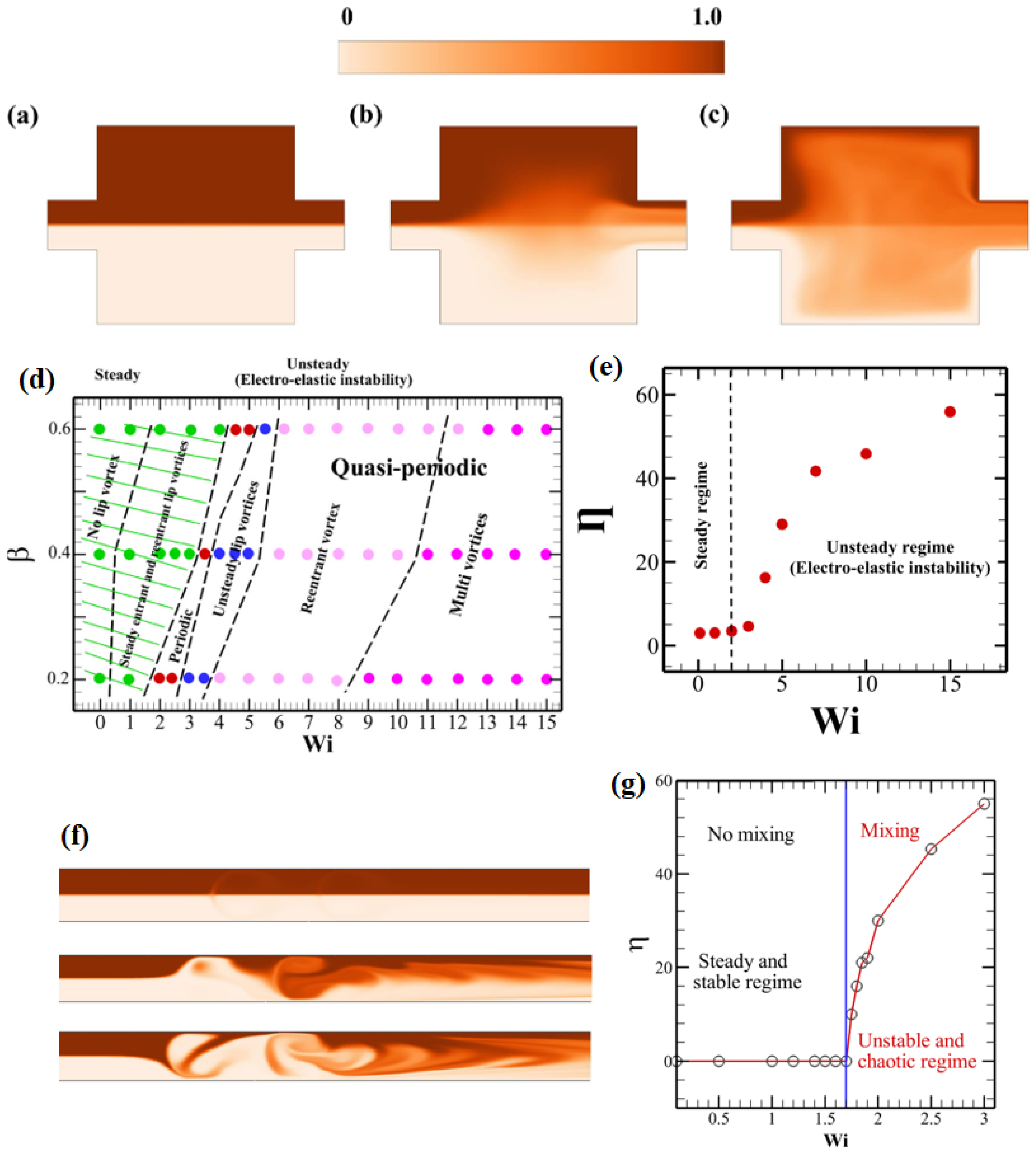
2. Current Status of Studies on EEI and EET
3. Conclusions and Future Directions
3.1. Scope in Fundamental Understanding
- In pressure-driven and rotationally driven shear flows, it is well established that when elastic instability arises, the flow field transitions to a more chaotic and fluctuating state, often leading to the onset of elastic turbulence as the fluid elasticity or flow strength increases [40,41]. However, for electro-osmotic flows, experimental investigations of electro-elastic turbulence remain largely limited in the literature. Although Pimenta and Alves [52] briefly mentioned this phenomenon in their study, they were unable to confirm its presence due to the absence of a detailed fixed-point data analysis of the fluctuating flow field. Thus, there is a significant need for further research into this regime. Future studies should include comprehensive statistical analyses of fixed-point fluctuating flow data and the temporal evolution of the entire flow field [67]. This can be achieved using advanced techniques such as micro-particle image velocimetry (-PIV) or other flow visualization methods, allowing for a more detailed characterization of the electro-elastic turbulence in electro-osmotic flows. Expanding the understanding of this regime could have important implications for enhancing transport processes in microfluidic applications. Along with experiments, further numerical simulations are needed to understand these EEI and EET phenomena better. However, the simulation of viscoelastic fluids remains a challenge due to the inherent “High Weissenberg Number Problem (HWNP)” associated with these fluids [68]. This problem leads to the loss of numerical stability at sufficiently high Weissenberg numbers, where EET flow is expected to exist. Some studies have used numerical stabilization techniques, such as the log-conformation tensor approach [69], and performed simulations in this regime [63,66]. More such stabilization techniques should be proposed to perform numerical simulations more efficiently at high Weissenberg numbers than possible with the currently available stabilization methods. However, simulations have been performed on these two phenomena so far using only the continuum approximation of the flow system. This approach cannot provide details on how fluid microstructure (such as polymer molecules in the case of polymer solutions) evolves in this EET regime, which could answer many questions related to this flow phenomenon. To do so, we must adopt a micro–macro- or multiscale simulation approach for viscoelastic fluids [70,71], which solves the governing equations of both the continuum solvent and dispersed phases, and, ultimately, solutions are coupled with each other through a proper algorithm. Although this simulation approach would provide more details, it will be more challenging to implement than the continuum approach. Therefore, a huge scope is present in this direction for future studies.
- A detailed investigation is required to determine whether significant differences exist in the evolution of the local and global flow fields over time or the onset mechanisms between electrokinetically driven and pressure-driven elastic instability and elastic turbulence phenomena. This question naturally arises because a significant difference exists in the flow dynamics between pressure- and electrokinetic-driven flows. For instance, the velocity field shows a parabolic profile in the former case, whereas a plug-like profile is seen in the latter case. This may cause different mechanisms for the onset of these instabilities for pressure- and electrokinetically driven flows. This clarification is very crucial as some experimental studies have suggested that EEI does not enhance mixing to the same degree as the elastic instability observed in pressure-driven or rotational shear flows [49,52]. A potential explanation for this difference lies in the variation in velocity profiles between the two flow types. Electrokinetically driven flows typically exhibit a plug-like velocity profile in microchannels [1], whereas pressure-driven flows tend to follow a parabolic velocity profile. These differing velocity distributions may lead to distinct flow behaviors once the EI and ET regimes are triggered. Therefore, further comparative studies, particularly focusing on temporal and spatial flow field characteristics in both these flow conditions, are necessary to understand the underlying dynamics and potential impacts on processes like mixing in a microscale system.
- When two non-Newtonian fluids with differing electrical conductivities flow under the influence of an applied electric field, the phenomenon of electrokinetic instability (EKI) often arises in microfluidic systems once the electric field strength and the conductivity gradient exceeds critical thresholds [72]. An intriguing area of research involves investigating the electro-elastic instabilities in two viscoelastic fluids, especially when these fluids also exhibit electrical conductivity gradients that could generate electrokinetic instabilities. A thorough statistical analysis of both the fixed-point fluctuating flow field data and the global flow field data is required to discern whether these two types of instabilities, electrokinetic and electro-elastic, behave similarly or if distinct differences exist between them. This investigation is crucial, as recent experimental and numerical studies have indicated that the viscoelastic properties of fluids tend to suppress the chaotic fluctuations associated with electrokinetic instability [73,74]. Understanding this suppression effect could have significant implications for controlling the instabilities in microfluidic systems.
- In the case of pressure-driven purely elastic instability and elastic turbulence phenomena, it has been observed that the shear-thinning properties (the apparent viscosity decreases with increasing deformation rate) of a viscoelastic fluid tend to suppress the chaotic behavior arising due to these instabilities and/or suppress the onset of these instabilities [75,76]. However, no detailed study has been performed on the corresponding electrokinetic-driven flows, emphasizing the influence of different non-linear rheological behaviors, such as shear-thinning or yield stress, on the onset of EEI and EET phenomena. Therefore, a great scope is present in this direction for further studies both in terms of experiments as well as numerical simulations.
3.2. Scope in Practical Applications
- Both electro-elastic instability and electro-elastic turbulence generate chaotic and fluctuating flow fields, which could enhance the mixing efficiency of two fluids in microfluidic systems. Chaotic flow patterns are known to significantly improve mixing, as demonstrated by several experimental and numerical studies investigating pressure-driven or rotationally driven elastic instabilities and elastic turbulence. These studies have shown a marked increase in mixing efficiency in viscoelastic fluids [43,44,45,54,77,78]. However, in the case of EEI and EET, the findings are less consistent. Numerical studies [63,64,66] suggest that these phenomena can lead to increased mixing efficiency, with significant improvements over Newtonian fluid behavior. On the other hand, some experimental studies [51,52] have reported either negligible increases or even decreases in mixing efficiency when EEI and EET are involved, particularly when compared to simple Newtonian fluids under similar conditions. These discrepancies between numerical and experimental results indicate that the mechanisms governing mixing in electro-elastic systems are not yet fully understood. To resolve these inconsistencies and clarify the role of EEI and EET in fluid mixing, further detailed studies, consisting of both experimental and numerical studies, are necessary. These investigations should focus on understanding the underlying flow dynamics and the conditions that lead to either enhancement in or suppression of mixing efficiency in microfluidic systems utilizing EEI and EET phenomena.
- Another promising application area deserving attention is microscale heat transfer through the utilization of electro-elastic instability and electro-elastic turbulence phenomena. Pressure-driven or rotationally driven elastic instability and elastic turbulence phenomena have already demonstrated significant enhancement in heat transfer rates in various microscale geometries when compared to simple Newtonian fluids under identical operating conditions [48,79,80,81,82,83,84,85]. The increased heat transfer efficiency results from the chaotic flow patterns generated by these instabilities, which lead to better heat distribution across the fluid. However, studies investigating microscale heat transfer using the corresponding EEI and EET phenomena are notably absent in the current literature. Exploring this area could provide valuable insights for enhancing the thermal performance of microscale systems, especially in applications where the precise control of heat transfer is critical. Potential applications include microfluidic heat exchangers, microfluidic cooling systems, microfluidic fuel cells, and microreactors. These systems frequently encounter heat transfer challenges due to their small dimensions and high heat generation rates. The introduction of EEI- and EET-based mechanisms could significantly improve thermal management by promoting enhanced convective heat transfer, thereby increasing the overall efficiency of these microscale devices. Further investigation into these phenomena could lead to new methods for optimizing the thermal performance of microfluidic systems, ultimately improving energy efficiency.
- Electrokinetic remediation (EKR) is an in situ environmental remediation technique that employs electrical currents to remove contaminants such as heavy metals, radioactive materials, and organic compounds from soils, sediments, or groundwater [8,86,87,88]. This process is driven primarily by electro-osmotic flow through porous media, which typically consist of soils or sediments. The introduction of electro-elastic instability and electro-elastic turbulence phenomena in these systems could enhance the contaminant removal efficiency, making this an area worthy of further investigation. This is particularly significant because studies on pressure-driven elastic instability and elastic turbulence in porous media have already demonstrated substantial improvements in oil displacement efficiency [89,90,91,92] and increased reaction rates [93], attributed to the chaotic and enhanced flow dynamics induced by these instabilities. Similar mechanisms could be leveraged in EKR, where the presence of EEI and EET may lead to more effective contaminant mobilization and transport through porous soils, improving overall remediation outcomes. Given the potential benefits, exploring the role of these elastic phenomena in EKR systems could open new avenues for optimizing contaminant removal, particularly in low-permeability soils where traditional methods struggle to achieve efficient remediation.
Funding
Conflicts of Interest
Abbreviations
| EOF | Electro-osmotic flows |
| EEI | Electro-elastic instability |
| EET | Electro-elastic turbulence |
| EDL | Electrical double-layer |
References
- Li, D. Electrokinetics in Microfluidics; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Wong, P.K.; Wang, T.H.; Deval, J.H.; Ho, C.M. Electrokinetics in micro devices for biotechnology applications. IEEE/ASME Trans. Mechatron. 2004, 9, 366–376. [Google Scholar] [CrossRef]
- Mir, M.; Martínez-Rodríguez, S.; Castillo-Fernández, O.; Homs-Corbera, A.; Samitier, J. Electrokinetic techniques applied to electrochemical DNA biosensors. Electrophoresis 2011, 32, 811–821. [Google Scholar] [CrossRef] [PubMed]
- Xuan, X. Recent advances in direct current electrokinetic manipulation of particles for microfluidic applications. Electrophoresis 2019, 40, 2484–2513. [Google Scholar] [CrossRef] [PubMed]
- Ghosal, S. Electrokinetic flow and dispersion in capillary electrophoresis. Annu. Rev. Fluid Mech. 2006, 38, 309–338. [Google Scholar] [CrossRef]
- Ocvirk, G.; Munroe, M.; Tang, T.; Oleschuk, R.; Westra, K.; Harrison, D.J. Electrokinetic control of fluid flow in native poly (dimethylsiloxane) capillary electrophoresis devices. Electrophor. Int. J. 2000, 21, 107–115. [Google Scholar] [CrossRef]
- Monnig, C.A.; Kennedy, R.T. Capillary electrophoresis. Anal. Chem. 1994, 66, 280–314. [Google Scholar] [CrossRef]
- Cameselle, C.; Gouveia, S. Electrokinetic remediation for the removal of organic contaminants in soils. Curr. Opin. Electrochem. 2018, 11, 41–47. [Google Scholar] [CrossRef]
- Rosestolato, D.; Bagatin, R.; Ferro, S. Electrokinetic remediation of soils polluted by heavy metals (mercury in particular). Chem. Eng. J. 2015, 264, 16–23. [Google Scholar] [CrossRef]
- Alshawabkeh, A.N. Electrokinetic soil remediation: Challenges and opportunities. Sep. Sci. Technol. 2009, 44, 2171–2187. [Google Scholar] [CrossRef]
- Chung, A.J.; Kim, D.; Erickson, D. Electrokinetic microfluidic devices for rapid, low power drug delivery in autonomous microsystems. Lab Chip 2008, 8, 330–338. [Google Scholar] [CrossRef]
- Fine, D.; Grattoni, A.; Zabre, E.; Hussein, F.; Ferrari, M.; Liu, X. A low-voltage electrokinetic nanochannel drug delivery system. Lab Chip 2011, 11, 2526–2534. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Choo, J.; Yan, B. The microfabricated electrokinetic pump: A potential promising drug delivery technique. Expert Opin. Drug Deliv. 2007, 4, 119–129. [Google Scholar] [CrossRef] [PubMed]
- Karimi, G.; Li, X. electro-osmotic flow through polymer electrolyte membranes in PEM fuel cells. J. Power Sources 2005, 140, 1–11. [Google Scholar] [CrossRef]
- Berning, T.; Lu, D.; Djilali, N. Three-dimensional computational analysis of transport phenomena in a PEM fuel cell. J. Power Sources 2002, 106, 284–294. [Google Scholar] [CrossRef]
- Masliyah, J.H.; Bhattacharjee, S. Electrokinetic and Colloid Transport Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Ramos, A. Electrokinetics and Electrohydrodynamics in Microsystems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 530. [Google Scholar]
- Pfohl, T.; Mugele, F.; Seemann, R.; Herminghaus, S. Trends in microfluidics with complex fluids. ChemPhysChem 2003, 4, 1291–1298. [Google Scholar] [CrossRef]
- Nghe, P.; Terriac, E.; Schneider, M.; Li, Z.; Cloitre, M.; Abecassis, B.; Tabeling, P. Microfluidics and complex fluids. Lab Chip 2011, 11, 788–794. [Google Scholar] [CrossRef]
- Stoecklein, D.; Di Carlo, D. Nonlinear microfluidics. Anal. Chem. 2018, 91, 296–314. [Google Scholar] [CrossRef]
- Waterman, H.; Blom, C.; Holterman, H.; ’s-Gravenmade, E.J.; Mellema, J. Rheological properties of human saliva. Arch. Oral Biol. 1988, 33, 589–596. [Google Scholar] [CrossRef]
- Brust, M.; Schaefer, C.; Doerr, R.; Pan, L.; Garcia, M.; Arratia, P.; Wagner, C. Rheology of human blood plasma: Viscoelastic versus Newtonian behavior. Phys. Rev. Lett. 2013, 110, 078305. [Google Scholar] [CrossRef]
- Thurston, G.B. Viscoelasticity of human blood. Biophys. J. 1972, 12, 1205–1217. [Google Scholar] [CrossRef]
- Juarez, G.; Arratia, P.E. Extensional rheology of DNA suspensions in microfluidic devices. Soft Matter 2011, 7, 9444–9452. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow and Applied Rheology: Engineering Applications; Butterworth-Heinemann: Oxford, UK, 2011. [Google Scholar]
- Bird, R.B.; Curtiss, C.F.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids, Volume 2: Kinetic Theory; Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Schroeder, C.M. Single polymer dynamics for molecular rheology. J. Rheol. 2018, 62, 371–403. [Google Scholar] [CrossRef]
- Beris, A.N.; Horner, J.S.; Jariwala, S.; Armstrong, M.; Wagner, N.J. Recent advances in blood rheology: A review. Soft Matter 2021, 17, 10591–10613. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, J.; Xu, M.; Zhang, K. Advances in the rheology of emulsion explosive. J. Mol. Liq. 2021, 336, 116854. [Google Scholar] [CrossRef]
- Fuhrmann, P.L.; Breunig, S.; Sala, G.; Sagis, L.; Stieger, M.; Scholten, E. Rheological behaviour of attractive emulsions differing in droplet-droplet interaction strength. J. Colloid Interface Sci. 2022, 607, 389–400. [Google Scholar] [CrossRef]
- Briceño-Ahumada, Z.; Mikhailovskaya, A.; Staton, J.A. The role of continuous phase rheology on the stabilization of edible foams: A review. Phys. Fluids 2022, 34, 031302. [Google Scholar] [CrossRef]
- Kim, D.; Seol, Y.; Kim, Y. Numerical study on rheology of two-dimensional dry foam. Phys. Fluids 2021, 33, 052111. [Google Scholar] [CrossRef]
- Jain, A.; Shaqfeh, E.S. Transient and steady shear rheology of particle-laden viscoelastic suspensions. J. Rheol. 2021, 65, 1269–1295. [Google Scholar] [CrossRef]
- Shewan, H.M.; Yakubov, G.E.; Bonilla, M.R.; Stokes, J.R. Viscoelasticity of non-colloidal hydrogel particle suspensions at the liquid–solid transition. Soft Matter 2021, 17, 5073–5083. [Google Scholar] [CrossRef]
- Rodd, L.; Cooper-White, J.; Boger, D.; McKinley, G.H. Role of the elasticity number in the entry flow of dilute polymer solutions in micro-fabricated contraction geometries. J.-Non-Newton. Fluid Mech. 2007, 143, 170–191. [Google Scholar] [CrossRef]
- Phan-Thien, N. Coaxial-disk flow of an Oldroyd-B fluid: Exact solution and stability. J.-Non-Newton. Fluid Mech. 1983, 13, 325–340. [Google Scholar] [CrossRef]
- Phan-Thien, N. Cone-and-plate flow of the Oldroyd-B fluid is unstable. J.-Non-Newton. Fluid Mech. 1985, 17, 37–44. [Google Scholar] [CrossRef]
- Larson, R.G.; Shaqfeh, E.S.; Muller, S.J. A purely elastic instability in Taylor–Couette flow. J. Fluid Mech. 1990, 218, 573–600. [Google Scholar] [CrossRef]
- Larson, R.G. Instabilities in viscoelastic flows. Rheol. Acta 1992, 31, 213–263. [Google Scholar] [CrossRef]
- Datta, S.S.; Ardekani, A.M.; Arratia, P.E.; Beris, A.N.; Bischofberger, I.; McKinley, G.H.; Eggers, J.G.; López-Aguilar, J.E.; Fielding, S.M.; Frishman, A.; et al. Perspectives on viscoelastic flow instabilities and elastic turbulence. Phys. Rev. Fluids 2022, 7, 080701. [Google Scholar] [CrossRef]
- Steinberg, V. Elastic turbulence: An experimental view on inertialess random flow. Annu. Rev. Fluid Mech. 2021, 53, 27–58. [Google Scholar] [CrossRef]
- Steinberg, V. New direction and perspectives in elastic instability and turbulence in various viscoelastic flow geometries without inertia. Low Temp. Phys. 2022, 48, 492–507. [Google Scholar] [CrossRef]
- Groisman, A.; Steinberg, V. Efficient mixing at low Reynolds numbers using polymer additives. Nature 2001, 410, 905–908. [Google Scholar] [CrossRef]
- Burghelea, T.; Segre, E.; Bar-Joseph, I.; Groisman, A.; Steinberg, V. Chaotic flow and efficient mixing in a microchannel with a polymer solution. Phys. Rev. E 2004, 69, 066305. [Google Scholar] [CrossRef]
- Gan, H.Y.; Lam, Y.C.; Nguyen, N.T.; Tam, K.C.; Yang, C. Efficient mixing of viscoelastic fluids in a microchannel at low Reynolds number. Microfluid. Nanofluid. 2007, 3, 101–108. [Google Scholar] [CrossRef]
- Whalley, R.; Abed, W.; Dennis, D.; Poole, R. Enhancing heat transfer at the micro-scale using elastic turbulence. Theor. Appl. Mech. Lett. 2015, 5, 103–106. [Google Scholar] [CrossRef]
- Traore, B.; Castelain, C.; Burghelea, T. Efficient heat transfer in a regime of elastic turbulence. J.-Non-Newton. Fluid Mech. 2015, 223, 62–76. [Google Scholar] [CrossRef]
- Abed, W.M.; Whalley, R.D.; Dennis, D.J.; Poole, R.J. Experimental investigation of the impact of elastic turbulence on heat transfer in a serpentine channel. J.-Non-Newton. Fluid Mech. 2016, 231, 68–78. [Google Scholar] [CrossRef]
- Bryce, R.; Freeman, M. Abatement of mixing in shear-free elongationally unstable viscoelastic microflows. Lab Chip 2010, 10, 1436–1441. [Google Scholar] [CrossRef]
- Bryce, R.; Freeman, M. Extensional instability in electro-osmotic microflows of polymer solutions. Phys. Rev.—Stat. Nonlinear Soft Matter Phys. 2010, 81, 036328. [Google Scholar] [CrossRef]
- Afonso, A.; Pinho, F.; Alves, M. Electro-osmosis of viscoelastic fluids and prediction of electro-elastic flow instabilities in a cross slot using a finite-volume method. J.-Non-Newton. Fluid Mech. 2012, 179, 55–68. [Google Scholar] [CrossRef]
- Pimenta, F.; Alves, M. Electro-elastic instabilities in cross-shaped microchannels. J.-Non-Newton. Fluid Mech. 2018, 259, 61–77. [Google Scholar] [CrossRef]
- Groisman, A.; Steinberg, V. Elastic turbulence in a polymer solution flow. Nature 2000, 405, 53–55. [Google Scholar] [CrossRef]
- Groisman, A.; Steinberg, V. Elastic turbulence in curvilinear flows of polymer solutions. New J. Phys. 2004, 6, 29. [Google Scholar] [CrossRef]
- Fouxon, A.; Lebedev, V. Spectra of turbulence in dilute polymer solutions. Phys. Fluids 2003, 15, 2060–2072. [Google Scholar] [CrossRef]
- Steinberg, V. Scaling relations in elastic turbulence. Phys. Rev. Lett. 2019, 123, 234501. [Google Scholar] [CrossRef] [PubMed]
- Qin, B.; Arratia, P.E. Characterizing elastic turbulence in channel flows at low Reynolds number. Phys. Rev. Fluids 2017, 2, 083302. [Google Scholar] [CrossRef]
- Sousa, P.; Pinho, F.; Alves, M. Purely-elastic flow instabilities and elastic turbulence in microfluidic cross-slot devices. Soft Matter 2018, 14, 1344–1354. [Google Scholar] [CrossRef]
- Beaumont, J.; Louvet, N.; Divoux, T.; Fardin, M.A.; Bodiguel, H.; Lerouge, S.; Manneville, S.; Colin, A. Turbulent flows in highly elastic wormlike micelles. Soft Matter 2013, 9, 735–749. [Google Scholar] [CrossRef]
- Jun, Y.; Steinberg, V. Elastic turbulence in a curvilinear channel flow. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2011, 84, 056325. [Google Scholar] [CrossRef]
- Sadek, S.H.; Pinho, F.T.; Alves, M.A. Electro-elastic flow instabilities of viscoelastic fluids in contraction/expansion micro-geometries. J.-Non-Newton. Fluid Mech. 2020, 283, 104293. [Google Scholar] [CrossRef]
- Song, L.; Yu, L.; Li, D.; Jagdale, P.P.; Xuan, X. Elastic instabilities in the electro-osmotic flow of non-Newtonian fluids through T-shaped microchannels. Electrophoresis 2020, 41, 588–597. [Google Scholar] [CrossRef]
- Khan, M.B.; Sasmal, C. Electro-elastic instability in electro-osmotic flows of viscoelastic fluids through a model porous system. Eur. J. Mech.-B/Fluids 2023, 97, 173–186. [Google Scholar] [CrossRef]
- Sasmal, C. A simple yet efficient approach for electrokinetic mixing of viscoelastic fluids in a straight microchannel. Sci. Rep. 2022, 12, 2395. [Google Scholar] [CrossRef]
- Ji, J.; Qian, S.; Liu, Z. electro-osmotic flow of viscoelastic fluid through a constriction microchannel. Micromachines 2021, 12, 417. [Google Scholar] [CrossRef]
- Khan, M.B.; Hamid, F.; Ali, N.; Mehandia, V.; Sasmal, C. Flow-switching and mixing phenomena in electro-osmotic flows of viscoelastic fluids. Phys. Fluids 2023, 35, 083101. [Google Scholar] [CrossRef]
- Mukherjee, S.; Pal, S.K.; Gopmandal, P.P.; Sarkar, S. Scaling Effects of the Weissenberg Number in Electrokinetic Oldroyd-B Fluid Flow Within a Microchannel. Electrophoresis 2024. Online ahead of print. [Google Scholar]
- Keunings, R. On the high Weissenberg number problem. J.-Non-Newton. Fluid Mech. 1986, 20, 209–226. [Google Scholar] [CrossRef]
- Afonso, A.; Oliveira, P.J.; Pinho, F.; Alves, M. The log-conformation tensor approach in the finite-volume method framework. J.-Non-Newton. Fluid Mech. 2009, 157, 55–65. [Google Scholar] [CrossRef]
- Le Bris, C.; Lelièvre, T. Micro-macro models for viscoelastic fluids: Modelling, mathematics and numerics. Sci. China Math. 2012, 55, 353–384. [Google Scholar] [CrossRef]
- Prakash, J.R. Micro and macro in the dynamics of dilute polymer solutions: Convergence of theory with experiment. Korea-Aust. Rheol. J. 2009, 21, 245–268. [Google Scholar]
- Lin, H. Electrokinetic instability in microchannel flows: A review. Mech. Res. Commun. 2009, 36, 33–38. [Google Scholar] [CrossRef]
- Sasmal, C. Fluid viscoelasticity suppresses chaotic convection and mixing due to electrokinetic instability. Phys. Fluids 2022, 34, 082011. [Google Scholar] [CrossRef]
- Song, L.; Jagdale, P.; Yu, L.; Liu, Z.; Li, D.; Zhang, C.; Xuan, X. Electrokinetic instability in microchannel viscoelastic fluid flows with conductivity gradients. Phys. Fluids 2019, 31, 082001. [Google Scholar] [CrossRef]
- Casanellas, L.; Alves, M.A.; Poole, R.J.; Lerouge, S.; Lindner, A. The stabilizing effect of shear thinning on the onset of purely elastic instabilities in serpentine microflows. Soft Matter 2016, 12, 6167–6175. [Google Scholar] [CrossRef]
- Shakeri, P.; Jung, M.; Seemann, R. Scaling purely elastic instability of strongly shear thinning polymer solutions. Phys. Rev. E 2022, 105, L052501. [Google Scholar] [CrossRef]
- Hong, S.O.; Park, K.S.; Kim, D.Y.; Lee, S.S.; Lee, C.S.; Kim, J.M. Gear-shaped micromixer for synthesis of silica particles utilizing inertio-elastic flow instability. Lab Chip 2021, 21, 513–520. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Sasmal, C. On designing a wavy sinusoidal micromixer for efficient mixing of viscoelastic fluids harnessing elastic instability and elastic turbulence phenomena. Chem. Eng. Sci. 2024, 295, 120126. [Google Scholar] [CrossRef]
- Li, D.Y.; Li, X.B.; Zhang, H.N.; Li, F.C.; Qian, S.Z.; Joo, S.W. Measuring heat transfer performance of viscoelastic fluid flow in curved microchannel using Ti–Pt film temperature sensor. Exp. Therm. Fluid Sci. 2016, 77, 226–233. [Google Scholar] [CrossRef]
- Li, D.Y.; Li, X.B.; Zhang, H.N.; Li, F.C.; Qian, S.; Joo, S.W. Efficient heat transfer enhancement by elastic turbulence with polymer solution in a curved microchannel. Microfluid. Nanofluid. 2017, 21, 10. [Google Scholar] [CrossRef]
- Copeland, D.; Ren, C.; Su, M.; Ligrani, P. Elastic turbulence influences and convective heat transfer within a miniature viscous disk pump. Int. J. Heat Mass Transf. 2017, 108, 1764–1774. [Google Scholar] [CrossRef]
- Yang, H.; Yao, G.; Wen, D. Flow resistance and convective heat transfer by elastic turbulence in 1D/2D/3D geometries. Int. J. Therm. Sci. 2022, 176, 107512. [Google Scholar] [CrossRef]
- Gupta, S.; Chauhan, A.; Sasmal, C. Influence of elastic instability and elastic turbulence on mixed convection of viscoelastic fluids in a lid-driven cavity. Int. J. Heat Mass Transf. 2022, 186, 122469. [Google Scholar] [CrossRef]
- Li, D.Y.; Zhang, H.; Cheng, J.P.; Li, X.B.; Li, F.C.; Qian, S.; Joo, S.W. Numerical simulation of heat transfer enhancement by elastic turbulence in a curvy channel. Microfluid. Nanofluid. 2017, 21, 25. [Google Scholar] [CrossRef]
- Gupta, S.; Sasmal, C. Effect of cavity aspect ratio on mixed convective heat transfer phenomenon inside a lid-driven cavity due to elastic turbulence. Phys. Fluids 2023, 35, 033114. [Google Scholar] [CrossRef]
- Acar, Y.B.; Alshawabkeh, A.N. Principles of electrokinetic remediation. Environ. Sci. Technol. 1993, 27, 2638–2647. [Google Scholar] [CrossRef]
- Acar, Y.B.; Gale, R.J.; Alshawabkeh, A.N.; Marks, R.E.; Puppala, S.; Bricka, M.; Parker, R. Electrokinetic remediation: Basics and technology status. J. Hazard. Mater. 1995, 40, 117–137. [Google Scholar] [CrossRef]
- Wen, D.; Fu, R.; Li, Q. Removal of inorganic contaminants in soil by electrokinetic remediation technologies: A review. J. Hazard. Mater. 2021, 401, 123345. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Du, D.; Pu, W.; Peng, Q.; Tao, Z.; Pang, Y. Viscoelastic displacement and anomalously enhanced oil recovery of a novel star-like amphiphilic polyacrylamide. Chem. Eng. Res. Des. 2019, 142, 369–385. [Google Scholar] [CrossRef]
- De, S.; Krishnan, P.; Van Der Schaaf, J.; Kuipers, J.; Peters, E.; Padding, J. Viscoelastic effects on residual oil distribution in flows through pillared microchannels. J. Colloid Interface Sci. 2018, 510, 262–271. [Google Scholar] [CrossRef]
- Zhong, H.; Li, Y.; Zhang, W.; Yin, H.; Lu, J.; Guo, D. Microflow mechanism of oil displacement by viscoelastic hydrophobically associating water-soluble polymers in enhanced oil recovery. Polymers 2018, 10, 628. [Google Scholar] [CrossRef]
- Mohamed, A.I.; Khishvand, M.; Piri, M. The role of injection fluid elasticity in microscopic displacement efficiency of residual non-wetting phase: An in-situ experimental investigation. Fuel 2023, 333, 126180. [Google Scholar] [CrossRef]
- Browne, C.A.; Datta, S.S. Harnessing elastic instabilities for enhanced mixing and reaction kinetics in porous media. Proc. Natl. Acad. Sci. USA 2024, 121, e2320962121. [Google Scholar] [CrossRef]
- James, D.F. Boger fluids. Annu. Rev. Fluid Mech. 2009, 41, 129–142. [Google Scholar] [CrossRef]
- McKinley, G.H.; Pakdel, P.; Öztekin, A. Rheological and geometric scaling of purely elastic flow instabilities. J.-Non-Newton. Fluid Mech. 1996, 67, 19–47. [Google Scholar] [CrossRef]
- Pakdel, P.; McKinley, G.H. Elastic instability and curved streamlines. Phys. Rev. Lett. 1996, 77, 2459. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sasmal, C. Electro-Elastic Instability and Turbulence in Electro-osmotic Flows of Viscoelastic Fluids: Current Status and Future Directions. Micromachines 2025, 16, 187. https://doi.org/10.3390/mi16020187
Sasmal C. Electro-Elastic Instability and Turbulence in Electro-osmotic Flows of Viscoelastic Fluids: Current Status and Future Directions. Micromachines. 2025; 16(2):187. https://doi.org/10.3390/mi16020187
Chicago/Turabian StyleSasmal, Chandi. 2025. "Electro-Elastic Instability and Turbulence in Electro-osmotic Flows of Viscoelastic Fluids: Current Status and Future Directions" Micromachines 16, no. 2: 187. https://doi.org/10.3390/mi16020187
APA StyleSasmal, C. (2025). Electro-Elastic Instability and Turbulence in Electro-osmotic Flows of Viscoelastic Fluids: Current Status and Future Directions. Micromachines, 16(2), 187. https://doi.org/10.3390/mi16020187




