Efficient Mask Optimization for DMD-Based Maskless Lithography Using a Genetic–Hippo Hybrid Algorithm
Abstract
1. Introduction
2. Theory and Modeling
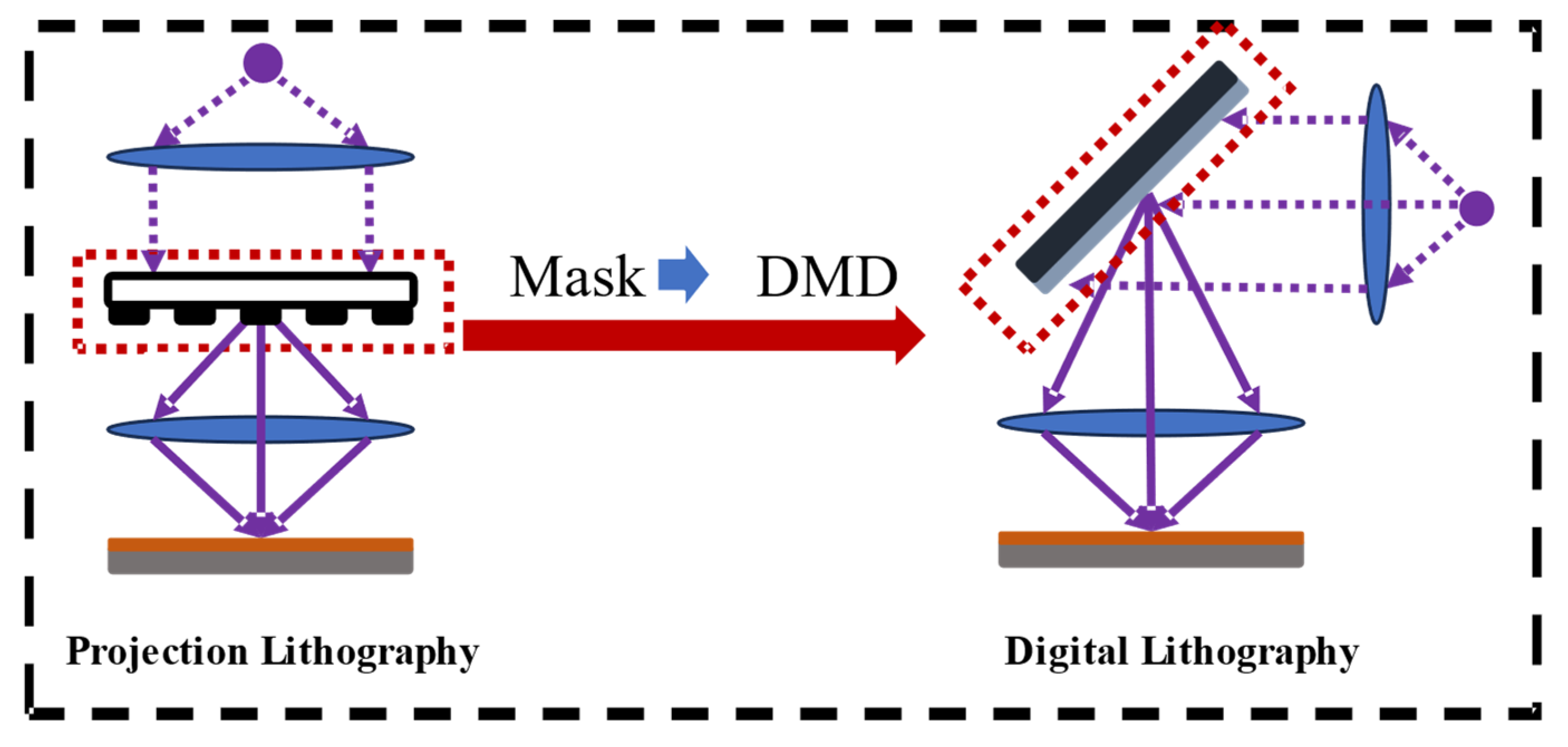
2.1. Spatial Imaging Model for DMD-Based Lithography Based on Abbe Theory
2.2. Optical Field Amplitude Modulation Model Based on DMD
2.3. Photoresist Exposure Model
3. Maskless Optimization Based on Genetic–Hippo Hybrid Algorithm
3.1. Genetic Algorithm
3.2. Hippo Optimization Algorithm
- Multi-Leader Guidance Mechanism.
- 2.
- Directed Gene Replacement:
- 3.
- Local Escape Mechanism.
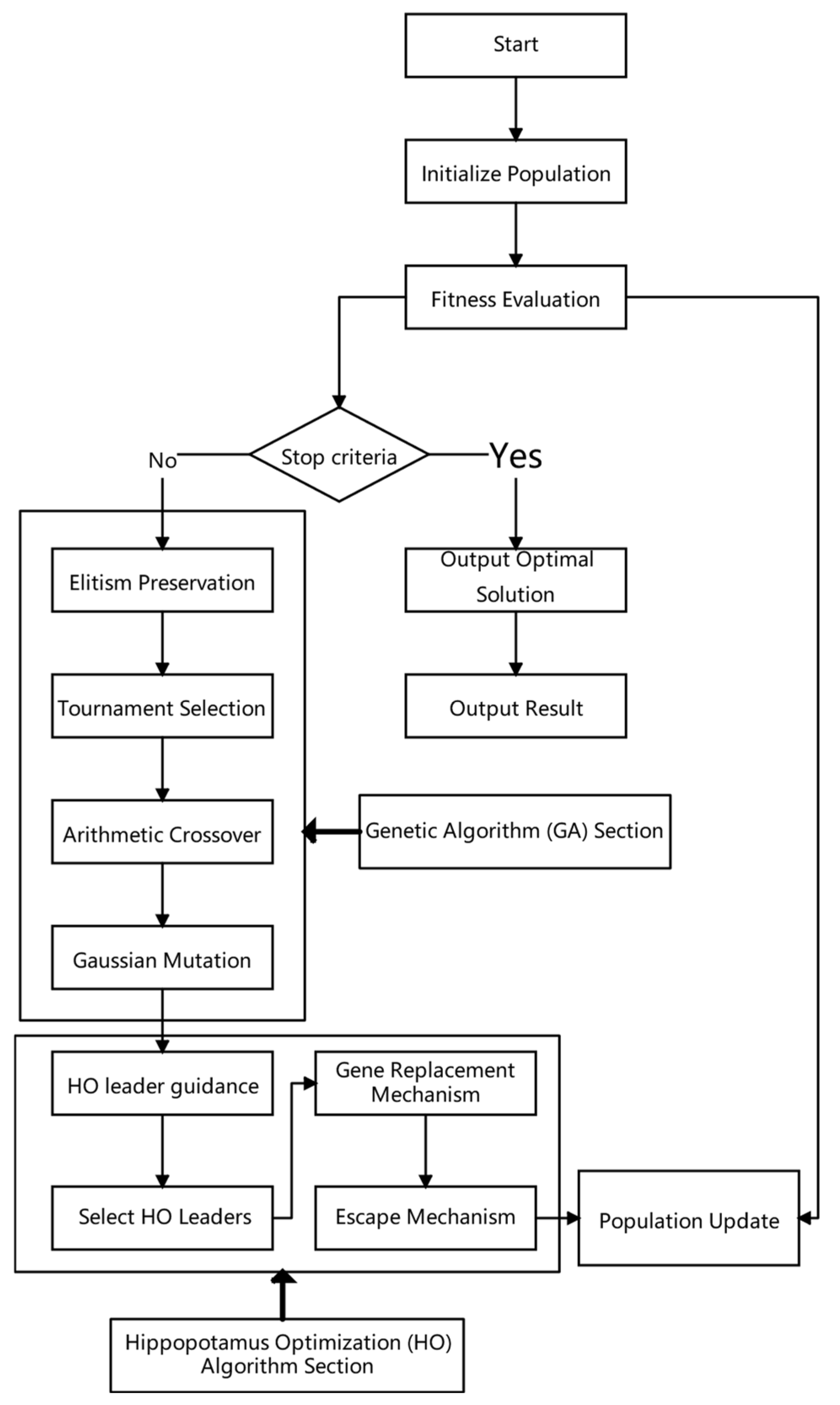
3.3. GA-HO Hybrid Optimization Structure
- Initialization: Randomly generate several mask grayscale matrices as the initial population and calculate their imaging fitness.
- Genetic Evolution: Perform selection, crossover, and mutation operations to produce a new generation of individuals.
- Hippo Enhancement: Select leaders from elite individuals and perform gene-guided local search.
- Adaptive Perturbation: If no improvement in the best fitness is observed over consecutive generations, trigger the drought (perturbation) mechanism to restore population diversity.
- Convergence Check: Terminate the algorithm when the rate of change in the best fitness falls below a preset threshold or the maximum number of iterations is reached.
3.4. Convergence and Adaptive Control Mechanisms
3.5. Mathematical Analysis and Synergistic Mechanism of the GA-HO Hybrid Optimization Algo-Rithm
4. Simulation Results and Analysis
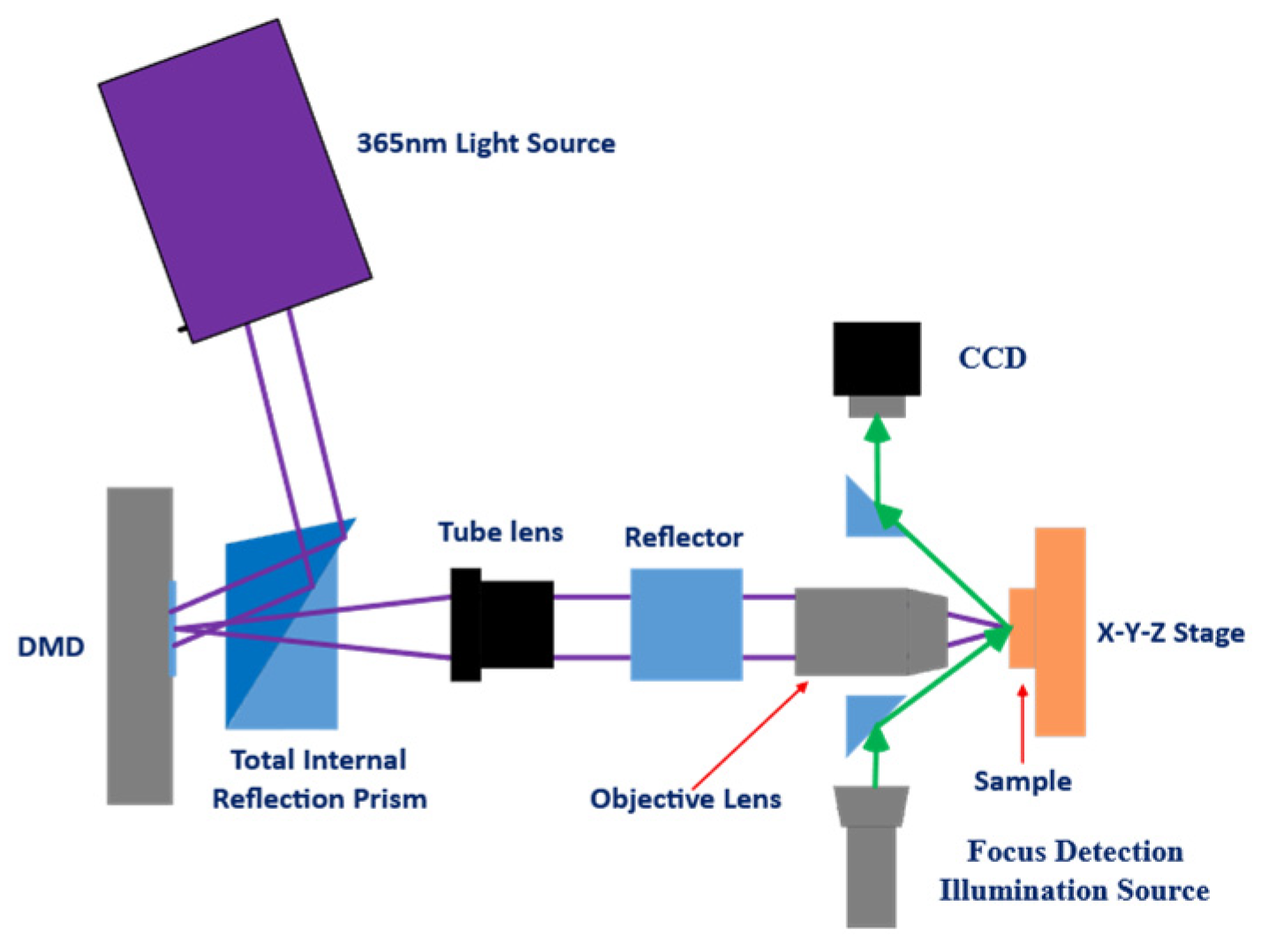
4.1. Simulation Setup
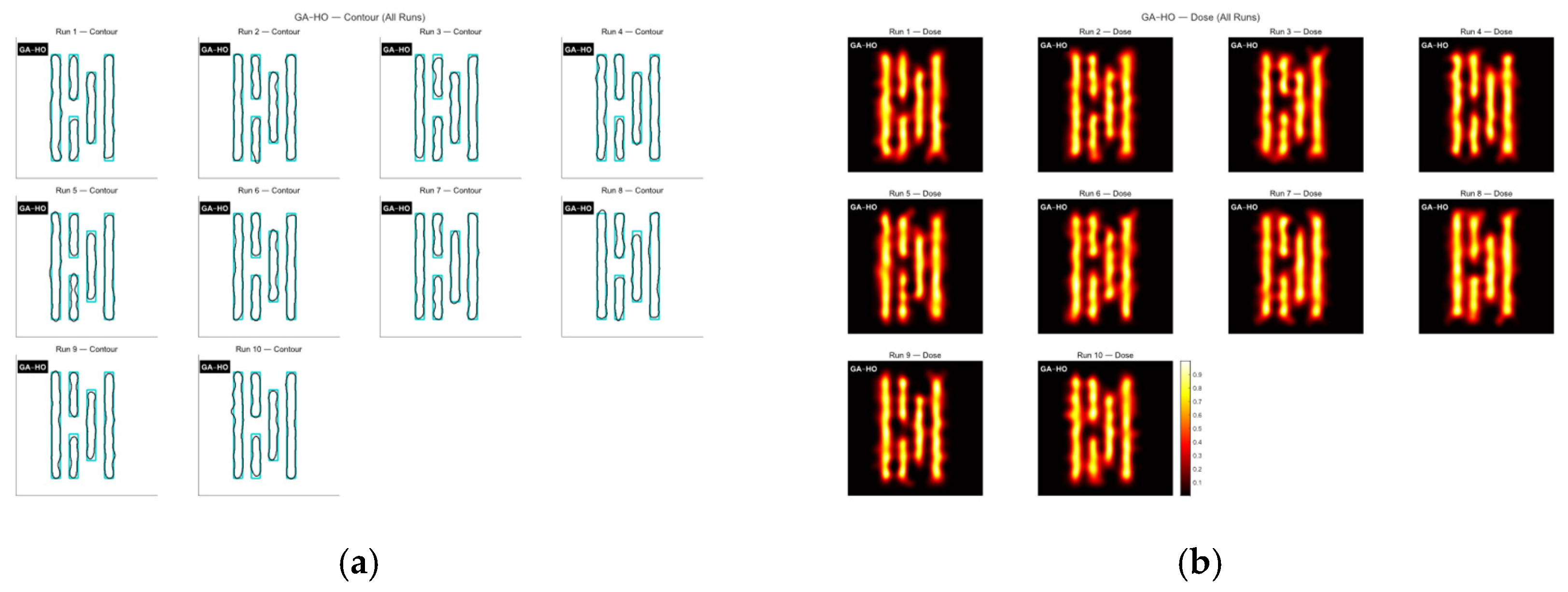
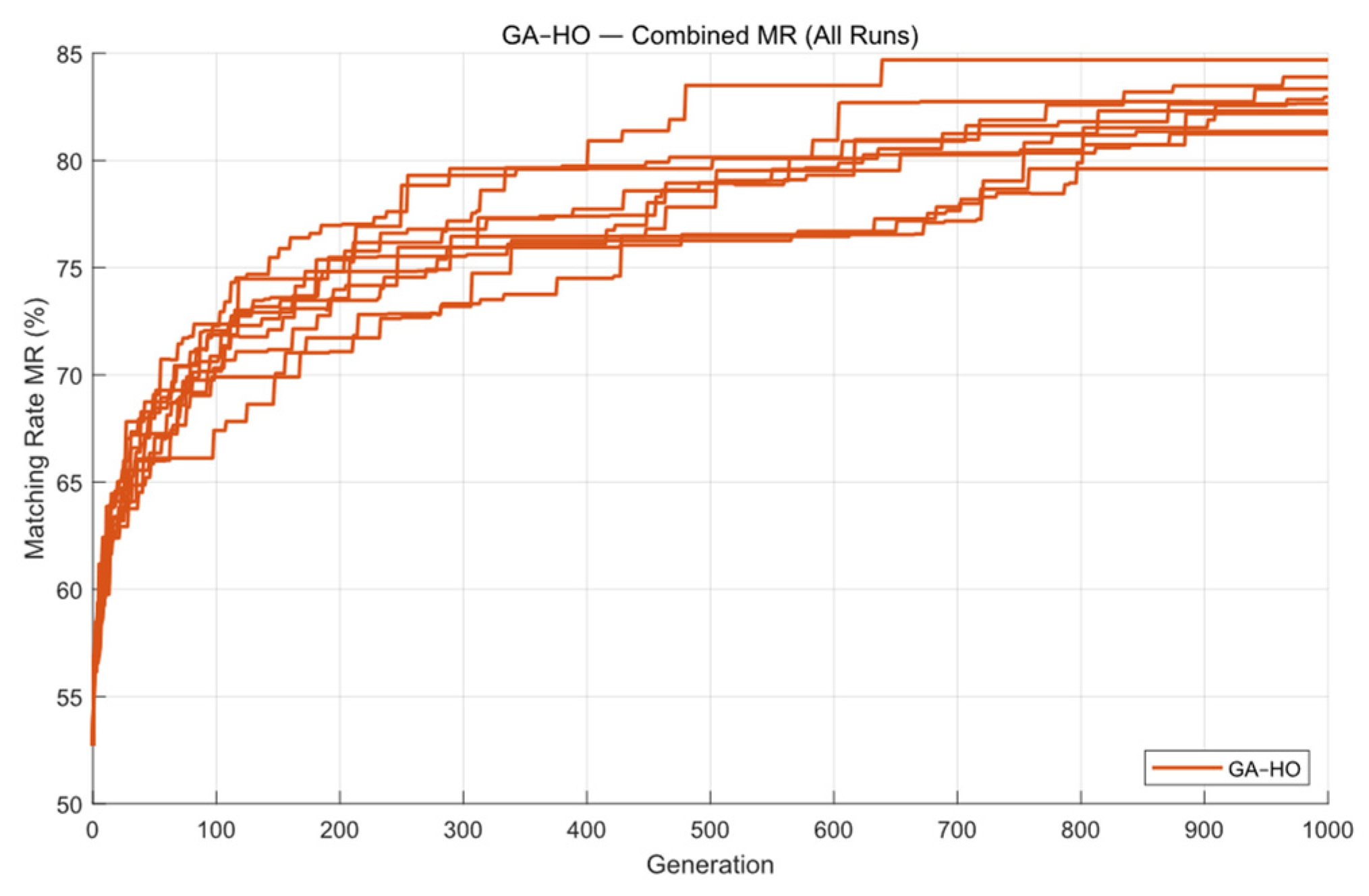
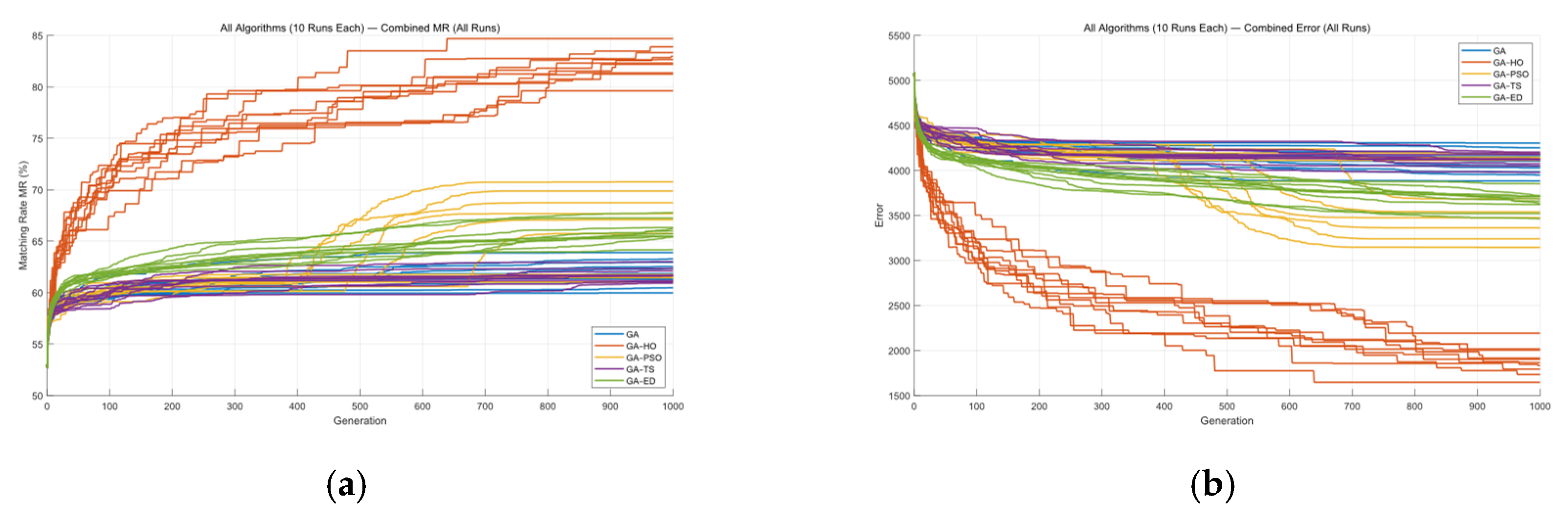
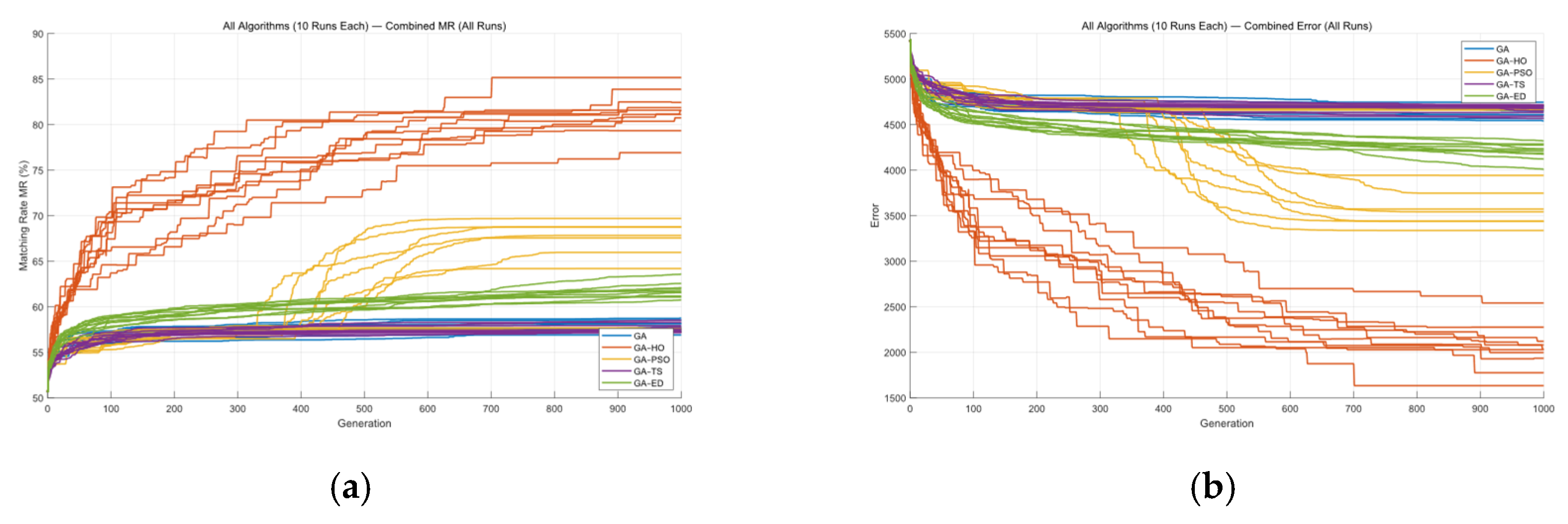
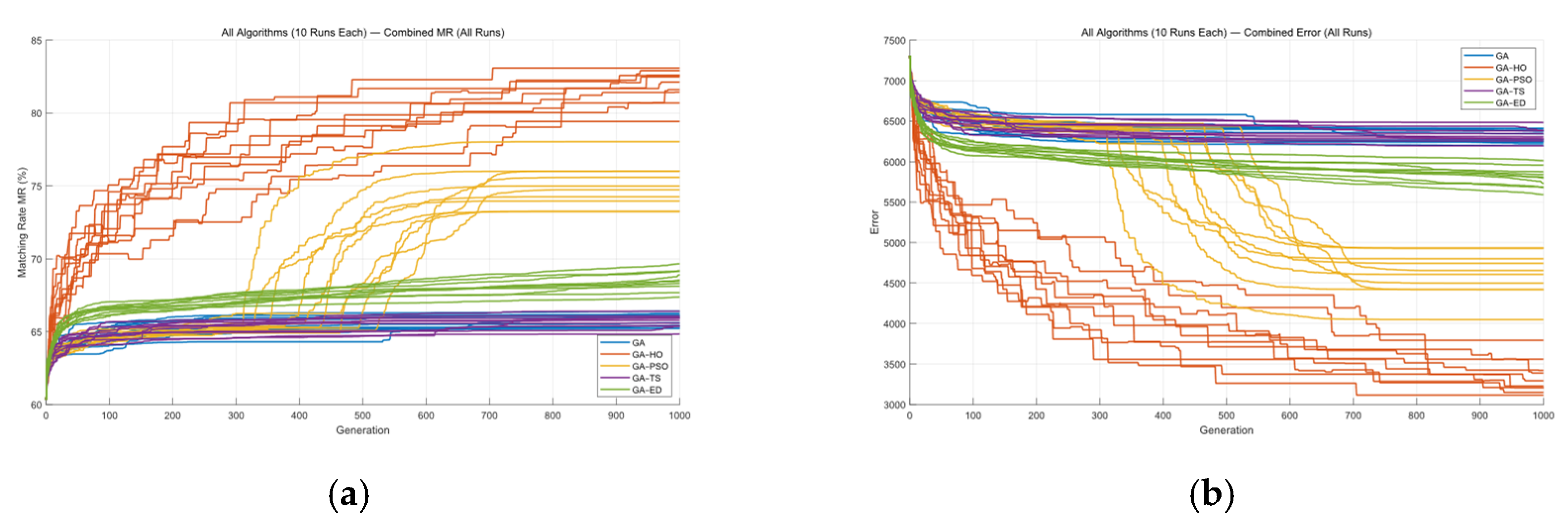
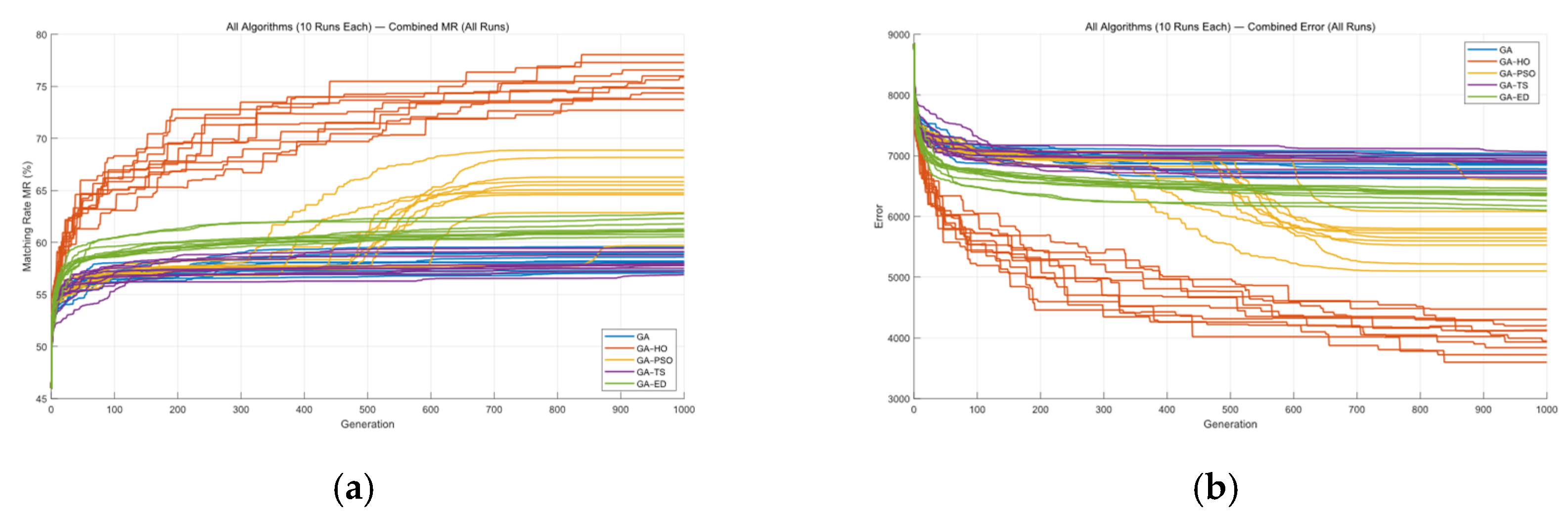
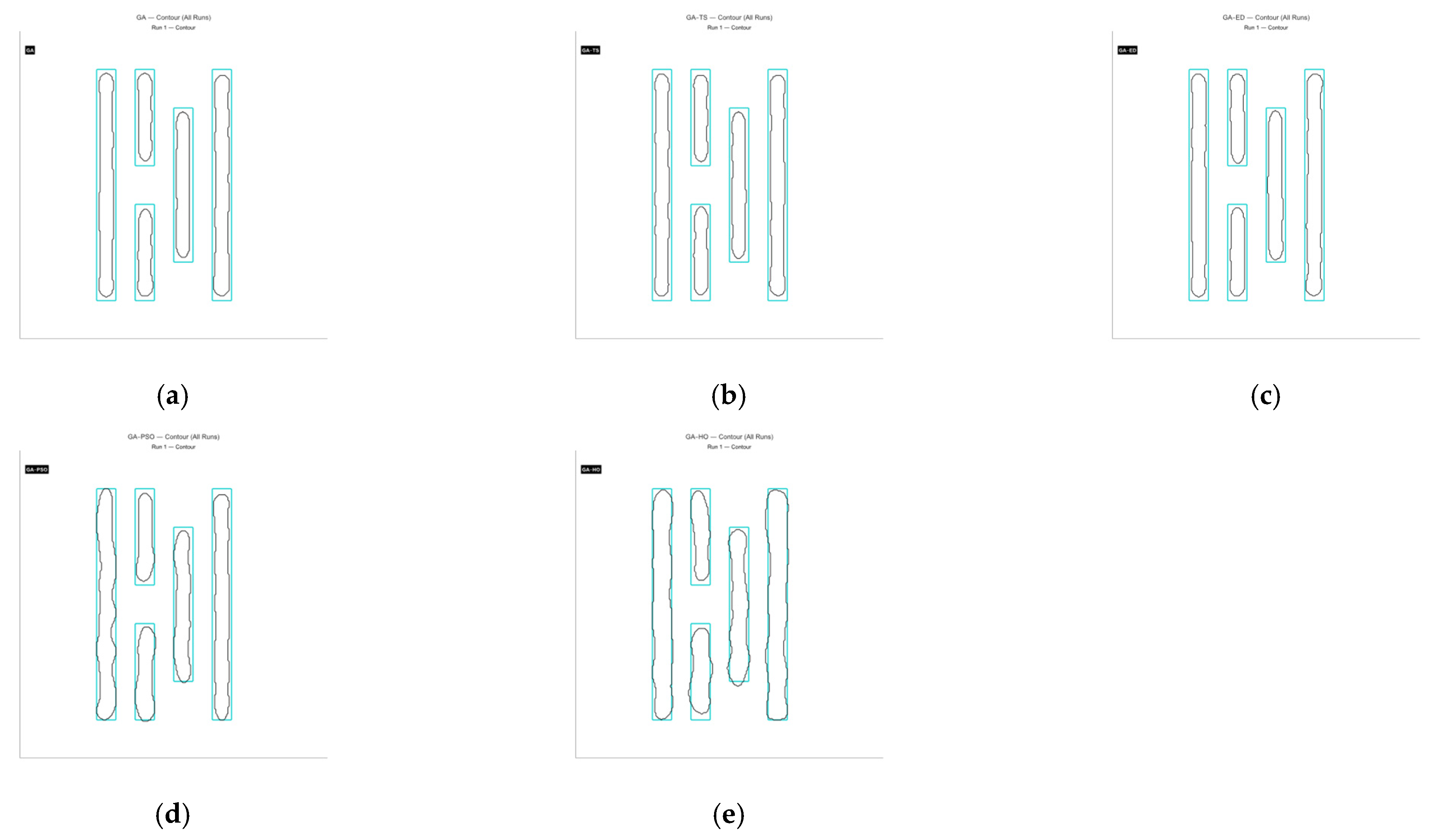
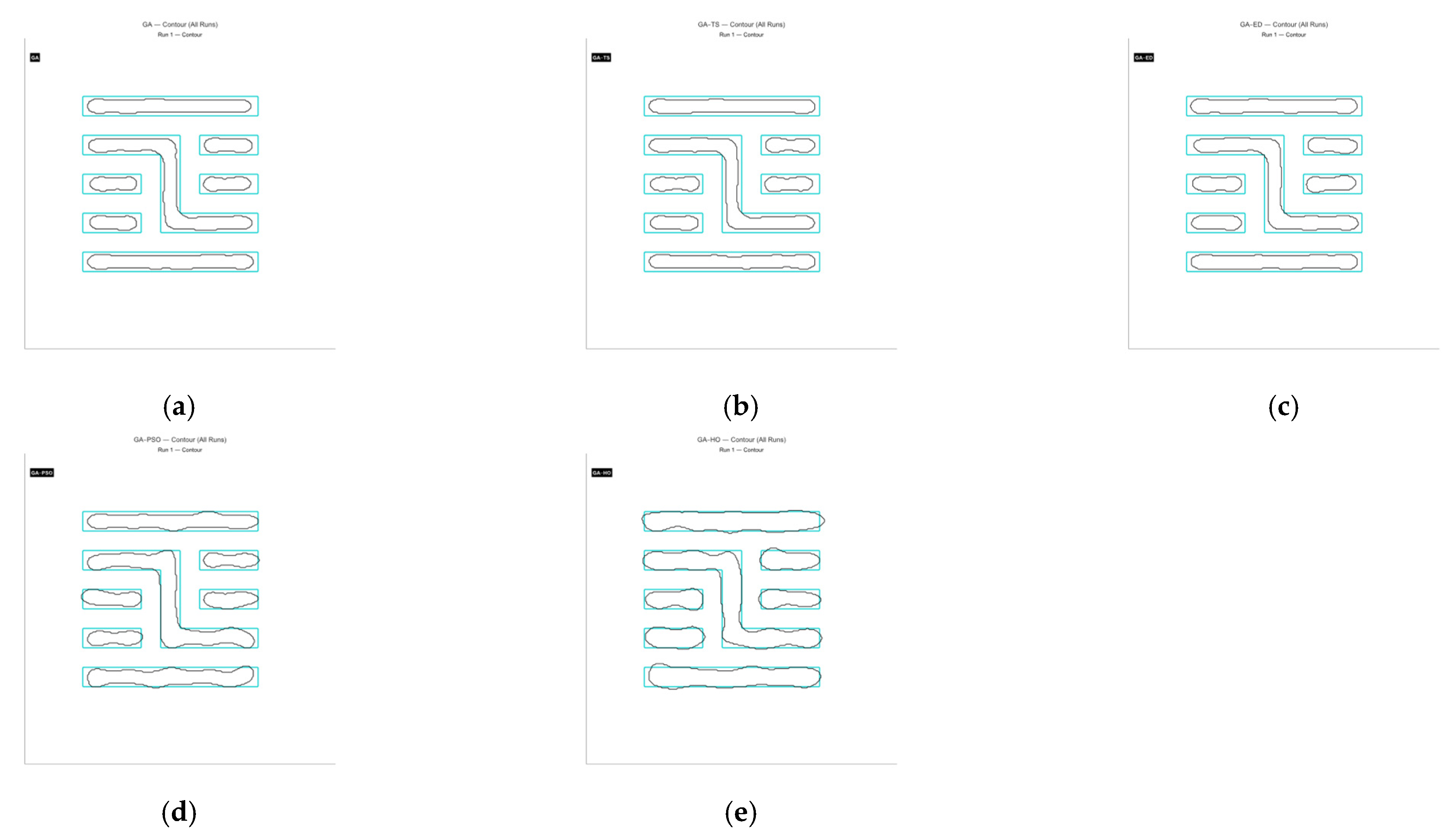
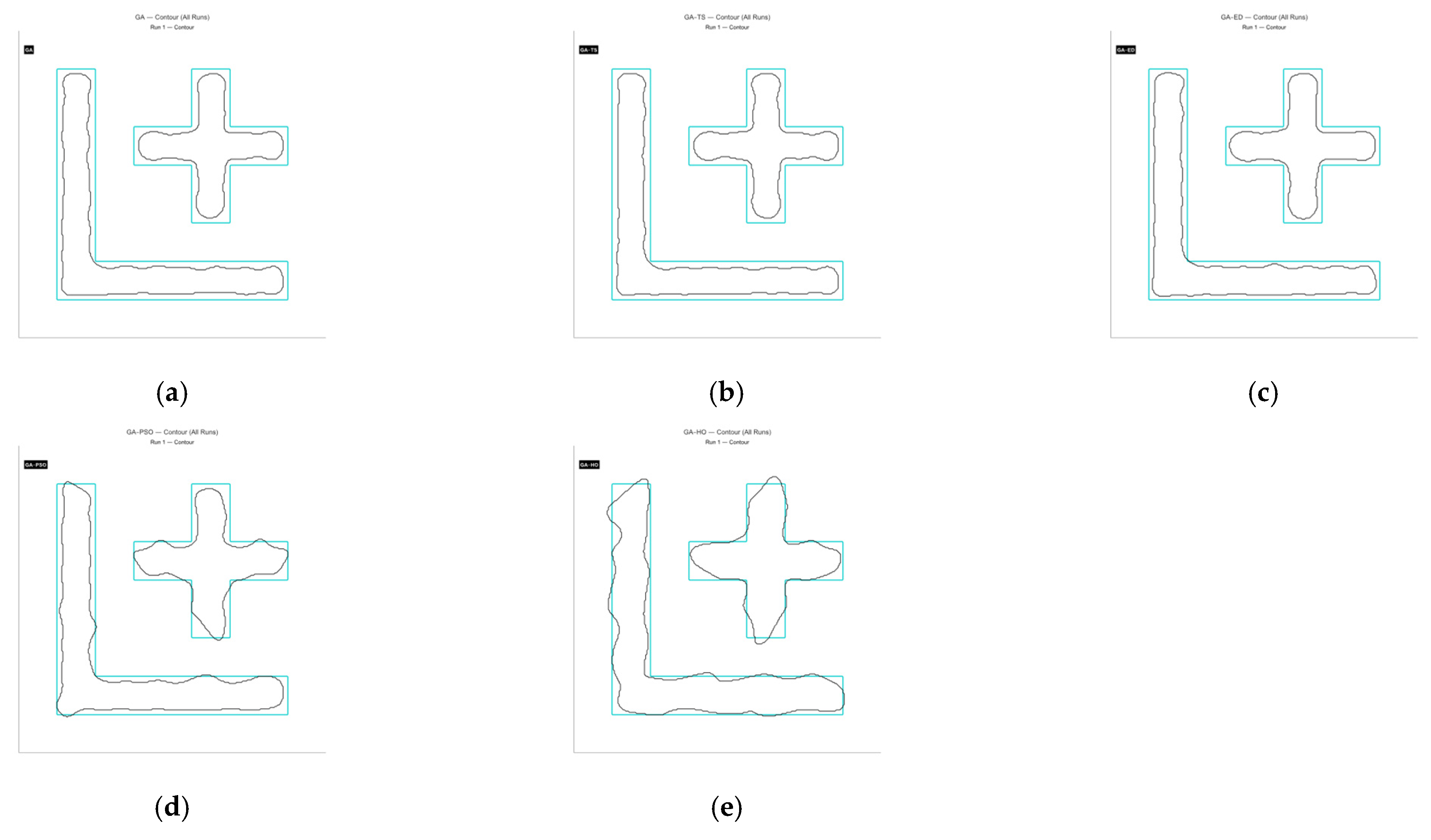
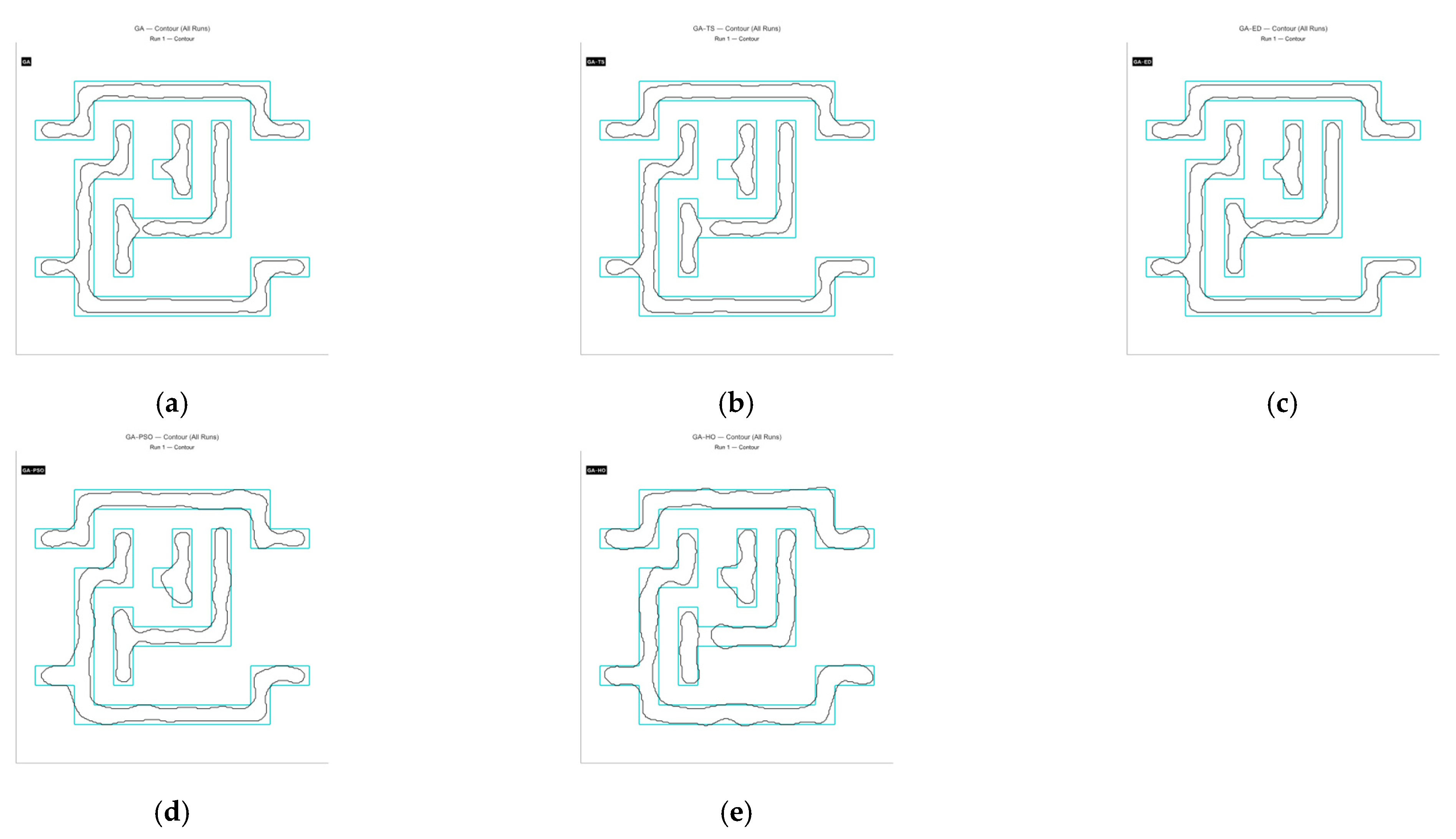
4.2. Simulation Results

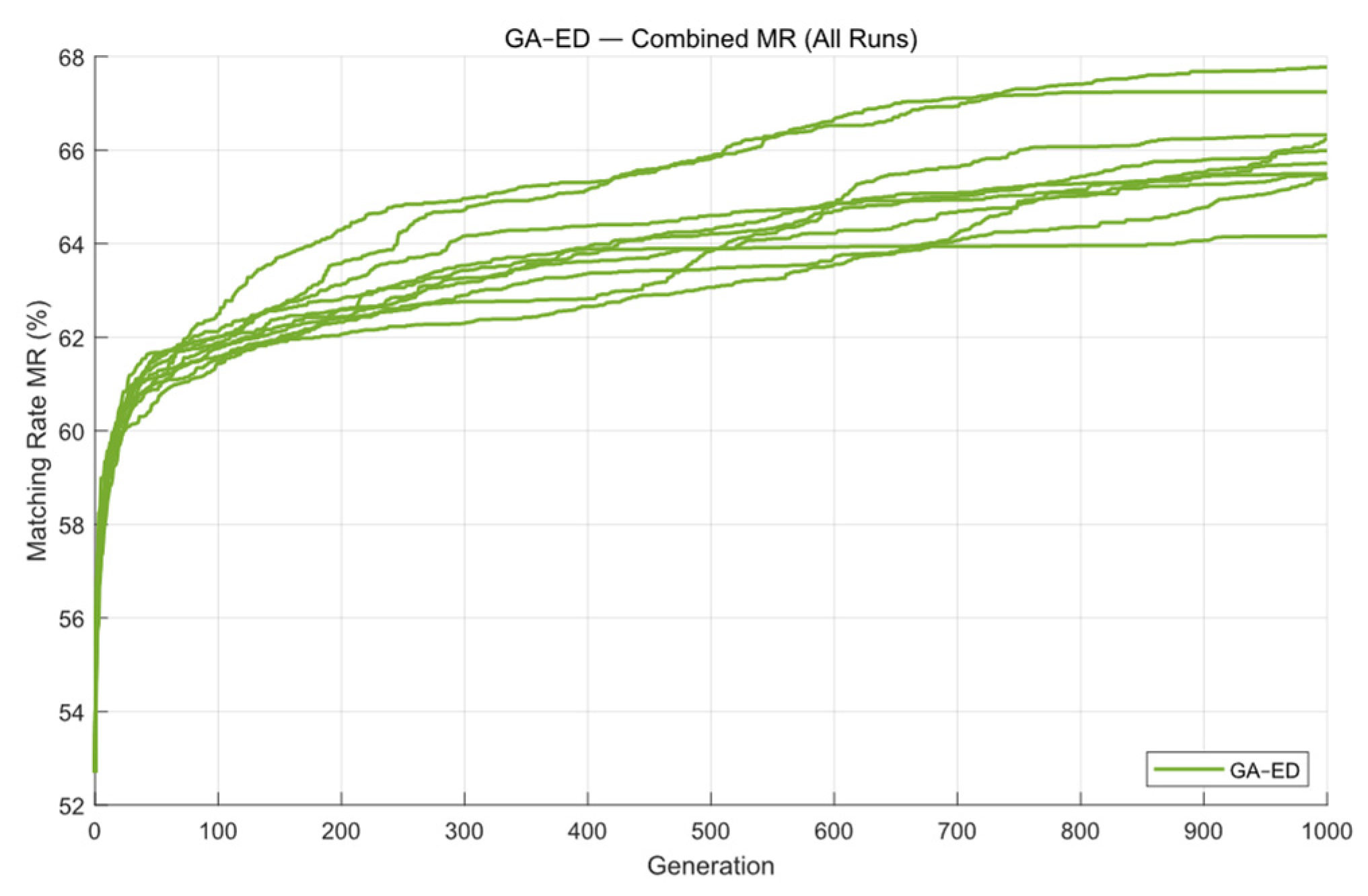
4.3. Analysis of Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bie, Y.-Q.; Grosso, G.; Heuck, M.; Furchi, M.M.; Cao, Y.; Zheng, J.; Bunandar, D.; Navarro-Moratalla, E.; Zhou, L.; Efetov, D.K.; et al. A MoTe2-based light-emitting diode and photodetector for silicon photonic integrated circuits. Nat. Nanotechnol. 2017, 12, 1124–1129. [Google Scholar] [CrossRef]
- Holler, M.; Guizar-Sicairos, M.; Tsai, E.H.R.; Dinapoli, R.; Müller, E.; Bunk, O.; Raabe, J.; Aeppli, G. High-resolution non-destructive three-dimensional imaging of integrated circuits. Nature 2017, 543, 402–406. [Google Scholar] [CrossRef]
- Xu, H.; Yu, C.; Wang, S.; Malyarchuk, V.; Xie, T.; Rogers, J.A. Deformable, programmable, and shape-memorizing micro-optics. Adv. Funct. Mater. 2013, 23, 3299–3306. [Google Scholar] [CrossRef]
- Jang, J.-S.; Javidi, B. Improved viewing resolution of three-dimensional integral imaging by use of nonstationary micro-optics. Opt. Lett. 2002, 27, 324–326. [Google Scholar] [CrossRef]
- Thiele, S.; Arzenbacher, K.; Gissibl, T.; Giessen, H.; Herkommer, A.M. 3D-printed eagle eye: Compound microlens system for foveated imaging. Sci. Adv. 2017, 3, e1602655. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Yan, X.; Yao, X.; Xu, L.; Zhang, K.; Zhang, J.; Yang, B.; Jiang, L. The dry-style antifogging properties of mosquito compound eyes and artificial analogues prepared by soft lithography. Adv. Mater. 2007, 19, 2213–2217. [Google Scholar] [CrossRef]
- Lin, D.M.; Fan, P.Y.; Hasman, E.; Brongersma, M.L. Dielectric gradient metasurface optical elements. Science 2014, 345, 298–302. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef]
- Ikai, T.; Yoshida, T.; Shinohara, K.-I.; Taniguchi, T.; Wada, Y.; Swager, T.M. Triptycene-based ladder polymers with one-handed helical geometry. J. Am. Chem. Soc. 2019, 141, 4696–4703. [Google Scholar] [CrossRef]
- Manna, J.; Shilpa, N.; Bandarapu, A.K.; Rana, R.K. Oxyanion-binding in a bio-inspired nanoparticle-assembled hybrid microsphere structure: Effective removal of arsenate/chromate from water. ACS Appl. Nano Mater. 2019, 2, 1525–1532. [Google Scholar] [CrossRef]
- Yao, Q.; Wang, Y.; Wang, J.; Chen, S.; Liu, H.; Jiang, Z.; Zhang, X.; Liu, S.; Yuan, Q.; Zhou, X. An ultrasensitive diagnostic biochip based on biomimetic periodic nanostructure-assisted rolling circle amplification. ACS Nano 2018, 12, 6777–6783. [Google Scholar] [CrossRef]
- Liang, L.; Zhou, J.; Lei, L.; Wang, B.; Wang, Q.; Wen, K. Suppression of imaging crack caused by the gap between micromirrors in maskless lithography. Opt. Eng. 2017, 56, 106102. [Google Scholar] [CrossRef]
- Zhang, Z.; Radtke, C.; Ruan, Y.; Zhong, K. Fast fabrication of curved microlens array using DMD-based lithography. AIP Adv. 2016, 6, 015319. [Google Scholar] [CrossRef]
- Guo, X.; Chen, J.T.; Zhao, Y.Y.; Cai, S.C.; Duan, X.M. Optical proximity correction of hot-spot patterns with subwavelength size in DMD maskless projection lithography. Opt. Lett. 2024, 49, 810–813. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.F.; Laidig, T.; Wampler, K.E.; Caldwell, R. Optical proximity correction for intermediate-pitch features using sub-resolution scattering bars. J. Vac. Sci. Technol. B 1997, 15, 2426–2433. [Google Scholar] [CrossRef]
- Dinh, D.H.; Chien, N.-Q. Maskless lithography based on digital micromirror device (DMD) and double-sided microlens and spatial filter array. Micromachines 2019, 10, 856. [Google Scholar] [CrossRef]
- Yang, Z.; Lin, J.; Liu, L.; Zhu, Z.; Zhang, R.; Wen, S.; Yin, Y.; Lan, C.; Li, C.; Liu, Y. Genetic algorithm-based optical proximity correction for DMD maskless lithography. Opt. Express 2023, 31, 23598–23607. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, T.; Wu, L.; Zhao, H. An improved particle swarm optimization algorithm for optical proximity correction in DMD-based maskless lithography. Micromachines 2024, 15, 527. [Google Scholar] [CrossRef]
- Xiao, L.; Yi, J.; Mao, Y.; Qi, X.; Hong, R.; Liu, Q.H. A Novel Optical Proximity Correction (OPC) System Based on Deep Learning Method for the Extreme Ultraviolet (EUV) Lithography. Prog. Electromagn. Res. 2023, 176, 95–108. [Google Scholar] [CrossRef]
- Chan, J.T.; Liu, R.; Lee, D.H. Deep learning-driven digital inverse lithography technology (DDILT) for maskless DMD systems. Optica 2025, 12, 221–230. [Google Scholar] [CrossRef]
- Amiri, M.H.; Mehrabi Hashjin, N.; Montazeri, M.; Mirjalili, S.; Khodadadi, N. Hippopotamus optimization algorithm: A novel nature-inspired optimization algorithm. Sci. Rep. 2024, 14, 5032. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics, 3rd ed.; Roberts & Company Publishers: Englewood, CO, USA, 2005. [Google Scholar]
- Huang, W.-C.; Lin, C.-H.; Kuo, C.-C.; Huang, C.-C.; Lin, J.-F.; Chen, J.-H.; Liu, R.-G.; Ku, Y.-C.; Lin, B.-J. Two threshold resist models for optical proximity correction. In Proceedings of the Optical Microlithography XVII; SPIE: Bellingham, WA, USA, 2004; Volume 5377. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Zhang, Z.; Li, S.; Wang, X.; Cheng, W.; Qi, Y. Source-mask optimization for extreme-ultraviolet lithography based on thick mask model and social learning particle swarm optimization algorithm. Opt. Express 2021, 29, 5448–5465. [Google Scholar] [CrossRef]
- Huang, S.; Wu, D.; Tang, Y.; Ren, B.; Pan, J.; Tian, Z.; Shao, Y.; He, S. Chaos-enhanced self-adaptive particle swarm optimization with simulated annealing for digital lithography mask optimization. J. Vac. Sci. Technol. B 2025, 43, 012601. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.; Wang, J.; Chen, Q. The Inverse Optimization of Lithographic Source and Mask via GA-APSO Hybrid Algorithm. Photonics 2023, 10, 638. [Google Scholar] [CrossRef]
- Mao, S.; Li, J.; Xu, H.; Zhang, Z. Lithography Tool Matching Based on Differential Evolution Algorithm. Acta Opt. Sin. 2019, 39, 1222002. [Google Scholar] [CrossRef]
- Sun, H.; Du, J.; Jin, C.; Quan, H.; Li, Y.; Tang, Y.; Wang, J.; Hu, S.; Liu, J. Global Optimisation of Source and Mask in Inverse Lithography via Tabu Search Combined with Genetic Algorithm. Opt. Express 2022, 30, 24166–24185. [Google Scholar] [CrossRef] [PubMed]
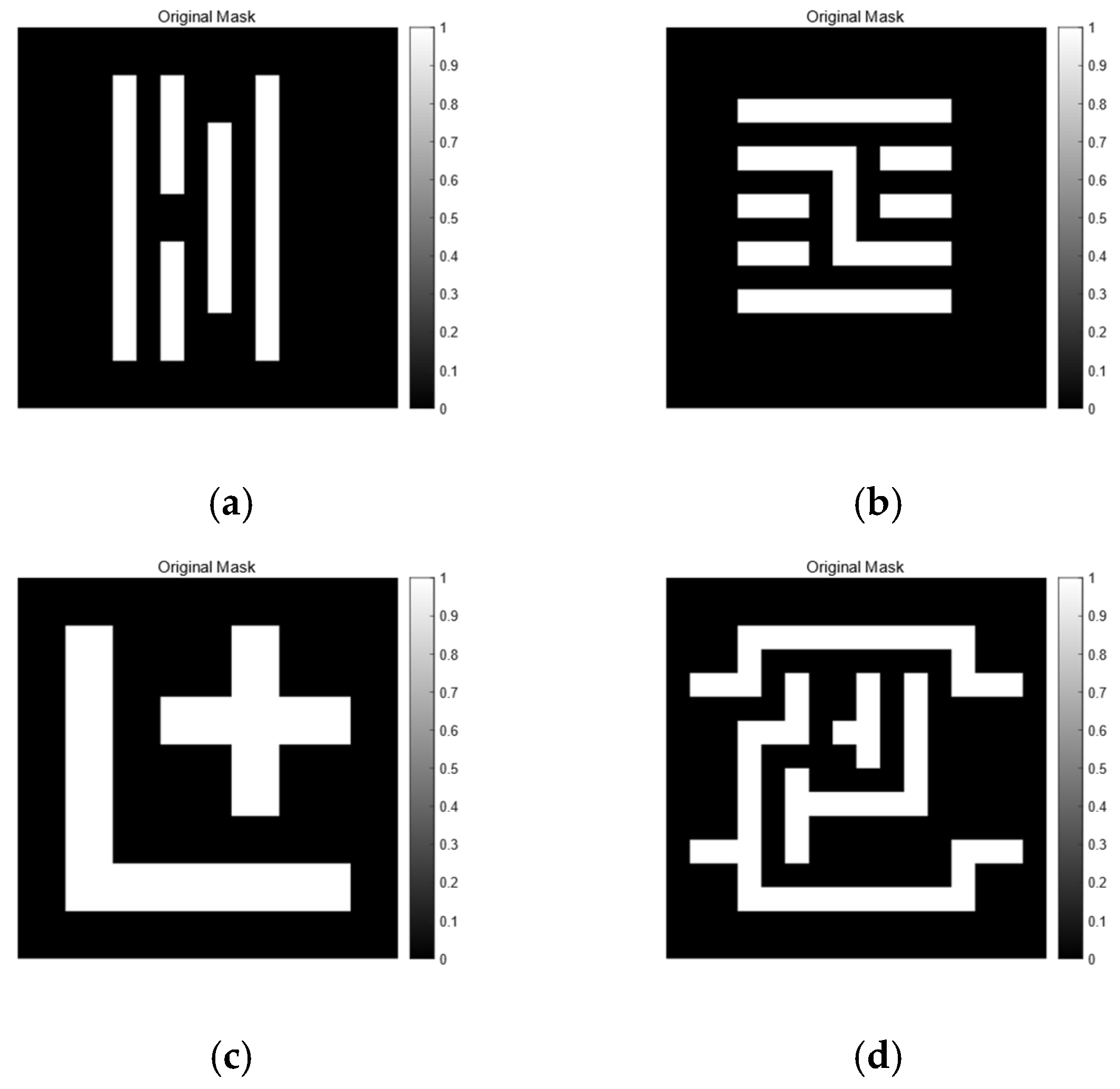
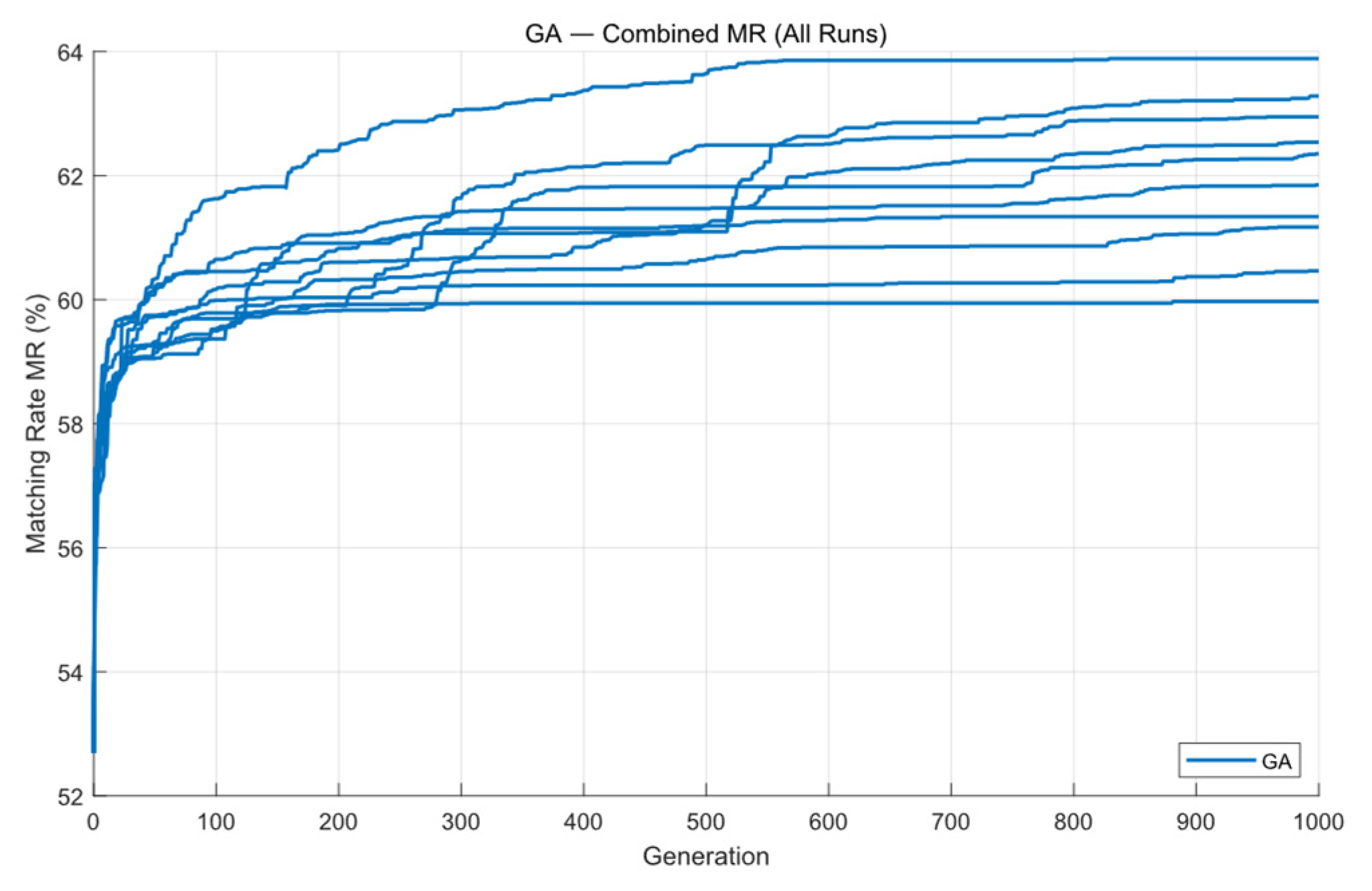
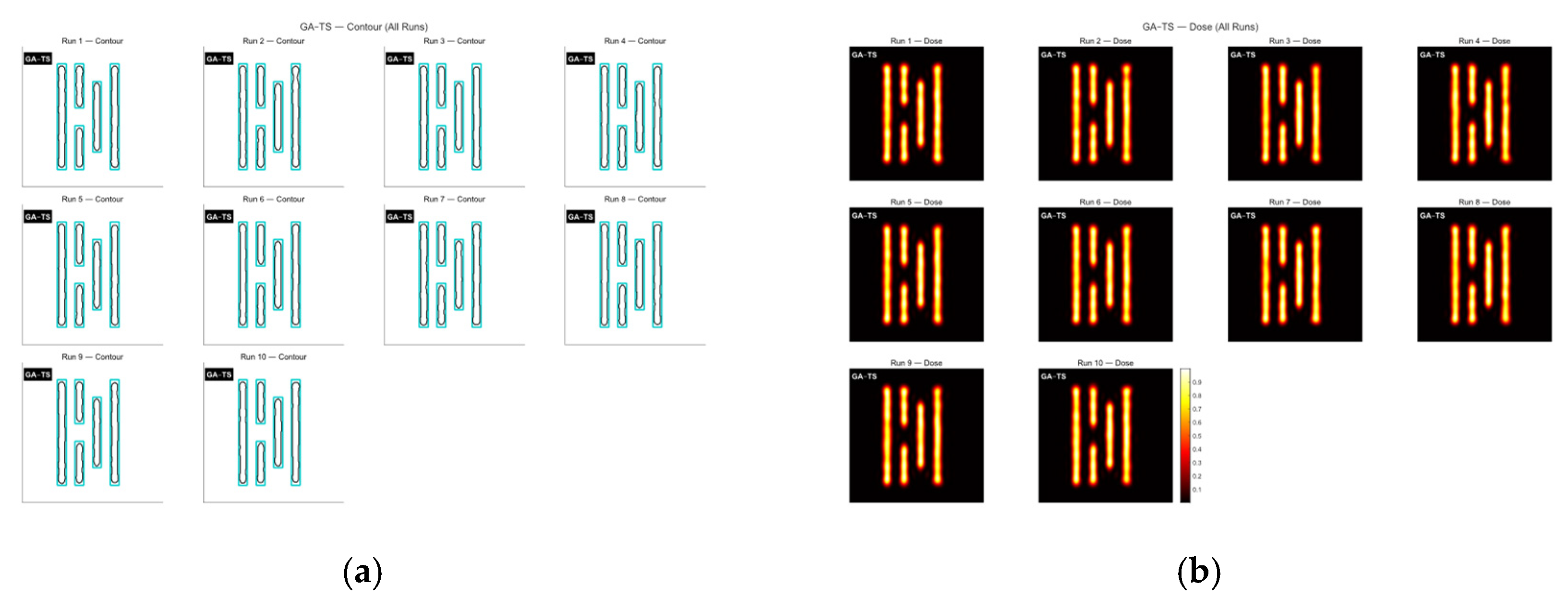
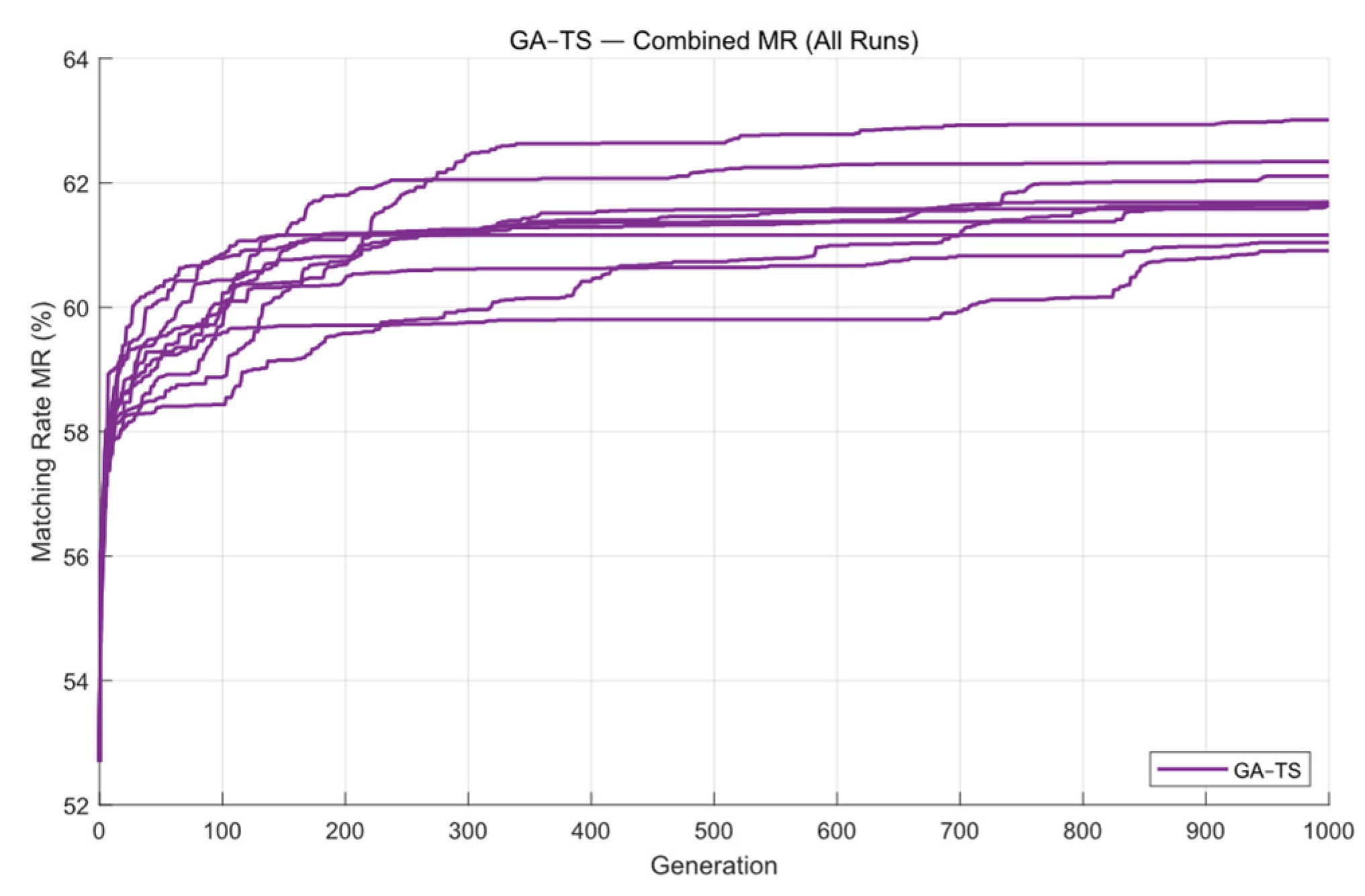
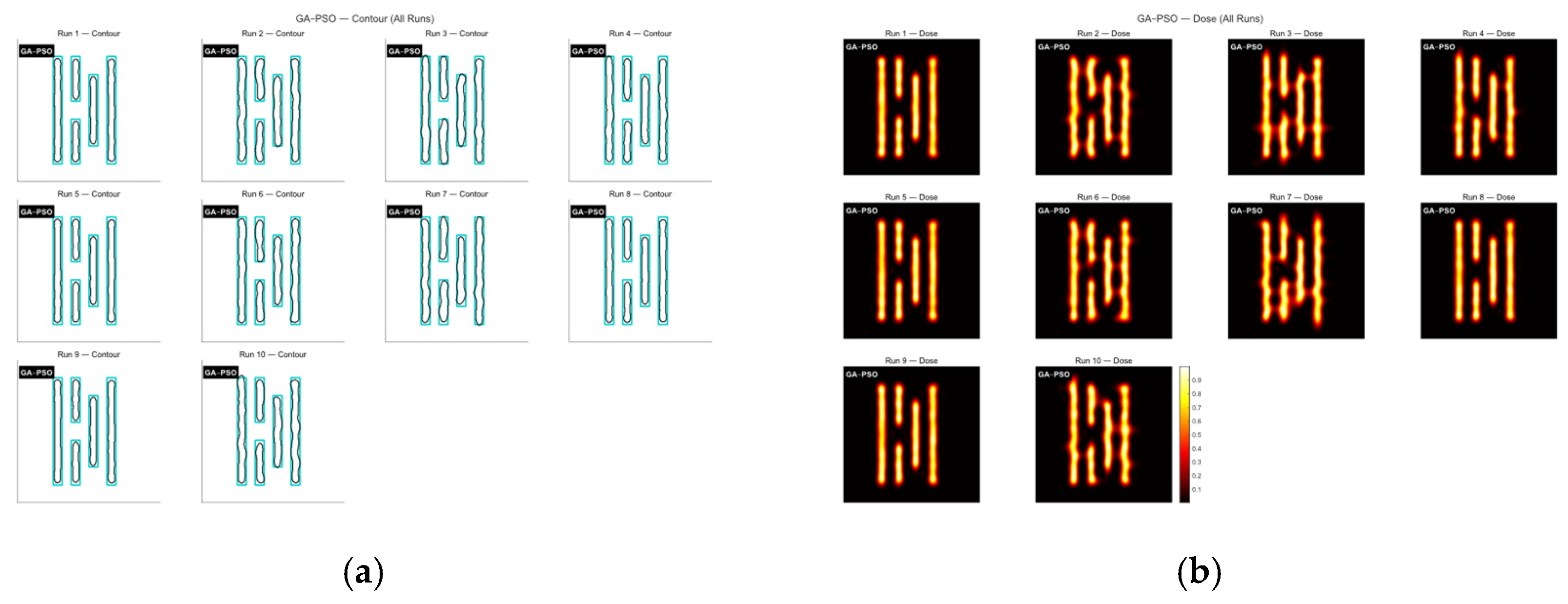
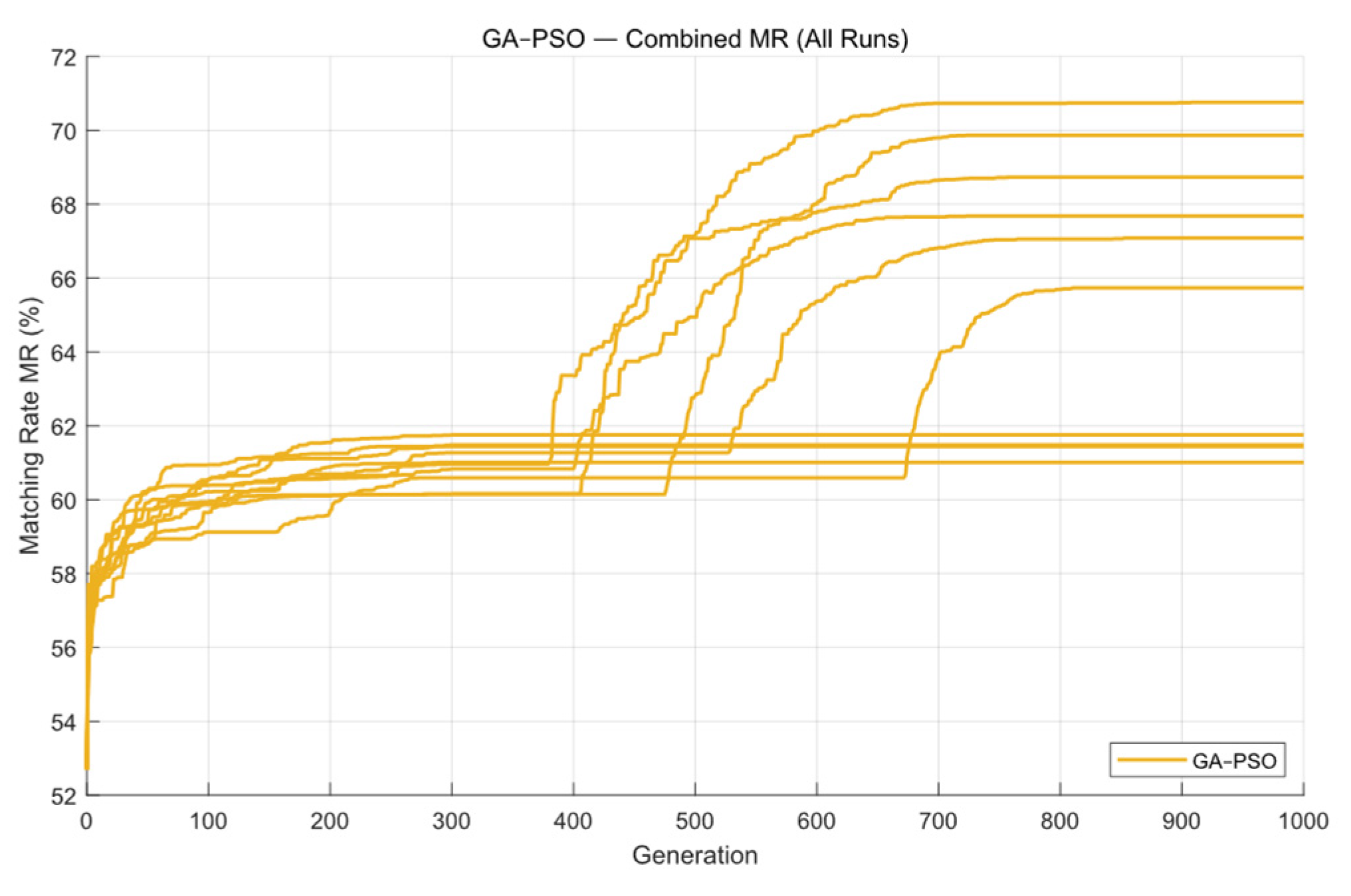
| Parameter | Value |
|---|---|
| Wavelength (λ) | 365 nm |
| Numerical Aperture (NA) | 0.3 |
| Partial Coherence Factor | 0.9 |
| Photoresist Exposure Threshold (Tp) | 0.5 |
| Mask Image Size | 16 × 16 |
| Population Size | 30 |
| Elite Retention Ratio | 0.1 |
| HO Leader Proportion | 0.5 |
| Maximum Iterations | 1000 |
| Loop | 10 |
| Algorithm | MR | ERR | Time |
|---|---|---|---|
| GA | 61.97% | 4088 | 55.31 s |
| GA-TS | 61.72% | 4102 | 48.32 s |
| GA-DE | 66.02% | 3657 | 61.98 s |
| GA-PSO | 68.13% | 3302 | 53.21 s |
| GA-HO | 82.39% | 1889 | 50.12 s |
| Algorithm | MR | ERR | Time |
|---|---|---|---|
| GA | 57.79% | 4646 | 61.79 s |
| GA-TS | 57.64% | 4712 | 45.62 s |
| GA-DE | 61.91% | 4302 | 63.98 s |
| GA-PSO | 64.51% | 3901 | 52.31 s |
| GA-HO | 81.45% | 2015 | 51.85 s |
| Algorithm | MR | ERR | Time |
|---|---|---|---|
| GA | 69.77% | 6308 | 62.15 s |
| GA-TS | 65.72% | 6702 | 39.32 s |
| GA-DE | 68.54% | 6232 | 66.98 s |
| GA-PSO | 75.01% | 4502 | 49.77 s |
| GA-HO | 81.90% | 3396 | 48.60 s |
| Algorithm | MR | ERR | Time |
|---|---|---|---|
| GA | 58.21% | 6846 | 59.38 s |
| GA-TS | 58.04% | 5707 | 45.77 s |
| GA-DE | 61.39% | 6336 | 64.39 s |
| GA-PSO | 65.18% | 5702 | 51.20 s |
| GA-HO | 75.42% | 4026 | 50.86 s |
| Algorithm | Comparison Metric | Mask A | Mask B | Mask C | Mask D |
|---|---|---|---|---|---|
| / | Original-mask MR | 52.70% | 50.64% | 60.25% | 45.98% |
| GA | MR | 61.97% | 57.79% | 69.77% | 58.21% |
| Time | 55.31 s | 61.79 s | 62.15 s | 59.38 s | |
| GA-TS | MR | 61.72% | 57.64% | 65.72% | 58.04% |
| Time | 48.32 s | 45.62 s | 39.32 s | 45.77 s | |
| GA-DE | MR | 66.02% | 61.91% | 68.54% | 61.39% |
| Time | 61.98 s | 63.98 s | 66.98 s | 64.39 s | |
| GA-PSO | MR | 68.13% | 64.51% | 75.01% | 65.18% |
| Time | 53.21 s | 52.31 s | 49.77 s | 51.20 s | |
| GA-HO | MR | 82.39% | 81.45% | 81.90% | 75.42% |
| Time | 50.12 s | 51.85 s | 48.60 s | 50.86 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Tu, C.; Sun, H.; Kang, X.; Liu, J.; Hu, S. Efficient Mask Optimization for DMD-Based Maskless Lithography Using a Genetic–Hippo Hybrid Algorithm. Micromachines 2025, 16, 1333. https://doi.org/10.3390/mi16121333
Chen Z, Tu C, Sun H, Kang X, Liu J, Hu S. Efficient Mask Optimization for DMD-Based Maskless Lithography Using a Genetic–Hippo Hybrid Algorithm. Micromachines. 2025; 16(12):1333. https://doi.org/10.3390/mi16121333
Chicago/Turabian StyleChen, Zhiyong, Chi Tu, Haifeng Sun, Xia Kang, Junbo Liu, and Song Hu. 2025. "Efficient Mask Optimization for DMD-Based Maskless Lithography Using a Genetic–Hippo Hybrid Algorithm" Micromachines 16, no. 12: 1333. https://doi.org/10.3390/mi16121333
APA StyleChen, Z., Tu, C., Sun, H., Kang, X., Liu, J., & Hu, S. (2025). Efficient Mask Optimization for DMD-Based Maskless Lithography Using a Genetic–Hippo Hybrid Algorithm. Micromachines, 16(12), 1333. https://doi.org/10.3390/mi16121333






