Abstract
A power amplifier (PA) stands as a central module within the electronic information system (EIS), and any variation in a PA’s specifications has a direct impact on the EIS’s performance, especially in the face of temperature fluctuations. In examining the influence of PA specification changes on the EIS, we employed support vector machine (SVM) to model the behavior of the temperature characteristics of 0.3–1.1 GHz complementary metal oxide semiconductor (CMOS) class-A broadband PAs. The results show that the parameters of S11, S12, S21, and S22 can be effectively modeled. SVM outperforms Elman and GRNN in terms of combined modeling time and modeling accuracy. This research can be extended to modeling the behavior of other types of power amplifiers or devices and circuits.
1. Introduction
Modern wireless communications have revolutionized our lives, and they are also becoming one of the critical supporting technologies in several areas of industry [1]. Power amplifiers (PAs) are the most critical element of modern wireless communication systems and significantly impact the performance of wireless communication systems [2]. PAs have a significant temperature dependence [3,4]. The degradation of the PA specification can lead to accelerated system failures if care is not taken to understand the effects of temperature changes on the PA [5,6]. Therefore, to avoid the system’s failure, the temperature characteristics of the PA need to be considered in advance during the optimization of the system design. To understand the temperature characteristics of a PA, there is a need to model the relationship between temperature variation and PA specifications.
Support vector machine (SVM) is a machine learning algorithm which was proposed by V. Vapnik et al. in the 1960s [7,8]. SVM can be used to describe the relationship between different variables. It is widely used in many fields as it minimizes real risk by seeking to minimize structural risk and pursues optimal results under limited information conditions [7,9]. For example, Chen et al. proposed a privacy-preserving medical diagnosis scheme based on a multi-class SVM [10]. The scheme is based on the Distributed Double Trapdoor Public Key Cryptosystem (DT-PKC) and the Boneh–Goh–Nissim (BGN) cryptosystem. Chen et al.’s scheme can deal with both linearly divisible data and nonlinear data, while preserving the privacy of the user’s data and support vectors. Chhavi Gupta et al. used a supervised machine learning (ML) approach to create a predictive model for the degree of work–life balance (on a scale of 1–5) of female professionals in information technology (IT) [11]. The results of the study showed that the optimized SVM model had the highest accuracy in work–life balance prediction. In addition, Chhavi Gupta et al. compared the predictive ability of the SVM model with that of the multiple regression model. A comparison of these two prediction models revealed that SVM was more accurate than multiple regression. Liu et al. proposed a self-induction method using a hybrid kernel function fuzzy support vector machine (FSVM) displacement prediction model to solve the problems of the large size, high cost, and low reliability of the displacement sensor in the magnetic levitation bearing system [12]. The simulation results show that the performance of the prediction model using the hybrid kernel function FSVM is significantly better than that of the prediction model using other kernel functions, and the predicted values in the x-direction and y-direction are about 93.35% and 95.5% of the actual values, respectively. Amyloid-based diagnostic biomarkers and assays provide only limited information about the disease process, and they are unable to identify diseased individuals before amyloid-β accumulates in the brain in large quantities. Chima et al. developed a method for early AD detection based on an SVM to identify potential blood-based, non-amyloid biomarkers [13]. Lu et al. has optimized the adhesive stamp mass transfer process for micro light-emitting diodes (micro-LEDs) using a support vector machine (SVM) model [14]. And from them, the separation speed and force between the stamp and the donor substrate were extracted as signal features. Finally, the classification accuracy based on the SVM model reached 85%, which implies that a more complex definition of the signal features is needed in future work. During the operation of an electric locomotive, a large amount of operational data will be stored by the analog-to-digital converter (ADC) and recording oscilloscope of the on-board traction control unit (TCU). It is of great significance to analyze data quality to detect slippage for energy saving, performance improvement, and safety of the traction control system of electric locomotives. Huang et al. proposed an SVM slippage detection method based on the EWT and FE algorithms after analyzing and summarizing the advantages of the Empirical Wavelet Transform (EWT) and the Fuzzy Entropy (FE) algorithms in data processing, as well as the classification theory of the support vector machines (SVMs) algorithm for SVM slip detection [15]. Brazil et al. developed an advanced method to classify load–pull contours for broadband high-efficiency PA designs using the technique of SVM [16]. This method achieves high efficiency and linearity over the entire operating bandwidth. Shi et al. proposed a model for PAs by adding a decomposed vector rotation (DVR) basis term to a support vector regression (SVR) model based on real-valued time delays [17]. This model achieves more than a 2 dB improvement in normalized mean square error (NMSE) and has better stability. Geng et al. proposed a PA model based on amplitude and phase-augmented time-delayed dual SVR [18]. The proposed model reduces CPU training time and provides efficient linearization performance with improved generalization capability. In summary, SVM has shown good application prospects and achieved remarkable results in many fields such as biology, medicine, electrical machinery, information statistics, device modeling, and optimization. Therefore, the emergence of SVM provides a new idea and opens up a new way to construct a nonlinear relationship between the specification of radio frequency (RF) power amplifiers and temperature change.
In this paper, the authors applied SVM for modeling based on the measured data of 0.3–1.1 GHz CMOS PAs at three different ambient temperatures (−40 °C, 25 °C, 125 °C). The experimental results show that the SVM can better describe the relationship between the S-parameters of the PA and the temperature variation. Meanwhile, the authors also compared the modeling results of SVM with those of Elman and Generalized Regression Neural Network (GRNN). The comparison results show that SVM outperforms Elman and GRNN under the combined consideration of modeling time and modeling accuracy.
2. Methodology
The SVM concept was first proposed in 1964 and then gradually theorized with the progress of pattern recognition and became a part of statistical learning theory [8]. It developed rapidly and derived a series of improved and extended algorithms in recent decades. Except for modeling PA behavior, this method is widely used in mortality prediction due to COVID-19 [19], coronary artery disease detection [20], wireless communication channel scenarios identification [21], image classification [22], power quality disturbance classification [23], etc. The regression is revealed as a branch of SVM. By creating a “margin” besides the linear function, the SVM model skips calculating the loss for these samples falling into it. The filtered support vector will impact its function and obtain the optimized model by maximizing the margin correlating to the loss function.
The SVM employs the principle of structural risk minimization, enabling the better avoidance of local optima and exhibiting lower generalization error. By utilizing a kernel function, SVM maps nonlinear problems from low-dimensional space to high-dimensional space, facilitating effective linear separation in the higher-dimensional realm and addressing complex nonlinear issues. Moreover, SVM demonstrates robustness against noise and outliers in the training data, efficiently handling noise present in input data. As a supervised learning algorithm, SVM exhibits excellent generalization performance in the training and learning of small-scale samples. Considering the scale of the data in this paper, SVM is chosen as the primary modeling method.
Here, we investigate the effect of SVM models on the behavioral modeling of the temperature characteristics of CMOS class-A broadband PAs, and the experimental data of a 0.3–1.1 GHz broadband PA are used as a modeling dataset. For the given training datasets {(f1, T1, S111, S121, S211, S221), (f2, T2, S112, S122, S212, S222), …, (fm, Tm, S11m, S12m, S21m, S22m)}, a regression SVM model f(x) = c∙x+d is hoped to get as close to yi as possible, where xi = (fi, Ti), yi = (S11i, S12i, S21i, S22i), f1 is the frequency, and T1 is the temperature. The weight factor c and the threshold value d will be determined during the process. Considering a deviation of ε between f(x) and yi in our required limit, the loss is calculated only if the absolute difference is greater than ε. The SVM model can be formalized as:
where R is the regularization constant, and l is the ε-insensitive loss function shown in Equation (2):
Equation (1) can be rewritten by introducing the slack variables and :
The loss function is transformed into a simpler dual calculation by introducing Lagrange multipliers.
where L is the Lagrange function, and , , , and are the Lagrange multipliers.
Assuming that the partial derivative of with respect to c, d, , and is set to zero, we can obtain:
Karush–Kuhn–Tucker (KKT) conditions should be met in the above process, namely
The solution of the SVM model is shown in Equation (7).
A robust approach is often adopted by averaging selected multiple samples that satisfy the condition 0 < αi < R that can solve d. Considering the feature mapping form, then:
where ϕ(xj) is the kernel function.
The SVM model can be expressed as:
where κ(xiTx) = ϕ(xi)T.
Compared with the general linear regression model, the SVM model creates a margin only if the differences between G(fi, Ti) and (S11i, S12i, S21i, S22i) are greater than ε. General linear regression optimizes the model by averaging after gradient descent, while SVM optimizes the model by maximizing the width of the margin and minimizing the total loss. Moreover, this model may be utilized as a powerful tool for modeling the temperature characteristics of PAs based on the feature of continuously approximating the nonlinear function.
3. Measurements
To investigate the effect of SVM on modeling for the temperature characteristics of CMOS class-A broadband PAs, the temperature characteristics of a 0.3–1.1 GHz broadband PA were measured. To obtain data for SVM modeling, the temperature characteristics of this PA were measured in an experimental environmental chamber in this paper, and the measurement environment is shown in Figure 1. A DC power supply from R&S and a vector network analyzer (VNA) were used during the measurements. The DC power supply provided the required DC bias for the PA, and the VNA was used for the S-parameter measurements and data acquisition.
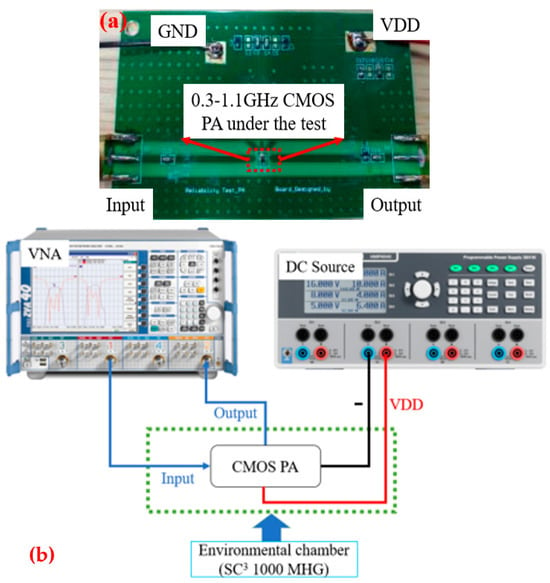
Figure 1.
Measurement environment: (a) PA to be measured; (b) measurement connection diagram.
This paper investigates the effect of SVM models on the behavioral modeling of the temperature characteristics of CMOS class-A broadband PAs. The experimental data of a 0.3–1.1 GHz broadband PA are used as a modeling dataset. According to the input SVM network, the input matrix is defined as
where f1 is the frequency and T1 is the temperature.
The output data are the characteristics of S11, S12, S21, and S22, which can be expressed as
It should be noted that only ¾ (75%) of the measurements are used for modeling, and this 75% is divided into training data (1/4, 25%) and validation data (1/2, 50%).
4. Results
4.1. S11
Figure 2 shows the modeling behavior of S11 at −40 °C, 25 °C, and 125 °C. The training time of the model is about 13 ms at all three temperatures, and the test errors of the model are 7.5948 × 10−2, 1.4313 × 10−1, and 2.3117 × 10−2, respectively. This indicates that for the behavioral modeling of the temperature characteristics of S11, the model’s accuracy can reach the order of 10−1 for all of them. However, in terms of model accuracy, the model accuracy of S11 at −40 °C and 125 °C is an order of magnitude higher than that at 25 °C. One possible reason for this is that the difference between the maximum and minimum values of S11 at −40 °C and 125 °C is smaller than that at 25 °C.
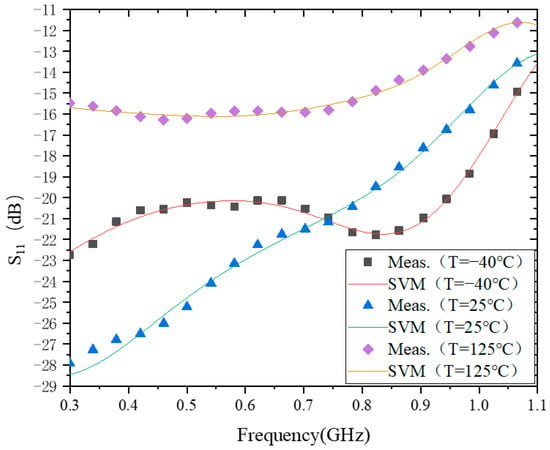
Figure 2.
The results of modeling S11.
In the 0.3–0.75 GHz range, |S11| does not vary monotonically with temperature. For example, from −40 °C to 25 °C, |S11| increases with temperature, while from 25 °C to 125 °C, |S11| decreases with temperature. In the range of 0.75 to 1.1 GHz, |S11| decreases with increasing temperature. The main reason for this phenomenon is that during the design process of the PA, the transistors and matching circuits are designed to consider impedance matching at 25 °C only. When the temperature changes, especially at low temperatures, the carrier mobility in the transistor increases with decreasing temperature, making the impedance of the transistor deviate far from the design value at 25 °C, which results in the variation in the characteristics of |S11| at −40 °C over the entire operating frequency range, though this is not quite the same as those at 25 °C and 125 °C.
4.2. S12
Figure 3 shows the modeling behavior of S12 at −40 °C, 25 °C, and 125 °C. The model accuracy of S12 at these three temperatures is 4.3359 × 10−1, 4.4285 × 10−1, and 1.6438, respectively. From this, the model accuracy at the two temperatures of −40 °C and 25 °C is one magnitude higher than that at 125 °C. One possible reason for this situation is that the difference between the maximum and minimum values of S12 at 125 °C is greater than the difference between the two temperatures of −40 °C and 25 °C. According to the model results of S11 and S12, if the difference between the maximum and minimum values of S11 or S12 is larger, then the corresponding model accuracy error will also be larger.
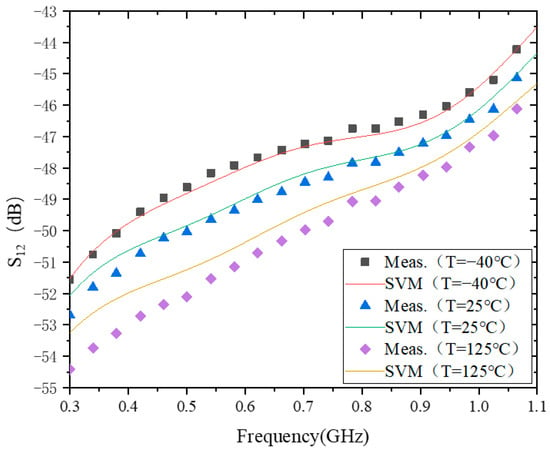
Figure 3.
The results of modeling of S12.
In addition, it can be seen from Figure 3 that |S12| increases with temperature in the frequency range of 0.3–1.1 GHz. This is different from the characteristic of |S11| with temperature. Because |S12| and |S11| are not defined in the same way, when the temperature changes, it does not necessarily produce the same phenomena as |S11| at −40 °C. However, the impedance of the transistors and matching circuits are designed for 25 °C. Therefore, when the temperature deviates from 25 °C, the value of |S12| will also deviate from the original design value.
4.3. S21
Figure 4 shows the modeling behavior of S21 at −40 °C, 25 °C, and 125 °C. The test errors of the model at these three temperatures are 1.9177 × 10−1, 2.1655 × 10−1, and 4.2388 × 10−1, respectively. From this, the model accuracy of S21 reaches 10−1 at all three temperatures. The difference between the maximum and minimum values of S21 is relatively small at all three temperatures. Therefore, there is no case of high errors at individual temperature points as in S11 and S12. In addition, from a time perspective, the training time of the model is about 13 ms at all three temperatures. This is the same as the case of S11 and S12.
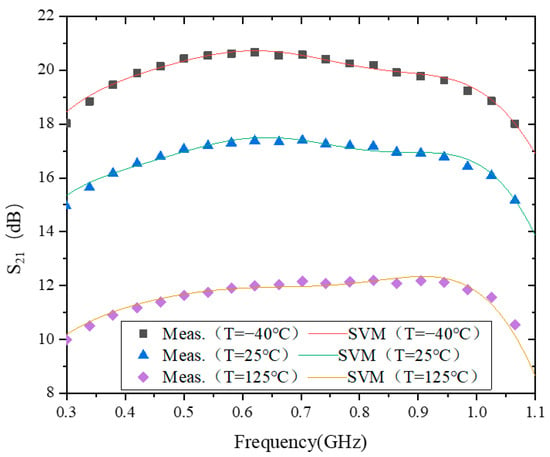
Figure 4.
The results of modeling S21.
As can be seen in Figure 4, |S21| decreases with increasing temperature. The main reason for this phenomenon is that the carrier mobility in the transistor decreases with increasing temperature. This is analyzed as follows.
Transduction in the unsaturated regions [24,25].
And the carrier mobility versus temperature can be expressed as [26].
where W is the gate width, μn is the carrier mobility, Cox is the gate oxide capacitance per unit area, L is the gate length, VGS is the gate voltage, VT is the threshold voltage, and VDS is the drain voltage, T0 = 300 K.
According to Equations (12) and (13), the transconductance of the transistor decreases with increasing temperature. And the transconductance is usually considered to be the gain of the transistor [25]. Thus, it can be observed that the S21 of the PA degrades with increasing temperature.
4.4. S22
Figure 5 shows the modeling behavior of S22 at −40 °C, 25 °C, and 125 °C. The validation errors of the model at three different ambient temperatures are 1.8112 × 10−1, 1.9015 × 10−1, and 2.2803 × 10−1, respectively. From the time perspective, the time required for model training at all three temperatures is about 13 ms.
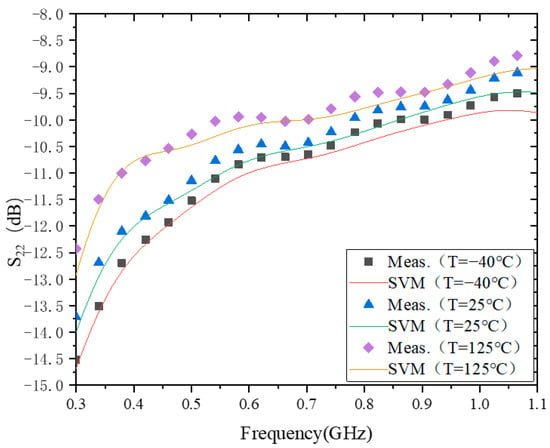
Figure 5.
The results of modeling S22.
In addition, it can be seen that |S22| decreases with increasing temperature. This is the same as the temperature-dependent characteristic of |S21|, but the exact opposite of the temperature-dependent characteristic of |S12|. However, the main reason for the change in |S22| with temperature is also due to the fact that the impedance matching at 25 °C was only considered during the design process. When the temperature changes, the impedance will also change, which is reflected by the fact that each S-parameter will deviate from the original design reference value. The specific trend of S11, S12, and S22 with temperature changes needs to be specifically analyzed and discussed in conjunction with their respective definitions, and it is also more complicated. The topic of this paper is to use SVM to model the measured data of RF PAs at different ambient temperatures, so we will not discuss this again. In the future, the authors will also specifically address this issue and report on the specific degradation trends and influencing factors.
To better evaluate the performance of the SVM method in modeling, we introduced Elman [27] and the Generalized Regression Neural Network (GRNN) [28] methods that are commonly used for PA modeling for comparison. The results are presented in Table 1. From Table 1, it can be seen that SVM has the shortest modeling time and Elman has the longest modeling time. The modeling accuracy of SVM is higher than Elman and GRNN.

Table 1.
Modeling results of 0.3–1.1 GHz CMOS class-A broadband PAs.
Table 1 shows that the SVM method performs well in the training and learning of small-scale samples, showcasing good generalization performance.
5. Conclusions
In this paper, SVM is applied to model the S-parameters of 0.3–1.1 GHz CMOS with measured data at different ambient temperatures. The modeling results show that SVM has a high accuracy and fast modeling speed compared with Elman and GRNN. The results of this paper show that SVM also shows good application prospects and achieves good modeling results in the field of RF PA modeling.
Author Contributions
Conceptualization, R.L., S.Z., C.Y. and J.W.; methodology, R.L., S.Z., C.Y. and J.W.; validation, R.L., S.Z., C.Y. and J.W.; formal analysis, J.W.; investigation, R.L., S.Z. and C.Y.; resources, J.W.; data curation, R.L., S.Z. and C.Y.; writing—original draft preparation, R.L. and S.Z.; writing—review and editing, S.Z., C.Y. and J.W.; visualization, R.L., S.Z. and C.Y.; supervision, J.W.; project administration, J.W.; funding acquisition, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Impedance Transformation Matching Techniques for Broadband Local Amplifier Standard Devices (No. XS-KF-2023-0004) and the AoShan Talents Outstanding Scientist Program (No. 2017ASTCP-OS03).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Amar, A.S.I.; Mamidanna, M.; Darwish, M.; El-Hennawy, H. High Gain Broadband Power Amplifier Design Based on Integrated Diplexing Networks. IEEE Microw. Wirel. Compon. Lett. 2022, 32, 133–136. [Google Scholar] [CrossRef]
- Piacibello, A.; Giofrè, R.; Quaglia, R.; Figueiredo, R.; Carvalho, N.; Colantonio, P.; Valenta, V.; Camarchia, V. A 5-W GaN Doherty Amplifier for Ka-Band Satellite Downlink With 4-GHz Bandwidth and 17-dB NPR. IEEE Microw. Wirel. Compon. Lett. 2022, 32, 964–967. [Google Scholar] [CrossRef]
- Rio, D.; Gurutzeaga, I.; Beriain, A.; Solar, H.; Berenguer, R. A Compact, Wideband, and Temperature Robust 67–90-GHz SiGe Power Amplifier with 30% PAE. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 351–353. [Google Scholar]
- Zhou, S. Experimentally investigating the degradations of the GaN PA indexes under different temperature conditions. Microw. Opt. Technol. Lett. 2021, 63, 758–763. [Google Scholar] [CrossRef]
- Yu, C.; Yuan, J.S. Electrical and Temperature Stress Effects on Class-AB Power Amplifier Performances. IEEE Trans. Electron Devices 2007, 54, 1346–1350. [Google Scholar]
- Zhou, S.H. Experimental investigation on the performance degradations of the GaN class-F power amplifier under humidity conditions. Semicond. Sci. Technol. 2021, 36, 035025. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, C.; Wang, J. Support Vector Machine–Based Model for 2.5–5.2 GHz CMOS Power Amplifier. Micromachines 2022, 13, 1012. [Google Scholar] [CrossRef] [PubMed]
- Cortes, C.; Vapnik, V. Support-vector network. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Boser, B.; Guyon, I.; Vapnik, V. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Chen, Y.; Mao, Q.; Wang, B.; Duan, P.; Zhang, B.; Hong, Z. Privacy-Preserving Multi-Class Support Vector Machine Model on Medical Diagnosis. IEEE J. Biomed. Health Inform. 2022, 26, 3342–3353. [Google Scholar] [CrossRef] [PubMed]
- Gupta, C.; Rao, K.V.S.R.; Datta, P. Support Vector Machine Based Prediction of Work-Life Balance among Women in Information Technology Organizations. IEEE Eng. Manag. Rev. 2022, 50, 147–155. [Google Scholar] [CrossRef]
- Liu, T.; Zhu, H.; Wu, M.; Zhang, W. Rotor Displacement Self-Sensing Method for Six-Pole Radial Hybrid Magnetic Bearing Using Mixed-Kernel Fuzzy Support Vector Machine. IEEE Trans. Appl. Supercond. 2020, 30, 3603404. [Google Scholar] [CrossRef]
- Eke, C.S.; Jammeh, E.; Li, X.; Carroll, C.; Pearson, S.; Ifeachor, E. Early Detection of Alzheimer’s Disease with Blood Plasma Proteins Using Support Vector Machines. IEEE J. Biomed. Health Inform. 2021, 25, 218–226. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Guo, W.; Su, C.; Li, X.; Lu, Y.; Chen, Z.; Zhu, L. Optimization on Adhesive Stamp Mass-Transfer of Micro-LEDs with Support Vector Machine Model. IEEE J. Electron Devices Soc. 2020, 8, 554–558. [Google Scholar] [CrossRef]
- Huang, J.; Jiang, B.; Xu, C.; Wang, N. Slipping Detection of Electric Locomotive Based on Empirical Wavelet Transform, Fuzzy Entropy Algorithm and Support Vector Machine. IEEE Trans. Veh. Technol. 2021, 70, 7558–7570. [Google Scholar] [CrossRef]
- Chen, P.; Brazil, T.J. Classifying load-pull contours of a broadband high-efficiency power amplifier using a support vector machine. In Proceedings of the 2017 Integrated Nonlinear Microwave and Millimetre-Wave Circuits Workshop (INMMiC), Graz, Austria, 20–21 April 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Hu, G.; Zhu, X.-W.; Xia, J.; Yu, C.; Shi, Y. A Vector Rotation-based Nonlinear Support Vector Regression Model for Envelope Tracking RF Power Amplifiers. In Proceedings of the 2019 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Guangzhou, China, 19–22 May 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Xu, J.; Jiang, W.; Ma, L.; Li, M.; Yu, Z.; Geng, Z. Augmented Time-Delay Twin Support Vector Regression-Based Behavioral Modeling for Digital Predistortion of RF Power Amplifier. IEEE Access 2019, 7, 59832–59843. [Google Scholar] [CrossRef]
- Abegaz, K.H.; Etikan, İ. Artificial Intelligence-Driven Ensemble Model for Predicting Mortality Due to COVID-19 in East Africa. Diagnostics 2022, 12, 2861. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Han, Y. A New Mixed-Gas-Detection Method Based on a Support Vector Machine Optimized by a Sparrow Search Algorithm. Sensors 2022, 22, 8977. [Google Scholar] [CrossRef] [PubMed]
- Zaki, A.; Métwalli, A.; Aly, M.H.; Badawi, W.K. Wireless Communication Channel Scenarios: Machine-Learning-Based Identification and Performance Enhancement. Electronics 2022, 11, 3253. [Google Scholar] [CrossRef]
- Tan, S.; Pan, J.; Zhang, J.; Liu, Y. CASVM: An Efficient Deep Learning Image Classification Method Combined with SVM. Appl. Sci. 2022, 12, 11690. [Google Scholar] [CrossRef]
- Lin, W.-M.; Wu, C.-H. Fast Support Vector Machine for Power Quality Disturbance Classification. Appl. Sci. 2022, 12, 11649. [Google Scholar] [CrossRef]
- Razavi, B. Design of Analog CMOS Integrated Circuits; McGraw Hill Higher Education: New York, NY, USA, 2003; pp. 17–21. [Google Scholar]
- Neamen, D.A. Semiconductor Physics and Devices: Basic Principles; McGraw Hill Higher Education: New York, NY, USA, 2012; pp. 395–419. [Google Scholar]
- Lee, T.H. The Design of CMOS Radio-Frequency Integrated Circuits; Cambridge University Press: Cambridge, UK, 2012; pp. 172–189. [Google Scholar]
- Mišić, J.; Marković, V.; Marinković, Z.; Budimir, D. Behavioral modeling of low noise amplifiers for LTE systems based on modified Elman neural networks. In Proceedings of the 2014 22nd Telecommunications Forum Telfor (TELFOR), Belgrade, Serbia, 25–27 November 2014; pp. 308–311. [Google Scholar] [CrossRef]
- Shah, J.; Patel, H.; Gajjar, R.; Panchal, D.; Patel, M.I. Aspect Ratio Estimation for MOS Amplifier using Machine Learning. In Proceedings of the 2021 IEEE 2nd International Conference on Applied Electromagnetics, Signal Processing, & Communication (AESPC), Bhubaneswar, India, 26–28 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).