Deep Learning Based Multiresponse Optimization Methodology for Dual-Axis MEMS Accelerometer
Abstract
1. Introduction
2. MEMS Accelerometer Design
3. Basics of Deep Learning Model
4. Proposed Deep-Neural-Network-Based Framework
4.1. Design, Response, and Desirability Value Details
4.2. General Working of the Proposed Optimization Framework
4.3. Output Response Prediction Model
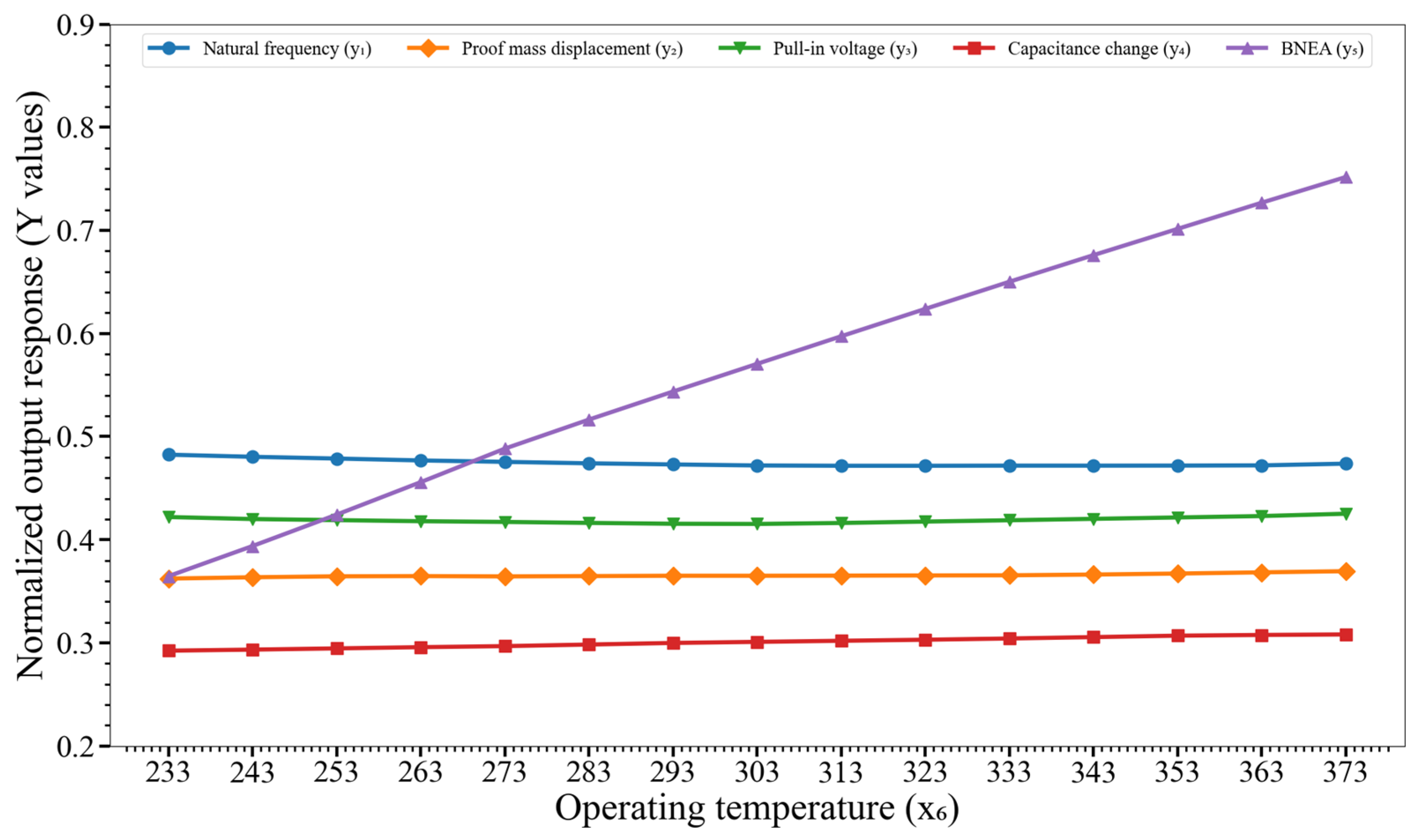
4.4. Effect of Design Parameters on the Output Responses
5. Multiresponse Optimization Using D Prediction Model
5.1. Training of the D Prediction Model
5.2. Multi-Response Optimization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, M.; Wang, Q.; Liu, D.; Zhao, B.; Tang, J.; Sun, J. Real-time gait phase recognition based on time domain features of multi-MEMS inertial sensors. IEEE Trans. Instrum. Meas. 2021, 70, 7504012. [Google Scholar] [CrossRef]
- Zheng, J.; Li, S.; Liu, S.; Guan, B.; Wei, D.; Fu, Q. Research on the Shearer Positioning Method Based on the MEMS Inertial Sensors/Odometer Integrated Navigation System and RTS Smoother. Micromachines 2021, 12, 1527. [Google Scholar] [CrossRef] [PubMed]
- Tsai, J.M.; Sun, I.C.; Chen, K.S. Realization and performance evaluation of a machine tool vibration monitoring module by multiple MEMS accelerometer integrations. Int. J. Adv. Manuf. Technol. 2021, 114, 465–479. [Google Scholar] [CrossRef]
- Di Nuzzo, F.; Brunelli, D.; Polonelli, T.; Benini, L. Structural health monitoring system with narrowband IoT and MEMS sensors. IEEE Sens. J. 2021, 21, 16371–16380. [Google Scholar] [CrossRef]
- Wang, C.; Hao, Y.; Sun, Z.; Zu, L.; Yuan, W.; Chang, H. Design of a Capacitive MEMS Accelerometer with Softened Beams. Micromachines 2022, 13, 459. [Google Scholar] [CrossRef] [PubMed]
- Tahir, M.A.; Saleem, M.M.; Bukhari, S.A.; Hamza, A.; Shakoor, R.I. An efficient design of dual-axis MEMS accelerometer considering microfabrication process limitations and operating environment variations. Microelectron. Int. 2021, 38, 144–156. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, B.; Cai, Y.; Liu, W.; Tovstopyat, A.; Sun, C. A novel tri-axial piezoelectric MEMS accelerometer with folded beams. Sensors 2021, 21, 453. [Google Scholar] [CrossRef]
- Kavitha, S.; Daniel, R.J.; Sumangala, K. High performance MEMS accelerometers for concrete SHM applications and comparison with COTS accelerometers. Mech. Syst. Signal Process. 2016, 66, 410–424. [Google Scholar] [CrossRef]
- Abozyd, S.; Toraya, A.; Gaber, N. Design and Modeling of Fiber-Free Optical MEMS Accelerometer Enabling 3D Measurements. Micromachines 2022, 13, 343. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Scudero, S.; Vitale, G. A review of the capacitive MEMS for seismology. Sensors 2019, 19, 3093. [Google Scholar] [CrossRef]
- Keshavarzi, M.; Yavand Hasani, J. Design and optimization of fully differential capacitive MEMS accelerometer based on surface micromachining. Microsyst. Technol. 2019, 25, 1369–1377. [Google Scholar] [CrossRef]
- Benmessaoud, M.; Nasreddine, M.M. Optimization of MEMS capacitive accelerometer. Microsyst. Technol. 2013, 19, 713–720. [Google Scholar] [CrossRef]
- Mohammed, Z.; Dushaq, G.; Chatterjee, A.; Rasras, M. An optimization technique for performance improvement of gap-changeable MEMS accelerometers. Mechatronics 2018, 54, 203–216. [Google Scholar] [CrossRef]
- Xu, X.; Wu, S.; Fang, W.; Yu, Z.; Jia, Z.; Wang, X.; Bai, J.; Lu, Q. Bandwidth Optimization of MEMS Accelerometers in Fluid Medium Environment. Sensors 2022, 22, 9855. [Google Scholar] [CrossRef]
- Pedersen, C.B.; Seshia, A.A. On the optimization of compliant force amplifier mechanisms for surface micromachined resonant accelerometers. J. Micromech. Microeng. 2004, 14, 1281. [Google Scholar] [CrossRef]
- Ramakrishnan, J.; Gaurav, P.R.; Chandar, N.S.; Sudharsan, N.M. Structural design, analysis and DOE of MEMS-based capacitive accelerometer for automotive airbag application. Microsyst. Technol. 2021, 27, 763–777. [Google Scholar] [CrossRef]
- Saghir, S.; Saleem, M.M.; Hamza, A.; Riaz, K.; Iqbal, S.; Shakoor, R.I. A Systematic Design Optimization Approach for Multiphysics MEMS Devices Based on Combined Computer Experiments and Gaussian Process Modelling. Sensors 2021, 21, 7242. [Google Scholar] [CrossRef]
- Shinde, P.P.; Shah, S. A Review of Machine Learning and Deep Learning Applications. In Proceedings of the 2018 Fourth International Conference on Computing Communication Control and Automation (ICCUBEA), Pune, India, 16–18 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Nguyen, G.; Dlugolinsky, S.; Bobák, M.; Tran, V.; López García, Á.; Heredia, I.; Malík, P.; Hluchý, L. Machine learning and deep learning frameworks and libraries for large-scale data mining: A survey. Artif. Intell. Rev. 2019, 52, 77–124. [Google Scholar] [CrossRef]
- Mathew, A.; Amudha, P.; Sivakumari, S. Deep Learning Techniques: An Overview. Advanced Machine Learning Technologies and Applications. Proc. AMLTA 2020, 2021, 599–608. [Google Scholar]
- Coşkun, M.; Yildirim, Ö.; Ayşegül, U.Ç.; Demir, Y. An overview of popular deep learning methods. Eur. J. Tech. 2017, 7, 165–176. [Google Scholar] [CrossRef]
- Cowen, A.; Hames, G.; Monk, D.; Wilcenski, S.; Hardy, B. SOIMUMPs Design Handbook; MEMSCAP Inc.: Durham, NC, USA, 2011; pp. 2002–2011. [Google Scholar]
- Le, X.L.; Kim, K.; Choa, S.H. Analysis of Temperature Stability and Change of Resonant Frequency of a Capacitive MEMS Accelerometer. Int. J. Precis. Eng. Manuf. 2022, 23, 347–359. [Google Scholar] [CrossRef]
- Derringer, G.; Suich, R. Simultaneous Optimization of Several Response Variables. J. Qual. Technol. 1980, 12, 214–219. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation functions in deep learning: A comprehensive survey and benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 2. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Del Castillo, E.; Montgomery, D.C.; McCarville, D.R. Modified Desirability Functions for Multiple Response Optimization. J. Qual. Technol. 1996, 28, 337–345. [Google Scholar] [CrossRef]
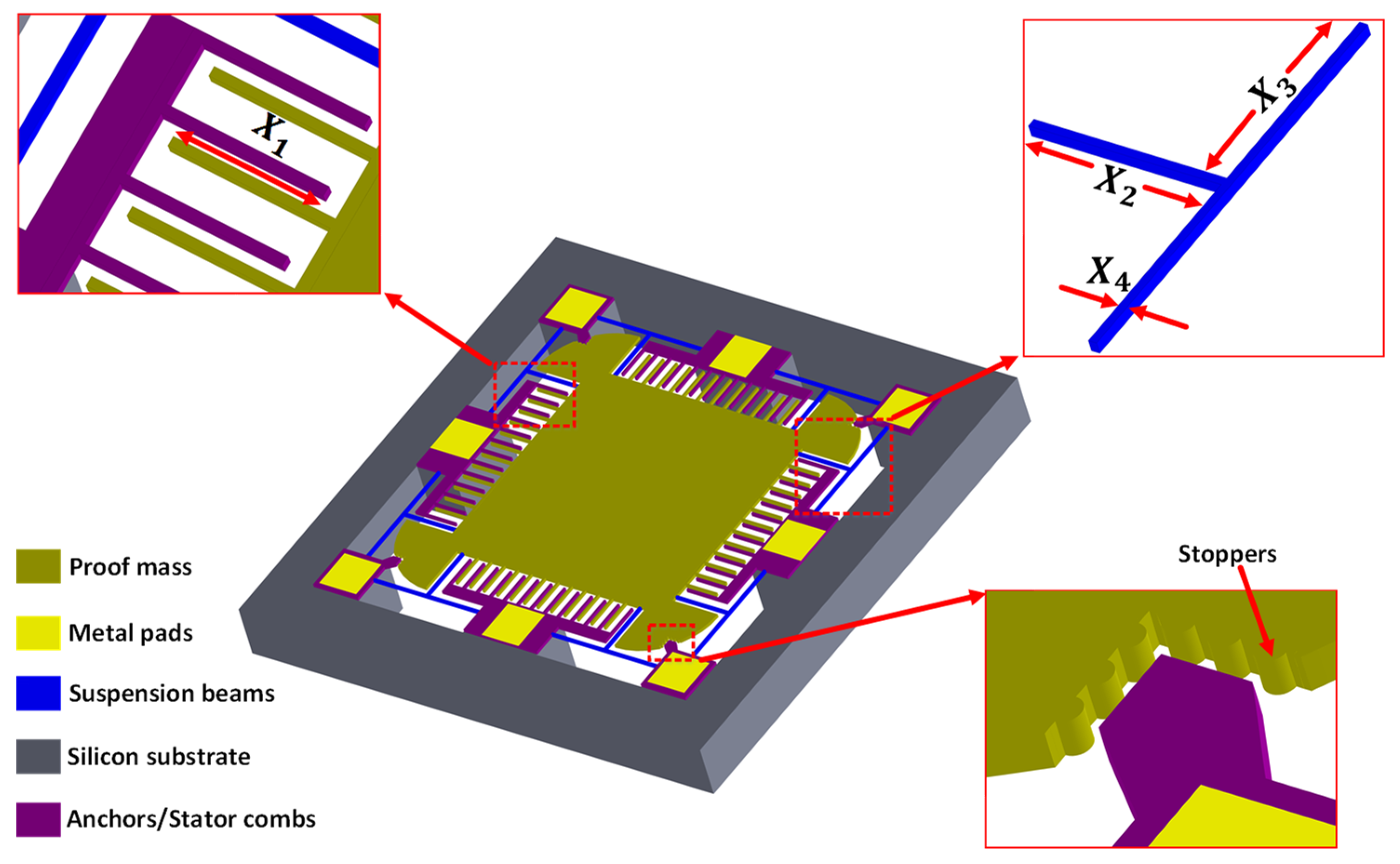














| Notation | Design Parameters | Low Level | High Level |
|---|---|---|---|
| x1 | Overlap length of comb | 150 μm | 250 μm |
| x2 | Length of suspension beam 1 | 400 μm | 500 μm |
| x3 | Length of suspension beam 2 | 500 μm | 500 μm |
| x4 | Width of suspension beam | 6 μm | 8 μm |
| x5 | Input acceleration | 1 g | 25 g |
| x6 | Operating temperature | 233.15 K | 373.15 K |
| x7 | Operating pressure | 100 Torr | 760 Torr |
| x8 | Frequency ratio | 0.1 | 0.5 |
| Output Response | MAE | RMSE | ||
|---|---|---|---|---|
| Proposed | [17] | Proposed | [17] | |
| Natural frequency (y1) | 12.67 Hz | 29.64 Hz | 15.41 Hz | 41.19 Hz |
| Proof mass displacement (y2) | 0.004 μm | 0.024 μm | 0.004 μm | 0.034 μm |
| Pull-in voltage (y3) | 0.065 V | 0.085 V | 0.072 V | 0.134 V |
| Capacitance change (y4) | 5.292 fF | 10.179 fF | 6.28 fF | 14.05 fF |
| BNEA (y5) | ||||
| Optimized Values Reported in [17] | ||||||||
|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |
| Design Parameters (X values) | 153.6 μm | 403.6 μm | 500 μm | 6.26 μm | 25 g | 300 K | 760 Torr | 0.50 |
| y1 | y2 | y3 | y4 | y5 | ||||
| Output Responses (Y values) | 3036.4 Hz | 0.903 μm | 6.76 V | 676.2 fF | ||||
| Optimized Values Obtained Using the Proposed Method. | ||||||||
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |
| Design Parameters (X values) | 150.0 μm | 430.0 μm | 500 μm | 6.40 μm | 25 g | 300 K | 760 Torr | 0.45 |
| y1 | y2 | y3 | y4 | y5 | ||||
| Output Responses (Y values) | 3160.0 Hz | 0.723 μm | 7.22 V | 571.0 fF | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mattoo, F.A.; Nawaz, T.; Saleem, M.M.; Khan, U.S.; Hamza, A. Deep Learning Based Multiresponse Optimization Methodology for Dual-Axis MEMS Accelerometer. Micromachines 2023, 14, 817. https://doi.org/10.3390/mi14040817
Mattoo FA, Nawaz T, Saleem MM, Khan US, Hamza A. Deep Learning Based Multiresponse Optimization Methodology for Dual-Axis MEMS Accelerometer. Micromachines. 2023; 14(4):817. https://doi.org/10.3390/mi14040817
Chicago/Turabian StyleMattoo, Fahad A., Tahir Nawaz, Muhammad Mubasher Saleem, Umar Shahbaz Khan, and Amir Hamza. 2023. "Deep Learning Based Multiresponse Optimization Methodology for Dual-Axis MEMS Accelerometer" Micromachines 14, no. 4: 817. https://doi.org/10.3390/mi14040817
APA StyleMattoo, F. A., Nawaz, T., Saleem, M. M., Khan, U. S., & Hamza, A. (2023). Deep Learning Based Multiresponse Optimization Methodology for Dual-Axis MEMS Accelerometer. Micromachines, 14(4), 817. https://doi.org/10.3390/mi14040817






