Elasto-Kinematics and Instantaneous Invariants of Compliant Mechanisms Based on Flexure Hinges
Abstract
1. Introduction
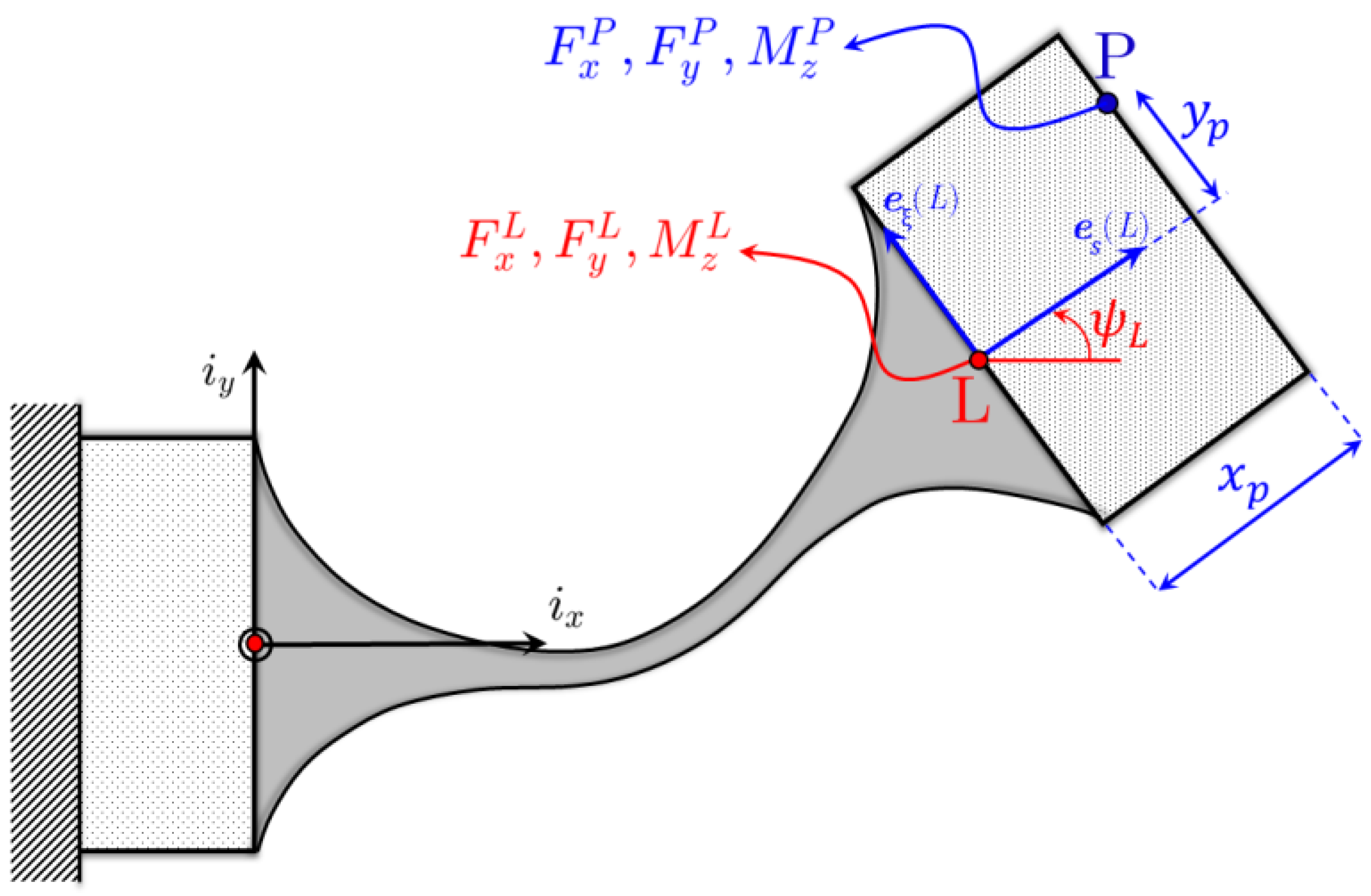
2. A Comprehensive Analytical Model of Flexure Hinge Kinematics
2.1. Analytical Solution
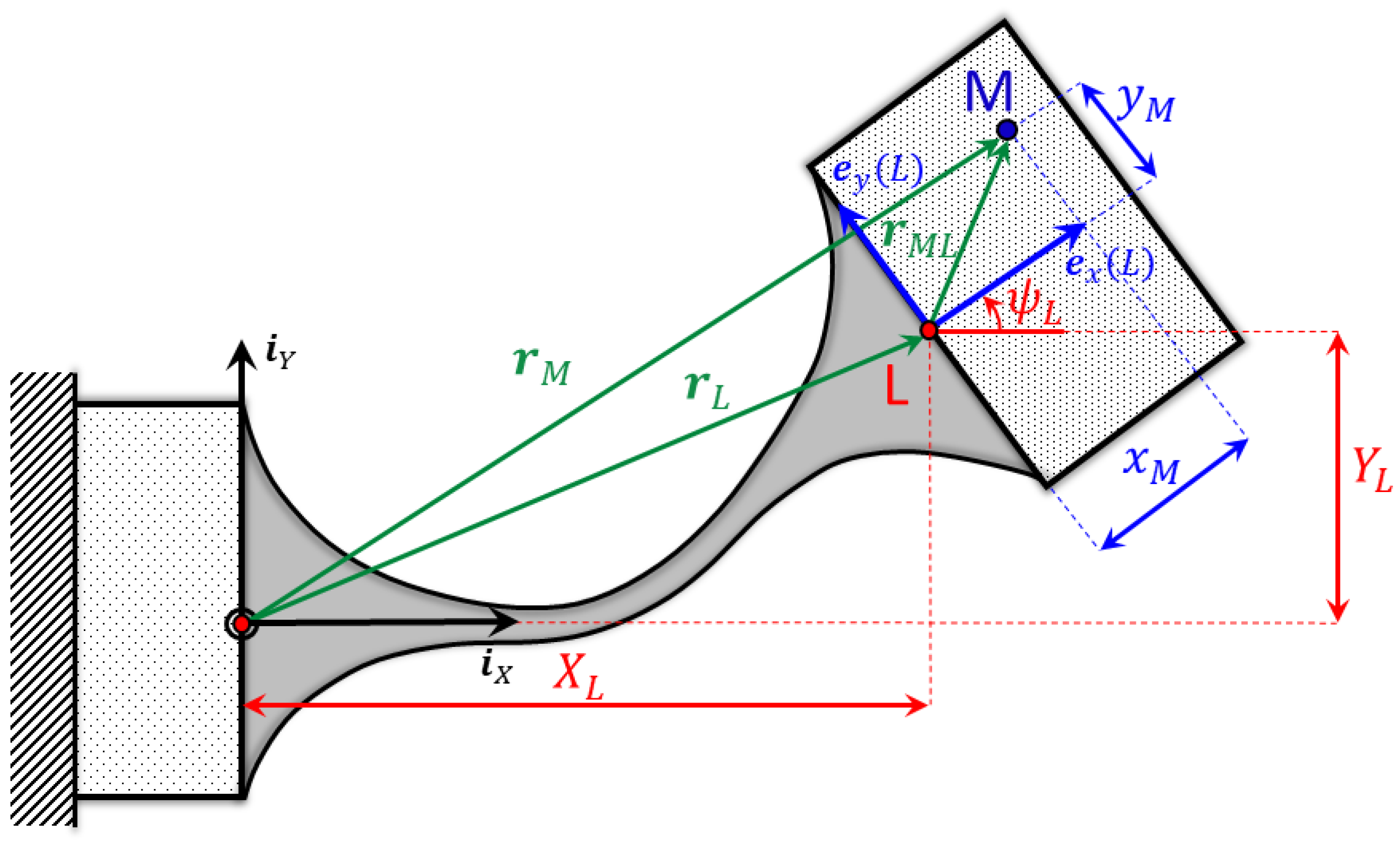
3. Analytical Deduction of Instantaneous Invariants for Compliant Mechanism
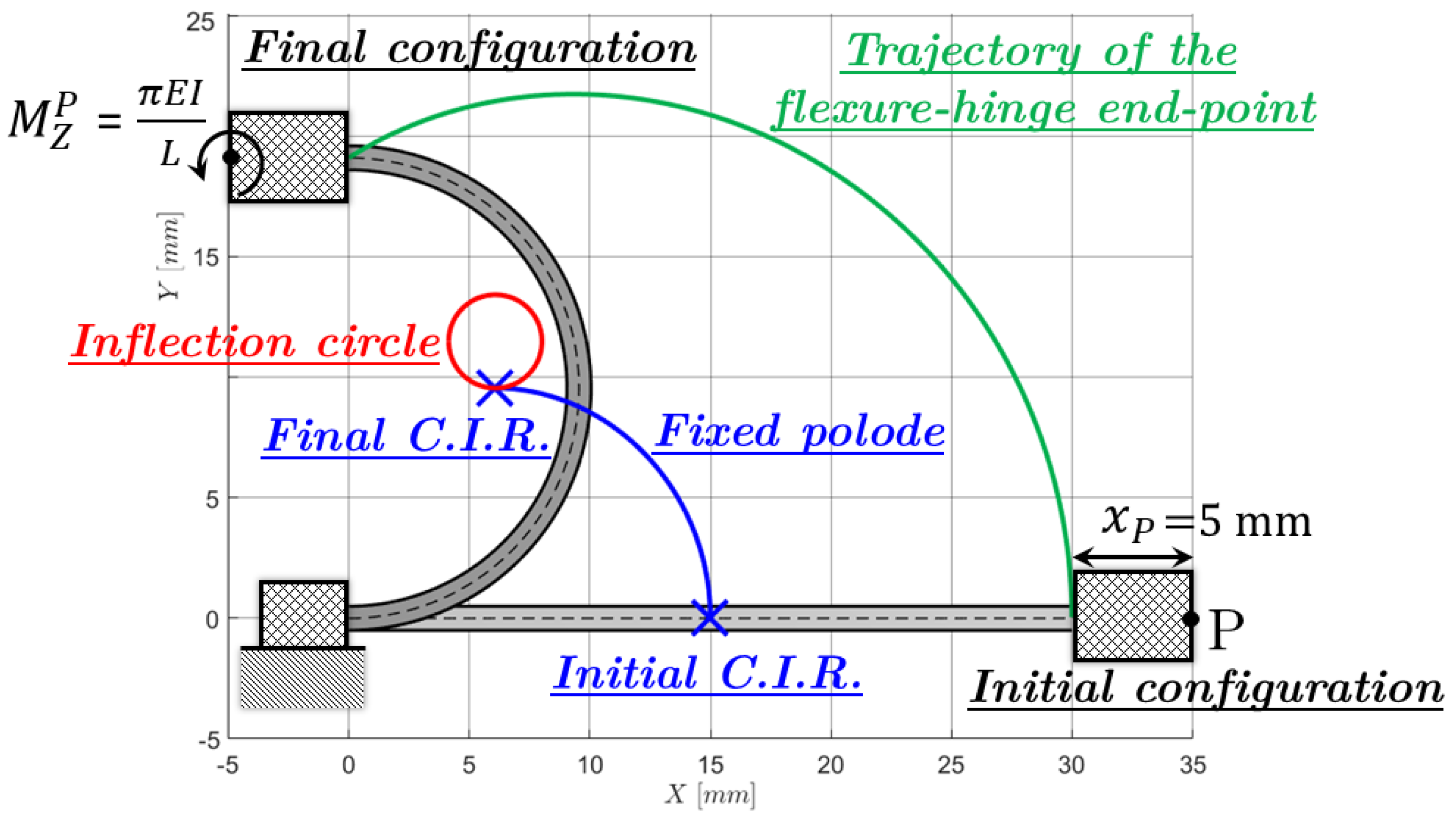
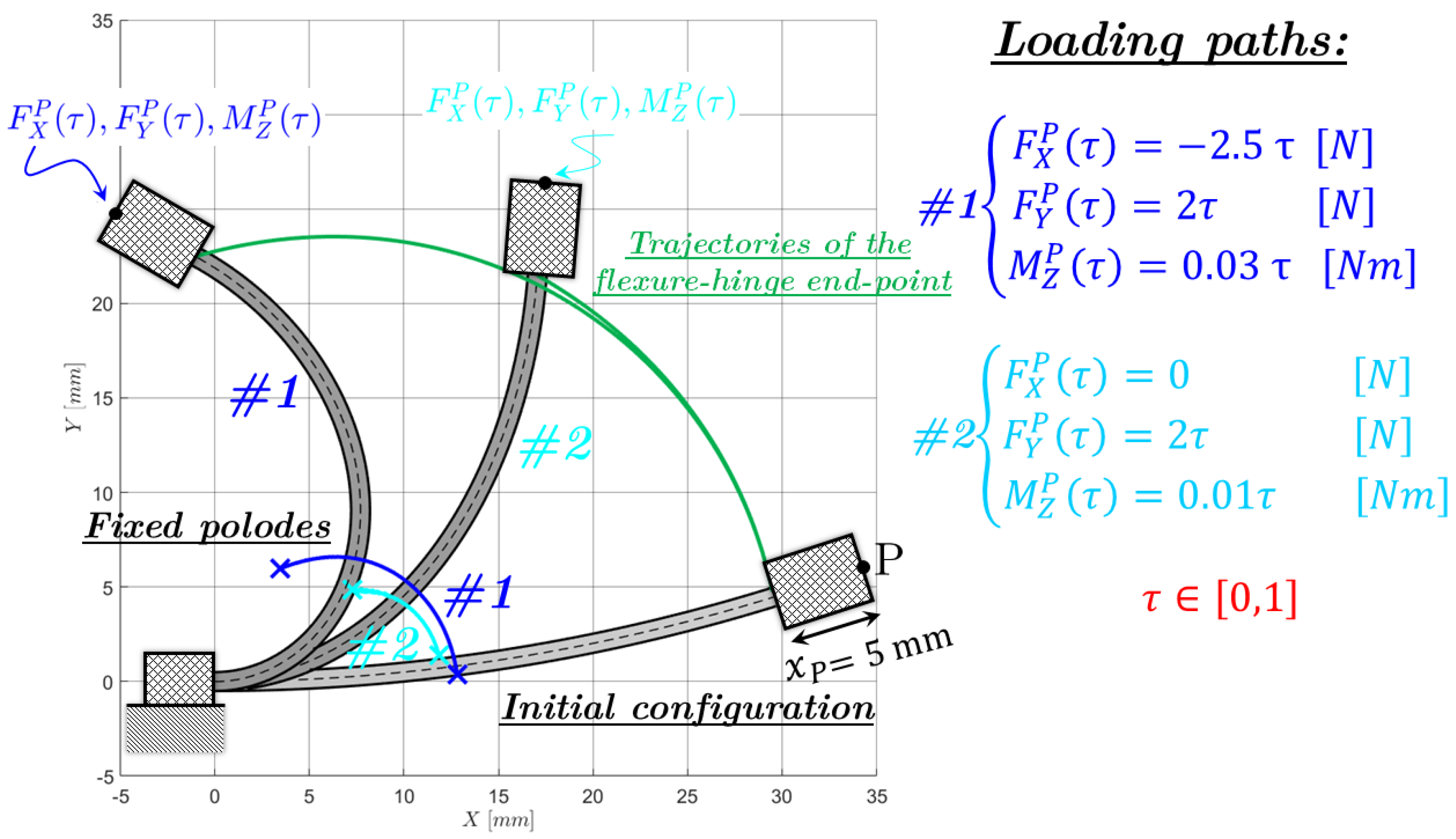
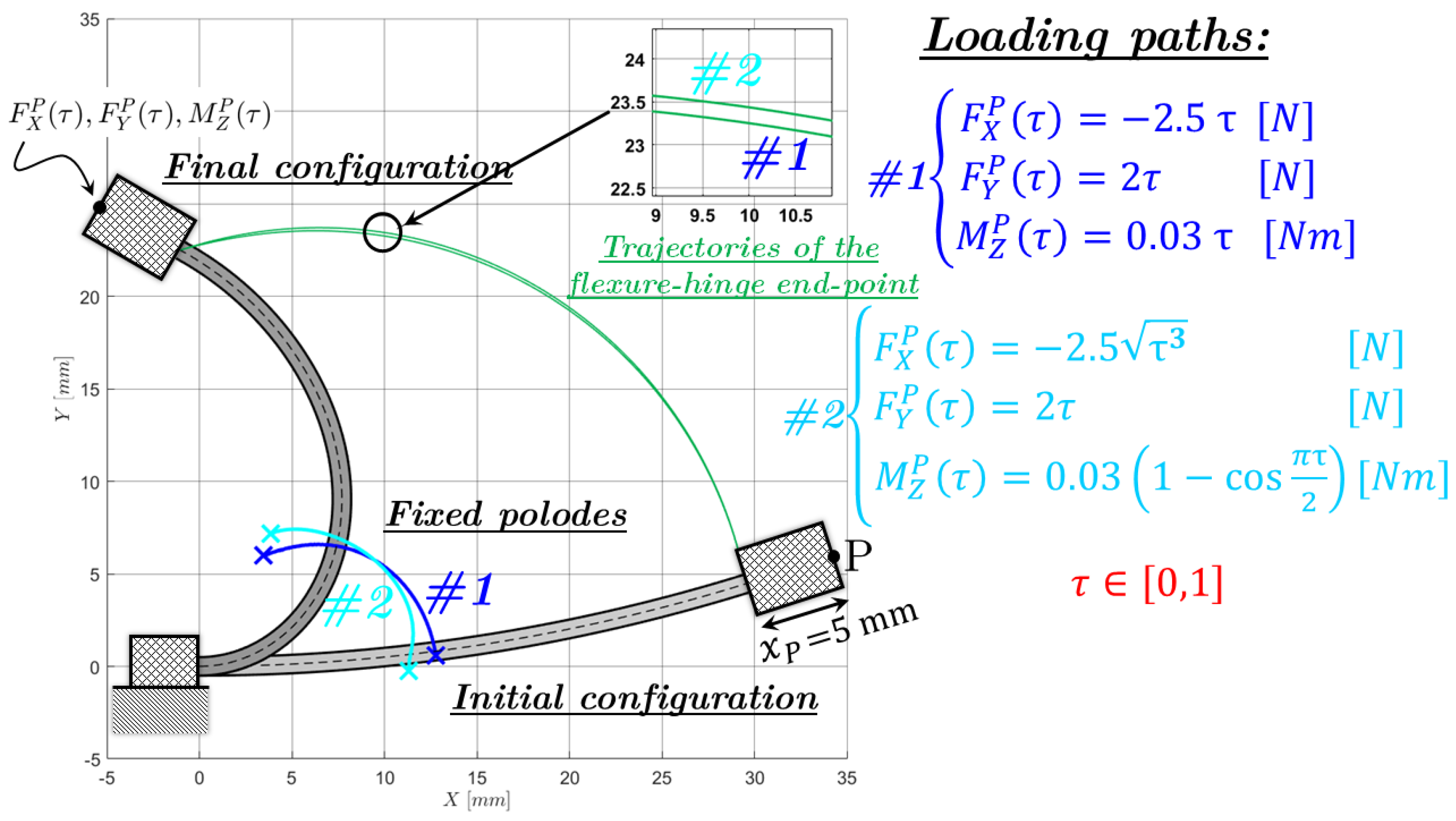
4. Numerical Examples and Experimental Evidence
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of the Skewness of the Curvature Tensor
Appendix B. Other Relations Regarding the Equilibrium
Appendix C. A Useful Trick to Avoid the Singularities of Some Integrals
Appendix D. Fully Analytical Solution of Polodes (Fixed and Mobile) and Inflection Circle for a Flexure Hinge Loaded by a Concentrated Moment
References
- Howell, L.L.; Magleby, S.P.; Olsen, B.M. Handbook of Compliant Mechanisms; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Howell, L.L. Compliant Mechanisms; John Wiley and Sons, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Alejandro, A.E.; Fachinotti, V.D.; Pucheta, M.A. A review on design methods for compliant mechanisms. Mec. Comput. 2010, 29, 59–72. [Google Scholar]
- Shuib, S.; Ridzwan, M.I.Z.; Kadarman, A.H. Methodology of compliant mechanisms and its current developments in applications: A review. Am. J. Appl. Sci. 2007, 4, 160–167. [Google Scholar] [CrossRef]
- Jagtap, S.P.; Deshmukh, B.B.; Pardeshi, S. Applications of compliant mechanism in today’s world—A review. J. Phys. Conf. Ser. 2021, 1969, 012013. [Google Scholar] [CrossRef]
- Wu, S.; Shao, Z.; Fu, H. A Substructure Condensed Approach for Kinetostatic Modeling of Compliant Mechanisms with Complex Topology. Micromachines 2022, 13, 1734. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Wang, J.; Xiong, W.; Hu, Q.; Liu, H.; Wang, Q. Design and Modeling of a Curved Beam Compliant Mechanism with Six Degrees of Freedom. Micromachines 2022, 13, 208. [Google Scholar] [CrossRef]
- Liu, T.; Hao, G. Design of Deployable Structures by Using Bistable Compliant Mechanisms. Micromachines 2022, 13, 651. [Google Scholar] [CrossRef]
- Xi, X.; Clancy, T.; Wu, X.; Sun, Y.; Liu, X. A MEMS XY-stage integrating compliant mechanism for nanopositioning at sub-nanometer resolution. J. Micromech. Microeng. 2016, 26, 025014. [Google Scholar] [CrossRef]
- Kota, S.; Joo, J.; Li, Z.; Rodgers, S.M.; Sniegowski, J. Design of Compliant Mechanisms: Applications to MEMS. Analog. Integr. Circuits Signal Process. 2001, 29, 7–15. [Google Scholar] [CrossRef]
- Parkinson, M.; Jensen, B.; Kurabayashi, K. Design of compliant force and displacement amplification micro-mechanisms. In Proceedings of the DETC ’01 ASME 2001 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Pittsburgh, PA, USA, 9–12 September 2001. [Google Scholar]
- Kahr, M.; Steiner, H.; Hortschitz, W.; Stifter, M.; Kainz, A.; Keplinger, F. 3D-Printed MEMS Magnetometer Featuring Compliant Mechanism. Proceedings 2018, 2, 784. [Google Scholar]
- Iqbal, S.; Lai, Y.; Shakoor, R.I.; Raffi, M.; Bazaz, S.A. Design, analysis, and experimental investigation of micro-displacement amplification compliant mechanism for micro-transducers. Rev. Sci. Instrum. 2021, 92, 105007. [Google Scholar] [CrossRef]
- Ursi, P.; Rossi, A.; Botta, F.; Belfiore, N.P. Analytical Modeling of a New Compliant Microsystem for Atherectomy Operations. Micromachines 2022, 13, 1094. [Google Scholar] [CrossRef] [PubMed]
- Botta, F.; Rossi, A.; Belfiore, N.P. A Cantilever-Based Piezoelectric MEMS for Arbitrary XY Path Generation. Micromachines 2022, 13, 1514. [Google Scholar] [CrossRef] [PubMed]
- Botta, F. A Piezoelectric MEMS Microgripper for Arbitrary XY Trajectory. Micromachines 2022, 13, 1888. [Google Scholar] [CrossRef]
- Botta, F.; Rossi, A.; Belfiore, N.P. A Feasibility Study of a Novel Piezo MEMS Tweezer for Soft Materials Characterization. Appl. Sci. 2019, 9, 2277. [Google Scholar] [CrossRef]
- Di Giamberardino, P.; Bagolini, A.; Bellutti, P.; Rudas, I.J.; Verotti, M.; Botta, F.; Belfiore, N.P. New MEMS Tweezers for the Viscoelastic Characterization of Soft Materials at the Microscale. Micromachines 2018, 9, 15. [Google Scholar] [CrossRef]
- Laszczyk, K.; Bargiel, S.; Gorecki, C.; Krezel, J.; Dziubana, P.; Kujawinskab, M.; Callet, D.; Frankd, S. A two directional electrostatic comb-drive X–Y micro-stage for MOEMS applications. Sens. Actuators A Phys. 2010, 163, 255–265. [Google Scholar] [CrossRef]
- Singh, J.; Teo, J.H.S.; Xu, Y.; Premachandran, C.S.; Chen, N.; Kotlanka, R.; Olivo, M.; Sheppard, C.J.R. A two axes scanning SOI MEMS micromirror for endoscopic bioimaging. J. Micromech. Microeng. 2008, 18, 025001. [Google Scholar] [CrossRef]
- Smith, S.T.; Chetwynd, D.G.; Bowen, D.K. Design and assessment of monolithic high precision translation mechanisms. J. Phys. E Sci. Instrum. 1987, 20, 977–983. [Google Scholar] [CrossRef]
- Linß, S.; Schorr, P.; Zentner, L. General design equations for the rotational stiffness, maximal angular deflection and rotational precision of various notch flexure hinges. Mech. Sci. 2017, 8, 29–49. [Google Scholar] [CrossRef]
- Hou, W. Analysis of three nodes flexure hinge element in ultra-precision positioning stage. In Proceedings of the 7th International Conference on Biomedical Engineering and Informatics, Dalian, China, 14–16 October 2014; pp. 527–533. [Google Scholar]
- Melgarejo, M.; Darnieder, M.; Linß, S.; Zentner, L.; Fröhlich, T.; Theska, R. On Modeling the Bending Stiffness of Thin Semi-Circular Flexure Hinges for Precision Applications. Actuators 2018, 7, 86. [Google Scholar] [CrossRef]
- Xu, Q. Micromachines for Biological Micromanipulation; Springer: Cham, Switzerland, 2018; ISBN 978-3-319-74620-3. [Google Scholar]
- Pan, P.; Wang, W.; Ru, C.; Sun, Y.; Liu, X. MEMS-based platforms for mechanical manipulation and characterization of cells. J. Micromech. Microeng. 2017, 27, 123003. [Google Scholar] [CrossRef]
- Ding, B.; Li, Y.; Xiao, X.; Tang, Y.; Li, B. Design and analysis of a 3-DOF planar micromanipulation stage with large rotational displacement for micromanipulation system. Mech. Sci. 2017, 8, 117–126. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Z. Design, analysis and simulation of a novel 3-DOF translational micromanipulator based on the PRB model. Mech. Mach. Theory 2016, 100, 235–258. [Google Scholar] [CrossRef]
- Udvardi, P.; Radó, J.; Straszner, A.; Ferencz, J.; Hajnal, Z.; Soleimani, S.; Schneider, M.; Schmid, U.; Révész, P.; Volk, J. Spiral-Shaped Piezoelectric MEMS Cantilever Array for Fully Implantable Hearing Systems. Micromachines 2017, 8, 311. [Google Scholar] [CrossRef]
- Abdalla, M.; Frecker, M.; Gürdal, Z.; Johnson, T.; Lindner, D.K. Design of a piezoelectric actuator and compliant mechanism combination for maximum energy efficiency. Smart Mater. Struct. 2005, 14, 1421. [Google Scholar] [CrossRef]
- Wei, H.; Shirinzadeh, B.; Li, W.; Clark, L.; Pinskier, J.; Wang, Y. Development of Piezo-Driven Compliant Bridge Mechanisms: General Analytical Equations and Optimization of Displacement Amplification. Micromachines 2017, 8, 238. [Google Scholar] [CrossRef]
- Pfusterschmied, G.; Toledo, J.; Kucera, M.; Steindl, W.; Zemann, S.; Ruiz-Díez, V.; Schneider, M.; Bittner, A.; Sanchez-Rojas, J.L.; Schmid, U. Potential of Piezoelectric MEMS Resonators for Grape Must Fermentation Monitoring. Micromachines 2017, 8, 200. [Google Scholar] [CrossRef]
- Zhou, Z.; Gao, Y.; Sun, L.; Dong, W.; Du, Z. A bistable mechanism with linear negative stiffness and large in-plane lateral stiffness: Design, modeling and case studies. Mech. Sci. 2020, 11, 75–89. [Google Scholar] [CrossRef]
- Ding, B.; Zhao, J.; Li, Y. Design of a spatial constant-force end-effector for polishing/deburring operations. Int. J. Adv. Manuf. Technol. 2021, 116, 3507–3515. [Google Scholar] [CrossRef]
- Cannon, B.R.; Lillian, T.D.; Magleby, S.P.; Howell, L.L.; Linford, M.R. A compliant end-effector for microscribing. Precis. Eng. 2005, 29, 86–94. [Google Scholar] [CrossRef]
- Deng, G.; Cui, W.; Zhou, C.; Li, J. A piezoelectric jetting dispenser with a pin joint. Optik 2018, 175, 163–171. [Google Scholar] [CrossRef]
- Iandiorio, C.; Salvini, P. Heavy Elastica soil-supported with lifting load and bending moment applied to an end: A new analytical approach for very large displacements and experimental validation. Int. J. Solids Struct. 2020, 206, 153–169. [Google Scholar] [CrossRef]
- Marotta, E.; Iandiorio, C.; Salvini, P. Experimental setup for the evaluation of large displacements in the inflected beams sustained to ground. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1038, 012078. [Google Scholar] [CrossRef]
- Iandiorio, C.; Salvini, P. Inflectional Heavy Elastica with Unilateral Contact constraint: Analytical Solution through the Curvilinear Abscissa Mapping approximation. Int. J. Solids Struct. 2022, 234–235, 111258. [Google Scholar] [CrossRef]
- De Bona, F.; Zelenika, S. A generalized elastica-type approach to the analysis of large displacements of spring-strips. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1997, 211, 509–517. [Google Scholar] [CrossRef]
- Ahuett-Garza, H.; Chaides, O.; Garcia, P.N.; Urbina, P. Studies about the use of semicircular beams as hinges in large deflection planar compliant mechanisms. Precis. Eng. 2014, 38, 711–727. [Google Scholar] [CrossRef]
- Linß, S.; Gräser, P.; Räder, T.; Henning, S.; Theska, R.; Zentner, L. Influence of geometric scaling on the elasto-kinematic properties of flexure hinges and compliant mechanisms. Mech. Mach. Theory 2018, 125, 220–239. [Google Scholar] [CrossRef]
- Henning, S.; Linß, S.; Gräser, P.; Theska, R.; Zentner, L. Non-linear analytical modeling of planar compliant mechanisms. Mech. Mach. Theory 2021, 155, 104067. [Google Scholar] [CrossRef]
- Valentini, P.P.; Pennestrì, E. Compliant four-bar linkage synthesis with second-order flexure hinge approximation. Mech. Mach. Theory 2018, 128, 225–233. [Google Scholar] [CrossRef]
- Valentini, P.P.; Cirelli, M.; Di Donato, S. The compliant centrifugal pendulum as the vibration absorber with second-order elasto-kinematic approximation. J. Vib. Control. Vol. 2021, 27, 1370–1381. [Google Scholar] [CrossRef]
- Valentini, P.P.; Pennestrì, E. Second-order approximation pseudo-rigid model of leaf flexure hinge. Mech. Mach. Theory 2017, 116, 352–359. [Google Scholar] [CrossRef]
- Cera, M.; Cirelli, M.; Colaiacovo, L.; Valentini, P.P. Second-order approximation pseudo-rigid model of circular arc flexure hinge. Mech. Mach. Theory 2022, 175, 104963. [Google Scholar] [CrossRef]
- Valentini, P.P.; Cirelli, M.; Pennestrì, E. Second-order approximation pseudo-rigid model of flexure hinge with parabolic variable thickness. Mech. Mach. Theory 2019, 136, 178–189. [Google Scholar] [CrossRef]
- Šalinić, S.; Nikolic, A.V. A new pseudo-rigid-body model approach for modeling the quasi-static response of planar flexure-hinge mechanisms. Mech. Mach. Theory 2018, 124, 150–161. [Google Scholar] [CrossRef]
- Meng, Q.; Li, Y.; Xu, J. A novel analytical model for flexure-based proportion compliant mechanisms. Precis. Eng. 2014, 38, 449–457. [Google Scholar] [CrossRef]
- Belfiore, N.P. Functional synthesis of a new class of micro electro-mechanical systems. In Advances in Soft Computing Intelligent Robotics and Control of Topics in Intelligent Engineering and Informatics; Fodor, J., Fullér, R., Eds.; Springer: Cham, Switzerland, 2014; Volume 8, pp. 81–93. [Google Scholar]
- Verotti, M. Analysis of the center of rotation in primitive flexures: Uniform cantilever beams with constant curvature. Mech. Mach. Theory 2016, 97, 29–50. [Google Scholar] [CrossRef]
- Iandiorio, C.; Salvini, P. An Analytical Solution for Large Displacements of End-Loaded Beams. In Lecture Notes in Mechanical Engineering, Proceedings of the 1st International Conference on Numerical Modelling in Engineering NME, Ghent University, Ghent, Belgium, 28–29 August 2018; Springer: Singapore, 2018. [Google Scholar] [CrossRef]
- Iandiorio, C.; Salvini, P. Large displacements of slender beams in plane: Analytical solution by means of a new hypergeometric function. Int. J. Solids Struct. 2020, 185–186, 467–484. [Google Scholar] [CrossRef]
- Batista, M. Analytical solution for large deflection of Reissner’s beam on two supports subjected to central concentrated force. Int. J. Mech. Sci. 2016, 107, 13–20. [Google Scholar] [CrossRef]
- Irschik, H.; Gerstmayr, J. A continuum mechanics based derivation of Reissner’s large-displacement finite-strain beam theory: The case of plane deformations of originally straight Bernoulli-Euler beams. Acta Mech. 2009, 206, 1–21. [Google Scholar] [CrossRef]
- Timoshenko, S.P. Strength of Materials (Parts I & II); David Van Nostrand Company: New York, NY, USA, 1940. [Google Scholar]
- Iandiorio, C.; Salvini, P. An Engineering Theory of thick Curved Beams loaded in-plane and out-of-plane: 3D Stress Analysis. Eur. J. Mech.-A/Solids 2022, 92, 104484. [Google Scholar] [CrossRef]
- Lacarbonara, W. Nonlinear Structural Mechanics; Springer: New York, NY, USA, 2013; ISBN 978-1-4419-1275-6. [Google Scholar]
- Rossi, A.; Botta, F. Optimised Voltage Distribution on Piezoelectric Actuators for Modal Excitations Damping in Tapered Beams. Actuators 2023, 12, 71. [Google Scholar] [CrossRef]
- Thabuis, A.; Thomas, S.; Martinez, T.; Germano, P.; Perriard, Y. Designing compliant mechanisms composed of shape memory alloy and actuated by induction heating. Smart Mater. Struct. 2021, 30, 095025. [Google Scholar] [CrossRef]
- Iandiorio, C.; Salvini, P. Updated Lagrangian Curvilinear Beam Element for 2D Large Displacement Analysis. In Lecture Notes in Mechanical Engineering, Proceedings of the 5th International Conference on Numerical Modelling in Engineering NME, Ghent University, Ghent, Belgium, 23–24 August 2022; Springer: Singapore, 2023. [Google Scholar]
- Iandiorio, C.; Salvini, P. Elastic-plastic analysis with pre-integrated beam finite element based on state diagrams: Elastic-perfectly plastic flow. Eur. J. Mech.-A/Solids 2023, 97, 104837. [Google Scholar] [CrossRef]
- Krause, M. Analysis der Ebenen Bewegung; Vereinigung Wissenschaftlicher Verlag: Berlin, Germany, 1920. [Google Scholar]
- Bottema, O. Some Remarks on theoretical Kinematics: Instantaneous Invariants. In Proceedings of the International Conference for Teachers of Mechanisms, New Haven, CT, USA, 27–30 March 1961; The Shoe String Press: New Haven, CT, USA, 1961. [Google Scholar]
- Veldkamp, G.R. Curvature Theory in Plane Kinematics. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1963. [Google Scholar]
- Woo, L.S.; Freudenstein, F. On the curves of synthesis in plane, instantaneous kinematics. In International Union of Theoretical and Applied Mechanics; Springer: Berlin, Germany, 1969. [Google Scholar] [CrossRef]
- Di Benedetto, A.; Pennestrì, E. Introduzione alla Cinematica dei Meccanismi; Casa Editrice Ambrosiana: Milano, Italy, 1993; Volume 2, ISBN 8808084701. [Google Scholar]
- Pennestrì, E.; Cera, M. Engineering Kinematics: Curvature Theory of Plane Motion. Independently Published; 2023; ISBN 979-8374816860. [Google Scholar]
- Roth, B.; Yang, A.T. Application of Instantaneous Invariants to the Analysis and Synthesis of Mechanisms. J. Eng. Ind. 1977, 99, 97–103. [Google Scholar] [CrossRef]
- Roth, B. On the advantages of instantaneous invariants and geometric kinematics. Mech. Mach. Theory 2015, 89, 5–13. [Google Scholar] [CrossRef]
- Figliolini, G.; Lanni, C. Geometric Loci for the Kinematic Analysis of Planar Mechanisms via the Instantaneous Geometric Invariants. In Mechanisms and Machine Science; Springer: Cham, Switzerland, 2019; Volume 66. [Google Scholar] [CrossRef]
- Belfiore, N.P.; Simeone, P. Inverse kinetostatic analysis of compliant four-bar linkages. Mech. Mach. Theory 2013, 69, 350–372. [Google Scholar] [CrossRef]
- Luck, K.; Rehwald, W. Historical Evolution of the Pole-Theory. In International Symposium on History of Machines and Mechanisms; Springer: Dordrecht, The Netherlands, 2004. [Google Scholar] [CrossRef]
- Bresse, J.A.C. Memoire sur un theoreme nouveau concernant les mouvements plans, et sur l’application de la cinematique a la determination des rayons de courbure. J. Ľecole Polytech. 1853, 35, 89. [Google Scholar]
- Beléndez, T.; Neipp, C.; Beléndez, A. An Integrated Project for Teaching the Post-Buckling of a Slender Cantilever Bar. Int. J. Mech. Eng. Educ. 2004, 32. [Google Scholar] [CrossRef]



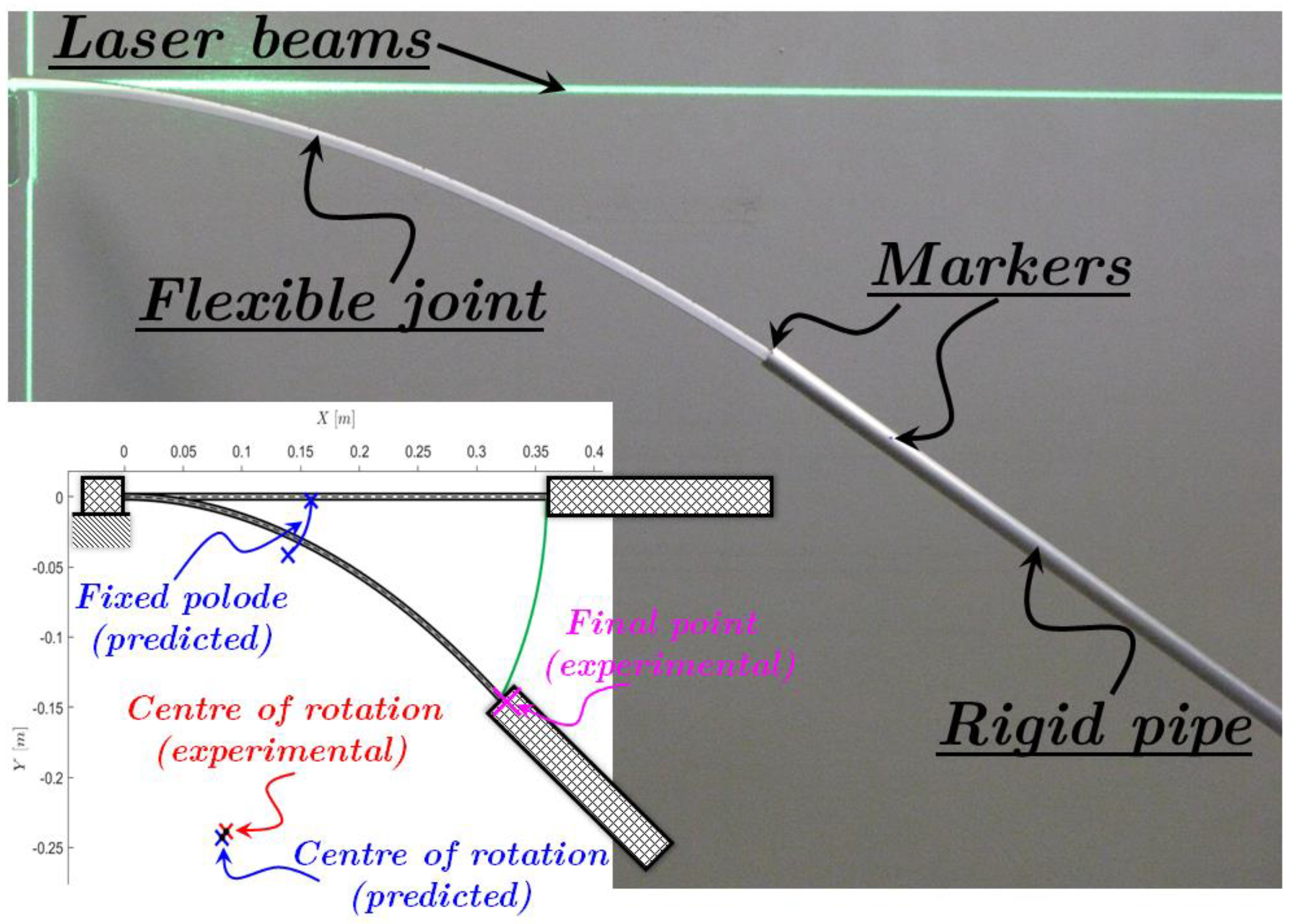
| Flexible Joint Lengths [mm] | Experimental Centre of Rotation [mm] | Predicted Centre of Rotation [mm] | Experimental Final Angle [deg] | Predicted Final Angle [deg] |
|---|---|---|---|---|
| 360 | (87.3, −238.6) | (83.7, −242.9) | 41.6 | 42.7 |
| 270 | (85.2, −169.4) | (85.3, −168.2) | 33.0 | 32.6 |
| 180 | (70.7, −100.1) | (71.4, −97.4) | 22.2 | 21.5 |
| 90 | (40.3, −47.1) | (41.5, −38.9) | 12.4 | 10.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iandiorio, C.; Salvini, P. Elasto-Kinematics and Instantaneous Invariants of Compliant Mechanisms Based on Flexure Hinges. Micromachines 2023, 14, 783. https://doi.org/10.3390/mi14040783
Iandiorio C, Salvini P. Elasto-Kinematics and Instantaneous Invariants of Compliant Mechanisms Based on Flexure Hinges. Micromachines. 2023; 14(4):783. https://doi.org/10.3390/mi14040783
Chicago/Turabian StyleIandiorio, Christian, and Pietro Salvini. 2023. "Elasto-Kinematics and Instantaneous Invariants of Compliant Mechanisms Based on Flexure Hinges" Micromachines 14, no. 4: 783. https://doi.org/10.3390/mi14040783
APA StyleIandiorio, C., & Salvini, P. (2023). Elasto-Kinematics and Instantaneous Invariants of Compliant Mechanisms Based on Flexure Hinges. Micromachines, 14(4), 783. https://doi.org/10.3390/mi14040783






