System Identification and Mathematical Modeling of A Piezoelectric Actuator through A Practical Three-Stage Mechanism
Abstract
1. Introduction
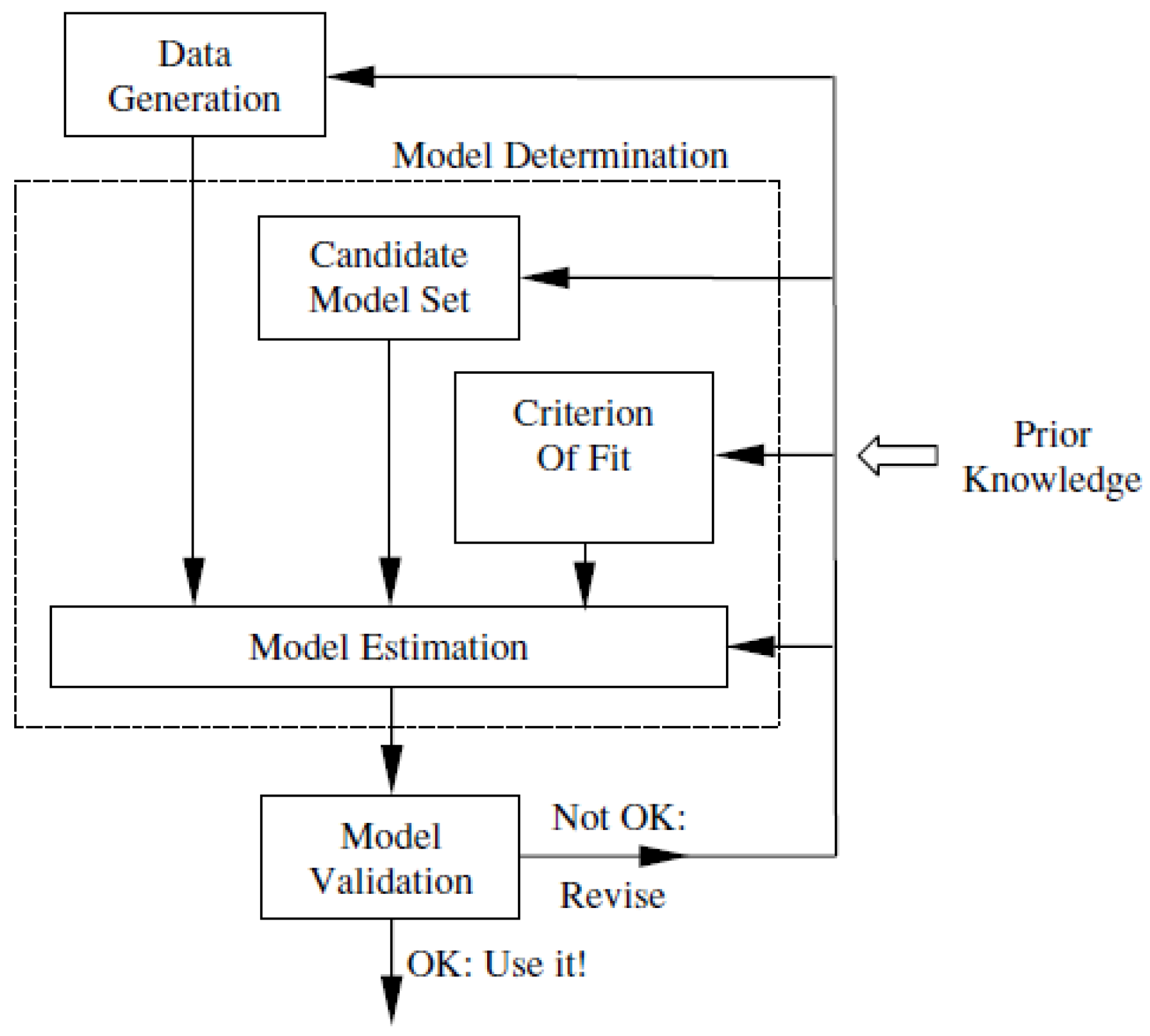
2. System Identification Methods
3. The Combined System Model
3.1. Piezoelectric Elements (PEMs)
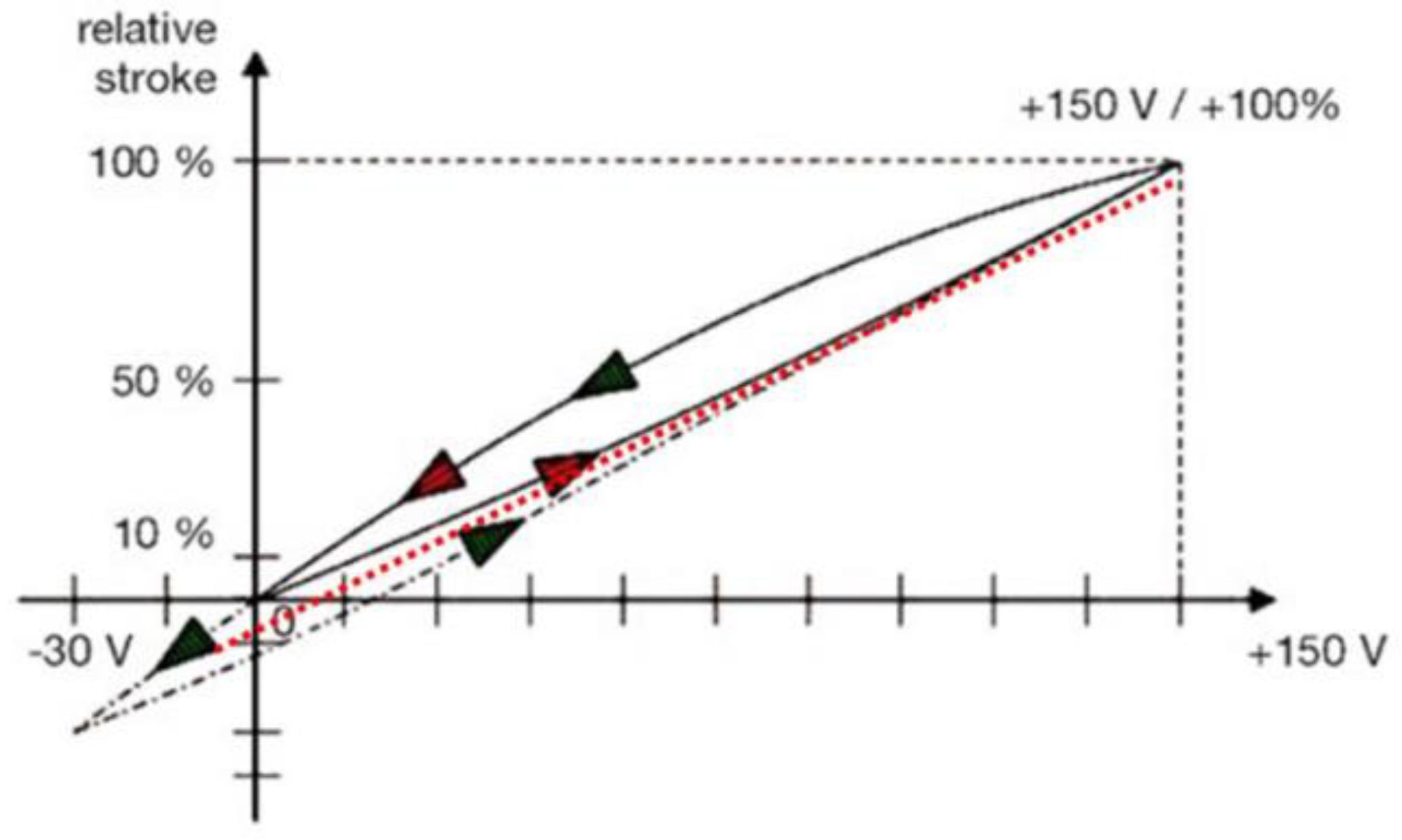
3.2. Hysteresis in Piezoelectric Materials
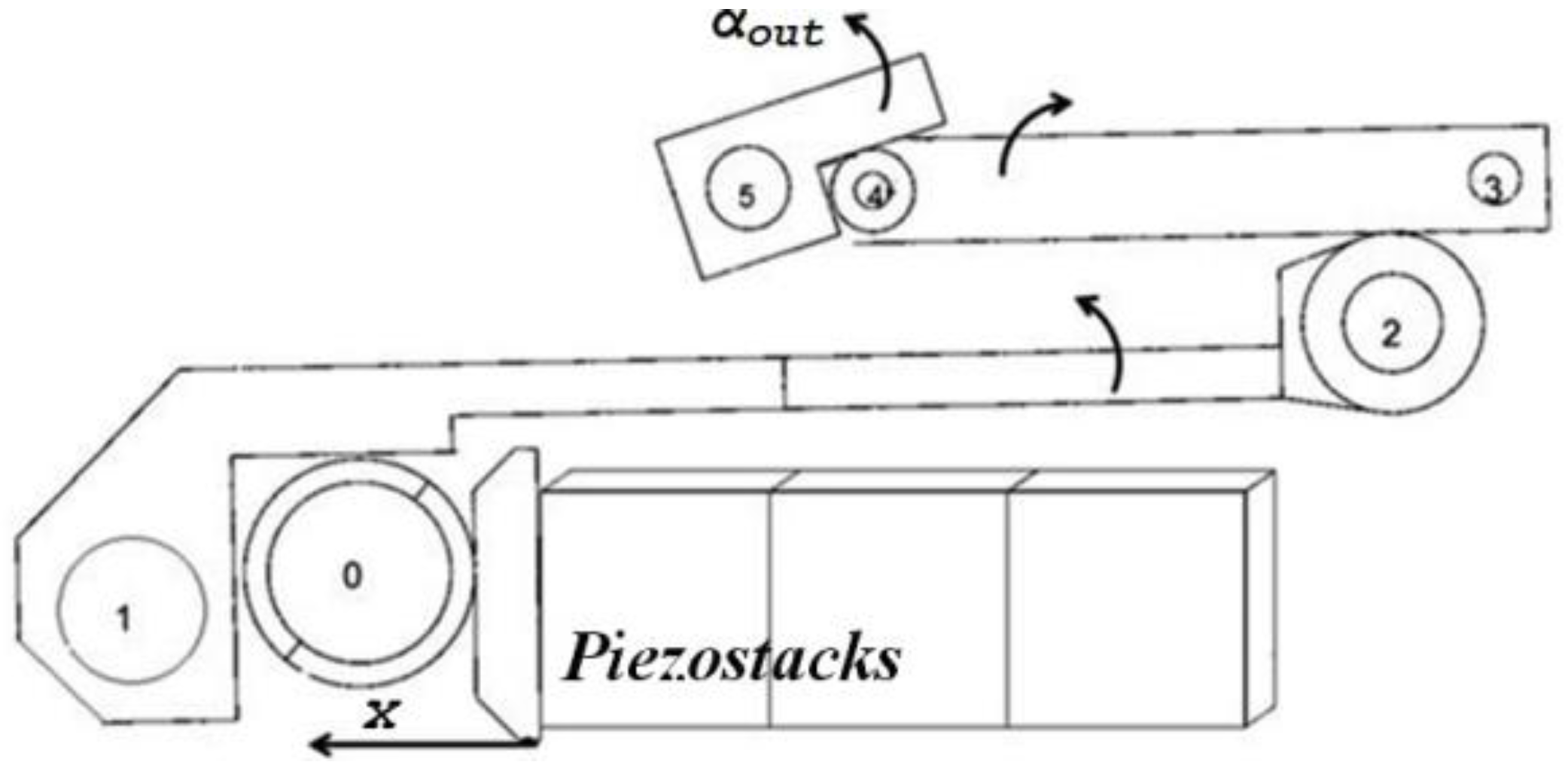
3.3. Amplification Mechanism
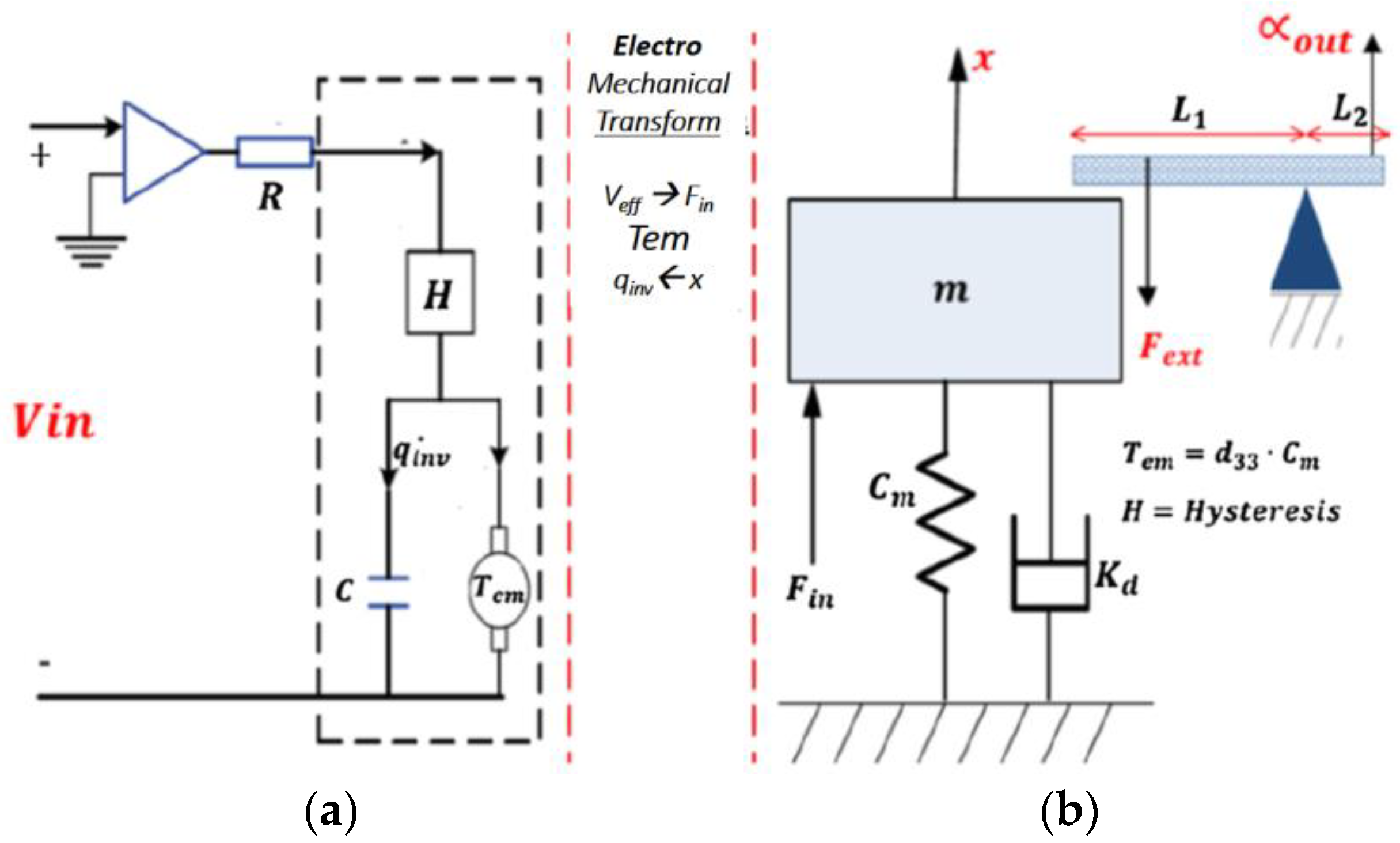
3.4. Electro-Mechanical Coupling
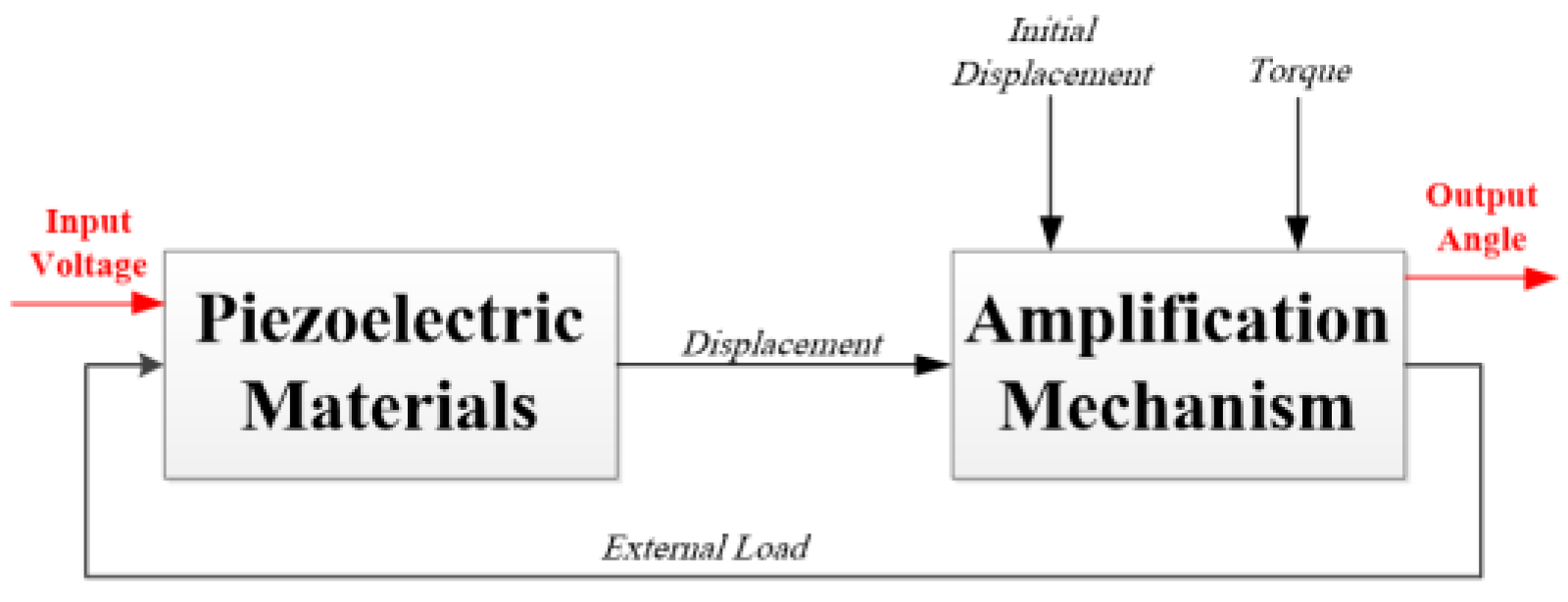
3.5. Combined System Model
4. System Identification Process Description
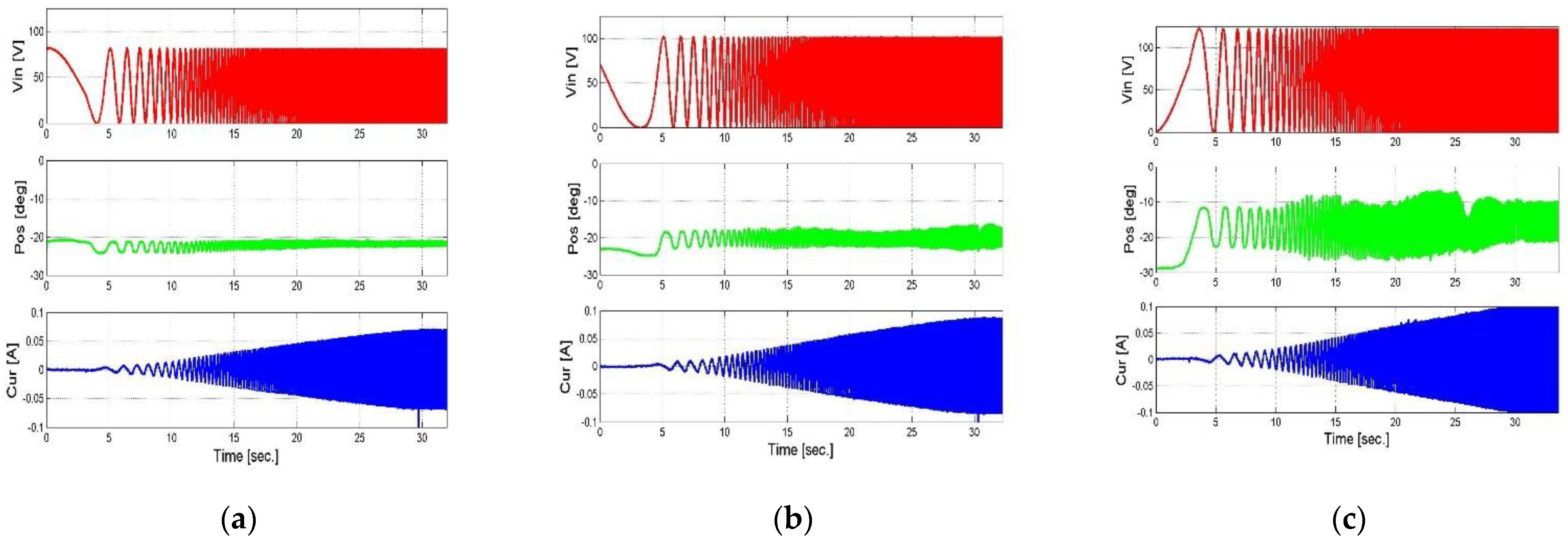
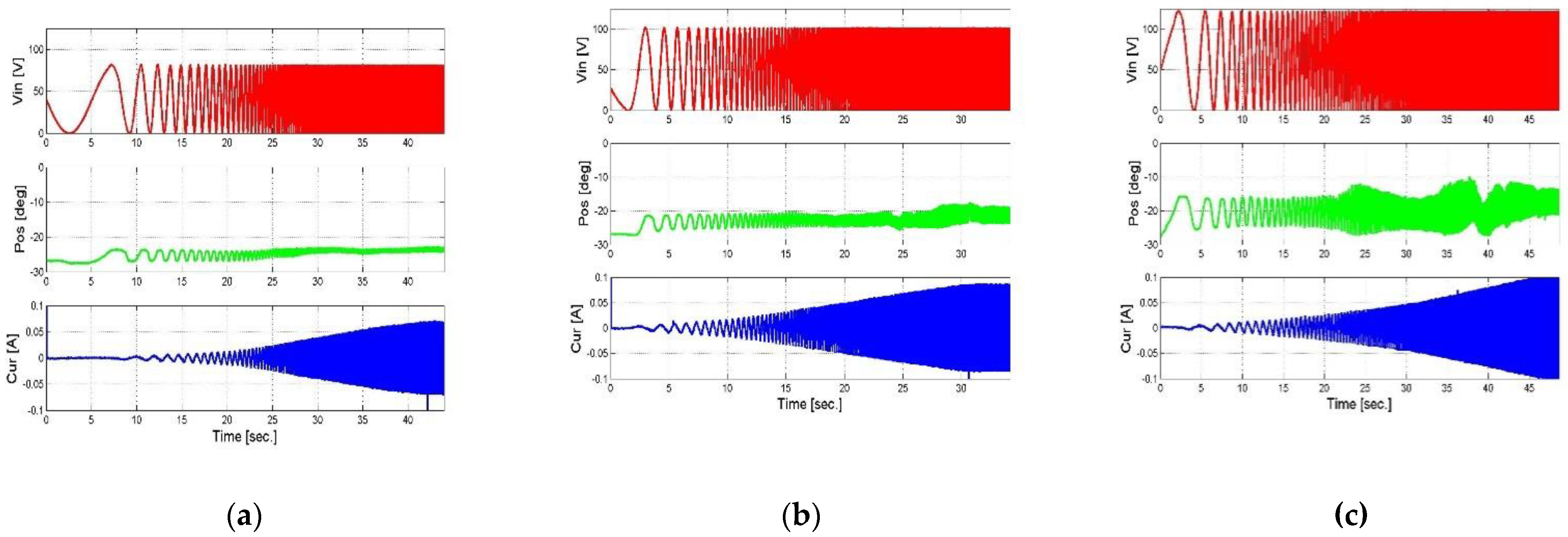
4.1. System Measurements
4.2. System Characterization
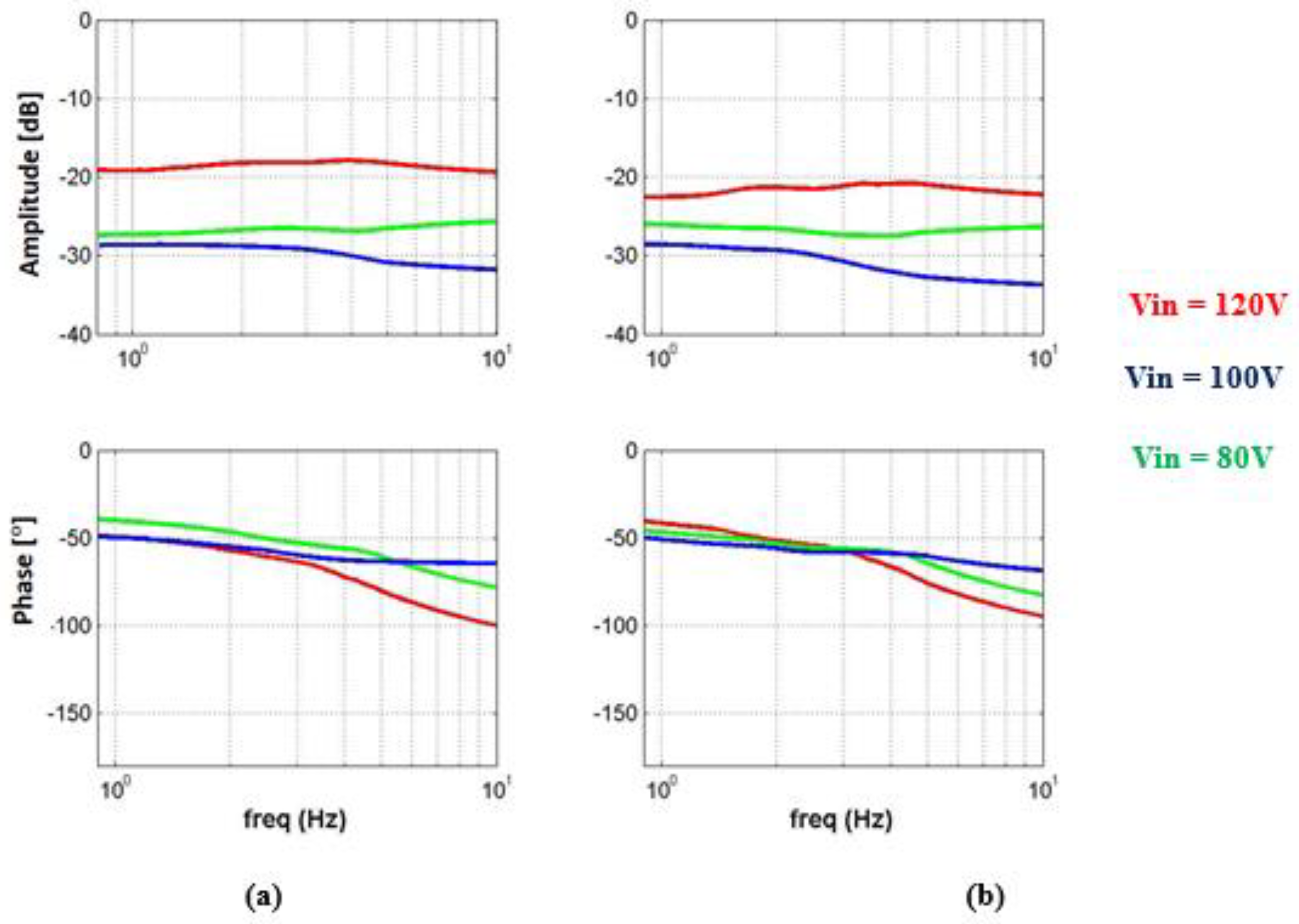
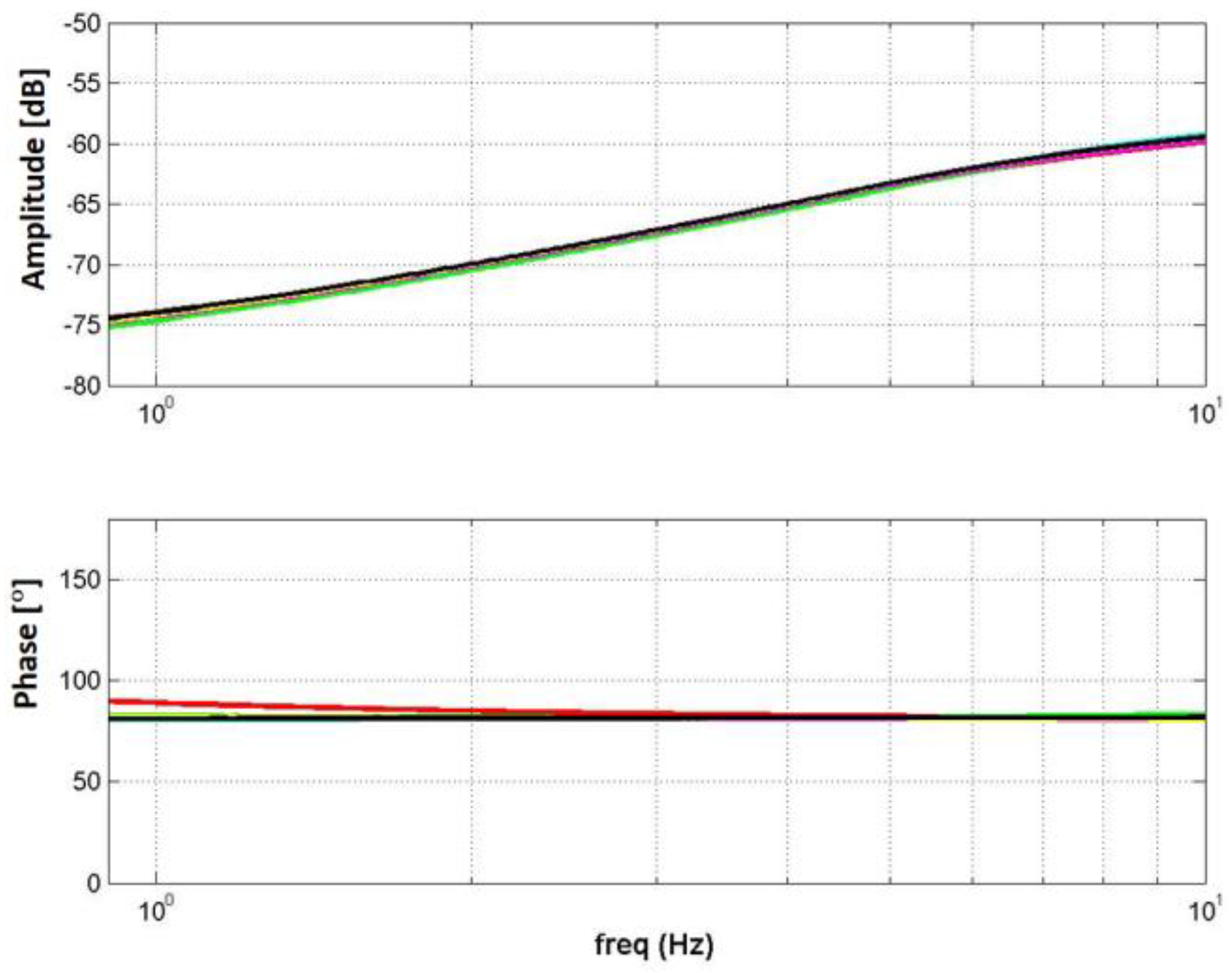
4.2.1. Evaluation of Transfer Function
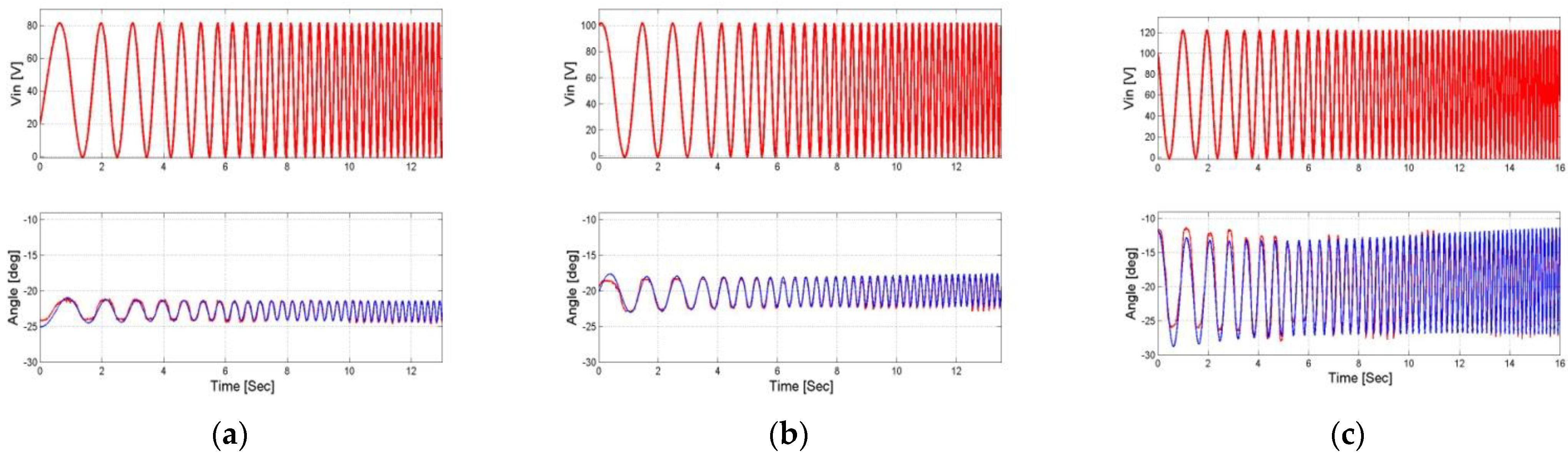
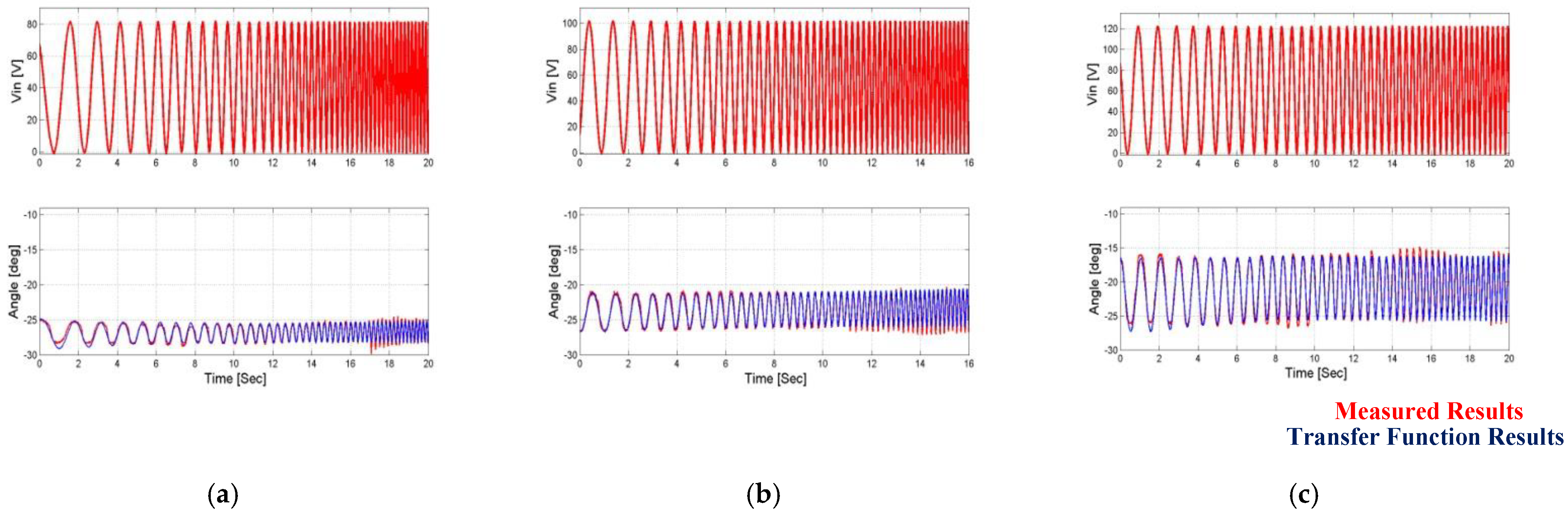
4.2.2. Position Feedback Transfer Function Adjustment
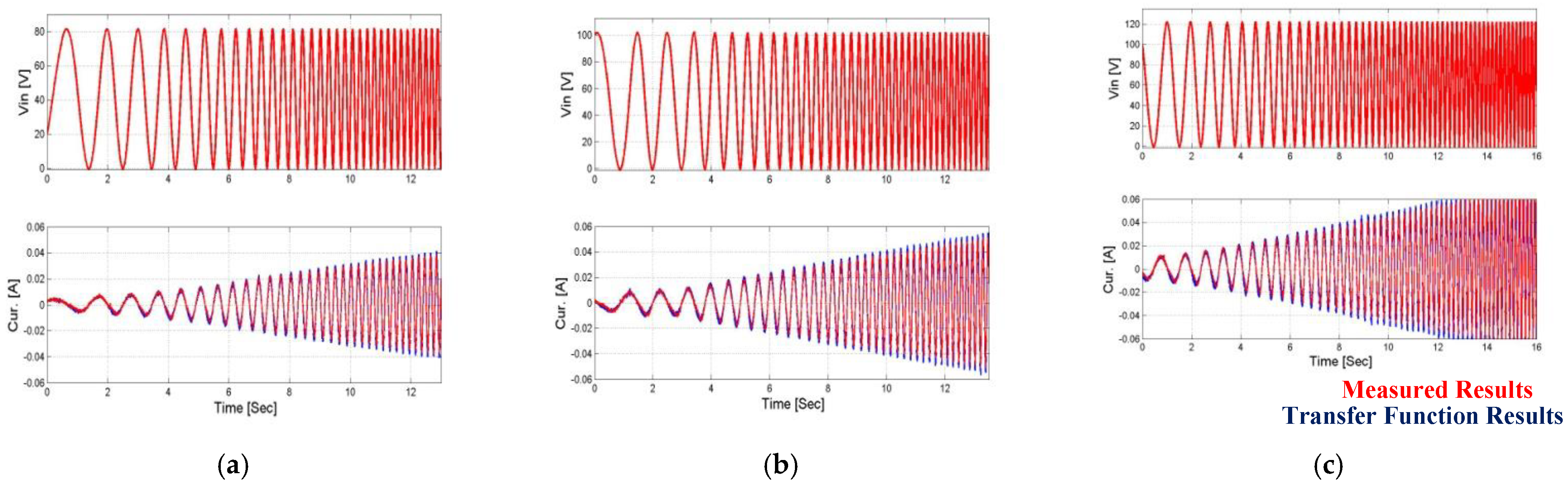
4.2.3. Current Feedback Transfer Function Adjustment
4.3. Model Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Preumont, A. Mechatronics Dynamics of Electromechanical and Piezoelectric Systems; Springer: Dordrecht, The Netherlands, 2006; pp. 95–130. [Google Scholar]
- Li, Y.; Xiao, S.; Xi, L.; Wu, Z. Design, Modeling, Control and Experiment for a 2-DOF Compliant Micro-Motion Stage. Int. J. Precis. Eng. Manuf. 2014, 15, 735–744. [Google Scholar] [CrossRef]
- Tian, X.; Liu, Y.; Deng, J.; Wang, L.; Chen, W. A review on piezoelectric ultrasonic motors for the past decade: Classification, operating principle, performance, and future work perspectives. Sens. Actuators A Phys. 2020, 306, 111971. [Google Scholar] [CrossRef]
- Wischnewski, M.; Delibas, B.; Wischnewski, A. Piezoelectric motor operated both in resonance and DC modes. In Proceedings of the ACTUATOR International Conference and Exhibition on New Actuator Systems and Applications, Online, 17–19 February 2021; pp. 1–4. [Google Scholar]
- Zhang, B.; Chen, F.; Li, H.; Du, Z.; Sun, L.; Dong, W. A friction-inertial-based rotary motor: Design, modelling and experiments. Materials. 2018, 11, 918. [Google Scholar] [CrossRef]
- Kim, C.; Shin, J.-W. Topology optimization of piezoelectric materials and application to the cantilever beams for vibration energy harvesting. Int. J. Precis. Eng. Manuf. 2013, 14, 1925–1931. [Google Scholar] [CrossRef]
- Kim, I.; Kim, Y.-S.; Park, E.-C. Sliding mode control of the inchworm displacement with hysteresis compensation. Int. J. Precis. Eng. Manuf. 2009, 10, 43–49. [Google Scholar] [CrossRef]
- Kim, M.S.; Park, Y.J.; Cho, K.J.; Ahn, S.H.; Chu, W.S.; Lee, K.T.; Song, S.H.; Han, M.W.; Lee, J.Y.; Kim, H.S. Review of Biomimetic Underwater Robots Using Smart Actuators. Int. J. Precis. Eng. Manuf. 2012, 13, 1281–1292. [Google Scholar]
- Ghemari, Z.; Saad, S.; Khettab, K. Improvement of the Vibratory Diagnostic Method by Evolution of the Piezoelectric Sensor Performances. Int. J. Precis. Eng. Manuf. 2019, 20, 1361–1369. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Design and testing of a new 3-DOF spatial flexure parallel micropositioning stage. Int. J. Precis. Eng. Manuf. 2018, 19, 109–118. [Google Scholar] [CrossRef]
- McCarty, R.; Mahmoodi, S.N. Dynamic mulitmode analysis of non-linear piezoelectric microcantilever probe in bistable region of tapping mode atomic force microscopy. Int. J. Non-Linear Mech. 2015, 74, 25–37. [Google Scholar] [CrossRef]
- Dong, W.; Chen, F.; Li, H.; Yang, M.; Du, Z. A two-dimensional nano-positioner: Design, modelling and experiments. Robot. Comput.-Integr. Manuf. 2017, 48, 167–173. [Google Scholar] [CrossRef]
- Guo, L.; Yan, W.; Xu, Y.; Chen, Y. Valveless Piezoelectric Micropump of Parallel Double Chambers. Int. J. Precis. Eng. Manuf. 2012, 13, 771–776. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, P.; Ouyang, G.; Zhou, J. Development of an Electromechanical Model for Piezo Actuated Common Rail Injectors. In Proceedings of the 2010 International Conference on Intelligent Computation Technology and Automation, Changsha, China, 11–12 May 2010; pp. 98–101. [Google Scholar] [CrossRef]
- Muir, E.R.; Liu, L.; Friedmann, P.P.; Kumar, D. Effect of Piezoelectric Actuator Hysteresis on Helicopter Vibration and Noise Reduction. J. Guid. Control. Dyn. 2012, 35, 1299–1311. [Google Scholar] [CrossRef]
- Zanoni, C.; Bortoluzzi, D. Experimental-Analytical Qualification of a Piezoelectric Mechanism for a Critical Space Application. IEEE/ASME Trans. Mechatron. 2015, 20, 427–437. [Google Scholar] [CrossRef]
- Kurniawan, R.; Ali, S.; Park, K.M.; Li, C.P.; Ko, T.J. Development of a Three-Dimensional Ultrasonic Elliptical Vibration Transducer (3D-UEVT) Based on Sandwiched Piezoelectric Actuator for Micro-grooving. Int. J. Precis. Eng. Manuf. 2019, 20, 1229–1240. [Google Scholar] [CrossRef]
- Kim, J.; Lee, H.; Kim, H.S. Beam vibration control using cellulose-based Electro-Active Paper sensor. Int. J. Precis. Eng. Manuf. 2010, 11, 823–827. [Google Scholar] [CrossRef]
- Yun, J.N.; Su, J.; Kim, Y.I.; Kim, Y.C. Robust Disturbance Observer for Two-Inertia System. IEEE Trans. Ind. Electron. 2012, 60, 2700–2710. [Google Scholar] [CrossRef]
- Kanno, I.; Kunisawa, T.; Suzuki, T.; Kotera, H. Development of Deformable Mirror Composed of Piezoelectric Thin Films for Adaptive Optics. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 155–161. [Google Scholar] [CrossRef]
- Niv, S.E.; Levy, D.A.; Oster, D. Integrated Model and Analysis of a Pneumatic Piezoelectric Actuator. In Proceedings of the 53th Israel Annual Conference on Aerospace Science, Haifa, Israel, 6–7 March 2013. [Google Scholar]
- Ben-Yaakov, S.; Lineykin, S. Maximum power tracking of piezoelectric transformer HV converters under load variations. IEEE Trans. Power Electron. 2006, 21, 73–78. [Google Scholar] [CrossRef]
- Lineykin, S.; Ben-Yaakov, S. Feedback isolation by piezoelectric transformers: Comparison of amplitude to frequency modulation. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; pp. 1834–1840. [Google Scholar] [CrossRef]
- Levy, D.A.; Shapiro, A. Model and Analysis of Piezoelectric Actuator in Practical Three-Stage Mechanism. Int. J. Precis. Eng. Manuf. 2020, 21, 1717–1728. [Google Scholar] [CrossRef]
- Zadeh, L.A. On the identification problem. IRE Trans. Circuit Theory 1956, 3, 277–281. [Google Scholar] [CrossRef]
- Klein, V.; Morelli, E.A. Aircraft System Identification: Theory and Practice; Williamsburg, VA: Sunflyte Enterprises, NY, USA, 2016. [Google Scholar] [CrossRef]
- Lai, Y.-C.; Ting, W.O. Design and Implementation of an Optimal Energy Control System for Fixed-Wing Unmanned Aerial Vehicles. Appl. Sci. 2016, 6, 369. [Google Scholar] [CrossRef]
- Naeem, W.; Sutton, R. Nonlinear modelling and control of an autonomous underwater vehicle. IFAC Proc. Vol. 2008, 41, 1–6. [Google Scholar] [CrossRef]
- Xiao, X.; Mullen, T.J.; Mukkamala, R. System identification: A multi-signal approach for probing neural cardiovascular regulation. Physiol. Meas. 2005, 26, R41–R71. [Google Scholar] [CrossRef] [PubMed]
- Ljung, L. System Identification Theory for the User, 2nd ed.; IEEE Prentice Hall: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Ghiaus, C.; Ghazal, R.; Joubert, P.; Hayyani, M.Y. Gray-box state-space model and parameter identification of desiccant wheels. Appl. Therm. Eng. 2013, 51, 742–752. [Google Scholar] [CrossRef]
- Cooper, J.E.; Wright, J.R. Spacecraft in orbit identification using eigensystem realization methods. J. Guid. Control. Dyn. 1992, 15, 352–359. [Google Scholar] [CrossRef]
- Maia, N.M.M.; Silva, J.M.M. Theoretical and Experimental Modal Analysis; Research Studies Press: London, UK, 1997. [Google Scholar]
- Spitznogle, F.R.; Quazi, A.H. Representation and analysis of time-limited signals using a complex exponential algorithm. J. Acoust. Soc. Am. 1970, 47, 1150–1155. [Google Scholar] [CrossRef]
- Allemang, R.J.; Brown, D.L. A correlation coefficient for modal vector analysis. In Proceedings of the First International Modal Analysis Conference, Orlando, FL, USA, 8–10 November 1982; pp. 110–116. [Google Scholar]
- Leuridan, J.M.; Brown, D.L.; Allemang, R.J. Time Domain Parameter Identification Methods for Linear Modal Analysis: A Unifying Approach. J. Vib. Acoust. 1986, 108, 1–8. [Google Scholar] [CrossRef]
- Van Overschee, P.; De Moor, B. N4SID: Subspace algorithms for the identification of combined deterministic-stochastic systems. Automatica 1994, 30, 75–93. [Google Scholar] [CrossRef]
- Cempel, C. Multidimensional Condition Monitoring of Mechanical Systems in Operation. Mech. Syst. Signal Process. 2003, 17, 1291–1303. [Google Scholar] [CrossRef]
- Ibrahim, S.R.; Mikulcik, E.C. A time domain modal vibration test technique. Shock. Vib. Bull. 1973, 43, 21–37. [Google Scholar]
- Ibrahim, S. Random Decrement Technique for Modal Identification of Structures. J. Spacecr. Rocket. 1977, 14, 696–700. [Google Scholar] [CrossRef]
- Lembregts, F.; Leuridan, J.; Van Brussel, H. Frequency Domain Direct Parameter Identification for Modal Analysis: State Space Formulation. Mech. Syst. Signal Process. 1990, 4, 65–75. [Google Scholar] [CrossRef]
- Ward, H.; Lammens, S.; Sas, P. Modal Analysis Theory and Testing; Faculty of Engineering, Department of Mechanical Engineering, Division of Production Engineering, Machine Design and Automation: Leuven, Belgium, 1998. [Google Scholar]
- Verboven, P. Frequency-Domain System Identifcation for Modal Analysis. Ph.D. Thesis, University of Brussels, Brussels, Belgium, 2002. [Google Scholar]
- Géradin, M.; Rixen, D.J. Mechanical Vibrations: Theory and Application to Structural Dynamics, 2nd ed.; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Guillaume, P.; Verboven, P.; Vanlanduit, S.; Van Der Auweraer, H.; Peeters, B. A poly-reference implementation of the least-squares complex frequency-domain estimator. In Proceedings of the 21st International Modal Analysis Conference (IMAC), Orlando, FL, USA; 2003; pp. 183–192. [Google Scholar]
- Cauberghe, B. Applied Frequency-Domain System Identification in the Field of Experimental and Operational Modal Analysis. Ph.D. Thesis, University of Brussels, Brussels, Belgium, 2004. [Google Scholar]
- Available online: https://www.mathworks.com/help/signal/ref/invfreqs.html (accessed on 1 September 2022).
- Kass, R.E.; Dennis, J.E.; Schnabel, R.B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations. J. Am. Stat. Assoc. 1985, 80, 247. [Google Scholar] [CrossRef]
- Available online: https://www.pi-usa.us/en/products/piezo-motors-stages-actuators/piezo-motion-control-tutorial/tutorial-4-16 (accessed on 1 September 2022).
- Designing with Piezoelectric Transducers: Nanopositioning Fundamentals-2005. Available online: www.pi.ws (accessed on 1 September 2022).
- Song, G.; Zhao, J.; Zhou, X.; De Abreu-Garcia, J. Tracking Control of a Piezoceramic Actuator with Hysteresis Compensation Using Inverse Preisach Model. IEEE/ASME Trans. Mechatronics 2005, 10, 198–209. [Google Scholar] [CrossRef]
- Kuhnen, K.; Krejci, P. Compensation of Complex Hysteresis and Creep Effects in Piezoelectrically Actuated Systems—A New Preisach Modeling Approach. IEEE Trans. Autom. Control. 2009, 54, 537–550. [Google Scholar] [CrossRef]
- Iyer, R.V.; Tan, X. Control of hysteretic systems through inverse compensation. IEEE Control Syst. 2009, 29, 83–99. [Google Scholar] [CrossRef]
- Nguyen, P.-B.; Choi, S.-B. Micro-position control of a piezostack actuator using rate-dependent hysteretic compensator. Int. J. Precis. Eng. Manuf. 2011, 12, 885–891. [Google Scholar] [CrossRef]
- Sivaselvan, M. Hysteretic models with stiffness and strength degradation in a mathematical programming format. Int. J. Non-linear Mech. 2013, 51, 10–27. [Google Scholar] [CrossRef]
- Villegas, F.; Hecker, R.L.; Peña, M. Two-state GMS-based friction model for precise control applications. Int. J. Precis. Eng. Manuf. 2016, 17, 553–564. [Google Scholar] [CrossRef]
- Kuhnen, K.; Janocha, H. Adaptive inverse control of piezoelectric actuators with hysteresis operators. In Proceedings of the 1999 European Control Conference (ECC), Karlsruhe, Germany, 31 August–3 September 1999; pp. 791–796. [Google Scholar] [CrossRef][Green Version]
- Dong, R.; Tan, Y. A modified Prandtl–Ishlinskii modeling method for hysteresis. Phys. B Condens. Matter 2009, 404, 1336–1342. [Google Scholar] [CrossRef]
- Jiang, H.; Ji, H.; Qiu, J.; Chen, Y. A modified prandtl-ishlinskii model for modeling asymmetric hysteresis of piezoelectric actuators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2010, 57, 1200–1210. [Google Scholar] [CrossRef] [PubMed]
- Ming, M.; Ling, J.; Feng, Z.; Xiao, X. A Model Prediction Control Design for Inverse Multiplicative Structure Based Feedforward Hysteresis Compensation of a Piezo Nanopositioning Stage. Int. J. Precis. Eng. Manuf. 2018, 19, 1699–1708. [Google Scholar] [CrossRef]
- Pickelmann, L. Low Voltage Co-Fired Multilayer Stacks, Rings and Chips for Actuation; Piezomechanik GmbH. Munich: Munich, Germany, 2004; p. 23. Available online: http://www.piezomechanik.com/en/products/ (accessed on 1 September 2022).
- Sun, L.; Ru, C.; Rong, W.; Chen, L.; Kong, M. Tracking control of piezoelectric actuator based on a new mathematical model. J. Micromech. Microeng. 2004, 14, 1439–1444. [Google Scholar] [CrossRef]
- Delibas, B.; Koc, B. Electromechanical Model for Bi-Phase Piezo Inertia Drives. In Proceedings of the Actuator 2022 International Conference and Exhibition on New Actuator Systems and Applications, Mannheim, Germany, 29–30 June 2022; pp. 1–4. [Google Scholar]
- Available online: https://www.piezomechanik.com/fileadmin/content_files/catalogs/piezomechanik-data-sheet.pdf (accessed on 1 September 2022).







| Name | Description | Units |
|---|---|---|
| Vin | Voltage developed on the piezostack electrodes | [Volt] |
| Vact | Total voltage in the PEM | [Volt] |
| Fact | Total force in the PEM | [Newton] |
| Fext | External force | [Newton] |
| v | PEM velocity | [meter/sec] |
| x | PEM displacement | [meter] |
| Name | Description | Units |
|---|---|---|
| d33 | Piezoelectric coefficient | [meter/Volt] or [Coulomb/Newton] |
| Cm | Mechanical stiffness | [Newton/meter] |
| m | Effective mass | [Kg] |
| Kd | Viscous friction | [Newton·sec/meter] |
| R | Actuator internal ohmic resistance | [Ohm] |
| C | Actuator capacitance | [F] |
| Descent Curve | Ascend Curve | ||||||
|---|---|---|---|---|---|---|---|
| Pdn1 | 1.7× 10−6 | Bdn1 | −17.67 × 10−3 | Pup1 | 42.36 × 10−6 | Bup1 | −23.55 × 10−3 |
| Pdn2 | 4.54 × 10−4 | Bdn2 | 2.1 | Pup2 | 3.65 × 10−3 | Bup2 | 2.41 |
| Pdn3 | 2.51 × 10−2 | Bdn3 | 0.53 | Pup3 | −53 × 10−3 | Bup3 | 1.72 |
| Pdn4 | 0.438 | Pup4 | 0.137 | ||||
| Pdn5 | 124.94 | ||||||
| Name | Description | Units |
|---|---|---|
| L1 | Arm of the first lever | mm |
| L2 | Arm of the second lever | mm |
| α34 | Angular movement of the second stage | deg |
| αout | Angular movement of the output stage | deg |
| Name | Description | Units |
|---|---|---|
| X12 | Distance between points 1 and 2 in a horizontal direction. | 60.43 |
| Y12 | Distance between points 1 and 2 in a vertical direction. | 13 |
| R12 | Distance between points 1 and 2. | 61.81 |
| Rb1 | Movement radius of the first lever. | 2 |
| X13 | Distance between points 1 and 3 in a horizontal direction. | 65.31 |
| Y13 | Distance between points 1 and 3 in a vertical direction. | 20.50 |
| Rb2 | Movement radius of the second lever. | 4.36 |
| R34 | Distance between points 3 and 4. | 30 |
| X35 | Distance between points 3 and 5 in a horizontal direction. | 36 |
| Y35 | Distance between points 3 and 5 in a vertical direction. | 0.044 |
| Rb3 | Radius of movement of the third lever. | 4.48 |
| (In this table, all the units are mm) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levy, D.A.; Shapiro, A. System Identification and Mathematical Modeling of A Piezoelectric Actuator through A Practical Three-Stage Mechanism. Micromachines 2023, 14, 88. https://doi.org/10.3390/mi14010088
Levy DA, Shapiro A. System Identification and Mathematical Modeling of A Piezoelectric Actuator through A Practical Three-Stage Mechanism. Micromachines. 2023; 14(1):88. https://doi.org/10.3390/mi14010088
Chicago/Turabian StyleLevy, Dror A., and Amir Shapiro. 2023. "System Identification and Mathematical Modeling of A Piezoelectric Actuator through A Practical Three-Stage Mechanism" Micromachines 14, no. 1: 88. https://doi.org/10.3390/mi14010088
APA StyleLevy, D. A., & Shapiro, A. (2023). System Identification and Mathematical Modeling of A Piezoelectric Actuator through A Practical Three-Stage Mechanism. Micromachines, 14(1), 88. https://doi.org/10.3390/mi14010088





