Darcy–Forchheimer Magnetized Nanofluid flow along with Heating and Dissipation Effects over a Shrinking Exponential Sheet with Stability Analysis
Abstract
1. Introduction
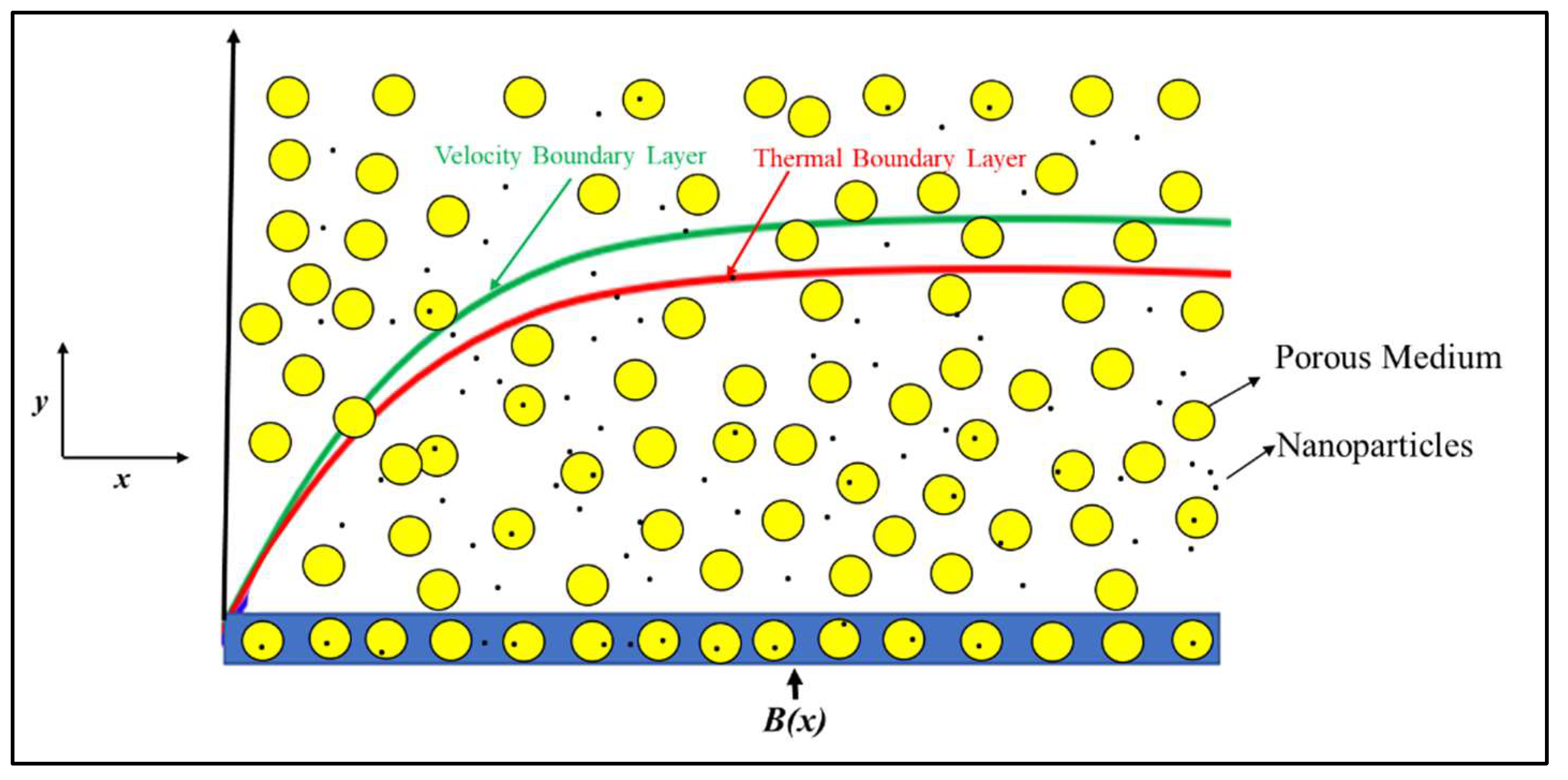
2. Mathematical Description of the Problem
3. Linear Stability Analysis
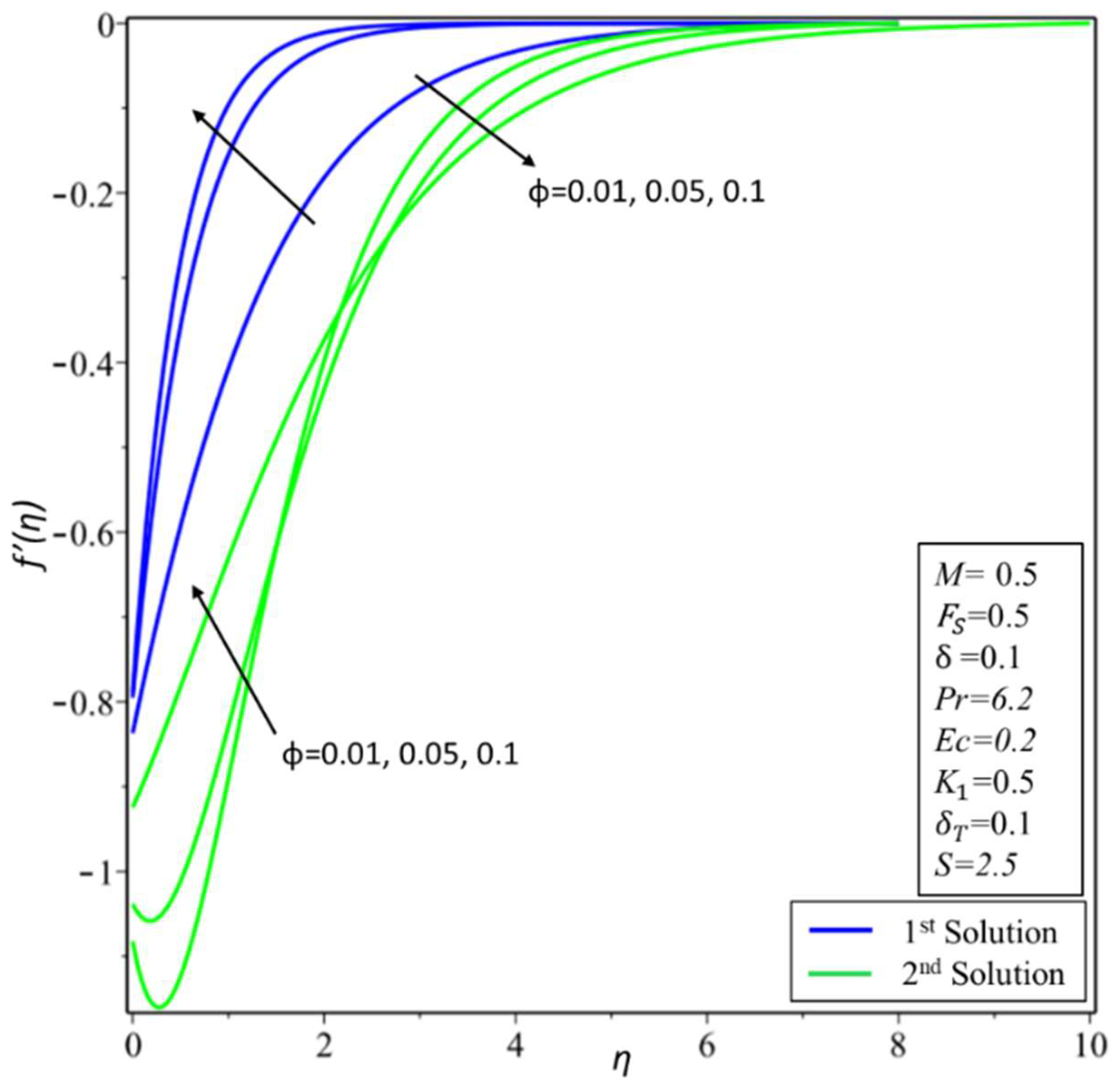
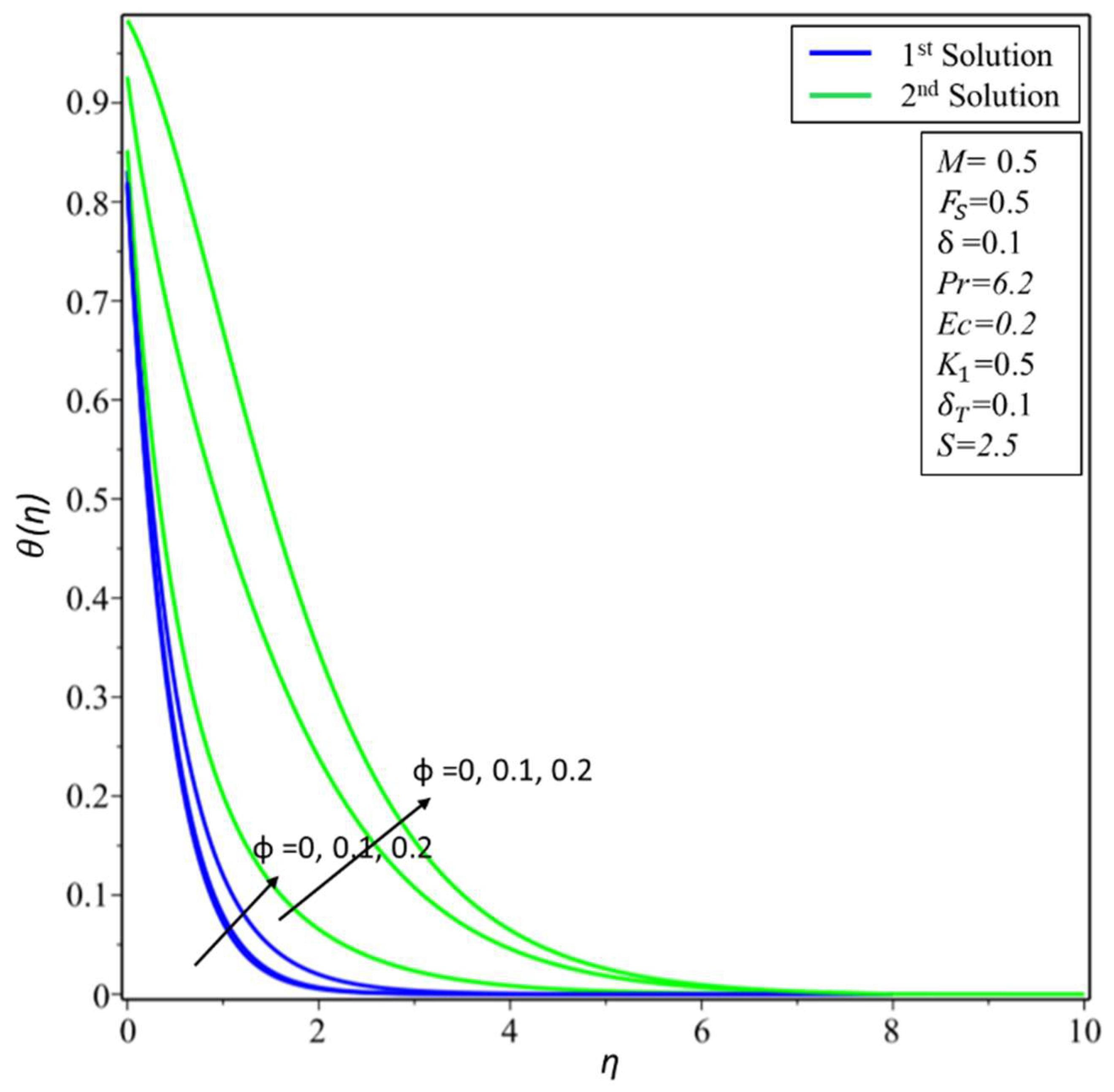
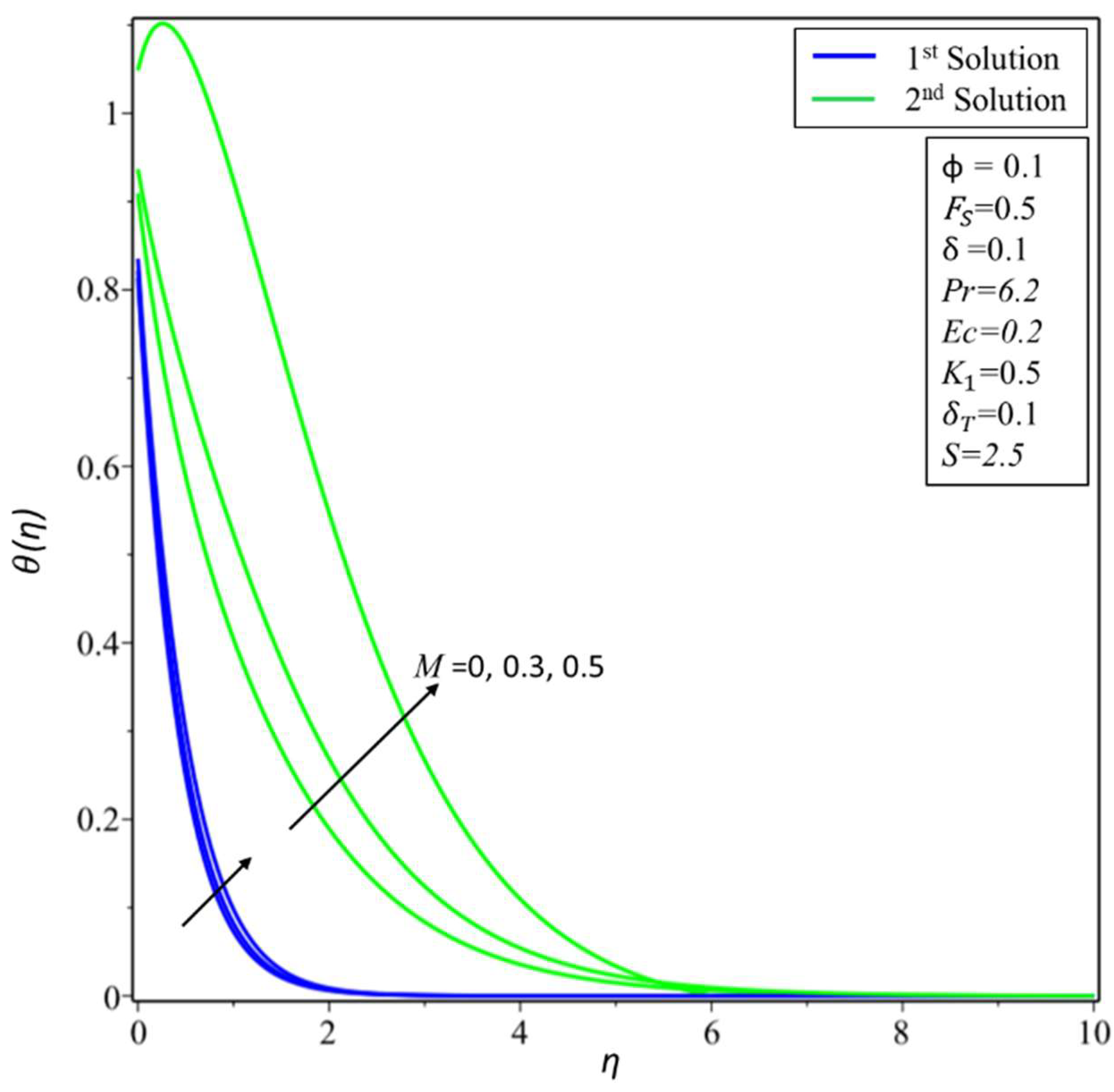
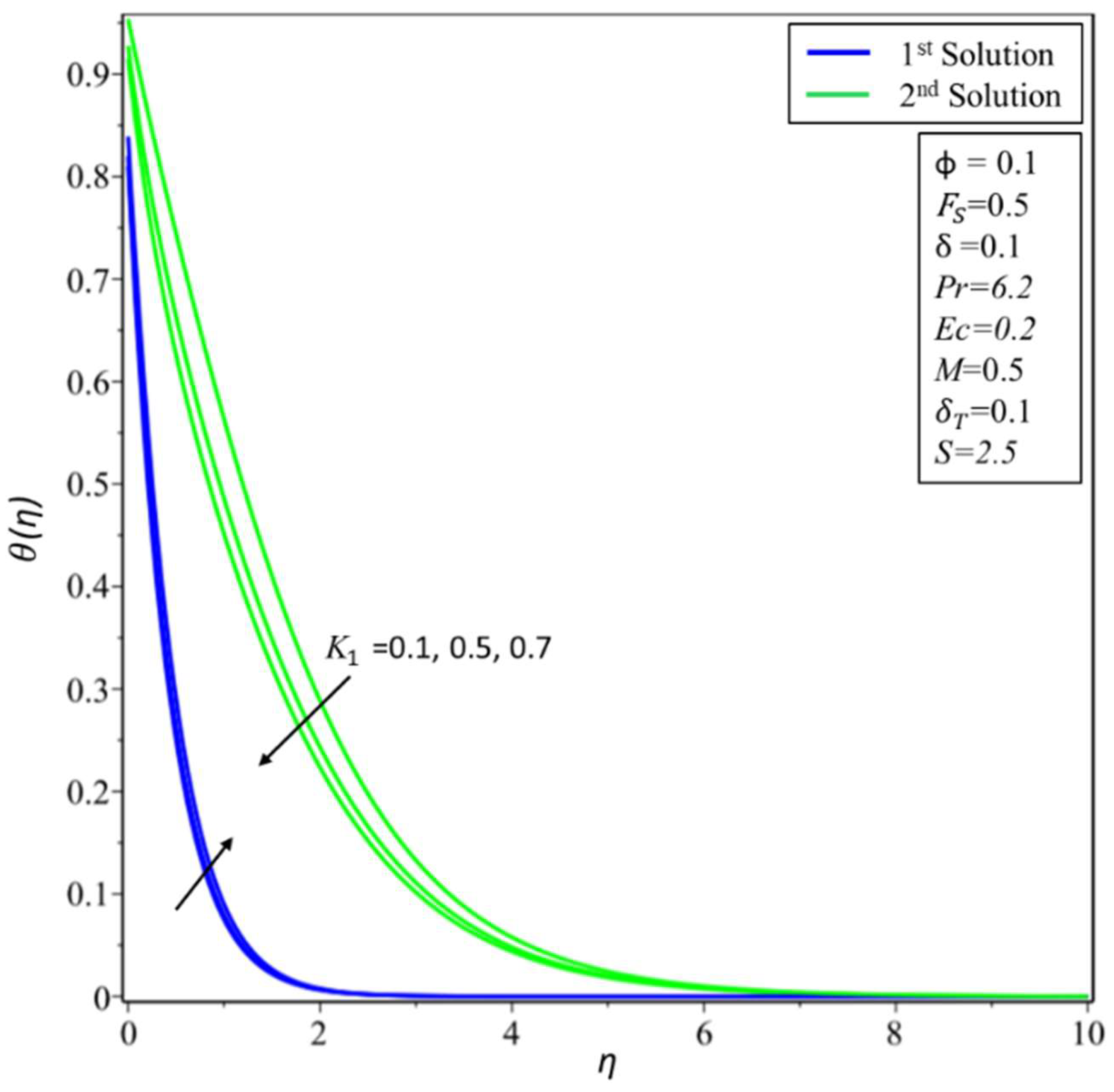
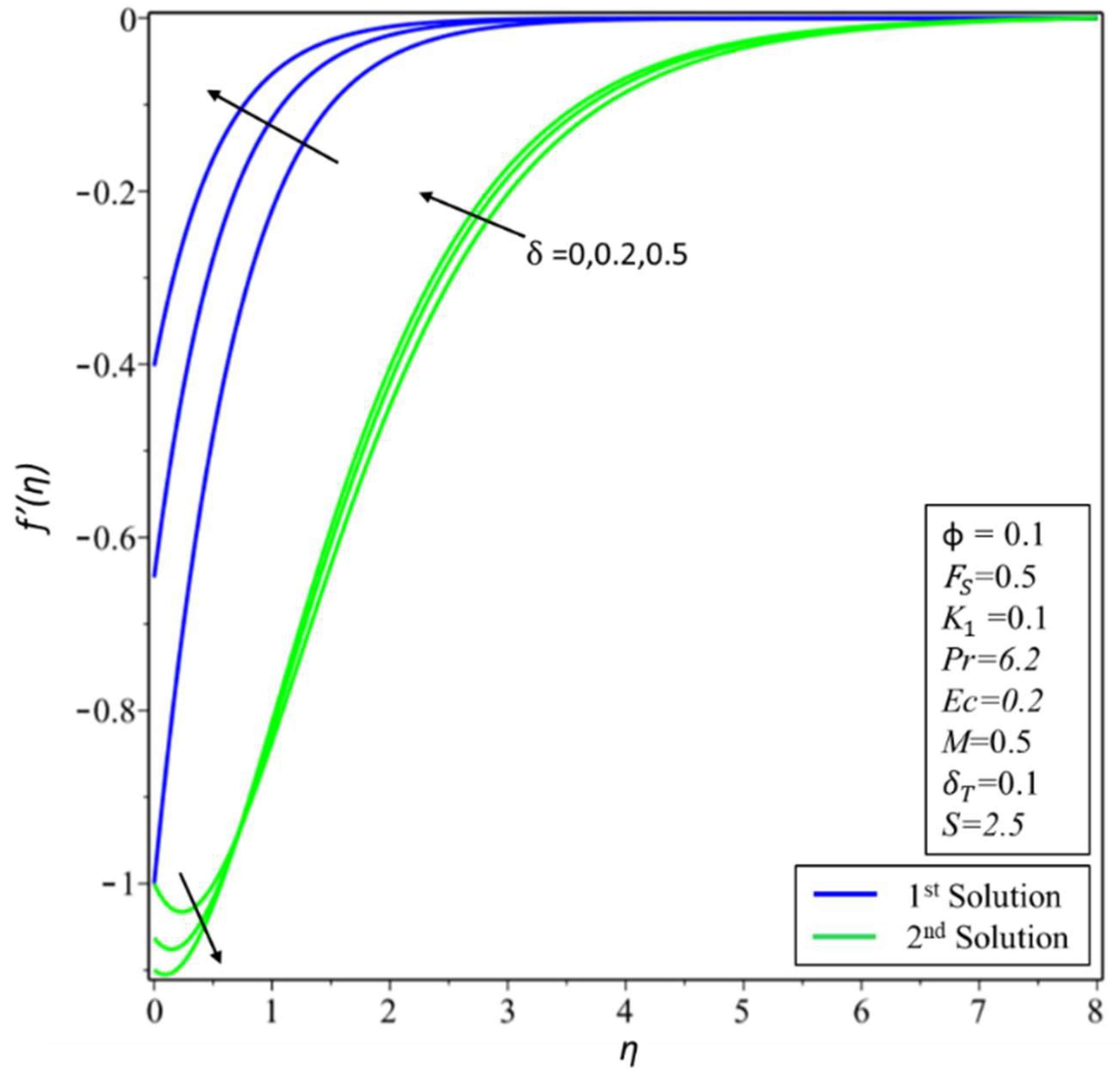
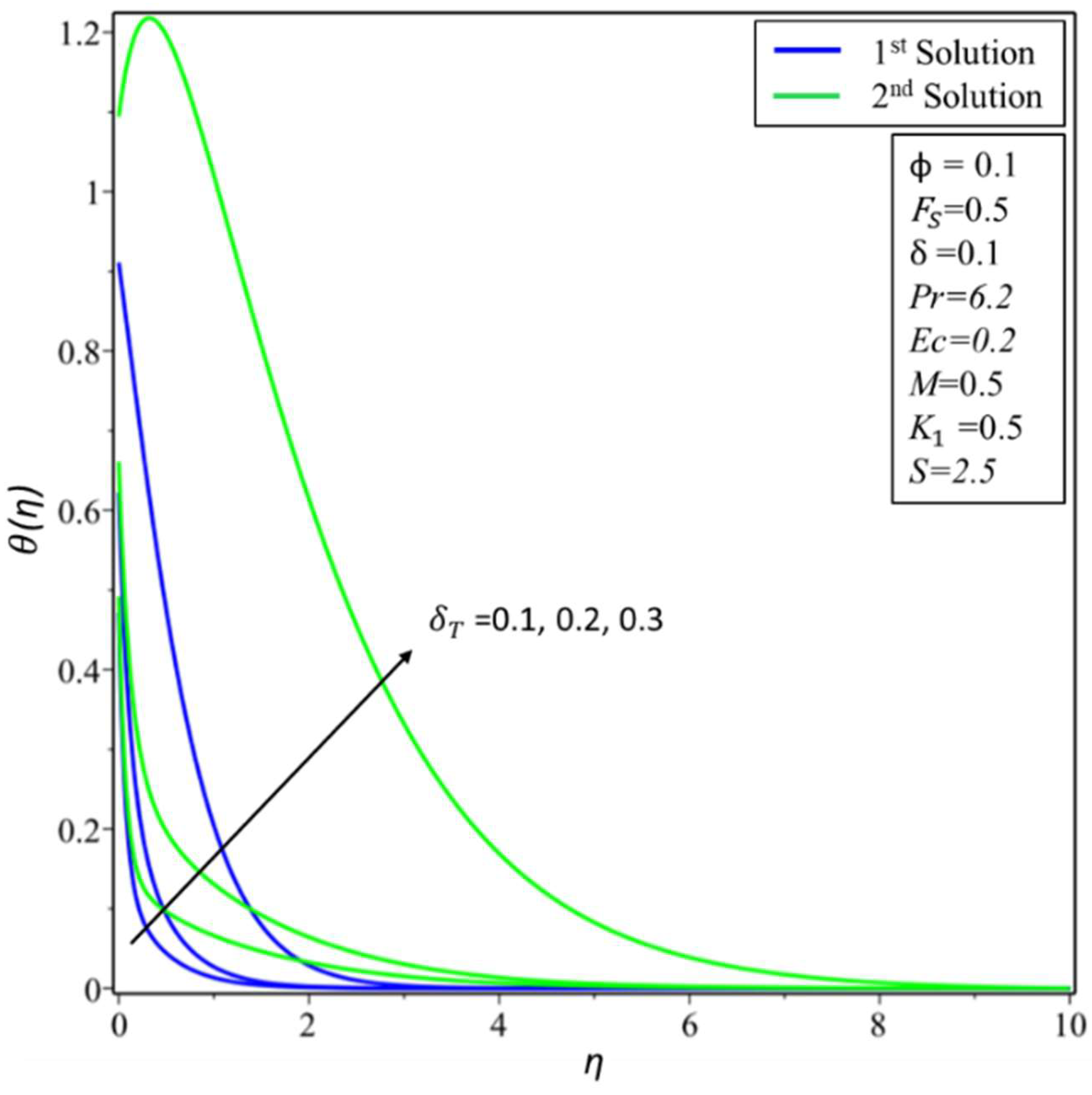
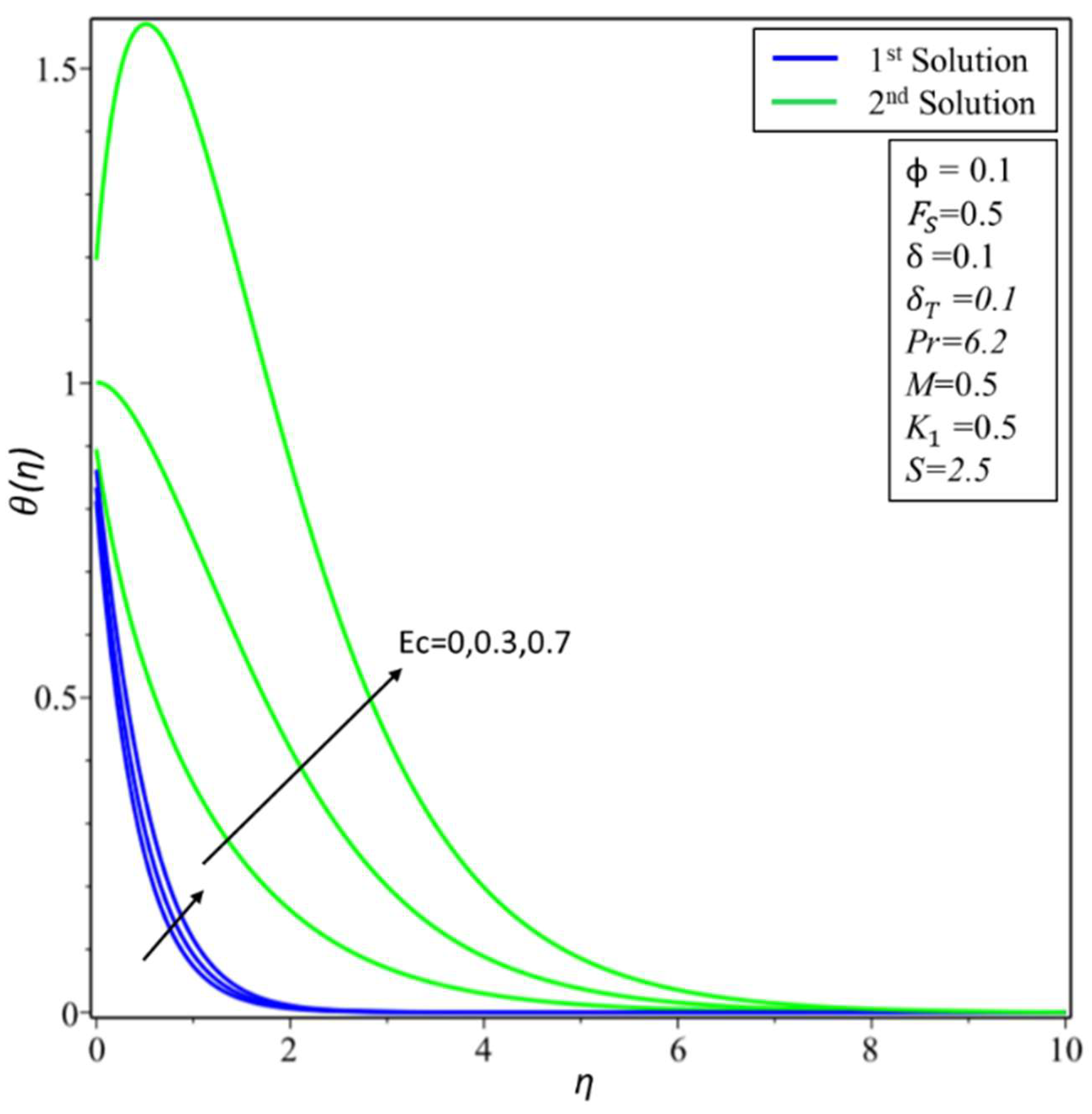
4. Result and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| FS | Forchheimmer parameter |
| K1 | permeability parameter |
| Nu | Nusselt number |
| lT∞ | ambient temperature (Kelvin) |
| Rex | Reynolds number |
| vw | suction/injection velocity (m/s) |
| δT | thermal slip |
| μnf | dynamic viscosity of nanofluid |
| ρnf | density of nanofluid(kg/m3) |
| ′ | differentiation with respect to η |
| M | Hartmann number |
| B(x) | magnetic field (Tesla) |
| Pr | Prandtl number |
| T | temperature (Kelvin) |
| S | suction/blowing parameter |
| K | permeability of the porous medium |
| u,v | velocity components (m/s) |
| ϕ | volume fraction of copper |
| ε | unknown eigenvalue |
| τ | stability transformed variable |
| Tw | variable temperature of sheet (Kelvin) |
| ε1 | smallest eigenvalue |
| T0 | a constant |
| uw | shrinking velocity of surface (m/s) |
| η | transformed variable |
| D | thermal slip factor |
| σ | electrical conductivity (S/m) |
| t | time (s) |
| B | velocity slip factor |
| ψ | stream function |
| δ | velocity slip |
| Cf | skin-friction coefficient |
| B0 | constant magnetic strength |
| b | local inertia coefficient |
| Ec | Eckert number |
| knf | nanofluid thermal conductivity (W/mK) |
References
- Muskat, M.; Meres, M.W. The flow of heterogeneous fluids through porous media. Physics 1936, 7, 346–363. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Hussain, S.; Zaydan, M.; Wakif, A.; Chamkha, A.J.; Bhutta, M.S. Significance of Rosseland’s radiative process on reactive Maxwell nanofluid flows over an isothermally heated stretching sheet in the presence of Darcy–Forchheimer and Lorentz forces: Towards a new perspective on Buongiorno’s model. Micromachines 2022, 13, 368. [Google Scholar] [CrossRef]
- Seddeek, M.A. Influence of viscous dissipation and thermophoresis on Darcy–Forchheimer mixed convection in a fluid saturated porous media. J. Colloid Interface Sci. 2006, 293, 137–142. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.F.; Zaib, A.; Ali, F.; Bafakeeh, O.T.; Tag-ElDin, E.S.M.; Guedri, K.; Elattar, S.; Khan, M.I. Numerical computation for gyrotactic microorganisms in MHD radiative Eyring–Powell nanomaterial flow by a static/moving wedge with Darcy–Forchheimer relation. Micromachines 2022, 13, 1768. [Google Scholar] [CrossRef]
- Pal, D.; Mondal, H. Hydromagnetic convective diffusion of species in Darcy–Forchheimer porous medium with non-uniform heat source/sink and variable viscosity. Int. Commun. Heat Mass Transf. 2012, 39, 913–917. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Thermal radiation effects on the time-dependent MHD permeable flow having variable viscosity. Int. J. Therm. Sci. 2011, 50, 88–96. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F. Free convection and radiation effects in nanofluid (Silicon dioxide and Molybdenum disulfide) with second order velocity slip, entropy generation, Darcy-Forchheimer porous medium. Int. J. Hydrogen Energy 2021, 46, 1362–1369. [Google Scholar] [CrossRef]
- Nagaraju, K.R.; Mahabaleshwar, U.S.; Krimpeni, A.A.; Sarris, I.E.; Lorenzini, G. Impact of mass transpiration on unsteady boundary layer flow of impulsive porous stretching. Math. Model. Eng. Probl. 2019, 6, 349–354. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab.(ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Hayat, T.; Shah, F.; Khan, M.I.; Alsaedi, A. Numerical simulation for aspects of homogeneous and heterogeneous reactions in forced convection flow of nanofluid. Results Phys. 2018, 8, 206–212. [Google Scholar] [CrossRef]
- Alotaibi, H.; Eid, M.R. Thermal analysis of 3D electromagnetic radiative nanofluid flow with suction/blowing: Darcy–Forchheimer scheme. Micromachines 2021, 12, 1395. [Google Scholar] [CrossRef]
- Qayyum, S.; Hayat, T.; Kanwal, M.; Alsaedi, A.; Khan, M.I. Transportation of entropy optimization in radiated chemically dissipative flow of Prandtl–Eyring nanofluid with activation energy. Comput. Methods Programs Biomed. 2020, 184, 105130. [Google Scholar] [CrossRef] [PubMed]
- Bang, I.C.; Chang, S.H. Boiling heat transfer performance and phenomena of Al2O3–water nano-fluids from a plain surface in a pool. Int. J. Heat Mass Transf. 2005, 48, 2407–2419. [Google Scholar] [CrossRef]
- Khan, U.; Ahmed, N.; Mohyud-Din, S.T.; Alsulami, M.D.; Khan, I. A novel analysis of heat transfer in the nanofluid composed by nanodimaond and silver nanomaterials: Numerical investigation. Sci. Rep. 2022, 12, 1284. [Google Scholar]
- Ravisha, M.; Alsulami, M.D.; Mamatha, A.L.; Shivakumara, I.S. Penetrative ferroconvection in a heterogeneous Brinkman porous medium. Int. J. Mod. Phys. B 2022, 37, 2350020. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Waini, I.; Zainal, N.A.; Hamzah, K.B.; Kasim, A.R.M.; Arifin, N.M.; Pop, I. Thermal Progress of Unsteady Separated Stagnation Point Flow with Magnetic Field and Heat Generation in Hybrid Ferrofluid. Nanomaterials 2022, 12, 3205. [Google Scholar] [CrossRef]
- Alzahrani, F.; Gowda, R.P.; Kumar, R.N.; Khan, M.I. Dynamics of thermosolutal Marangoni convection and nanoparticle aggregation effects on Oldroyd-B nanofluid past a porous boundary with homogeneous-heterogeneous catalytic reactions. J. Indian Chem. Soc. 2022, 99, 100458. [Google Scholar] [CrossRef]
- Rizwan, M.; Hassan, M.; Asjad, M.I.; Tag-ElDin, E.M. Flow Characteristics of Heat and Mass for Nanofluid under Different Operating Temperatures over Wedge and Plate. Micromachines 2022, 13, 2080. [Google Scholar] [CrossRef]
- Sneha, K.N.; Vanitha, G.P.; Mahabaleshwar, U.S.; Laroze, D. Effect of Couple Stress and Mass Transpiration on Ternary Hybrid Nanoliquid over a Stretching/Shrinking Sheet with Heat Transfer. Micromachines 2022, 13, 1694. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Effects of thermal radiation, viscous and Joule heating on electrical MHD nanofluid with double stratification. Chin. J. Phys. 2017, 55, 630–651. [Google Scholar] [CrossRef]
- Alrihieli, H.; Areshi, M.; Alali, E.; Megahed, A.M. MHD dissipative Williamson nanofluid flow with chemical reaction due to a slippery elastic sheet which was contained within a porous medium. Micromachines 2022, 13, 1879. [Google Scholar] [CrossRef]
- Kumaran, G.; Sandeep, N.; Ali, M.E. Computational analysis of magnetohydrodynamic Casson and Maxwell flows over a stretching sheet with cross diffusion. Results Phys. 2017, 7, 147–155. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Heat and mass transfer on the unsteady magnetohydrodynamic flow due to a porous rotating disk subject to a uniform outer radial flow. J. Heat Transf. 2010, 132, 061703. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. MHD fluid flow and heat transfer due to a stretching rotating disk. Int. J. Therm. Sci. 2012, 51, 195–201. [Google Scholar] [CrossRef]
- Waqas, M.; Farooq, M.; Khan, M.I.; Alsaedi, A.; Hayat, T.; Yasmeen, T. Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretched sheet with convective condition. Int. J. Heat Mass Transf. 2016, 102, 766–772. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, S.A.; Alsaedi, A. Irreversibility characterization in nanoliquid flow with velocity slip and dissipation by a stretchable cylinder. Alex. Eng. J. 2021, 60, 2835–2844. [Google Scholar] [CrossRef]
- Nayak, M.K.; Akbar, N.S.; Tripathi, D.; Pandey, V.S. Three dimensional MHD flow of nanofluid over an exponential porous stretching sheet with convective boundary conditions. Therm. Sci. Eng. Prog. 2017, 3, 133–140. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Heat generation/absorption effect on MHD flow of hybrid nanofluid over bidirectional exponential stretching/shrinking sheet. Chin. J. Phys. 2021, 69, 118–133. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Turkyilmazoglu, M.; Arifin, N.M.; Rosali, H. Analytical and stability analysis of MHD flow past a nonlinearly deforming vertical surface in Carbon Nanotubes. Alex. Eng. J. 2020, 59, 497–507. [Google Scholar] [CrossRef]
- Mabood, F.; Yusuf, T.A.; Sarris, I.E. Entropy generation and irreversibility analysis on free convective unsteady MHD Casson fluid flow over a stretching sheet with Soret/Dufour in porous media. Spec. Top. Rev. Porous Media Int. J. 2020, 11, 595–611. [Google Scholar] [CrossRef]
- Asogwa, K.K.; Alsulami, M.D.; Prasannakumara, B.C.; Muhammad, T. Double diffusive convection and cross diffusion effects on Casson fluid over a Lorentz force driven Riga plate in a porous medium with heat sink: An analytical approach. Int. Commun. Heat Mass Transf. 2022, 131, 105761. [Google Scholar] [CrossRef]
- Umavathi, J.C.; Prakasha, D.G.; Alanazi, Y.M.; Lashin, M.M.; Al-Mubaddel, F.S.; Kumar, R.; Punith Gowda, R.J. Magnetohydrodynamic squeezing Casson nanofluid flow between parallel convectively heated disks. Int. J. Mod. Phys. B 2022, 2350031. [Google Scholar] [CrossRef]
- Gangaiah, T.; Saidulu, N.; Lakshmi, A.V. Magnetohydrodynamic flow of nanofluid over an exponentially stretching sheet in presence of viscous dissipation and chemical reaction. J. Nanofluids 2018, 7, 439–448. [Google Scholar] [CrossRef]
- Sarada, K.; Gamaoun, F.; Abdulrahman, A.; Paramesh, S.O.; Kumar, R.; Prasanna, G.D.; Gowda, R.P. Impact of exponential form of internal heat generation on water-based ternary hybrid nanofluid flow by capitalizing non-Fourier heat flux model. Case Stud. Therm. Eng. 2022, 38, 102332. [Google Scholar]
- Jamil, M.; Khan, N.A. Slip effects on fractional viscoelastic fluids. Int. J. Differ. Equ. 2011, 2011, 193813. [Google Scholar] [CrossRef]
- Andersson, H.I. Slip flow past a stretching surface. Acta Mech. 2002, 158, 121–125. [Google Scholar] [CrossRef]
- Wang, F.; Ahmad, S.; Al Mdallal, Q.; Alammari, M.; Khan, M.N.; Rehman, A. Natural bio-convective flow of Maxwell nanofluid over an exponentially stretching surface with slip effect and convective boundary condition. Sci. Rep. 2022, 12, 2220. [Google Scholar] [CrossRef] [PubMed]
- Saleem, S.; Abd El-Aziz, M. Entropy generation and convective heat transfer of radiated non-Newtonian power-law fluid past an exponentially moving surface under slip effects. Eur. Phys. J. Plus 2019, 134, 184. [Google Scholar] [CrossRef]
- Haider, S.; Saeed Butt, A.; Li, Y.Z.; Imran, S.M.; Ahmad, B.; Tayyaba, A. Study of entropy generation with multi-slip effects in MHD unsteady flow of viscous fluid past an exponentially stretching surface. Symmetry 2020, 12, 426. [Google Scholar] [CrossRef]
- Imran, M.A.; Riaz, M.B.; Shah, N.A.; Zafar, A.A. Boundary layer flow of MHD generalized Maxwell fluid over an exponentially accelerated infinite vertical surface with slip and Newtonian heating at the boundary. Results Phys. 2018, 8, 1061–1067. [Google Scholar] [CrossRef]
- Reddy, J.R.; Sugunamma, V.; Sandeep, N. Thermophoresis and Brownian motion effects on unsteady MHD nanofluid flow over a slendering stretching surface with slip effects. Alex. Eng. J. 2018, 57, 2465–2473. [Google Scholar] [CrossRef]
- Reddy, M.G.; Reddy, K.V. Influence of Joule heating on MHD peristaltic flow of a nanofluid with compliant walls. Procedia Eng. 2015, 127, 1002–1009. [Google Scholar] [CrossRef]
- Maskeen, M.M.; Zeeshan, A.; Mehmood, O.U.; Hassan, M. Heat transfer enhancement in hydromagnetic alumina–copper/water hybrid nanofluid flow over a stretching cylinder. J. Therm. Anal. Calorim. 2019, 138, 1127–1136. [Google Scholar] [CrossRef]
- Sajid, M.; Iqbal, S.A.; Naveed, M.; Abbas, Z. Joule heating and magnetohydrodynamic effects on ferrofluid (Fe3O4) flow in a semi-porous curved channel. J. Mol. Liq. 2016, 222, 1115–1120. [Google Scholar] [CrossRef]
- Patel, H.R.; Singh, R. Thermophoresis, Brownian motion and non-linear thermal radiation effects on mixed convection MHD micropolar fluid flow due to nonlinear stretched sheet in porous medium with viscous dissipation, joule heating and convective boundary condition. Int. Commun. Heat Mass Transf. 2019, 107, 68–92. [Google Scholar] [CrossRef]
- Kamran, A.; Hussain, S.; Sagheer, M.; Akmal, N. A numerical study of magnetohydrodynamics flow in Casson nanofluid combined with Joule heating and slip boundary conditions. Results Phys. 2017, 7, 3037–3048. [Google Scholar] [CrossRef]
- Gholinia, M.; Hoseini, M.E.; Gholinia, S. A numerical investigation of free convection MHD flow of Walters-B nanofluid over an inclined stretching sheet under the impact of Joule heating. Therm. Sci. Eng. Prog. 2019, 11, 272–282. [Google Scholar] [CrossRef]
- Khan, M.I.; Qayyum, S.; Hayat, T.; Khan, M.I.; Alsaedi, A. Entropy optimization in flow of Williamson nanofluid in the presence of chemical reaction and Joule heating. Int. J. Heat Mass Transf. 2019, 133, 959–967. [Google Scholar] [CrossRef]
- Khan, I.; Malik, M.Y.; Hussain, A.; Khan, M. Magnetohydrodynamics Carreau nanofluid flow over an inclined convective heated stretching cylinder with Joule heating. Results Phys. 2017, 7, 4001–4012. [Google Scholar] [CrossRef]
- Hussain, A.; Malik, M.Y.; Salahuddin, T.; Bilal, S.; Awais, M. Combined effects of viscous dissipation and Joule heating on MHD Sisko nanofluid over a stretching cylinder. J. Mol. Liq. 2017, 231, 341–352. [Google Scholar] [CrossRef]
- Yan, L.; Dero, S.; Khan, I.; Mari, I.A.; Baleanu, D.; Nisar, K.S.; Sherif, E.-S.M.; Abdo, H.S. Dual solutions and stability analysis of magnetized hybrid nanofluid with joule heating and multiple slip conditions. Processes 2020, 8, 332. [Google Scholar] [CrossRef]
- Khan, Z.; Rasheed, H.U.; Abbas, T.; Khan, W.; Khan, I.; Baleanu, D.; Sooppy Nisar, K. Analysis of Eyring–Powell fluid flow used as a coating material for wire with variable viscosity effect along with thermal radiation and joule heating. Crystals 2020, 10, 168. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Mixed convection flow over an exponentially stretching/shrinking vertical surface in a hybrid nanofluid. Alex. Eng. J. 2020, 59, 1881–1891. [Google Scholar] [CrossRef]



| Properties | Nanofluid |
|---|---|
| Dynamic viscosity | |
| Density | , where subscript s indicates the solid properties of the copper. |
| Thermal conductivity | |
| Heat capacity |
| Material | ρ/(kg·m−1) | Cp/(J·kg−1·m−1) | k/(W·m−1·K−1) |
|---|---|---|---|
| Copper | 8933 | 385 | 401 |
| Water | 997.1 | 4179 | 0.613 |
| Waini et al. [56] | Current Results | |||
|---|---|---|---|---|
| S | f″(0) | −θ(0) | f″(0) | −θ(0) |
| 0 | −1.28181 | 4.97911 | −1.28181 | 4.97911 |
| 0.2 | −1.37889 | 5.65473 | −1.37889 | 5.65473 |
| 0.6 | −1.59824 | 7.22487 | −1.59824 | 7.22487 |
| 1 | −1.84983 | 9.03715 | −1.84983 | 9.03715 |
| 1st Solution | 2nd Solution | ||
|---|---|---|---|
| S | ε1 | ||
| 2.5 | 0.01 | 0.78456 | −0.94592 |
| 0.1 | 0.64948 | −0.89248 | |
| 3 | 0.05 | 0.85310 | −0.894601 |
| 0.1 | 0.68092 | −0.87253 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lund, L.A.; Chandio, A.F.; Vrinceanu, N.; Yashkun, U.; Shah, Z.; Alshehri, A. Darcy–Forchheimer Magnetized Nanofluid flow along with Heating and Dissipation Effects over a Shrinking Exponential Sheet with Stability Analysis. Micromachines 2023, 14, 106. https://doi.org/10.3390/mi14010106
Lund LA, Chandio AF, Vrinceanu N, Yashkun U, Shah Z, Alshehri A. Darcy–Forchheimer Magnetized Nanofluid flow along with Heating and Dissipation Effects over a Shrinking Exponential Sheet with Stability Analysis. Micromachines. 2023; 14(1):106. https://doi.org/10.3390/mi14010106
Chicago/Turabian StyleLund, Liaquat Ali, Abdul Fattah Chandio, Narcisa Vrinceanu, Ubaidullah Yashkun, Zahir Shah, and Ahmed Alshehri. 2023. "Darcy–Forchheimer Magnetized Nanofluid flow along with Heating and Dissipation Effects over a Shrinking Exponential Sheet with Stability Analysis" Micromachines 14, no. 1: 106. https://doi.org/10.3390/mi14010106
APA StyleLund, L. A., Chandio, A. F., Vrinceanu, N., Yashkun, U., Shah, Z., & Alshehri, A. (2023). Darcy–Forchheimer Magnetized Nanofluid flow along with Heating and Dissipation Effects over a Shrinking Exponential Sheet with Stability Analysis. Micromachines, 14(1), 106. https://doi.org/10.3390/mi14010106









