A Novel Approach for Measurement of Free-Form Optical Elements with Digital Holographic Microscopy
Abstract
1. Introduction
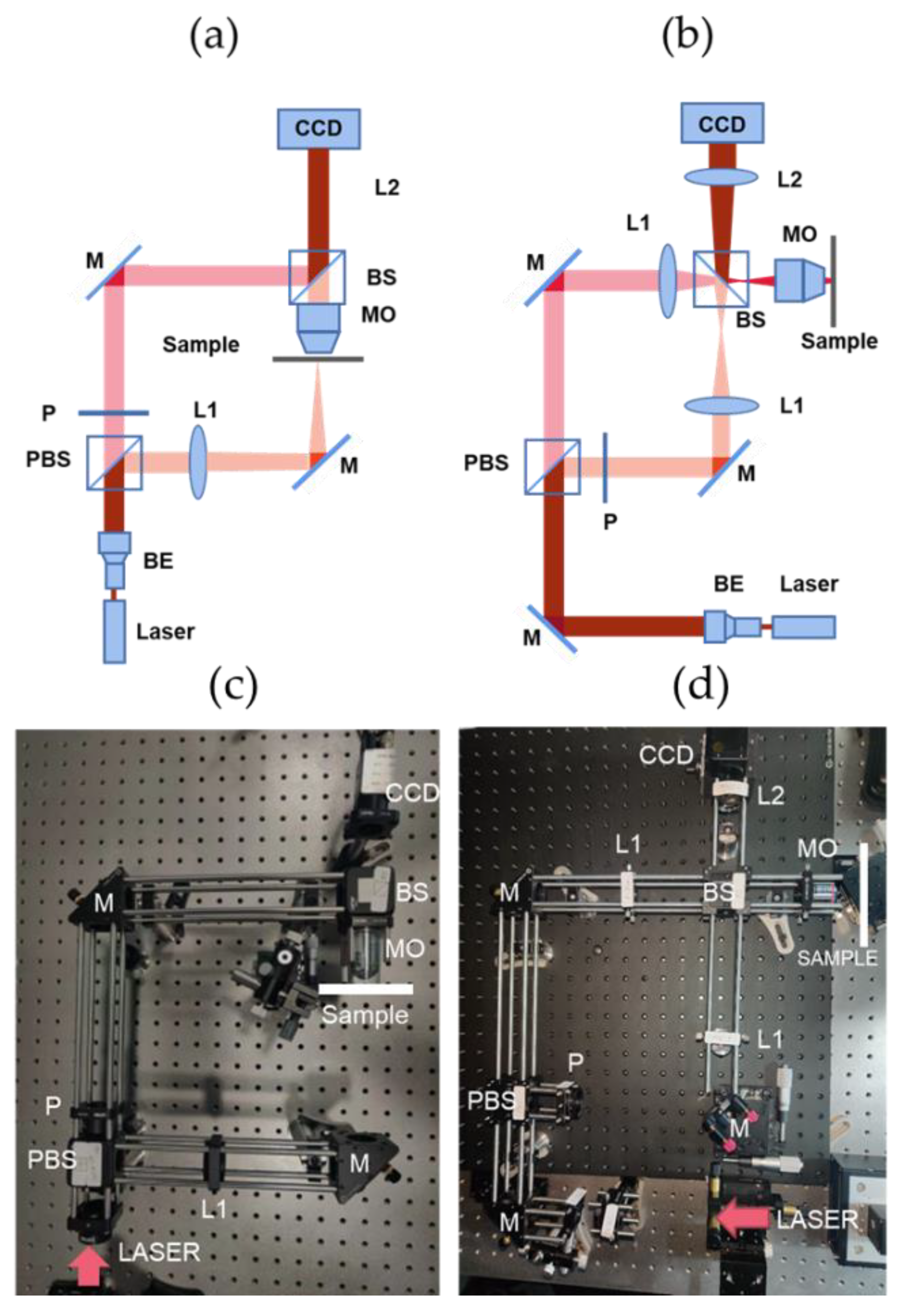
2. Materials and Methods
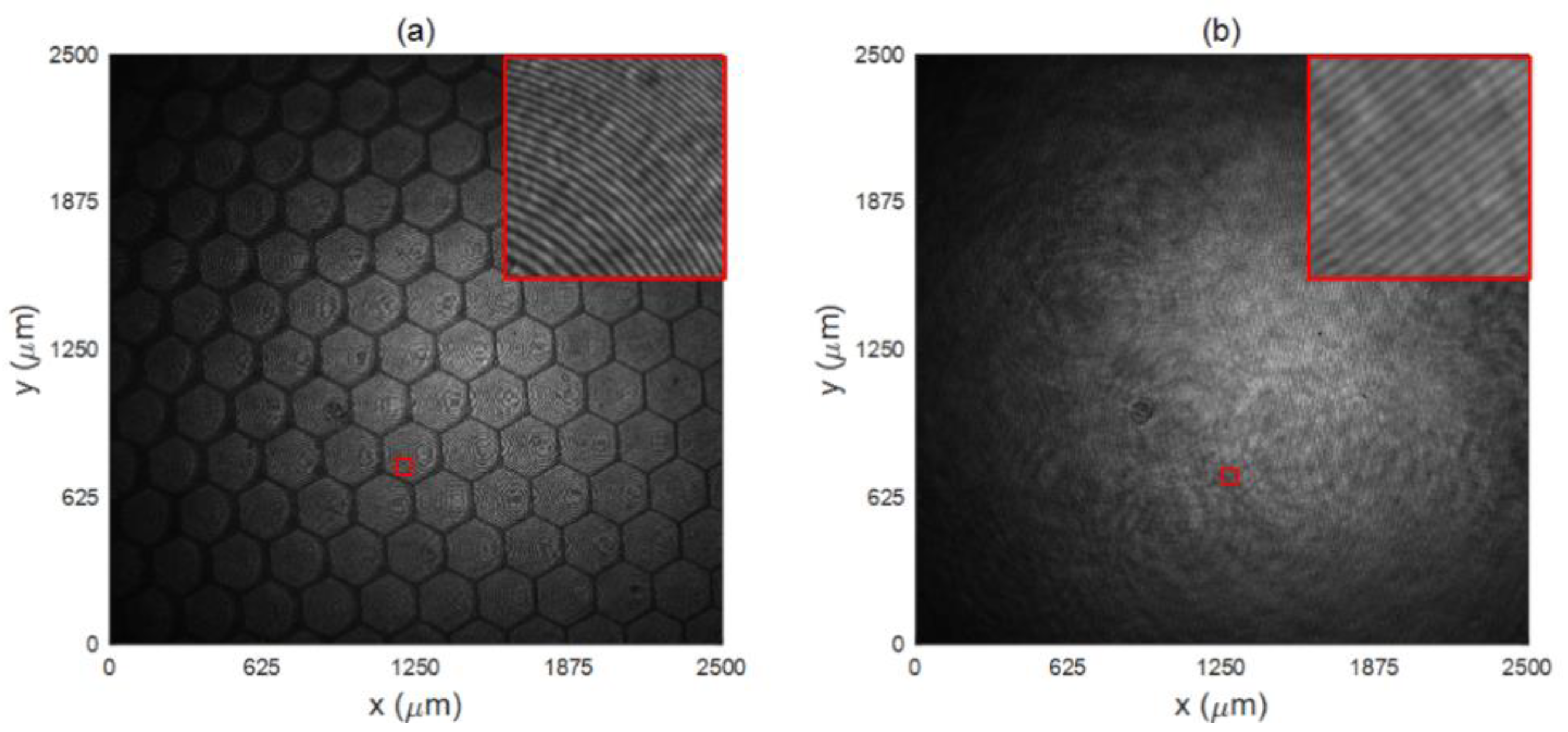
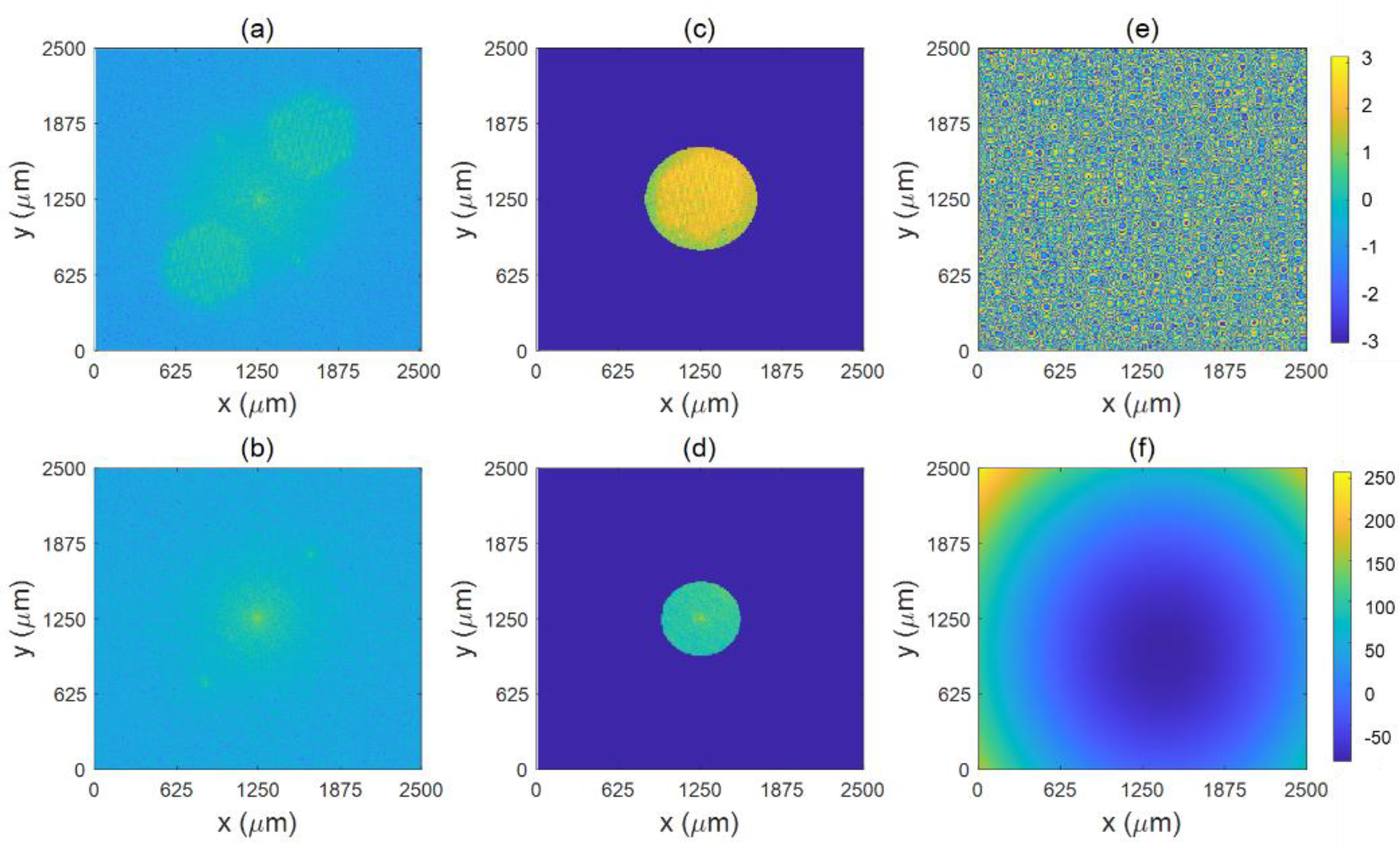
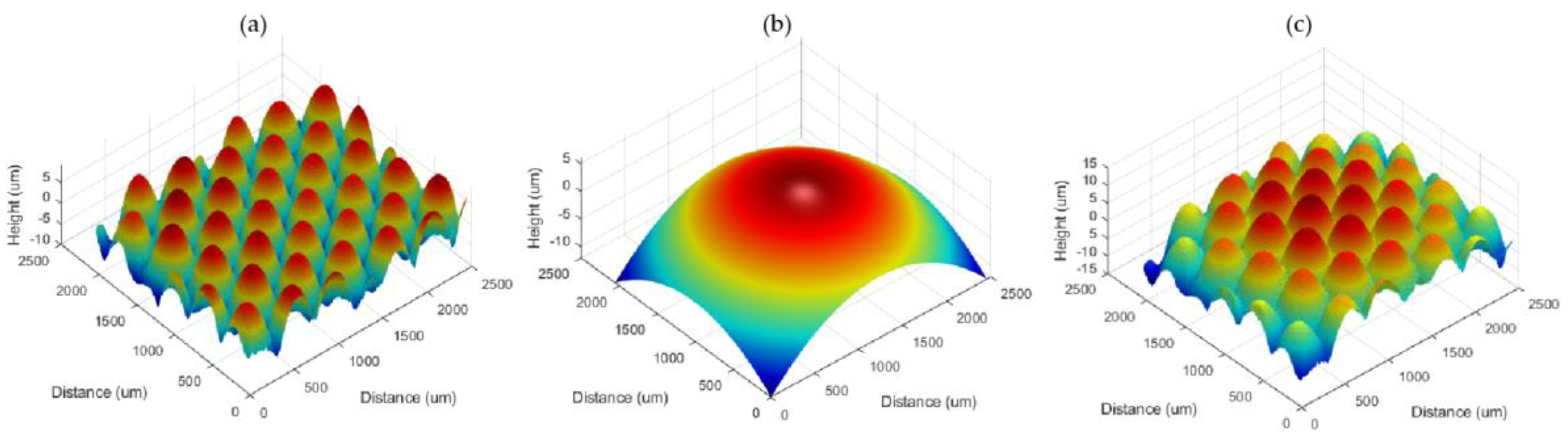
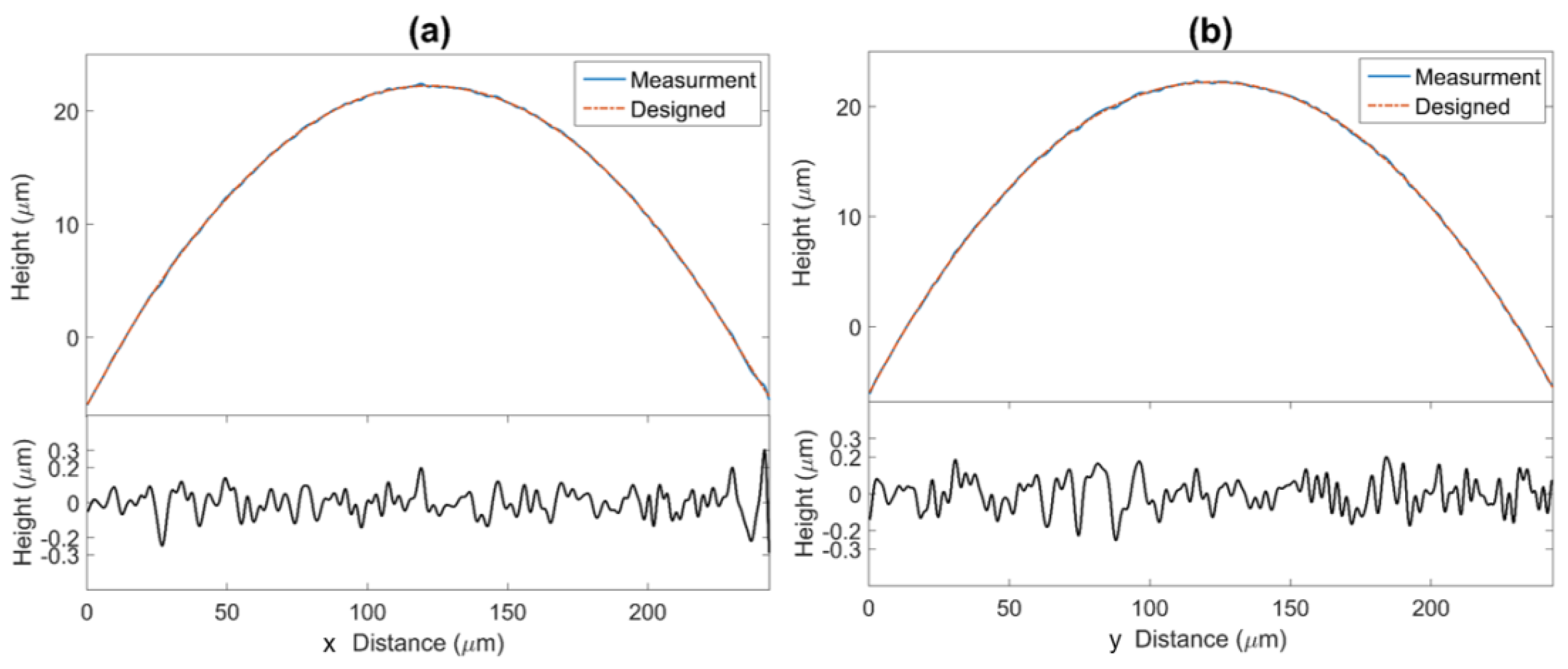
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wei, S.L.; Zhu, Z.B.; Fan, Z.C.; Yan, Y.M.; Ma, D.L. Multr surface catadioptric freeform lens design for ultra-efficient off-axis road illumination. Opt. Express 2019, 27, A779–A789. [Google Scholar] [CrossRef]
- Wu, R.; Yang, L.; Ding, Z.; Zhao, L.; Wang, D.; Li, K.; Wu, F.; Li, Y.; Zheng, Z.; Liu, X. Precise light control in highly tilted geometry by freeform illumination optics. Opt. Lett. 2019, 44, 2887–2890. [Google Scholar] [CrossRef]
- Zhu, Z.; Ma, D.; Hu, Q.; Tang, Y.; Liang, R. Catadioptric freeform optical system design for LED off-axis road illumination applications. Opt. Express 2018, 26, A54–A65. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, X.M.; Ge, P.; Yu, J.D. A high-efficiency freeform reflector for a light emitting diode low-beam headlamp. Light. Res. Technol. 2016, 48, 1005–1016. [Google Scholar] [CrossRef]
- Wang, Q.; Cheng, D.; Wang, Y.; Hua, H.; Jin, G. Design, tolerance and fabrication of an optical see-through head-mounted display with free-form surface elements. Appl. Opt. 2013, 52, C88. [Google Scholar] [CrossRef]
- Meng, X.; Liu, W.; Zhang, D.; Jiang, G.; Zhu, X.; Yang, J. Design of wide field-of-view head-mounted display optical system with double freeform surfaces. Infrared Laser Eng. 2016, 45, 0418004. [Google Scholar] [CrossRef]
- Wei, L.; Li, Y.; Jing, J.; Feng, L.; Zhou, J. Design and fabrication of a compact off axis see-through head-mounted display using a freeform surface. Opt. Express 2018, 26, 8550–8565. [Google Scholar] [CrossRef]
- Liu, J.; Huang, W. Optical system design of reflective head mounted display using freeform surfaces. Infrared Laser Eng. 2016, 45, 1018001. [Google Scholar]
- Wang, J.H.; Liang, Y.C.; Xu, M. Design of a see-through head mounted display with a freeform surface. J. Opt. Soc. Korea 2015, 19, 614–618. [Google Scholar] [CrossRef][Green Version]
- Bian, Y.; Li, H.; Wang, Y.; Zheng, Z.; Liu, X. Method to design two aspheric surfaces for a wide field of view imaging system with low distortion. Appl. Opt. 2015, 54, 8241–8247. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, X.; Li, H. Design of laser projection display illumination system based on freeform surface array. Acta Optica Sinica 2018, 38, 0622001. [Google Scholar] [CrossRef]
- Yu, B.; Tian, Z.; Su, D.; Sui, Y.; Yang, H. Design and engineering verification of an ultrashort throw ratio projection system with a freeform mirror. Appl. Opt. 2019, 58, 3575–3581. [Google Scholar] [CrossRef]
- Yu, B.H. Research on Key Technology of Ultra Short Focus Projection Objective System Based on Freeform Surfaces. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2019. [Google Scholar]
- Nie, Y.; Mohedano, R.; Benítez, P.; Chaves, J.; Miñano, J.C.; Thienpont, H.; Duerr, F. Multifield direct design method for ultrashort throw ratio projection optics with two tailored mirrors. Appl. Opt. 2016, 55, 3794–3800. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Y. Study on free-form optical testing. Chin. Opt. 2008, 1, 92–99. [Google Scholar]
- Li, Y.; Chen, Y.; Dai, F. Inspection of free-form optics. Nanotechnol. Precis. Eng. 2005, 3, 126–136. [Google Scholar]
- Zhang, L.; Liu, D.; Shi, T.; Yang, Y.Y.; Li, J.S.; Yu, B.L. Optical free-form surface shape measurement technology. China Opt. 2017, 10, 283–299. [Google Scholar] [CrossRef]
- Colomb, T.; Kühn, J.; Charriere, F.; Depeursinge, C.; Marquet, P.; Aspert, N. Total aberrations compensation in digital holographic microscopy with a reference conjugated hologram. Opt. Express 2006, 14, 4300–4306. [Google Scholar] [CrossRef]
- Dev, K.; Singh, V.R.; Asundi, A. Full-field phase modulation characterization of liquid-crystal spatial light modulator using digital holography. Appl. Opt. 2011, 50, 1593–1600. [Google Scholar] [CrossRef]
- Khmaladze, A.; Kim, M.; Lo, C.M. Phase imaging of cells by simultaneous dual-wavelength reflection digital holography. Opt. Express 2008, 16, 10900–10911. [Google Scholar] [CrossRef]
- Cheng, C. Recent progress in digital holographic microscopy: From superresolution to ultrafast imaging. In 2017 OPJ-OSA Joint Symposia on Nanophotonics and Digital Photonics; Omatsu, T., Ed.; OSA Technical Digest/Optica Publishing Group: Online, 2017; p. 31aOD1. [Google Scholar]
- Marquet, P.; Rappaz, B.; Magistretti, P.J.; Cuche, E.; Emery, Y.; Colomb, T.; Depeursinge, C. Digital holographic microscopy: A noninvasive contrast imaging technique allowing quantitative visualization of living cells with subwavelength axial accuracy. Opt. Lett. 2005, 30, 468–470. [Google Scholar] [CrossRef]
- He, X.; Nguyen, C.V.; Pratap, M.; Zheng, Y.; Wang, Y.; Nisbet, D.R.; Williams, R.J.; Rug, M.; Maier, A.G.; Lee, W.M. Automated Fourier space region-recognition filtering for off-axis digital holographic microscopy. Biomed. Opt. Express 2016, 7, 3111–3123. [Google Scholar] [CrossRef]
- Howes, W.L.; Buchele, D.R. Optical Interferometry of Inhomogeneous Gases. J. Opt. Soc. Am. 1966, 56, 1517–1528. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, C.; Dai, S.; Di, J.; Li, Y.; Xi, T.; Zhao, J. Transmission and total internal reflection integrated digital holographic microscopy. Opt. Lett. 2016, 41, 3844–3847. [Google Scholar] [CrossRef]
- Olszak, A. Lateral scanning white-light interferometer. Appl. Opt. 2000, 39, 3906–3913. [Google Scholar] [CrossRef]
- Wagner, C.; Osten, W.; Seebacher, S. Direct shape measurement by digital wavefront reconstruction and multiwavelength contouring. Opt. Eng. 2000, 39, 79–85. [Google Scholar] [CrossRef]


| Parameters | Theoretical Value (Tolerance) | Average | Value of 5 Points |
|---|---|---|---|
| 2a | ) | 241.96 μm, 242.20 μm, 241.97 μm, 241.86 μm, 242.01 μm | |
| r | ) | 900.90 μm, 900.00 μm, 898.26 μm, 899.86 μm, 897.98 μm | |
| R1 | 31.80 mm ) | 31.51 μm, 31.41 μm, 31.47 μm, 31.44 μm, 31.52 μm | |
| R2 | 33.30 mm ) | 32.96 μm, 32.98 μm, 32.91 μm, 33.02μm, 32.98 μm | |
| Sag | ) | 10.79 μm, 10.80 μm, 10.79 μm, 10.81 μm, 10.81 μm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wu, C.; Chen, L.; Chen, G.; Zheng, G. A Novel Approach for Measurement of Free-Form Optical Elements with Digital Holographic Microscopy. Micromachines 2022, 13, 1719. https://doi.org/10.3390/mi13101719
Zhang X, Wu C, Chen L, Chen G, Zheng G. A Novel Approach for Measurement of Free-Form Optical Elements with Digital Holographic Microscopy. Micromachines. 2022; 13(10):1719. https://doi.org/10.3390/mi13101719
Chicago/Turabian StyleZhang, Xuhui, Chonglin Wu, Lei Chen, Gengliang Chen, and Guoliang Zheng. 2022. "A Novel Approach for Measurement of Free-Form Optical Elements with Digital Holographic Microscopy" Micromachines 13, no. 10: 1719. https://doi.org/10.3390/mi13101719
APA StyleZhang, X., Wu, C., Chen, L., Chen, G., & Zheng, G. (2022). A Novel Approach for Measurement of Free-Form Optical Elements with Digital Holographic Microscopy. Micromachines, 13(10), 1719. https://doi.org/10.3390/mi13101719







