Molecular Dynamics Study of Ion Transport in Polymer Electrolytes of All-Solid-State Li-Ion Batteries
Abstract
1. Introduction
2. Simulation Methods
2.1. Molecular Models
2.2. Simulation Conditions
3. Results and Discussion
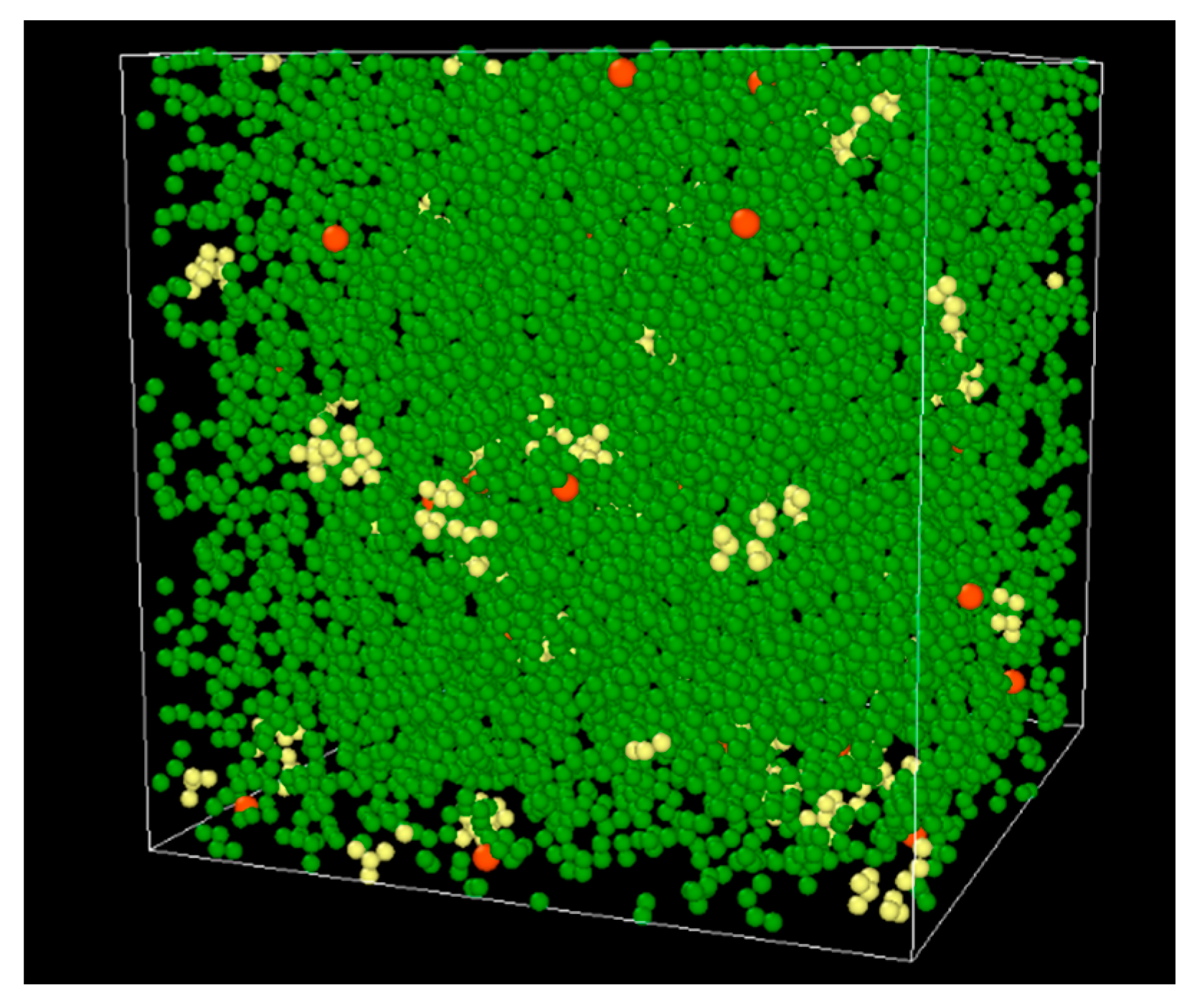
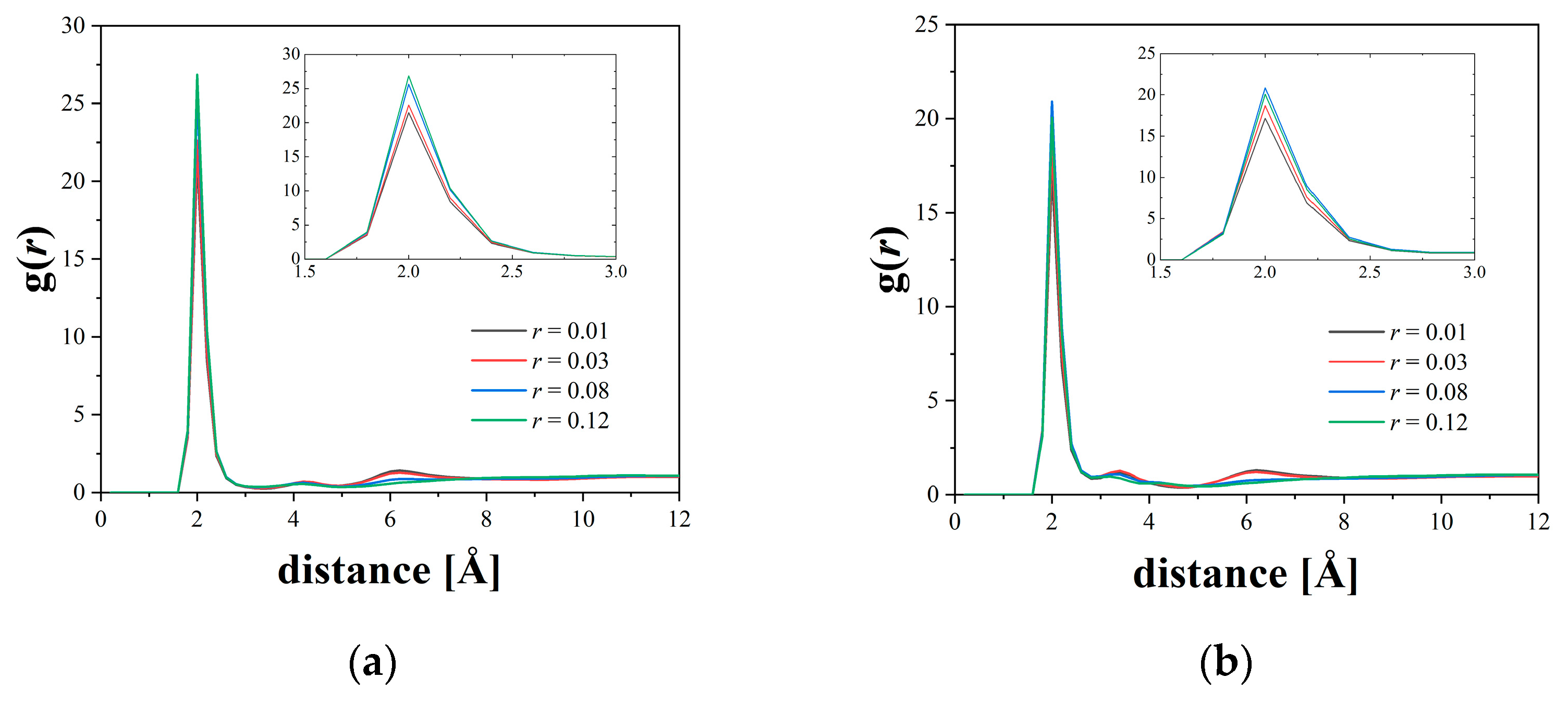
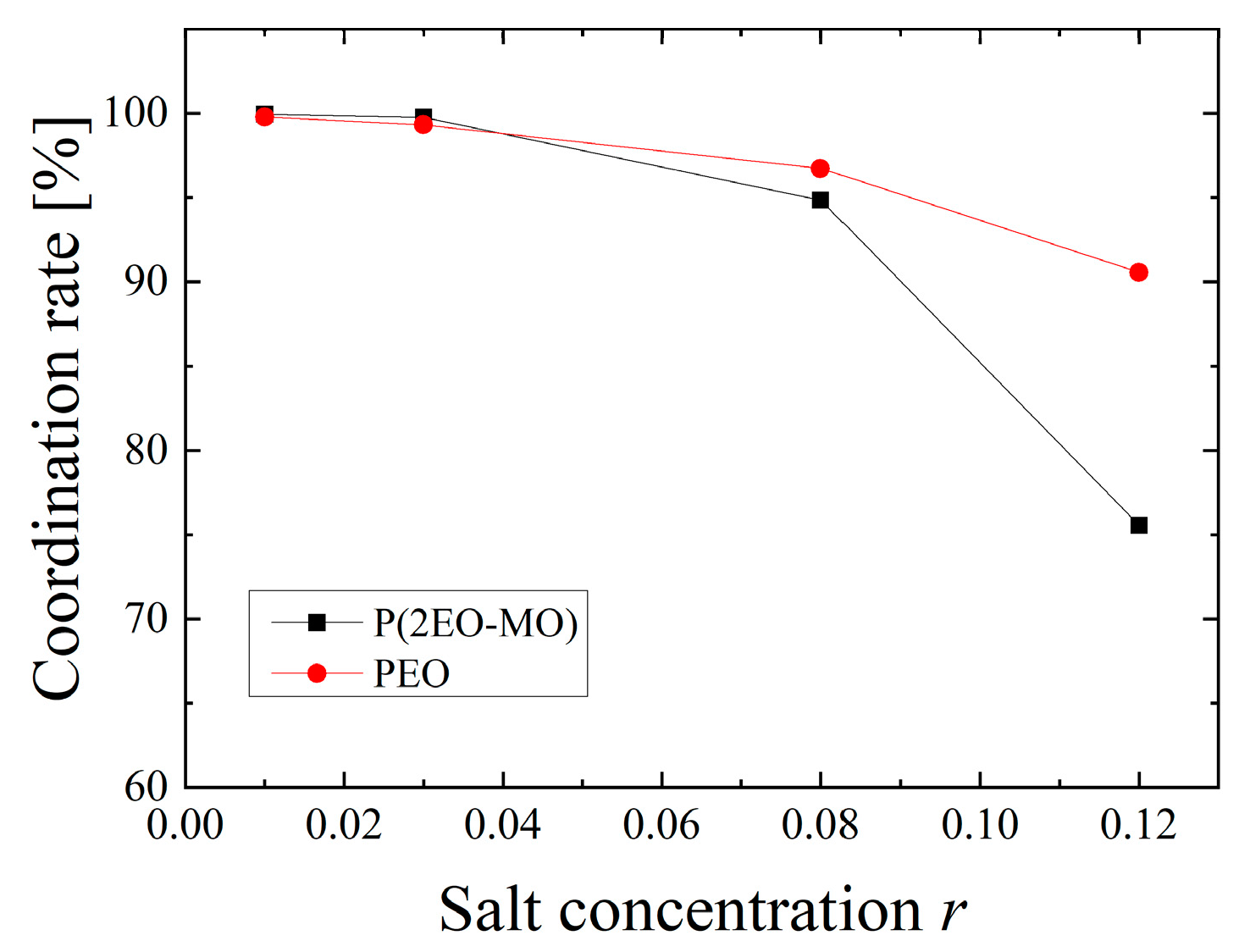
3.1. Structural Characteristics around Li Ions
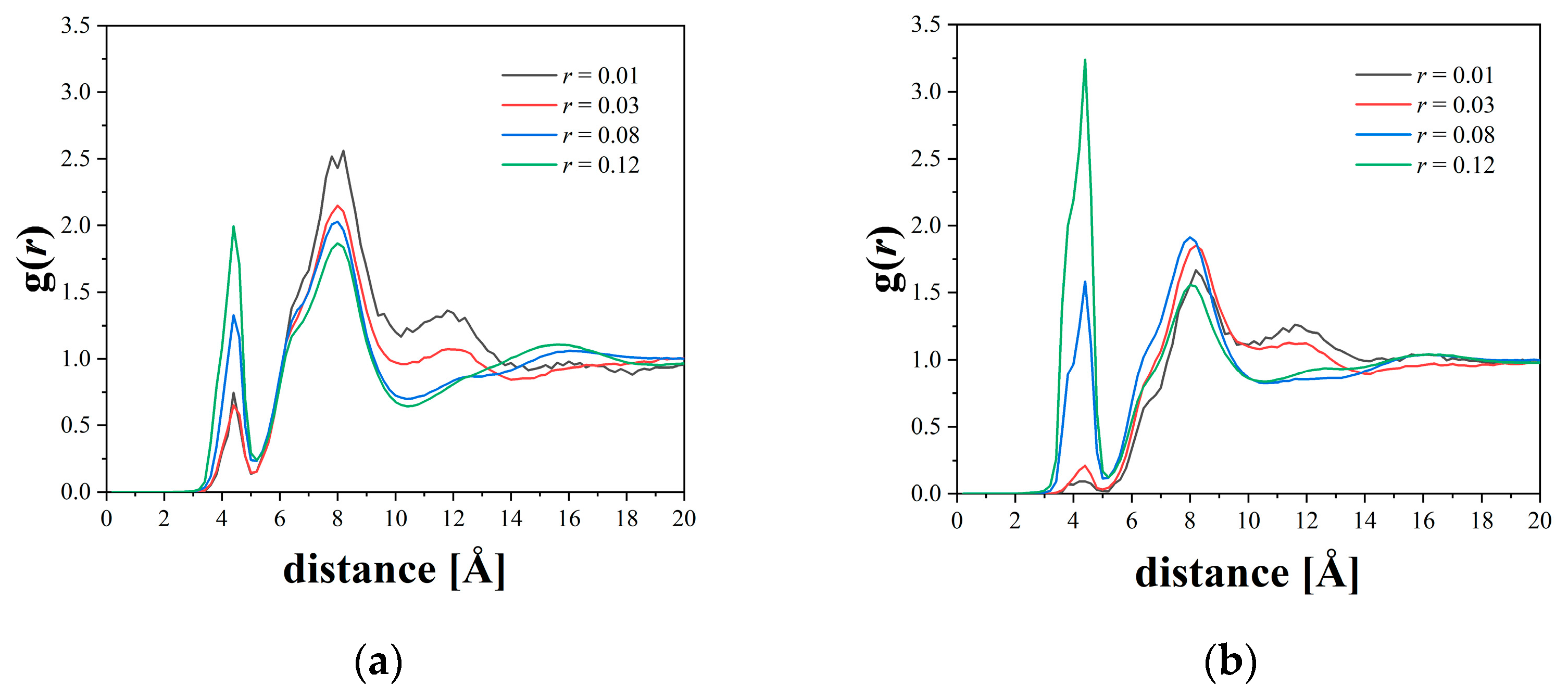
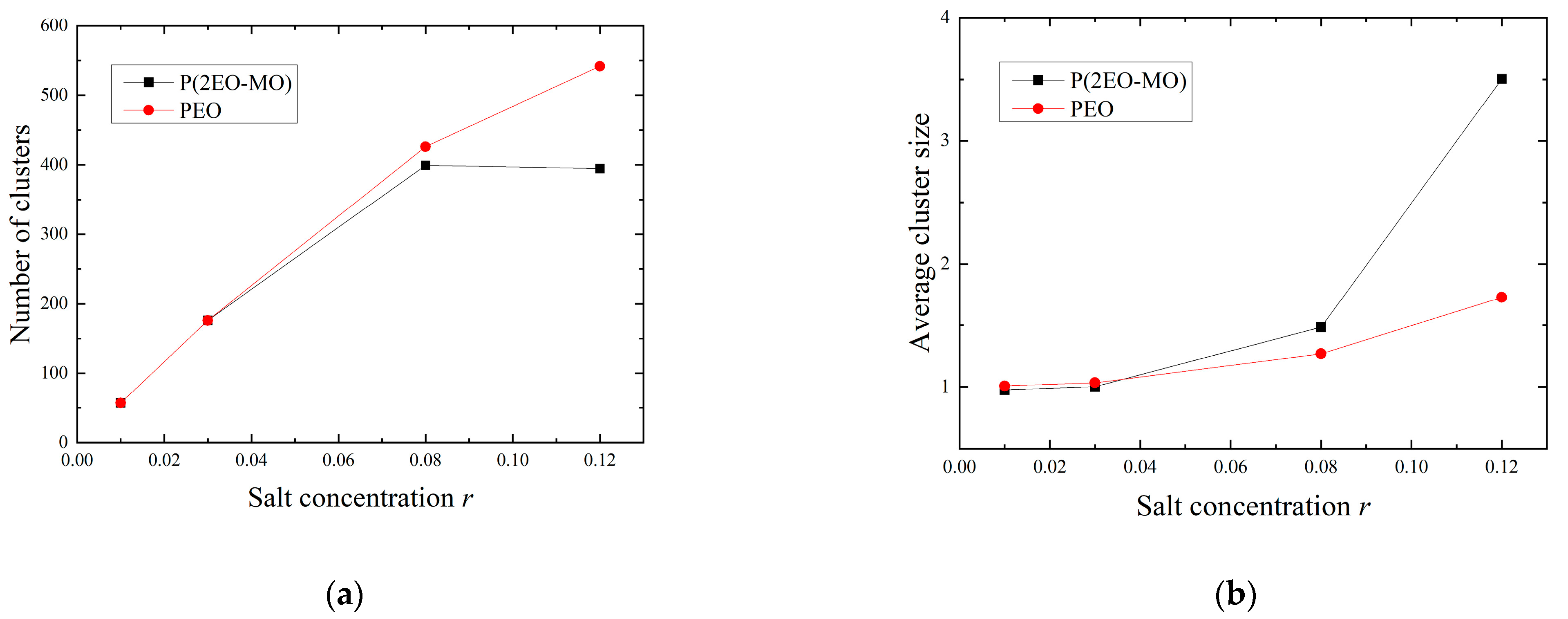
3.2. Cluster Analysis
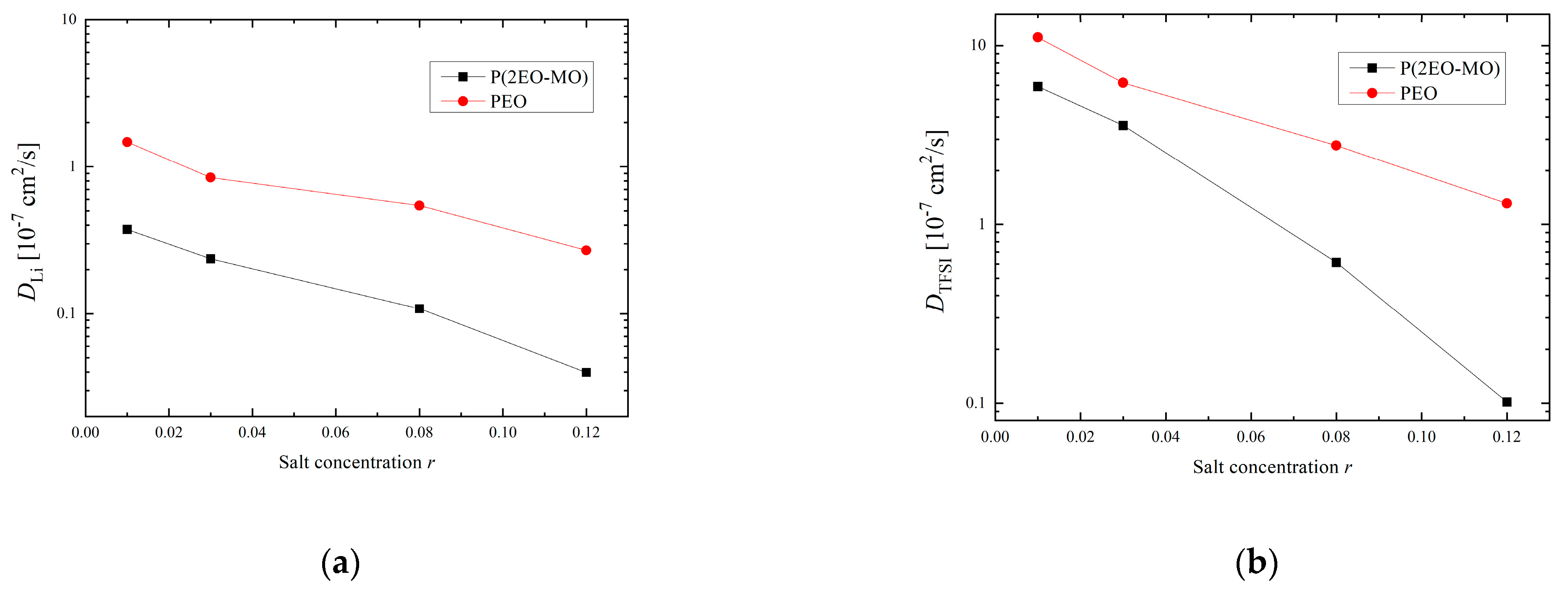
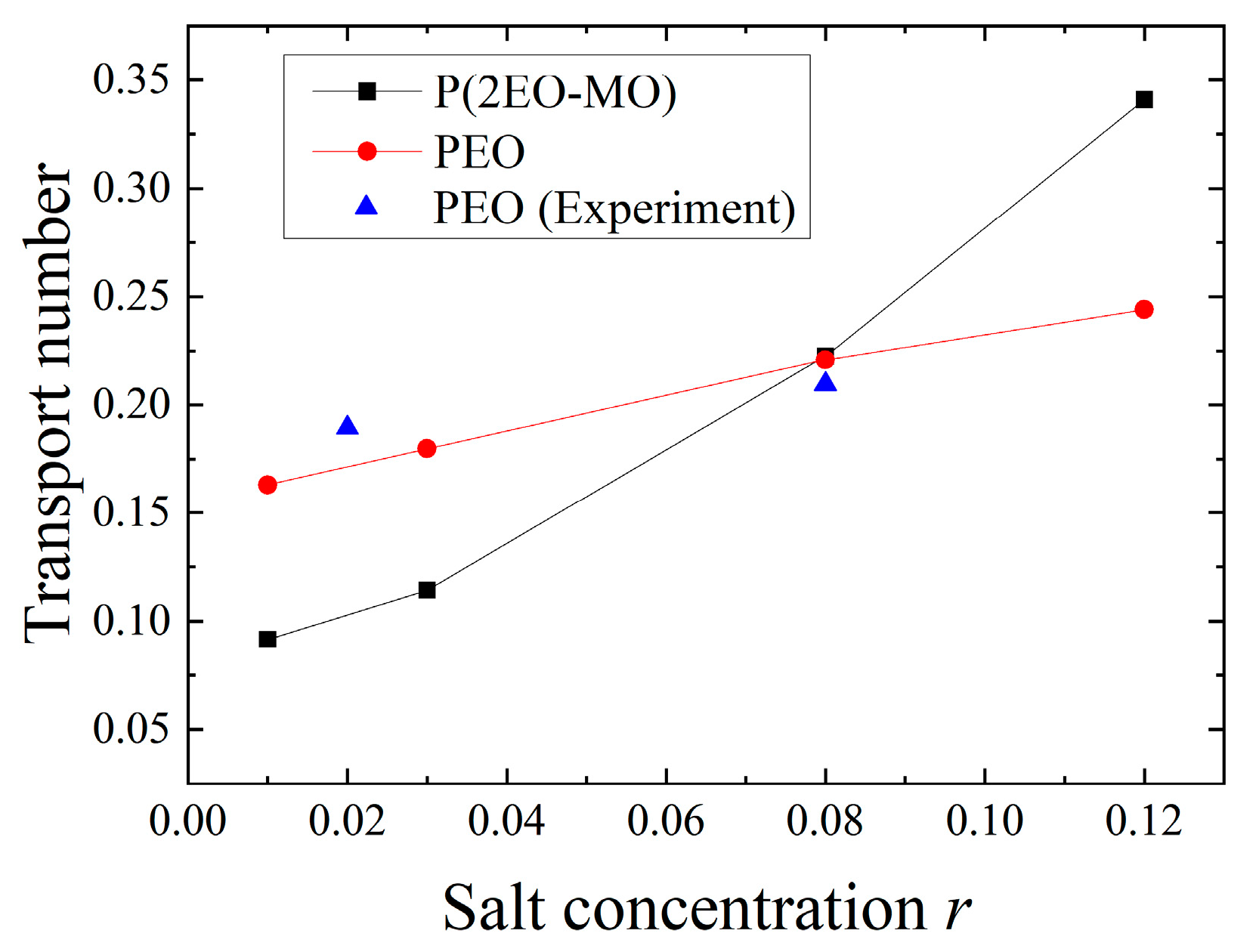
3.3. Transport Characteristics and Transport Number of Li Ions
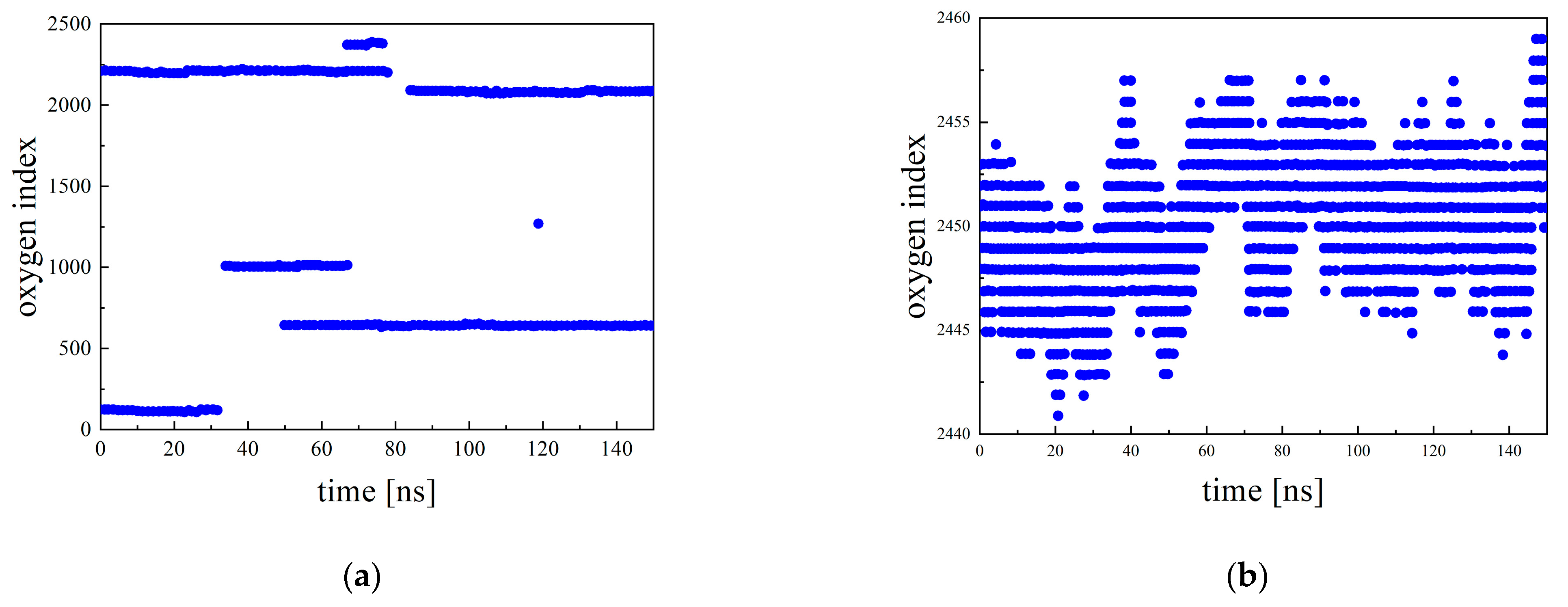
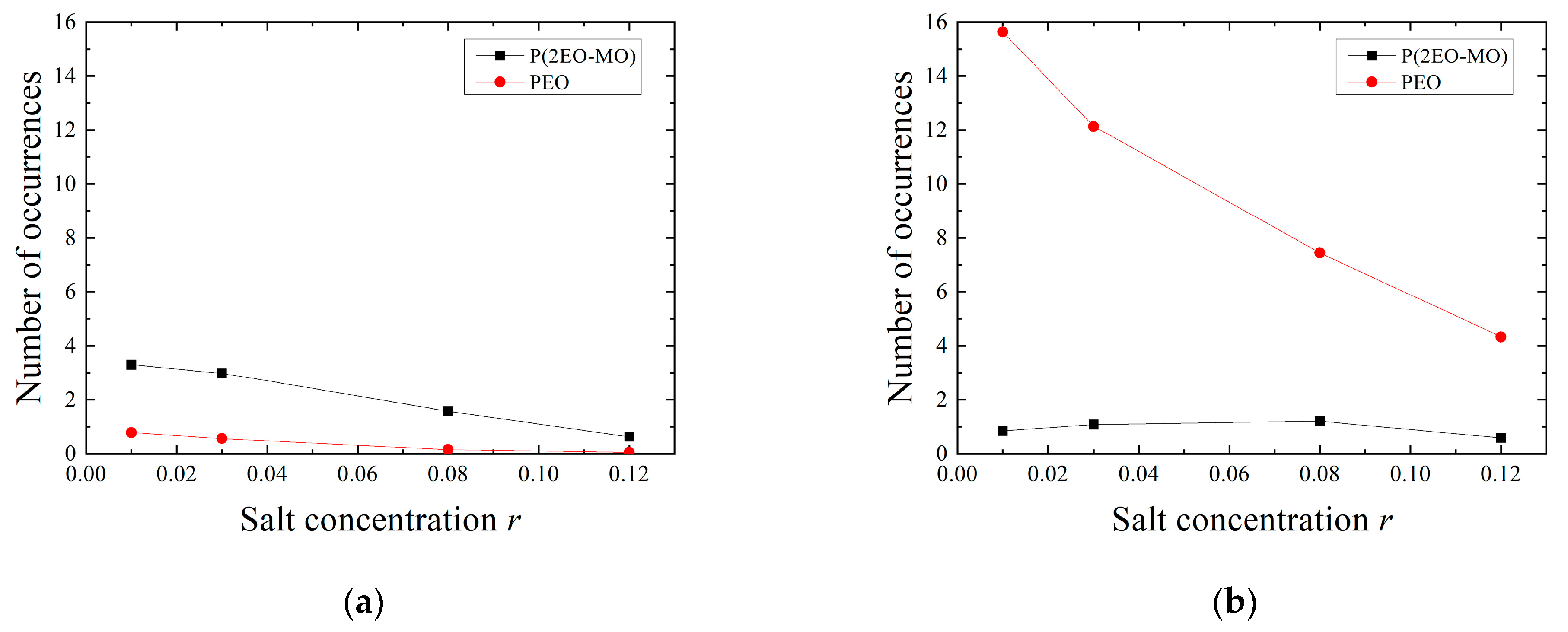
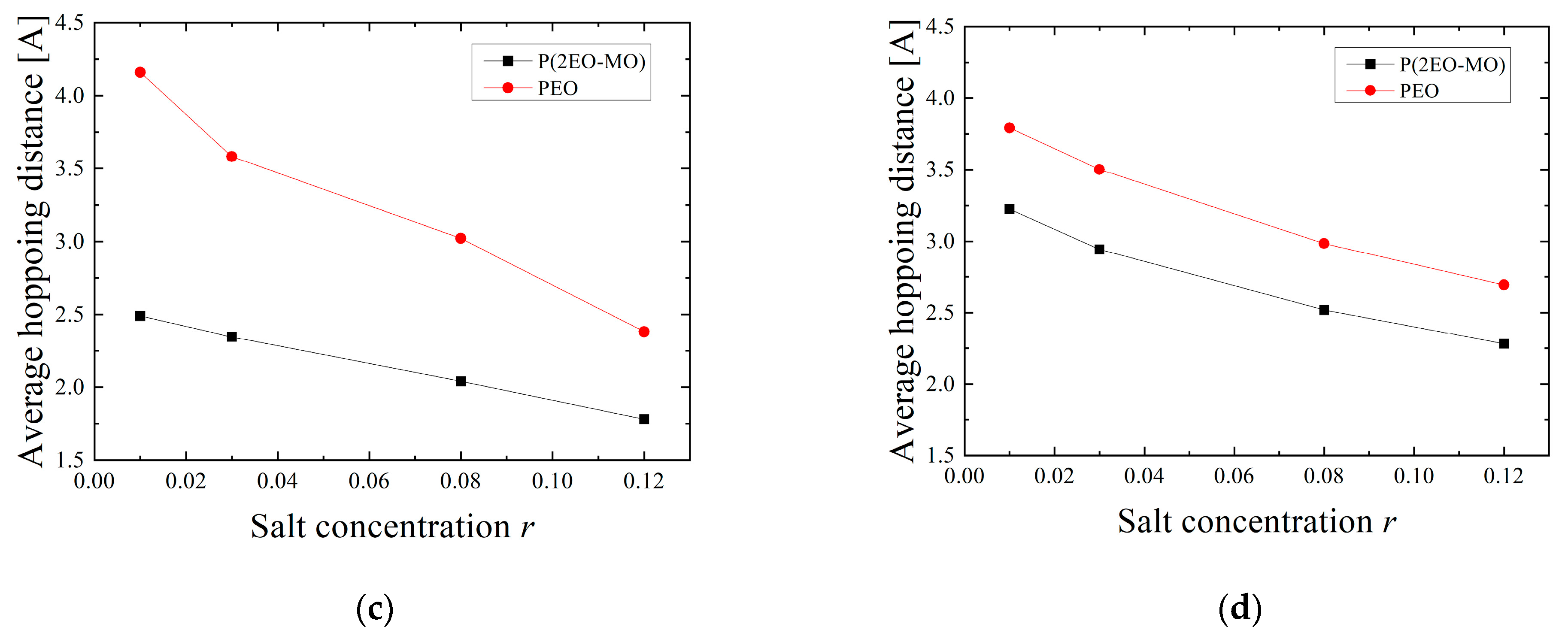
3.4. Hopping Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Tarascon, J.M.; Armand, M. Issues and challenges facing rechargeable lithium batteries. Nature 2001, 414, 359–367. [Google Scholar] [CrossRef] [PubMed]
- Buriez, O.; Han, Y.B.; Hou, J.; Kerr, J.B.; Qiao, J.; Sloop, S.E.; Tian, M.; Wang, S. Performance limitations of polymer electrolytes based on ethylene oxide polymers. J. Power Sources 2000, 89, 149–155. [Google Scholar] [CrossRef]
- Diddens, D.; Heuer, A.; Borodin, O. Understanding the lithium transport within a rouse-based model for a peo/litfsi polymer electrolyte. Macromolecules 2010, 43, 2028–2036. [Google Scholar] [CrossRef]
- Xue, Z.; He, D.; Xie, X. Poly(ethylene oxide)-based electrolytes for lithium-ion batteries. J. Mater. Chem. A 2015, 3, 19218–19253. [Google Scholar] [CrossRef]
- Volel, M.; Armand, M.; Gorecki, W. Influence of sample history on the morphology and transport properties of peo−lithium salt complexes. Macromolecules 2004, 37, 8373–8380. [Google Scholar] [CrossRef]
- Pożyczka, K.; Marzantowicz, M.; Dygas, J.R.; Krok, F. Ionic conductivity and lithium transference number of poly(ethylene oxide):Litfsi system. Electrochim. Acta 2017, 227, 127–135. [Google Scholar] [CrossRef]
- Devaux, D.; Bouchet, R.; Glé, D.; Denoyel, R. Mechanism of ion transport in peo/litfsi complexes: Effect of temperature, molecular weight and end groups. Solid State Ion. 2012, 227, 119–127. [Google Scholar] [CrossRef]
- Croce, F.; Appetecchi, G.B.; Persi, L.; Scrosati, B. Nanocomposite polymer electrolytes for lithium batteries. Nature 1998, 394, 456–458. [Google Scholar] [CrossRef]
- Jiang, K.; Liu, X.; Lou, G.; Wen, Z.; Liu, L. Parameter sensitivity analysis and cathode structure optimization of a non-aqueous li–o2 battery model. J. Power Source 2020, 451, 227821. [Google Scholar] [CrossRef]
- Liu, C.; Gao, Y.; Liu, L. Toward safe and rapid battery charging: Design optimal fast charging strategies thorough a physics-based model considering lithium plating. Int. J. Energy Res. 2021, 45, 2303–2320. [Google Scholar] [CrossRef]
- Mu, W.; Liu, X.; Wen, Z.; Liu, L. Numerical simulation of the factors affecting the growth of lithium dendrites. J. Energy Storage 2019, 26, 100921. [Google Scholar] [CrossRef]
- O'Malley, R.; Liu, L.; Depcik, C. Comparative study of various cathodes for lithium ion batteries using an enhanced peukert capacity model. J. Power Sources 2018, 396, 621–631. [Google Scholar] [CrossRef]
- Brooks, D.J.; Merinov, B.V.; Goddard, W.A.; Kozinsky, B.; Mailoa, J. Atomistic description of ionic diffusion in peo–litfsi: Effect of temperature, molecular weight, and ionic concentration. Macromolecules 2018, 51, 8987–8995. [Google Scholar] [CrossRef]
- Webb, M.A.; Savoie, B.M.; Wang, Z.-G.; Miller Iii, T.F. Chemically specific dynamic bond percolation model for ion transport in polymer electrolytes. Macromolecules 2015, 48, 7346–7358. [Google Scholar] [CrossRef]
- Webb, M.A.; Jung, Y.; Pesko, D.M.; Savoie, B.M.; Yamamoto, U.; Coates, G.W.; Balsara, N.P.; Wang, Z.-G.; Miller, T.F. Systematic computational and experimental investigation of lithium-ion transport mechanisms in polyester-based polymer electrolytes. ACS Cent. Sci. 2015, 1, 198–205. [Google Scholar] [CrossRef]
- Zheng, Q.; Pesko, D.M.; Savoie, B.M.; Timachova, K.; Hasan, A.L.; Smith, M.C.; Miller, T.F.; Coates, G.W.; Balsara, N.P. Optimizing ion transport in polyether-based electrolytes for lithium batteries. Macromolecules 2018, 51, 2847–2858. [Google Scholar] [CrossRef]
- Mabuchi, T.; Tokumasu, T. Effect of bound state of water on hydronium ion mobility in hydrated nafion using molecular dynamics simulations. J. Chem. Phys. 2014, 141, 104904. [Google Scholar] [CrossRef] [PubMed]
- Mabuchi, T.; Tokumasu, T. Molecular dynamics simulation of proton transport in polymer electrolyte membrane. J. Nanosci. Nanotechnol. 2015, 15, 2958–2963. [Google Scholar] [CrossRef]
- Mabuchi, T.; Tokumasu, T. Relationship between proton transport and morphology of perfluorosulfonic acid membranes: A reactive molecular dynamics approach. J. Phys. Chem. B 2018, 122, 5922–5932. [Google Scholar] [CrossRef] [PubMed]
- Mabuchi, T.; Tokumasu, T. Effects of water nanochannel diameter on proton transport in proton-exchange membranes. J. Polym. Sci. Part B Polym. Phys. 2019, 57, 867–878. [Google Scholar] [CrossRef]
- Aochi, J.; Mabuchi, T.; Tokumasu, T. Molecular dynamics study of the effect of wettability of the carbon support on proton transport in nafion ionomer thin films. J. Therm. Sci. Technol. 2016, 11, JTST0045. [Google Scholar] [CrossRef][Green Version]
- Mabuchi, T.; Tokumasu, T. Dependence of electroosmosis on polymer structure in proton exchange membranes. Mech. Eng. J. 2017, 4, 17–00054. [Google Scholar] [CrossRef]
- Timachova, K.; Watanabe, H.; Balsara, N.P. Effect of molecular weight and salt concentration on ion transport and the transference number in polymer electrolytes. Macromolecules 2015, 48, 7882–7888. [Google Scholar] [CrossRef]
- Molinari, N.; Mailoa, J.P.; Kozinsky, B. Effect of salt concentration on ion clustering and transport in polymer solid electrolytes: A molecular dynamics study of peo–litfsi. Chem. Mater. 2018, 30, 6298–6306. [Google Scholar] [CrossRef]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmüller, H.; MacKerell, A.D. Charmm36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Wu, H.; Wick, C.D. Computational investigation on the role of plasticizers on ion conductivity in poly(ethylene oxide) litfsi electrolytes. Macromolecules 2010, 43, 3502–3510. [Google Scholar] [CrossRef]
- Polak, E.; Ribière, G. Note sur la convergence de directions conjuguée. Rev. Fr. Inf. Rech. Oper. 3e Année 1969, 16, 35–43. [Google Scholar]
- Nosé, S. A molecular-dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Constant-pressure equations of motion. Phys. Rev. A 1986, 34, 2499–2500. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Mao, G.; Saboungi, M.-L.; Price, D.L.; Armand, M.B.; Howells, W.S. Structure of liquid peo-litfsi electrolyte. Phys. Rev. Lett. 2000, 84, 5536–5539. [Google Scholar] [CrossRef] [PubMed]
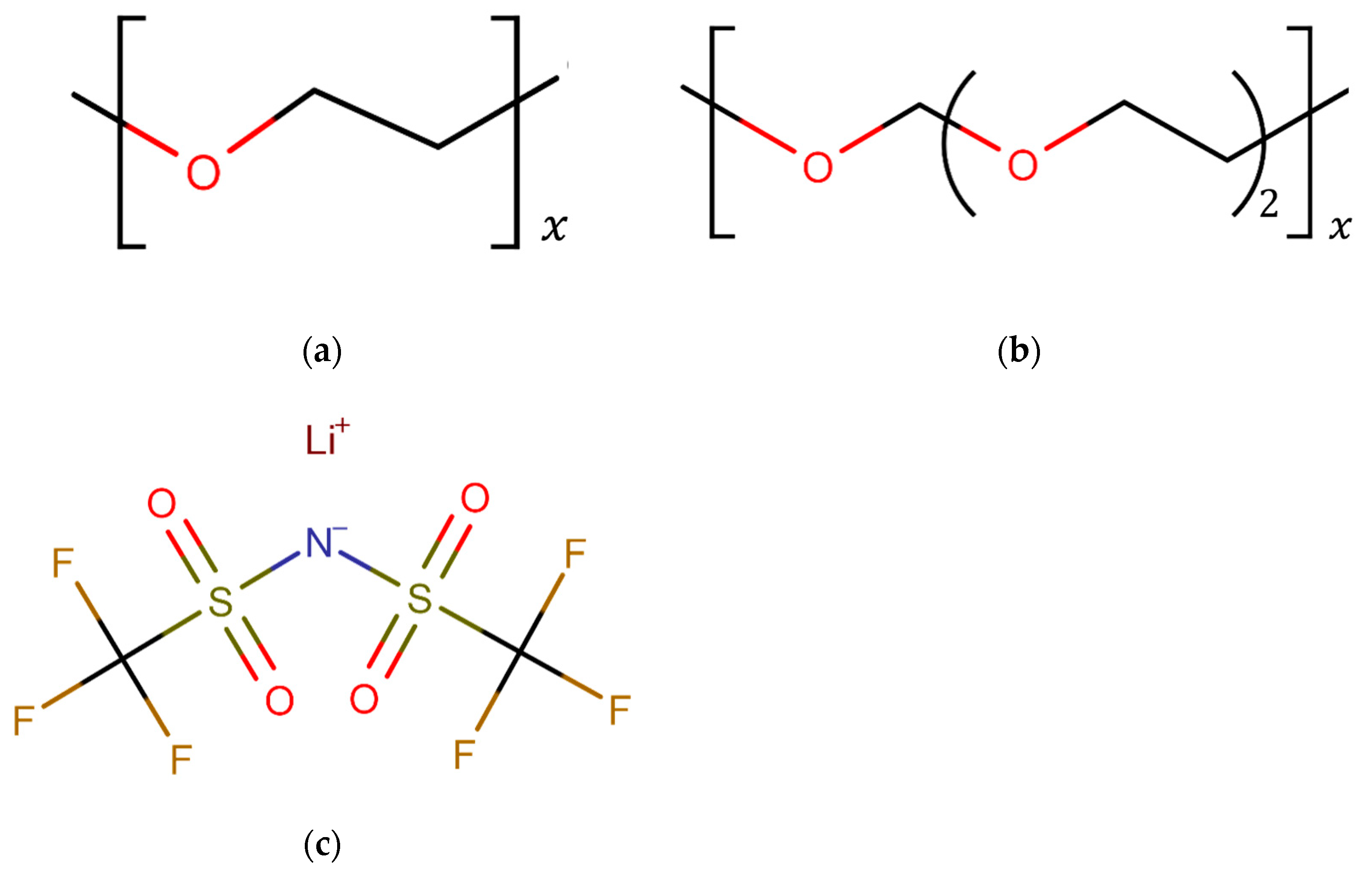
| Salt Concentration, r | 0.01 | 0.03 | 0.08 | 0.12 |
|---|---|---|---|---|
| PEO | 1.09 | 1.16 | 1.28 | 1.37 |
| P(2EO-MO) | 1.16 | 1.22 | 1.35 | 1.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mabuchi, T.; Nakajima, K.; Tokumasu, T. Molecular Dynamics Study of Ion Transport in Polymer Electrolytes of All-Solid-State Li-Ion Batteries. Micromachines 2021, 12, 1012. https://doi.org/10.3390/mi12091012
Mabuchi T, Nakajima K, Tokumasu T. Molecular Dynamics Study of Ion Transport in Polymer Electrolytes of All-Solid-State Li-Ion Batteries. Micromachines. 2021; 12(9):1012. https://doi.org/10.3390/mi12091012
Chicago/Turabian StyleMabuchi, Takuya, Koki Nakajima, and Takashi Tokumasu. 2021. "Molecular Dynamics Study of Ion Transport in Polymer Electrolytes of All-Solid-State Li-Ion Batteries" Micromachines 12, no. 9: 1012. https://doi.org/10.3390/mi12091012
APA StyleMabuchi, T., Nakajima, K., & Tokumasu, T. (2021). Molecular Dynamics Study of Ion Transport in Polymer Electrolytes of All-Solid-State Li-Ion Batteries. Micromachines, 12(9), 1012. https://doi.org/10.3390/mi12091012






