Fluorescence Anisotropy as a Temperature-Sensing Molecular Probe Using Fluorescein
Abstract
:1. Introduction
2. Materials and Methods
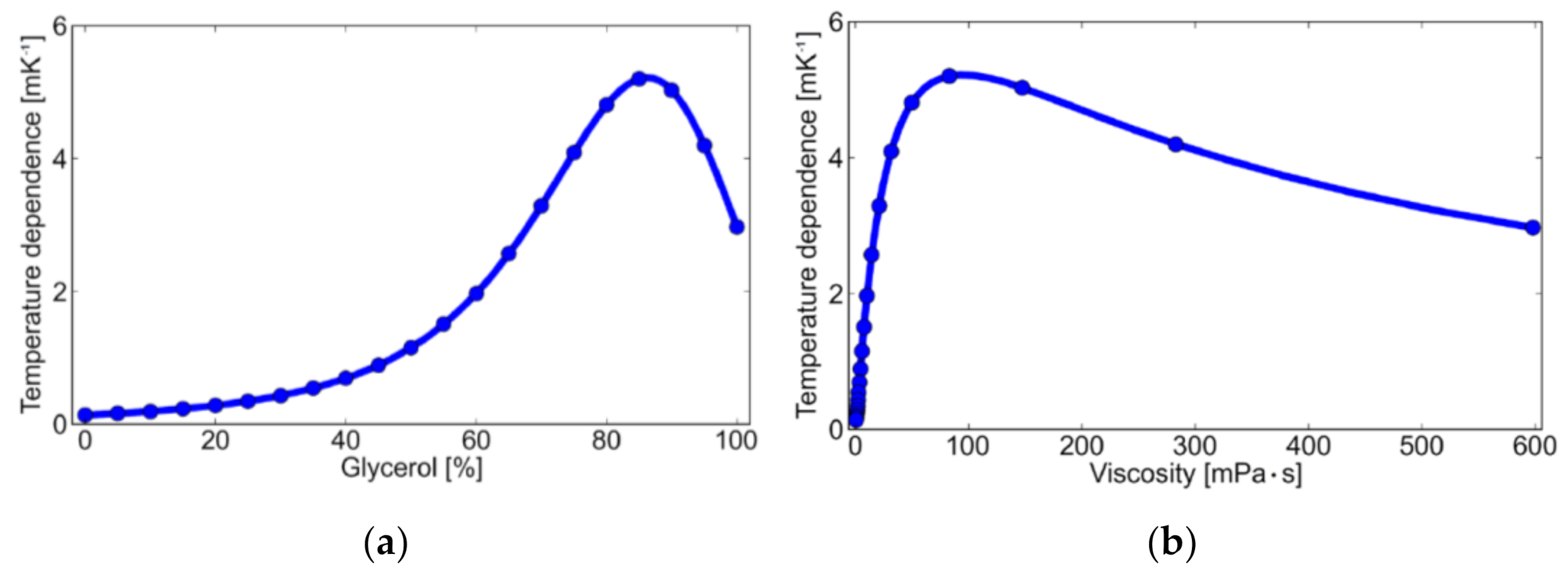
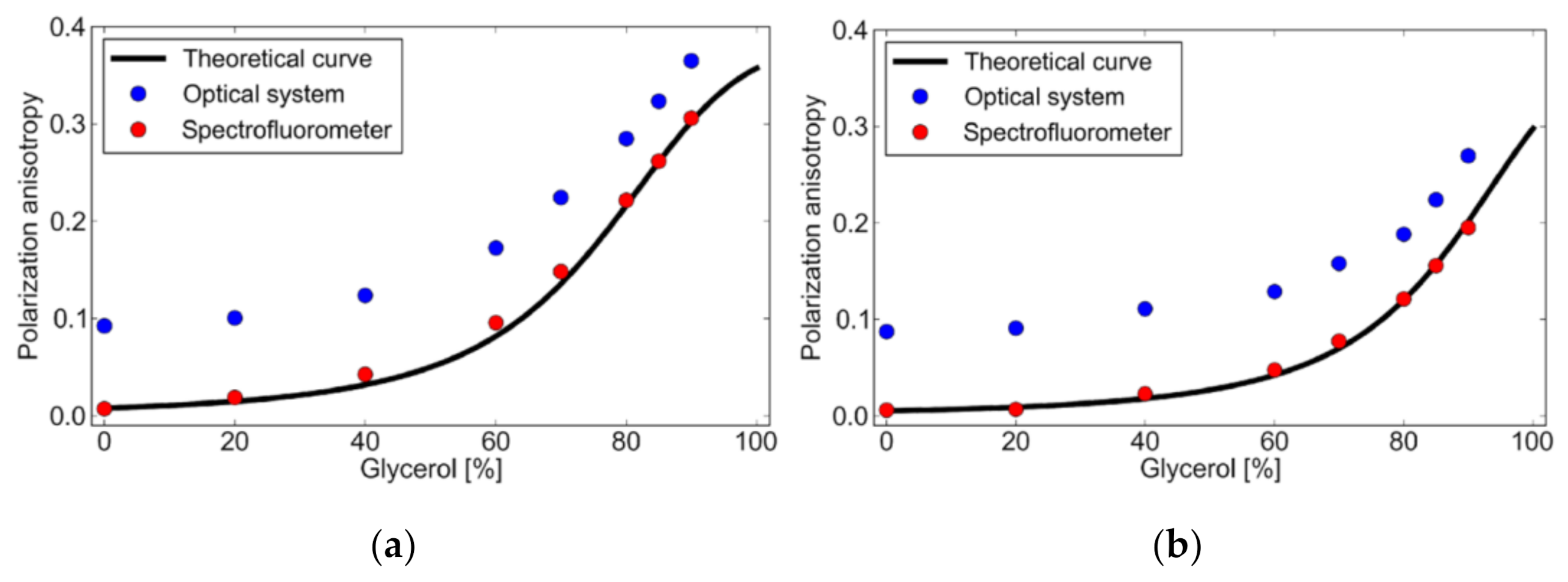
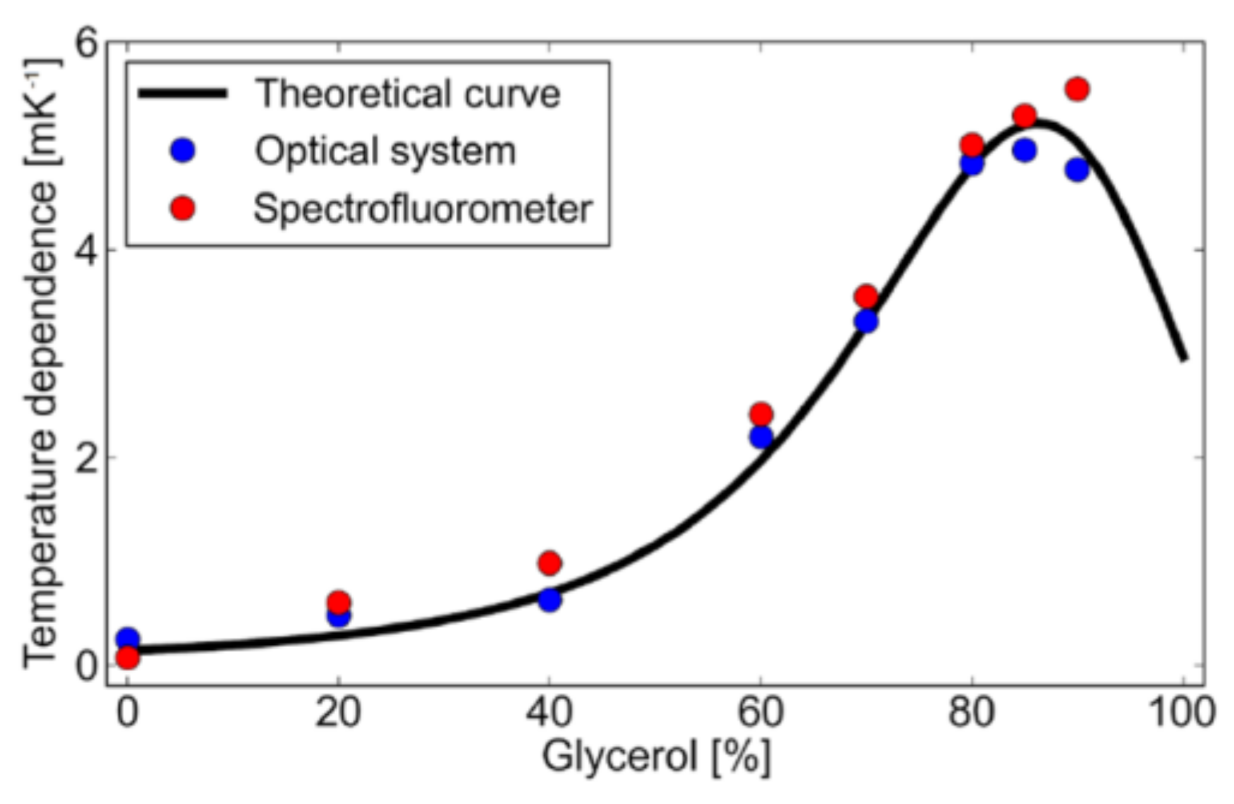
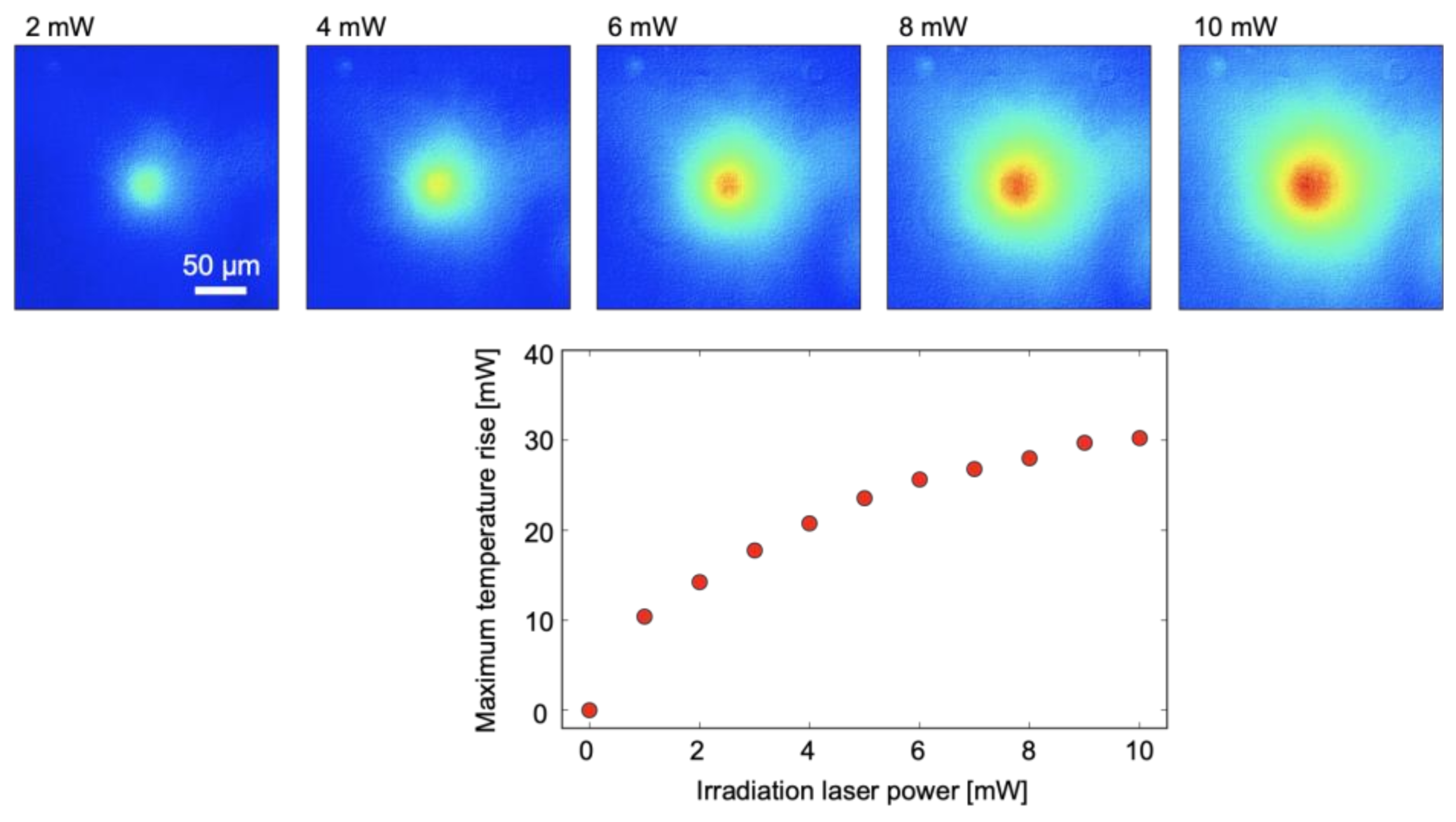
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tabling, P. Introduction to Microfluidics, 3rd ed.; Oxford University Press: New York, NY, USA, 2011; pp. 24–69. [Google Scholar]
- Alex, H. Lab-on-a-Chip Technologies for the Single Cell Level: Separation, Analysis, and Diagnostics. Micromachines 2020, 11, 468–501. [Google Scholar]
- Miralles, V.; Huerre, A.; Malloggi, F.; Jullien, M.-C. A Review of Heating and Temperature Control in Microfluidic Systems: Techniques and Applications. Diagnostics 2013, 3, 33–67. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Yang, N.; Huo, X.; Xu, S. Thermal sensing in fluid at micro-nano-scales. Biomicrofluidics 2018, 12, 041501. [Google Scholar] [CrossRef]
- Niidome, T.; Akiyama, Y.; Yamagata, M.; Kawano, T.; Mori, T.; Niidome, Y.; Katayama, Y. Poly(ethylene glycol)-modified gold nanorods as a photothermal nanodevice for hyperthermia. J. Biomater. Sci. Polym. Ed. 2009, 20, 1203–1215. [Google Scholar] [CrossRef]
- Zhang, W.; Ling, G.; Liangpiao, Z.; Liang, Z. The effect of reducing the thermal contact resistance on the performance of battery thermal management system. Int. J. Energy Res. 2021, 45, 9970–9982. [Google Scholar] [CrossRef]
- Watanabe, M.S.; Kakuta, N.; Mabuchi, K.; Yamada, Y. Micro-thermocouple probe for measurement of cellular thermal responses. In Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 1–4 September 2005. [Google Scholar]
- Ross, D.; Gaitan, M.; Locascio, L. Temperature measurement in microfluidic systems using a temperature-dependent fluorescent dye. Anal. Chem. 2001, 73, 4117–4123. [Google Scholar] [CrossRef] [PubMed]
- Motosuke, M.; Akutsu, D.; Honami, S. Temperature measurement of microfluids with high temporal resolution by laser-induced fluorescence. J. Mech. Sci. Technol. 2009, 23, 1821–1828. [Google Scholar] [CrossRef]
- Hoang, V.N.; Kaigala, G.V.; Backhouse, C.J. Dynamic temperature measurement in microfluidic devices using thermochromic liquid crystals. Lab Chip 2008, 8, 484–487. [Google Scholar] [CrossRef] [PubMed]
- Guan, Y.; Zhang, L.; Wang, D.; West, J.-L.; Fu, W. Preparation of thermochromic liquid crystal microcapsules for intelligent functional fiber. Mater. Des. 2018, 147, 28–34. [Google Scholar] [CrossRef]
- Gabbarini, V.; Rossi, R.; Ciparisse, J.F.; Andrea Malizia, A.; Divizia, A.; Filippis, D.P.; Anselmi, M.; Carestia, M.; Palombi, L.; Divizia, M.; et al. Laser-induced fluorescence (LIF) as a smart method for fast environmental virological analyses: Validation on Picornaviruses. Sci. Rep. 2019, 9, 12598. [Google Scholar] [CrossRef] [Green Version]
- Ruttinger, S.; Spille, C.; Hoffmann, M.; Schluter, M. Laser-Induced Fluorescence in Multiphase Systems. Chem. Bio. Eng. Rev. 2018, 5, 253–269. [Google Scholar]
- Natrajan, V.K.; Christensen, K.T. Two-color laser-induced fluorescent thermometry for microfluidic systems. Meas. Sci. Technol. 2009, 20, 015401–015412. [Google Scholar] [CrossRef] [Green Version]
- Gradinaru, C.C.; Marushchak, D.O.; Samin, M.; Krull, U.J. Fluorescence anisotropy: From single molecules to live cells. Analyst 2010, 135, 452–459. [Google Scholar] [CrossRef] [Green Version]
- Stawska, I.H.; Popenda, A.M. Fluorescence Anisotropy Sensor Comprising a Dual Hollow-Core Antiresonant Fiber Polarization Beam Splitter. Sensors 2020, 20, 3321. [Google Scholar] [CrossRef]
- Vinegoni, C.; Feruglio, F.P.; Gryczynski, I.; Mazitschek, R.; Weissleder, R. Fluorescence anisotropy imaging in drug discovery. Adv. Drug Deliv. Rev. 2019, 151, 262–288. [Google Scholar] [CrossRef]
- Donner, J.; Thompson, S.; Kreuzer, M.; Baffou, G.; Quidant, R. Mapping Intracellular Temperature Using Green Fluorescent Protein. Nano Lett. 2012, 12, 2107–2111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Valeur, B.; Santos, N. Molecular Fluorescence Principles and Applications, 3rd ed.; Wiley-VCH: Darmstadt, Germany, 2006; pp. 125–154. [Google Scholar]
- Flecha, F.L.G.; Levi, V. Determination of the Molecular Size of BSA by Fluorescence Anisotropy. Biochem. Mol. Biol. Educ. 2003, 31, 319–322. [Google Scholar] [CrossRef]
- Lakowicz, J. Principles of Fluorescence Spectroscopy, 2nd ed.; Kluwer Academic/Prenum Publishers: New York, NY, USA, 1999; pp. 291–306. [Google Scholar]
- Holde, K.; Johnson, W.; Ho, P. Principles of Physical Biochemistry, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1998; pp. 452–483. [Google Scholar]
- Liu, H.; Ma, L.; Ma, C.; Du, J.; Wang, M.; Wang, K. Quencher-Free Fluorescence Method for the Detection of Mercury(II) Based on Polymerase-Aided Photoinduced Electron Transfer Strategy. Sensors 2016, 16, 1945. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moura-Melo, S.; Miranda-Castro, R.; De-los-Santos-Álvarez, N.; Miranda-Ordieres, J.A.; Junior, S.D.R.J.; Fonseca, S.A.R.; Lobo-Castañón, J.M. A Quantitative PCR-Electrochemical Genosensor Test for the Screening of Biotech Crops. Sensors 2017, 17, 881. [Google Scholar] [CrossRef] [Green Version]
- Leung, W.-H.; Pang, C.-C.; Pang, S.-N.; Weng, S.-X.; Lin, Y.-L.; Chiou, Y.-E.; Pang, S.-T.; Weng, W.-H. High-sensitivity dual-probe detection of urinary miR-141 in cancer patients via a modified screen-printed carbon electrode-based electrochemical biosensor. Sensors 2021, 21, 3183. [Google Scholar] [CrossRef] [PubMed]
- Ali, H.R.H.; Hassan, I.A.; Hassan, F.Y.; El-Wekil, M.M. One pot fabrication of fluorescein functionalized manganese dioxide for fluorescence “Turn OFF–ON” sensing of hydrogen peroxide in water and cosmetic samples. RSC Adv. 2020, 10, 17506. [Google Scholar] [CrossRef]
- Al-Senani, M.G.; Al-Kadhi, S.N. Studies on adsorption of fluorescein dye from aqueous solutions using wild herbs. Int. J. Anal. Chem. 2020, 2020, 8019274. [Google Scholar] [CrossRef]
- Khan, T.F.; Price, B.L.; Morgan, P.B.; Maldonado-Codina, C.; Dobson, C.B. Cellular fluorescein hyperfluorescence is dynamin-dependent and increased by Tetronic 1107 treatment. Int. J. Biochem. Cell. Biol. 2018, 101, 54–63. [Google Scholar] [CrossRef] [Green Version]
- Ojha, N.; Rainey, K.H.; Patterson, G.H. Imaging of fluorescence anisotropy during photoswitching provides a simple readout for protein self-association. Nat. Commun. 2020, 11, 21. [Google Scholar] [CrossRef] [Green Version]
- Loura, L.M.S.; Prieto, M. FRET in membrane biophysics: An overview. Front. Physiol. 2011, 2, 82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chin, S.F.; Azman, A.; Pang, S.C.; Ng, S.M. Fluorescein-labeled starch maleate nanoparticles as sensitive fluorescent sensing probes for metal ions. J. Nanomater. 2014, 2014, 1. [Google Scholar] [CrossRef] [Green Version]
- Tatsumi, K.; Hsu, C.H.; Suzuki, A.; Nakabe, K. Liquid temperature measurement method in microchannels by using fluorescence polarization. Heat Mass Transf. 2018, 54, 2607–2616. [Google Scholar] [CrossRef]
- Sanchez, F.G.; Diaz, A.N.; Ruiz, C.C.; Guerrero, M.M.L. Fluid viscosity determination based on frequency domain time-resolved fluorescence anisotropy. J. Mol. Liq. 2010, 155, 121–126. [Google Scholar] [CrossRef]
- Ludwanowski, S.; Samanta, A.; Loescher, S.; Barner-Kowollik, C.; Walther, A. A Modular fluorescent probe for viscosity and polarity sensing in DNA hybrid mesostructures. Adv. Sci. 2020, 8, 2003740. [Google Scholar] [CrossRef] [PubMed]
- Cheng, N.S. Formula for the viscosity of a glycerol−water mixture. Ind. Eng. Chem. Res. 2008, 47, 3285–3288. [Google Scholar] [CrossRef]

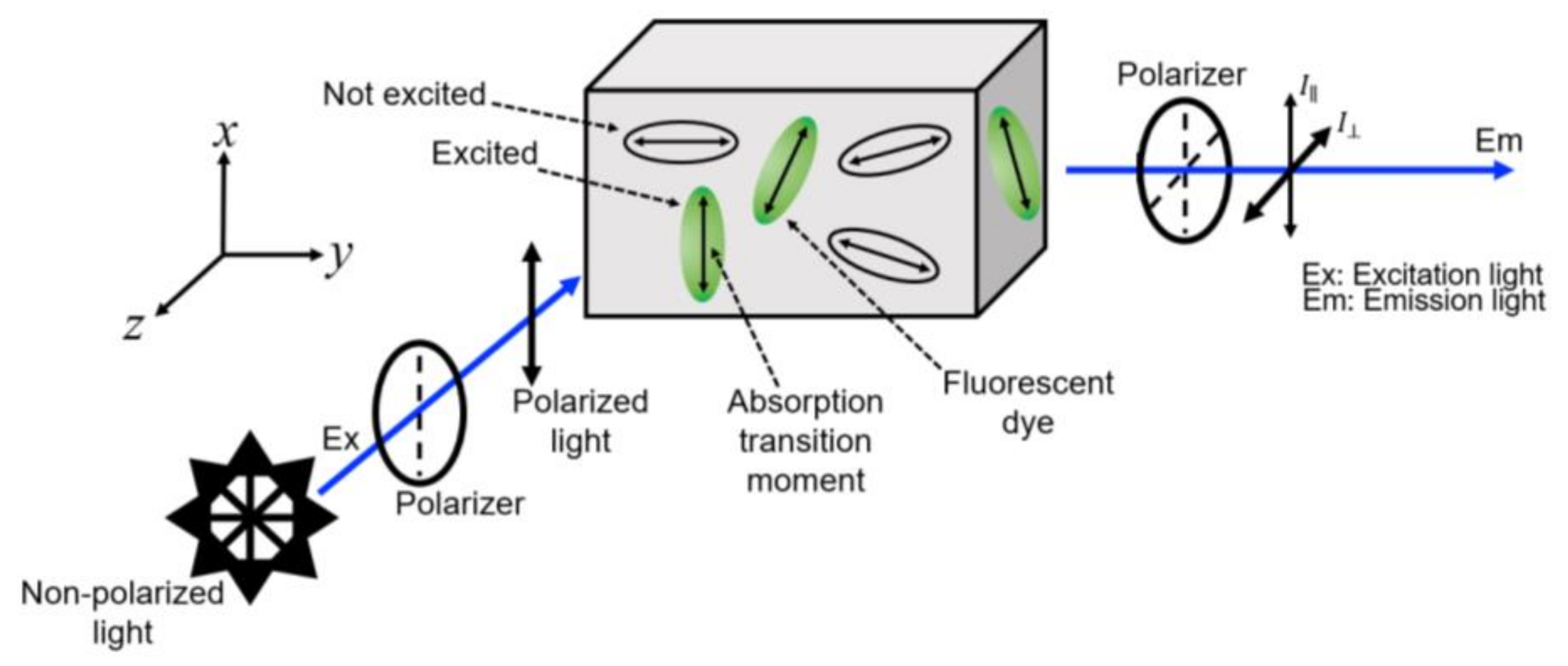
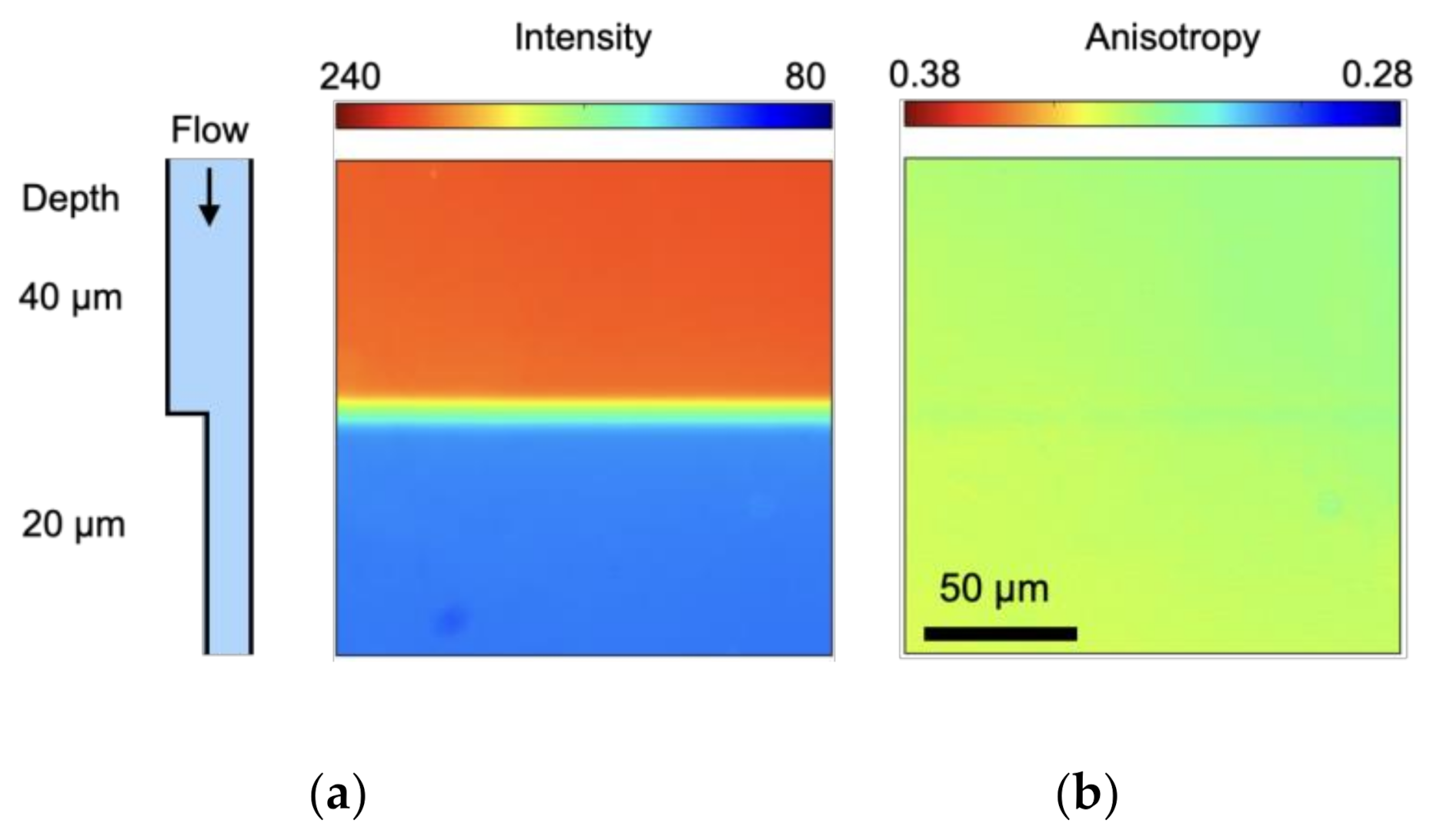
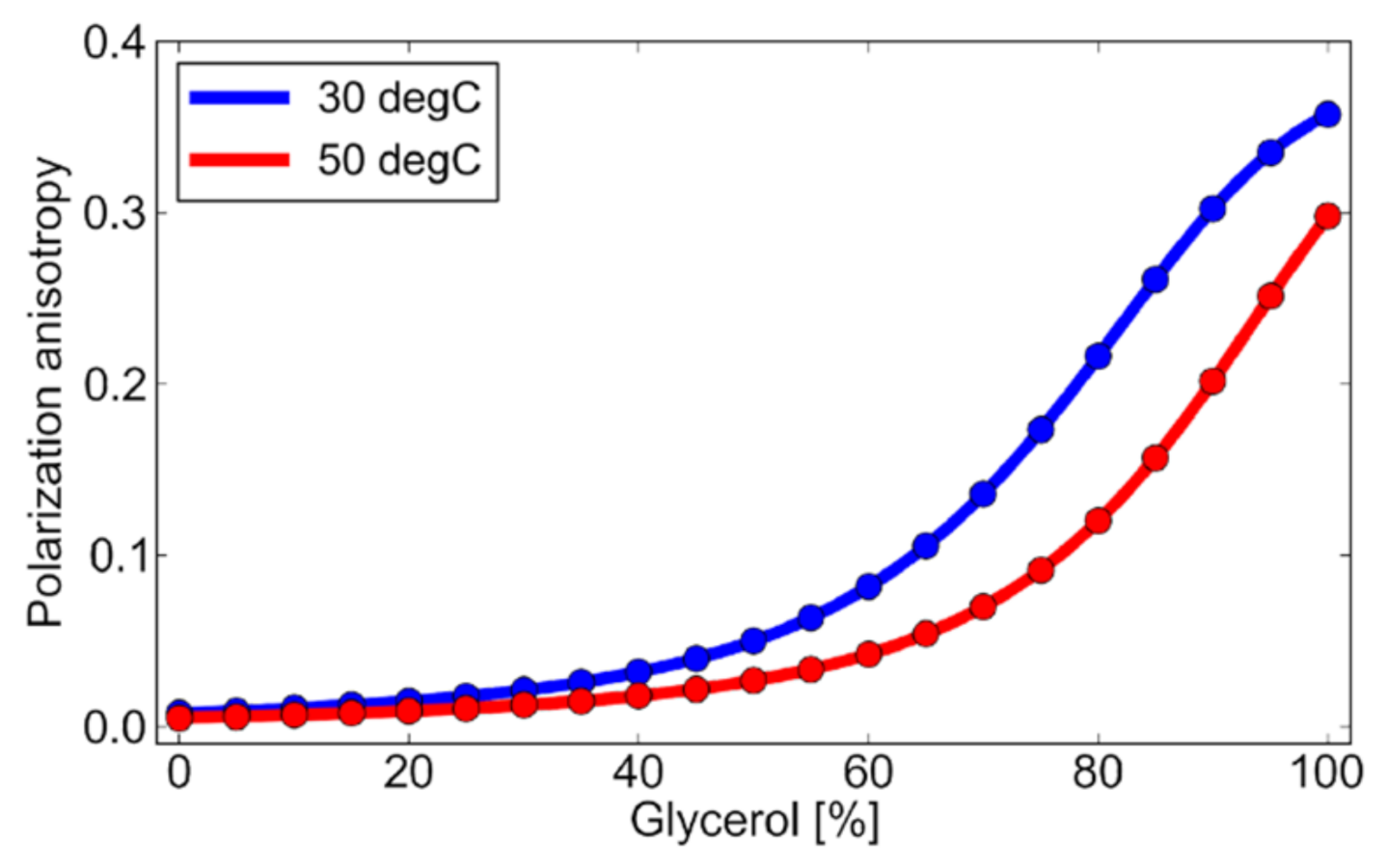
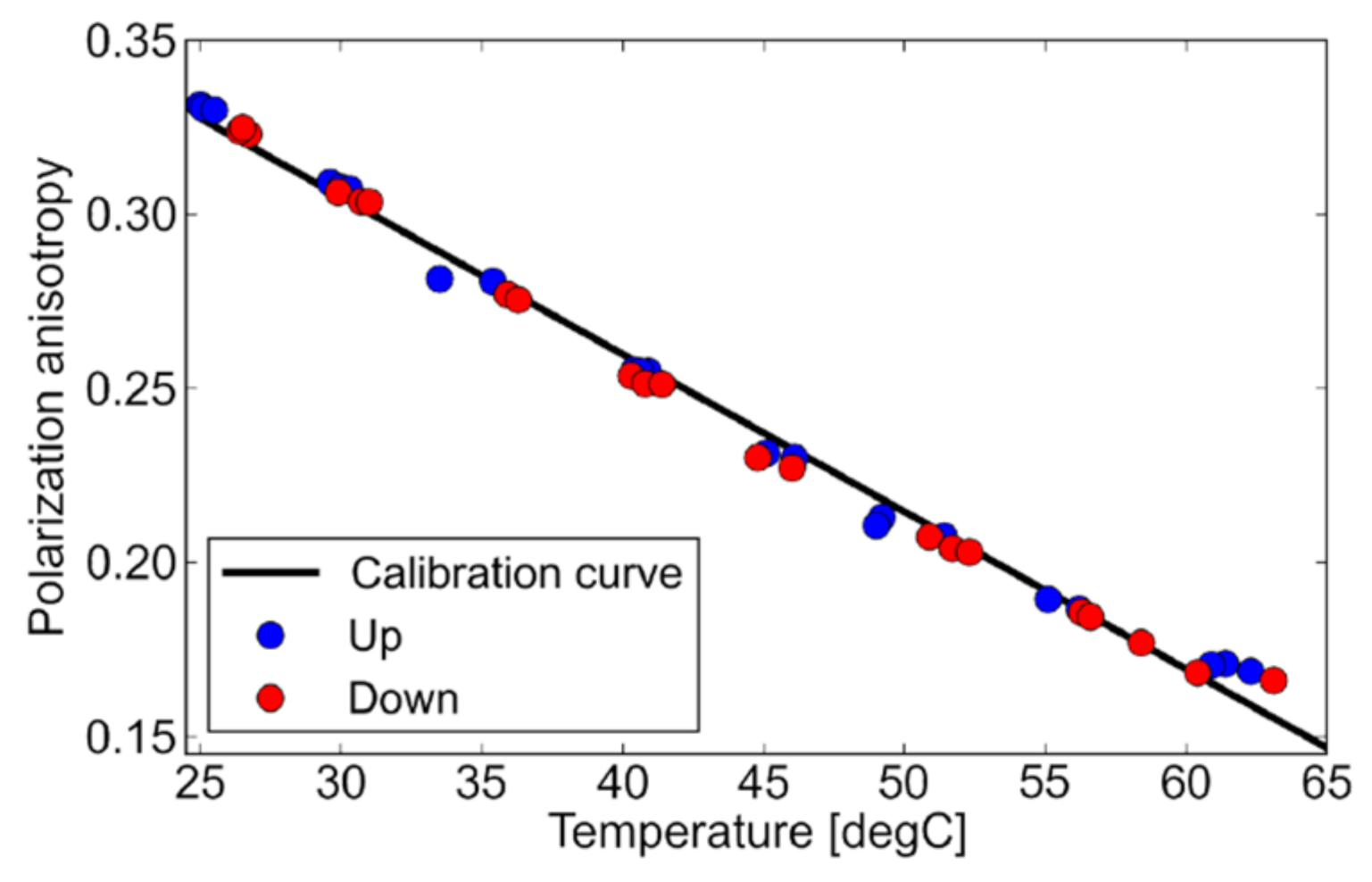
| Parameter | Value |
|---|---|
| Limiting anisotropy, r0 | 0.38 |
| Fluorescent lifetime, τ | 3.7 ns |
| Volume, V | 0.41 nm3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jain, P.; Aida, T.; Motosuke, M. Fluorescence Anisotropy as a Temperature-Sensing Molecular Probe Using Fluorescein. Micromachines 2021, 12, 1109. https://doi.org/10.3390/mi12091109
Jain P, Aida T, Motosuke M. Fluorescence Anisotropy as a Temperature-Sensing Molecular Probe Using Fluorescein. Micromachines. 2021; 12(9):1109. https://doi.org/10.3390/mi12091109
Chicago/Turabian StyleJain, Puneet, Takuya Aida, and Masahiro Motosuke. 2021. "Fluorescence Anisotropy as a Temperature-Sensing Molecular Probe Using Fluorescein" Micromachines 12, no. 9: 1109. https://doi.org/10.3390/mi12091109
APA StyleJain, P., Aida, T., & Motosuke, M. (2021). Fluorescence Anisotropy as a Temperature-Sensing Molecular Probe Using Fluorescein. Micromachines, 12(9), 1109. https://doi.org/10.3390/mi12091109






