Significant Involvement of Double Diffusion Theories on Viscoelastic Fluid Comprising Variable Thermophysical Properties
Abstract
1. Introduction
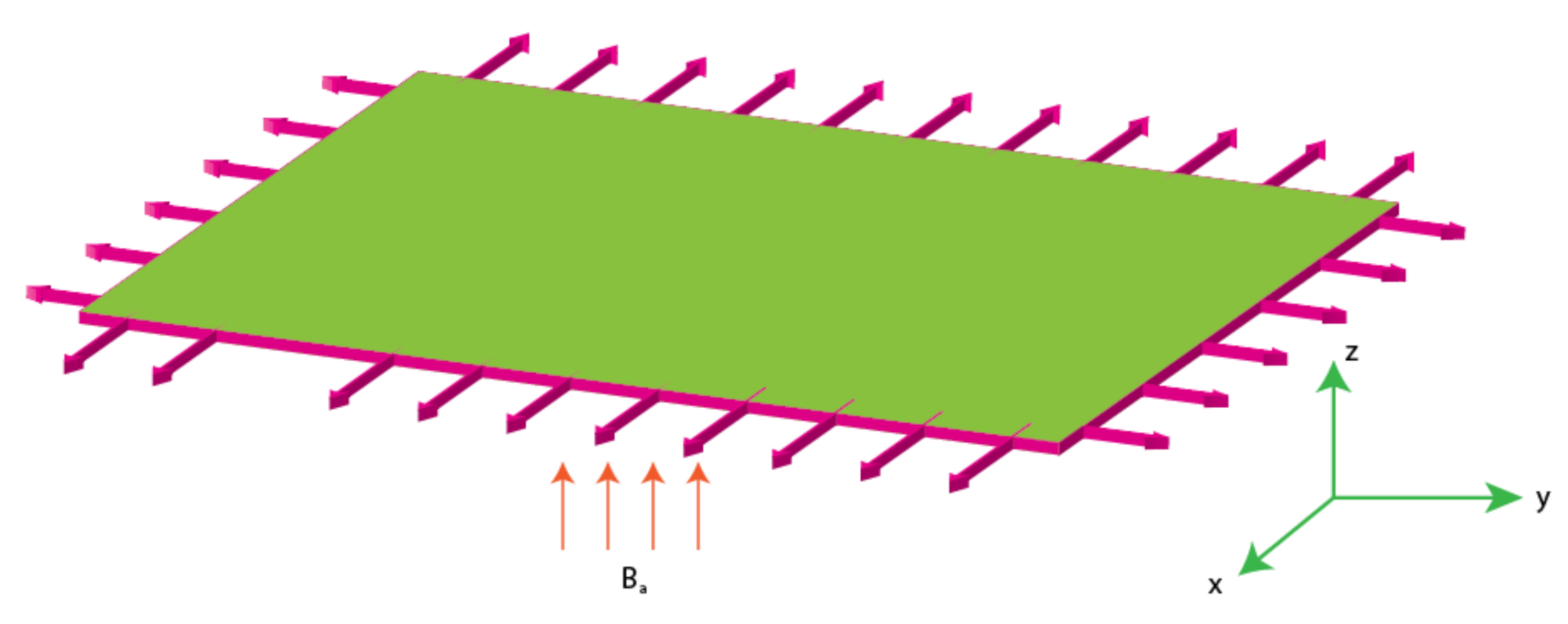
2. Mathematical Drafting of Viscoelastic Fluid with Thermal and Mass Transport
- ❖
- Three-dimensional flow;
- ❖
- Bi-directional elastic surface;
- ❖
- Incompressible fluid;
- ❖
- Steady flow;
- ❖
- Viscoelastic second grade fluid;
- ❖
- Heat flux via generalized theory of Cattaneo–Christov;
- ❖
- Temperature-dependent thermal conductivity model;
- ❖
- Space-dependent magnetic field;
- ❖
- Updated mass flux model with temperature dependent diffusion coefficient;
Physical Quantities
3. Numerical Method for Solution
- ❖
- Linear operator selection;
- ❖
- Using the boundary data;
- ❖
- Determination of unknown constants;
- ❖
- Adopting of initial guesses;
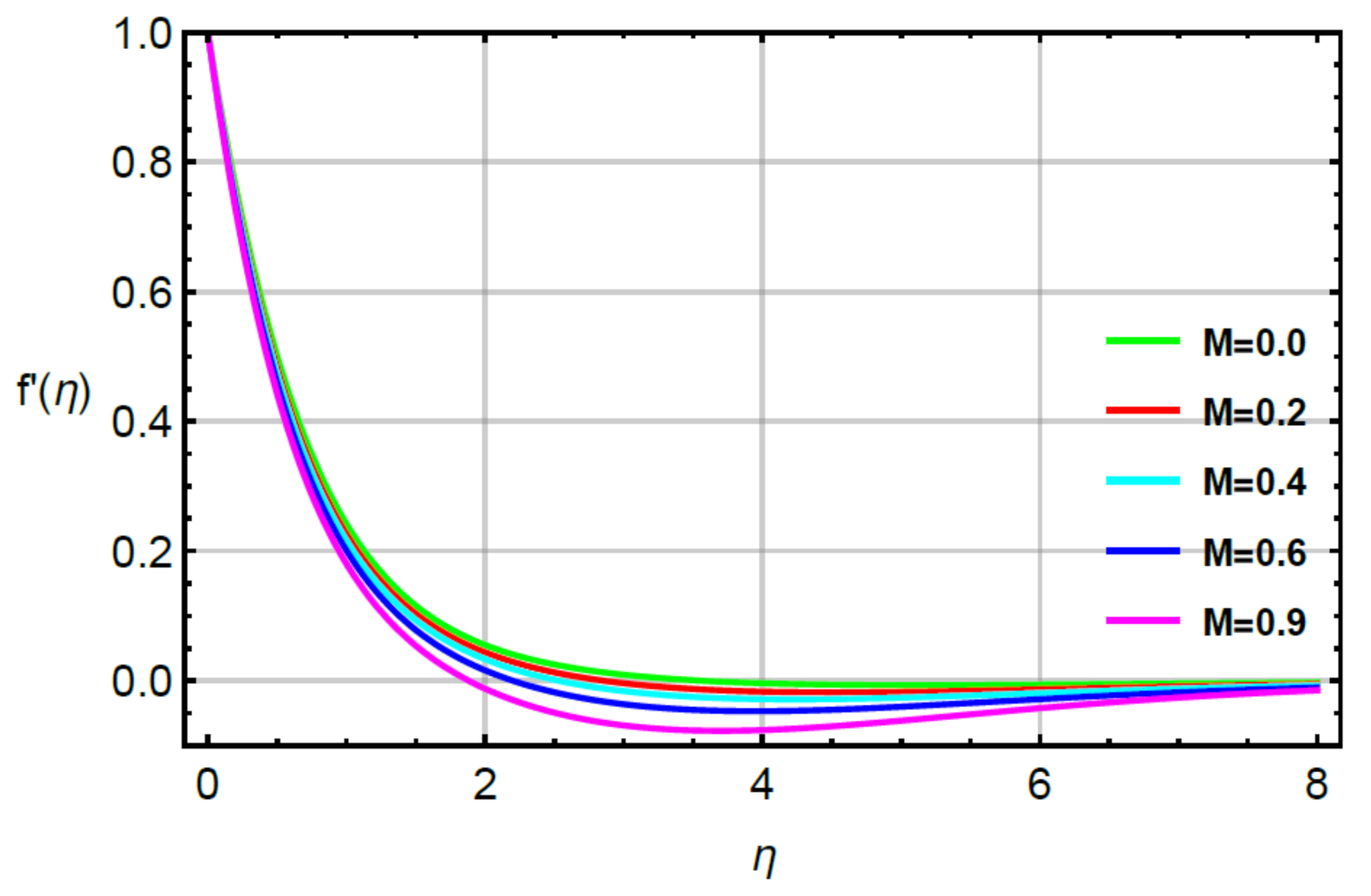
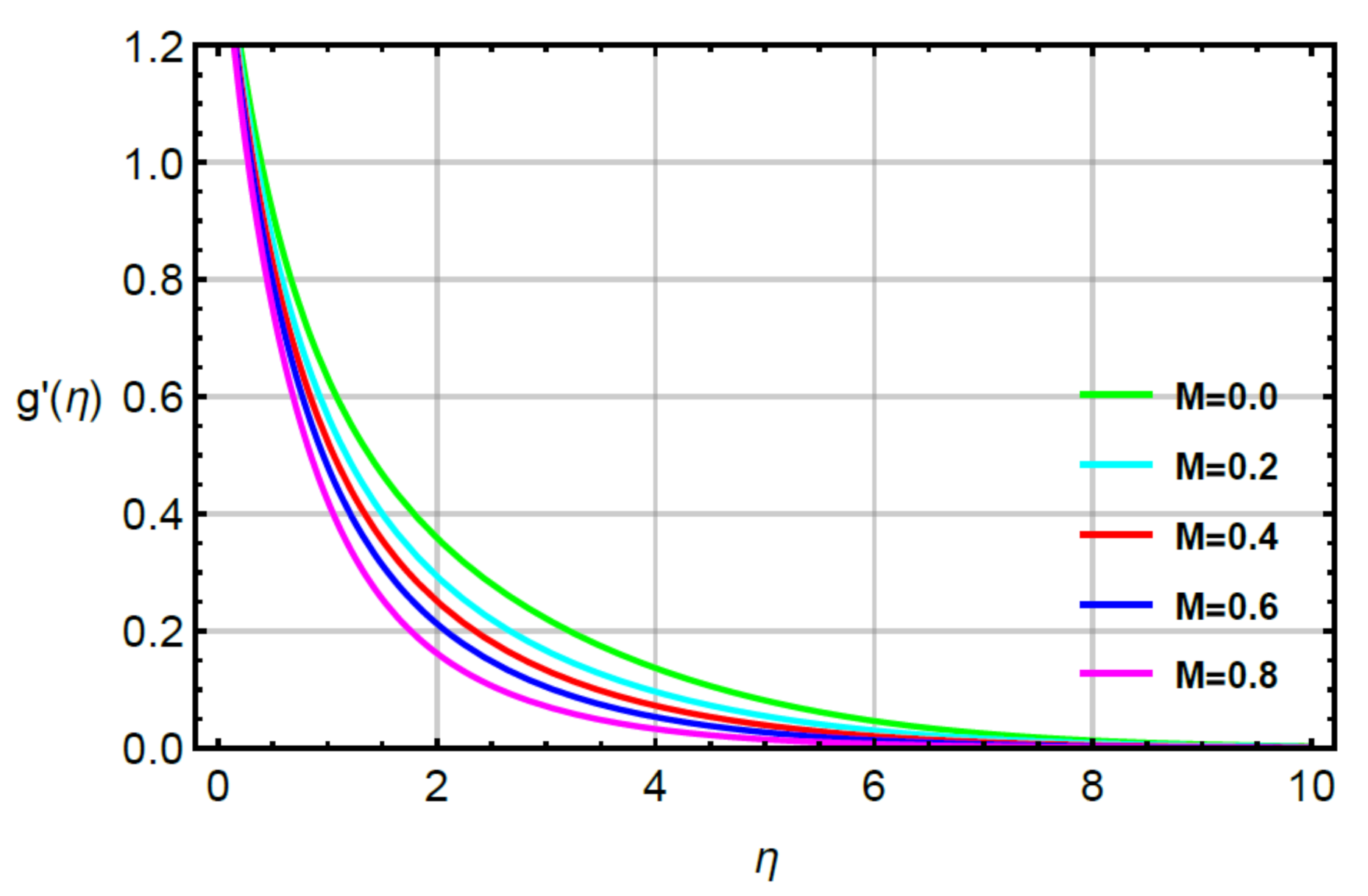
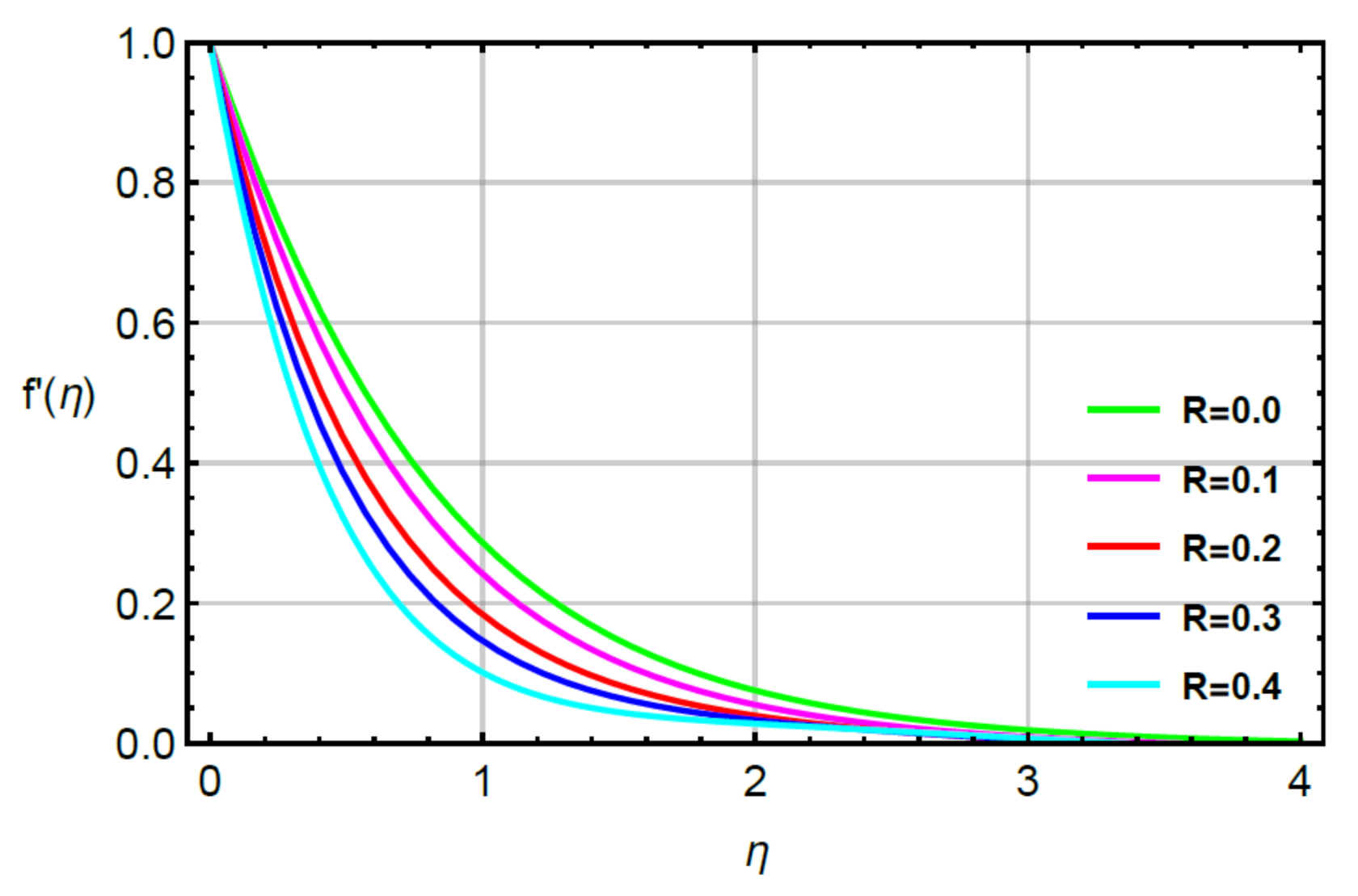
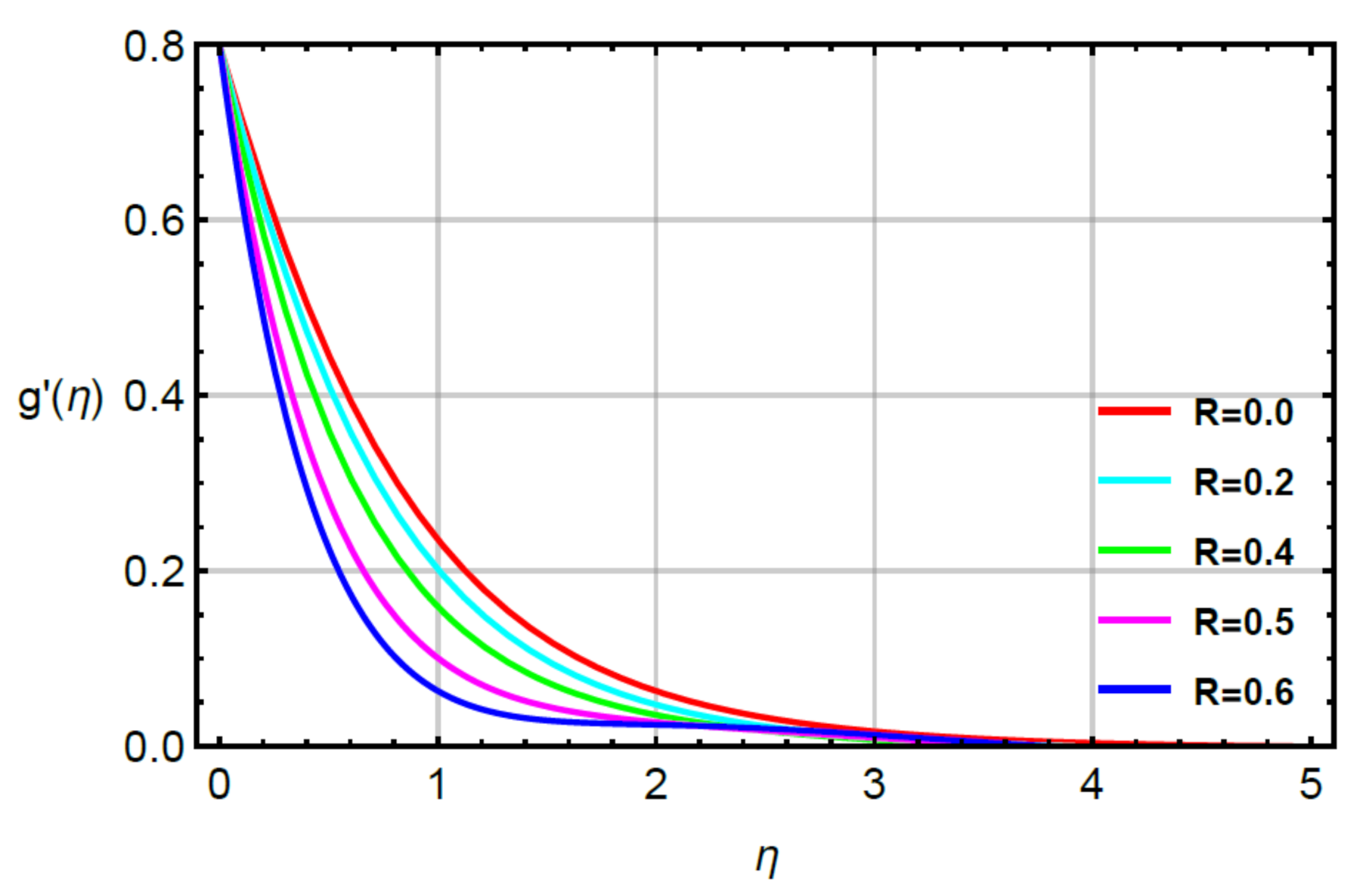
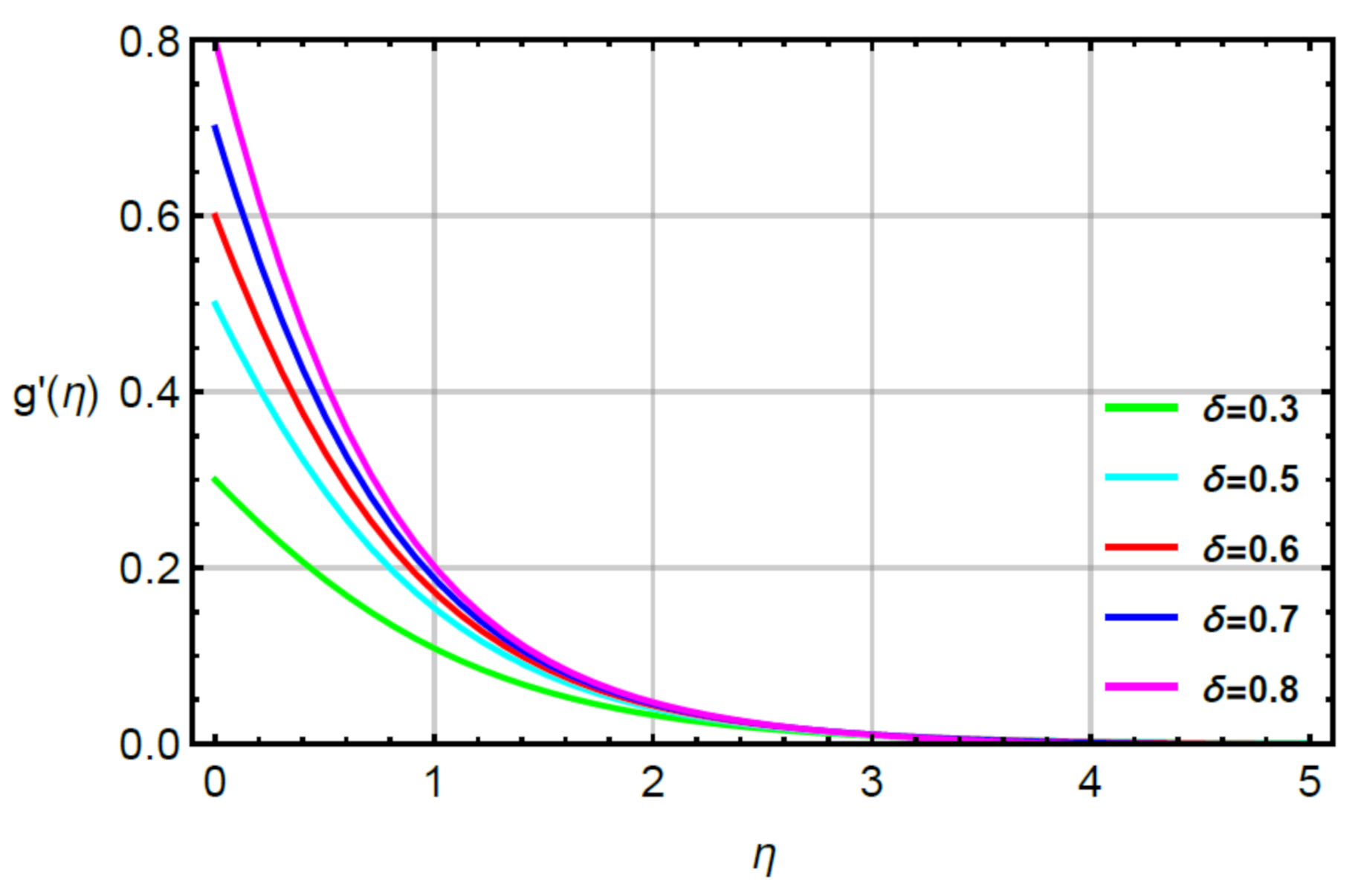
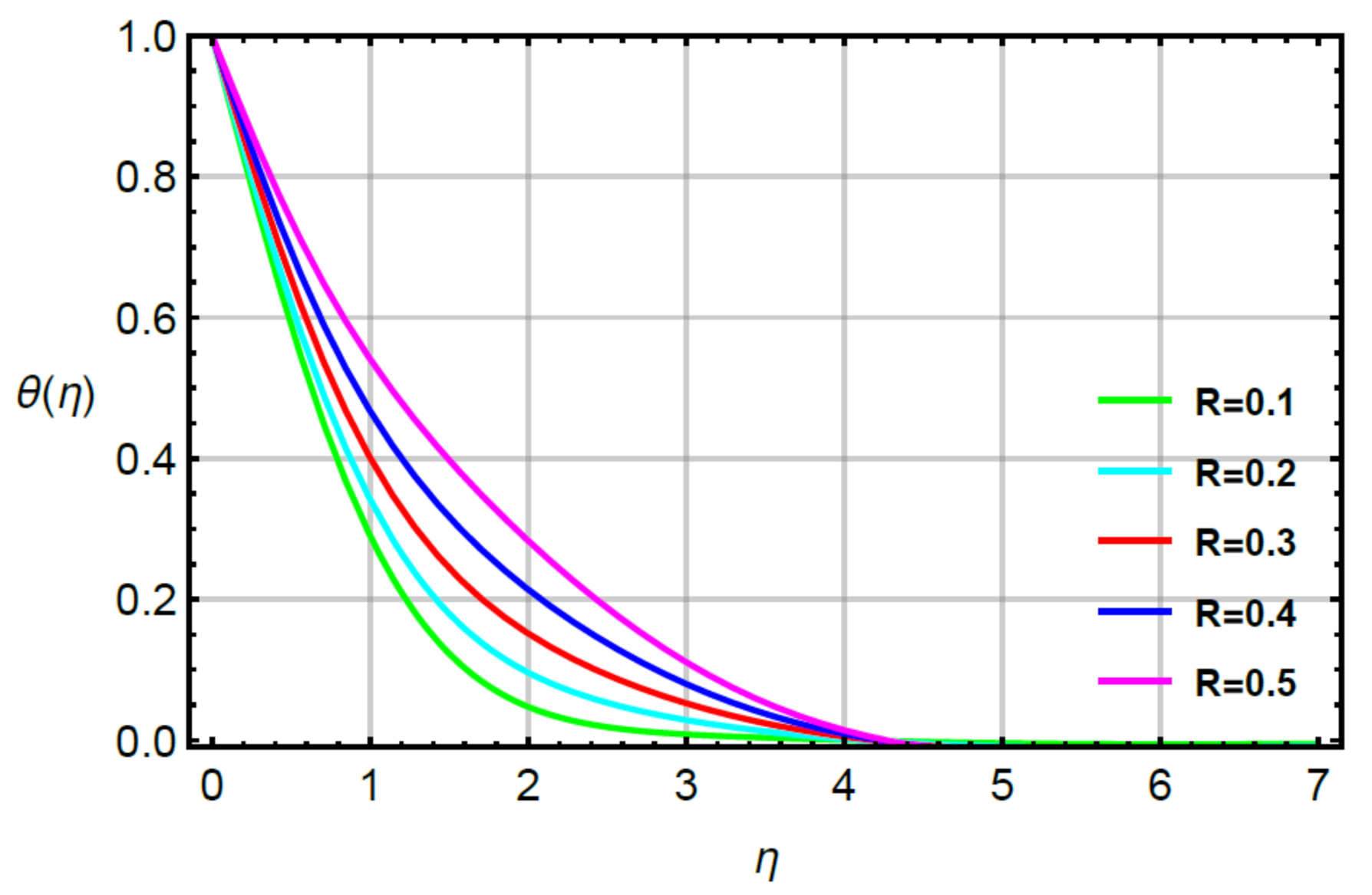
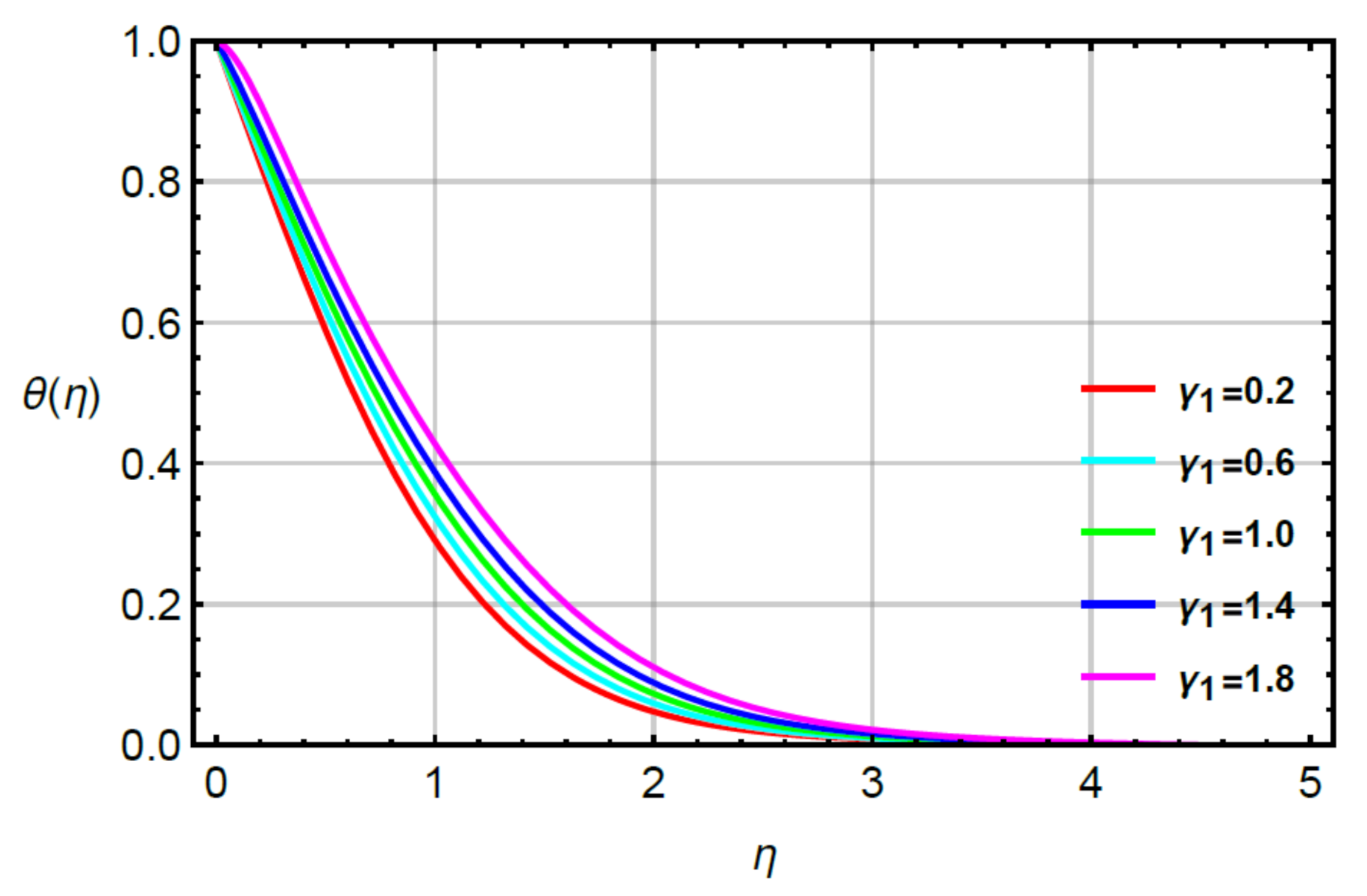
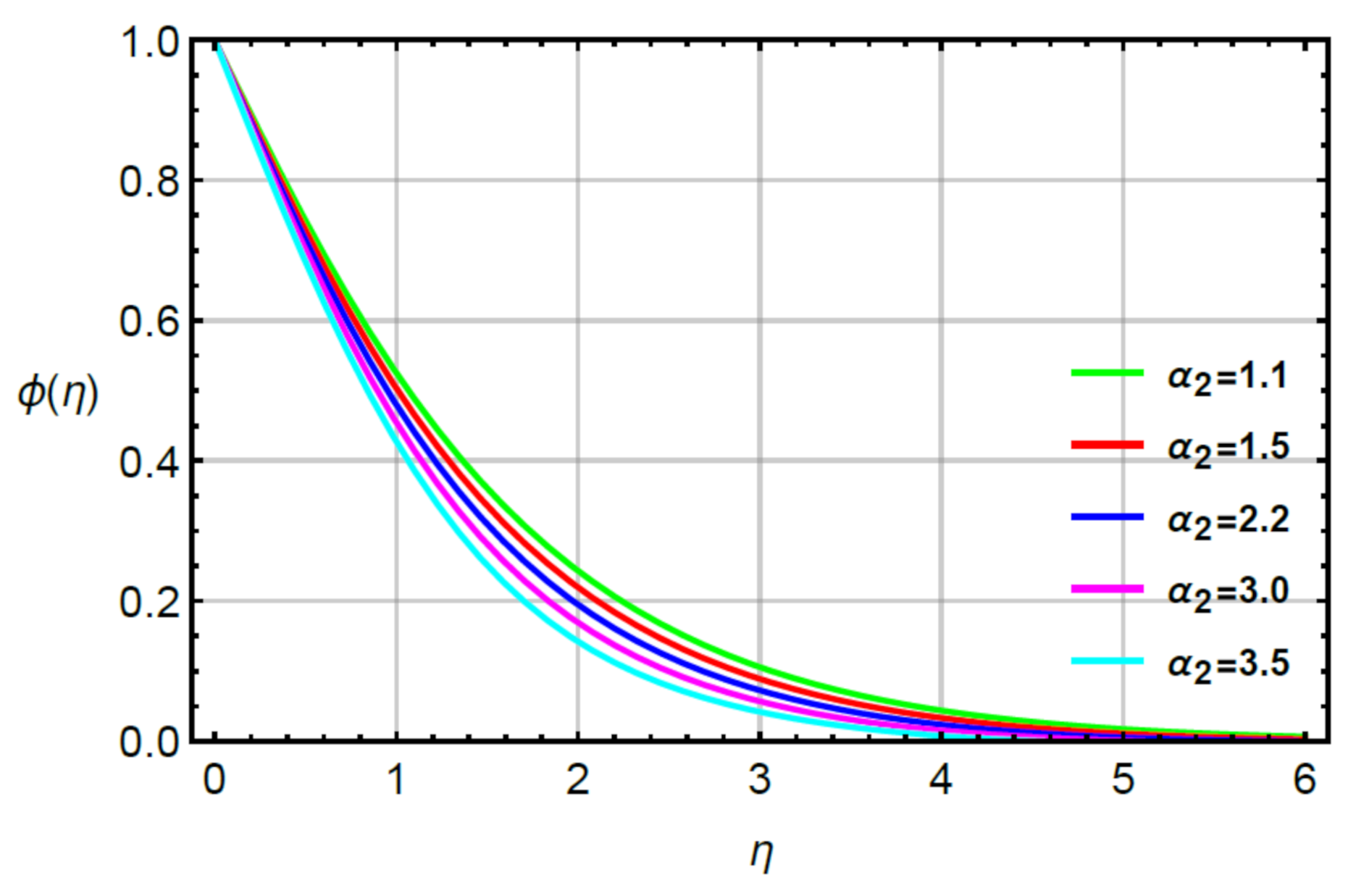
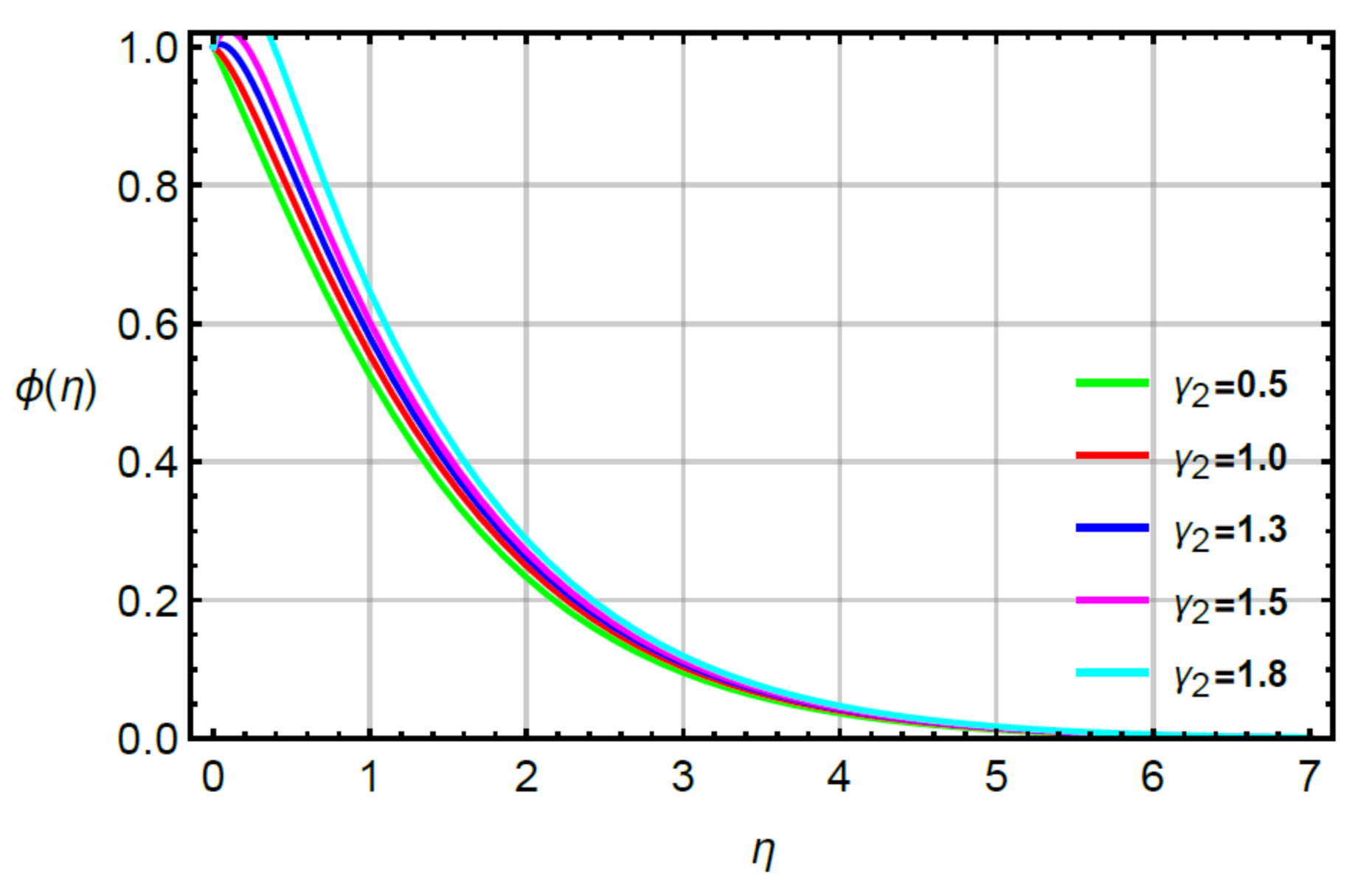
4. Analysis and Discussion
5. Conclusions and Key Findings of the Investigation Performed
- The improvement in motion of fluid particles was captured via large values of second grade fluid and stretching ratio numbers while a decrement in flow behavior was conducted via enlargement in magnetic number;
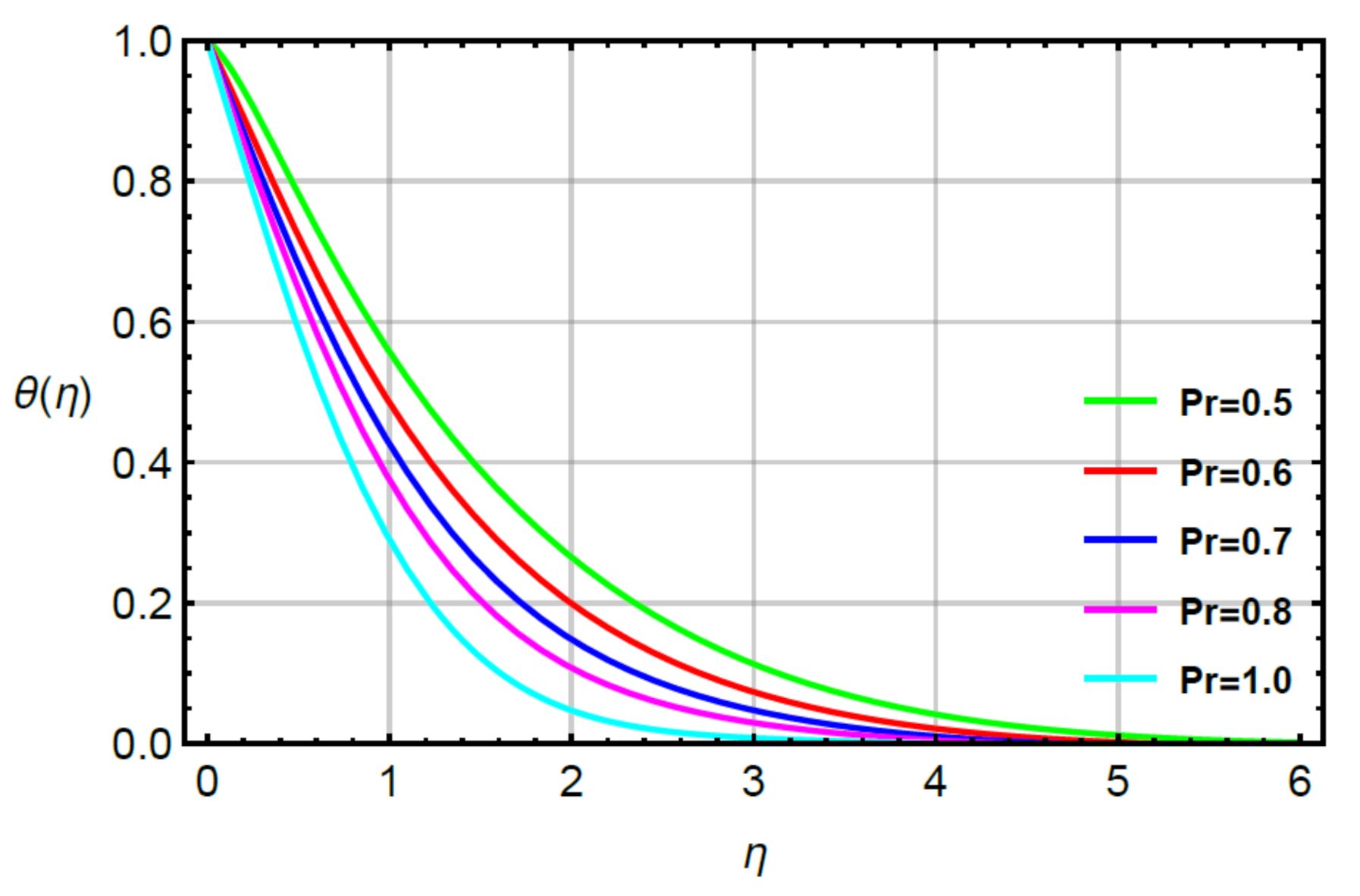
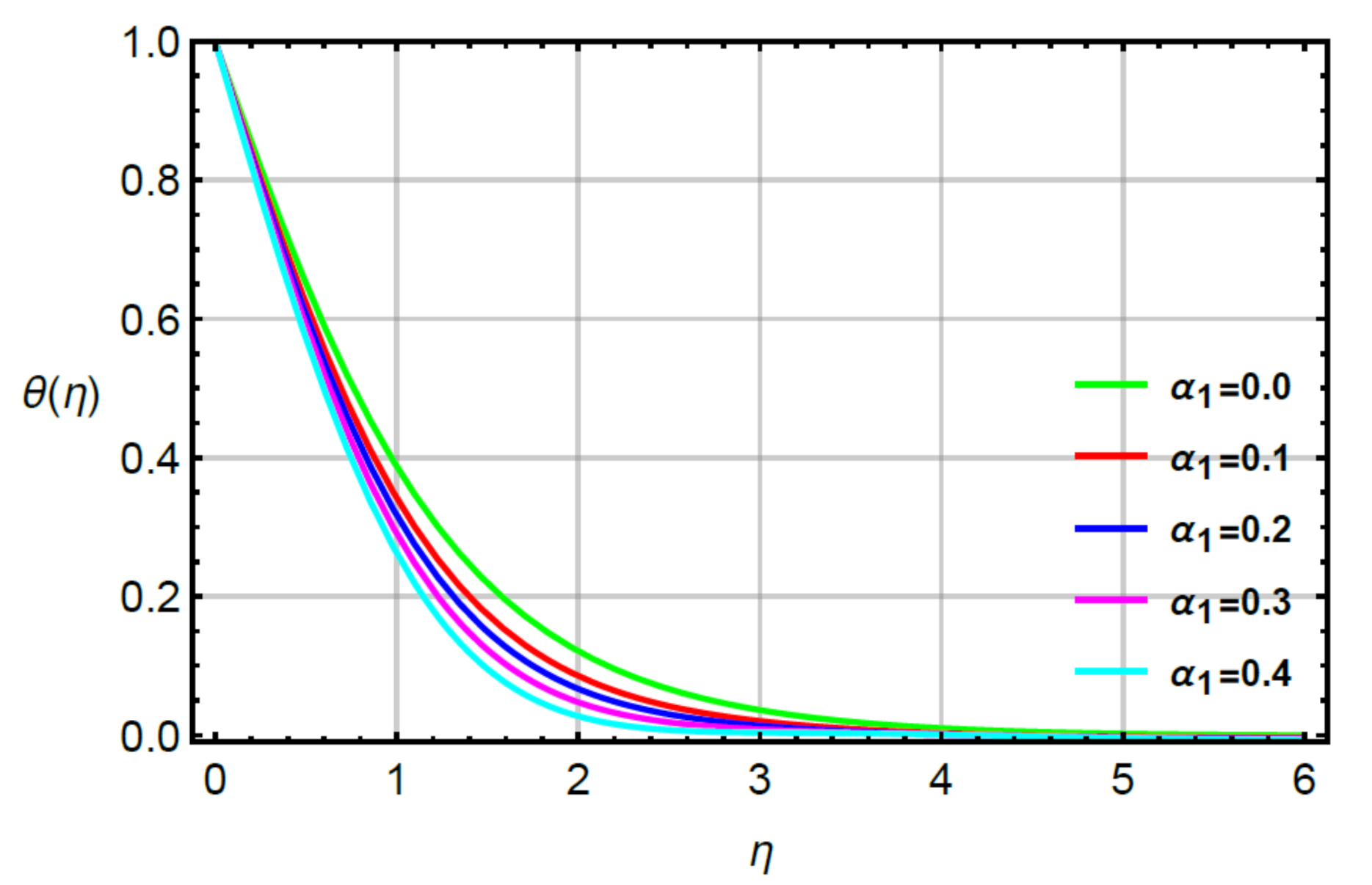
- The mechanism of heat energy became maximum using higher values of second grade fluid number but an opposite trend was captured via large values of time relaxation, Prandtl and very small numbers;
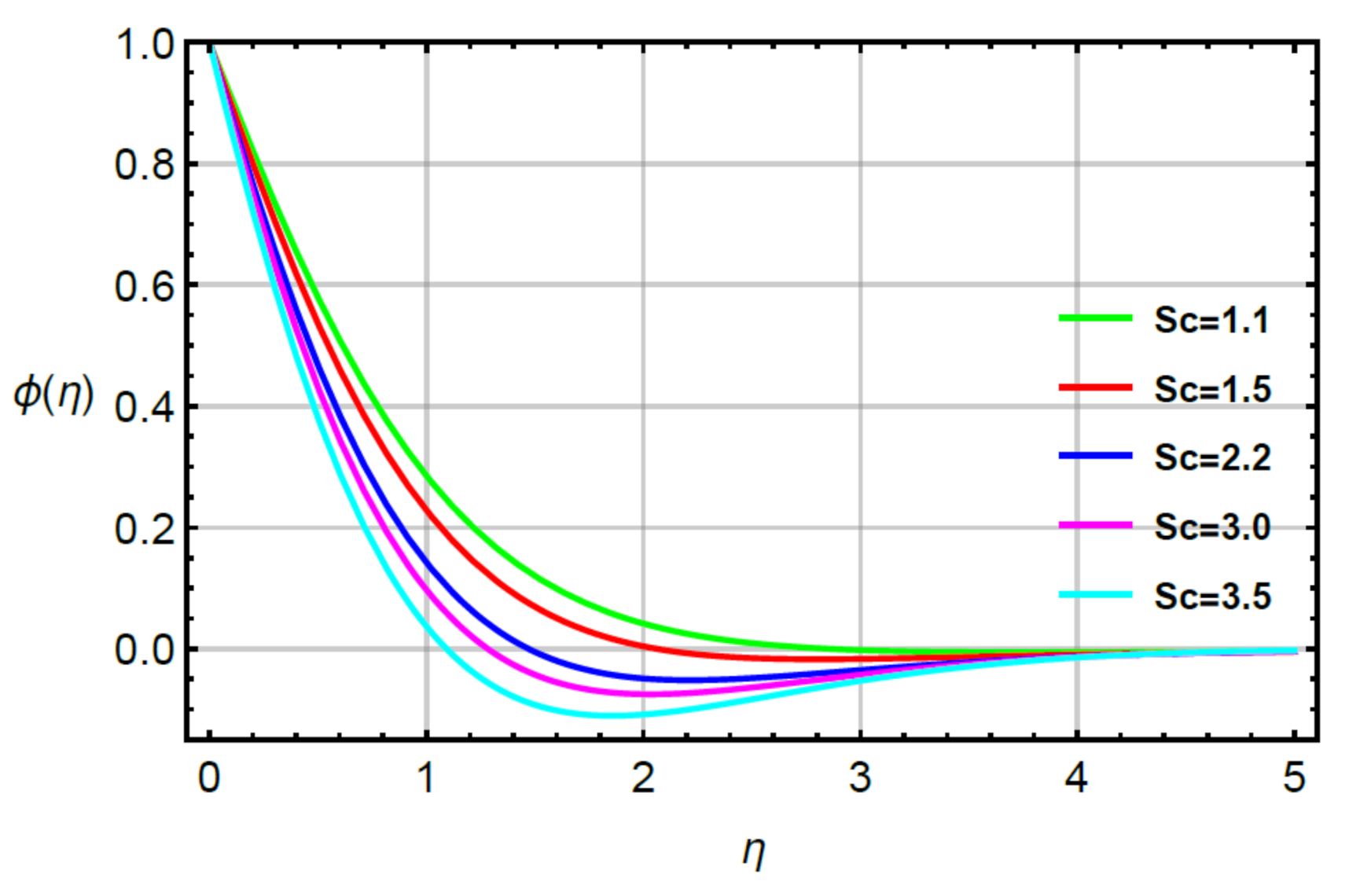
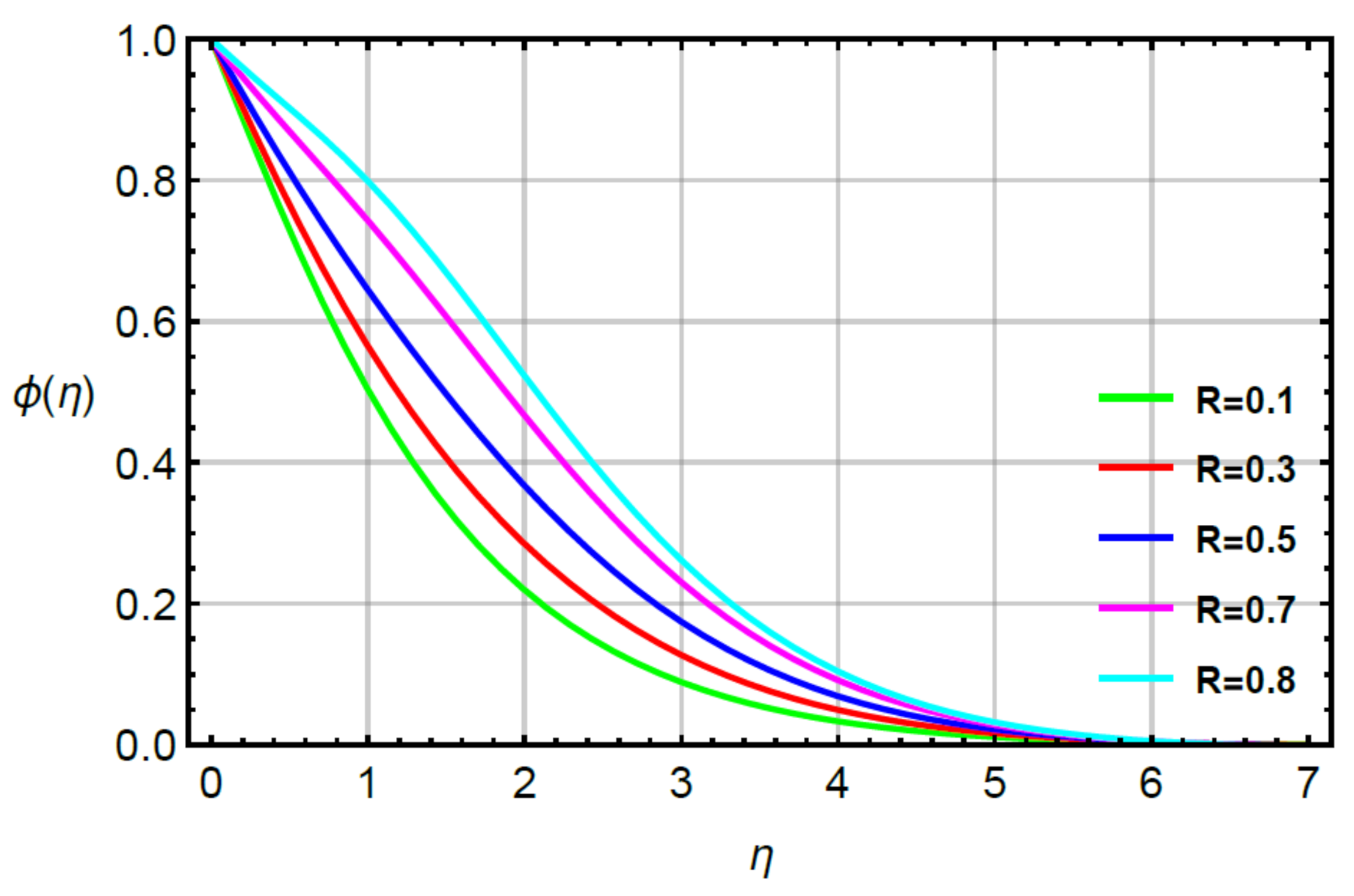
- The solute became fast considering large values of second grade fluid, time relaxation and very small numbers. The reduction in solute became slow against variation in Schmidt number;
- An incline in rate of solute and gradient temperature was addressed against higher values of time relaxation numbers;
- The surface force was enhanced near the wall of the hot surface via large values of second grade liquid and flow stretching parameters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Used for | Symbols | Used for |
| and | Velocity at wall | Space coordinates | |
| Dimensional velocity | Kinematic viscosity | ||
| Non-uniform magnetic field | Electrical conductivity | ||
| Fluid density | stretching ratio number | ||
| Heat transfer rate | Mass transportation rate | ||
| TBL | Thermal boundary layer | MBL | Momentum boundary layer |
| Linear operators | Initial guesses | ||
| Dimensionless concentration | Dimensionless temperature | ||
| Dimensionless independent variable | Prandtl number | ||
| Concentration relaxation time | Temperature relaxation time | ||
| Schmidt number | Dimensionless velocity | ||
| Fluid parameter | Magnetic parameter |
References
- Hayat, T.; Anwar, M.S.; Farooq, M.; Alsaedi, A. Mixed convection flow of viscoelastic fluid by a stretching cylinder with heat transfer. PLoS ONE 2015, 10, e0118815. [Google Scholar] [CrossRef]
- Massoudi, M.; Vaidya, A.; Wulandana, R. Natural convection flow of a generalized second grade fluid between two vertical walls. Nonlinear Anal. Real World Appl. 2008, 9, 80–93. [Google Scholar] [CrossRef]
- Fetecau, C.; Nazar, A.; Khan, I.; Shah, N.A. First exact solution for a second grade fluid subject to an oscillating shear stress induced by a sphere. J. Nonlinear Sci. 2018, 19, 186–195. [Google Scholar]
- Kamran, M.; Imran, M.; Athar, M. Analytical Solutions for the Flow of a Fractional Second Grade Fluid due to a Rotational Constantly Accelerating Shear. Int. Sch. Res. Not. 2012, 2012. [Google Scholar] [CrossRef][Green Version]
- Mohamad, A.Q.; Khan, I.; Zin, N.A.M.; Ismail, Z.; Shafie, S. The unsteady mixed convection flow of rotating second grade fluid in porous medium with ramped wall temperature. Malays. J. Fundam. Appl. Sci. 2017, 13, 798–802. [Google Scholar] [CrossRef]
- Chauhan, D.S.; Kumar, V. Unsteady flow of a non-Newtonian second grade fluid in a channel partially filled by a porous medium. Adv. Appl. Sci. Res. 2012, 2, 1–2. [Google Scholar]
- Hayat, T.; Ayub, T.; Muhammad, T.; Alsaedi, A. Three-dimensional flow with Cattaneo–Christov double diffusion and homogeneous-heterogeneous reactions. Results Phys. 2017, 7, 2812–2820. [Google Scholar] [CrossRef]
- Moon, J.H.; Kim, D.Y.; Lee, S.H. Spreading and receding characteristics of a non-Newtonian droplet impinging on a heated surface. Exp. Therm. Fluid Sci. 2014, 57, 94–101. [Google Scholar] [CrossRef]
- German, G.; Bertola, V. The free-fall of viscoplastic drops. J. Non Newton. Fluid Mech. 2010, 165, 825–828. [Google Scholar] [CrossRef]
- An, S.M.; Lee, S.Y. Observation of the spreading and receding behavior of a shear-thinning liquid drop impacting on dry solid surfaces. Exp. Therm. Fluid Sci. 2012, 37, 37–45. [Google Scholar] [CrossRef]
- Moon, J.H.; Choi, C.K.; Allen, J.S.; Lee, S.H. Observation of a mixed regime for an impinging droplet on a sessile droplet. Int. J. Heat Mass Transf. 2018, 127, 130–135. [Google Scholar] [CrossRef]
- Zhao, J.; Khayat, R.E. Spread of a non-Newtonian liquid jet over a horizontal plate. J. Fluid Mech. 2008, 613, 411–443. [Google Scholar] [CrossRef]
- Moon, J.H.; Lee, J.B.; Lee, S.H. Dynamic behavior of non-Newtonian droplets impinging on solid surfaces. Mater. Trans. 2013, 54, 260–265. [Google Scholar] [CrossRef]
- Naseem, A.; Shafiq, A.; Zhao, L.; Farooq, M.U. Analytical investigation of third grade nanofluidic flow over a riga plate using Cattaneo-Christov model. Results Phys. 2018, 9, 961–969. [Google Scholar] [CrossRef]
- Sahoo, B.; Poncet, S. Blasius flow and heat transfer of fourth-grade fluid with slip. Appl. Math. Mech. 2013, 34, 1465–1480. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Gireesha, B.J.; Bagewadi, C.S. MHD flow of a dusty fluid near the stagnation point over a permeable stretching sheet with non-uniform source/sink. Int. J. Heat Mass Transf. 2012, 55, 4900–4907. [Google Scholar] [CrossRef]
- Qiu, S.; Xie, Z.; Chen, L.; Yang, A.; Zhou, J. Entropy generation analysis for convective heat transfer of nanofluids in tree-shaped network flowing channels. Therm. Sci. Eng. Prog. 2018, 5, 546–554. [Google Scholar] [CrossRef]
- Khan, M.I.; Kiyani, M.Z.; Malik, M.Y.; Yasmeen, T.; Khan, M.W.A.; Abbas, T. Numerical investigation of magnetohydrodynamic stagnation point flow with variable properties. Alex. Eng. J. 2016, 55, 2367–2373. [Google Scholar] [CrossRef]
- Sohail, M.; Naz, R. Modified heat and mass transmission models in the magnetohydrodynamic flow of Sutterby nanofluid in stretching cylinder. Phys. A Stat. Mech. Appl. 2020, 549, 124088. [Google Scholar] [CrossRef]
- Sohail, M.; Raza, R. Analysis of radiative magneto nano pseudo-plastic material over three dimensional nonlinear stretched surface with passive control of mass flux and chemically responsive species. Multidiscip. Modeling Mater. Struct. 2020, 16, 1061–1083. [Google Scholar] [CrossRef]
- Sohail, M.; Tariq, S. Dynamical and optimal procedure to analyze the attributes of yield exhibiting material with double diffusion theories. Multidiscip. Modeling Mater. Struct. 2019, 16, 557–580. [Google Scholar] [CrossRef]
- Sohail, M.; Naz, R.; Bilal, S. Thermal performance of an MHD radiative Oldroyd-B nanofluid by utilizing generalized models for heat and mass fluxes in the presence of bioconvective gyrotactic microorganisms and variable thermal conductivity. Heat Transf. Asian Res. 2019, 48, 2659–2675. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Non-standard Lagrangians in rotational dynamics and the modified Navier–Stokes equation. Nonlinear Dyn. 2015, 79, 2055–2068. [Google Scholar] [CrossRef]
- Sohail, M.; Nazir, U.; Chu, Y.M.; Alrabaiah, H.; Al-Kouz, W.; Thounthong, P. Computational exploration for radiative flow of Sutterby nanofluid with variable temperature-dependent thermal conductivity and diffusion coefficient. Open Phys. 2020, 18, 1073–1083. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Fractional Navier-Stokes equation from fractional velocity arguments and its implications in fluid flows and microfilaments. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 449–459. [Google Scholar] [CrossRef]
| 1 | ||||
| 4 | ||||
| 8 | ||||
| 12 | ||||
| 16 | ||||
| 20 |
[7] | Present | [7] | Present | ||
|---|---|---|---|---|---|
| 0.0 | 0.1 | 1.0203 | 1.0209 | 0.0669 | 0.0668 |
| 0.15 | - | 1.6510 | 1.6519 | 0.0785 | 0.0784 |
| 0.2 | - | 1.8970 | 1.8975 | 0.0806 | 0.0803 |
| 0.1 | 0.0 | 1.3703 | 1.3707 | 0.0000 | 0.0000 |
| - | 0.2 | 1.4798 | 1.4798 | 0.1762 | 0.1769 |
| - | 0.5 | 1.6510 | 1.6516 | 0.6317 | 0.6312 |
[7] | Present Results | |
|---|---|---|
| 0.0 | 0.6051 | 0.6059 |
| 0.2 | 0.6258 | 0.6256 |
| 0.4 | 0.6483 | 0.6489 |
| 0.6 | 0.6727 | 0.6729 |
[7] | Present Results | |
|---|---|---|
| 0.0 | 0.3668 | 0.3669 |
| 0.2 | 0.3764 | 0.3760 |
| 0.4 | 0.3864 | 0.3862 |
| 0.6 | 0.3973 | 0.3978 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sohail, M.; Nazir, U.; Bazighifan, O.; El-Nabulsi, R.A.; Selim, M.M.; Alrabaiah, H.; Thounthong, P. Significant Involvement of Double Diffusion Theories on Viscoelastic Fluid Comprising Variable Thermophysical Properties. Micromachines 2021, 12, 951. https://doi.org/10.3390/mi12080951
Sohail M, Nazir U, Bazighifan O, El-Nabulsi RA, Selim MM, Alrabaiah H, Thounthong P. Significant Involvement of Double Diffusion Theories on Viscoelastic Fluid Comprising Variable Thermophysical Properties. Micromachines. 2021; 12(8):951. https://doi.org/10.3390/mi12080951
Chicago/Turabian StyleSohail, Muhammad, Umar Nazir, Omar Bazighifan, Rami Ahmad El-Nabulsi, Mahmoud M. Selim, Hussam Alrabaiah, and Phatiphat Thounthong. 2021. "Significant Involvement of Double Diffusion Theories on Viscoelastic Fluid Comprising Variable Thermophysical Properties" Micromachines 12, no. 8: 951. https://doi.org/10.3390/mi12080951
APA StyleSohail, M., Nazir, U., Bazighifan, O., El-Nabulsi, R. A., Selim, M. M., Alrabaiah, H., & Thounthong, P. (2021). Significant Involvement of Double Diffusion Theories on Viscoelastic Fluid Comprising Variable Thermophysical Properties. Micromachines, 12(8), 951. https://doi.org/10.3390/mi12080951










