A Low-g MEMS Accelerometer with High Sensitivity, Low Nonlinearity and Large Dynamic Range Based on Mode-Localization of 3-DoF Weakly Coupled Resonators
Abstract
1. Introduction
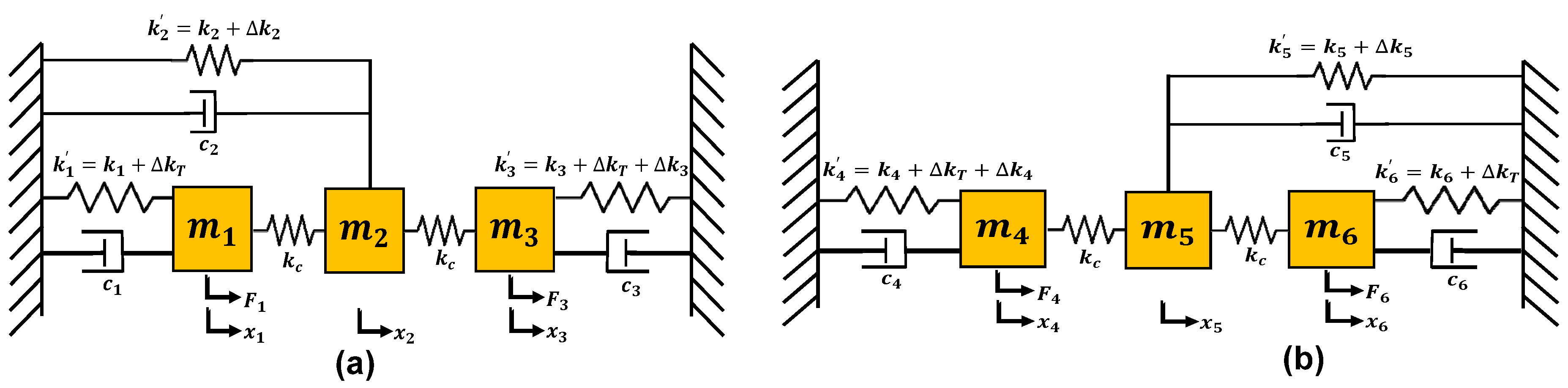
2. Structural Design and Working Principle
3. Mathematical Model
4. Performance Analysis of the MEMS Accelerometer Design
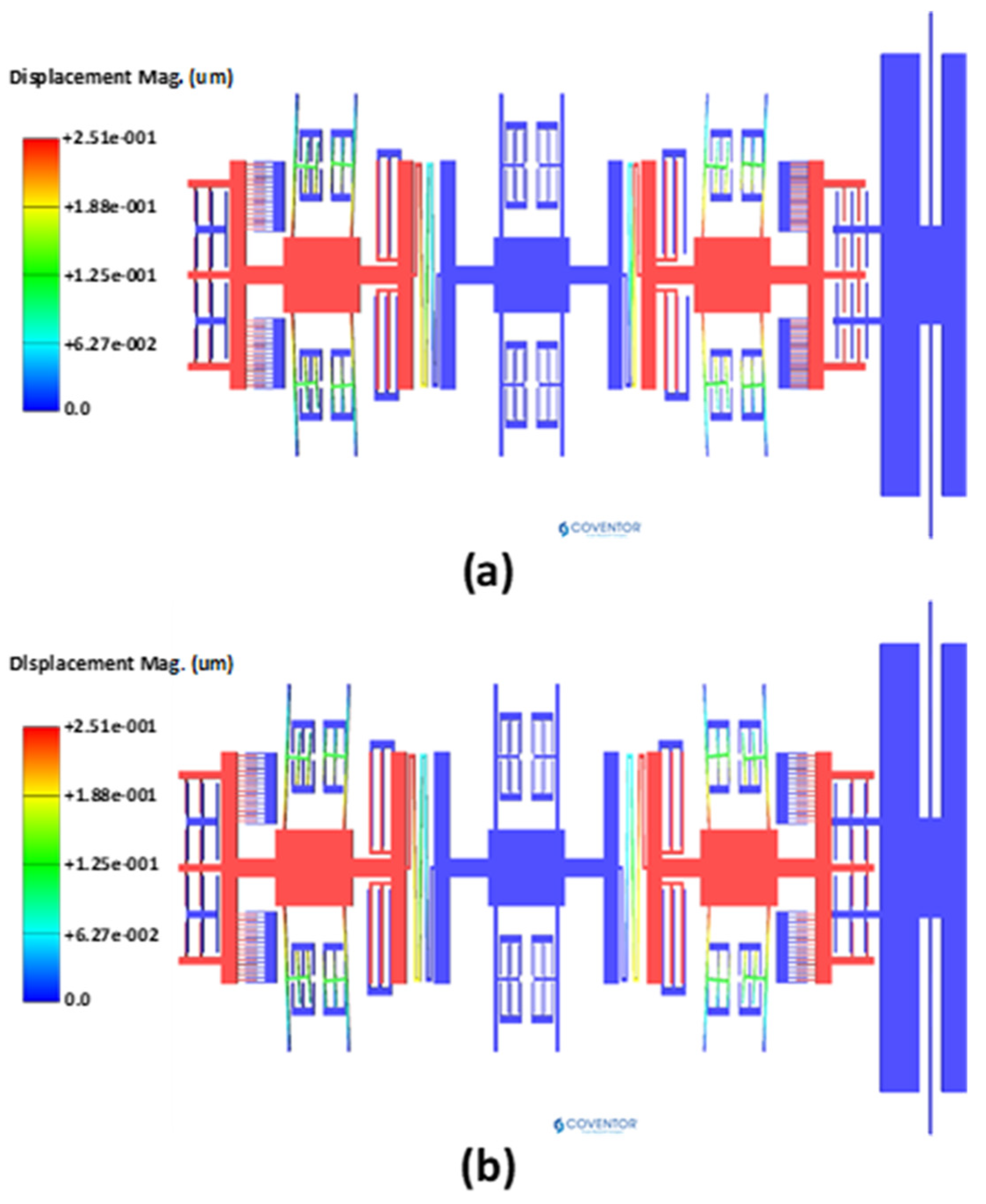
4.1. Natural Frequency Analysis
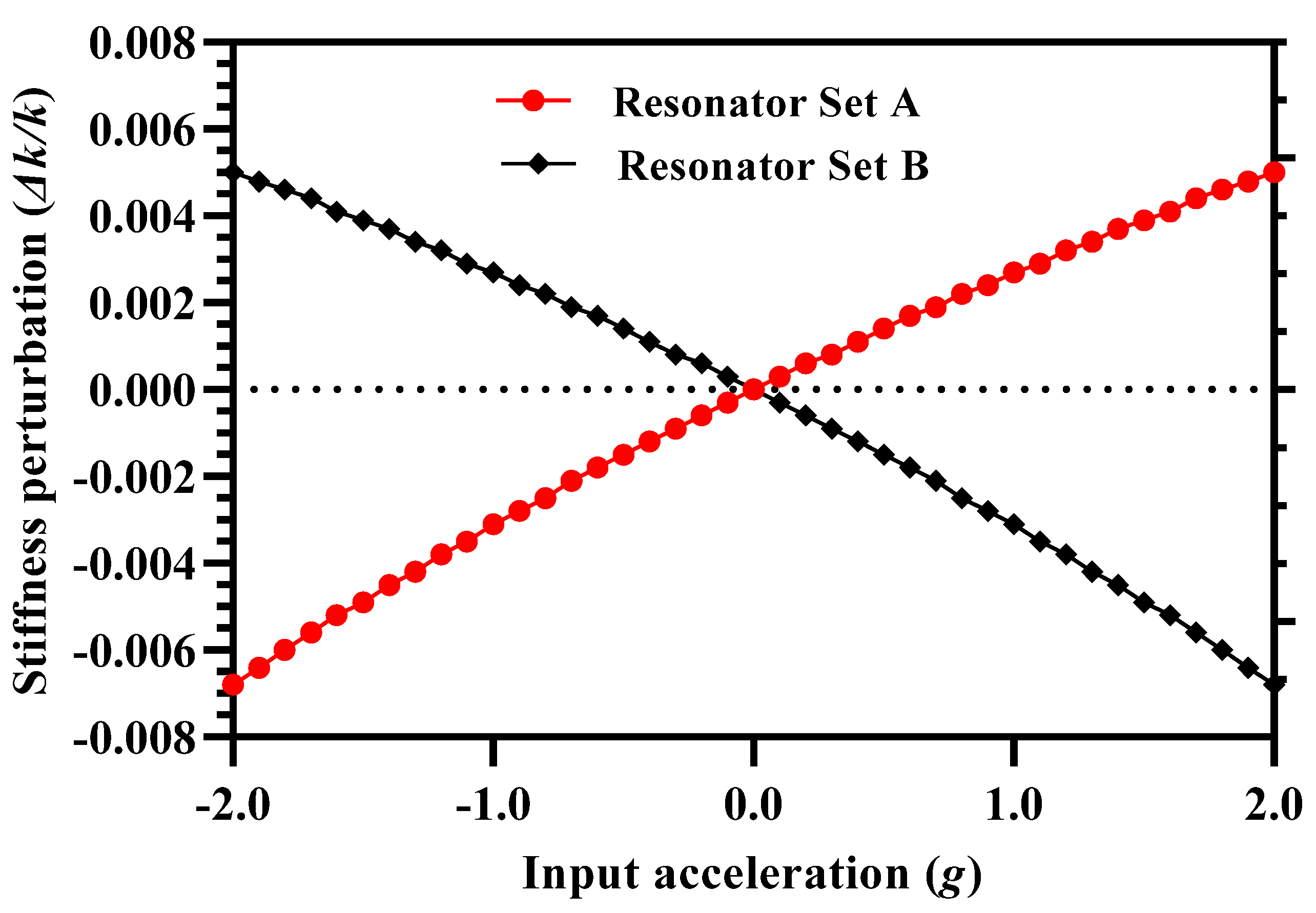
4.2. Stiffness Perturbation in the the Inner Resonators of 3-DoF Resonator Sets
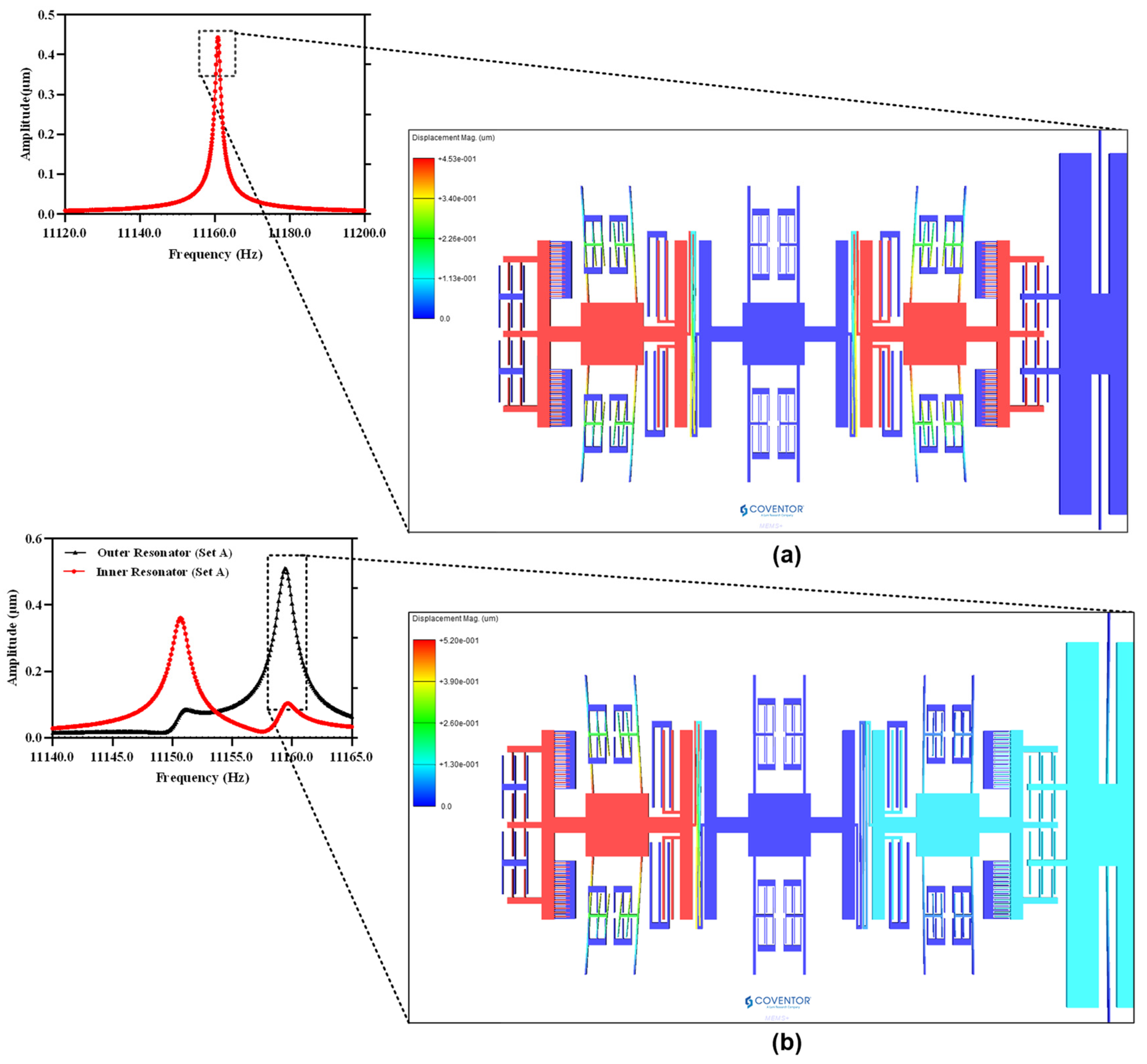
4.3. Dynamic Response and Mode Localization
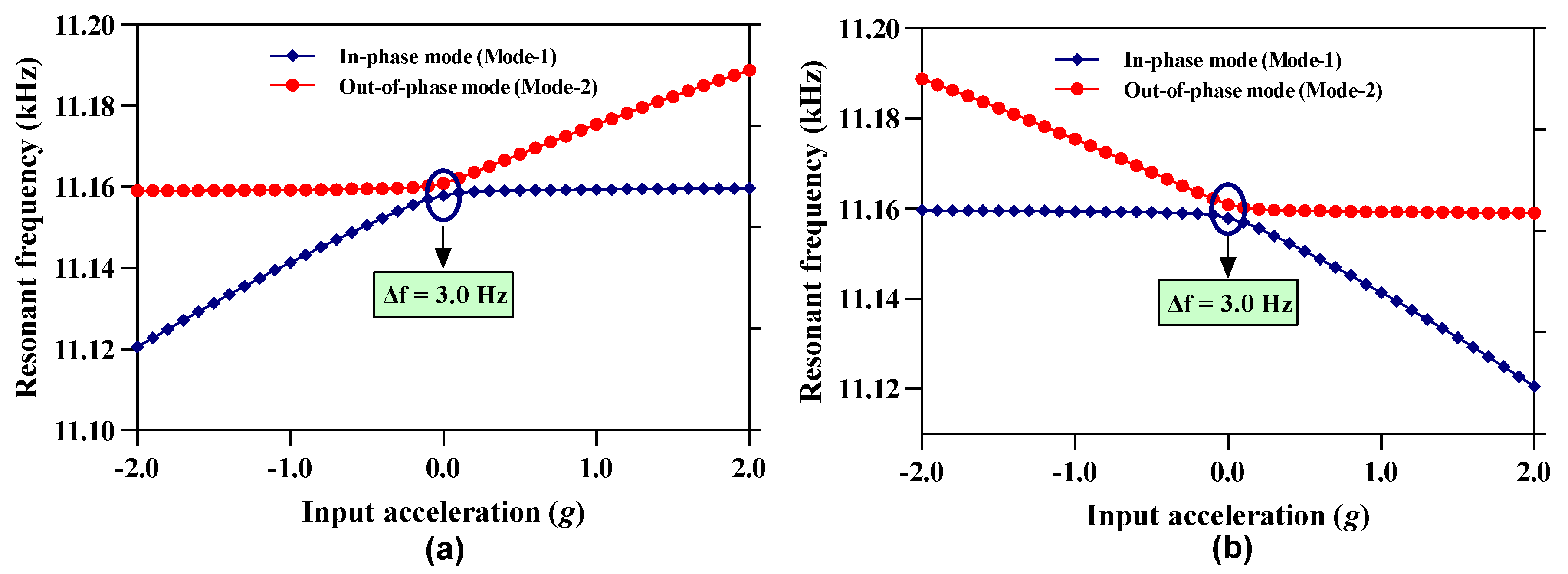
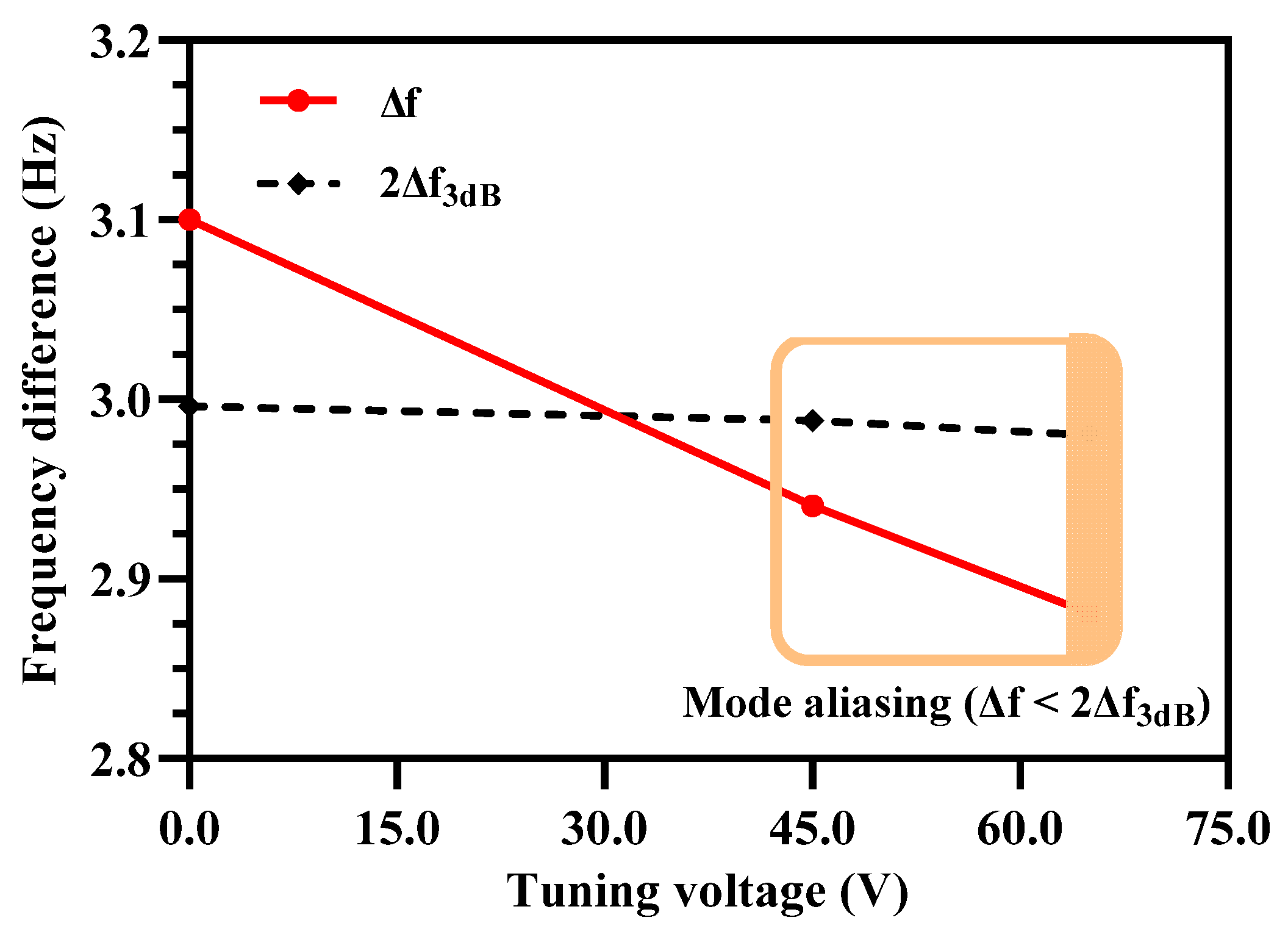
4.4. Mode Aliasing and Frequency Based Sensitivity Analysis
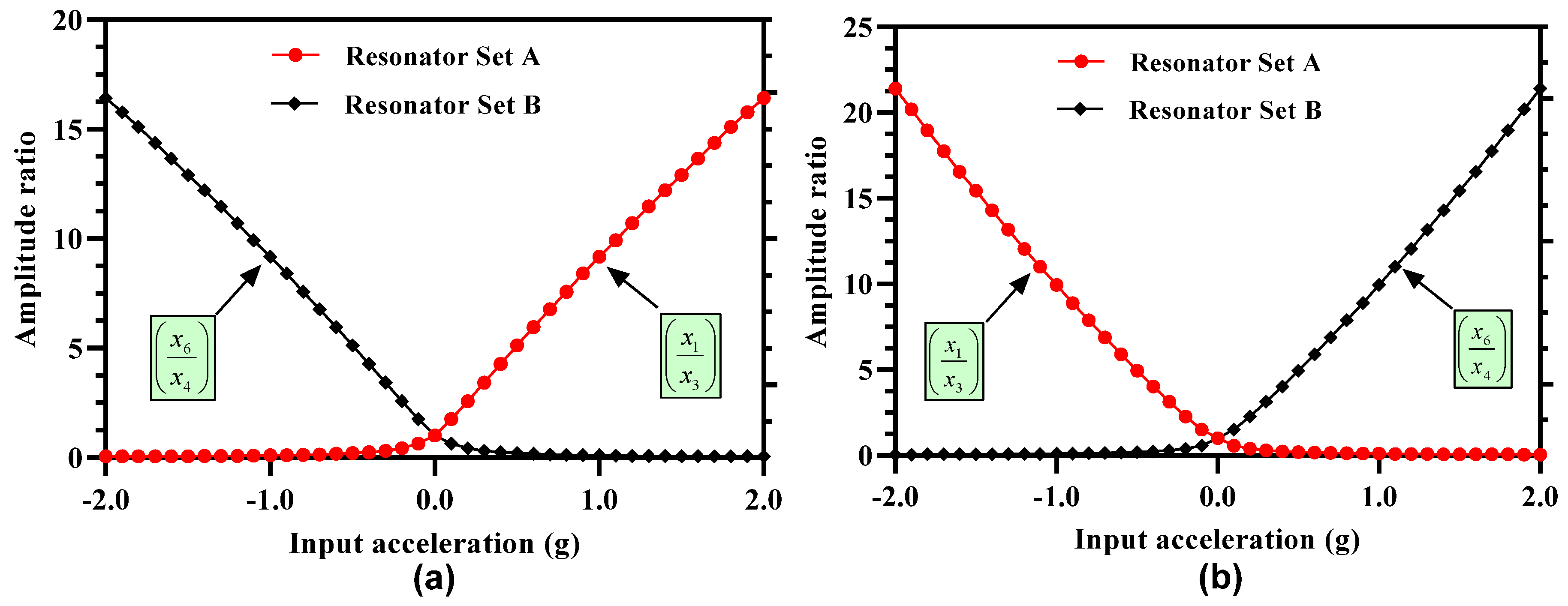
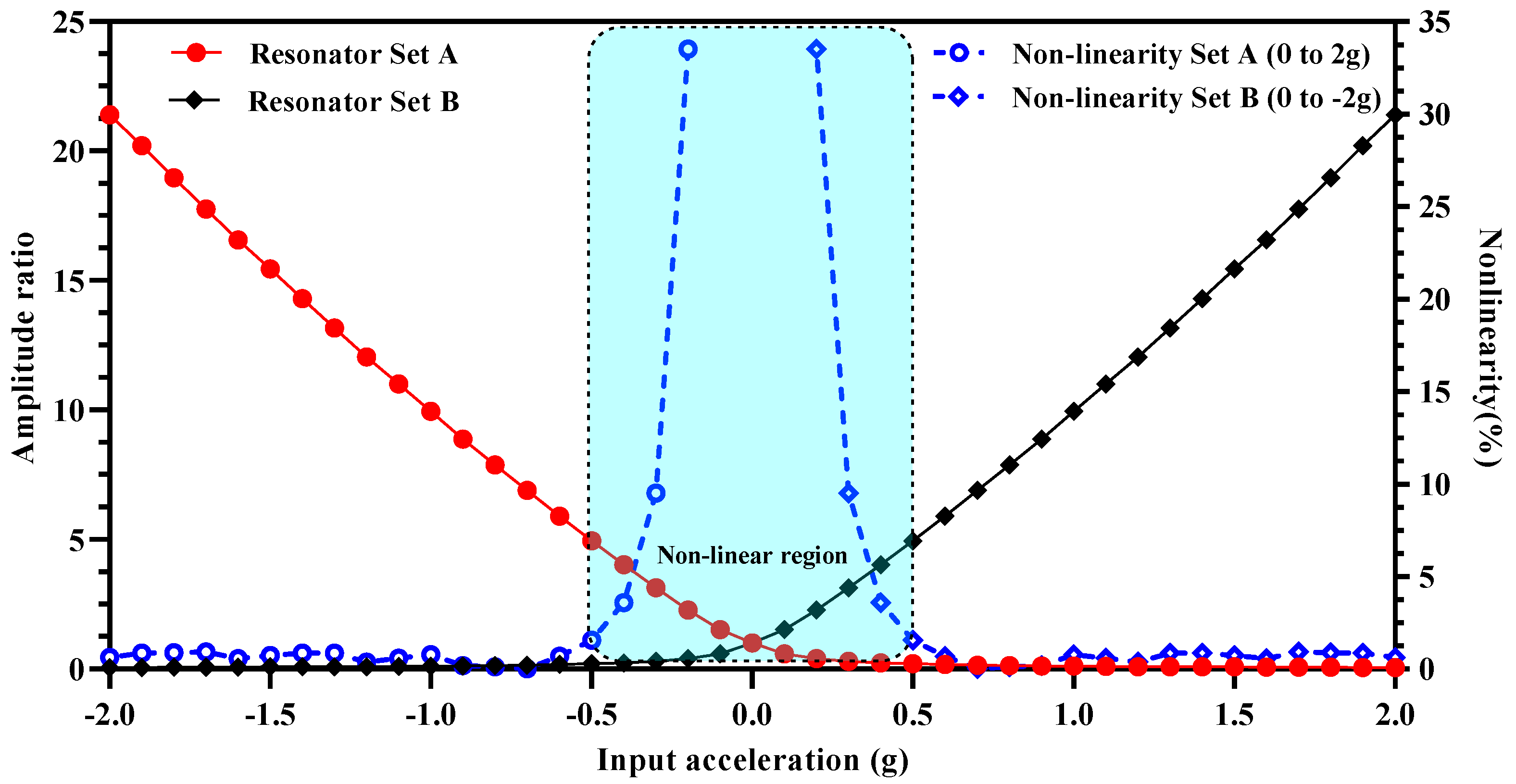
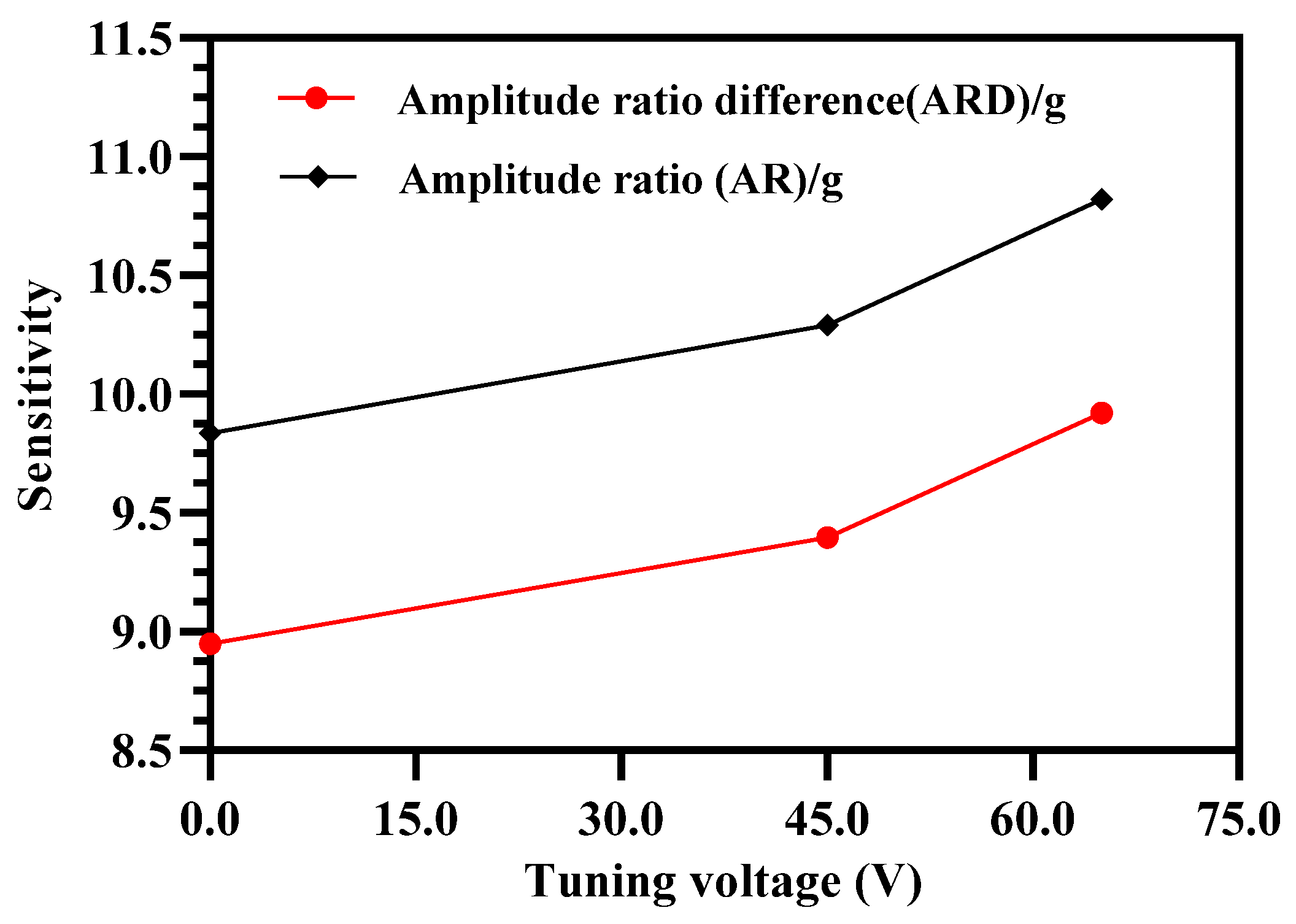
4.5. Amplitude Ratio of 3-DoF Resonators as Sensitivity Metric
4.6. Amplitude Ratio Difference of 3-DoF Resonators as Sensitivity Metric
5. Sensitivity Tuning of MEMS Accelerometer
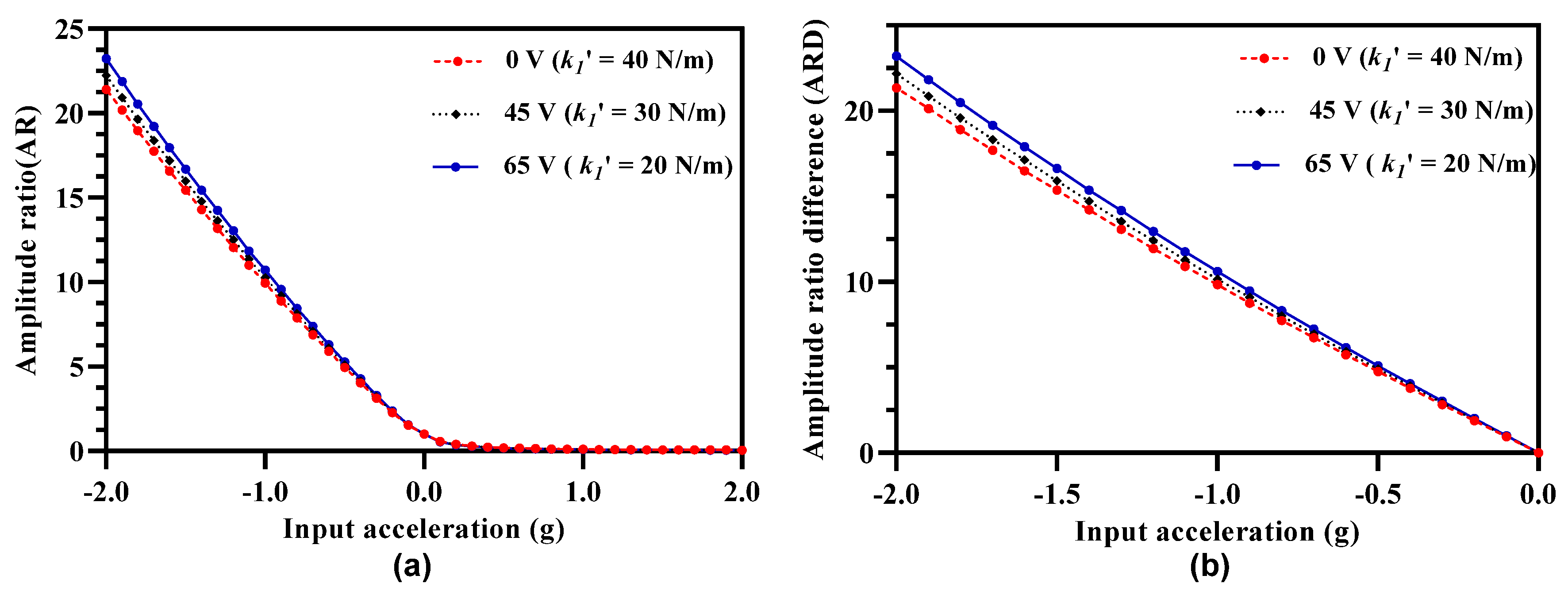
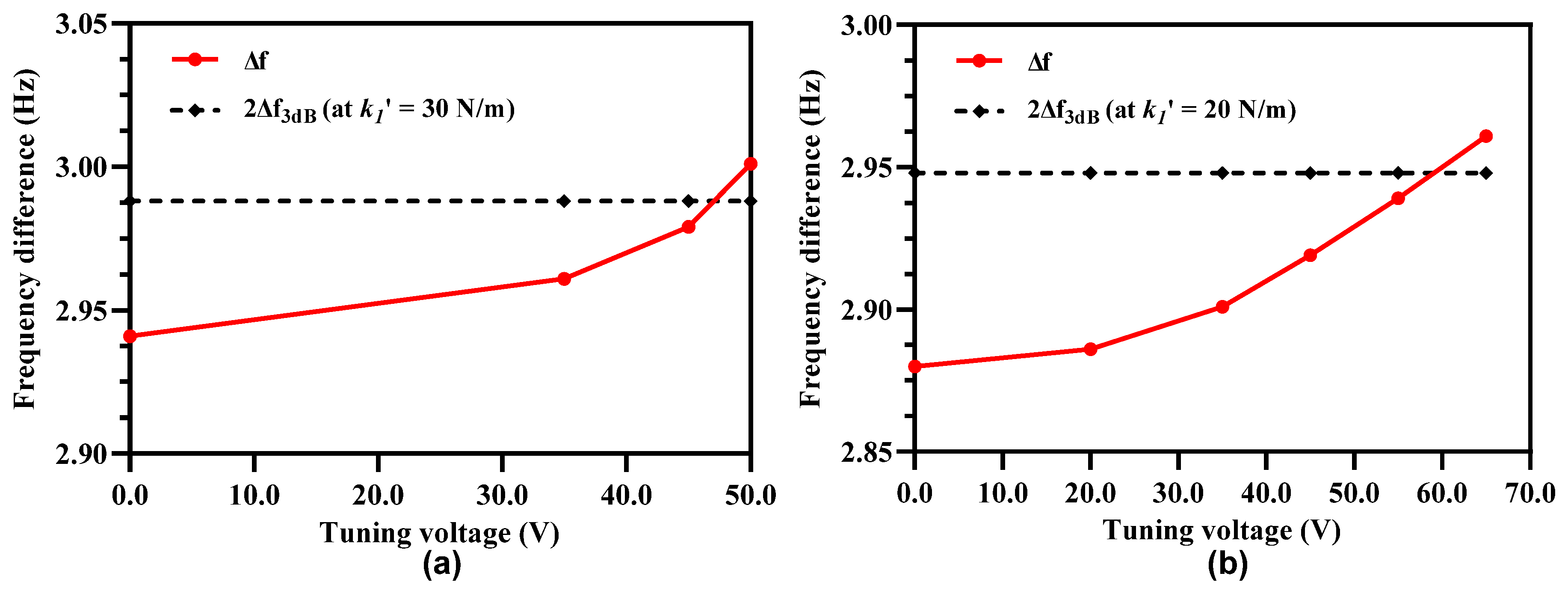
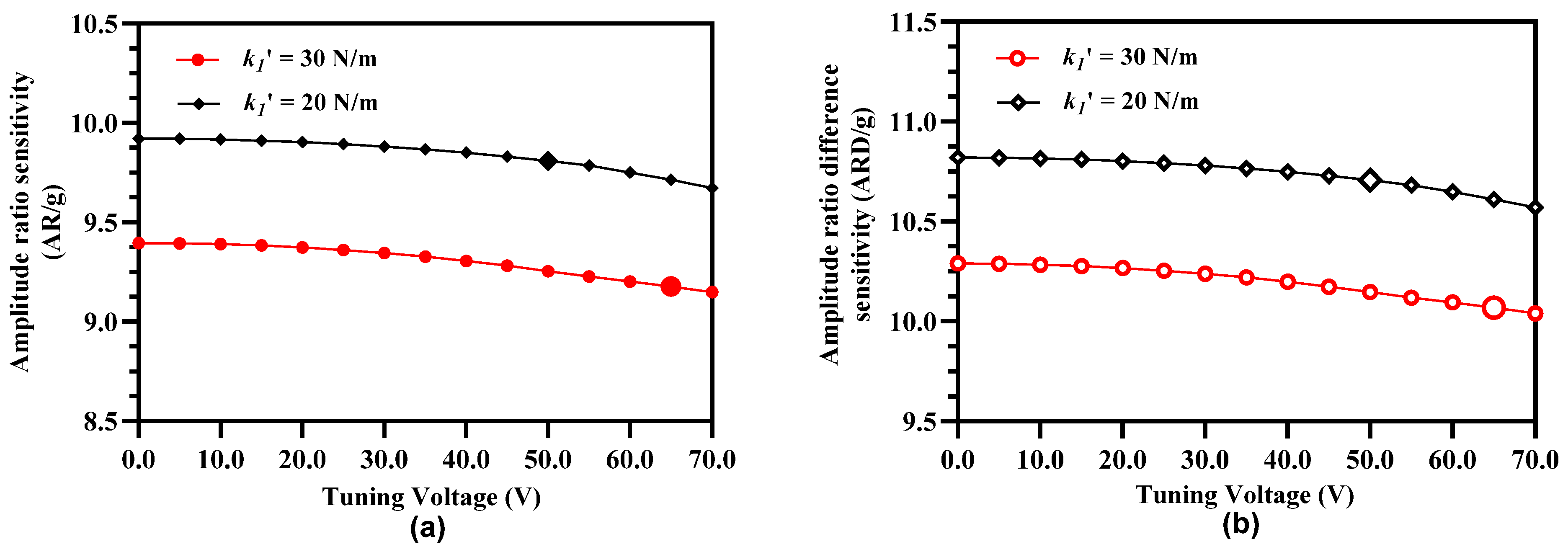
5.1. Electrostatic Stiffness Tuning of Inner/Outer Resonators
5.2. Electrostatic Stiffness Tuning of Middle Resonators in 3-DoF Weakly Coupled Resonators
5.3. Dynamic Range and Resolution of MEMS Accelerometer
6. Discussion
6.1. Comparison of 3-DoF Weakly Coupled MEMS Resonators Based Accelerometer Designs
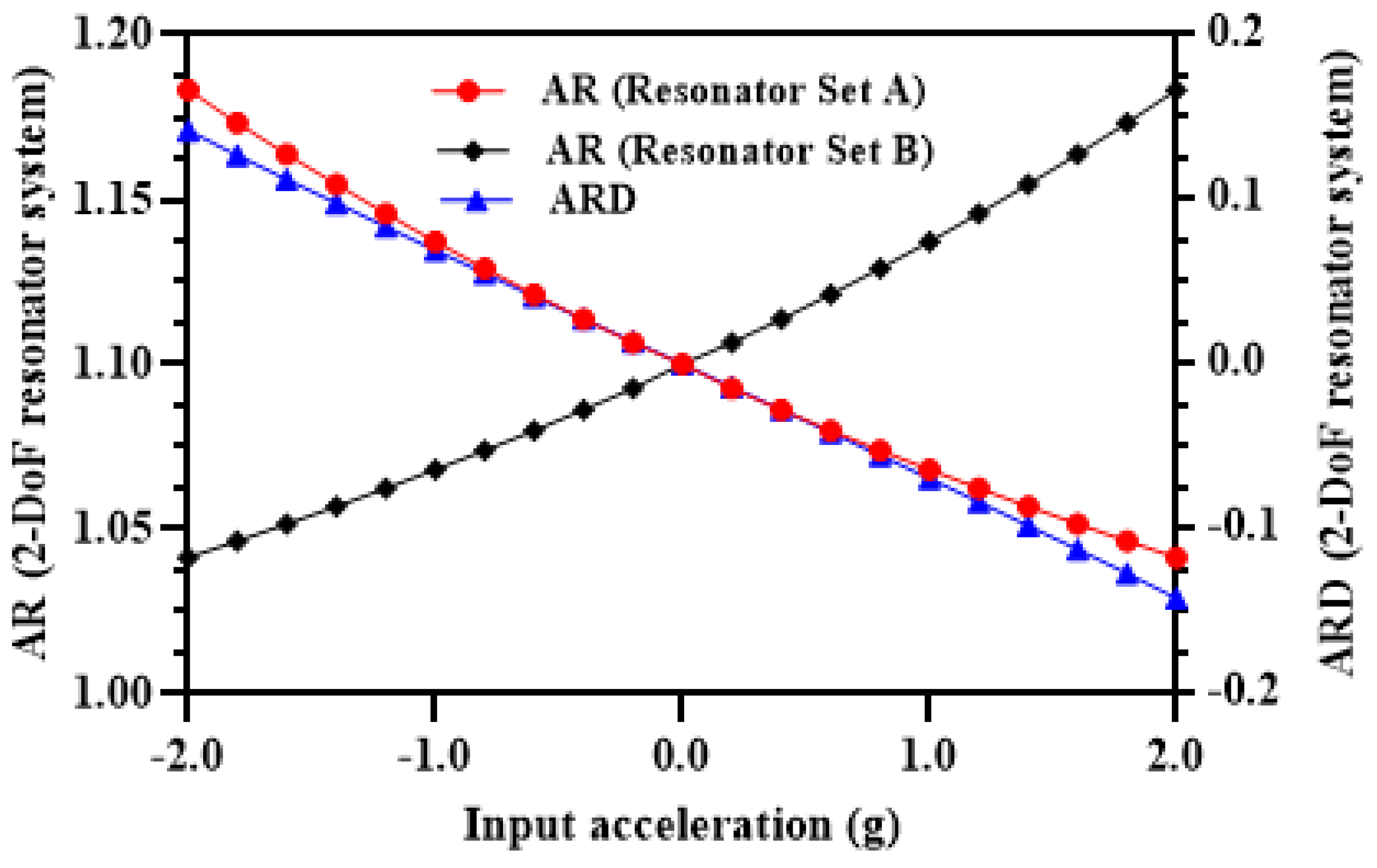
6.2. Comparison of 3-DoF and 2-DoF Weakly Coupled MEMS Resonators Based MEMS Accelerometer Designs
6.3. Effect of Microfabrication Process Tolerances on the MEMS Accelerometer
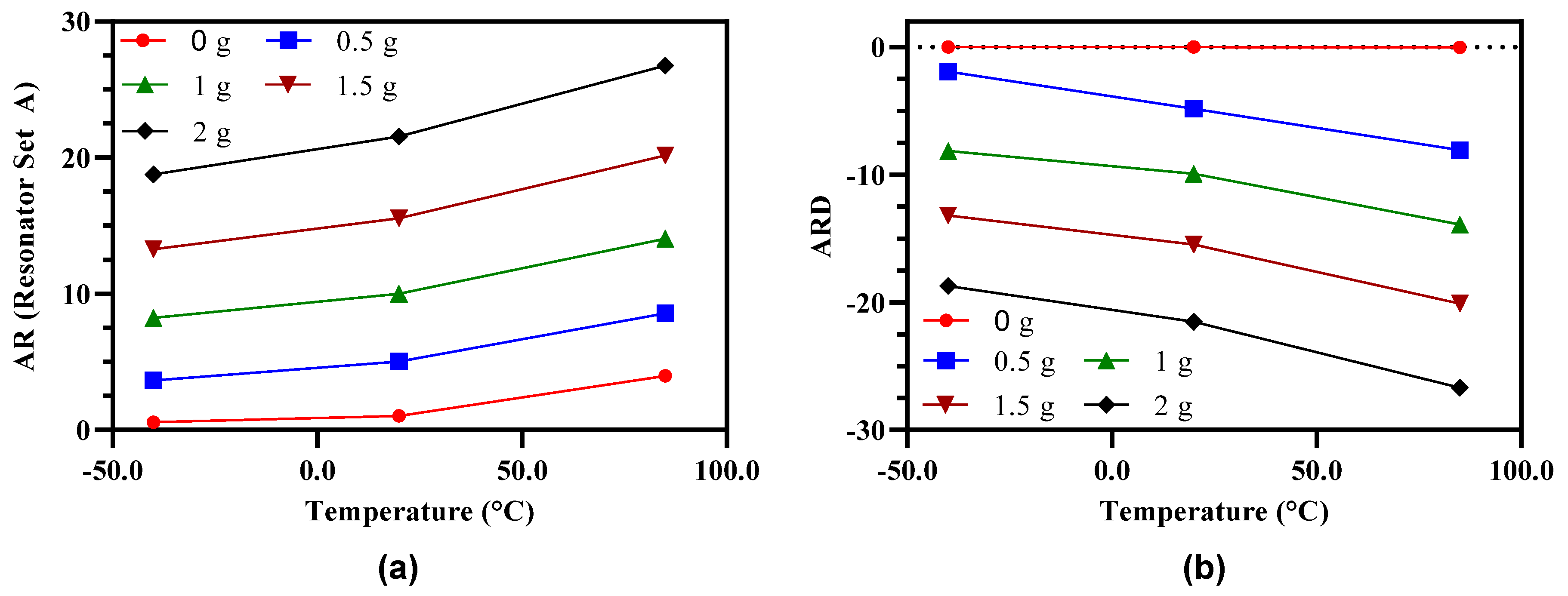
6.4. Effect of Operating Temperature on Performance of the MEMS Accelerometer
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kavitha, S.; Daniel, R.J.; Sumangala, K. Design and Analysis of MEMS Comb Drive Capacitive Accelerometer for SHM and Seismic Applications. Measurement 2016, 93, 327–339. [Google Scholar] [CrossRef]
- Wang, S.; Wei, X.; Zhao, Y.; Jiang, Z.; Shen, Y. A MEMS resonant accelerometer for low-frequency vibration detection. Sens. Actuators A Phys. 2018, 283, 151–158. [Google Scholar] [CrossRef]
- Yin, Y.; Fang, Z.; Han, F.; Yan, B.; Dong, J.; Wu, Q. Design and test of a micromachined resonant accelerometer with high scale factor and low noise. Sens. Actuators A Phys. 2017, 268, 52–60. [Google Scholar] [CrossRef]
- Su, S.; Yang, H.; Agogino, A. A resonant accelerometer with two-stage microleverage mechanisms fabricated by SOI-MEMS technology. IEEE Sens. J. 2005, 5, 1214–1223. [Google Scholar] [CrossRef]
- Huang, L.; Yang, H.; Gao, Y.; Zhao, L.; Liang, J. Design and Implementation of a Micromechanical Silicon Resonant Accelerometer. Sensors 2013, 13, 15785–15804. [Google Scholar] [CrossRef] [PubMed]
- Godthi, V.; Reddy, J.; Pratap, R. A Study of Pressure-Dependent Squeeze Film Stiffness as a Resonance Modulator Using Static and Dynamic Measurements. J. Microelectromech. Syst. 2015, 24, 1712–1719. [Google Scholar] [CrossRef]
- Zotov, S.A.; Simon, B.R.; Trusov, A.A.; Shkel, A.M. High Quality Factor Resonant MEMS Accelerometer With Continuous Thermal Compensation. IEEE Sens. J. 2015, 15, 5045–5052. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, W.; Shen, Y.; Ren, J.; Gu, H.; Wei, X. Temperature compensation for MEMS resonant accelerometer based on genetic algorithm optimized backpropagation neural network. Sens. Actuators A Phys. 2020, 316, 112393. [Google Scholar] [CrossRef]
- Zhao, C.; Wood, G.S.; Xie, J.; Chang, H.; Pu, S.H.; Kraft, M. A force sensor based on three weakly coupled resonators with ultrahigh sensitivity. Sens. Actuators A Phys. 2015, 232, 151–162. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, C.; Wang, C.; Cerica, D.; Baijot, M.; Xiao, Q.; Stoukatch, S.; Kraft, M. A mass sensor based on 3-DOF mode localized coupled resonator under atmospheric pressure. Sens. Actuators A Phys. 2018, 279, 254–262. [Google Scholar] [CrossRef]
- Zhao, C.; Wood, G.S.; Xie, J.; Chang, H.; Pu, S.H.; Chong, H.M.H.; Kraft, M. A sensor for stiffness change sensing based on three weakly coupled resonators with enhanced sensitivity. In Proceedings of the 2015 28th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Estoril, Portugal, 18–22 January 2015; pp. 881–884. [Google Scholar]
- Thiruvenkatanathan, P.; Seshia, A.A. Mode-Localized Displacement Sensing. J. Microelectromech. Syst. 2012, 21, 1016–1018. [Google Scholar] [CrossRef]
- Manav, M.; Phani, A.S.; Cretu, E. Mode Localization and Sensitivity in Weakly Coupled Resonators. IEEE Sens. J. 2018, 19, 2999–3007. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, W.; Li, B.; Hao, Y.; Kraft, M.; Chang, H. A novel resonant accelerometer based on mode localization of weakly coupled resonators. In Proceedings of the 2015 Transducers—2015 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Anchorage, AK, USA, 21–25 June 2015; pp. 1073–1076. [Google Scholar]
- Yang, J.; Zhong, J.; Chang, H. A Closed-Loop Mode-Localized Accelerometer. J. Microelectromech. Syst. 2018, 27, 210–217. [Google Scholar] [CrossRef]
- Kang, H.; Yang, J.; Chang, H. A Closed-Loop Accelerometer Based on Three Degree-of-Freedom Weakly Coupled Resonator With Self-Elimination of Feedthrough Signal. IEEE Sens. J. 2018, 18, 3960–3967. [Google Scholar] [CrossRef]
- Peng, B.; Hu, K.-M.; Shao, L.; Yan, H.; Li, L.; Wei, X.; Zhang, W.-M. A Sensitivity Tunable Accelerometer Based on Series-Parallel Electromechanically Coupled Resonators Using Mode Localization. J. Microelectromech. Syst. 2019, 29, 3–13. [Google Scholar] [CrossRef]
- Pandit, M.; Zhao, C.; Sobreviela, G.; Zou, X.; Seshia, A. A High Resolution Differential Mode-Localized MEMS Accelerometer. J. Microelectromech. Syst. 2019, 28, 782–789. [Google Scholar] [CrossRef]
- Cowen, A.; Hames, G.; Monk, D.; Wilcenski, S.; Hardy, B. SOIMUMPs Design Handbook (Revision 8.0.). Available online: http://www.memscap.com (accessed on 27 November 2020).
- Zhao, C.; Wood, G.S.; Xie, J.; Chang, H.; Pu, S.H.; Kraft, M. A Comparative Study of Output Metrics for an MEMS Resonant Sensor Consisting of Three Weakly Coupled Resonators. J. Microelectromech. Syst. 2016, 25, 626–636. [Google Scholar] [CrossRef]
- CoventorWare Analyzer Field Solver Reference; Coventor Inc.: Cary, NC, USA, 2018.
- Zhang, H.; Li, B.; Yuan, W.; Kraft, M.; Chang, H. An Acceleration Sensing Method Based on the Mode Localization of Weakly Coupled Resonators. J. Microelectromech. Syst. 2016, 25, 286–296. [Google Scholar] [CrossRef]
- Perelló-Roig, R.; Verd, J.; Bota, S.; Segura, J. Thermomechanical Noise Characterization in Fully Monolithic CMOS-MEMS Resonators. Sensors 2018, 18, 3124. [Google Scholar] [CrossRef]
- Thiruvenkatanathan, P.; Woodhouse, J.H.; Yan, J.; Seshia, A.A. Limits to mode-localized sensing using micro- and nanomechanical resonator arrays. J. Appl. Phys. 2011, 109, 104903. [Google Scholar] [CrossRef]
- Zhu, L.; Fu, Y.; Chow, R.; Spencer, B.F.; Park, J.W.; Mechitov, K. Development of a high-sensitivity wireless accelerometer for struc-tural health monitoring. Sensors 2018, 18, 262. [Google Scholar] [CrossRef]
- Grimaldi, G.; Manto, M. Neurological Tremor: Sensors, Signal Processing and Emerging Applications. Sensors 2010, 10, 1399–1422. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, P.; Lueth, T.C. Quantitative Assessment of Parkinsonian Tremor Based on an Inertial Measurement Unit. Sensors 2015, 15, 25055–25071. [Google Scholar] [CrossRef]
- Nof, R.N.; Chung, A.I.; Rademacher, H.; Dengler, L.; Allen, R.M. MEMS Accelerometer Mini-Array (MAMA): A low-cost imple-mentation for earthquake early warning enhancement. Earthq. Spectra 2019, 35, 21–38. [Google Scholar] [CrossRef]
- Younis, S.; Saleem, M.M.; Zubair, M.; Zaidi, S.M.T. Multiphysics design optimization of RF-MEMS switch using response surface methodology. Microelectron. J. 2018, 71, 47–60. [Google Scholar] [CrossRef]
- Saleem, M.M.; Farooq, U.; Izhar, U.; Khan, U.S. Multi-response optimization of electrothermal micromirror using desirability func-tion-based response surface methodology. Micromachines 2017, 8, 107. [Google Scholar] [CrossRef]
- Acar, C.; Shkel, A.M. Experimental evaluation and comparative analysis of commercial variable-capacitance MEMS accel-erometers. J. Micromech. Microeng. 2003, 13, 634. [Google Scholar] [CrossRef]
- Bukhari, S.A.R.; Saleem, M.M.; Khan, U.S.; Hamza, A.; Iqbal, J.; Shakoor, R.I. Microfabrication Process-Driven Design, FEM Analysis and System Modeling of 3-DoF Drive Mode and 2-DoF Sense Mode Thermally Stable Non-Resonant MEMS Gyroscope. Micromachines 2020, 11, 862. [Google Scholar] [CrossRef]
- Gysin, U.; Rast, S.; Ruff, P.; Meyer, E.; Lee, D.W.; Vettiger, P.; Gerber, C. Temperature dependence of the force sensitivity of silicon cantilevers. Phys. Rev. B 2004, 69, 045403. [Google Scholar] [CrossRef]



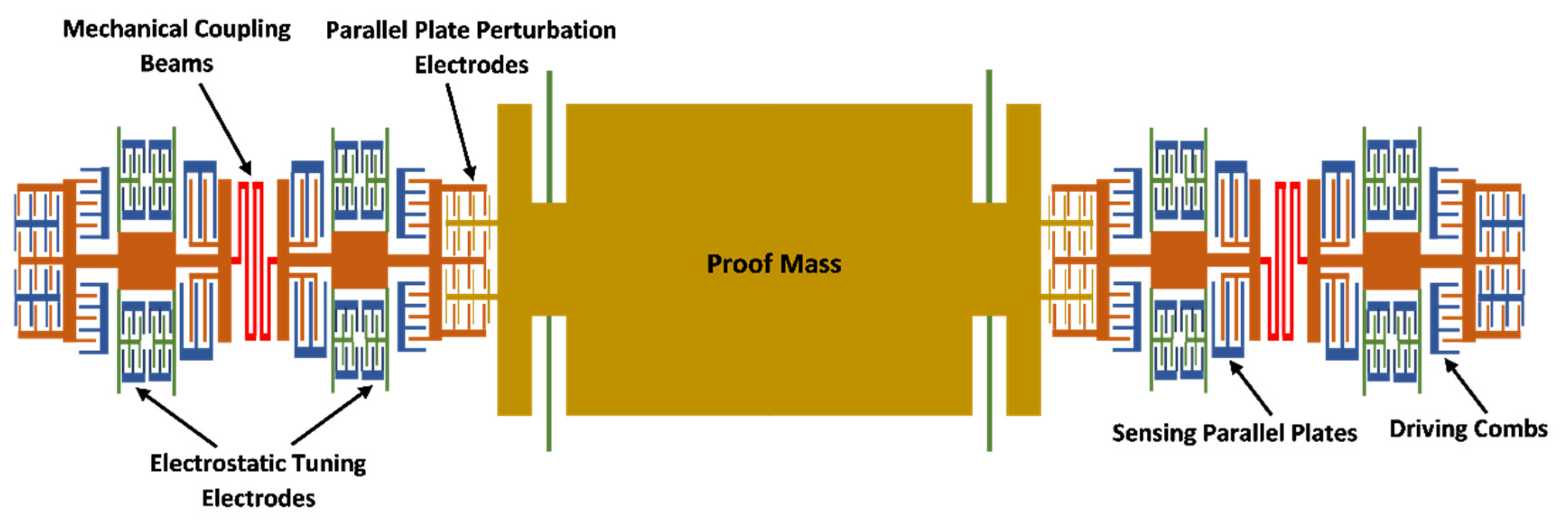



| Parameters | Values |
|---|---|
| Overall device area | 5.58 1.38 mm2 |
| Central proof mass dimensions | 1.96 1.16 mm2 |
| Mass of central proof mass | 1.36 10−7 Kg |
| Mechanical stiffness of proof mass suspension beams | 9.25 N/m |
| Overlap length of perturbation electrodes ) | 80 m |
| Width of perturbation electrodes | 3 m |
| Number of parallel plate perturbation electrodes () | 8 |
| Mechanical stiffness of inner and outer resonators ) | 40 N/m |
| Mechanical stiffness of middle resonator | 258 N/m |
| Mechanical stiffness of coupling beams ) | 1.06 N/m |
| Number of driving combs attached to inner and outer resonators | 28 |
| Number of electrostatic tuning plate pairs attached to each resonator | 16 |
| Overlap area of electrostatic tuning plates | 1500 µm2 |
| Number of parallel sensing plates attached to inner and outer resonators | 2 |
| Reference | DoF of Coupled Resonators | Output Metric | Dynamic Range | Sensitivity | Resolution | Size |
|---|---|---|---|---|---|---|
| Zhang et al. [14] | 2 | Amplitude ratio | ±1 g | 1.26/g | 0.619 mg | - |
| Yang et al. [15] | 2 | Amplitude ratio | ±1 g | 1.32/g | 7.608 | - |
| Kang et al. [16] | 3 | Amplitude ratio | ±1 g | 4.38/g | 1.1 | - |
| Peng et al. [17] | 4 | Amplitude ratio | 0-1 g | 23.37/g | - | - |
| Pandit et al. [18] | 2 | Amplitude ratio difference | ±1 g | 6/g | - | 10 × 10 mm2 |
| This work | 3 | Amplitude ratio difference | ±2 g | 10.61/g | 0.22 | 5.58 1.38 mm2 |
| 23.75 ( 5%) | 25 (0%) | 26.25 ( 5%) | |
|---|---|---|---|
| 1.004 N/m | 1.06 N/m | 1.11 N/m | |
| 38 N/m | 40 N/m | 42 N/m | |
| 244.8 N/m | 258 N/m | 270.6 N/m |
| No. | AR | ARD | |||||
|---|---|---|---|---|---|---|---|
| 1 | 26.25 | 23.75 | 23.75 | 19.975 | −19.909 | 3.401 | 2.956 |
| 2 | 26.25 | 23.75 | 26.25 | 21.683 | −21.622 | 3.001 | 2.956 |
| 3 | 26.25 | 25 | 25 | 19.923 | −19.857 | 3.302 | 2.912 |
| 4 | 23.75 | 23.75 | 23.75 | 23.105 | −23.049 | 2.801 | 2.976 |
| 5 | 25 | 26.25 | 25 | 20.487 | −20.423 | 3.102 | 2.956 |
| 6 | 25 | 25 | 25 | 21.396 | −21.335 | 3.001 | 2.920 |
| 7 | 26.25 | 26.25 | 23.75 | 18.259 | −18.187 | 3.502 | 2.944 |
| 8 | 26.25 | 26.25 | 26.25 | 19.864 | −19.798 | 3.202 | 2.944 |
| 9 | 23.75 | 26.25 | 23.75 | 21.188 | −21.126 | 2.901 | 2.968 |
| 10 | 25 | 25 | 26.25 | 22.259 | −22.200 | 2.901 | 2.920 |
| 11 | 23.75 | 25 | 25 | 23.004 | −22.947 | 2.701 | 2.932 |
| 12 | 25 | 25 | 23.75 | 20.552 | −20.488 | 3.201 | 2.920 |
| 13 | 23.75 | 26.25 | 26.25 | 22.897 | −22.839 | 2.601 | 2.968 |
| 14 | 25 | 23.75 | 25 | 22.399 | −22.340 | 2.902 | 2.968 |
| 15 | 25 | 25 | 25 | 21.396 | −21.335 | 3.001 | 2.920 |
| 16 | 23.75 | 23.75 | 26.25 | 24.858 | −24.805 | 2.501 | 2.976 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saleem, M.M.; Saghir, S.; Bukhari, S.A.R.; Hamza, A.; Shakoor, R.I.; Bazaz, S.A. A Low-g MEMS Accelerometer with High Sensitivity, Low Nonlinearity and Large Dynamic Range Based on Mode-Localization of 3-DoF Weakly Coupled Resonators. Micromachines 2021, 12, 310. https://doi.org/10.3390/mi12030310
Saleem MM, Saghir S, Bukhari SAR, Hamza A, Shakoor RI, Bazaz SA. A Low-g MEMS Accelerometer with High Sensitivity, Low Nonlinearity and Large Dynamic Range Based on Mode-Localization of 3-DoF Weakly Coupled Resonators. Micromachines. 2021; 12(3):310. https://doi.org/10.3390/mi12030310
Chicago/Turabian StyleSaleem, Muhammad Mubasher, Shayaan Saghir, Syed Ali Raza Bukhari, Amir Hamza, Rana Iqtidar Shakoor, and Shafaat Ahmed Bazaz. 2021. "A Low-g MEMS Accelerometer with High Sensitivity, Low Nonlinearity and Large Dynamic Range Based on Mode-Localization of 3-DoF Weakly Coupled Resonators" Micromachines 12, no. 3: 310. https://doi.org/10.3390/mi12030310
APA StyleSaleem, M. M., Saghir, S., Bukhari, S. A. R., Hamza, A., Shakoor, R. I., & Bazaz, S. A. (2021). A Low-g MEMS Accelerometer with High Sensitivity, Low Nonlinearity and Large Dynamic Range Based on Mode-Localization of 3-DoF Weakly Coupled Resonators. Micromachines, 12(3), 310. https://doi.org/10.3390/mi12030310






