Analysis of Parametric and Subharmonic Excitation in Push-Pull Driven Disk Resonator Gyroscopes
Abstract
1. Introduction
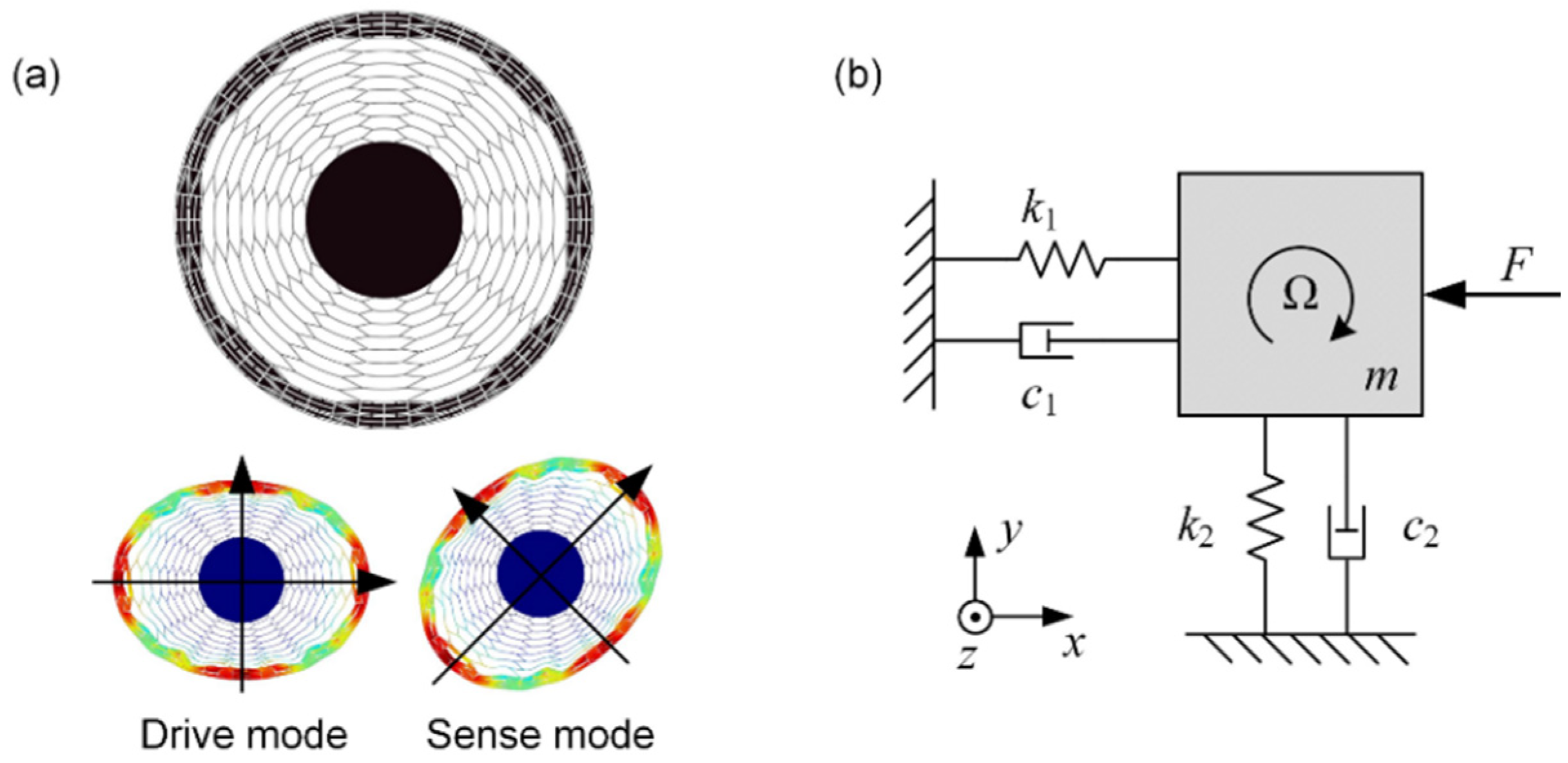
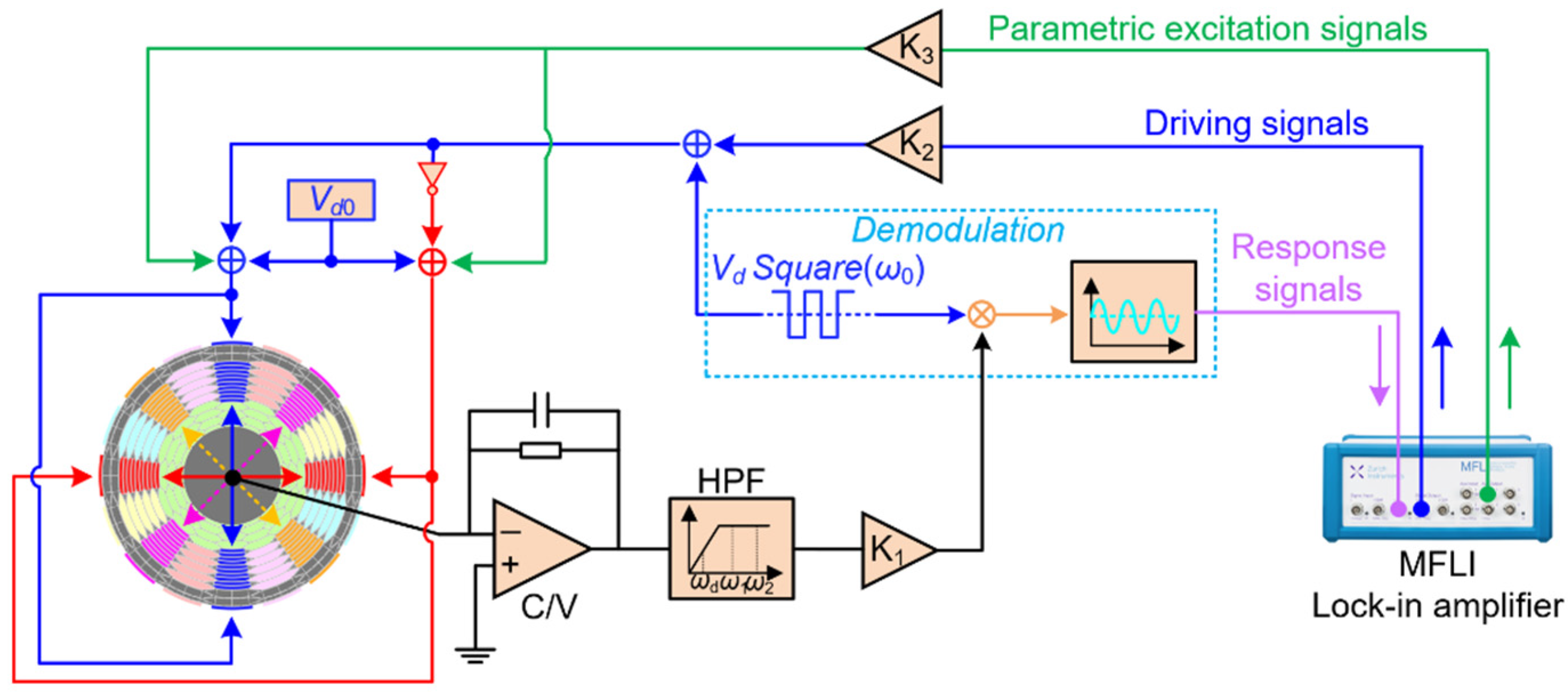
2. The Device Description and Dynamic Model of the DRG
3. Parametric Excitation in the Push-Pull Driven DRG
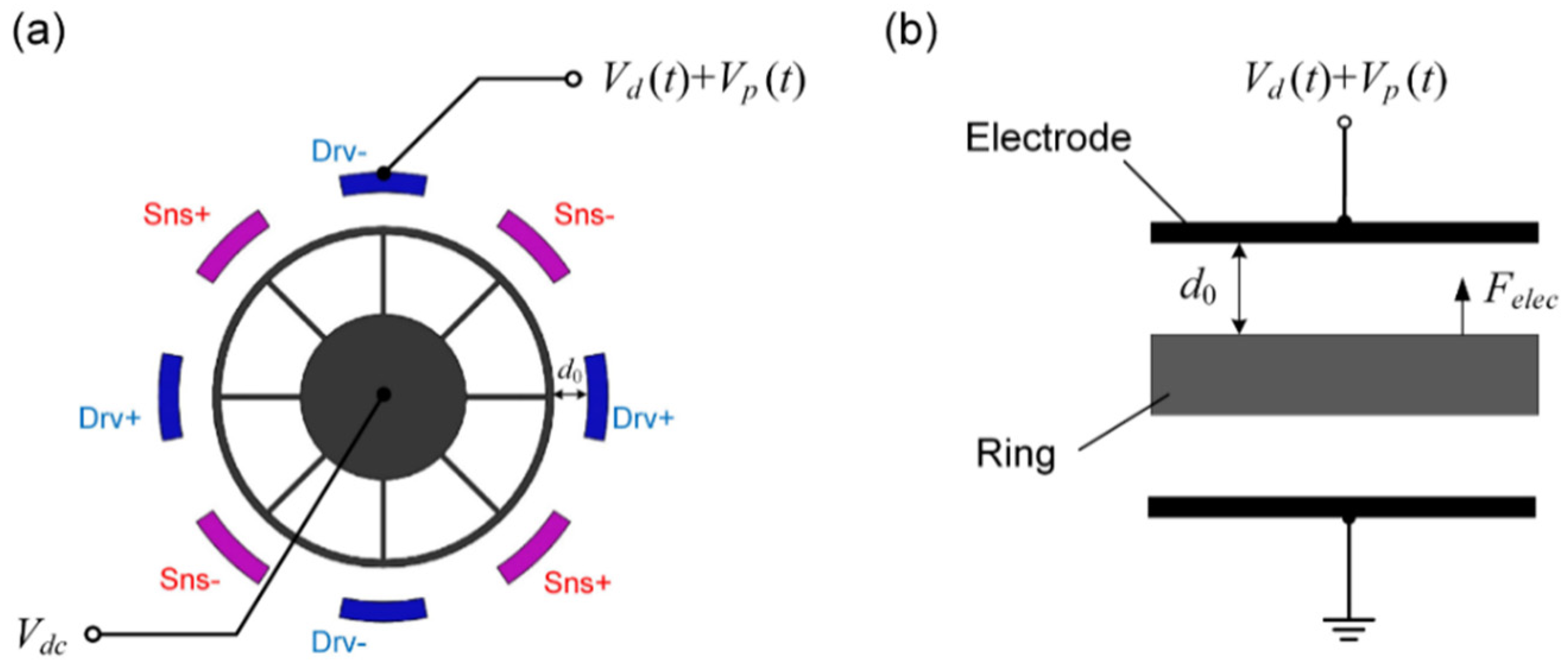
3.1. Parametric Excitation by a Single Electrode
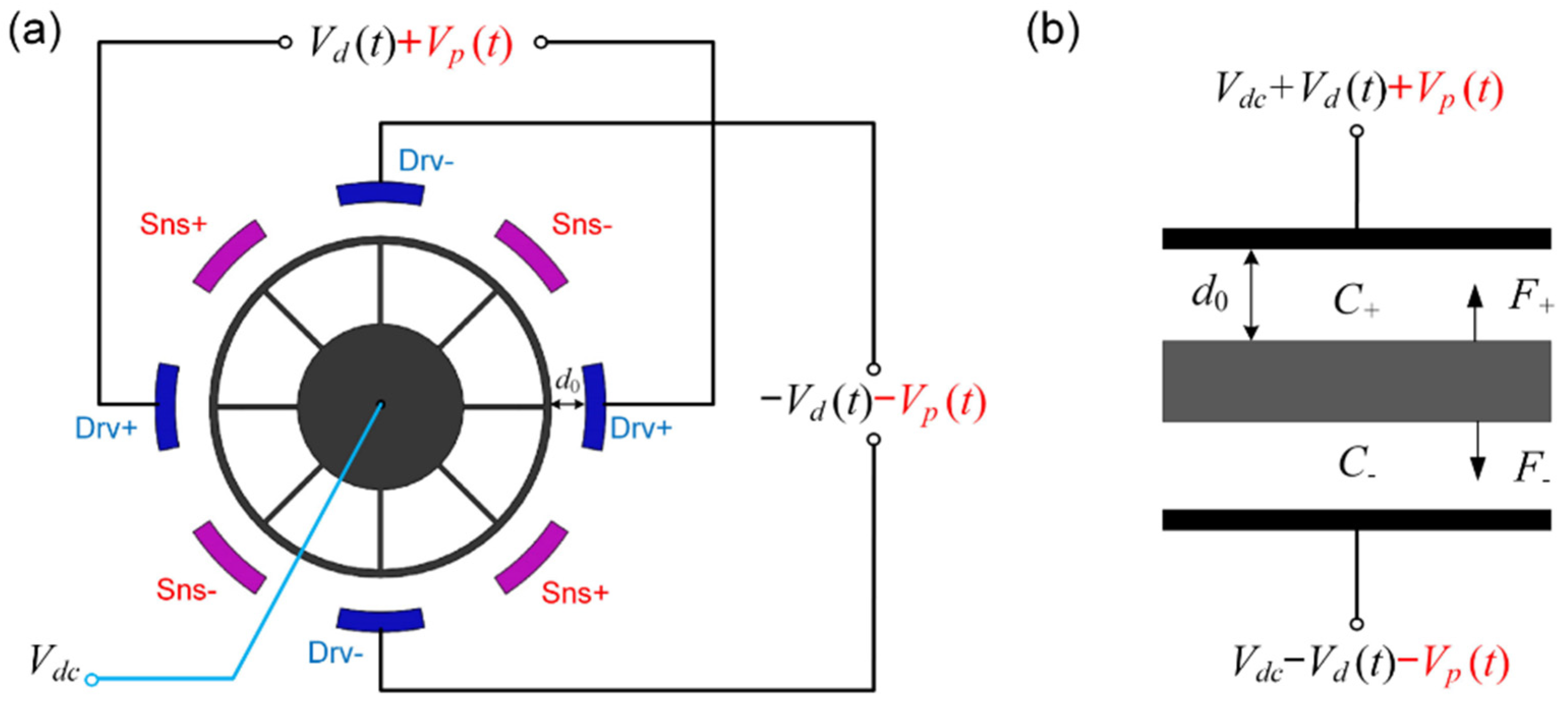
3.2. Parametric Excitation in Traditional Push-Pull Driving
3.2.1. Triple-Frequency Parametric Excitation in Push-Pull Driving
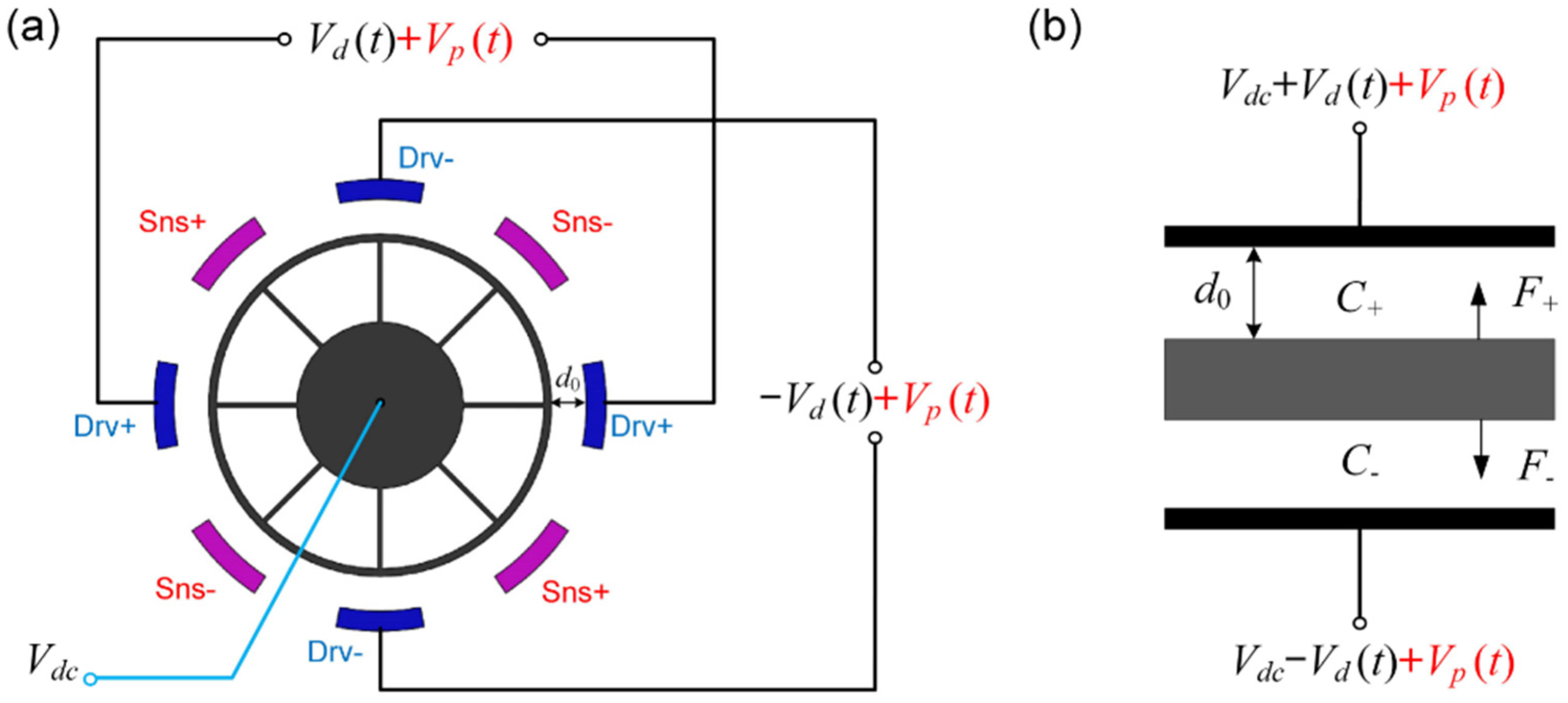
3.2.2. The Non-Differential Parametric Excitation in Push-Pull Driving
4. Subharmonic Resonance
4.1. The Analysis of the Threshold Voltage in Parametric Excitation
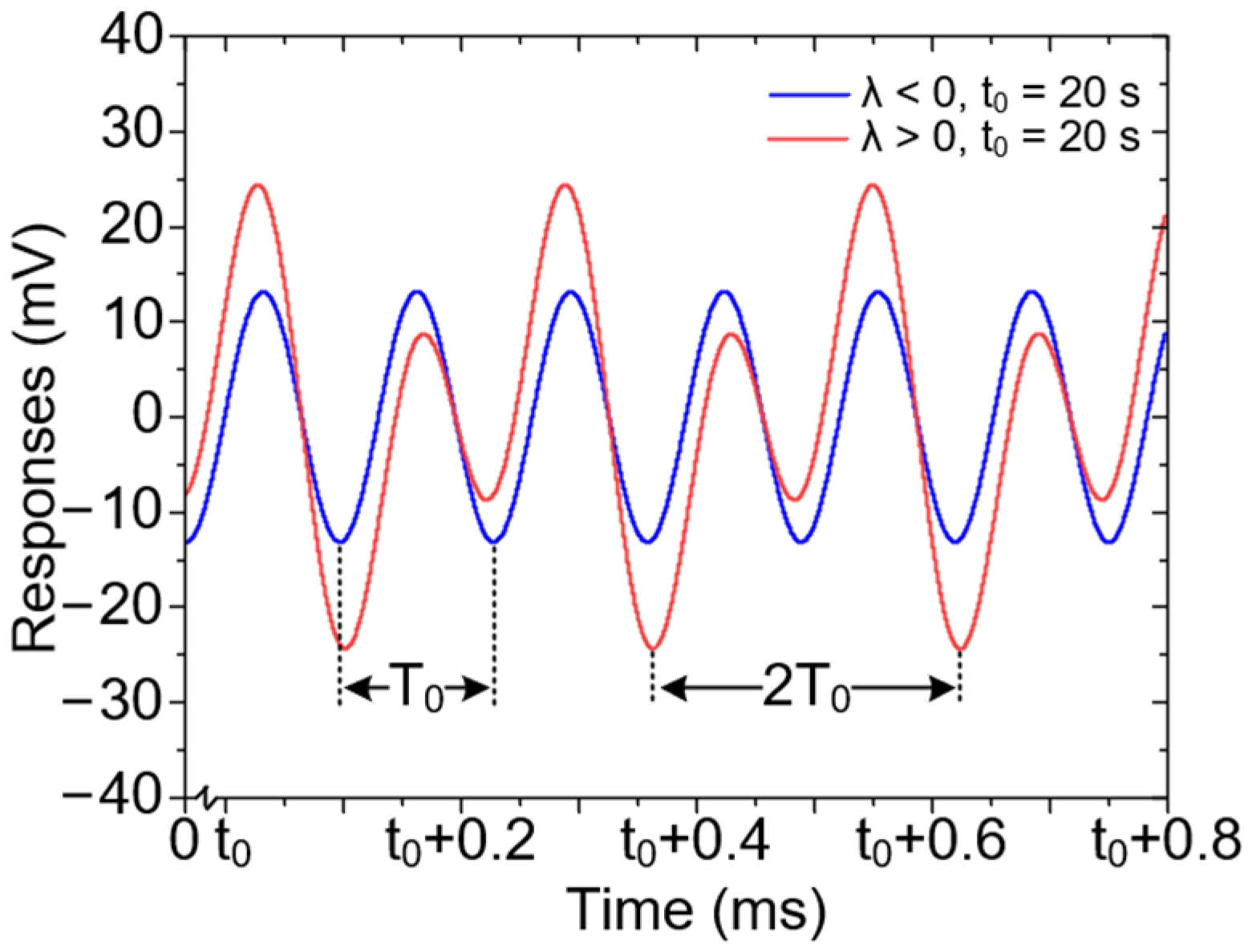
4.2. The Analysis of Subharmonic Excitation
5. Experimental Results
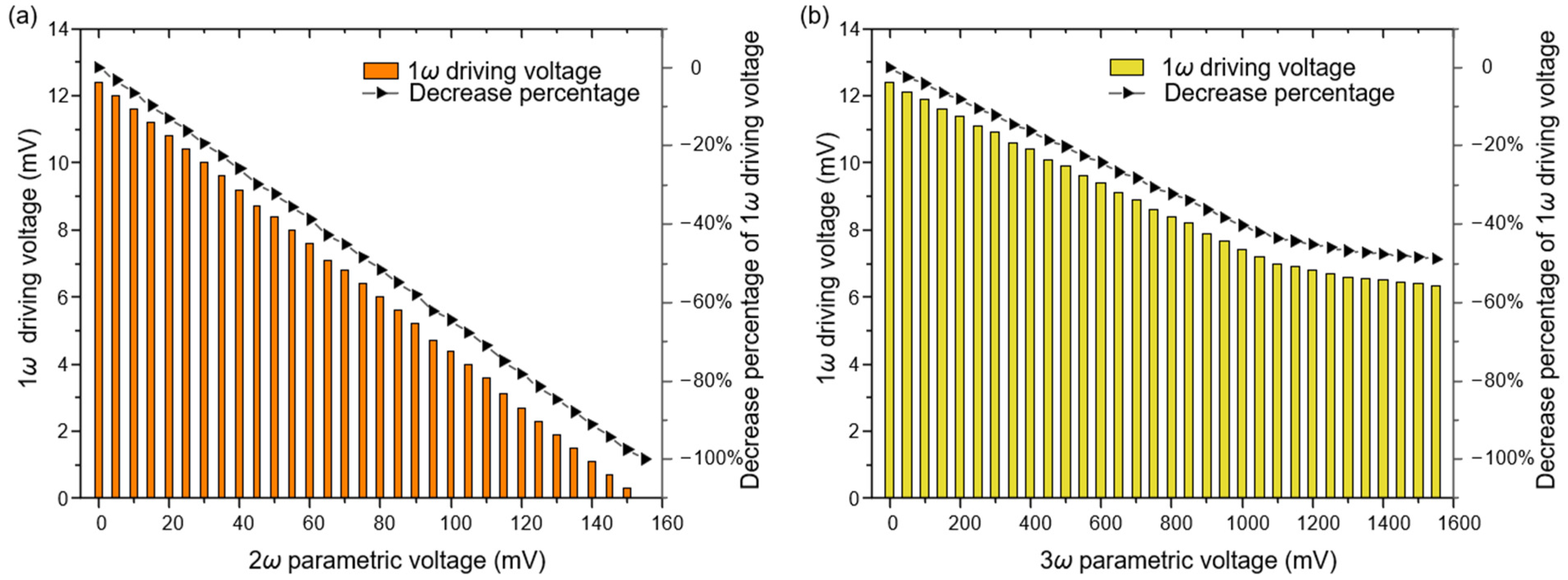
5.1. The Reduction of the Driving Voltage
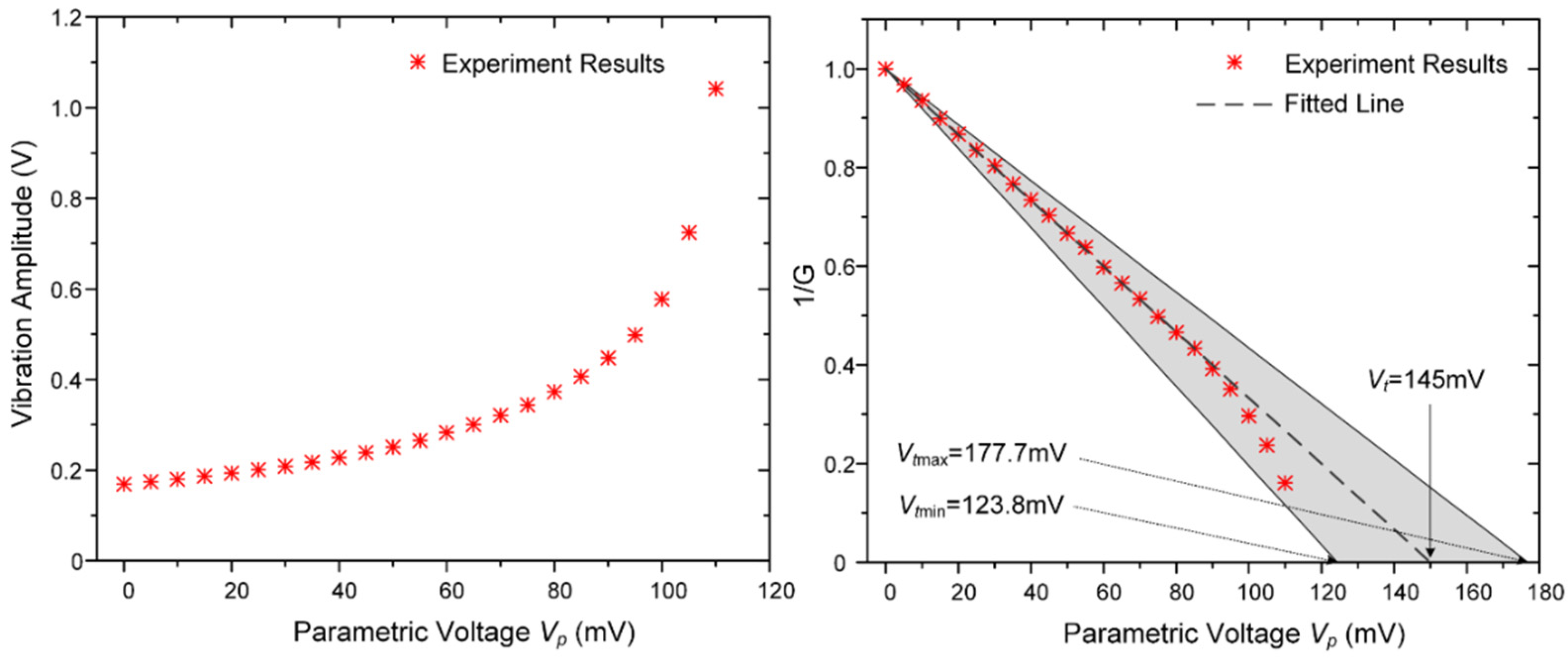
5.2. The Stability Boundary and Threshold Voltage
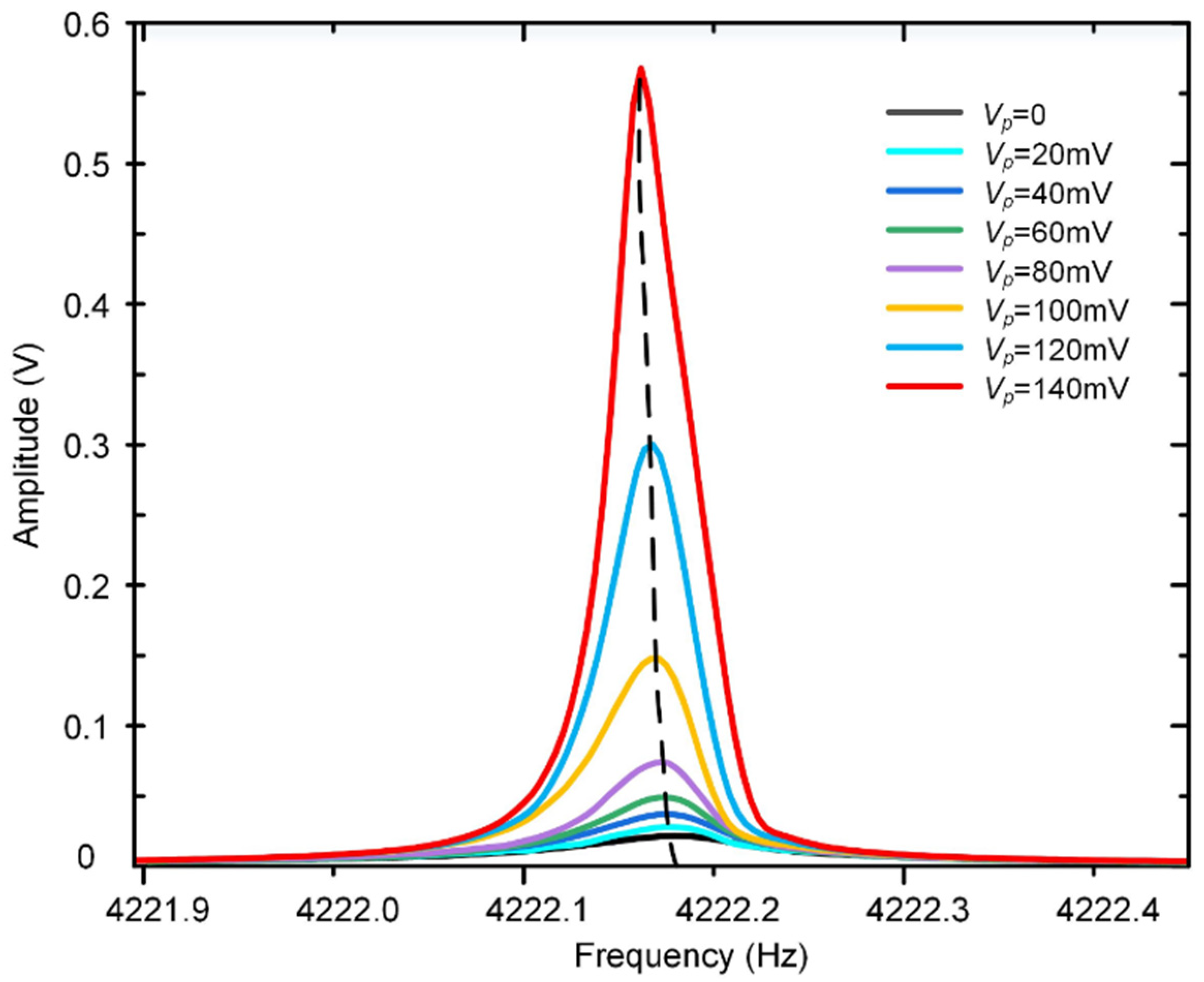
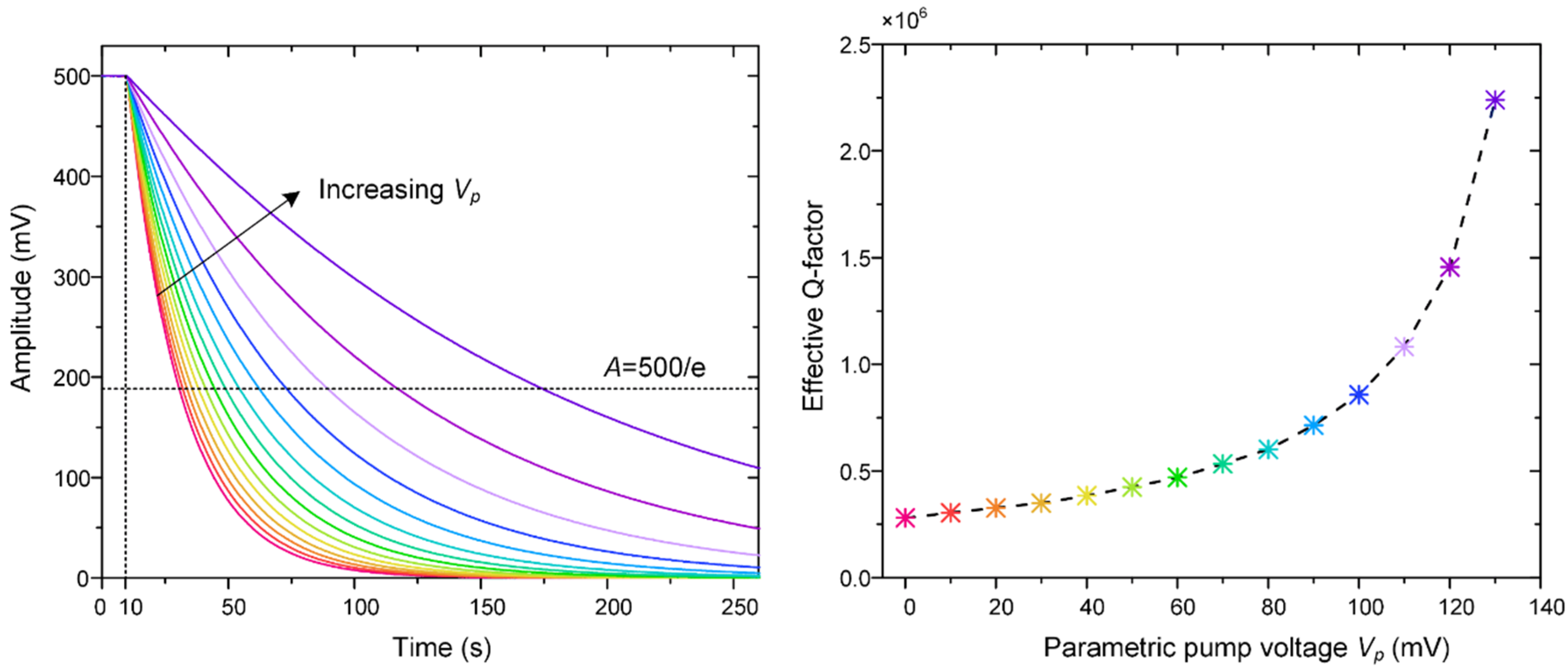
5.3. The Improvement of the “Effective Q”
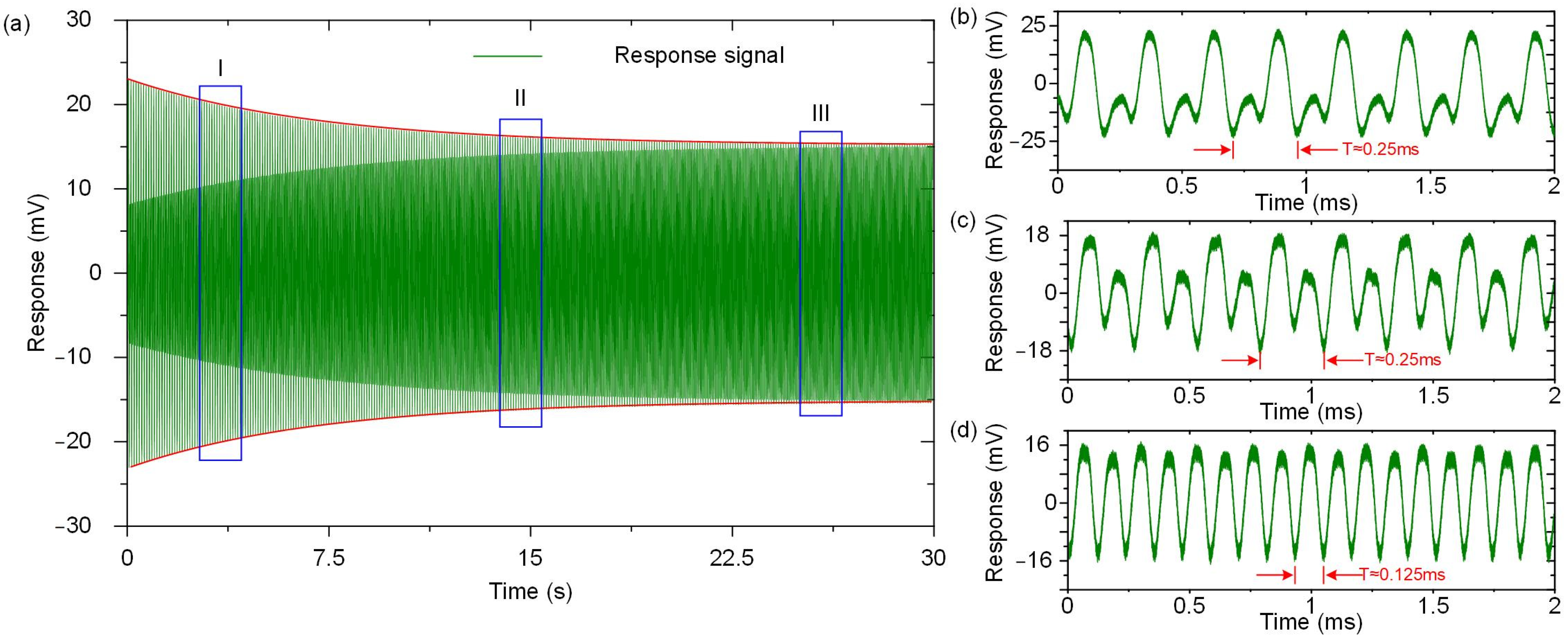
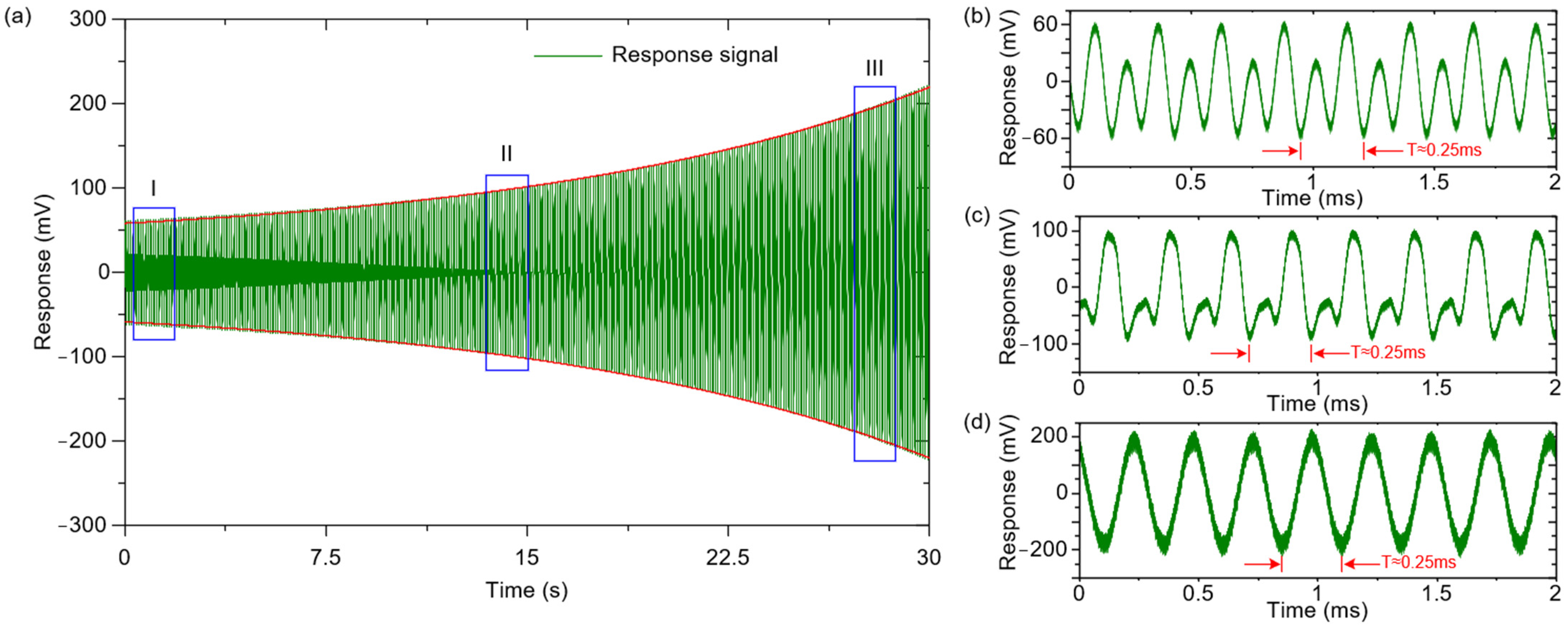
5.4. The Subharmonic Resonance
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, Q.; Xiao, D.; Zhou, X.; Xu, Y.; Zhuo, M.; Hou, Z.; He, K.; Zhang, Y.; Wu, X. 0.04 degree-per-hour MEMS disk resonator gyroscope with high-quality factor (510 k) and long decaying time constant (74.9 s). Microsyst. Nanoeng. 2018, 4, 32. [Google Scholar] [CrossRef]
- Bao, M.; Yang, H. Squeeze film air damping in MEMS. Sens. Actuators Phys. 2007, 136, 3–27. [Google Scholar] [CrossRef]
- Unterreithmeier, Q.P.; Faust, T.; Kotthaus, J.P. Damping of nanomechanical resonators. Phys. Rev. Lett. 2010, 105, 027205. [Google Scholar] [CrossRef]
- Zhou, X.; Xiao, D.; Li, Q.; Hu, Q.; Hou, Z.; He, K.; Chen, Z.; Zhao, C.; Wu, Y.; Wu, X.; et al. Investigation on the quality factor limit of the (111) silicon based disk resonator. Micromachines 2018, 9, 25. [Google Scholar] [CrossRef]
- Turner, K.L.; Miller, S.A.; Hartwell, P.G.; MacDonald, N.C.; Strogatz, S.H.; Adams, S.G. Five parametric resonances in a microelectromechanical system. Nature 1998, 396, 149–152. [Google Scholar] [CrossRef]
- Rugar, D.; Grütter, P. Mechanical parametric amplification and thermomechanical noise squeezing. Phys. Rev. Lett. 1991, 67, 699–702. [Google Scholar] [CrossRef] [PubMed]
- Karabalin, R.B.; Lifshitz, R.; Cross, M.C.; Matheny, M.H.; Masmanidis, S.C.; Roukes, M.L. Signal amplification by sensitive control of bifurcation topology. Phys. Rev. Lett. 2011, 106, 094102. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Baskaran, R.; Turner, K.L. Effect of cubic nonlinearity on auto-parametrically amplified resonant MEMS mass sensor. Sens. Actuators Phys. 2002, 102, 139–150. [Google Scholar] [CrossRef]
- Kacem, N.; Hentz, S.; Baguet, S.; Dufour, R. Forced large amplitude periodic vibrations of non-linear mathieu resonators for microgyroscope applications. Int. J. Non-Linear Mech. 2011, 46, 1347–1355. [Google Scholar] [CrossRef]
- Tiwari, S.; Candler, R.N. Using flexural MEMS to study and exploit nonlinearities: A review. J. Micromech. Microeng. 2019, 29, 083002. [Google Scholar] [CrossRef]
- Sobreviela, G.; Zhao, C.; Pandit, M.; Do, C.; Du, S.; Zou, X.; Seshia, A. Parametric noise reduction in a high-order nonlinear MEMS resonator utilizing its bifurcation points. J. Microelectromech. Syst. 2017, 26, 1189–1195. [Google Scholar] [CrossRef]
- Han, M.; Zhang, Q.; Hao, S.; Li, W. Parametric characteristics and bifurcation analysis of multi-degree-of-freedom micro gyroscope with drive stiffness nonlinearity. Micromachines 2019, 10, 578. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Xu, P.; Han, G.; Si, C.; Ning, J.; Yang, F. The characteristics and locking process of nonlinear MEMS gyroscopes. Micromachines 2020, 11, 233. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Zhao, C.; Xiao, D.; Sun, J.; Sobreviela, G.; Gerrard, D.D.; Chen, Y.; Flader, I.; Kenny, T.W.; Wu, X.; et al. Dynamic modulation of modal coupling in microelectromechanical gyroscopic ring resonators. Nat. Commun. 2019, 10, 4980. [Google Scholar] [CrossRef] [PubMed]
- Mahboob, I.; Yamaguchi, H. Piezoelectrically pumped parametric amplification and Q enhancement in an electromechanical oscillator. Appl. Phys. Lett. 2008, 92, 173109. [Google Scholar] [CrossRef]
- Harish, K.M.; Gallacher, B.J.; Burdess, J.S.; Neasham, J.A. Experimental investigation of parametric and externally forced motion in resonant MEMS sensors. J. Micromech. Microeng. 2009, 19, 15–21. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, A.D. Nonlinear Oscillations; John Wiley & Sons: Toronto, ON, Canada, 1979; pp. 258–348. [Google Scholar]
- Ahn, C.H.; Nitzan, S.; Ng, E.J.; Hong, V.A.; Yang, Y.; Kimbrell, T.; Horsley, D.A.; Kenny, T.W. Encapsulated high frequency (235 kHz), high-Q (100 k) disk resonator gyroscope with electrostatic parametric pump. Appl. Phys. Lett. 2014, 105, 586–593. [Google Scholar] [CrossRef]
- Gallacher, B.J.; Burdess, J.S.; Harish, K.M. A control scheme for a MEMS electrostatic resonant gyroscope excited using combined parametric excitation and harmonic forcing. J. Micromech. Microeng. 2006, 16, 320–331. [Google Scholar] [CrossRef]
- Hu, Z.X.; Gallacher, B.J.; Burdess, J.S.; Fell, C.P.; Townsend, K. A parametrically amplified MEMS rate gyroscope. Sens. Actuators Phys. 2011, 167, 249–260. [Google Scholar] [CrossRef]
- DeMartini, B.E.; Rhoads, J.F.; Turner, K.L.; Shaw, S.W.; Moehlis, J. Linear and nonlinear tuning of parametrically excited MEMS oscillators. J. Microelectromech. Syst. 2007, 16, 310–318. [Google Scholar] [CrossRef]
- Oropeza-Ramos, L.A.; Burgner, C.B.; Turner, K.L. Robust micro-rate sensor actuated by parametric resonance. Sens. Actuators Phys. 2009, 152, 80–87. [Google Scholar] [CrossRef]
- Sharma, M.; Sarraf, E.H.; Baskaran, R.; Cretu, E. Parametric resonance: Amplification and damping in MEMS gyroscopes. Sens. Actuators Phys. 2012, 177, 79–86. [Google Scholar] [CrossRef]
- Nitzan, S.H.; Zega, V.; Li, M.; Ahn, C.H.; Corigliano, A.; Kenny, T.W.; Horsley, D.A. Self-induced parametric amplification arising from nonlinear elastic coupling in a micromechanical resonating disk gyroscope. Sci. Rep. 2015, 5, 9036. [Google Scholar] [CrossRef] [PubMed]
- Harish, K.M.; Gallacher, B.J.; Burdess, J.S.; Neasham, J.A. Simple parametric resonance in an electrostatically actuated microelectromechanical gyroscope: Theory and experiment. Arch. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2008, 222, 43–52. [Google Scholar] [CrossRef]
- Miller, J.M.L.; Ansari, A.; Heinz, D.B.; Chen, Y.; Flader, I.B.; Shin, D.D.; Villanueva, L.G.; Kenny, T.W. Effective quality factor tuning mechanisms in micromechanical resonators. Appl. Phys. Rev. 2018, 5, 041307. [Google Scholar] [CrossRef]
- Zheng, X.; Wu, H.; Lin, Y.; Ma, Z.; Jin, Z. Linear parametric amplification/attenuation for MEMS vibratory gyroscopes based on triangular area-varying capacitors. J. Micromech. Microeng. 2020, 30, 045010. [Google Scholar] [CrossRef]
- Awrejcewicz, J. (Ed.) Applied Non-Linear Dynamical Systems; Springer Proceedings in Mathematics & Statistics; Springer International Publishing: Cham, Switzerland, 2014; Volume 93. [Google Scholar]
- Xu, Y.; Li, Q.; Zhang, Y.; Zhou, X.; Wu, X.; Xiao, D. Honeycomb-like disk resonator gyroscope. IEEE Sens. J. 2020, 20, 85–94. [Google Scholar] [CrossRef]
- Acar, C.; Shkel, A. MEMS Vibratory Gyroscopes; MEMS Reference Shelf; Springer: Boston, MA, USA, 2009. [Google Scholar]
- Szemplińska-Stupnicka, W. The generalized harmonic balance method for determining the combination resonance in the parametric dynamic systems. J. Sound Vib. 1978, 58, 347–361. [Google Scholar] [CrossRef]
- Li, Q.; Sun, J.; Xu, Y.; Wang, P.; Zhou, X.; Lu, K.; Wu, X.; Xiao, D. A novel nonlinearity reduction method in disk resonator gyroscopes based on thevibration amplification effect. In Proceedings of the 20th International Conference on Solid-State Sensors, Berlin, Germany, 23–27 June 2019; pp. 586–589. [Google Scholar]
- Dolleman, R.J.; Houri, S.; Chandrashekar, A.; Alijani, F.; van der Zant, H.S.J.; Steeneken, P.G. Opto-thermally excited multimode parametric resonance in graphene membranes. Sci. Rep. 2018, 8, 9366. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Radius of the outermost ring r | 4 mm ± 1 μm |
| Height of the ring h | 150 μm ± 1 μm |
| Gap between ring and outer electrodes d0 | 12 μm ± 0.5 μm |
| Effective (modal) mass m | 1.8 mg ± 0.1 mg |
| Frequency of drive mode f1 | 4222.2 Hz |
| Frequency of sense mode f2 | 4220.1 Hz |
| Quality factor of drive mode Q1 | 292,995 |
| Quality factor of sense mode Q2 | 286,489 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, K.; Lu, K.; Li, Q.; Zhang, Y.; Zhuo, M.; Yu, S.; Wu, X.; Xiao, D. Analysis of Parametric and Subharmonic Excitation in Push-Pull Driven Disk Resonator Gyroscopes. Micromachines 2021, 12, 61. https://doi.org/10.3390/mi12010061
Wu K, Lu K, Li Q, Zhang Y, Zhuo M, Yu S, Wu X, Xiao D. Analysis of Parametric and Subharmonic Excitation in Push-Pull Driven Disk Resonator Gyroscopes. Micromachines. 2021; 12(1):61. https://doi.org/10.3390/mi12010061
Chicago/Turabian StyleWu, Kai, Kuo Lu, Qingsong Li, Yongmeng Zhang, Ming Zhuo, Sheng Yu, Xuezhong Wu, and Dingbang Xiao. 2021. "Analysis of Parametric and Subharmonic Excitation in Push-Pull Driven Disk Resonator Gyroscopes" Micromachines 12, no. 1: 61. https://doi.org/10.3390/mi12010061
APA StyleWu, K., Lu, K., Li, Q., Zhang, Y., Zhuo, M., Yu, S., Wu, X., & Xiao, D. (2021). Analysis of Parametric and Subharmonic Excitation in Push-Pull Driven Disk Resonator Gyroscopes. Micromachines, 12(1), 61. https://doi.org/10.3390/mi12010061





