External Disturbances Rejection for Vector Field Sensors in Attitude and Heading Reference Systems
Abstract
1. Introduction
2. Previous Works
2.1. MARG Sensor Error Modeling
2.2. MARG Sensor Data Fusion
2.3. Switching Filters
- -
- The norm of (or ): it is the most widely used criterion, due to its high convenience and feasibility.
- -
- The deviation between and (or and ): it is another frequently used criterion, which can be easily acquired from the residual (or innovation) in the state correction step of KF. However, it may be affected by the filter’s instability.
- -
- The angular velocity: it can be used to detect rotational acceleration (especially the centripetal acceleration) [28], but it is not always reliable since the turning radius is usually unknown.
- -
- (a)
- (b)
- (c)
2.4. External Disturbances Estimation
- (1)
- Assuming that the a posteriori estimation of and at the (k − 1)th time step are already available (denoted as and ), the a priori estimations at the kth time step (denoted as and ) are calculated according to Equation (3). Please note that the coefficient and are both between 0 and 1.
- (2)
- Using and , the measurements and are corrected according to Equation (4).
- (3)
- Once the a posteriori estimation and are provided by KF, the estimations of and can be updated according to Equation (5).
3. Novel Attitude Filter Design
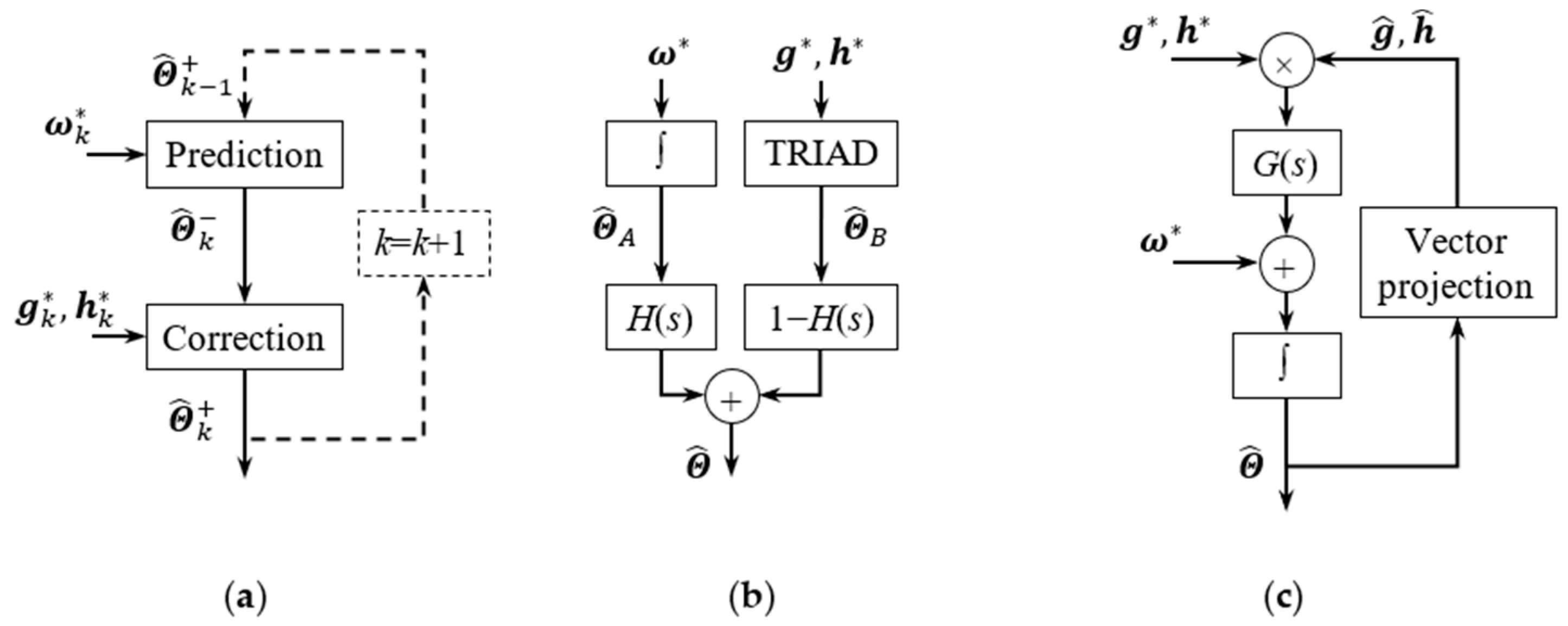
3.1. Attitude Filter Architecture
3.2. External Disturbances Estimation
- Step 1: Predict the disturbances and . This step is the same as (3).
- Step 2: Subtract and from the corresponding measurements (i.e., and ) to get the corrected vectors (denoted as and ). This step is the same as (4).
- Step 3: Get the estimated vectors and according to , , and through a certain algorithm (KF or CF).
- Step 4: Update the estimated disturbances and according to and , i.e., and . Then and go to Step 1.
3.3. Specific Implementations
3.3.1. The Proposed Method with Kalman Filter (Abbreviated as PM-KF Hereafter)
- PM-KF Step 1: Get a priori estimation according to Equation (8), in which the state transition matrix is calculated as . The matrix satisfies for any 3 × 1 vector , and is the sampling period.
- PM-KF Step 2: Calculate a priori covariance matrices according to (9). The process covariance matrices are defined as and , with denoting the noise of gyroscope.
- PM-KF Step 3: Get a posteriori estimation according to Equations (10)–(12). The measurement covariance matrices are defined as and , with and denoting the noise of accelerometer and magnetometer, respectively.
- PM-KF Step 4: Calculate a posteriori covariance matrix according to Equation (13).
3.3.2. The Proposed Method with Complementary Filter (Abbreviated as PM-CF Hereafter)
- PM-CF Step 1: Correct the angular velocity according to Equation (14).
- PM-CF Step 2: Update gravity and geomagnetic vectors using to the corrected angular velocity, as described by Equations (15)–(17).
- PM-CF Step 3: Compensate external disturbances and calculate equivalent angular velocity errors, as described by Equations (18) and (19). denotes the sampling period.
3.4. Remarks
4. Experiments
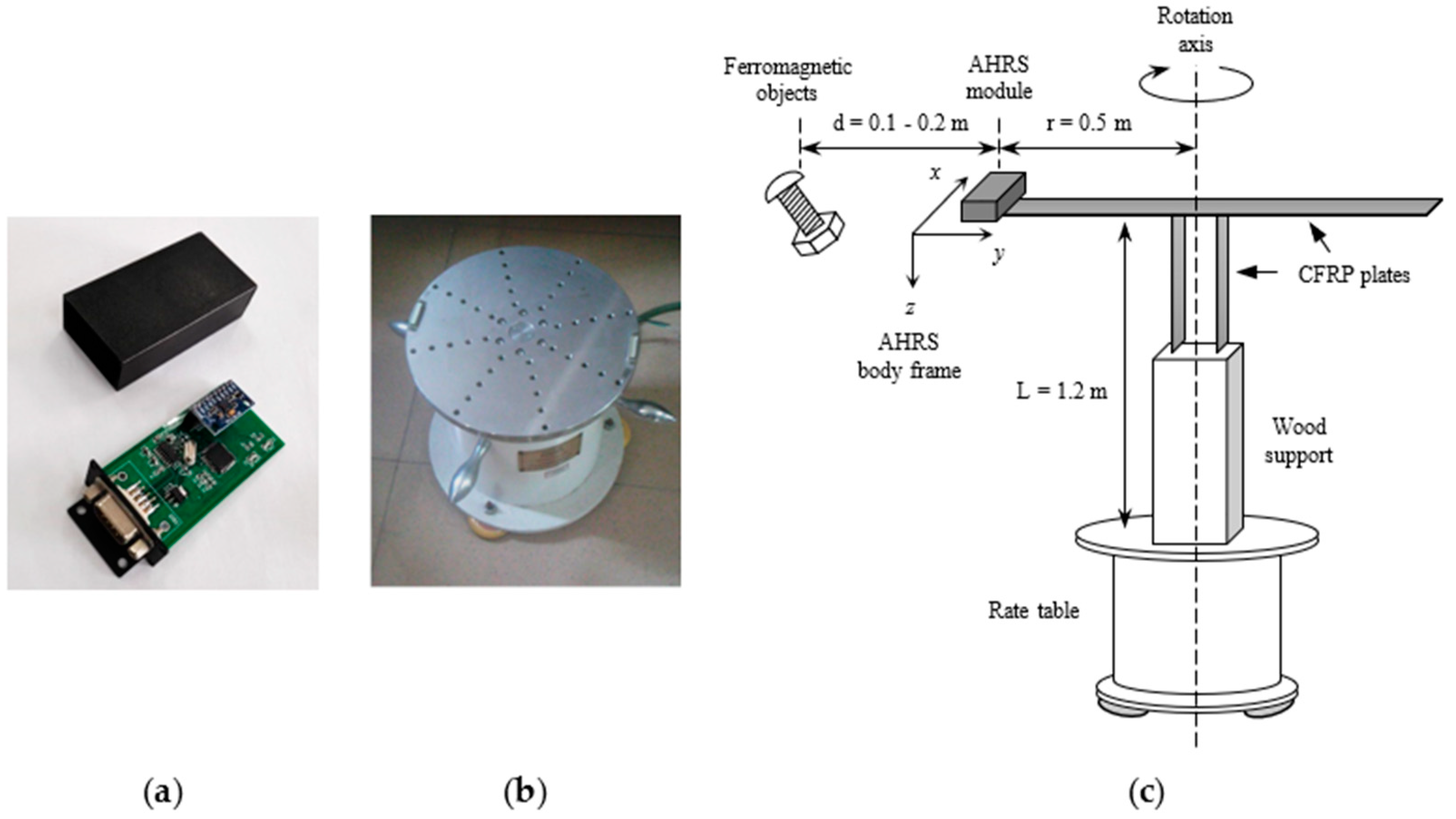
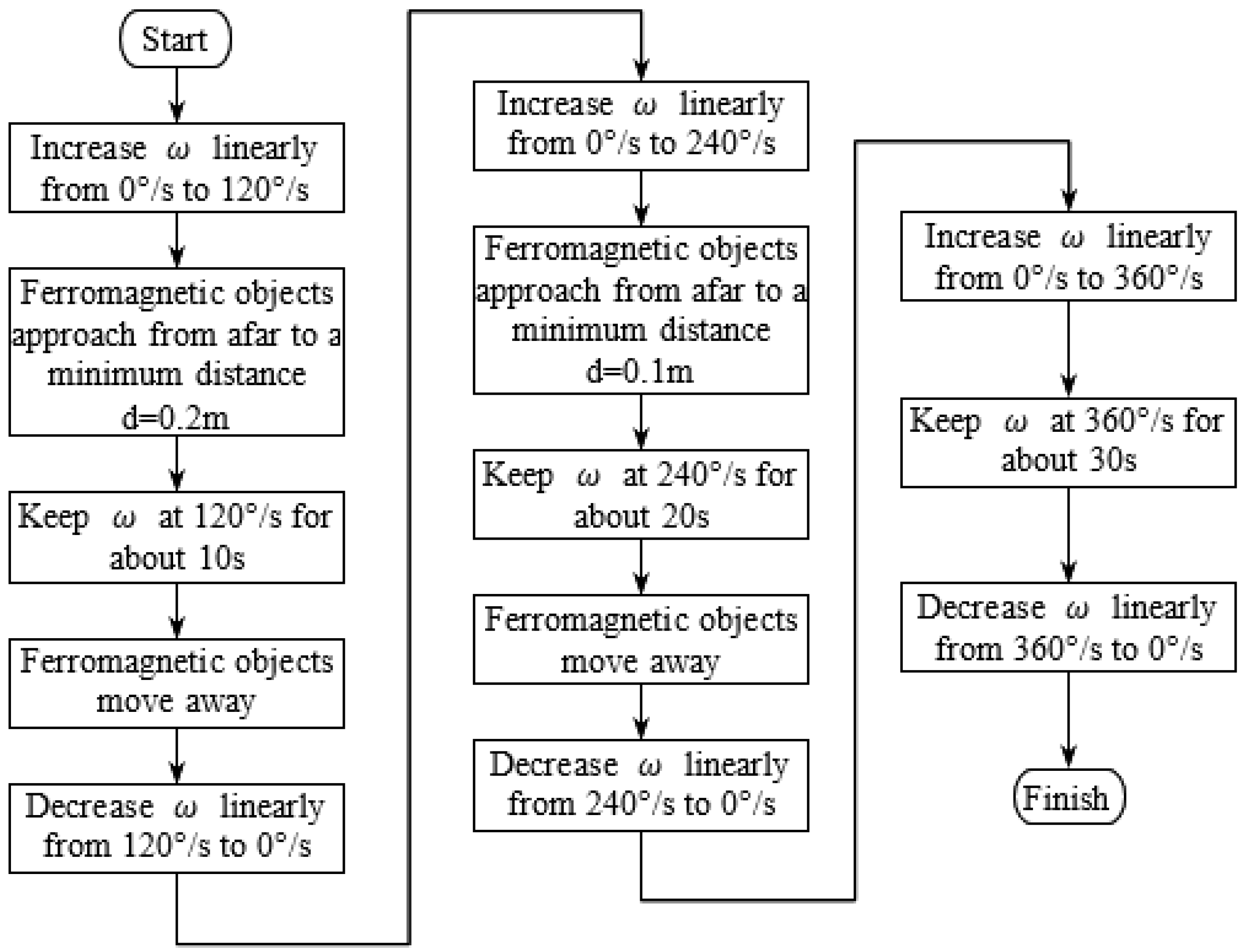
4.1. Basic Settings
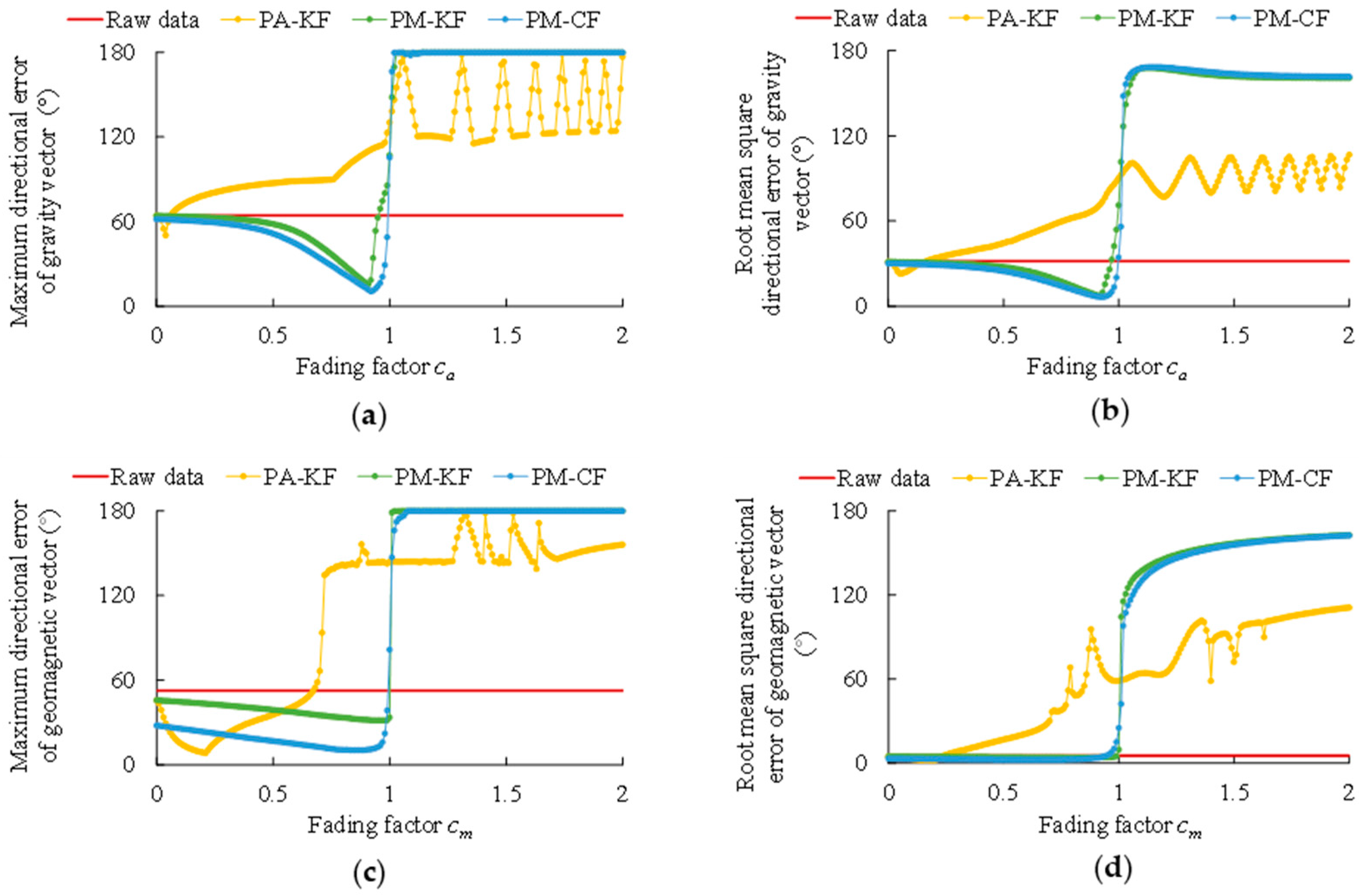
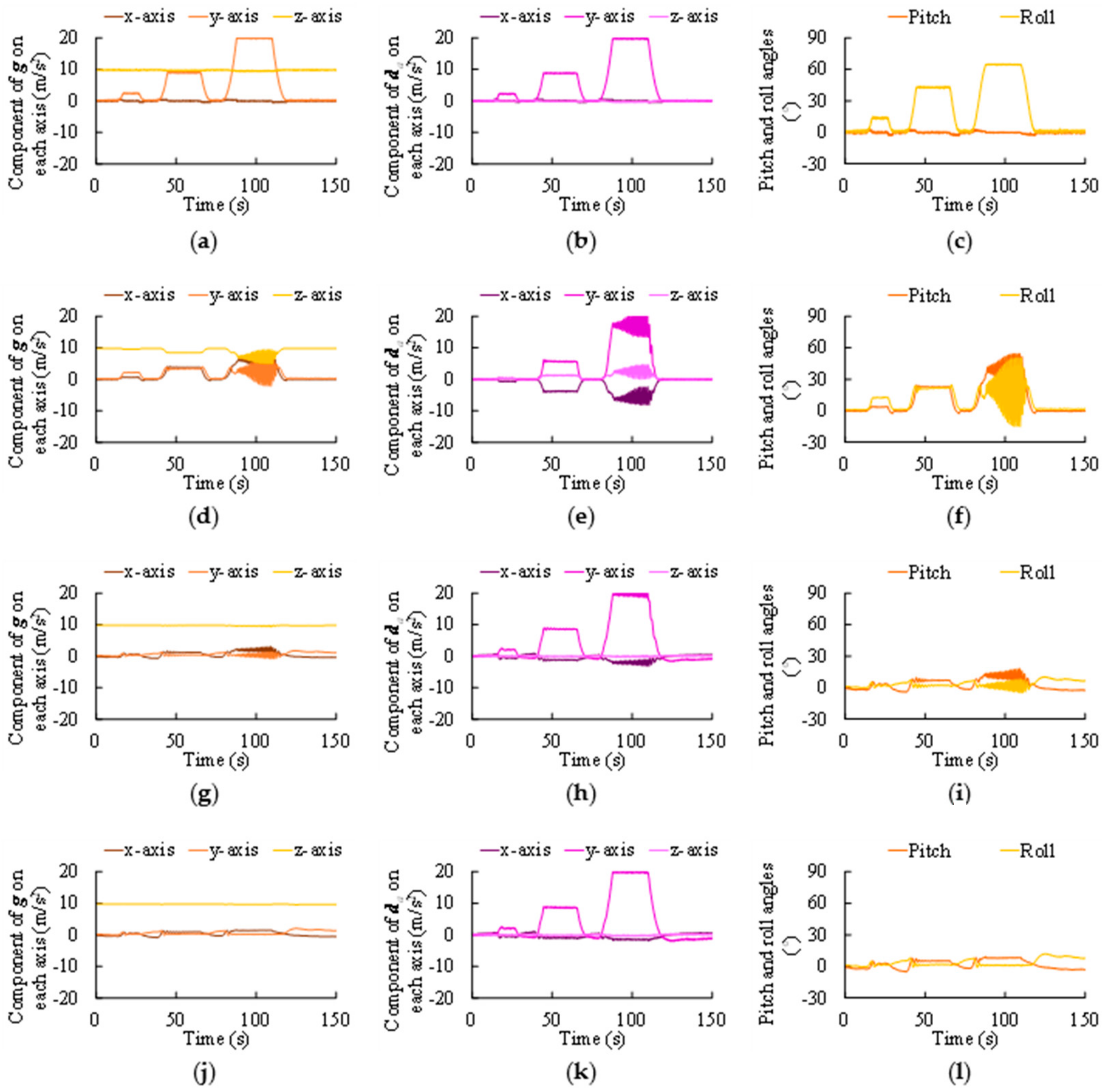
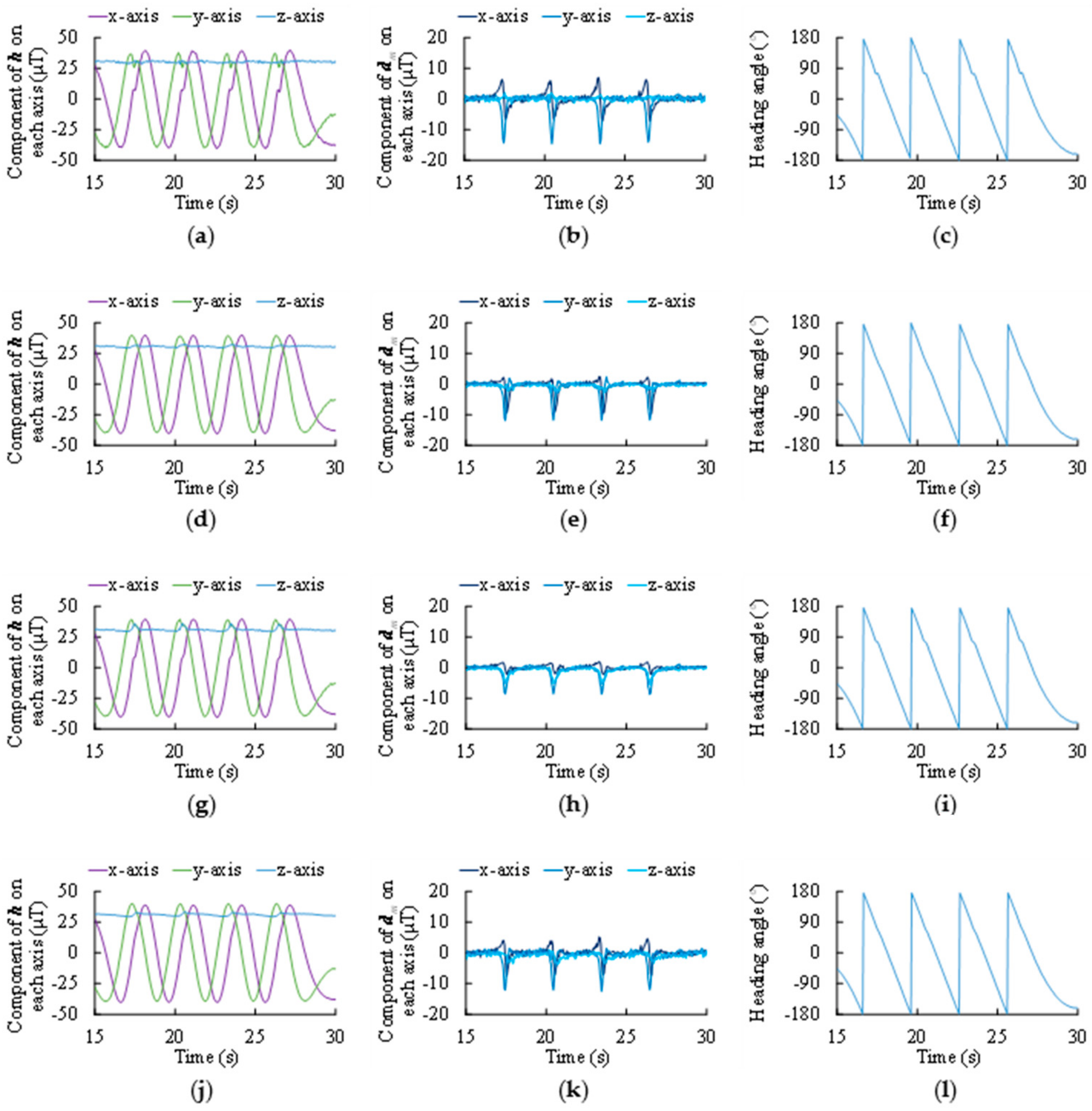
4.2. Experiment Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jurman, D.; Jankovec, M.; Kamnik, R.; Topic, M. Calibration and data fusion solution for the miniature attitude and heading reference system. Sens. Actuators A Phys. 2007, 138, 411–420. [Google Scholar] [CrossRef]
- Pourtakdoust, S.H.; Asl, H.G. An adaptive unscented Kalman filter for quaternion-based orientation estimation in low-cost AHRS. Aircr. Eng. Aerosp. Technol. 2007, 79, 485–493. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, Y.; Lai, J.; Yu, Y. Inner Attitude integration algorithm based on fault detection for strapdown inertial attitude and heading reference system. Chin. J. Aeronaut. 2010, 23, 68–74. [Google Scholar]
- Martin, P.; Salaun, E. Design and implementation of a low-cost observer-based attitude and heading reference system. Control Eng. Pract. 2010, 18, 712–722. [Google Scholar] [CrossRef]
- Ligorio, G.; Sabatini, A.M. Dealing with magnetic disturbances in human motion capture: A survey of techniques. Micromachines 2016, 7, 43. [Google Scholar] [CrossRef]
- Blachuta, M.; Grygiel, R.; Czyba, R.; Szafranski, G. Attitude and Heading Reference System Based on 3D Complementary Filter. In Proceedings of the 2014 19th International Conference on Methods and Models in Automation and Robotics (MMAR 2014), Miedzyzdroje, Poland, 2–5 September 2014; pp. 851–856. [Google Scholar]
- Valenti, R.G.; Dryanovski, I.; Xiao, J. A linear Kalman filter for MARG orientation estimation using the algebraic quaternion algorithm. IEEE Trans. Instrum. Meas. 2016, 65, 467–481. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, Z.; Chen, J.; Fourati, H.; Li, R. Fast complementary filter for attitude estimation using low-cost MARG sensors. IEEE Sens. J. 2016, 16, 6997–7007. [Google Scholar] [CrossRef]
- Valenti, R.G.; Dryanovski, I.; Xiao, J. Keeping a good attitude: A quaternion-based orientation filter for IMUs and MARGs. Sensors 2015, 15, 19302–19330. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R.; Sun, D.; Zhou, Z.; Wang, D. A linear fusion algorithm for attitude determination using low cost MEMS-based sensors. Meas. J. Int. Meas. Confed. 2007, 40, 322–328. [Google Scholar] [CrossRef]
- Sipos, M.; Paces, P.; Rohac, J.; Novacek, P. Analyses of triaxial accelerometer calibration algorithms. IEEE Sens. J. 2012, 12, 1157–1165. [Google Scholar] [CrossRef]
- Hemerly, E.M.; Coelho, F.A.A. Explicit solution for magnetometer calibration. IEEE Trans. Instrum. Meas. 2014, 63, 2093–2095. [Google Scholar] [CrossRef]
- Liu, Z.; Song, J. A low-cost calibration strategy for measurement-while-drilling system. IEEE Trans. Ind. Electron. 2018, 65, 3559–3567. [Google Scholar]
- Renaudin, V.; Afzal, M.H.; Lachapelle, G. Complete triaxis magnetometer calibration in the magnetic domain. J. Sens. 2010, 2010, 967245. [Google Scholar] [CrossRef]
- Secer, G.; Barshan, B. Improvements in deterministic error modeling and calibration of inertial sensors and magnetometers. Sens. Actuators A Phys. 2016, 247, 522–538. [Google Scholar] [CrossRef]
- Yang, D.; You, Z.; Li, B.; Duan, W.; Yuan, B. Complete tri-axis magnetometer calibration with a gyro auxiliary. Sensors 2017, 17, 1223. [Google Scholar] [CrossRef]
- Sarkka, O.; Nieminen, T.; Suuriniemi, S.; Kettunen, L. A multi-position calibration method for consumer-grade accelerometers, gyroscopes, and magnetometers to field conditions. IEEE Sens. J. 2017, 17, 3470–3481. [Google Scholar] [CrossRef]
- Mahony, R.; Hamel, T.; Pflimlin, J.M. Nonlinear complementary filters on the special orthogonal group. IEEE Trans. Autom. Control. 2008, 53, 1203–1218. [Google Scholar] [CrossRef]
- Benziane, L.; Hadri, A.E.; Seba, A.; Benallegue, A.; Chitour, Y. Attitude estimation and control using linearlike complementary filters: Theory and experiment. IEEE Trans. Control. Syst. Technol. 2016, 24, 2133–2140. [Google Scholar] [CrossRef]
- Januz, W.; Czyba, R.; Niezabitowski, M.; Grzejszczak, T. Expansion of Attitude Determination Algorithms via Complementary Filtering. In Proceedings of the 25th Mediterranean Conference on Control and Automation (MED 2017), Valletta, Malta, 3–6 July 2017; pp. 607–612. [Google Scholar]
- Lee, J.; Lim, J.; Lee, J. Compensated heading angles for outdoor mobile robots in magnetically disturbed environment. IEEE Trans. Instrum. Meas. 2018, 65, 1408–1419. [Google Scholar] [CrossRef]
- Sabatini, A.M. Quaternion-based extended Kalman filter for determining orientation by inertial and magnetic sensing. IEEE Trans. Biomed. Eng. 2006, 53, 1346–1356. [Google Scholar] [CrossRef]
- Suh, Y.S.; Park, S.K.; Kang, H.J.; Ro, Y.S. Attitude Estimation adaptively compensating external acceleration. JSME Int. J. Ser. C 2006, 49, 172–179. [Google Scholar] [CrossRef]
- Suh, Y.S. Orientation estimation using a quaternion-based indirect Kalman filter with adaptive estimation of external acceleration. IEEE Trans. Instrum. Meas. 2010, 59, 3296–3305. [Google Scholar] [CrossRef]
- Suh, Y.S.; Ro, Y.S.; Kang, H.J. Quaternion-Based Indirect Kalman Filter Discarding Pitch and Roll Information Contained in Magnetic Sensors. IEEE Trans. Instrum. Meas. 2012, 61, 1786–1792. [Google Scholar] [CrossRef]
- Nemec, D.; Janota, A.; Hruboš, M.; Šimák, V. Intelligent real-time MEMS sensor fusion and calibration. IEEE Sens. J. 2016, 16, 7150–7160. [Google Scholar] [CrossRef]
- Fan, B.; Li, Q.; Wang, C.; Liu, T. An adaptive orientation estimation method for magnetic and inertial sensors in the presence of magnetic disturbances. Sensors 2017, 17, 1161. [Google Scholar] [CrossRef] [PubMed]
- Kang, C.W.; Kim, H.J.; Park, C.G. A human motion tracking algorithm using adaptive EKF based on Markov chain. IEEE Sens. J. 2016, 16, 8953–8962. [Google Scholar] [CrossRef]
- Königseder, F.; Kemmetmüller, W.; Kugi, A. Attitude estimation using redundant inertial measurement units for the control of a camera stabilization platform. IEEE Trans. Control. Syst. Technol. 2016, 24, 1837–1844. [Google Scholar] [CrossRef]
- Fan, B.; Li, Q.; Liu, T. Improving the accuracy of wearable sensor orientation using a two-step complementary filter with state machine-based adaptive strategy. Meas. Sci. Technol. 2018, 29, 115104. [Google Scholar] [CrossRef]
- Ligorio, G.; Sabatini, A.M. A novel Kalman filter for human motion tracking with an inertial-based dynamic inclinometer. IEEE Trans. Biomed. Eng. 2015, 62, 2033–2043. [Google Scholar] [CrossRef]
- Yuan, Q.; Asadi, E.; Lu, Q.; Yang, G.; Chen, I.M. Uncertainty-based IMU orientation tracking algorithm for dynamic motions. IEEE ASME Trans. Mechatron. 2019, 24, 872–882. [Google Scholar] [CrossRef]
- Lee, J.K.; Park, E.J.; Robinovitch, S.N. Estimation of attitude and external acceleration using inertial sensor measurement during various dynamic conditions. IEEE Trans. Instrum. Meas. 2012, 61, 2262–2273. [Google Scholar] [CrossRef]
- Ahmed, H.; Tahir, M. Improving the accuracy of human body orientation estimation with wearable IMU sensors. IEEE Trans. Instrum. Meas. 2017, 66, 535–542. [Google Scholar] [CrossRef]
- Ahmed, H.; Tahir, M. Accurate attitude estimation of a moving land vehicle using low-cost MEMS IMU sensors. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1723–1739. [Google Scholar] [CrossRef]
- Rosario, M.B.D.; Khamis, H.; Ngo, P.; Lovell, N.H.; Redmond, S.J. Computationally efficient adaptive error-state Kalman filter for attitude estimation. IEEE Sens. J. 2018, 18, 9332–9342. [Google Scholar] [CrossRef]
- Lee, J.K. A Parallel attitude-heading Kalman filter without state augmentation of model-based disturbance components. IEEE Trans. Instrum. Meas. 2019, 68, 2668–2670. [Google Scholar] [CrossRef]
- Błachuta, M.; Czyba, R.; Janusz, W.; Szafranski, G. Data fusion algorithm for the altitude and vertical speed estimation of the VTOL platform. J. Intell. Rob. Syst. Theor. Appl. 2014, 74, 413–420. [Google Scholar] [CrossRef]
- Huang, W.; Xie, H.; Shen, C.; Li, J. A robust strong tracking cubature Kalman filter for spacecraft attitude estimation with quaternion constraint. Acta Astronaut. 2016, 121, 153–163. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman filters. IEEE Trans. Autom. Control. 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Batista, P.; Silvestre, C.; Oliveira, P. Vector-based attitude filter for space navigation. J. Intell. Rob. Syst. Theor. Appl. 2011, 64, 221–243. [Google Scholar] [CrossRef]
- Batista, P.; Silvestre, C.; Oliveira, P. Sensor-based globally asymptotically stable filters for attitude estimation: Analysis, design, and performance evaluation. IEEE Trans. Autom. Control. 2012, 57, 2095–2100. [Google Scholar] [CrossRef]
- Shuster, M.D. The TRIAD algorithm as maximum likelihood estimation. J. Astronaut. Sci. 2006, 54, 113–123. [Google Scholar] [CrossRef]
- Li, X.; Song, B.; Wang, Y.; Niu, J.; Li, Z. Calibration and alignment of tri-axial magnetometers for attitude determination. IEEE Sens. J. 2018, 18, 7399–7406. [Google Scholar] [CrossRef]
- Li, X.; Li, Z. Vector-aided in-field calibration method for low-end MEMS gyros in attitude and heading reference systems. IEEE Trans. Instrum. Meas. 2014, 63, 2675–2681. [Google Scholar] [CrossRef]

| Algorithm | Raw Data | PA-KF | PM-KF | PM-CF | |
|---|---|---|---|---|---|
| Gravity vector | Maximum error/ | 64.36°/− | 50.34°/0.04 | 15.63°/0.91 | 10.58°/0.92 |
| RMSE/ | 31.72°/− | 22.97°/0.05 | 7.41°/0.92 | 6.46°/0.93 | |
| Geomagnetic vector | Maximum error/ | 52.75°/− | 8.24°/0.21 | 31.31°/0.96 | 10.26°/0.87 |
| RMSE/ | 5.24°/− | 1.76°/0.20 | 3.82°/0.83 | 2.18°/0.64 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, Z.; Li, X. External Disturbances Rejection for Vector Field Sensors in Attitude and Heading Reference Systems. Micromachines 2020, 11, 803. https://doi.org/10.3390/mi11090803
Wang Y, Li Z, Li X. External Disturbances Rejection for Vector Field Sensors in Attitude and Heading Reference Systems. Micromachines. 2020; 11(9):803. https://doi.org/10.3390/mi11090803
Chicago/Turabian StyleWang, Yongjun, Zhi Li, and Xiang Li. 2020. "External Disturbances Rejection for Vector Field Sensors in Attitude and Heading Reference Systems" Micromachines 11, no. 9: 803. https://doi.org/10.3390/mi11090803
APA StyleWang, Y., Li, Z., & Li, X. (2020). External Disturbances Rejection for Vector Field Sensors in Attitude and Heading Reference Systems. Micromachines, 11(9), 803. https://doi.org/10.3390/mi11090803






