Influence of the Nose Radius on the Machining Forces Induced during AISI-4140 Hard Turning: A CAD-Based and 3D FEM Approach
Abstract
1. Introduction
2. Materials and Methods
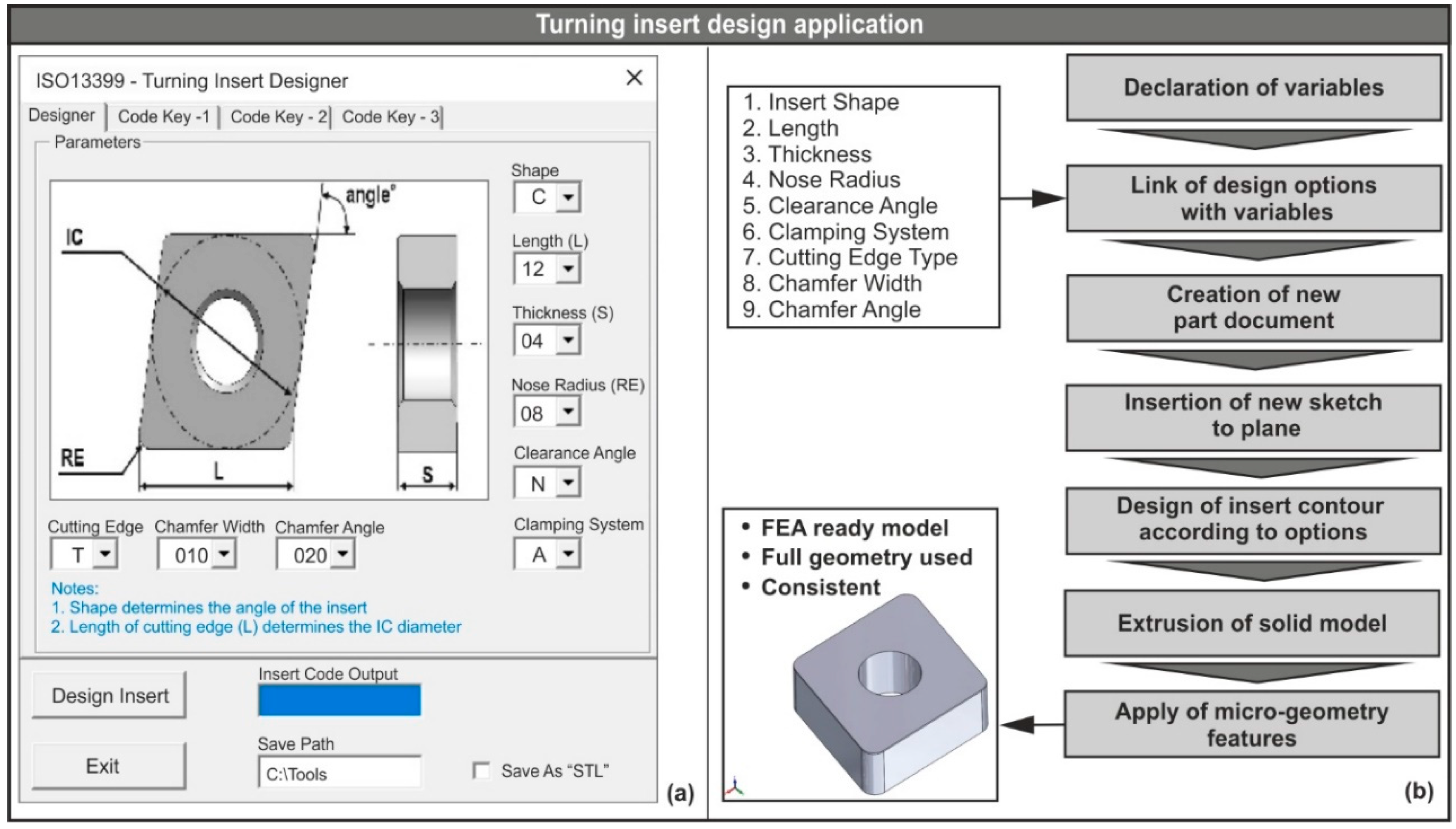
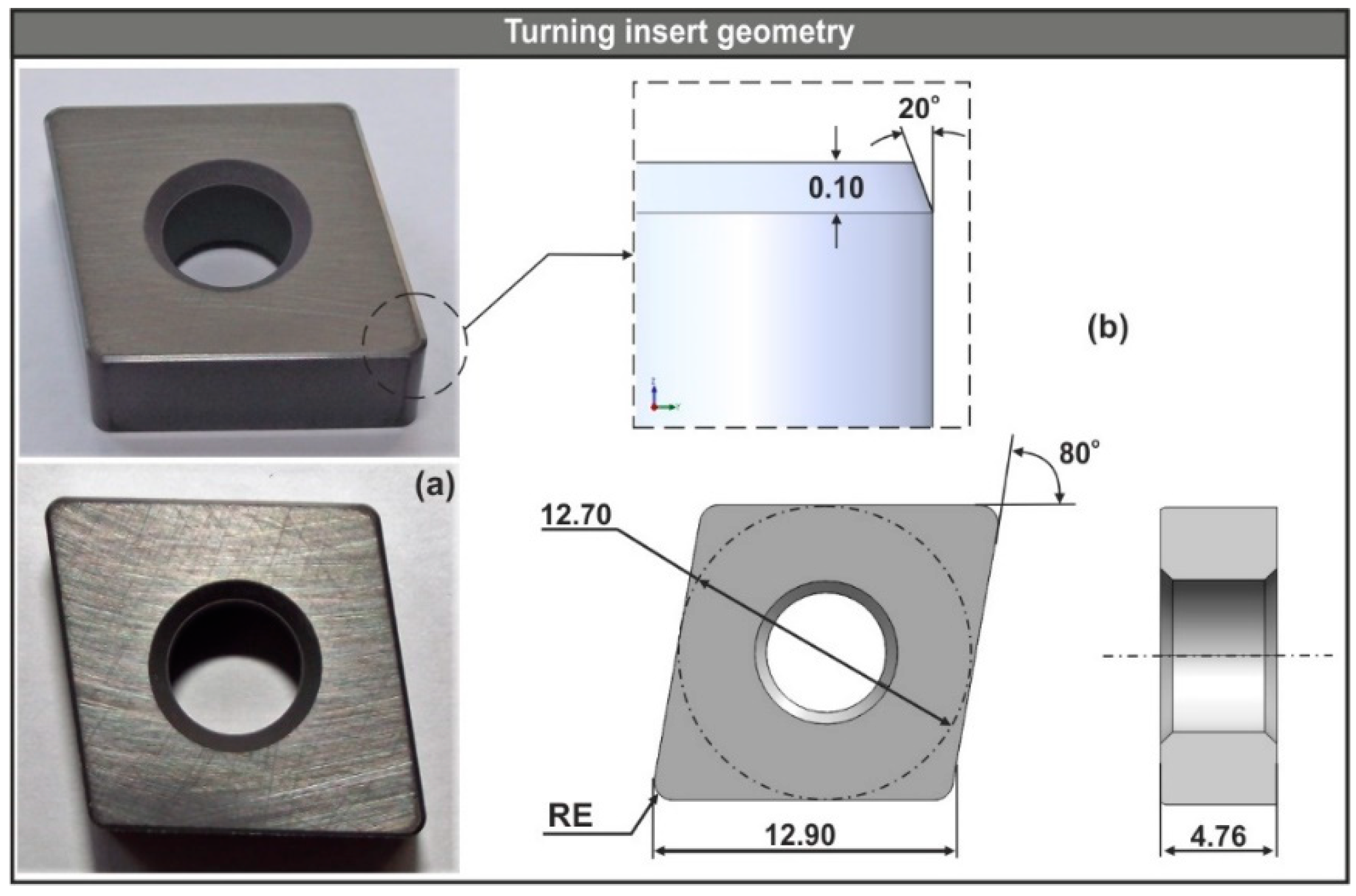
2.1. CAD-Based Application for Designing Turning Inserts
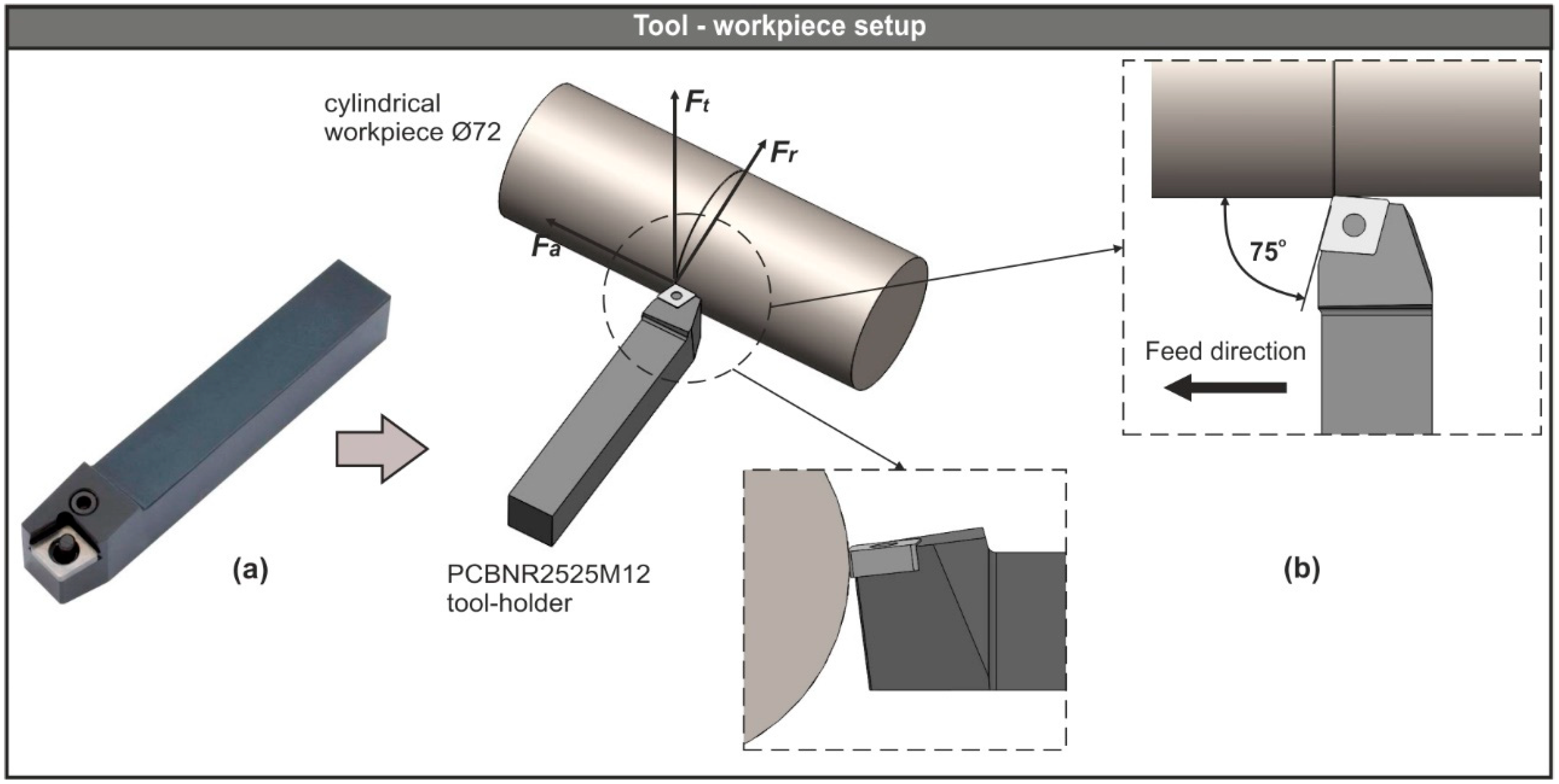
2.2. CAD-Based Layout of the Turning Process
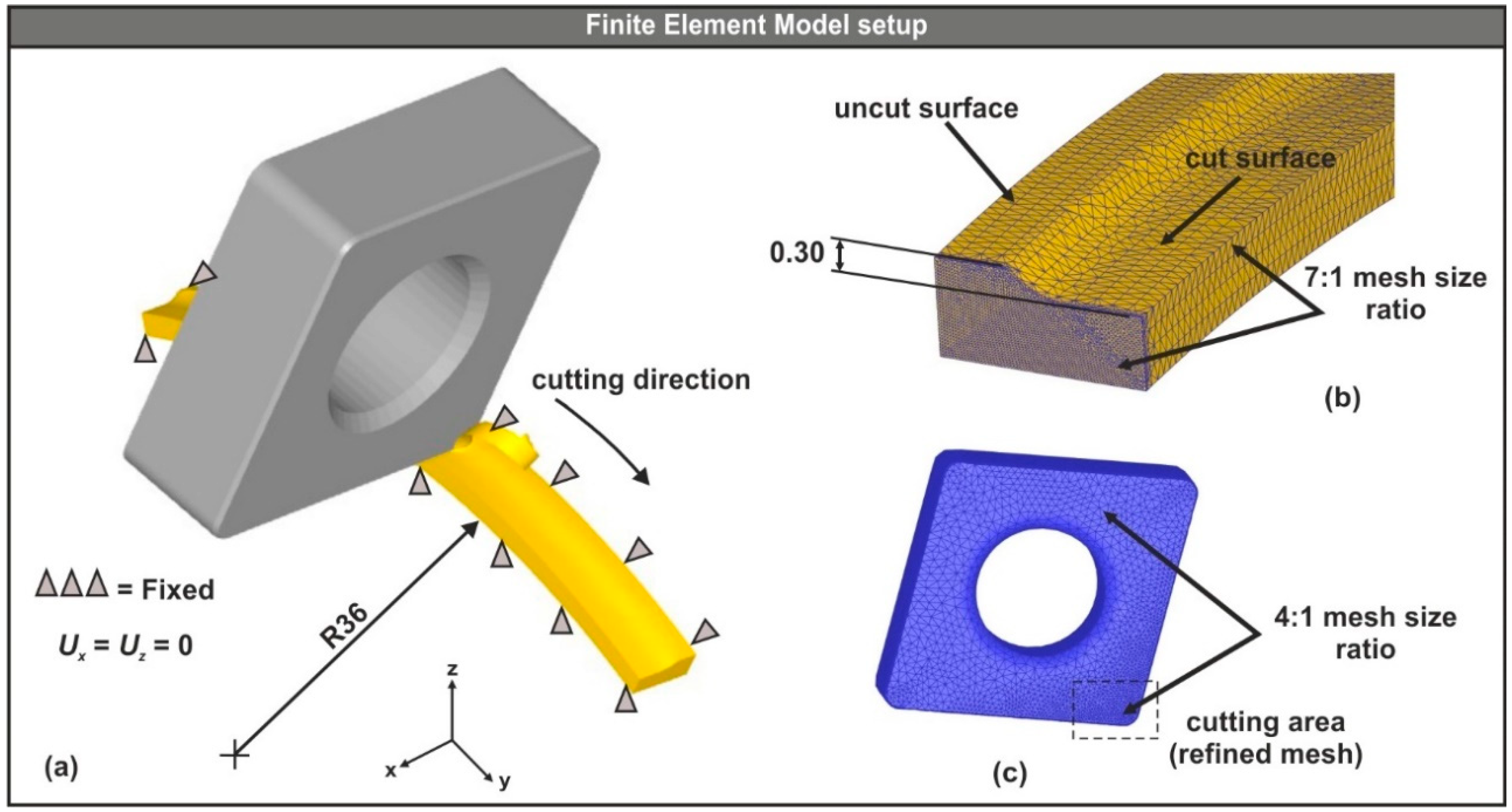
2.3. Pre-Processing of the 3D FE Turning Model
2.3.1. Configuration of the Insert-Workpiece Interface
2.3.2. Modeling of the Insert-Workpiece Materials
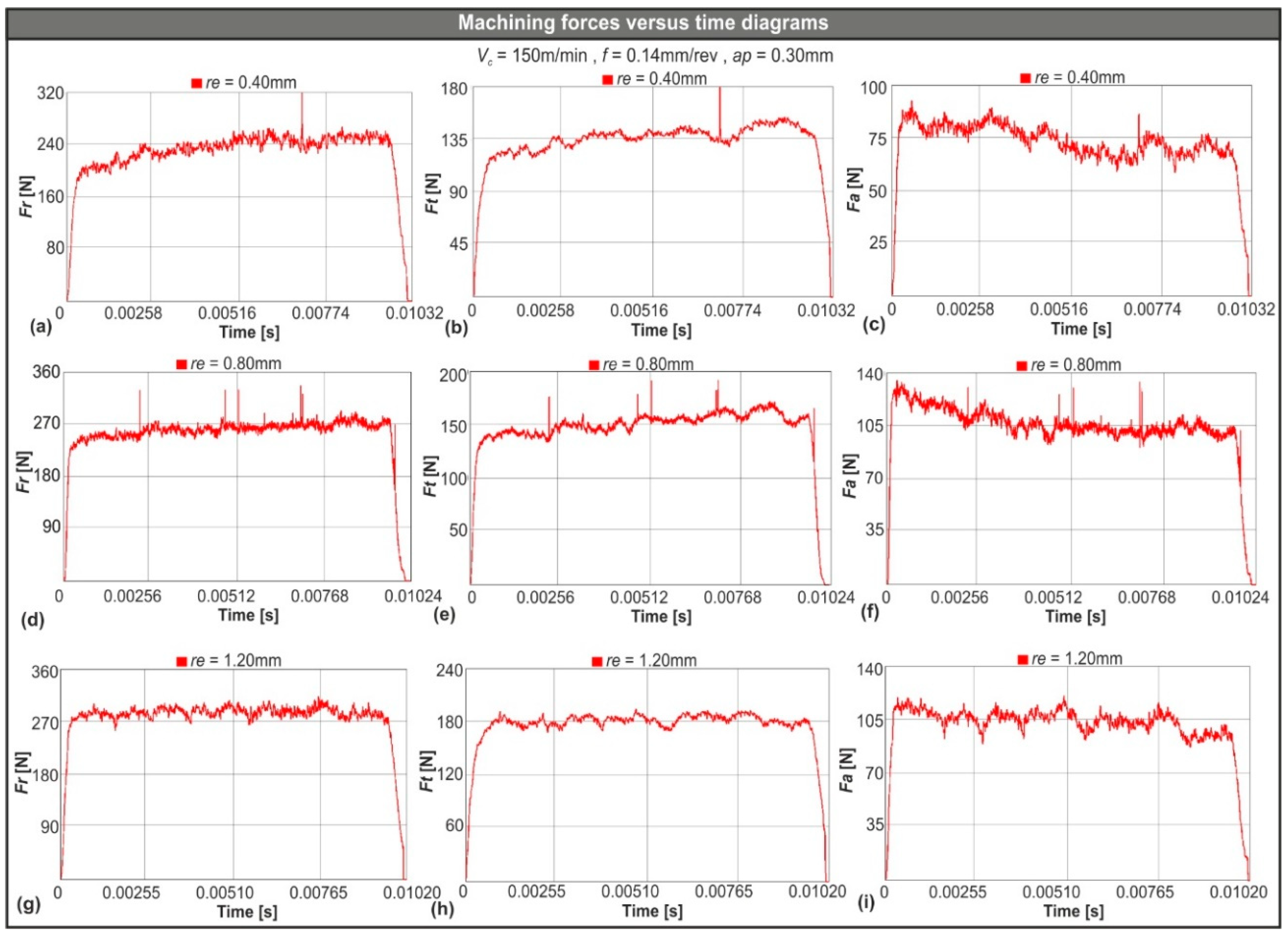
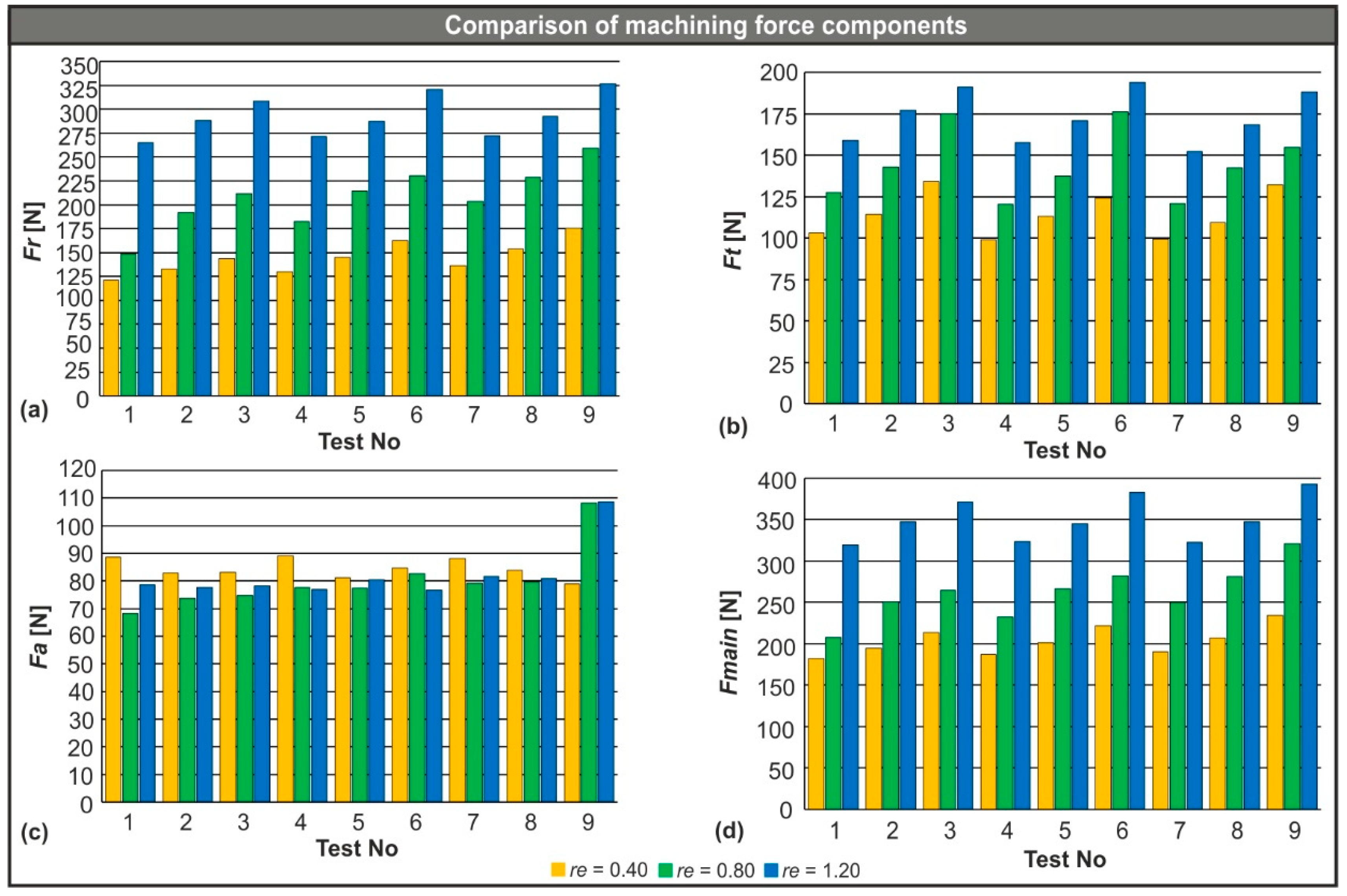
3. Results and Discussion
3.1. Assessment of the Cutting Force Components Using FEM
- The radial force is the component that contributes to the resultant machining force the most. In test number nine, for example, this contribution was approximately 56.6%, 65.3%, and 69.2% for each value of nose radius of 0.40 mm, 0.80 mm, and 1.20 mm, respectively. The same trend was observed in the rest of the tests.
- Any increase in feed rate affects all forces except the feed force. Even though the amount of change is not significant, it cannot be considered negligible either. Specifically, an increase in the feed rate from 0.08 mm/rev to 0.11 mm/rev increased the resultant machining force by about 7.6%, 16.0%, and 7.7% for each nose radius (0.40 mm, 0.80 mm, and 1.20 mm, respectively). Similarly, when the feed rate changed from 0.11 mm/rev to 0.14 mm/rev, the feed rate rose by approximately 10.9%, 13.7%, and 10.4% for the same nose radii, respectively.
- In contrast, the nose radius of the inserts had a notable impact on the generated cutting forces. The main machining force increased by 28% on average when the nose radius of the tool changed from 0.40 mm to 0.80 mm. Furthermore, the tool with the 1.20 mm nose radius produced even higher forces. The change from the 0.80 mm nose radius to the 1.20 mm increased Fmain by 35% on average.
- Finally, any change in cutting speed had a limited effect on the turning forces. A slight decrease in cutting forces was noted as lower cutting speeds were applied. In particular, by lowering cutting speed from 150 m/min to 115 m/min, the decrease was estimated as approximately 4.5% and for the equivalent shift from 115 m/min to 80 m/min, the reduction was found to be close to 3.4%.
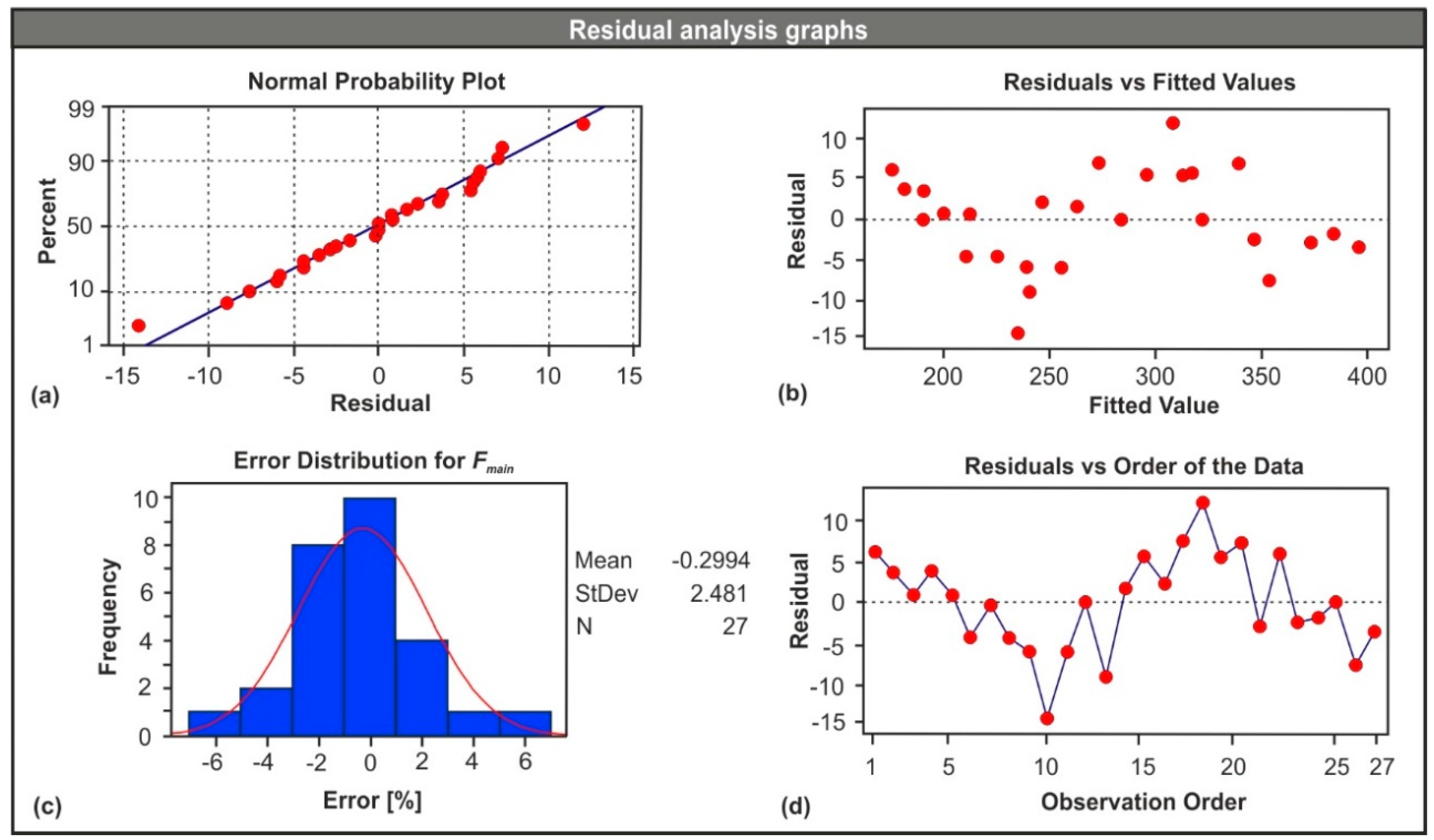
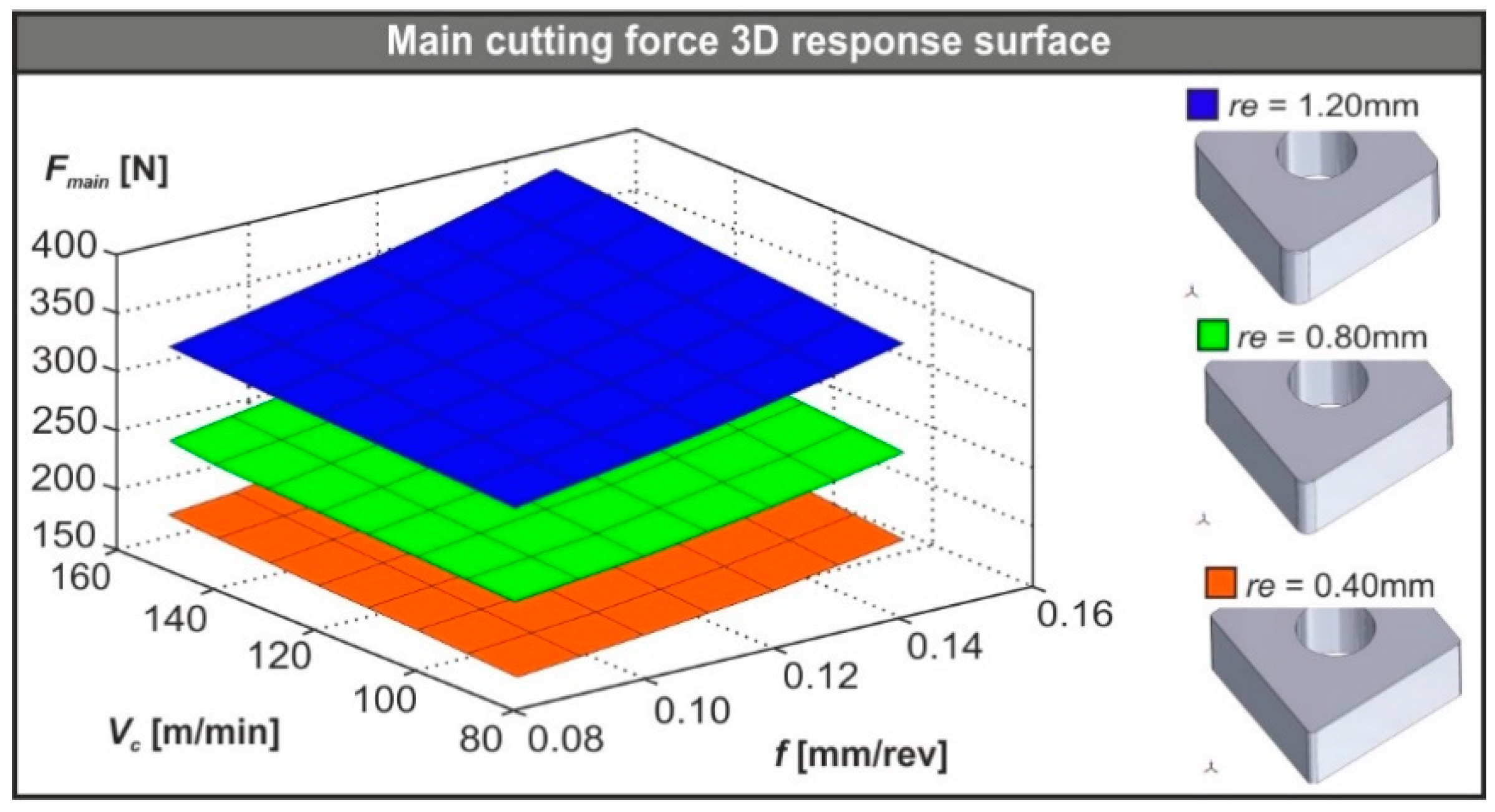
3.2. Modelling of the Resultant Cutting Force Using RSM
3.3. Validation of the RSM Based Model
- The nose radius had a strong impact on the resultant turning force. In fact, an increase from 0.40 mm to 1.20 mm almost doubled the resultant force regardless of the conditions.
- Any increase in feed rate acts as increasing the main cutting force, but at a much lower grade compared to the effect of the nose radius.
- Finally, any change in the cutting speed did not seem to have a significant influence on the main cutting force.
4. Conclusions
- Fr is the governing force during hard turning of AISI-4140, which in most cases represents two-thirds of the produced resultant machining force.
- When feed rate changed from 0.08 mm/rev to 0.11 mm/rev Fmain gained an average increase of about 10.4%. Similarly, a shift from 0.11 mm/rev to 0.14 mm/rev increased Fmain by approximately 11.7%, regardless of the nose radius value.
- The nose radius of the cutting edge affects the generated cutting forces substantially. It was highlighted that a higher value of nose radius leads to higher values of cutting forces, and depending on the applied cutting conditions, the increase percentage exceeded 30% in most cases.
- Finally, changing the cutting speed did not seem to influence the main cutting force notably.
Author Contributions
Funding
Conflicts of Interest
References
- Sayuti, M.; Sarhan, A.A.D.; Salem, F. Novel uses of SiO2 nano-lubrication system in hard turning process of hardened steel AISI4140 for less tool wear, surface roughness and oil consumption. J. Clean. Prod. 2014, 67, 265–276. [Google Scholar] [CrossRef]
- Gaitonde, V.N.; Karnik, S.R.; Figueira, L.; Davim, J.P. Analysis of machinability during hard turning of cold work tool steel (type: AISI D2). Mater. Manuf. Process. 2009, 24, 1373–1382. [Google Scholar] [CrossRef]
- Meddour, I.; Yallese, M.A.; Bensouilah, H.; Khellaf, A.; Elbah, M. Prediction of surface roughness and cutting forces using RSM, ANN, and NSGA-II in finish turning of AISI 4140 hardened steel with mixed ceramic tool. Int. J. Adv. Manuf. Technol. 2018, 97, 1931–1949. [Google Scholar] [CrossRef]
- Elkaseer, A.; Abdelaziz, A.; Saber, M.; Nassef, A. FEM-based study of precision hard turning of stainless steel 316L. Materials 2019, 12, 2522. [Google Scholar] [CrossRef] [PubMed]
- Meddour, I.; Yallese, M.A.; Khattabi, R.; Elbah, M.; Boulanouar, L. Investigation and modeling of cutting forces and surface roughness when hard turning of AISI 52100 steel with mixed ceramic tool: Cutting conditions optimization. Int. J. Adv. Manuf. Technol. 2015, 77, 1387–1399. [Google Scholar] [CrossRef]
- Davim, J.P.; Figueira, L. Machinability evaluation in hard turning of cold work tool steel (D2) with ceramic tools using statistical techniques. Mater. Des. 2007, 28, 1186–1191. [Google Scholar] [CrossRef]
- Saez-de-Buruaga, M.; Soler, D.; Aristimuño, P.X.; Esnaola, J.A.; Arrazola, P.J. Determining tool/chip temperatures from thermography measurements in metal cutting. Appl. Therm. Eng. 2018, 145, 305–314. [Google Scholar] [CrossRef]
- Ye, G.G.; Chen, Y.; Xue, S.F.; Dai, L.H. Critical cutting speed for onset of serrated chip flow in high speed machining. Int. J. Mach. Tools Manuf. 2014, 86, 18–33. [Google Scholar] [CrossRef]
- Shuang, F.; Chen, X.; Ma, W. Numerical analysis of chip formation mechanisms in orthogonal cutting of Ti6Al4V alloy based on a CEL model. Int. J. Mater. Form. 2018, 11, 185–198. [Google Scholar] [CrossRef]
- Arrazola, P.J.; Villar, A.; Ugarte, D.; Marya, S. Serrated chip prediction in finite element modeling of the chip formation process. Mach. Sci. Technol. 2007, 11, 367–390. [Google Scholar] [CrossRef]
- Klocke, F.; Raedt, H.-W.; Hoppe, S. 2D-FEM Simulation of the Orthogonal High Speed Cutting Process. Mach. Sci. Technol. 2001, 5, 323–340. [Google Scholar] [CrossRef]
- Calamaz, M.; Coupard, D.; Girot, F. A new material model for 2D numerical simulation of serrated chip formation when machining titanium alloy Ti-6Al-4V. Int. J. Mach. Tools Manuf. 2008, 48, 275–288. [Google Scholar] [CrossRef]
- DEFORM, version 11.3 (PC); Documentation; Scientific Forming Technologies Corporation: Columbus, OH, USA, 2016.
- Arrazola, P.J.; Özel, T.; Umbrello, D.; Davies, M.; Jawahir, I.S. Recent advances in modelling of metal machining processes. CIRP Ann. Manuf. Technol. 2013, 62, 695–718. [Google Scholar] [CrossRef]
- Tzotzis, A.; García-hernández, C.; Kyratsis, P. FEM based mathematical modelling of thrust force during drilling of Al7075-T6. Mech. Ind. 2020, 415, 1–14. [Google Scholar] [CrossRef]
- Arisoy, Y.M.; Özel, T. Prediction of machining induced microstructure in Ti-6Al-4V alloy using 3-D FE-based simulations: Effects of tool micro-geometry, coating and cutting conditions. J. Mater. Process. Technol. 2015, 220, 1–26. [Google Scholar] [CrossRef]
- Davoudinejad, A.; Tosello, G.; Parenti, P.; Annoni, M. 3D finite element simulation of micro end-milling by considering the effect of tool run-out. Micromachines 2017, 8, 187. [Google Scholar] [CrossRef]
- Guo, Y.B.; Liu, C.R. 3D FEA modeling of hard turning. J. Manuf. Sci. Eng. Trans. ASME 2002, 124, 189–199. [Google Scholar] [CrossRef]
- Karpat, Y.; Ozel, T. Process simulations for 3D turning using uniform and variable microgeometry PCBN tools. Int. J. Mach. Mach. Mater. 2008, 4, 26–38. [Google Scholar] [CrossRef]
- Malakizadi, A.; Gruber, H.; Sadik, I.; Nyborg, L. An FEM-based approach for tool wear estimation in machining. Wear 2016, 368–369, 10–24. [Google Scholar] [CrossRef]
- Lotfi, M.; Jahanbakhsh, M.; Farid, A.A. Wear estimation of ceramic and coated carbide tools in turning of Inconel 625: 3D FE analysis. Tribol. Int. 2016, 99, 107–116. [Google Scholar] [CrossRef]
- Hu, H.J.; Huang, W.J. Effects of turning speed on high-speed turning by ultrafine-grained ceramic tool based on 3D finite element method and experiments. Int. J. Adv. Manuf. Technol. 2013, 67, 907–915. [Google Scholar] [CrossRef]
- Magalhães, F.C.; Ventura, C.E.H.; Abrão, A.M.; Denkena, B. Experimental and numerical analysis of hard turning with multi-chamfered cutting edges. J. Manuf. Process. 2020, 49, 126–134. [Google Scholar] [CrossRef]
- Aouici, H.; Elbah, M.; Yallese, M.A.; Fnides, B.; Meddour, I.; Benlahmidi, S. Performance comparison of wiper and conventional ceramic inserts in hard turning of AISI 4140 steel: Analysis of machining forces and flank wear. Int. J. Adv. Manuf. Technol. 2016, 87, 2221–2244. [Google Scholar] [CrossRef]
- Vijayaraghavan, A. Automated Drill Design Software; Consortium on Deburring and Edge Finishing. Berkeley University: Berkeley, CA, USA, 2006. [Google Scholar]
- Oancea, G.; Haba, S.-A. Software Tool Used in CAPP/CAM Systems for Rotational Parts. Sci. Bull. Ser. C Fascicle Mech. Tribol. Mach. Manuf. Technol. 2016, 30, 75. [Google Scholar]
- Kyratsis, P.; Tzotzis, A.; Tzetzis, D.; Sapidis, N. Pneumatic cylinder design using cad-based programming. Acad. J. Manuf. Eng. 2018, 16, 107–113. [Google Scholar]
- Gardner, J.D.; Dornfeld, D. Finite Element Modeling of Drilling Using DEFORM; Consortium on Deburring and Edge Finishing. Berkeley University: Berkeley, CA, USA, 2006. [Google Scholar]
- Tzotzis, A.; Garcia-Hernandez, C.; Talón, J.L.H.; Kyratsis, P. 3D FE Modelling of Machining Forces during AISI 4140 Hard Turning. Strojniški Vestn. J. Mech. Eng. 2020, 66, 467–478. [Google Scholar] [CrossRef]
- Melkote, S.N.; Grzesik, W.; Outeiro, J.; Rech, J.; Schulze, V.; Attia, H.; Arrazola, P.J.; M’Saoubi, R.; Saldana, C. Advances in material and friction data for modelling of metal machining. CIRP Ann. Manuf. Technol. 2017, 66, 731–754. [Google Scholar] [CrossRef]
- Hu, H.J.; Huang, W.J. Tool life models of nano ceramic tool for turning hard steel based on FEM simulation and experiments. Ceram. Int. 2014, 40, 8987–8996. [Google Scholar] [CrossRef]
- Cockcroft, M.G.; Latham, D.J. Ductility and the Workability of Metals. J. Institue Met. 1968, 96, 33–39. [Google Scholar]
- Kobayashi, S.; Lee, C. Deformation mechanics and workability in upsetting solid circular cylinders. Proc. North. Am. Metalwork. Res. Conf. 1973, 1, 185–204. [Google Scholar]
- Oh, S.; Chen, C.; Kobayashi, S. Ductile fracture in axisymmetric extrusion and drawing—Part 2: Workability in extrusion and drawing. J. Manuf. Sci. Eng. ASME 1979, 101, 36–44. [Google Scholar] [CrossRef]
- Oyane, M.; Sato, T.; Okimoto, K.; Shima, S. Criteria for ductile fracture and their applications. J. Mech. Work. Technol. 1980, 4, 65–81. [Google Scholar] [CrossRef]
- Zorev, N.N. Inter-relationship between shear processes occurring along tool face and shear plane in metal cutting. Int. Res. Prod. Eng. 1963, 49, 143–152. [Google Scholar]
- Agmell, M. Applied FEM of Metal Removal and Forming, 1st ed.; Studentlitteratur: Lund, Sweden, 2018; ISBN 978-91-44-12507-7. [Google Scholar]
- Arrazola, P.J.; Meslin, F.; Marya, S. A technique for the identification of friction at tool/chip interface during machining. In Proceedings of the 6th CIRP International Workshop on Modeling of Machining Operations, Hamilton, ON, Canada, 20 May 2003; pp. 1–6. [Google Scholar]
- Haglund, A.J.; Kishawy, H.A.; Rogers, R.J. An exploration of friction models for the chip-tool interface using an Arbitrary Lagrangian—Eulerian finite element model. Wear. 2008, 265, 452–460. [Google Scholar] [CrossRef]
- Astakhov, V.P. Tribology of Metal Cutting, 1st ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2006; ISBN 0080451497. [Google Scholar]
- Aouici, H.; Bouchelaghem, H.; Yallese, M.A.; Elbah, M. Machinability investigation in hard turning of AISI D3 cold work steel with ceramic tool using response surface methodology. Int. J. Adv. Manuf. Technol. 2014, 73, 1775–1788. [Google Scholar] [CrossRef]
- Aouici, H.; Yallese, M.A.; Chaoui, K.; Mabrouki, T.; Rigal, J.F. Analysis of surface roughness and cutting force components in hard turning with CBN tool: Prediction model and cutting conditions optimization. Meas. J. Int. Meas. Confed. 2012, 45, 344–353. [Google Scholar] [CrossRef]
- Quiza, R.; Figueira, L.; Davim, J.P. Comparing statistical models and artificial neural networks on predicting the tool wear in hard machining D2 AISI steel. Int. J. Adv. Manuf. Technol. 2008, 37, 641–648. [Google Scholar] [CrossRef]
- Sahu, N.K.; Andhare, A.B. Prediction of residual stress using RSM during turning of Ti–6Al–4V with the 3D FEM assist and experiments. SN Appl. Sci. 2019, 1, 1–14. [Google Scholar] [CrossRef]
- Efkolidis, N.; Hernández, C.G.; Talón, J.L.H.; Kyratsis, P. Modelling and prediction of thrust force and torque in drilling operations of Al7075 using ANN and RSM methodologies. Strojniški Vestn. J. Mech. Eng. 2018, 64, 351–361. [Google Scholar] [CrossRef]
- Chmielewski, T.; Swiercz, D.O. Multi-Response Optimization of Electrical Discharge Machining Using the Desirability Function. Micromachines 2019, 10, 72. [Google Scholar] [CrossRef]
| Level | Vc (m/min) | f (mm/rev) | re (mm) |
|---|---|---|---|
| I | 80 | 0.08 | 0.40 |
| II | 115 | 0.11 | 0.80 |
| III | 150 | 0.14 | 1.20 |
| A (MPa) | B (MPa) | C | n | m | T0 (°C) | Tm (°C) |
|---|---|---|---|---|---|---|
| 106 | 1167 | 0.0352 | 0.1424 | 0.763 | 20 | 1547 |
| Mechanical Properties | AISI-4140 | Ceramic |
| Young’s Modulus (GPa) | 212 @ 20 °C | 415 |
| 192 @ 300 °C | ||
| 164 @ 600 °C | ||
| Density (kg/m3) | 7850 | 3500 |
| Poisson’s ratio | 0.30 | 0.22 |
| Hardness (HRC) | 60 | − |
| Thermal Properties | AISI-4140 | Ceramic |
| Heat capacity (J/kgK) | 362 @ 20 °C | 334 |
| 446 @ 300 °C | ||
| 610 @ 600 °C | ||
| Thermal expansion (μm/mK) | 11.9 @ 20 °C | 8.4 |
| 13.6 @ 300 °C | ||
| 14.9 @ 600 °C | ||
| Thermal conductivity (W/mK) | 41.7 @ 20 °C | 7.5 |
| 41.4 @ 300 °C | ||
| 34.1 @ 600 °C |
| Cutting Parameters | Fmain (N) | ||||||
|---|---|---|---|---|---|---|---|
| Std Order | Vc (m/min) | f (mm/rev) | ap (mm) | re (mm) | Experiments | FE Model | Relative Error (%) |
| 1 | 80 | 0.08 | 0.30 | 0.80 | 189.8 | 207.7 | 9.4 |
| 2 | 80 | 0.11 | 0.30 | 0.80 | 244.6 | 250.2 | 2.3 |
| 3 | 80 | 0.14 | 0.30 | 0.80 | 282.3 | 264.5 | −6.3 |
| 4 | 115 | 0.08 | 0.30 | 0.80 | 225.7 | 232.1 | 2.8 |
| 5 | 115 | 0.11 | 0.30 | 0.80 | 264.1 | 266.2 | 0.8 |
| 6 | 115 | 0.14 | 0.30 | 0.80 | 300.9 | 281.5 | −6.4 |
| 7 | 150 | 0.08 | 0.30 | 0.80 | 238.0 | 249.6 | 4.9 |
| 8 | 150 | 0.11 | 0.30 | 0.80 | 267.7 | 281.2 | 5.1 |
| 9 | 150 | 0.14 | 0.30 | 0.80 | 316.9 | 320.7 | 1.2 |
| Cutting Parameters | Fmain (N) | ||||
|---|---|---|---|---|---|
| Std Order | Vc (m/min) | F (mm/rev) | re (mm) | FE Model | RegressionModel |
| 1 | 80 | 0.08 | 0.40 | 182.3 | 176.3 |
| 2 | 80 | 0.11 | 0.40 | 194.1 | 190.6 |
| 3 | 80 | 0.14 | 0.40 | 213.6 | 212.9 |
| 4 | 115 | 0.08 | 0.40 | 186.5 | 182.8 |
| 5 | 115 | 0.11 | 0.40 | 201.0 | 200.3 |
| 6 | 115 | 0.14 | 0.40 | 221.3 | 225.8 |
| 7 | 150 | 0.08 | 0.40 | 190.2 | 190.5 |
| 8 | 150 | 0.11 | 0.40 | 206.5 | 211.1 |
| 9 | 150 | 0.14 | 0.40 | 233.7 | 239.8 |
| 10 | 80 | 0.08 | 0.80 | 207.7 | 236.0 |
| 11 | 80 | 0.11 | 0.80 | 250.2 | 256.2 |
| 12 | 80 | 0.14 | 0.80 | 284.5 | 284.5 |
| 13 | 115 | 0.08 | 0.80 | 232.1 | 241.2 |
| 14 | 115 | 0.11 | 0.80 | 266.2 | 264.6 |
| 15 | 115 | 0.14 | 0.80 | 301.5 | 296.1 |
| 16 | 150 | 0.08 | 0.80 | 249.6 | 247.5 |
| 17 | 150 | 0.11 | 0.80 | 281.2 | 274.1 |
| 18 | 150 | 0.14 | 0.80 | 320.7 | 308.8 |
| 19 | 80 | 0.08 | 1.20 | 319.1 | 313.7 |
| 20 | 80 | 0.11 | 1.20 | 346.9 | 339.9 |
| 21 | 80 | 0.14 | 1.20 | 371.3 | 374.3 |
| 22 | 115 | 0.08 | 1.20 | 323.3 | 317.6 |
| 23 | 115 | 0.11 | 1.20 | 344.4 | 347.0 |
| 24 | 115 | 0.14 | 1.20 | 382.6 | 384.5 |
| 25 | 150 | 0.08 | 1.20 | 322.4 | 322.7 |
| 26 | 150 | 0.11 | 1.20 | 347.4 | 355.2 |
| 27 | 150 | 0.14 | 1.20 | 392.3 | 395.9 |
| Source | Degree of Freedom | Sum of Squares | Mean Square | f-Value | p-Value |
| Regression | 9 | 113,045 | 12,560.6 | 238.87 | 0.000 |
| Residual Error | 17 | 894 | 52.6 | ||
| Total | 26 | 113,939 | |||
| R-sq (adj) = 98.80% | |||||
| Term | PE Coefficient | SE Coefficient | t-Value | p-Value | |
| Constant | 158.1 | 59.8 | 2.64 | 0.017 | |
| V | −0.109 | 0.611 | −0.18 | 0.861 | |
| f | −822 | 774 | −1.06 | 0.303 | |
| re | 48.8 | 39.5 | 1.24 | 0.233 | |
| V2 | 0.00046 | 0.00242 | 0.19 | 0.853 | |
| f2 | 4504 | 3289 | 1.37 | 0.189 | |
| re2 | 56.6 | 18.5 | 3.06 | 0.007 | |
| V × f | 3.03 | 1.99 | 1.52 | 0.147 | |
| V × re | −0.093 | 0.150 | −0.62 | 0.540 | |
| f × re | 498 | 174 | 2.86 | 0.011 | |
| Test No. | Simulated Fmain (N) | Predicted Fmain (N) | Relative Error (%) |
|---|---|---|---|
| I | 197.4 | 189.7 | −3.9 |
| II | 242.1 | 257.0 | 6.2 |
| III | 316.4 | 341.3 | 7.9 |
| IV | 217.6 | 203.1 | −6.6 |
| V | 248.8 | 275.6 | 10.8 |
| VI | 385.7 | 365.1 | −5.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzotzis, A.; García-Hernández, C.; Huertas-Talón, J.-L.; Kyratsis, P. Influence of the Nose Radius on the Machining Forces Induced during AISI-4140 Hard Turning: A CAD-Based and 3D FEM Approach. Micromachines 2020, 11, 798. https://doi.org/10.3390/mi11090798
Tzotzis A, García-Hernández C, Huertas-Talón J-L, Kyratsis P. Influence of the Nose Radius on the Machining Forces Induced during AISI-4140 Hard Turning: A CAD-Based and 3D FEM Approach. Micromachines. 2020; 11(9):798. https://doi.org/10.3390/mi11090798
Chicago/Turabian StyleTzotzis, Anastasios, César García-Hernández, José-Luis Huertas-Talón, and Panagiotis Kyratsis. 2020. "Influence of the Nose Radius on the Machining Forces Induced during AISI-4140 Hard Turning: A CAD-Based and 3D FEM Approach" Micromachines 11, no. 9: 798. https://doi.org/10.3390/mi11090798
APA StyleTzotzis, A., García-Hernández, C., Huertas-Talón, J.-L., & Kyratsis, P. (2020). Influence of the Nose Radius on the Machining Forces Induced during AISI-4140 Hard Turning: A CAD-Based and 3D FEM Approach. Micromachines, 11(9), 798. https://doi.org/10.3390/mi11090798






