Quantifying Heterogeneity According to Deformation of the U937 Monocytes and U937-Differentiated Macrophages Using 3D Carbon Dielectrophoresis in Microfluidics
Abstract
1. Introduction
2. Materials and Methods
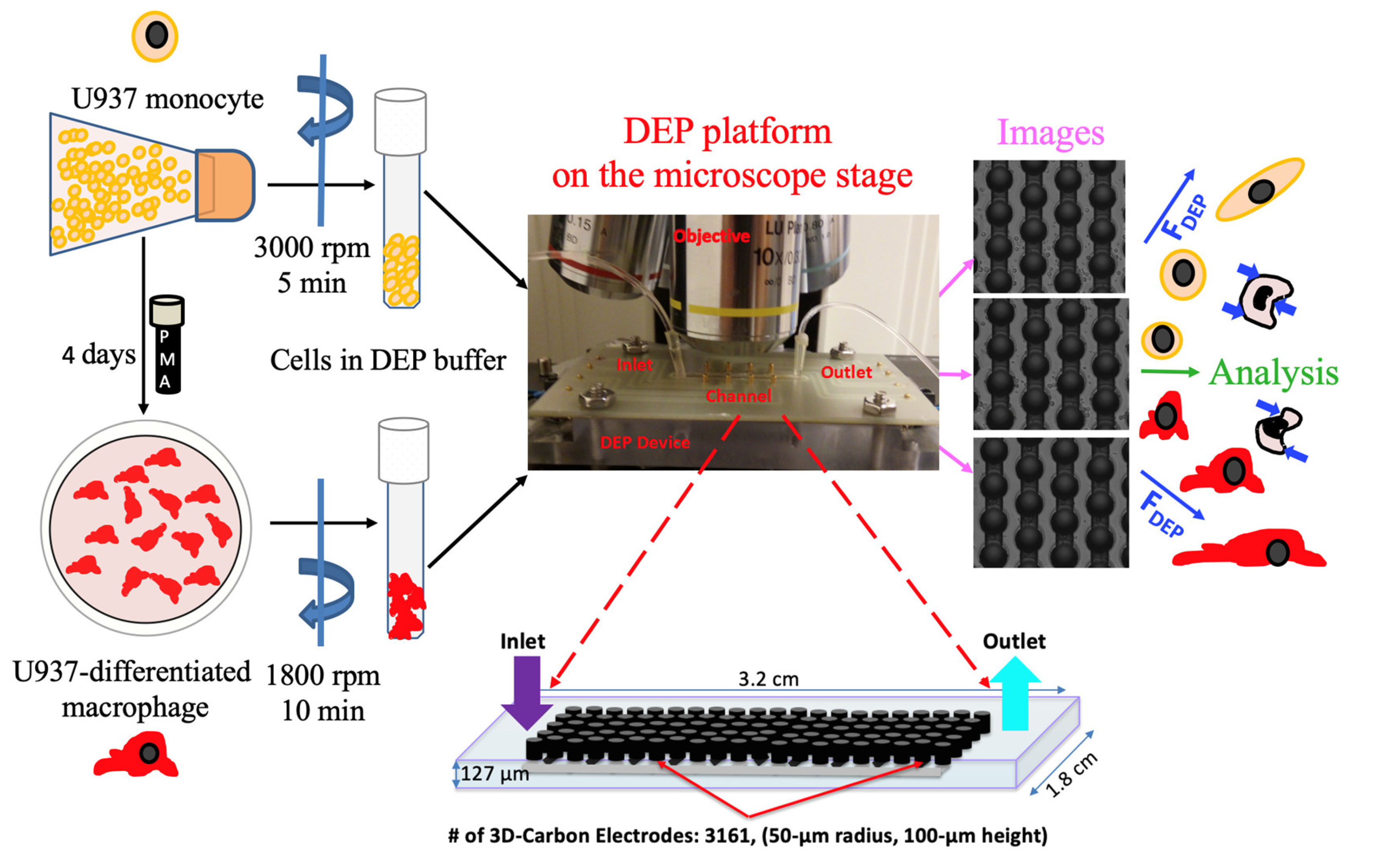
2.1. DEP Buffer Preparation and Conductivity Measurement
2.2. Cell Culture
2.3. 3D Carbon DEP Device
2.4. Experimental Setup
2.5. Image Acquisition and Data Analysis
3. Results
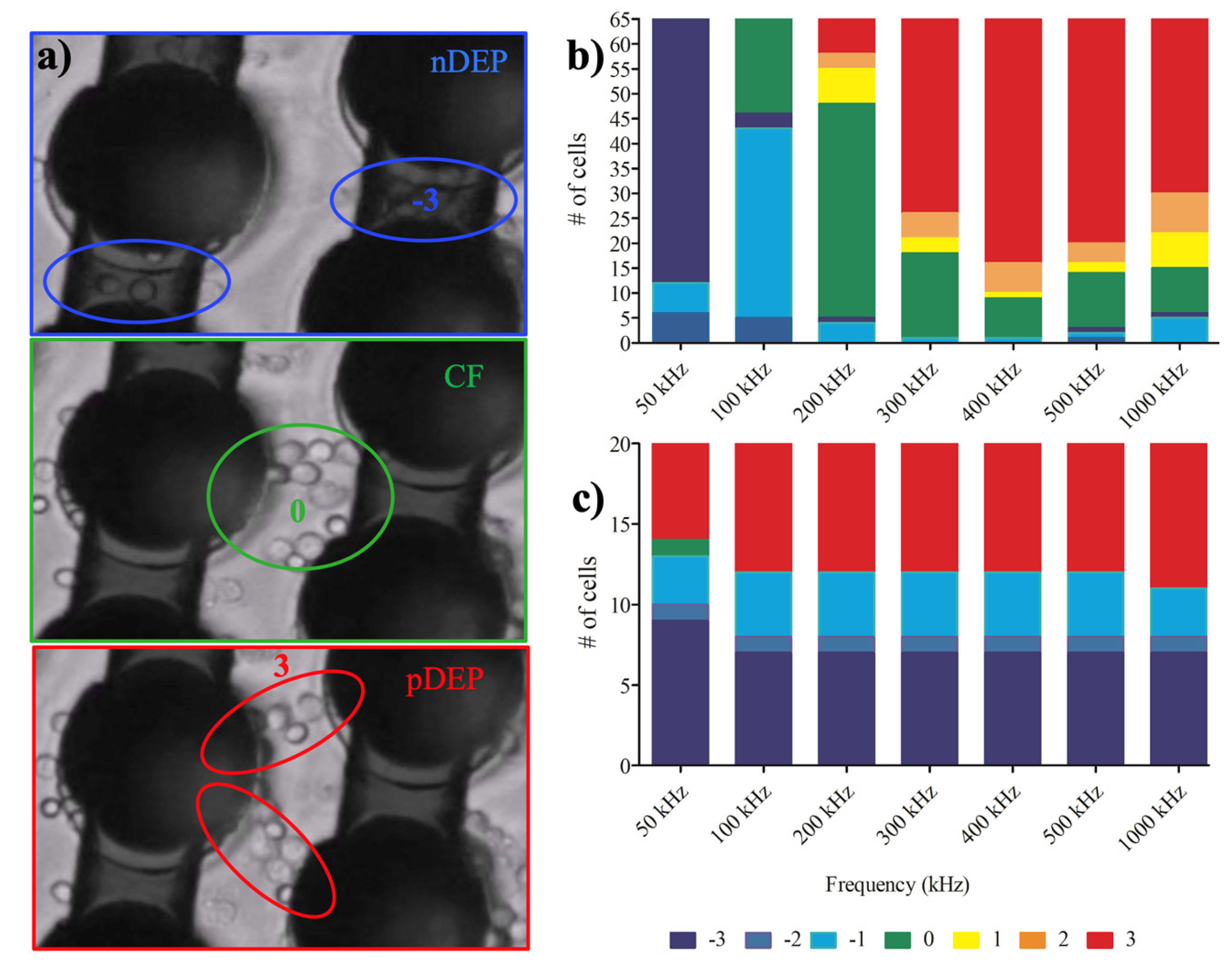
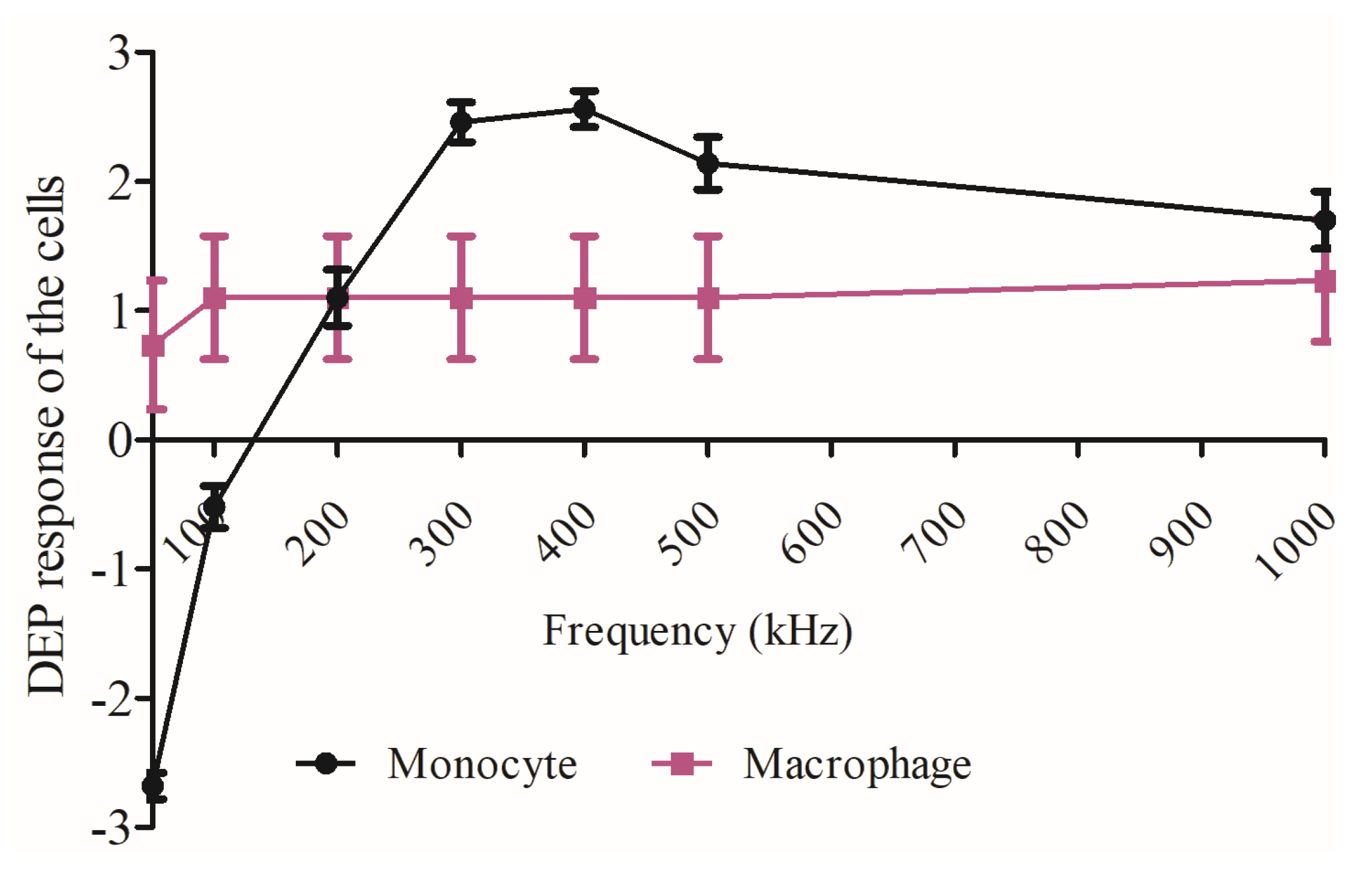
3.1. Dielectrophoretic Movement
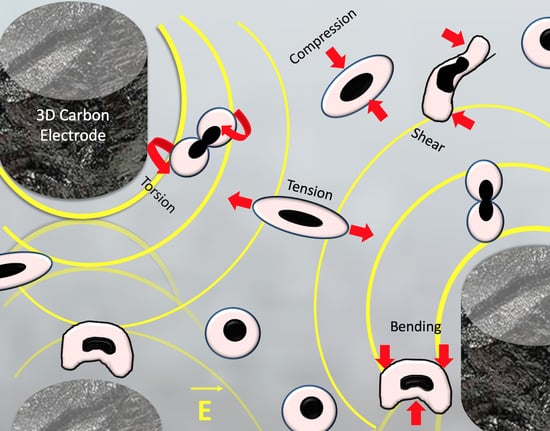
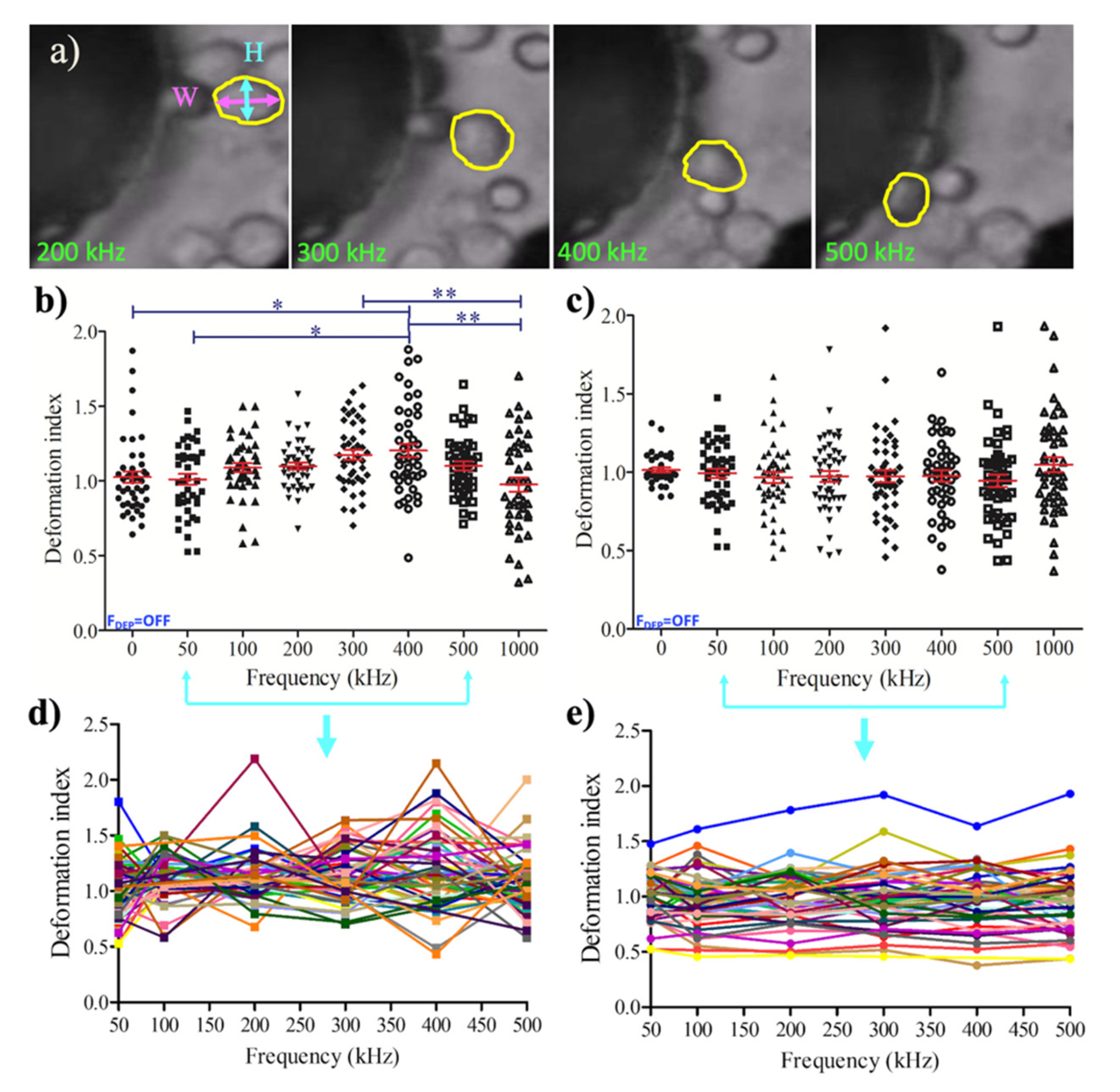
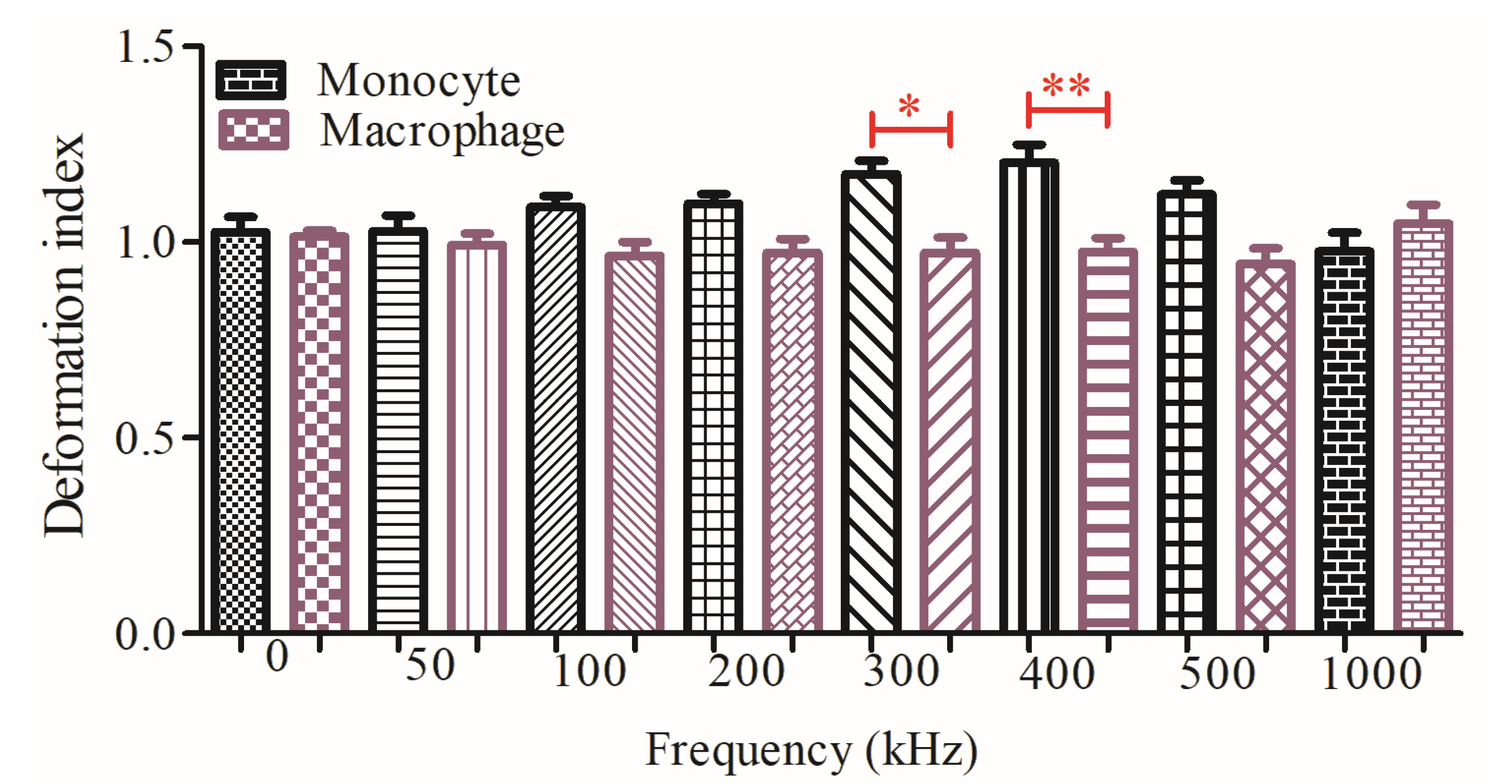
3.2. Dielectrophoretic Deformation Index
3.3. Dielectric Mobility and Membrane Relaxation Time
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Adekanmbi, E.O.; Srivastava, S.K. Dielectrophoretic applications for disease diagnostics using lab-on-a-chip platforms. Lab Chip 2016, 16, 2148–2167. [Google Scholar] [CrossRef]
- Mulhall, H.J.; Labeed, F.H.; Kazmi, B.; Costea, D.E.; Hughes, M.P.; Lewis, M.P. Cancer, pre-cancer and normal oral cells distinguished by dielectrophoresis. Anal. Bioanal. Chem. 2011, 401, 2455–2463. [Google Scholar] [CrossRef]
- Hur, S.C.; Henderson-Maclennan, N.K.; Mccabe, E.R.B.; Carlo, D.D. Deformability-based cell classification and enrichment using inertial microfluidics. Lab Chip 2011, 11, 912–920. [Google Scholar] [CrossRef]
- Suresh, S.; Spatz, J.; Mills, J.; Micoulet, A.; Dao, M.; Lim, C.; Seufferlein, T. Connections between single-cell biomechanics and human disease states: Gastrointestinal cancer and malaria. Acta Biomater. 2005, 1, 15–30. [Google Scholar] [CrossRef]
- Suresh, S. Biomechanics and biophysics of cancer cells. Acta Biomater. 2007, 3, 413–438. [Google Scholar] [CrossRef]
- Pohl, H.A. The Motion and Precipitation of Suspensoids in Divergent Electric Fields. J. Appl. Phys. 1951, 22, 869–871. [Google Scholar] [CrossRef]
- Pethig, R. Review Article—Dielectrophoresis: Status of the theory, technology, and applications. Biomicrofluidics 2010, 4, 022811. [Google Scholar] [CrossRef]
- Cross, S.E.; Jin, Y.-S.; Rao, J.; Gimzewski, J.K. Nanomechanical analysis of cells from cancer patients. Nat. Nanotechnol. 2007, 2, 780–783. [Google Scholar] [CrossRef]
- Hoffman, B.D.; Crocker, J.C. Cell Mechanics: Dissecting the Physical Responses of Cells to Force. Ann. Rev. Biomed. Eng. 2009, 11, 259–288. [Google Scholar] [CrossRef]
- Chauviere, A.; Preziosi, L.; Byrne, H. A model of cell migration within the extracellular matrix based on a phenotypic switching mechanism. Math. Med. Biol. 2009, 27, 255–281. [Google Scholar] [CrossRef]
- Taylor, P.R.; Gordon, S. Monocyte Heterogeneity and Innate Immunity. Immunity 2003, 19, 2–4. [Google Scholar] [CrossRef]
- Hume, D.A. Plenary Perspective: The complexity of constitutive and inducible gene expression in mononuclear phagocytes. J. Leukoc. Biol. 2012, 92, 433–444. [Google Scholar] [CrossRef]
- Lichtman, M.A.; Williams, W.J. Biochemistry and function of monocytes and macrophages. In Williams Hematology; McGraw-Hill Medical: New York, NY, USA, 2006; pp. 971–978. [Google Scholar]
- Hulsmans, M.; Clauss, S.; Xiao, L.; Aguirre, A.D.; King, K.R.; Hanley, A.; Nahrendorf, M. Macrophages Facilitate Electrical Conduction in the Heart. Cell 2017, 169. [Google Scholar] [CrossRef]
- Pittet, M.J.; Swirski, F.K. Monocytes link atherosclerosis and cancer. Eur. J. Immunol. 2011, 41, 2519–2522. [Google Scholar] [CrossRef]
- Etzerodt, A.; Tsalkitzi, K.; Maniecki, M.; Damsky, W.; Delfini, M.; Baudoin, E.; Lawrence, T. Specific targeting of CD163 TAMs mobilizes inflammatory monocytes and promotes T cell–mediated tumor regression. J. Exp. Med. 2019, 216, 2394–2411. [Google Scholar] [CrossRef]
- Thiriot, J.D.; Martinez-Martinez, Y.B.; Endsley, J.J.; Torres, A.G. Hacking the host: Exploitation of macrophage polarization by intracellular bacterial pathogens. Pathog. Dis. 2020, 78. [Google Scholar] [CrossRef]
- Eming, S.A.; Krieg, T.; Davidson, J.M. Inflammation in Wound Repair: Molecular and Cellular Mechanisms. J. Investig. Dermatol. 2007, 127, 514–525. [Google Scholar] [CrossRef]
- Swirski, F.K.; Nahrendorf, M.; Etzrodt, M.; Wildgruber, M.; Cortez-Retamozo, V.; Panizzi, P.; Pittet, M.J. Identification of Splenic Reservoir Monocytes and Their Deployment to Inflammatory Sites. Science 2009, 325, 612–616. [Google Scholar] [CrossRef]
- Muller, P.A.; Koscsó, B.; Rajani, G.M.; Stevanovic, K.; Berres, M.-L.; Hashimoto, D.; Bogunovic, M. Crosstalk between Muscularis Macrophages and Enteric Neurons Regulates Gastrointestinal Motility. Cell 2014, 158, 300–313. [Google Scholar] [CrossRef]
- Wynn, T.A.; Chawla, A.; Pollard, J.W. Macrophage biology in development, homeostasis and disease. Nature 2013, 496, 445–455. [Google Scholar] [CrossRef]
- Epelman, S.; Lavine, K.J.; Randolph, G.J. Origin and Functions of Tissue Macrophages. Immunity 2014, 41, 21–35. [Google Scholar] [CrossRef]
- Okabe, Y.; Medzhitov, R. Tissue-Specific Signals Control Reversible Program of Localization and Functional Polarization of Macrophages. Cell J. 2014, 157, 832–844. [Google Scholar] [CrossRef]
- Xue, J.; Schmidt, S.V.; Sander, J.; Draffehn, A.; Krebs, W.; Quester, I.; Schultze, J.L. Transcriptome-Based Network Analysis Reveals a Spectrum Model of Human Macrophage Activation. Immunity 2014, 40, 274–288. [Google Scholar] [CrossRef]
- Eisenberg, S.; Ben-Or, S.; Doljanski, F. Electro-kinetic properties of cells in growth processes. Exp. Cell Res. 1962, 26, 451–461. [Google Scholar] [CrossRef]
- Petty, H.; Ware, B.; Liebes, L.; Pelle, E.; Silber, R. Electrophoretic mobility distributions distinguish hairy cells from other mononuclear blood cells and provide evidence for the heterogeneity of normal monocytes. Blood 1981, 57, 250–255. [Google Scholar] [CrossRef]
- Bauer, J.; Hannig, K. Changes of the electrophoretic mobility of human monocytes are regulated by lymphocytes. Electrophoresis 1984, 5, 269–274. [Google Scholar] [CrossRef]
- Yang, J.; Huang, Y.; Wang, X.; Wang, X.-B.; Becker, F.F.; Gascoyne, P.R. Dielectric Properties of Human Leukocyte Subpopulations Determined by Electrorotation as a Cell Separation Criterion. Biophys. J. 1999, 76, 3307–3314. [Google Scholar] [CrossRef]
- Yang, J.; Huang, Y.; Wang, X.-B.; Becker, F.F.; Gascoyne, P.R. Differential Analysis of Human Leukocytes by Dielectrophoretic Field-Flow-Fractionation. Biophys. J. 2000, 78, 2680–2689. [Google Scholar] [CrossRef]
- Elitas, M.; Yildizhan, Y.; Islam, M.; Martinez-Duarte, R.; Ozkazanc, D. Dielectrophoretic characterization and separation of monocytes and macrophages using 3D carbon-electrodes. Electrophoresis 2018, 40, 315–321. [Google Scholar] [CrossRef]
- Yildizhan, Y.; Erdem, N.; Islam, M.; Martinez-Duarte, R.; Elitas, M. Dielectrophoretic Separation of Live and Dead Monocytes Using 3D Carbon-Electrodes. Sensors 2017, 17, 2691. [Google Scholar] [CrossRef]
- Erdem, N.; Yildizhan, Y.; Elitas, M. A numerical approach for dielectrophoretic characterization and separation human hematopoietic cells. Int. J. Eng. Res. 2017, 6, 1079–1082. [Google Scholar] [CrossRef]
- Tonin, M.; Bálint, S.; Mestres, P.; Martìnez, I.A.; Petrov, D. Electrophoretic mobility of a growing cell studied by photonic force microscope. Appl. Phys. Lett. 2010, 97, 203704. [Google Scholar] [CrossRef]
- Song, H.; Rosano, J.M.; Wang, Y.; Garson, C.J.; Prabhakarpandian, B.; Pant, K.; Lai, E. Continuous-flow sorting of stem cells and differentiation products based on dielectrophoresis. Lab Chip 2015, 15, 1320–1328. [Google Scholar] [CrossRef]
- Salmanzadeh, A.; Kittur, H.; Sano, M.B.; Roberts, P.C.; Schmelz, E.M.; Davalos, R.V. Dielectrophoretic differentiation of mouse ovarian surface epithelial cells, macrophages, and fibroblasts using contactless dielectrophoresis. Biomicrofluidics 2012, 6, 024104. [Google Scholar] [CrossRef]
- Polizzi, S.; Laperrousaz, B.; Perez-Reche, F.J.; Nicolini, F.E.; Satta, V.M.; Arneodo, A.; Argoul, F. A minimal rupture cascade model for living cell plasticity. New J. Phys. 2018, 20, 053057. [Google Scholar] [CrossRef]
- Agrawal, R.; Smart, T.; Nobre-Cardoso, J.; Richards, C.; Bhatnagar, R.; Tufail, A.; Pavesio, C. Assessment of red blood cell deformability in type 2 diabetes mellitus and diabetic retinopathy by dual optical tweezers stretching technique. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
- Fabry, B.; Maksym, G.N.; Hubmayr, R.D.; Butler, J.P.; Fredberg, J.J. Implications of heterogeneous bead behavior on cell mechanical properties measured with magnetic twisting cytometry. J. Magn. Magn. Mater. 1999, 194, 120–125. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, K.; Park, Y. Measurement Techniques for Red Blood Cell Deformability: Recent Advances. Blood Cell 2012. [Google Scholar] [CrossRef]
- Popescu, G.; Ikeda, T.; Dasari, R.R.; Feld, M.S. Diffraction phase microscopy for quantifying cell structure and dynamics. Opt. Lett. 2006, 31, 775–777. [Google Scholar] [CrossRef]
- Shin, S.; Ku, Y.-H.; Ho, J.-X.; Kim, Y.-K.; Suh, J.-S.; Singh, M. Progressive impairment of erythrocyte deformability as indicator of microangiopathy in type 2 diabetes mellitus. Clin. Hemorheol. Microcirc. 2007, 36, 253–261. [Google Scholar]
- Zeng, N.F.; Mancuso, J.E.; Zivkovic, A.M.; Smilowitz, J.T.; Ristenpart, W.D. Red Blood Cells from Individuals with Abdominal Obesity or Metabolic Abnormalities Exhibit Less Deformability upon Entering a Constriction. PLoS ONE 2016, 11. [Google Scholar] [CrossRef] [PubMed]
- Pinho, D.; Campo-Deaño, L.; Lima, R.; Pinho, F.T. In vitroparticulate analogue fluids for experimental studies of rheological and hemorheological behavior of glucose-rich RBC suspensions. Biomicrofluidics 2017, 11, 054105. [Google Scholar] [CrossRef] [PubMed]
- Guido, I.; Xiong, C.; Jaeger, M.S.; Duschl, C. Microfluidic system for cell mechanics analysis through dielectrophoresis. Microelectron. Eng. 2012, 97, 379–382. [Google Scholar] [CrossRef]
- Du, E.; Dao, M.; Suresh, S. Quantitative biomechanics of healthy and diseased human red blood cells using dielectrophoresis in a microfluidic system. Extreme Mech. Lett. 2014, 1, 35–41. [Google Scholar] [CrossRef]
- Pires-Afonso, Y.; Niclou, S.P.; Michelucci, A. Revealing and Harnessing Tumour-Associated Microglia/Macrophage Heterogeneity in Glioblastoma. Int. J. Mol. Sci. 2020, 21, 689. [Google Scholar] [CrossRef]
- Armistead, F.J.; Pablo, J.G.D.; Gadêlha, H.; Peyman, S.A.; Evans, S.D. Cells Under Stress: An Inertial-Shear Microfluidic Determination of Cell Behavior. Biophys. J. 2019, 116, 1127–1135. [Google Scholar] [CrossRef]
- Martinez-Duarte, R. SU-8 Photolithography as a Toolbox for Carbon MEMS. Micromachines 2014, 5, 766–782. [Google Scholar] [CrossRef]
- Martinez-Duarte, R.; Renaud, P.; Madou, M.J. A novel approach to dielectrophoresis using carbon electrodes. Electrophoresis 2011. [Google Scholar] [CrossRef]
- Martinez-Duarte, R.; Cito, S.; Collado-Arrendondo, E.; Martinez, S.O.; Madou, M.J. Fluido-dynamic and Electromagnetic Characterization of 3D Carbon Dielectrophoresis with Finite Element Analysis. Sens. Transducers J. 2008, 3, 25–36. [Google Scholar]
- Natu, R.; Martinez-Duarte, R. Numerical Model of Streaming DEP for Stem Cell Sorting. Micromachines 2016, 7, 217. [Google Scholar] [CrossRef]
- Nakano, A.; Ros, A. Protein dielectrophoresis: Advances, challenges, and applications. Electrophoresis 2013, 34, 1085–1096. [Google Scholar] [CrossRef] [PubMed]
- Pohl, H.A.; Pollock, K.; Crane, J.S. Dielectrophoretic force: A comparison of theory and experiment. J. Biol. Phys. 1978, 6, 133–160. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, X.-B.; Becker, F.F.; Gascoyne, P.R. Membrane changes associated with the temperature-sensitive P85gag-mos-dependent transformation of rat kidney cells as determined by dielectrophoresis and electrorotation. Biochim. Biophys. Acta 1996, 1282, 76–84. [Google Scholar] [CrossRef]
- Liang, W.; Liu, J.; Yang, X.; Zhang, Q.; Yang, W.; Zhang, H.; Liu, L. Microfluidic-based cancer cell separation using active and passive mechanisms. Microfluid. Nanofluid. 2020, 24. [Google Scholar] [CrossRef]
- Vargas, F.F.; Osorio, M.H.; Ryan, U.S.; Jesus, M.D. Surface Charge of Endothelial Cells Estimated from Electrophoretic Mobility. J. Membr. Biochem. 1989, 8, 221–227. [Google Scholar] [CrossRef] [PubMed]
- Ohshima, H.; Kondo, T. On the electrophoretic mobility of biological cells. Biophys. Chem. 1991, 39, 191–198. [Google Scholar] [CrossRef]
- Wal, A.V.D.; Minor, M.; Norde, W.; Zehnder, A.J.B.; Lyklema, J. Electrokinetic Potential of Bacterial Cells. Langmuir 1997, 13, 165–171. [Google Scholar] [CrossRef]
- Weiss, N.G.; Jones, P.V.; Mahanti, P.; Chen, K.P.; Taylor, T.J.; Hayes, M.A. Dielectrophoretic mobility determination in DC insulator-based dielectrophoresis. Electrophoresis 2011. [Google Scholar] [CrossRef]
- Harrison, H.; Lu, X.; Patel, S.; Thomas, C.; Todd, A.; Johnson, M.; Xuan, X. Electrokinetic preconcentration of particles and cells in microfluidic reservoirs. Analyst 2015, 140, 2869–2875. [Google Scholar] [CrossRef]
- Cummings, E.B.; Singh, A.K. Dielectrophoresis in Microchips Containing Arrays of Insulating Posts: Theoretical and Experimental Results. Analy. Chem. 2003, 75, 4724–4731. [Google Scholar] [CrossRef]
- Crowther, C.V.; Hayes, M.A. Refinement of insulator-based dielectrophoresis. Analyst 2017, 142, 1608–1618. [Google Scholar] [CrossRef]
- Pillet, F.; Dague, E.; Ilić, J.P.; Ružić, I.; Rols, M.-P.; Denardis, N.I. Changes in nanomechanical properties and adhesion dynamics of algal cells during their growth. Bioelectrochemistry 2019, 127, 154–162. [Google Scholar] [CrossRef]
- Ferrari, M.; Cirisano, F.; Morán, M.C. Mammalian Cell Behavior on Hydrophobic Substrates: Influence of Surface Properties. Colloids Interfaces 2019, 3, 48. [Google Scholar] [CrossRef]
- Hess, B.; van der Vegt, N.F.A. Cation specific binding with protein surface charges. Proc. Natl. Acad. Sci. USA 2009, 106, 13296–13300. [Google Scholar] [CrossRef] [PubMed]
- Birant, G.; Wild, J.D.; Meuris, M.; Poortmans, J.; Vermang, B. Dielectric-Based Rear Surface Passivation Approaches for Cu (In,Ga)Se2 Solar Cells—A Review. Appl. Sci. 2019, 9, 677. [Google Scholar] [CrossRef]
- Cottet, J.; Fabregue, O.; Berger, C.; Buret, F.; Renaud, P.; Frénéa-Robin, M. MyDEP: A New Computational Tool for Dielectric Modeling of Particles and Cells. Biophys. J. 2019, 116, 12–18. [Google Scholar] [CrossRef]
- Crowther, C.V.; Hilton, S.H.; Kemp, L.; Hayes, M.A. Isolation and identification of Listeria monocytogenes utilizing DC insulator-based dielectrophoresis. Anal. Chim. Acta 2019, 1068, 41–51. [Google Scholar] [CrossRef]
- Punjiya, M.; Nejad, H.R.; Mathews, J.; Levin, M.; Sonkusale, S. A flow through device for simultaneous dielectrophoretic cell trapping and AC electroporation. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef] [PubMed]
- Holmes, D.; Pettigrew, D.; Reccius, C.H.; Gwyer, J.D.; Berkel, C.V.; Holloway, J.; Morgan, H. Leukocyte analysis and differentiation using high speed microfluidic single cell impedance cytometry. Lab Chip 2009, 9, 2881–2889. [Google Scholar] [CrossRef] [PubMed]
- Sano, M.B.; Henslee, E.A.; Schmelz, E.; Davalos, R.V. Contactless dielectrophoretic spectroscopy: Examination of the dielectric properties of cells found in blood. Electrophoresis 2011, 32, 3164–3171. [Google Scholar] [CrossRef]
- Khoshmanesh, K.; Nahavandi, S.; Baratchi, S.; Mitchell, A.; Kalantar-Zadeh, K. Dielectrophoretic platforms for bio-microfluidic systems. Biosens. Bioelectron. 2011, 26, 1800–1814. [Google Scholar] [CrossRef] [PubMed]
| Parameters (Units) | Values | Resources |
|---|---|---|
| (m) | 1.15 × 10−5 | Measured |
| (m) | 1.5 × 10−5 | Measured |
| 0.976 | Calculated [67] | |
| 0.979 | Calculated [67] | |
| (C/V.m) | 6.90 × 10−10 | - |
| (kg/s.m) | 8.90 × 10−4 | - |
| (S/m) | 2 × 10−3 | Measured |
| (S/m) | 7 × 10−13 | [70] |
| (S/m) | 7 × 10−13 | [70] |
| (S/m) | 7 × 10−13 | Assumed |
| (F/m2) | 0.016 ± 0.002 | [70,71] |
| (F/m2) | 0.013 ± 0.001 | [70,71] |
| (s) | 2.63 × 105 | Calculated |
| (s) | 2.73 × 105 | Calculated |
| (m4/V2s) | 6.99 × 10−18 | Calculated |
| (m4/V2s) | 12.40 × 10−18 | Calculated |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elitas, M.; Sengul, E. Quantifying Heterogeneity According to Deformation of the U937 Monocytes and U937-Differentiated Macrophages Using 3D Carbon Dielectrophoresis in Microfluidics. Micromachines 2020, 11, 576. https://doi.org/10.3390/mi11060576
Elitas M, Sengul E. Quantifying Heterogeneity According to Deformation of the U937 Monocytes and U937-Differentiated Macrophages Using 3D Carbon Dielectrophoresis in Microfluidics. Micromachines. 2020; 11(6):576. https://doi.org/10.3390/mi11060576
Chicago/Turabian StyleElitas, Meltem, and Esra Sengul. 2020. "Quantifying Heterogeneity According to Deformation of the U937 Monocytes and U937-Differentiated Macrophages Using 3D Carbon Dielectrophoresis in Microfluidics" Micromachines 11, no. 6: 576. https://doi.org/10.3390/mi11060576
APA StyleElitas, M., & Sengul, E. (2020). Quantifying Heterogeneity According to Deformation of the U937 Monocytes and U937-Differentiated Macrophages Using 3D Carbon Dielectrophoresis in Microfluidics. Micromachines, 11(6), 576. https://doi.org/10.3390/mi11060576