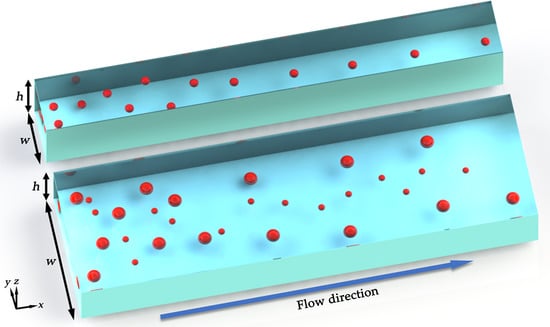
Three-Dimensional Numerical Simulation of Particle Focusing and Separation in Viscoelastic Fluids
Abstract
1. Introduction
2. Numerical Methods
2.1. 3D Lattice Boltzmann Method (LBM) of Viscoelastic Fluid
2.2. IBM for the Interaction between Particles and Fluid
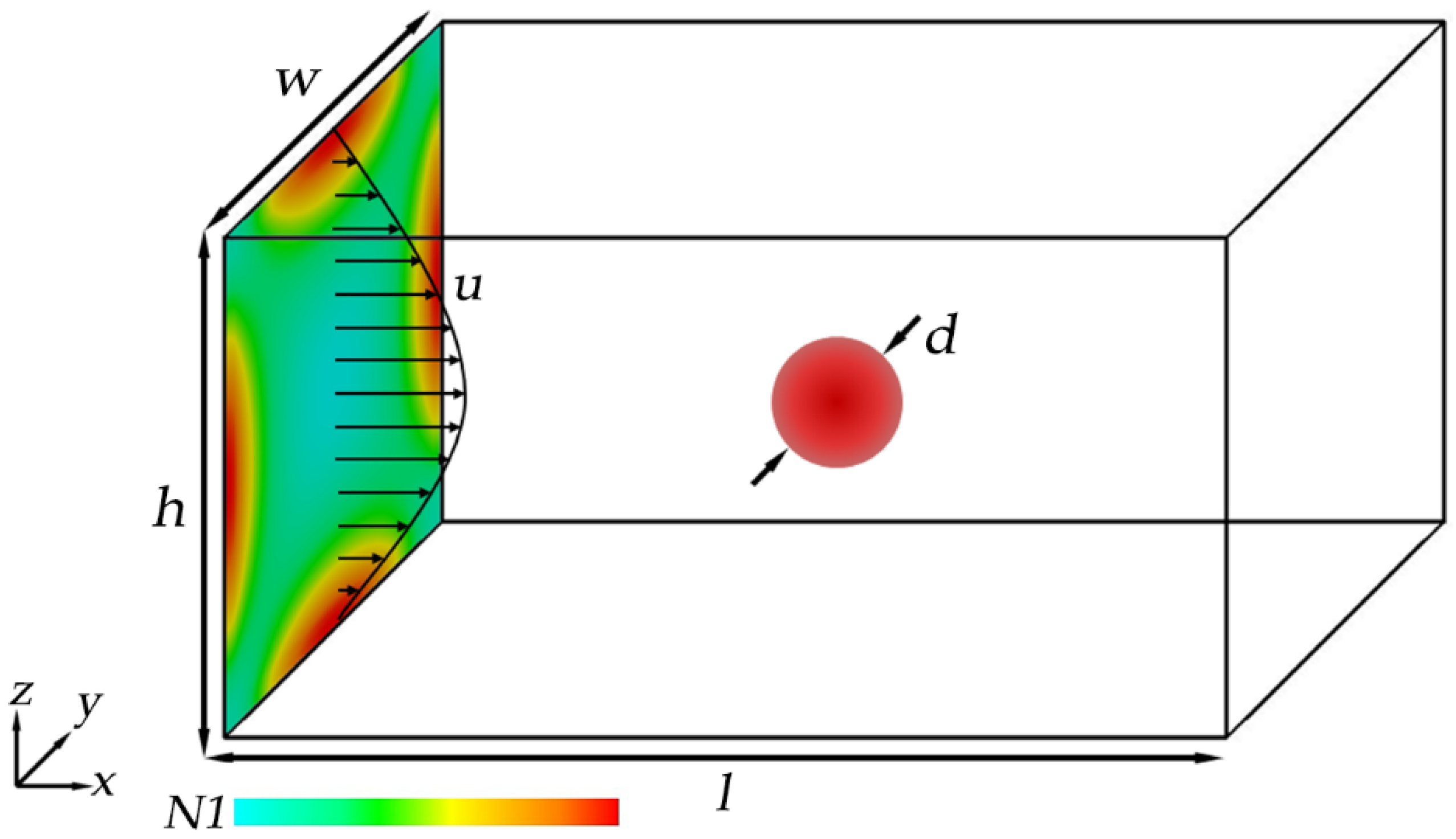
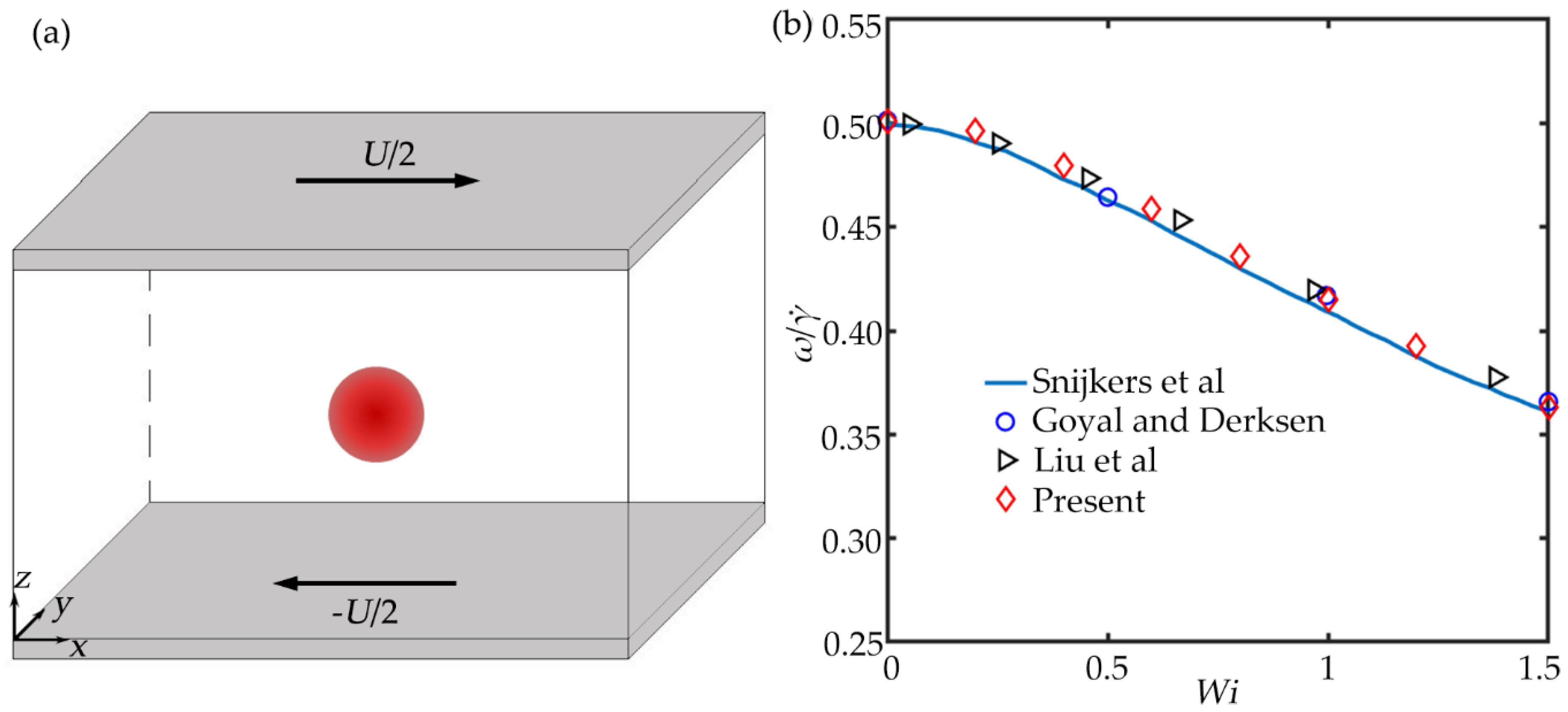
2.3. Channel Model and Validation
3. Results and Discussion
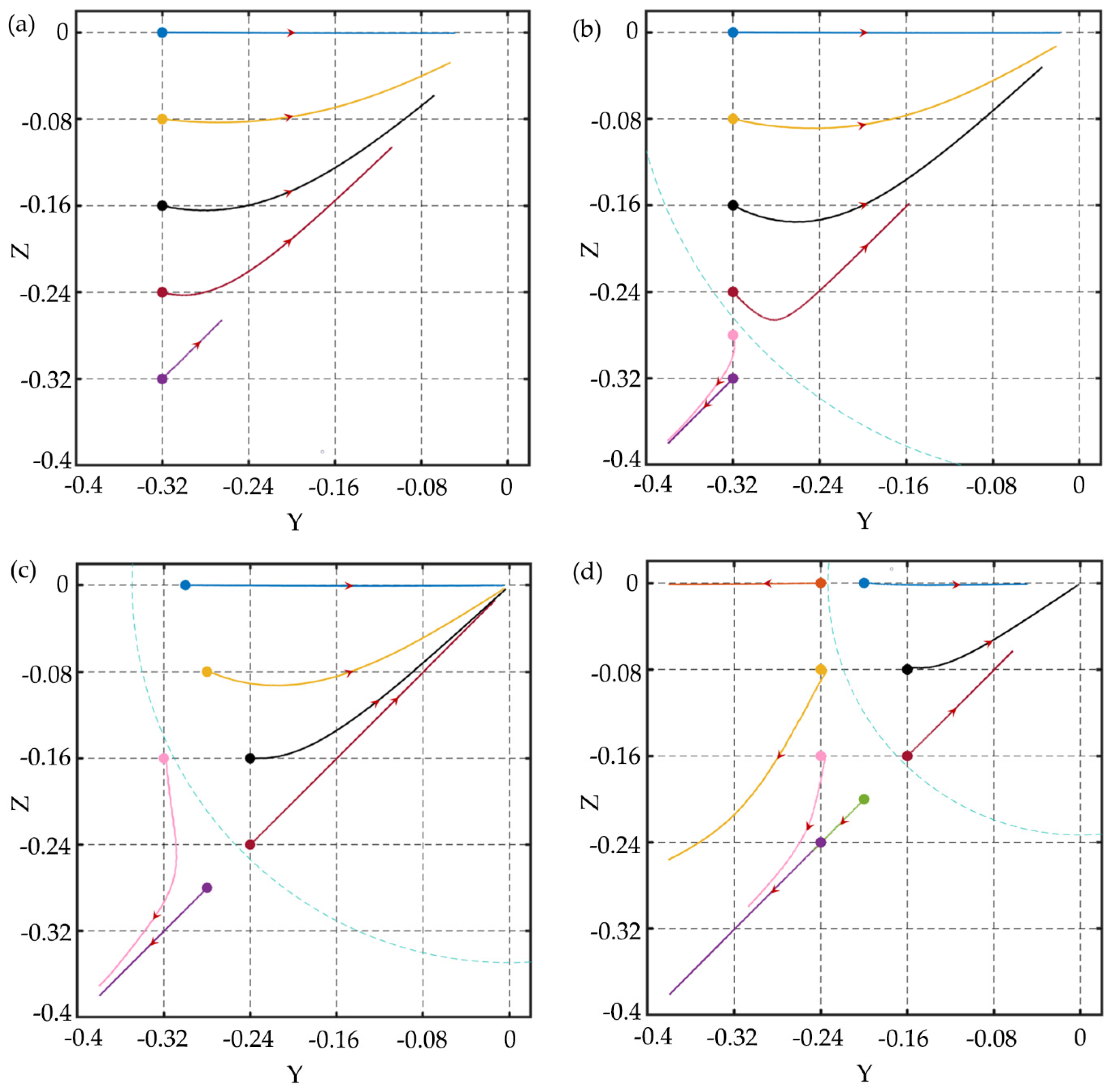
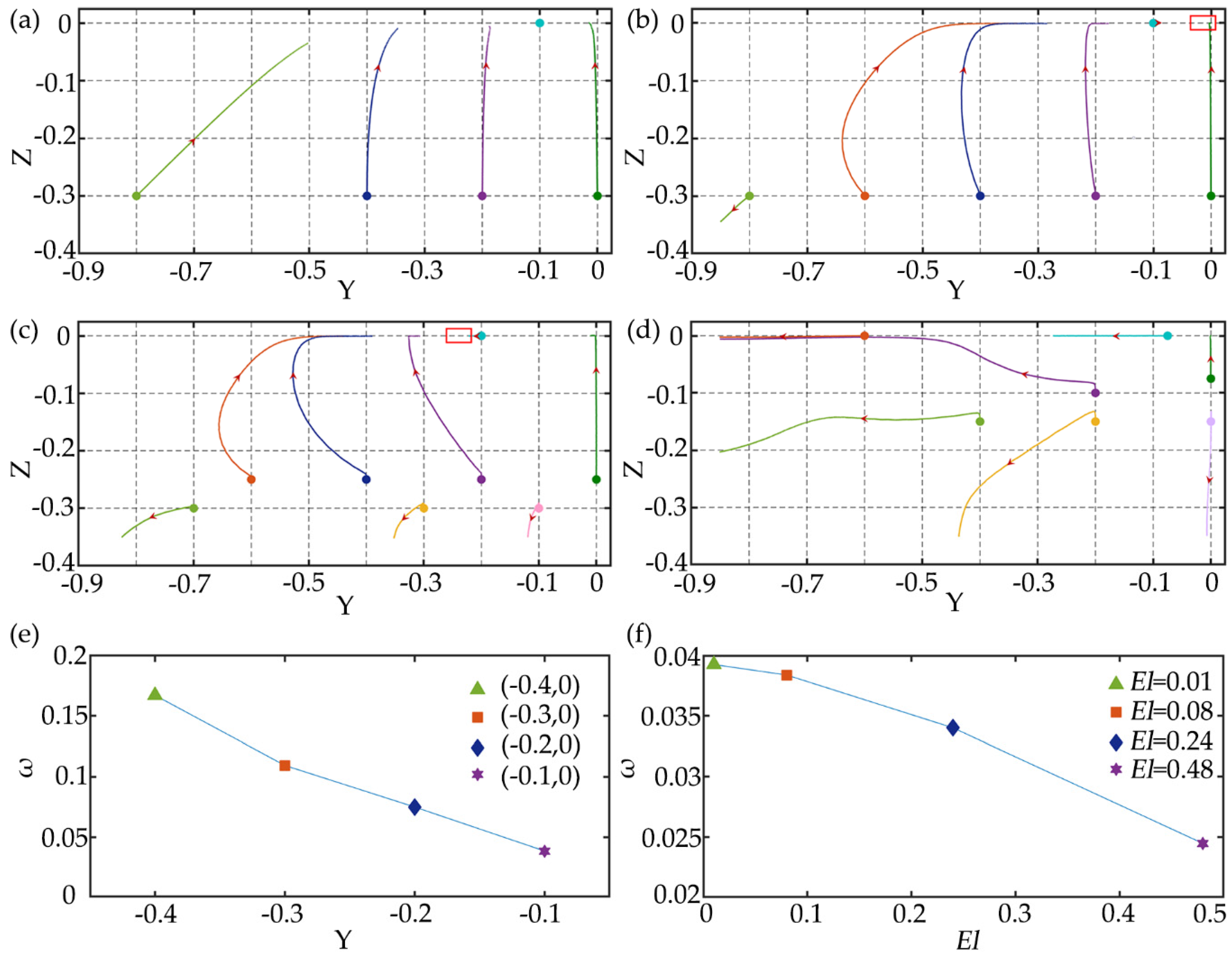
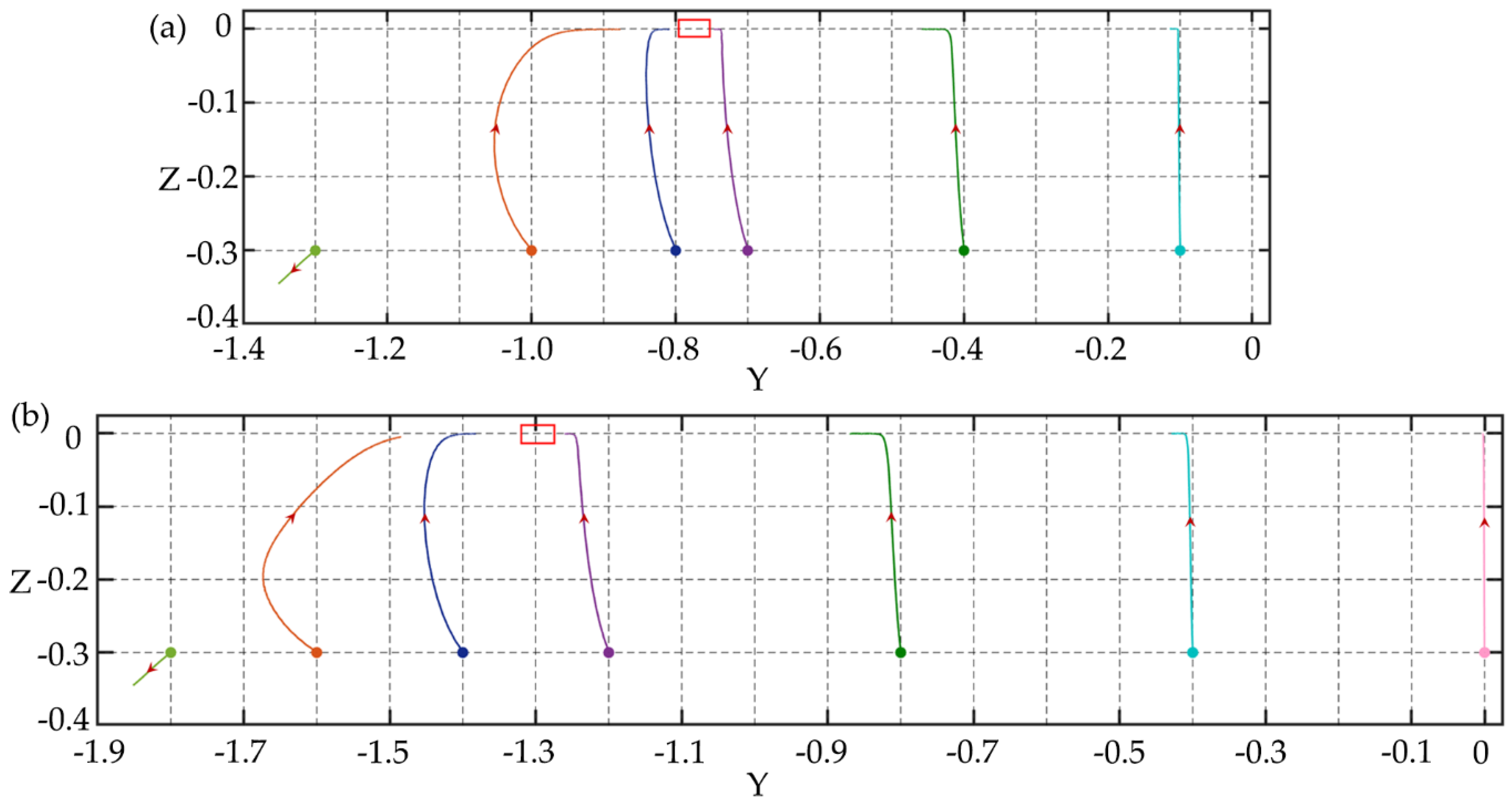
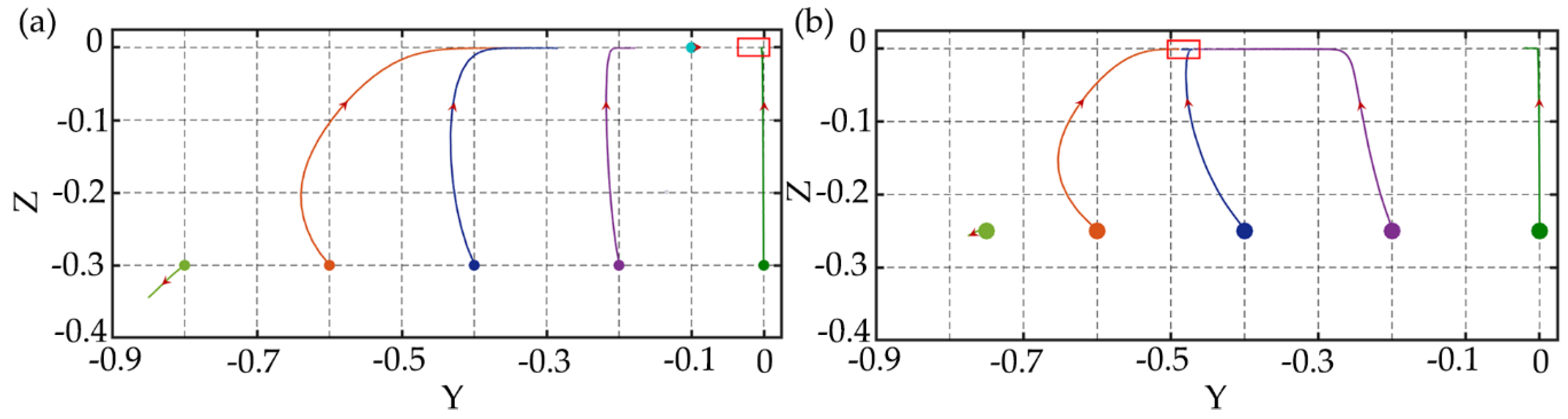
3.1. Particle Focusing
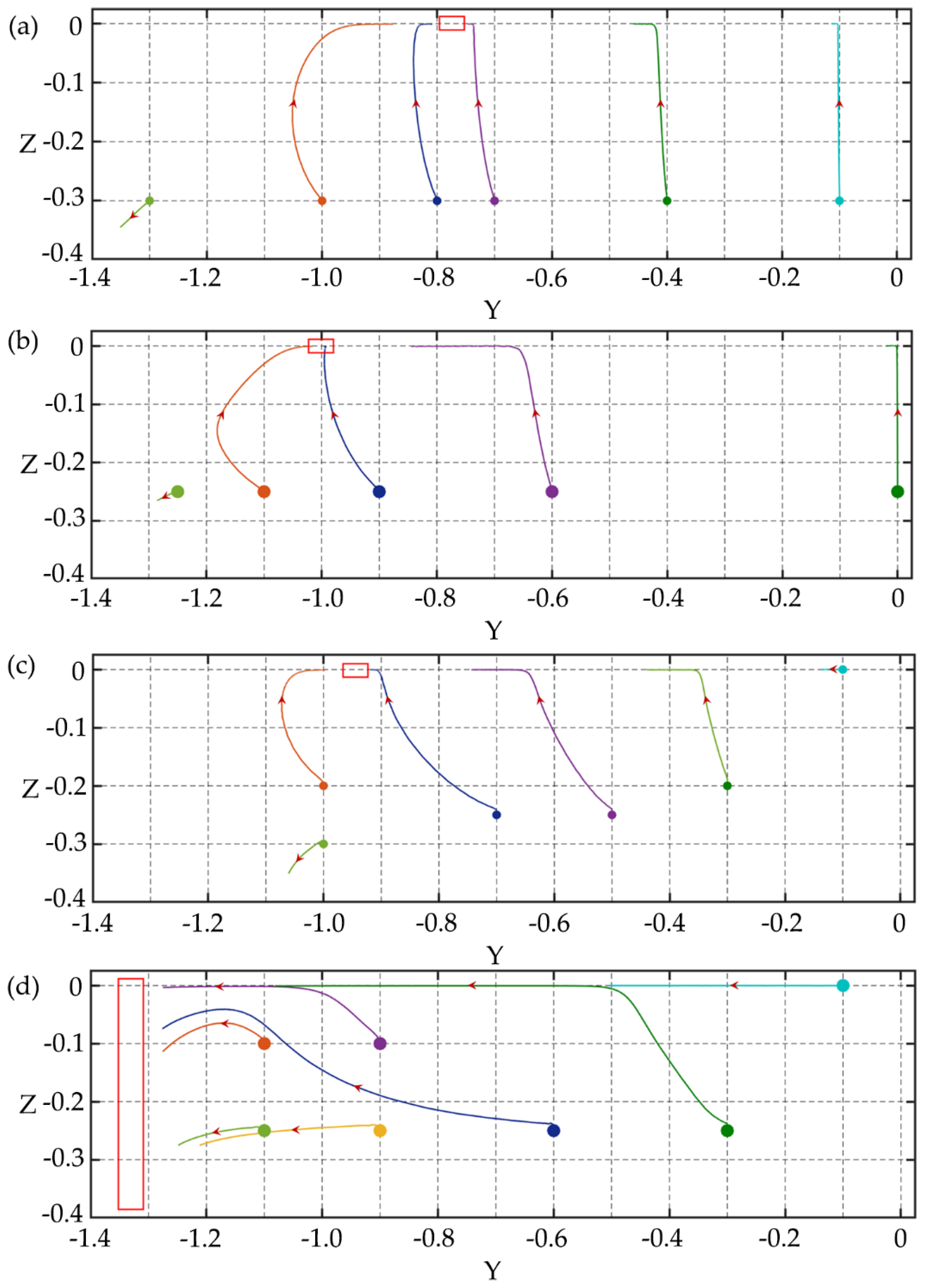
3.2. Particle Separation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xuan, X.; Zhu, J.; Church, C. Particle focusing in microfluidic devices. Microfluid. Nanofluid. 2010, 9, 1–16. [Google Scholar] [CrossRef]
- Lim, H.; Nam, J.; Shin, S. Lateral migration of particles suspended in viscoelastic fluids in a microchannel flow. Microfluid. Nanofluid. 2014, 17, 683–692. [Google Scholar] [CrossRef]
- Amini, H.; Lee, W.; Carlo, D.D. Inertial microfluidic physics. Lab. Chip 2014, 14, 2739–2761. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Tan, S.H.; Li, Y.; Tang, S.; Teo, A.J.T.; Zhang, J.; Zhao, Q.; Yuan, D.; Sluyter, R.; Nguyen, N.T. A portable, hand-powered microfluidic device for sorting of biological particles. Microfluid. Nanofluid. 2018, 22, 8. [Google Scholar] [CrossRef]
- Di Carlo, D. Inertial microfluidics. Lab. Chip 2009, 9, 3038. [Google Scholar] [CrossRef]
- Tang, W.; Jiang, D.; Li, Z.; Zhu, L.; Shi, J.; Yang, J.; Xiang, N. Recent advances in microfluidic cell sorting techniques based on both physical and biochemical principles. Electrophoresis 2019, 40, 930–954. [Google Scholar] [CrossRef]
- Seungyoung, Y.; Jae Young, K.; Seong Jae, L.; Sung Sik, L.; Min, K.J. Sheathless elasto-inertial particle focusing and continuous separation in a straight rectangular microchannel. Lab. Chip 2011, 11, 266–273. [Google Scholar]
- D’Avino, G.; Romeo, G.; Villone, M.M.; Greco, F.; Netti, P.A.; Maffettone, P.L. Single line particle focusing induced by viscoelasticity of the suspending liquid: Theory, experiments and simulations to design a micropipe flow-focuser. Lab. Chip 2012, 12, 1638. [Google Scholar] [CrossRef]
- Xiang, N.; Dai, Q.; Ni, Z. Multi-train elasto-inertial particle focusing in straight microfluidic channels. Appl. Phys. Lett. 2016, 109, 134101. [Google Scholar] [CrossRef]
- Yang, S.H.; Lee, D.J.; Youn, J.R.; Song, Y.S. Multiple-line particle focusing under viscoelastic flow in a microfluidic device. Anal. Chem. 2017, 89, 3639–3647. [Google Scholar] [CrossRef]
- Seo, K.W.; Ha, Y.R.; Lee, S.J. Vertical focusing and cell ordering in a microchannel via viscoelasticity: Applications for cell monitoring using a digital holographic microscopy. Appl. Phys. Lett. 2014, 104, 213702. [Google Scholar]
- Liu, C.; Guo, J.; Tian, F.; Yang, N.; Yan, F.; Ding, Y.; Wei, J.; Hu, G.; Nie, G.; Sun, J. Field-free isolation of exosomes from extracellular vesicles by microfluidic viscoelastic flows. ACS Nano 2017, 11, 6968–6976. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Ma, Z.; Tayebi, M.; Ai, Y. Submicron particle focusing and exosome sorting by wavy microchannel structures within viscoelastic fluids. Anal. Chem. 2019, 91, 4577–4584. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Xuan, X. Elasto-inertial pinched flow fractionation for continuous shape-based particle separation. Anal. Chem. 2015, 87, 11523–11530. [Google Scholar] [CrossRef]
- Liu, C.; Xue, C.; Chen, X.; Shan, L.; Tian, Y.; Hu, G. Size-Based separation of particles and cells utilizing viscoelastic effects in straight microchannels. Anal. Chem. 2015, 87, 6041–6048. [Google Scholar] [CrossRef]
- Nam, J.; Jang, W.S.; Hong, D.H.; Lim, C.S. Viscoelastic separation and concentration of fungi from blood for highly sensitive molecular diagnostics. Sci. Rep. UK 2019, 9, 3067. [Google Scholar] [CrossRef]
- Villone, M.M.; D’Avino, G.; Hulsen, M.A.; Greco, F.; Maffettone, P.L. Simulations of viscoelasticity-induced focusing of particles in pressure-driven micro-slit flow. J. Non-Newton Fluid 2011, 166, 1396–1405. [Google Scholar] [CrossRef]
- Villone, M.M.; D’Avino, G.; Hulsen, M.A.; Greco, F.; Maffettone, P.L. Particle motion in square channel flow of a viscoelastic liquid: Migration vs. secondary flows. J. Non-Newton Fluid 2013, 195, 1–8. [Google Scholar] [CrossRef]
- Raffiee, A.H.; Ardekani, A.M.; Dabiri, S. Numerical investigation of elasto-inertial particle focusing patterns in viscoelastic microfluidic devices. J. Non-Newton Fluid 2019, 272, 104166. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, P.; Lin, J.; Hu, H.H. Equilibrium positions of the elasto-inertial particle migration in rectangular channel flow of Oldroyd-B viscoelastic fluids. J. Fluid Mech. 2019, 868, 316–340. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, X.B.; Li, Q.; Jiang, X.S.; Zhou, H.P. Study of three-dimensional electro-osmotic flow with curved boundary via lattice Boltzmann method. Int. J. Mod. Phys. C 2016, 27. [Google Scholar] [CrossRef]
- Su, J.; Ma, L.; Ouyang, J.; Feng, C. Simulations of viscoelastic fluids using a coupled lattice Boltzmann method: Transition states of elastic instabilities. AIP Adv. 2017, 7, 115013. [Google Scholar] [CrossRef]
- Feng, Z.G.; Michaelides, E.E. The immersed boundary-lattice Boltzmann method for solving fluid-particles interaction problems. J. Comput. Phys. 2004, 195, 602–628. [Google Scholar] [CrossRef]
- Takeishi, N.; Ito, H.; Kaneko, M.; Wada, S. Deformation of a red blood cell in a narrow rectangular microchannel. Micromachines 2019, 10, 199. [Google Scholar] [CrossRef]
- Ma, J.; Wang, Z.; Young, J.; Lai, J.C.S.; Tian, F.B. An immersed boundary-lattice Boltzmann method for fluid-structure interaction problems involving viscoelastic fluids and complex geometries. J. Comput. Phys. 2020, 415, 109487. [Google Scholar] [CrossRef]
- Ma, Q.; Xu, Q.; Chen, Q.; Chen, Z.; Su, H.; Zhang, W. Lattice Boltzmann model for complex transfer behaviors in porous electrode of all copper redox flow battery with deep eutectic solvent electrolyte. Appl. Therm. Eng. 2019, 160, 114015. [Google Scholar] [CrossRef]
- Qian, Y.H.; D’Humières, D.; Lallemand, P. Lattice bgk models for navier-stokes equation. Europhys. Lett. 1992, 17, 479. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 2002, 65, 46308. [Google Scholar] [CrossRef]
- Guo, Z.L.; Zheng, C.G.; Shi, B.C. Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method. Chin. Phys. 2002, 11, 366–374. [Google Scholar]
- Krüger, T. Computer Simulation Study of Collective Phenomena in Dense Suspensions of Red Blood Cells under Shear; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Snijkers, F.; D’Avino, G.; Maffettone, P.L.; Greco, F.; Hulsen, M.A.; Vermant, J. Effect of viscoelasticity on the rotation of a sphere in shear flow. J. Non-Newton Fluid 2011, 166, 363–372. [Google Scholar] [CrossRef]
- Goyal, N.; Derksen, J.J. Direct simulations of spherical particles sedimenting in viscoelastic fluids. J. Non-Newton Fluid 2012, 183, 1–13. [Google Scholar] [CrossRef]
- Liu, B.; Lin, J.; Ku, X.; Yu, Z. Migration of spherical particles in a confined shear flow of Giesekus fluid. Rheol. Acta 2019, 58, 639–646. [Google Scholar] [CrossRef]
- Kim, J.Y.; Ahn, S.W.; Lee, S.S.; Kim, J.M. Lateral migration and focusing of colloidal particles and DNA molecules under viscoelastic flow. Lab. Chip 2012, 12, 2807–2814. [Google Scholar] [PubMed]
- Seo, K.W.; Kang, Y.J.; Lee, S.J. Lateral migration and focusing of microspheres in a microchannel flow of viscoelastic fluids. Phys. Fluids 2014, 26, 63301. [Google Scholar] [CrossRef]
- Wang, P.; Yu, Z.; Lin, J. Numerical simulations of particle migration in rectangular channel flow of Giesekus viscoelastic fluids. J. Non-Newton Fluid 2018, 262, 142–148. [Google Scholar] [CrossRef]
- Zhang, A.; Murch, W.L.; Einarsson, J.; Shaqfeh, E.S.G. Lift and drag force on a spherical particle in a viscoelastic shear flow. J. Non-Newton Fluid 2020, 280, 104279. [Google Scholar] [CrossRef]
- Lu, X.; Liu, C.; Hu, G.; Xuan, X. Particle manipulations in non-Newtonian microfluidics: A review. J. Colloid Interface Sci. 2017, 500, 182–201. [Google Scholar] [CrossRef]
- Nam, J.; Namgung, B.; Lim, C.T.; Bae, J.; Leo, H.L.; Cho, K.S.; Kim, S. Microfluidic device for sheathless particle focusing and separation using a viscoelastic fluid. J. Chromatogr. A 2015, 1406, 244–250. [Google Scholar] [CrossRef]
- Nam, J.; Shin, Y.; Tan, J.K.; Lim, Y.B.; Lim, C.T.; Kim, S. High-throughput malaria parasite separation using a viscoelastic fluid for ultrasensitive PCR detection. Lab. Chip 2016, 16, 2086. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, C.; Jiang, D. Three-Dimensional Numerical Simulation of Particle Focusing and Separation in Viscoelastic Fluids. Micromachines 2020, 11, 908. https://doi.org/10.3390/mi11100908
Ni C, Jiang D. Three-Dimensional Numerical Simulation of Particle Focusing and Separation in Viscoelastic Fluids. Micromachines. 2020; 11(10):908. https://doi.org/10.3390/mi11100908
Chicago/Turabian StyleNi, Chen, and Di Jiang. 2020. "Three-Dimensional Numerical Simulation of Particle Focusing and Separation in Viscoelastic Fluids" Micromachines 11, no. 10: 908. https://doi.org/10.3390/mi11100908
APA StyleNi, C., & Jiang, D. (2020). Three-Dimensional Numerical Simulation of Particle Focusing and Separation in Viscoelastic Fluids. Micromachines, 11(10), 908. https://doi.org/10.3390/mi11100908