Auxiliary Optomechanical Tools for 3D Cell Manipulation
Abstract
1. Introduction
2. Materials and Methods
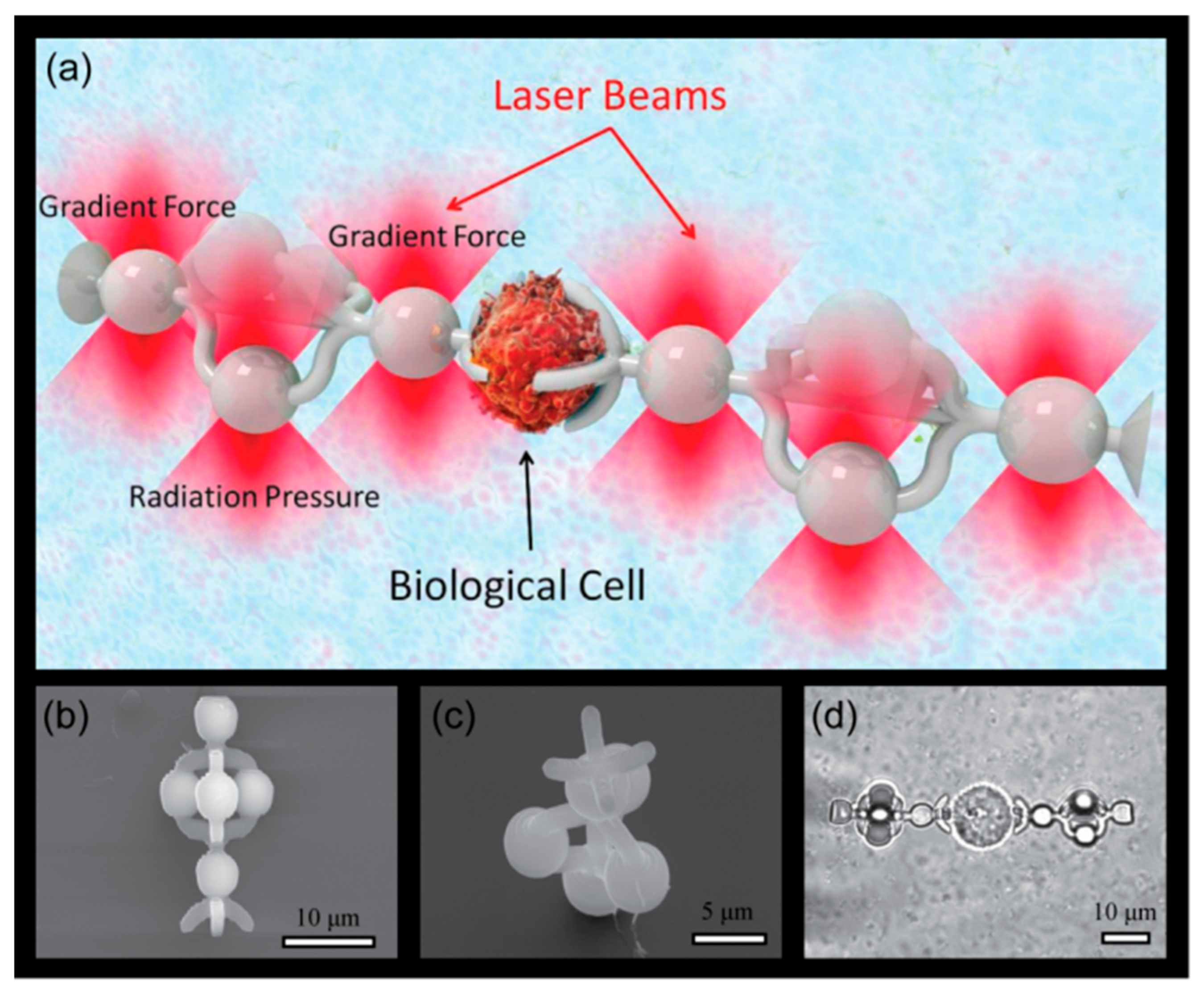
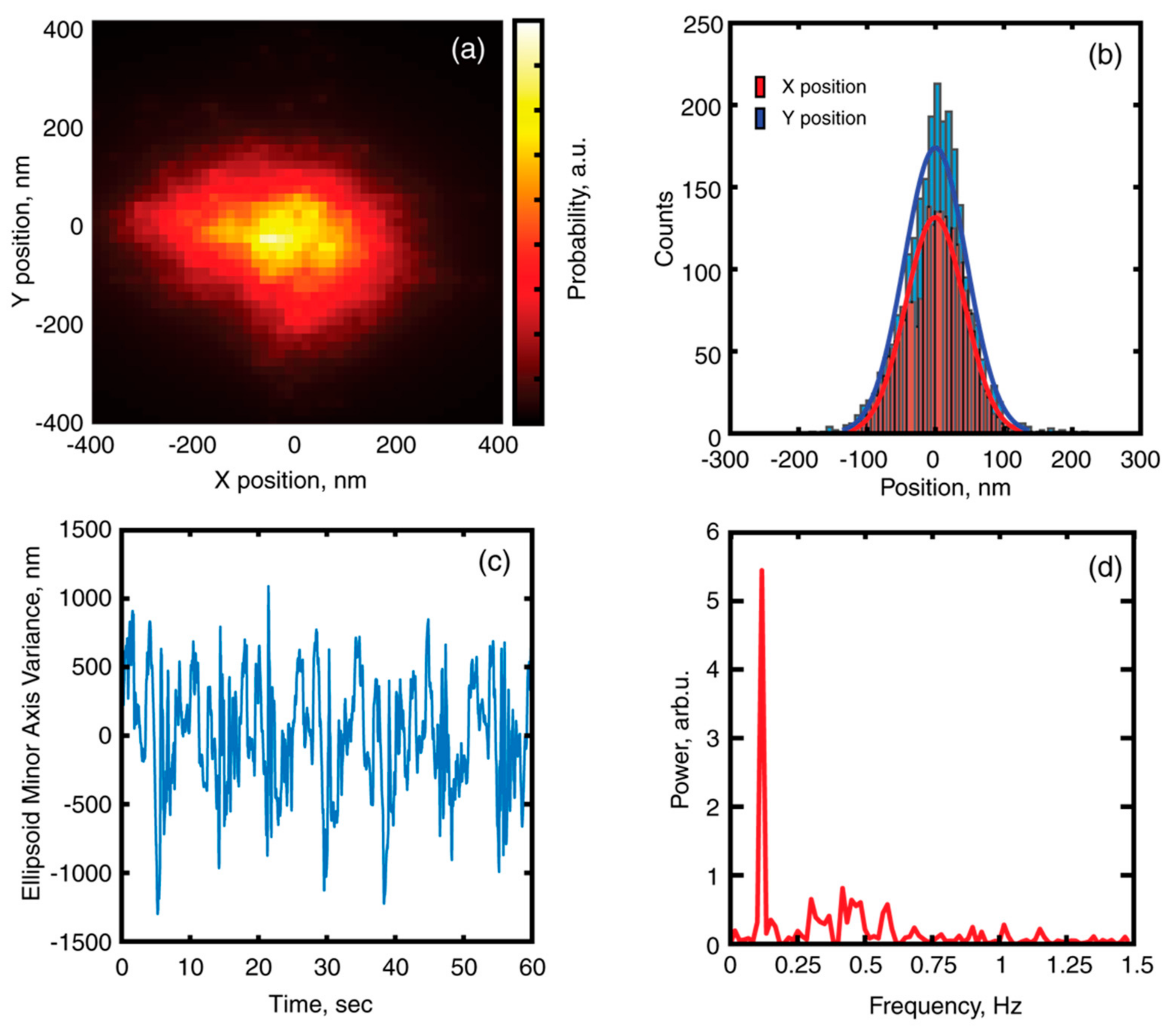
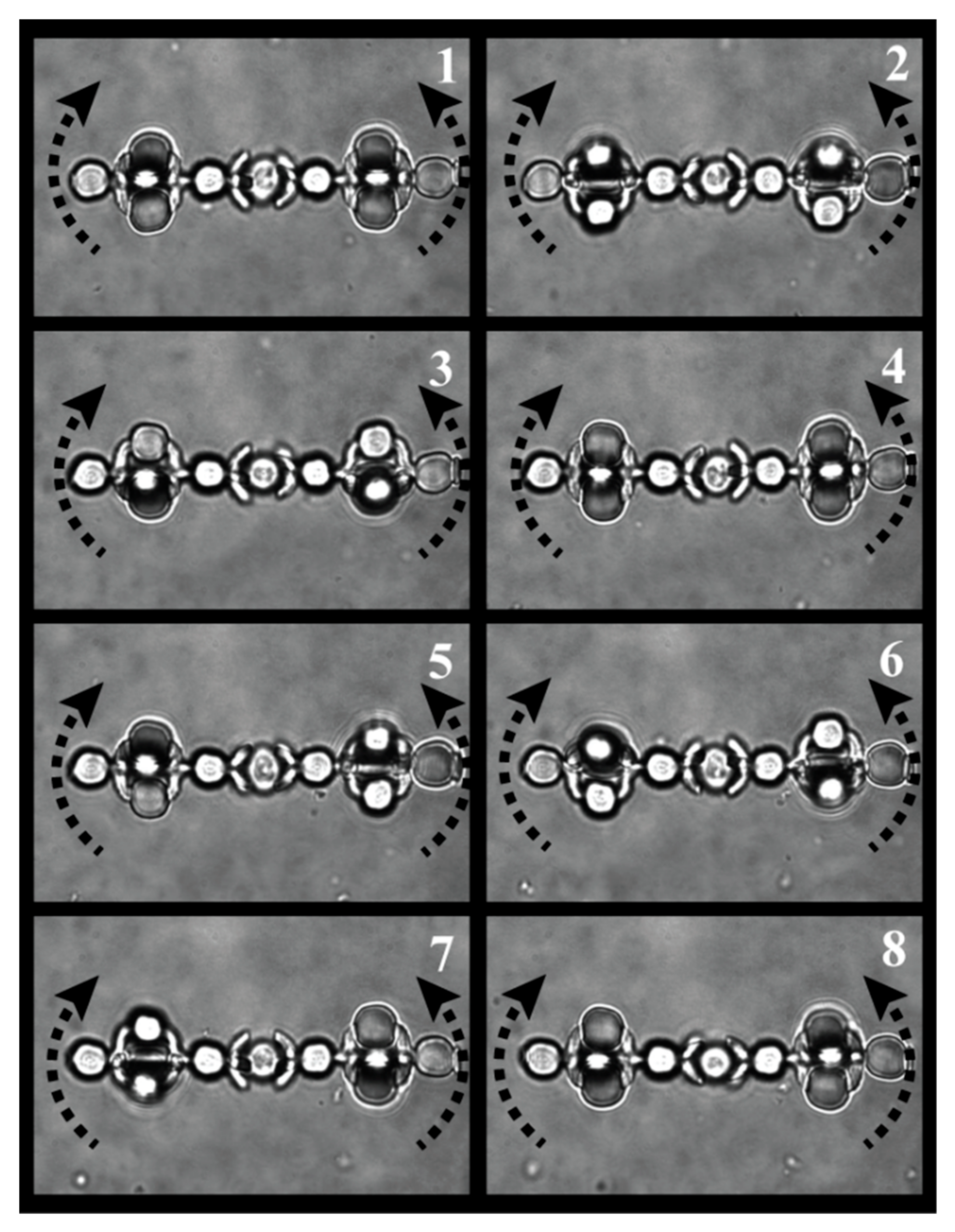
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Pawley, J.B. Handbook Of Biological Confocal Microscopy; Springer: Boston, MA, USA, 2006. [Google Scholar]
- Denk, W.; Strickler, J.H.; Webb, W.W. Two-photon laser scanning fluorescence microscopy. Science 1990, 248, 73–76. [Google Scholar] [CrossRef]
- Egner, A.; Hell, S.W. Fluorescence microscopy with super-resolved optical sections. Trends Cell Biol. 2005, 15, 207–215. [Google Scholar] [CrossRef]
- Choi, W.J.; Park, K.S.; Eom, T.J.; Oh, M.-K.; Lee, B.H. Tomographic imaging of a suspending single live cell using optical tweezer-combined full-field optical coherence tomography. Opt. Lett. 2012, 37, 2784. [Google Scholar] [CrossRef] [PubMed]
- Fauver, M.; Seibel, E.; Rahn, J.R.; Meyer, M.; Patten, F.; Neumann, T.; Nelson, A. Three-dimensional imaging of single isolated cell nuclei using optical projection tomography. Opt. Express 2005, 13, 4210–4223. [Google Scholar] [CrossRef] [PubMed]
- Kus, A.; Dudek, M.; Kemper, B.; Kujawinska, M.; Vollmer, A. Tomographic phase microscopy of living three-dimensional cell cultures. J. Biomed. Opt. 2014, 19, 46009. [Google Scholar] [CrossRef] [PubMed]
- Carmon, G.; Feingold, M. Rotation of single bacterial cells relative to the optical axis using optical tweezers. Opt. Lett. 2011, 36, 40. [Google Scholar] [CrossRef]
- Tanaka, Y.; Wakida, S. Controlled 3D rotation of biological cells using optical multiple-force clamps. Biomed. Opt. Express 2014, 5, 2341. [Google Scholar] [CrossRef]
- Habaza, M.; Gilboa, B.; Roichman, Y.; Shaked, N.T. Tomographic phase microscopy with 180° rotation of live cells in suspension by holographic optical tweezers. Opt. Lett. 2015, 40, 1881–1884. [Google Scholar] [CrossRef]
- Kreysing, M.K.; Kießling, T.; Fritsch, A.; Dietrich, C.; Guck, J.R.; Käs, J.A. The optical cell rotator. Opt. Express 2008, 16, 16984. [Google Scholar] [CrossRef]
- Kreysing, M.; Ott, D.; Schmidberger, M.J.; Otto, O.; Schürmann, M.; Martín-Badosa, E.; Whyte, G.; Guck, J. Dynamic operation of optical fibres beyond the single-mode regime facilitates the orientation of biological cells. Nat. Commun. 2014, 5, 5481. [Google Scholar] [CrossRef]
- Müller, P.; Schürmann, M.; Chan, C.J.; Guck, J. Single-Cell Diffraction Tomography with Optofluidic Rotation about a Tilted Axis. In Proceedings of the SPIE 9548, Optical Trapping and Optical Micromanipulation XII, San Diego, CA, USA, 25 August 2015; p. 95480U. [Google Scholar]
- Cao, B.; Kelbauskas, L.; Chan, S.; Shetty, R.M.; Smith, D.; Meldrum, D.R. Rotation of single live mammalian cells using dynamic holographic optical tweezers. Opt. Lasers Eng. 2017, 92, 70–75. [Google Scholar]
- Phys, J.A. A microfluidic chip for single-cell 3D rotation enabling self-adaptive spatial localization A micro fl uidic chip for single-cell 3D rotation enabling self-adaptive spatial localization. J. Appl. Phys. 2019, 126, 234702. [Google Scholar]
- Liu, Y.; Cheng, D.K.; Sonek, G.J.; Berns, M.W.; Chapman, C.F.; Tromberg, B.J. Evidence for localized cell heating induced by infrared optical tweezers. Biophys. J. 1995, 68, 2137–2144. [Google Scholar] [CrossRef]
- Mohanty, S.K.; Sharma, M.; Gupta, P.K. Generation of ROS in cells on exposure to CW and pulsed near-infrared laser tweezers. Photochem. Photobiol. Sci. 2006, 5, 134–139. [Google Scholar] [CrossRef] [PubMed]
- Konig, K.; Liang, H.; Berns, M.W.; Tromberg, B.J. Cell damage in near-infrared multimode optical traps as a result of multiphoton absorption. Opt. Lett. 1996, 21, 1090–1092. [Google Scholar] [CrossRef] [PubMed]
- Kawata, S.; Sun, H.B.; Tanaka, T.; Takada, K. Finer features for functional microdevices. Nature 2001, 412, 697–698. [Google Scholar] [CrossRef] [PubMed]
- Goppert-Mayer, M. Uber Elementarakte mit zwei Quantensprungen. Ann. Phys. 1931, 401, 273–294. [Google Scholar] [CrossRef]
- Maruo, S.; Nakamura, O.; Kawata, S. Three-dimensional microfabrication with two-photon-absorbed photopolymerization. Opt. Lett. 1997, 22, 132–134. [Google Scholar] [CrossRef]
- Phillips, D.B.; Simpson, S.H.; Grieve, J.A.; Bowman, R.; Gibson, G.M.; Padgett, M.J.; Rarity, J.G.; Hanna, S.; Miles, M.J.; Carberry, D.M. Force sensing with a shaped dielectric micro-tool. EPL 2012, 99, 58004. [Google Scholar] [CrossRef]
- Gibson, G.M.; Bowman, R.W.; Linnenberger, A.; Dienerowitz, M.; Phillips, D.B. A compact holographic optical tweezers instrument. Rev. Sci. Instrum. 2012, 8, 113107. [Google Scholar] [CrossRef]
- Phillips, D.B.; Padgett, M.J.; Hanna, S.; Ho, Y.L.D.; Carberry, D.M.; Miles, M.J.; Simpson, S.H. Shape-induced force fields in optical trapping. Nat. Photonics 2014, 8, 400–405. [Google Scholar] [CrossRef]
- Villangca, M.J.; Palima, D.; Bañas, A.R.; Glückstad, J. Light-driven micro-tool equipped with a syringe function. Nat. Publ. Gr. 2016, 5, e16148-7. [Google Scholar] [CrossRef] [PubMed]
- Palima, D.; Bañas, A.R.; Vizsnyiczai, G.; Kelemen, L.; Ormos, P.; Glückstad, J. Wave-guided optical waveguides. Opt. Express 2012, 20, 2004–2014. [Google Scholar] [CrossRef] [PubMed]
- Asavei, T.; Nieminen, T.A.; Loke, V.L.Y.; Stilgoe, A.B.; Bowman, R.; Preece, D.; Padgett, M.J.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Optically trapped and driven paddle-wheel. New J. Phys. 2013, 15, 63016. [Google Scholar] [CrossRef]
- Phillips, D.B.; Gibson, G.M.; Bowman, R.; Padgett, M.; Rarity, J.G.; Carberry, D.M.; Hanna, S.; Miles, M.J.; Simpson, S.H. Fashioning Microscopic Tools. In Proceedings of the Optics in the Life Sciences, Washington, DC, USA, 14–18 April 2013; p. TM2D.3. [Google Scholar]
- Grier, D.G.; Roichman, Y. Holographic optical trapping. Appl. Opt. 2006, 45, 880–887. [Google Scholar] [CrossRef]
- Guck, J.; Ananthakrishnan, R.; Mahmood, H.; Moon, T.J.; Cunningham, C.C.; Käs, J. The optical stretcher: A novel laser tool to micromanipulate cells. Biophys. J. 2001, 81, 767–784. [Google Scholar] [CrossRef]
- Sung, Y.; Choi, W.; Fang-Yen, C.; Badizadegan, K.; Dasari, R.R.; Feld, M.S. Optical diffraction tomography for high resolution live cell imaging. Opt. Express 2009, 17, 266. [Google Scholar] [CrossRef]
- Choi, W.; Fang-yen, C.; Badizadegan, K.; Oh, S.; Lue, N.; Dasari, R.R.; Feld, M.S. Tomographic phase microscopy. Nat. Methods 2007, 4, 717–719. [Google Scholar] [CrossRef]
- Charrière, F.; Marian, A.; Montfort, F.; Kuehn, J.; Colomb, T.; Cuche, E.; Marquet, P.; Depeursinge, C. Cell refractive index tomography by digital holographic microscopy. Opt. Lett. 2006, 31, 178. [Google Scholar] [CrossRef]
- Kawata, S.; Nakamura, O.; Minami, S. Optical microscope tomography I Support constraint. J. Opt. Soc. Am. A 1987, 4, 292. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shishkin, I.; Markovich, H.; Roichman, Y.; Ginzburg, P. Auxiliary Optomechanical Tools for 3D Cell Manipulation. Micromachines 2020, 11, 90. https://doi.org/10.3390/mi11010090
Shishkin I, Markovich H, Roichman Y, Ginzburg P. Auxiliary Optomechanical Tools for 3D Cell Manipulation. Micromachines. 2020; 11(1):90. https://doi.org/10.3390/mi11010090
Chicago/Turabian StyleShishkin, Ivan, Hen Markovich, Yael Roichman, and Pavel Ginzburg. 2020. "Auxiliary Optomechanical Tools for 3D Cell Manipulation" Micromachines 11, no. 1: 90. https://doi.org/10.3390/mi11010090
APA StyleShishkin, I., Markovich, H., Roichman, Y., & Ginzburg, P. (2020). Auxiliary Optomechanical Tools for 3D Cell Manipulation. Micromachines, 11(1), 90. https://doi.org/10.3390/mi11010090




