Transient Simulation for the Thermal Design Optimization of Pulse Operated AlGaN/GaN HEMTs
Abstract
1. Introduction
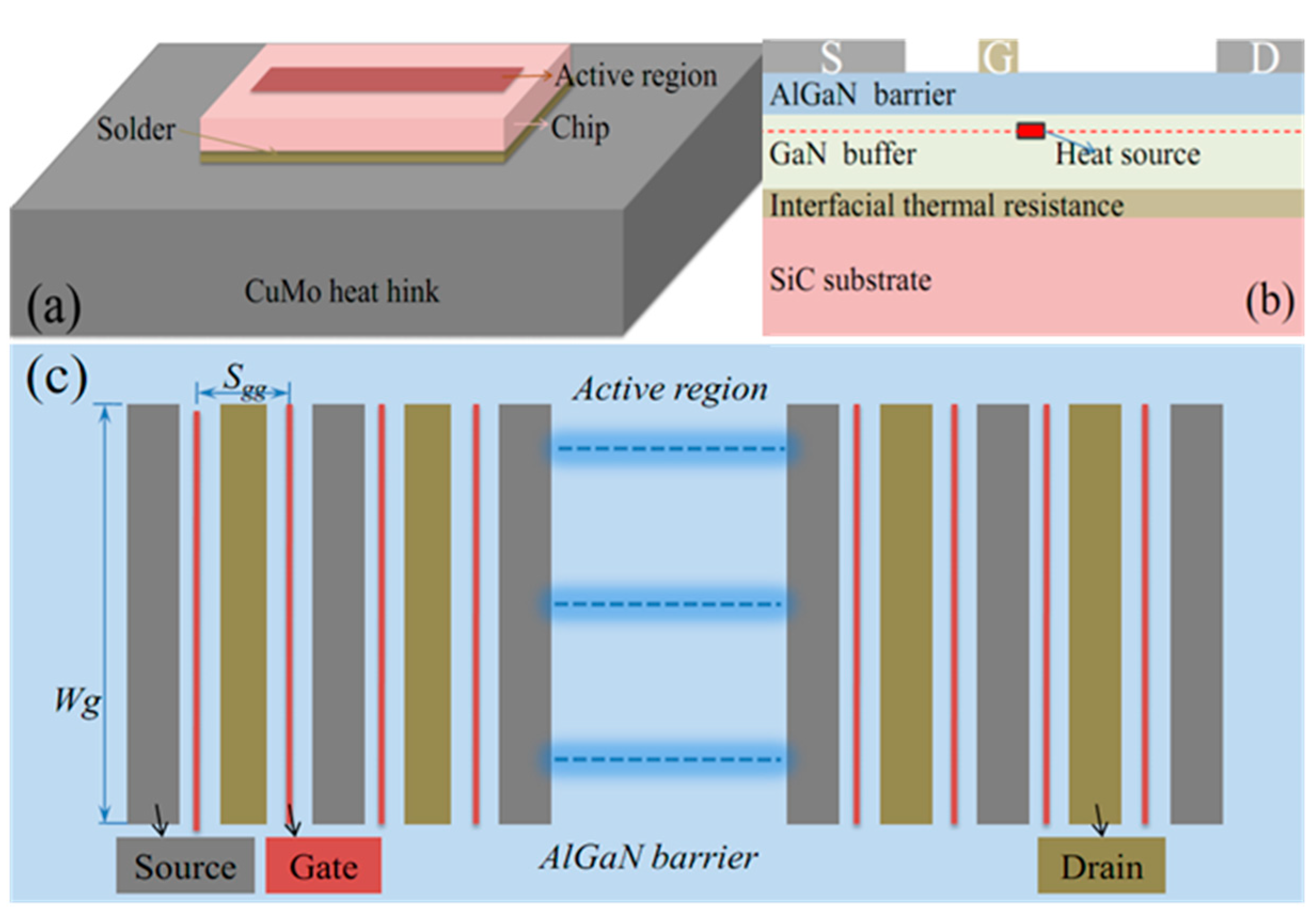
2. Device Details and Simulation Methods
3. Simulation Results and Discussion
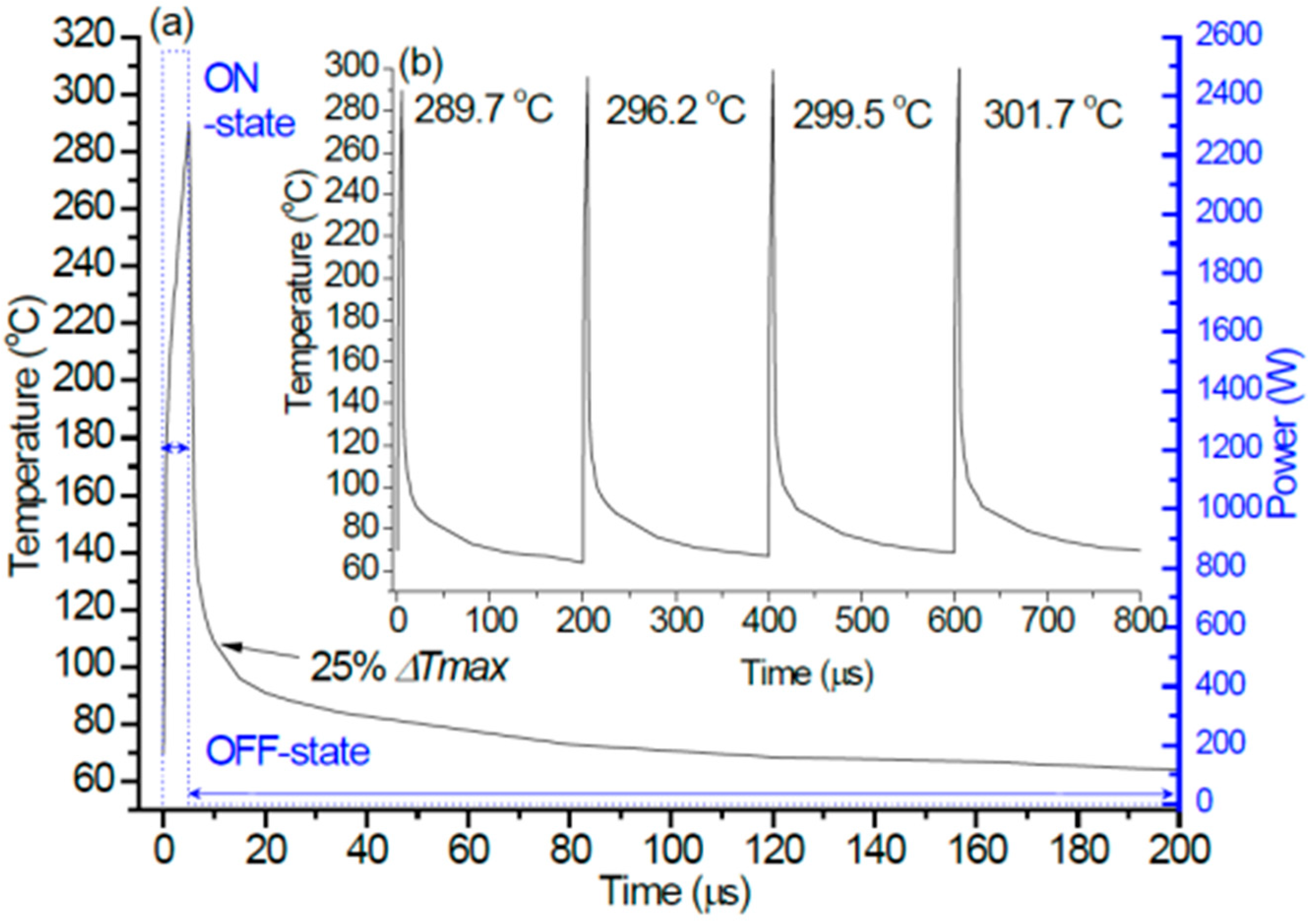
3.1. Transient Channel Temperature in Pulsed Operation
3.2. The Pulse Width Effect
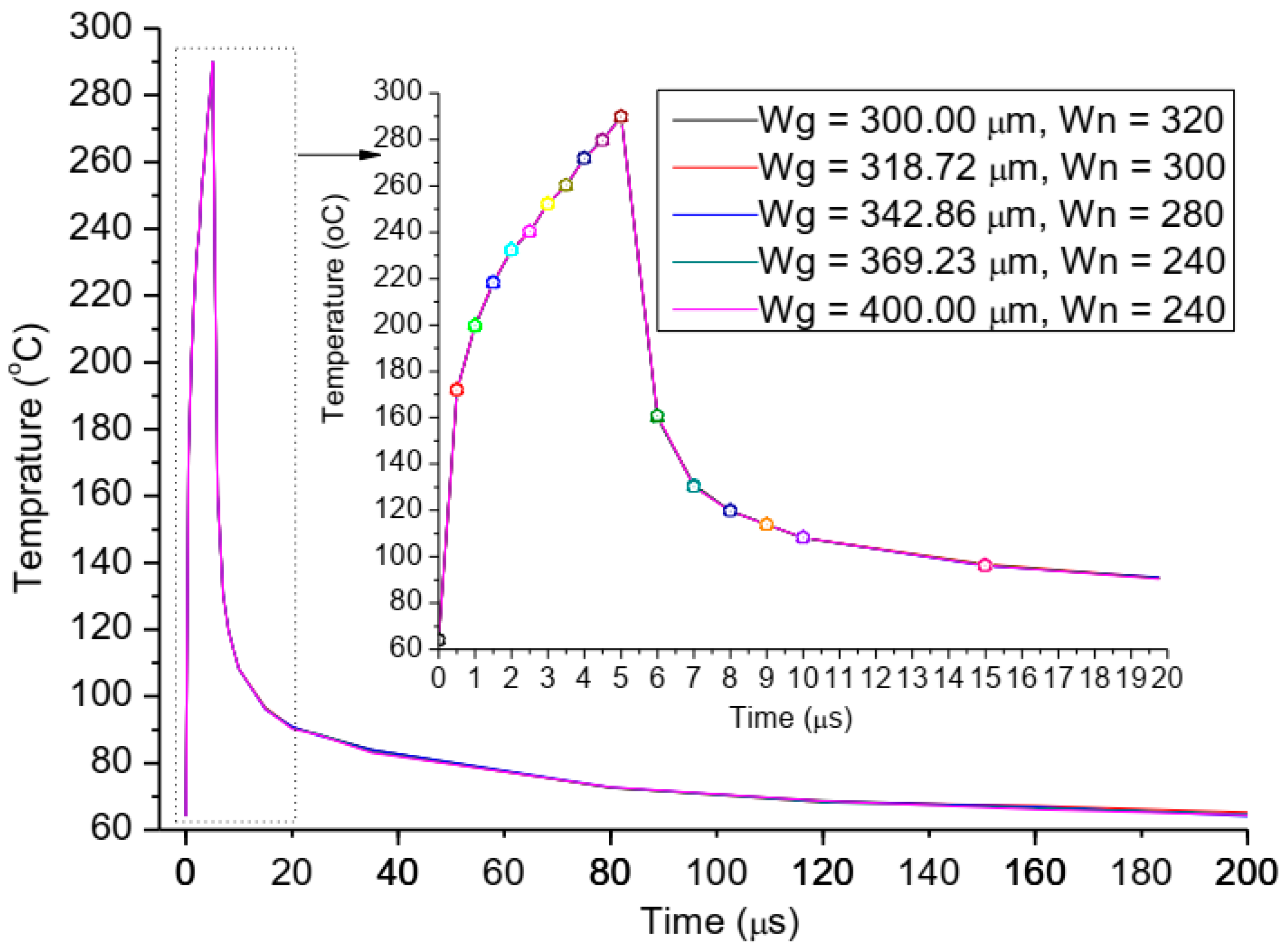
3.3. The Gate Structures Effect
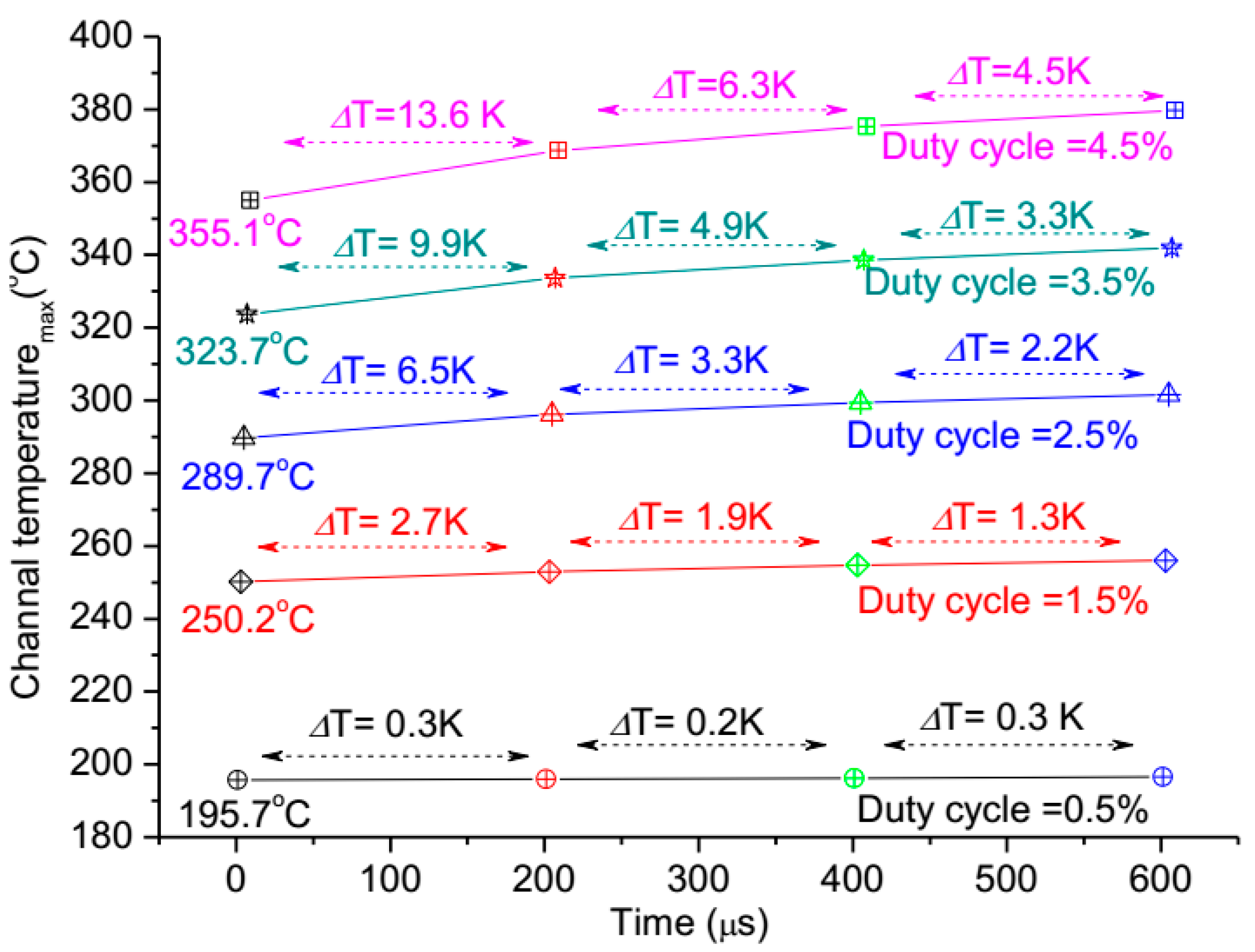
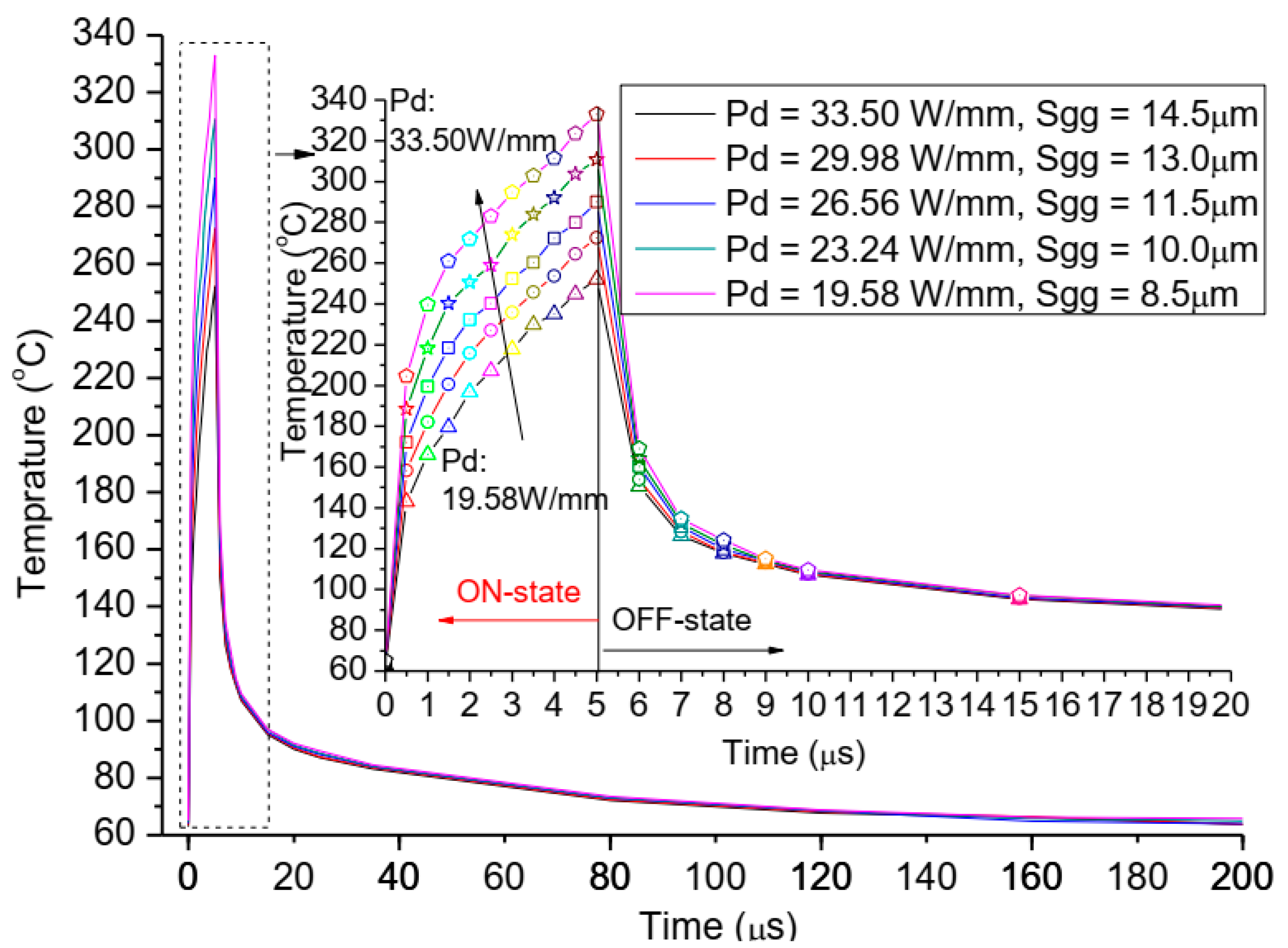
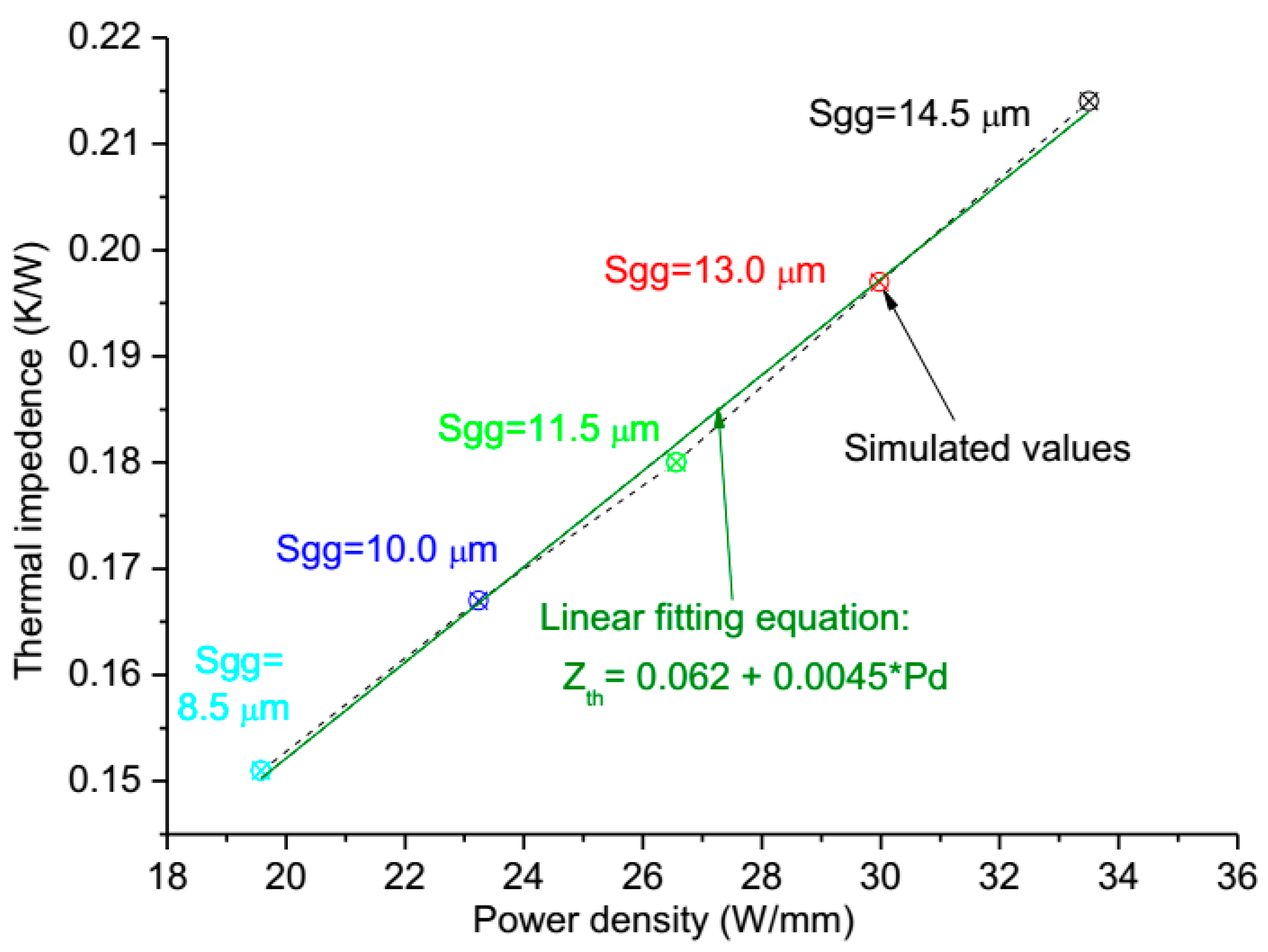
3.4. The Power Density Effect
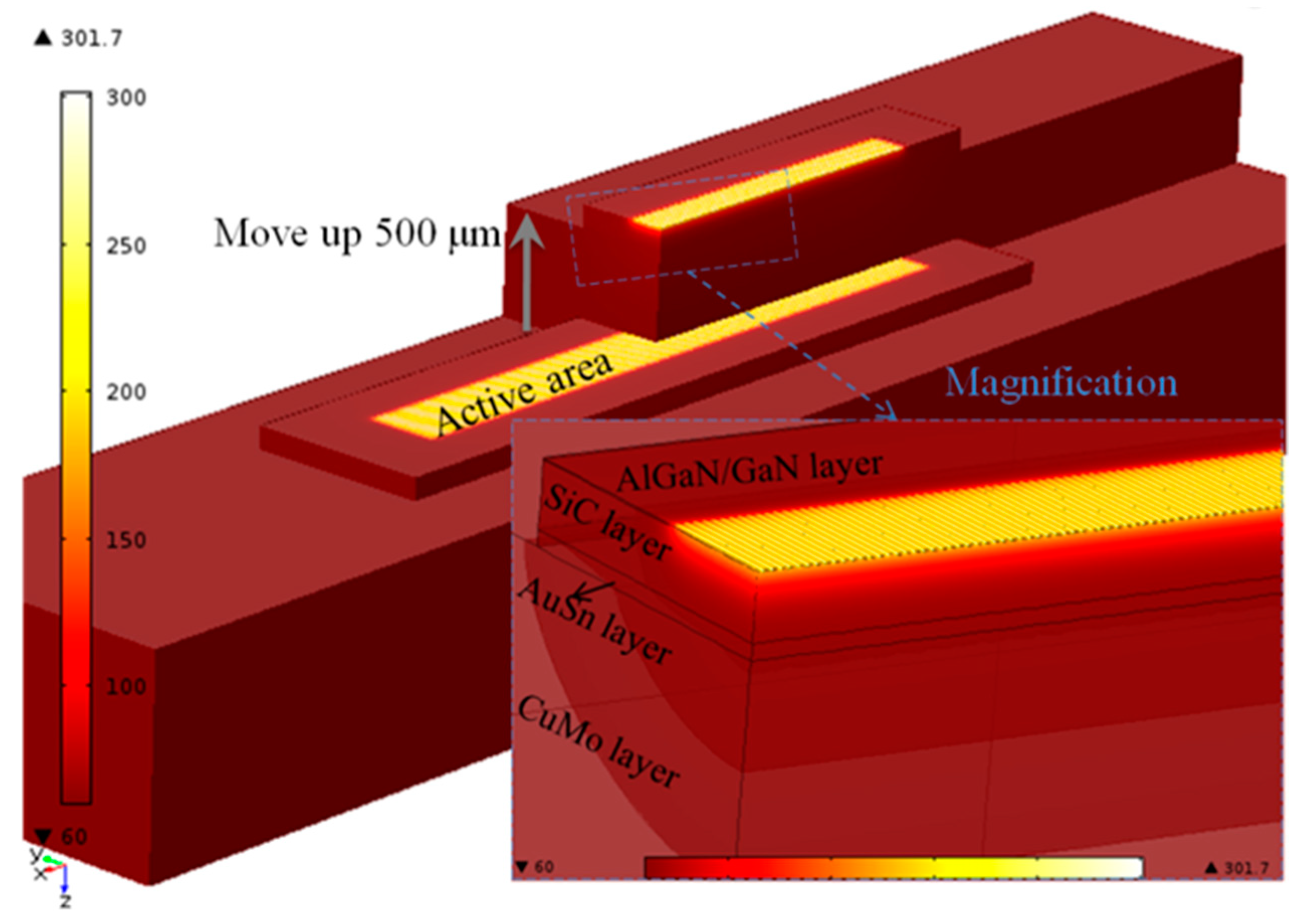
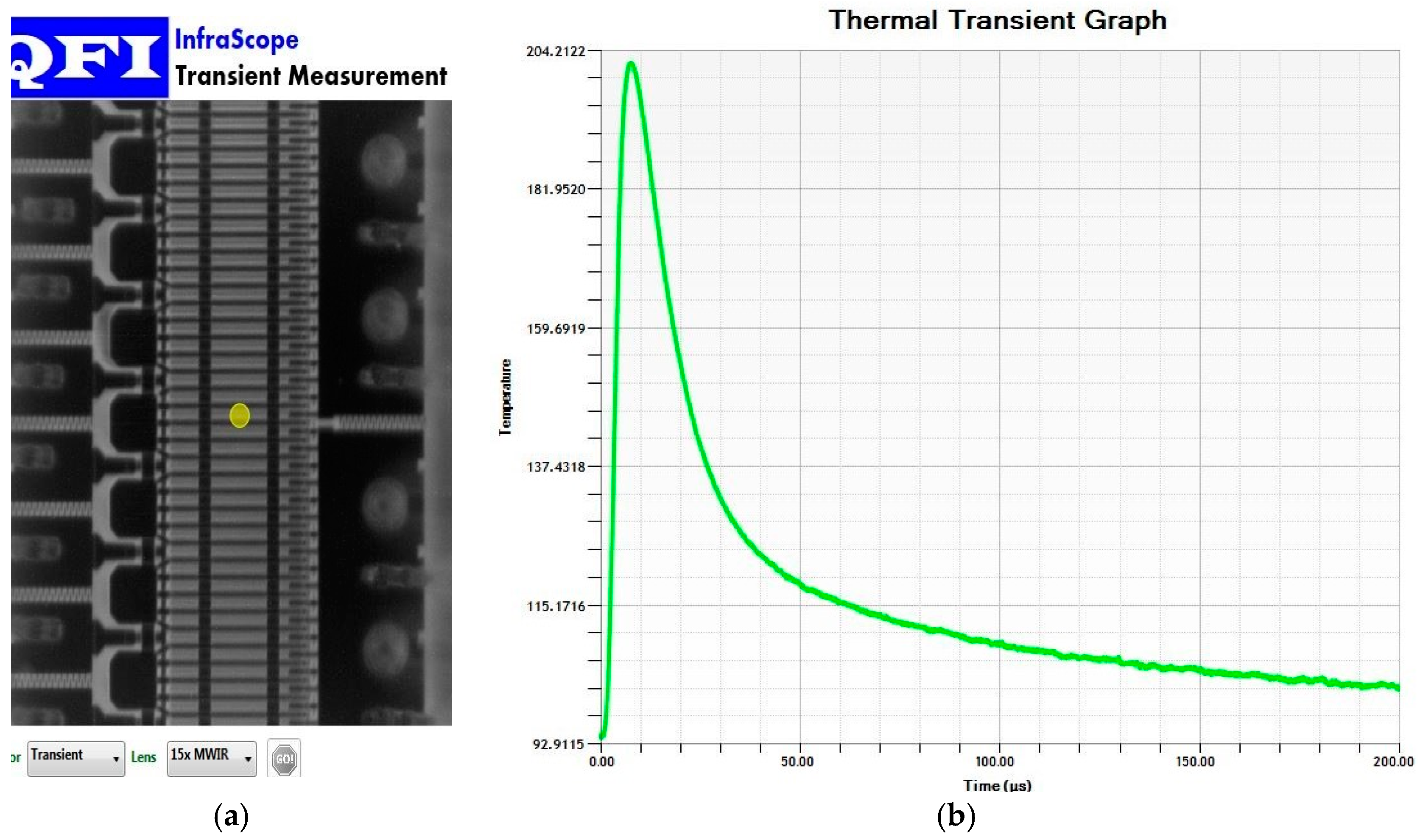
4. Experimental Test
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Amano, H.; Baines, Y.; Beam, E.; Borga, M.; Bouchet, T.; Chalker, P.R.; Charles, M.; Chen, K.J.; Chowdhury, N.; Chu, R.; et al. The 2018 GaN power electronics roadmap. J. Phys. D Appl. Phys. 2018, 51, 163001. [Google Scholar] [CrossRef]
- Baczkowski, L.; Jacquet, J.C.; Jardel, O.; Gaquière, C.; Moreau, M.; Carisetti, D.; Brunel, L.; Vouzelaud, F.; Mancuso, Y. Thermal characterization using optical methods of AlGaN/GaN HEMTs on SiC substrate in RF operating conditions. IEEE Trans. Electron Devices 2015, 62, 3992–3998. [Google Scholar] [CrossRef]
- Guo, H.; Kong, Y.; Chen, T. Thermal simulation of high power GaN-on-diamond substrates for HEMT applications. Diam. Relat. Mater. 2017, 73, 260–266. [Google Scholar] [CrossRef]
- Michael, F.; Patrick, M.; Avram, B. Modeling thermal microspreading resistance in via arrays. J. Electron. Packag. 2016, 138, 010909. [Google Scholar]
- Pavlidis, G.; Pavlidis, G.; Heller, E.R.; Moore, E.A.; Vetury, R.; Graham, S. Characterization of AlGaN/GaN HEMTs using gate resistance thermometry. IEEE Trans. Electron Devices 2017, 64, 78–83. [Google Scholar] [CrossRef]
- Chou, H.P.; Cheng, S.; Cheng, C.H.; Chuang, C.W. Thermal behavior investigation of cascode GaN HEMTs. In Proceedings of the 3rd International Conference on Industrial Application Engineering, Kitayushu, Japan, 28–31 March 2015. [Google Scholar]
- Nigam, A.; Bhat, T.N.; Rajamani, S.; Dolmanan, S.B.; Tripathy, S.; Kumar, M. Effect of self-heating on electrical characteristics of AlGaN/GaN HEMT on Si (111) substrate. AIP Adv. 2017, 7, 085015. [Google Scholar] [CrossRef]
- Jones, J.P.; Heller, E.; Dorsey, D.; Graham, S. Transient stress characterization of AlGaN/GaN HEMTs due to electrical and thermal effects. Microelectron. Reliab. 2015, 55, 2634–2639. [Google Scholar] [CrossRef]
- Ishizaki, T.; Yanase, M.; Kuno, A.; Satoh, T.; Usui, M.; Osawa, F.; Yamada, Y. Thermal simulation of joints with high thermal conductivities for power electronic devices. Microelectron. Reliab. 2015, 55, 1060–1066. [Google Scholar] [CrossRef]
- Asubar, J.T.; Yatabe, Z.; Hashizume, T. Reduced thermal resistance in AlGaN/GaN multi-mesa-channel high electron mobility transistors. Appl. Phys. Lett. 2014, 105, 053510. [Google Scholar] [CrossRef]
- Darwish, A.; Bayba, A.J.; Hung, H.A. Channel temperature analysis of GaN HEMTs with nonlinear thermal conductivity. IEEE Trans. Electron Devices 2015, 62, 840–846. [Google Scholar] [CrossRef]
- Schwitter, B.K.; Parker, A.E.; Mahon, S.J.; Fattorini, A.P.; Heimlich, M.C. Impact of bias and device structure on gate junction temperature in AlGaN/GaN-on-Si HEMTs. IEEE Trans. Electron Devices 2014, 61, 1327–1334. [Google Scholar] [CrossRef]
- Bertoluzza, F.; Delmonte, N.; Menozzi, R. Three-dimensional finite element thermal simulation of GaN-based HEMTs. Microelectron. Reliab. 2009, 49, 468–473. [Google Scholar] [CrossRef]
- Chen, X.P.; Donmezer, F.N.; Kumar, S.; Graham, S. A numerical study on comparing the active and passive cooling of AlGaN/GaN HEMTs. IEEE Trans. Electron Devices 2014, 61, 4056–4061. [Google Scholar] [CrossRef]
- Wang, A.; Tadjer, M.J.; Anderson, T.J.; Baranyai, R.; Pomeroy, J.W.; Feygelson, T.I.; Hobart, K.D.; Pate, B.B.; Calle, F. Impact of intrinsic stress in diamond capping layers on the electrical behavior of AlGaN/GaN HEMTs. IEEE Trans. Electron Devices 2013, 60, 3149–3156. [Google Scholar] [CrossRef]
- Guo, H.; Han, P.; Chen, T. Study of thermal simulation technology for GaN power device. Res. Prog. SSE 2017, 37, 176–181. [Google Scholar]
- Agarwal, G.; Kazior, T.; Kenny, T.; Weinstein, D. Modeling and analysis for thermal management in gallium nitride HEMTs using microfluidic cooling. J. Electron. Packag. 2017, 139, 1–11. [Google Scholar] [CrossRef]
- Heller, E.; Crespo, A. Electro-thermal modeling of multifinger AlGaN/GaN HEMT device operation including thermal substrate effects. Microelectron. Reliab. 2013, 75, 45–50. [Google Scholar] [CrossRef]
- Donmezer, N.; Islam, M.; Yoder, P.D. The impact of nongray thermal transport on the temperature of AlGaN/GaN HFETs. IEEE Trans. Electron Devices 2015, 62, 2437–2444. [Google Scholar] [CrossRef]
- García, S.; Torre, I.; Mateos, J.; González, T.; Pérez, S. Impact of substrate and thermal boundary resistance on the performance of AlGaN/GaN HEMTs analyzed by means of electro-thermal Monte Carlo simulations. Semicond. Sci. Technol. 2016, 31, 065005. [Google Scholar] [CrossRef]
- Denu, G.A.; Mirani, J.H.; Fu, J. FEM thermal analysis of Cu/diamond/Cu and diamond/SiC heat spreaders. AIP Adv. 2017, 7, 035102. [Google Scholar] [CrossRef]

| Definition | Value | Definition | Value |
|---|---|---|---|
| Length of chip | 4000 μm | AlGaN barrier thickness | 20 nm |
| Width of chip | 860 μm | GaN buffer thickness | 2.0 μm |
| Length of heat hink | 8000 μm | SiC substrate thickness | 80 μm |
| Width of heat hink | 1720μm | Solder thickness | 20 μm |
| Heat sink thickness | 1000 μm | Pulse period | 200 μs |
| Power efficiency | 50% | Pulse width | Variables |
| Total power | 2550 W | Power density, and gate pitch spacing | Variables |
| Active area of heat sources region | 1.104 mm2 | Gate fingers, and gate width | Variables |
| Material | Thermal Conductivity (W/m·K) | Material | Thermal Conductivity (W/m·K) |
|---|---|---|---|
| AlGaN | 25 × (T/300)−1.44 | SiC | 387 × (T/293)−1.49 |
| GaN | 150 × (T/300)−1.42 | CuMo | 167 |
| AuSn | 57 | - | - |
| Interfacial thermal resistance | 10 K·m2/GW | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Chen, T.; Shi, S. Transient Simulation for the Thermal Design Optimization of Pulse Operated AlGaN/GaN HEMTs. Micromachines 2020, 11, 76. https://doi.org/10.3390/mi11010076
Guo H, Chen T, Shi S. Transient Simulation for the Thermal Design Optimization of Pulse Operated AlGaN/GaN HEMTs. Micromachines. 2020; 11(1):76. https://doi.org/10.3390/mi11010076
Chicago/Turabian StyleGuo, Huaixin, Tangsheng Chen, and Shang Shi. 2020. "Transient Simulation for the Thermal Design Optimization of Pulse Operated AlGaN/GaN HEMTs" Micromachines 11, no. 1: 76. https://doi.org/10.3390/mi11010076
APA StyleGuo, H., Chen, T., & Shi, S. (2020). Transient Simulation for the Thermal Design Optimization of Pulse Operated AlGaN/GaN HEMTs. Micromachines, 11(1), 76. https://doi.org/10.3390/mi11010076




