Temperature-Dependent Growth Characteristics of Nb- and CoFe-Based Nanostructures by Direct-Write Using Focused Electron Beam-Induced Deposition
Abstract
1. Introduction
2. Results
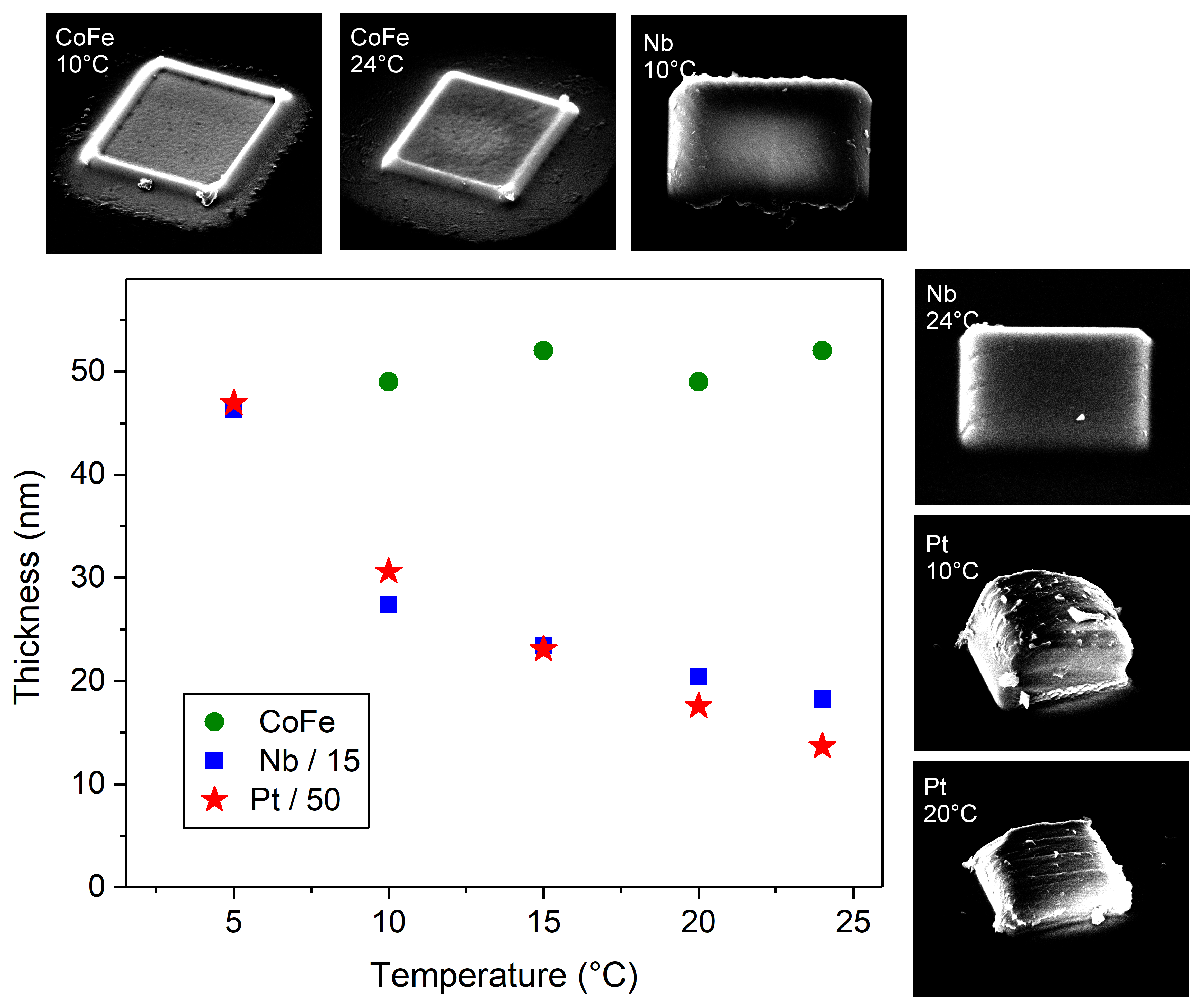
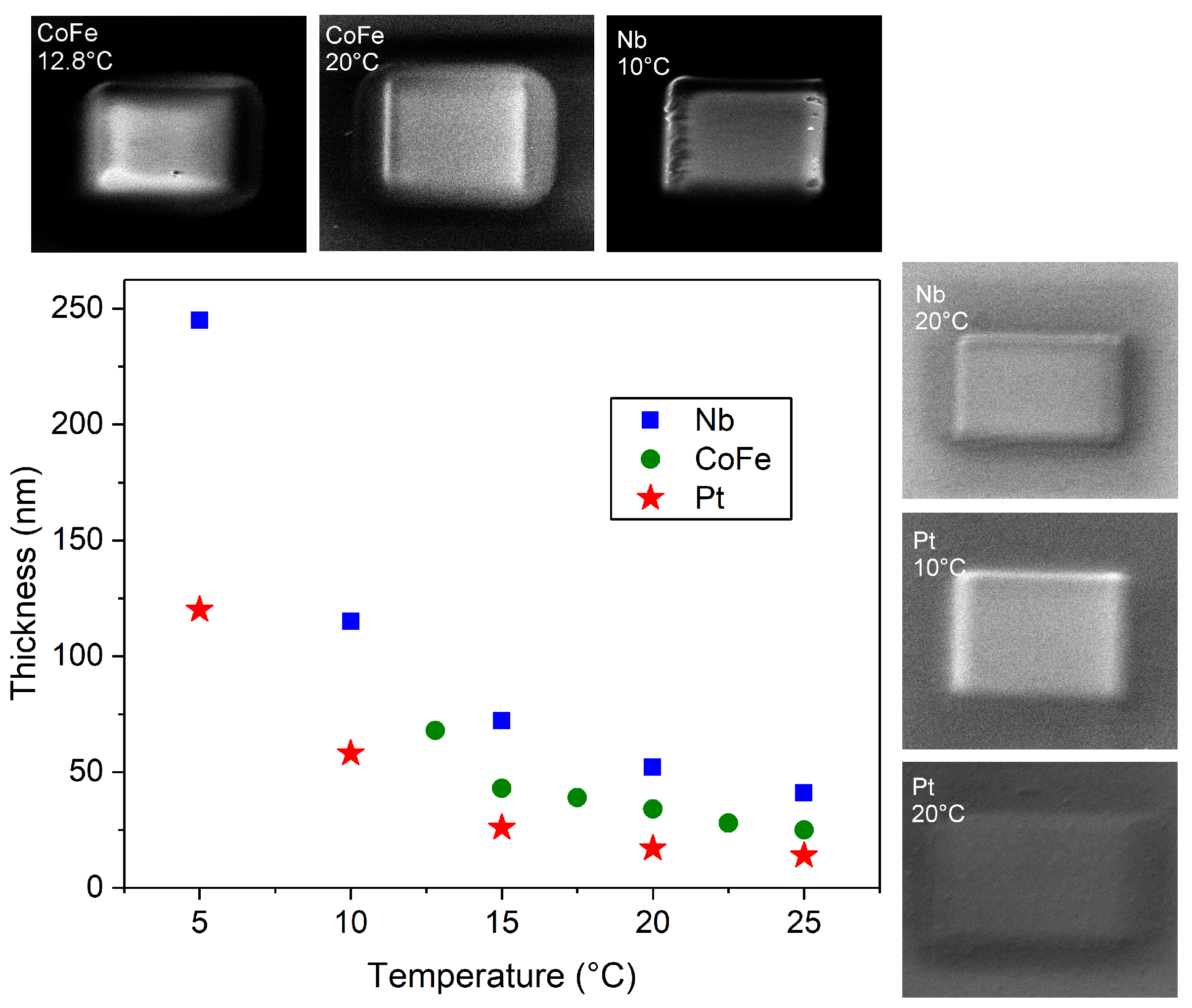
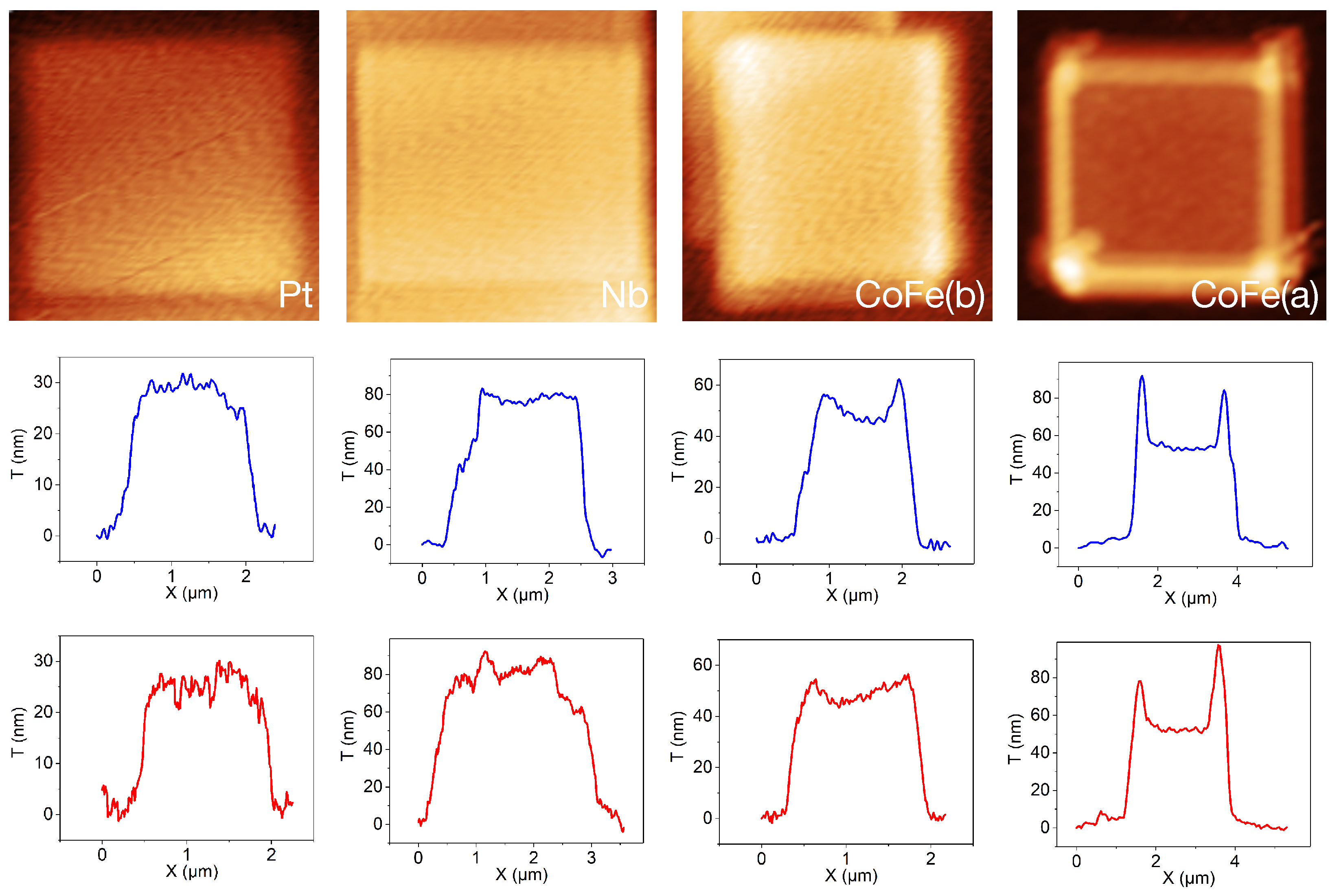
2.1. Fabrication, Height, and Composition Analysis
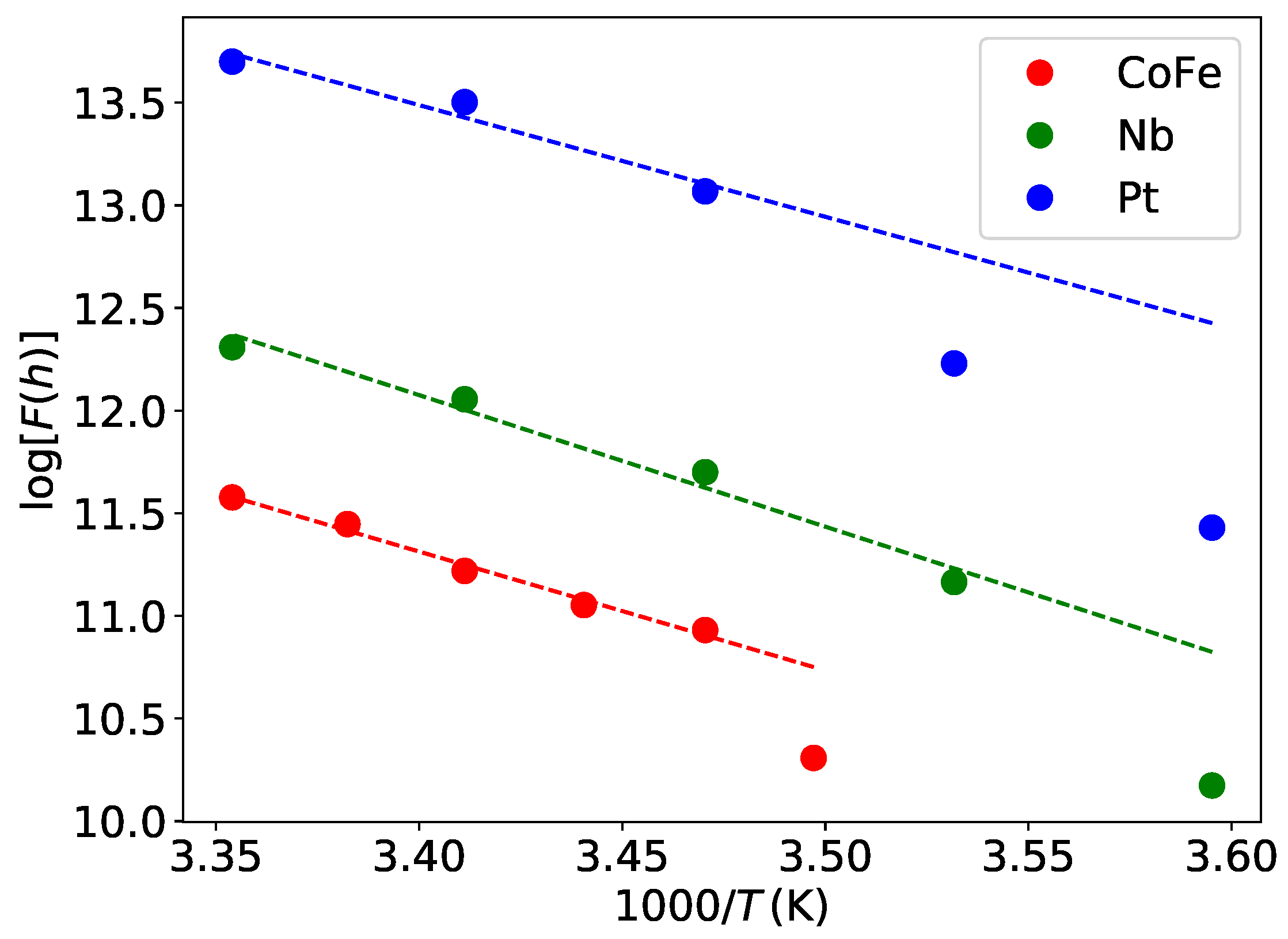
2.2. Analysis of Thermally-Induced Desorption
3. Discussion
4. Materials and Methods
4.1. Precursors
4.2. Fabrication and Height and Composition Analysis
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fernández-Pacheco, A.; Serrano-Ramón, L.; Michalik, J.M.; Ibarra, M.R.; De Teresa, J.M.; O’Brien, L.; Petit, D.; Lee, J.; Cowburn, R.P. Three dimensional magnetic nanowires grown by focused electron-beam induced deposition. Sci. Rep. 2013, 3, 1492. [Google Scholar] [CrossRef]
- Fernández-Pacheco, A.; Streubel, R.; Fruchart, O.; Hertel, R.; Fischer, P.; Cowburn, R.P. Three-dimensional nanomagnetism. Nat. Commun. 2017, 8, 15756. [Google Scholar] [CrossRef]
- Keller, L.; Al Mamoori, M.K.I.; Pieper, J.; Gspan, C.; Stockem, I.; Schröder, C.; Barth, S.; Winkler, R.; Plank, H.; Pohlit, M.; et al. Direct-write of free-form building blocks for artificial magnetic 3D lattices. Sci. Rep. 2018, 8, 6160. [Google Scholar] [CrossRef] [PubMed]
- Al Mamoori, M.; Keller, L.; Pieper, J.; Barth, S.; Winkler, R.; Plank, H.; Müller, J.; Huth, M. Magnetic Characterization of Direct-Write Free-Form Building Blocks for Artificial Magnetic 3D Lattices. Materials 2018, 11, 289. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Tasco, V.; Cuscunà, M.; Todisco, F.; Benedetti, A.; Tarantini, I.; Giorgi, M.D.; Sanvitto, D.; Passaseo, A. Nanoscale 3D Chiral Plasmonic Helices with Circular Dichroism at Visible Frequencies. ACS Photon. 2015, 2, 105–114. [Google Scholar] [CrossRef]
- Winkler, R.; Schmidt, F.P.; Haselmann, U.; Fowlkes, J.D.; Lewis, B.B.; Kothleitner, G.; Rack, P.D.; Plank, H. Direct-Write 3D Nanoprinting of Plasmonic Structures. ACS Appl. Mater. Interfaces 2017, 9, 8233–8240. [Google Scholar] [CrossRef] [PubMed]
- Porrati, F.; Barth, S.; Sachser, R.; Dobrovolskiy, O.V.; Seybert, A.; Frangakis, A.S.; Huth, M. Crystalline Niobium Carbide Superconducting Nanowires Prepared by Focused Ion Beam Direct Writing. ACS Nano 2019, 13, 6287–6296. [Google Scholar] [CrossRef] [PubMed]
- Córdoba, R.; Mailly, D.; Rezaev, R.O.; Smirnova, E.I.; Schmidt, O.G.; Fomin, V.M.; Zeitler, U.; Guillamón, I.; Suderow, H.; De Teresa, J.M. Three-Dimensional Superconducting Nanohelices Grown by He+-Focused-Ion-Beam Direct Writing. Nano Lett. 2019. [Google Scholar] [CrossRef]
- Huth, M.; Porrati, F.; Dobrovolskiy, O. Focused electron beam induced deposition meets materials science. Microelectron. Eng. 2018, 185–186, 9–28. [Google Scholar] [CrossRef]
- Skoric, L.; Sanz-Hernández, D.; Meng, F.; Donnelly, C.; Merino-Aceituno, S.; Fernández-Pacheco, A. Layer-by-layer growth of complex-shaped three-dimensional nanostructures with focused electron beams. arXiv 2019, arXiv:1908.10819. [Google Scholar] [CrossRef]
- Fowlkes, J.D.; Winkler, R.; Lewis, B.B.; Stanford, M.G.; Plank, H.; Rack, P.D. Simulation-Guided 3D Nanomanufacturing via Focused Electron Beam Induced Deposition. ACS Nano 2016, 10, 6163–6172. [Google Scholar] [CrossRef] [PubMed]
- Winkler, R.; Fowlkes, J.; Rack, P.; Plank, H. 3D nanoprinting via focused electron beams. J. Appl. Phys. 2019, 125, 210901. [Google Scholar] [CrossRef]
- Córdoba, R.; Sharma, N.; Kölling, S.; Koenraad, P.M.; Koopmans, B. High-purity 3D nano-objects grown by focused-electron-beam induced deposition. Nanotechnology 2016, 27, 355301. [Google Scholar] [CrossRef] [PubMed]
- Córdoba, R.; Ibarra, A.; Mailly, D.; De Teresa, J.M. Vertical Growth of Superconducting Crystalline Hollow Nanowires by He+ Focused Ion Beam Induced Deposition. Nano Lett. 2018, 18, 1379–1386. [Google Scholar] [CrossRef] [PubMed]
- Toth, M.; Lobo, C.; Friedli, V.; Szkudlarek, A.; Utke, I. Continuum models of focused electron beam induced processing. Beilstein J. Nanotechnol. 2015, 6, 1518–1540. [Google Scholar] [CrossRef] [PubMed]
- Porrati, F.; Pohlit, M.; Müller, J.; Barth, S.; Biegger, F.; Gspan, C.; Plank, H.; Huth, M. Direct writing of CoFe alloy nanostructures by focused electron beam induced deposition from a heteronuclear precursor. Nanotechnology 2015, 26, 475701. [Google Scholar] [CrossRef]
- Huth, M.; Porrati, F.; Schwalb, C.; Winhold, M.; Sachser, R.; Dukic, M.; Adams, J.; Fantner, G. Focused Electron Beam Induced Deposition: A Perspective. Beilstein J. Nanotechnol. 2012, 3, 597–619. [Google Scholar] [CrossRef]
- Utke, I.; Hoffmann, P.; Melngailis, J. Gas-Assisted Focused Electron Beam and Ion Beam Processing and Fabrication. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2008, 26, 1197–1276. [Google Scholar] [CrossRef]
- Friedli, V.; Utke, I. Optimized molecule supply from nozzle-based gas injection systems for focused electron- and ion-beam induced deposition and etching: simulation and experiment. J. Phys. D Appl. Phys. 2009, 42, 125305. [Google Scholar] [CrossRef]
- Cullen, J.; Bahm, A.; Lobo, C.J.; Ford, M.J.; Toth, M. Localized Probing of Gas Molecule Adsorption Energies and Desorption Attempt Frequencies. J. Phys. Chem. C 2015, 119, 15948–15953. [Google Scholar] [CrossRef]
- Engmann, S.; Stano, M.; Matejcik, S.; Ingólfsson, O. Gas phase low energy electron induced decomposition of the focused electron beam induced deposition (FEBID) precursor trimethyl (methylcyclopentadienyl) platinum(iv) (MeCpPtMe3). Phys. Chem. Chem. Phys. 2012, 14, 14611–14618. [Google Scholar] [CrossRef] [PubMed]
- Ragesh Kumar, R.K.; Bjornsson, R.; Barth, S.; Ingólfsson, O. Formation and decay of negative ion states up to 11 eV above the ionization energy of the nanofabrication precursor HFeCo3(CO)12. Chem. Sci. 2017, 8, 5949–5952. [Google Scholar] [CrossRef]
- Thorman, R.M.; Ragesh Kumar, T.P.; Fairbrother, D.H.; Ingólfsson, O. The role of low-energy electrons in focused electron beam induced deposition: four case studies of representative precursors. Beilstein J. Nanotechnol. 2015, 6, 1904–1926. [Google Scholar] [CrossRef] [PubMed]
- Cullen, J.; Lobo, C.J.; Ford, M.J.; Toth, M. Electron-Beam-Induced Deposition as a Technique for Analysis of Precursor Molecule Diffusion Barriers and Prefactors. ACS Appl. Mater. Interfaces 2015, 7, 21408–21415. [Google Scholar] [CrossRef] [PubMed]
- Mutunga, E.; Winkler, R.; Sattelkow, J.; Rack, P.D.; Plank, H.; Fowlkes, J.D. Impact of Electron-Beam Heating during 3D Nanoprinting. ACS Nano 2019, 13, 5198–5213. [Google Scholar] [CrossRef]
- Chini, P.; Colli, L.; Peraldo, M. Preparazione e proprieta’ dell’idrocarbonile HFeCo3(CO)12 e di alcuni composti derivati dall’Anione [FeCo3(CO)12]. Gazz. Chim. Ital. 1960, 90, 1005–1020. [Google Scholar]
- Baunemann, A.; Bekermann, D.; Thiede, T.B.; Parala, H.; Winter, M.; Gemel, C.; Fischer, R.A. Mixed Amido/Imido/Guanidinato Complexes of Niobium: Potential Precursors for MOCVD of Niobium Nitride Thin Films. Dalton Trans. 2008, 3715–3722. [Google Scholar] [CrossRef]
| Precursor | d (nm) | (nm) | (nms) | (nm) | V (nm) |
|---|---|---|---|---|---|
| HCoFe(CO) | 0.83 | 1.85 | 0.011 | 0.05 | |
| Nb(NMe)(N-t-Bu) | 0.77 | 2.15 | 0.015 | 0.13 | |
| MeCpMePt | 0.78 | 2.09 | 0.022 | 0.2 |
| Precursor | (eV) | (s) |
|---|---|---|
| HCoFe(CO) | 0.50 | |
| Nb(NMe)(N-t-Bu) | 0.55 | |
| MeCpMePt | 0.47 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huth, M.; Porrati, F.; Gruszka, P.; Barth, S. Temperature-Dependent Growth Characteristics of Nb- and CoFe-Based Nanostructures by Direct-Write Using Focused Electron Beam-Induced Deposition. Micromachines 2020, 11, 28. https://doi.org/10.3390/mi11010028
Huth M, Porrati F, Gruszka P, Barth S. Temperature-Dependent Growth Characteristics of Nb- and CoFe-Based Nanostructures by Direct-Write Using Focused Electron Beam-Induced Deposition. Micromachines. 2020; 11(1):28. https://doi.org/10.3390/mi11010028
Chicago/Turabian StyleHuth, Michael, Fabrizio Porrati, Peter Gruszka, and Sven Barth. 2020. "Temperature-Dependent Growth Characteristics of Nb- and CoFe-Based Nanostructures by Direct-Write Using Focused Electron Beam-Induced Deposition" Micromachines 11, no. 1: 28. https://doi.org/10.3390/mi11010028
APA StyleHuth, M., Porrati, F., Gruszka, P., & Barth, S. (2020). Temperature-Dependent Growth Characteristics of Nb- and CoFe-Based Nanostructures by Direct-Write Using Focused Electron Beam-Induced Deposition. Micromachines, 11(1), 28. https://doi.org/10.3390/mi11010028






