Analysis and Optimization of a Microchannel Heat Sink with V-Ribs Using Nanofluids for Micro Solar Cells
Abstract
1. Introduction
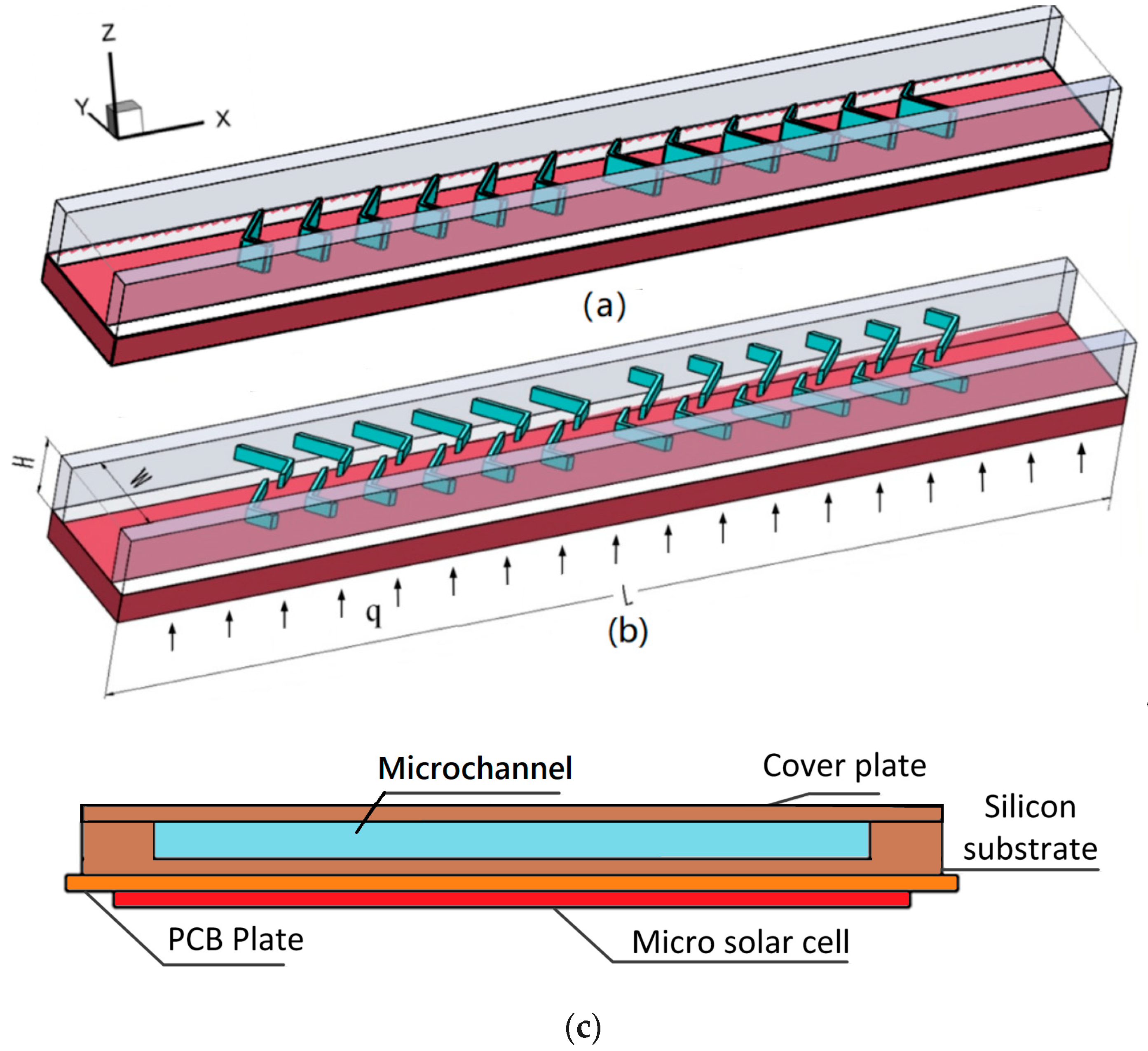
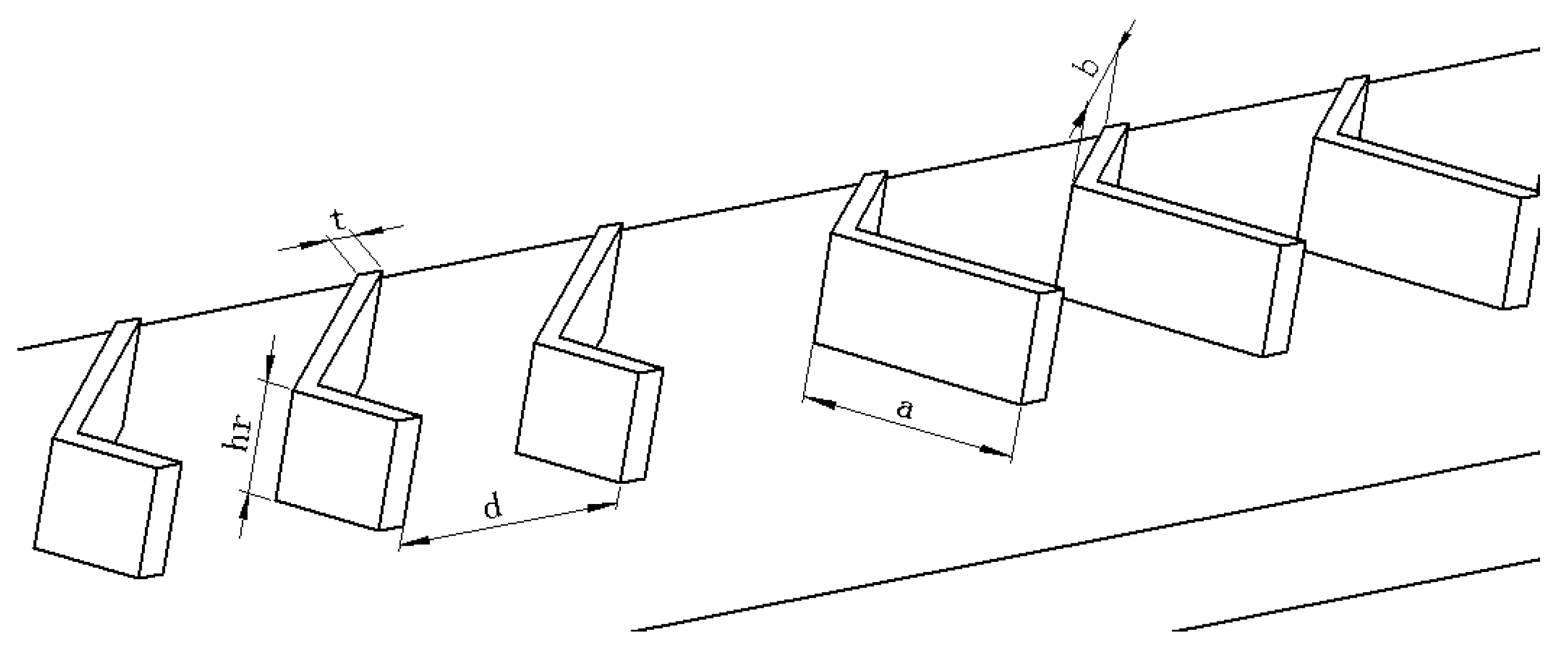
2. Geometrical Model
3. Numerical Analysis
3.1. Numerical Model
3.2. Parameter Settings
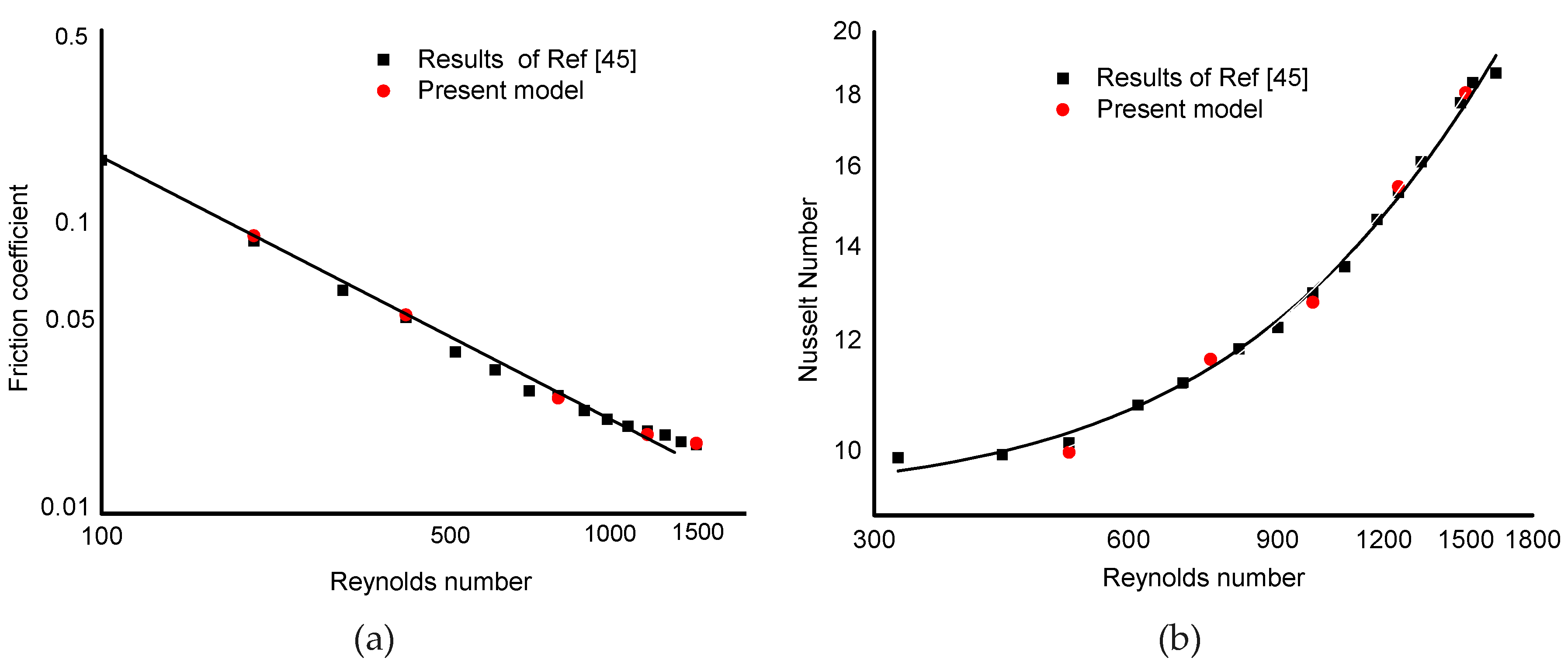
3.3. Validity of the Numerical Model
4. Results and Discussion
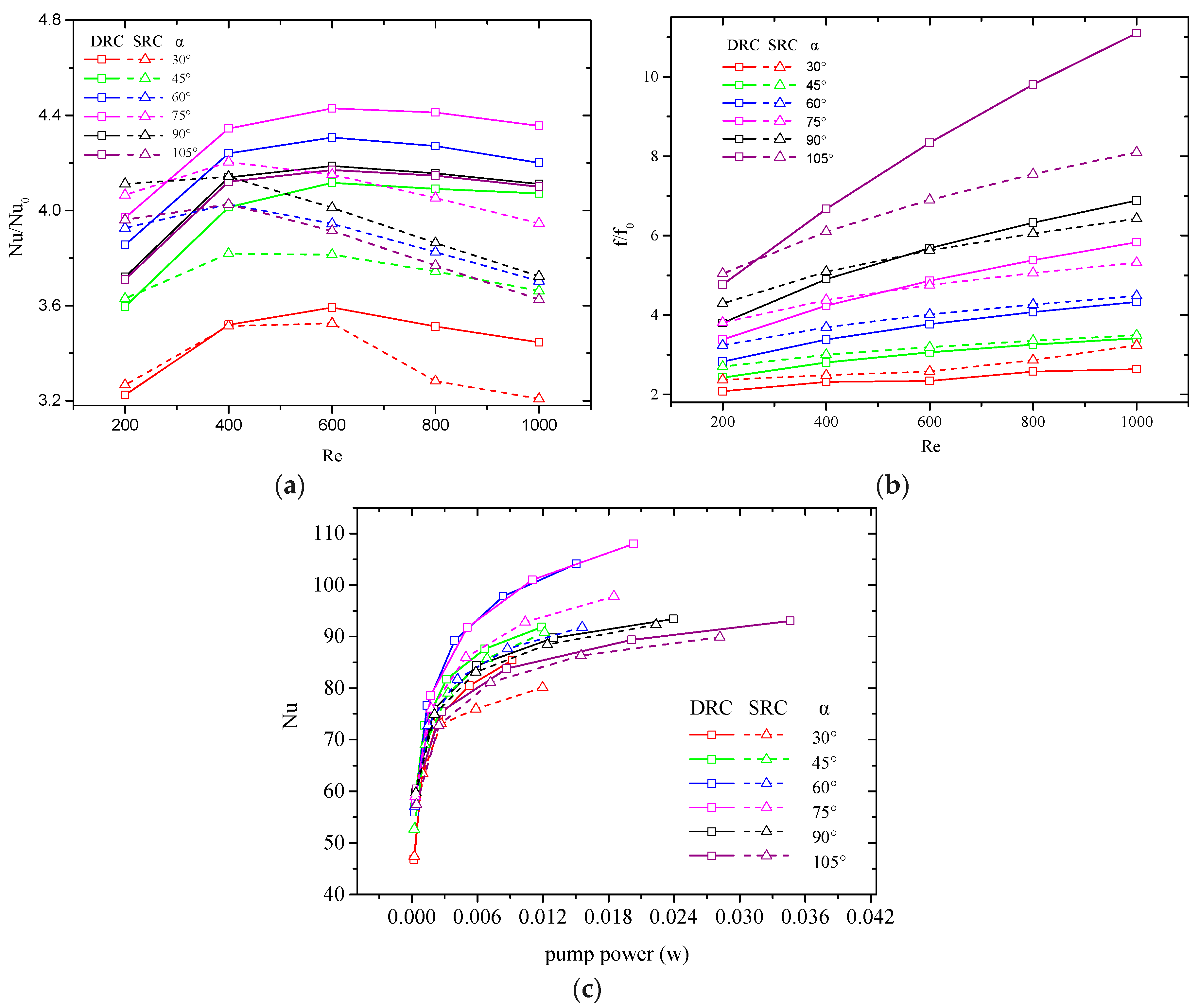
4.1. Definition of Relevant Parameters
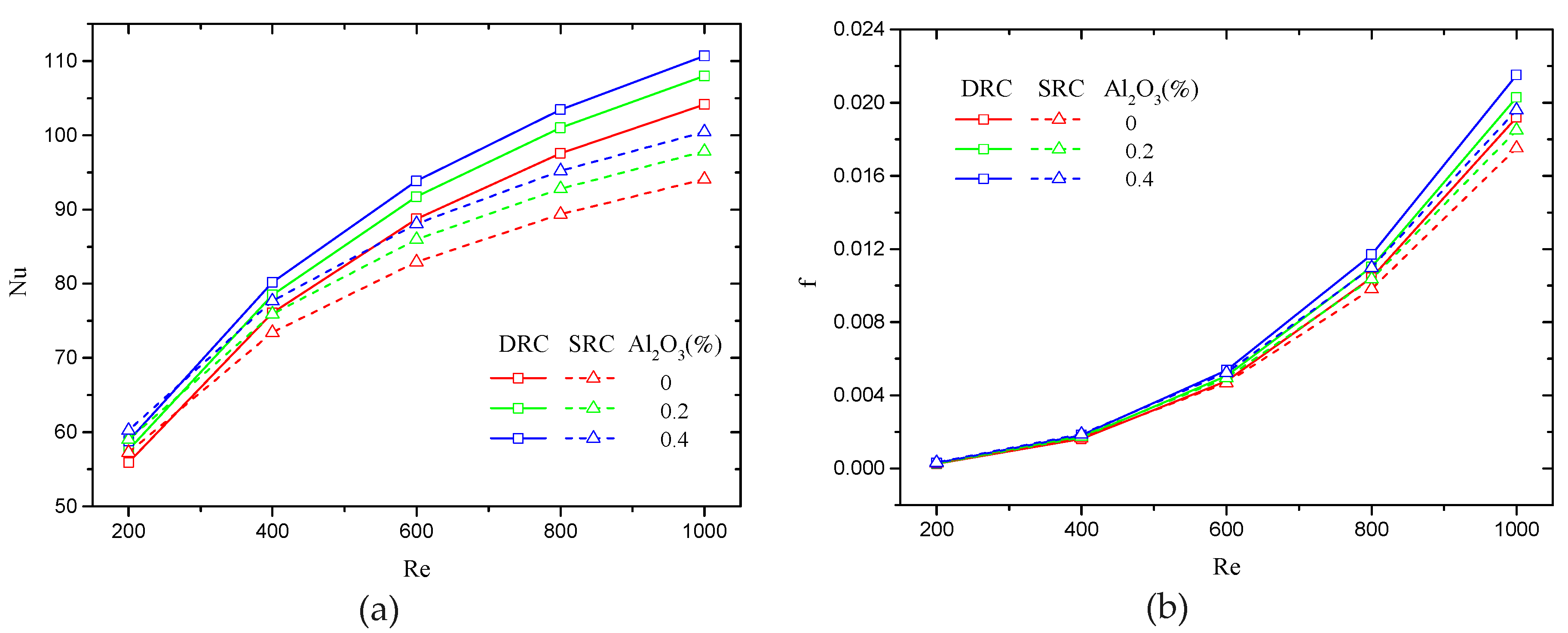
4.2. Effect of Volume Fraction of Nanoparticles
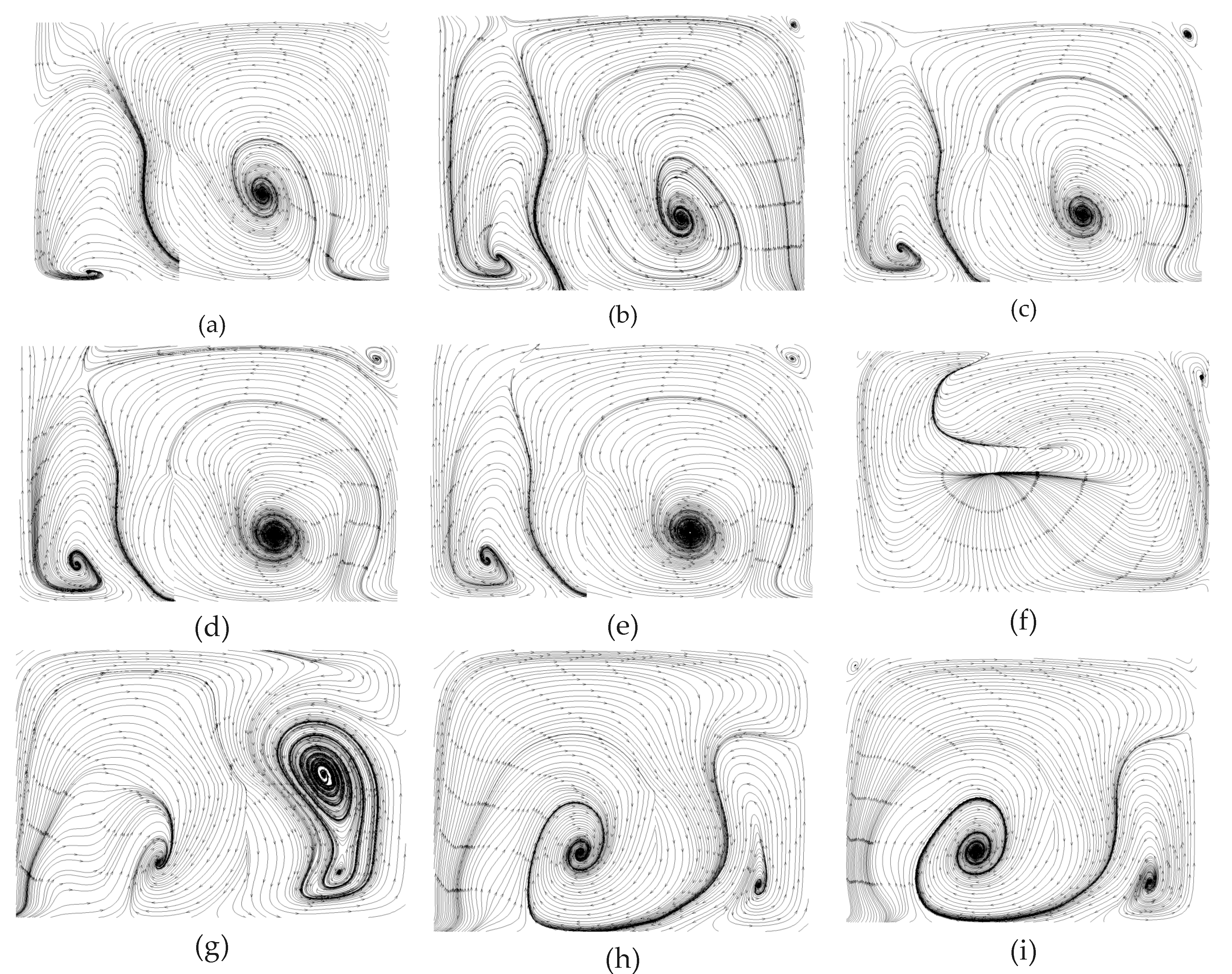
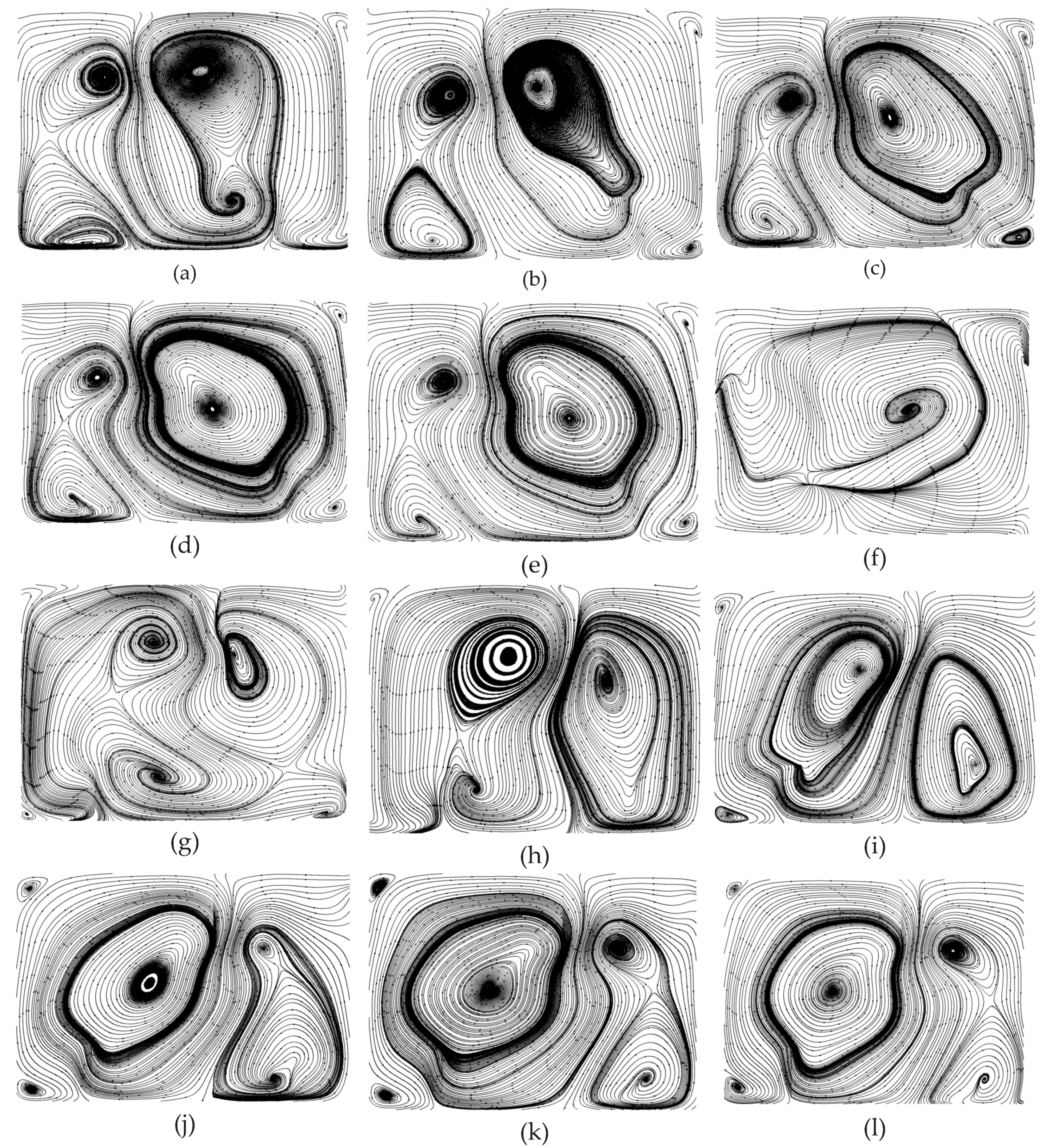
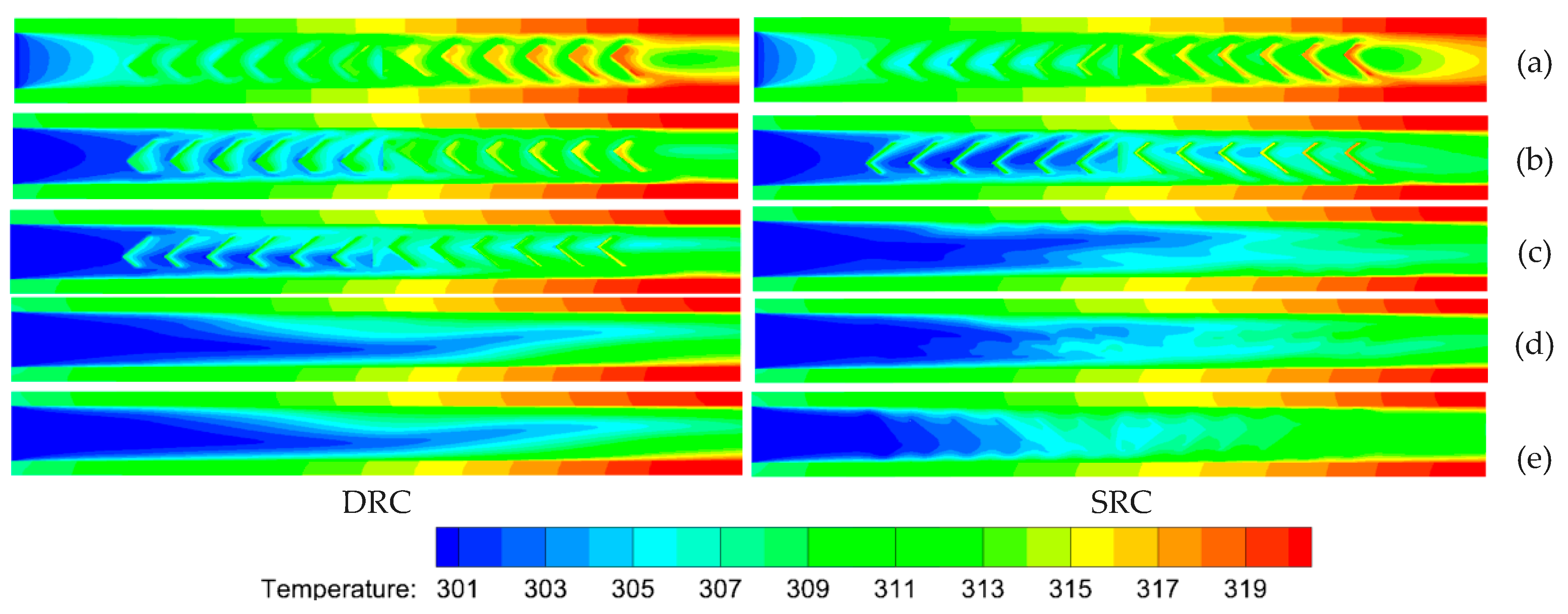
4.3. Overall Flow Patterns in a Microchannel
4.4. Overall Flow Patterns in Microchannel
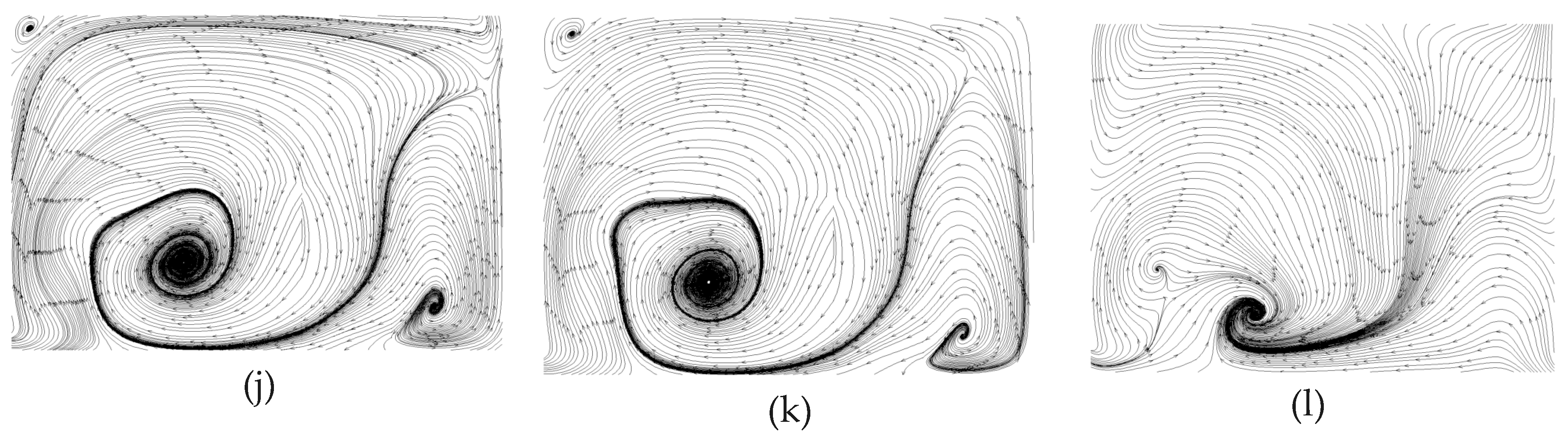
4.5. Planar Flow Patterns in the DRC
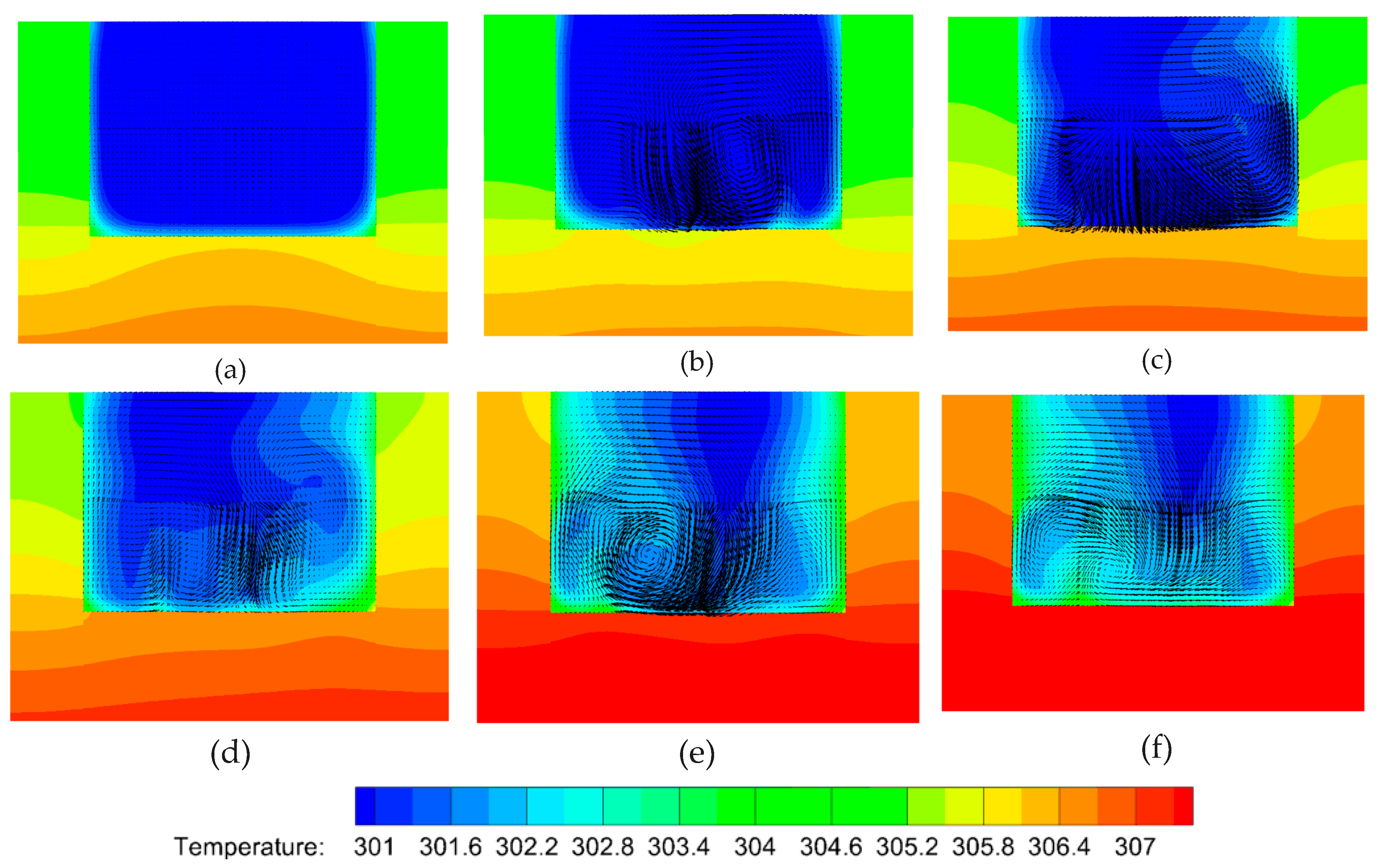
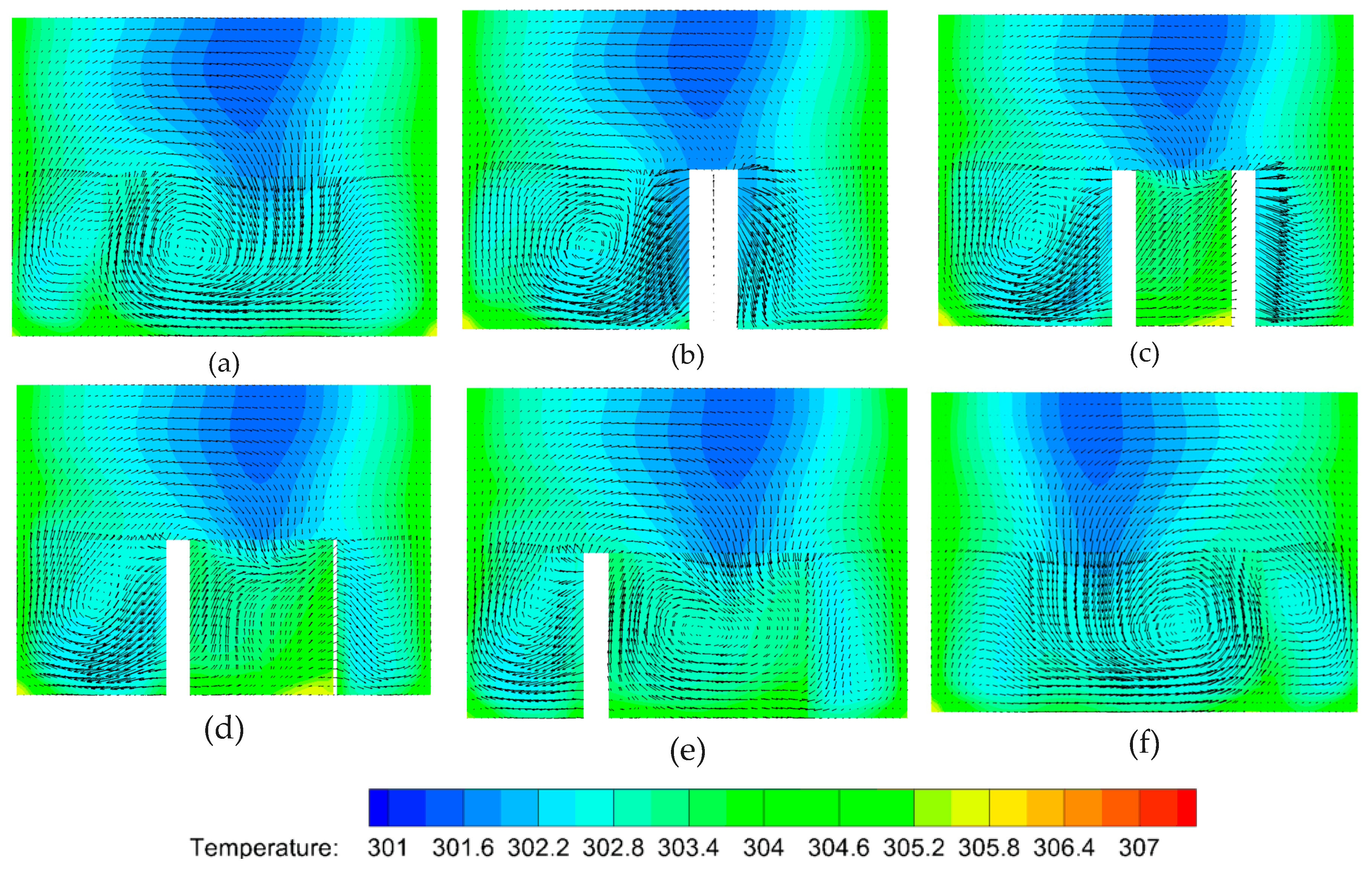
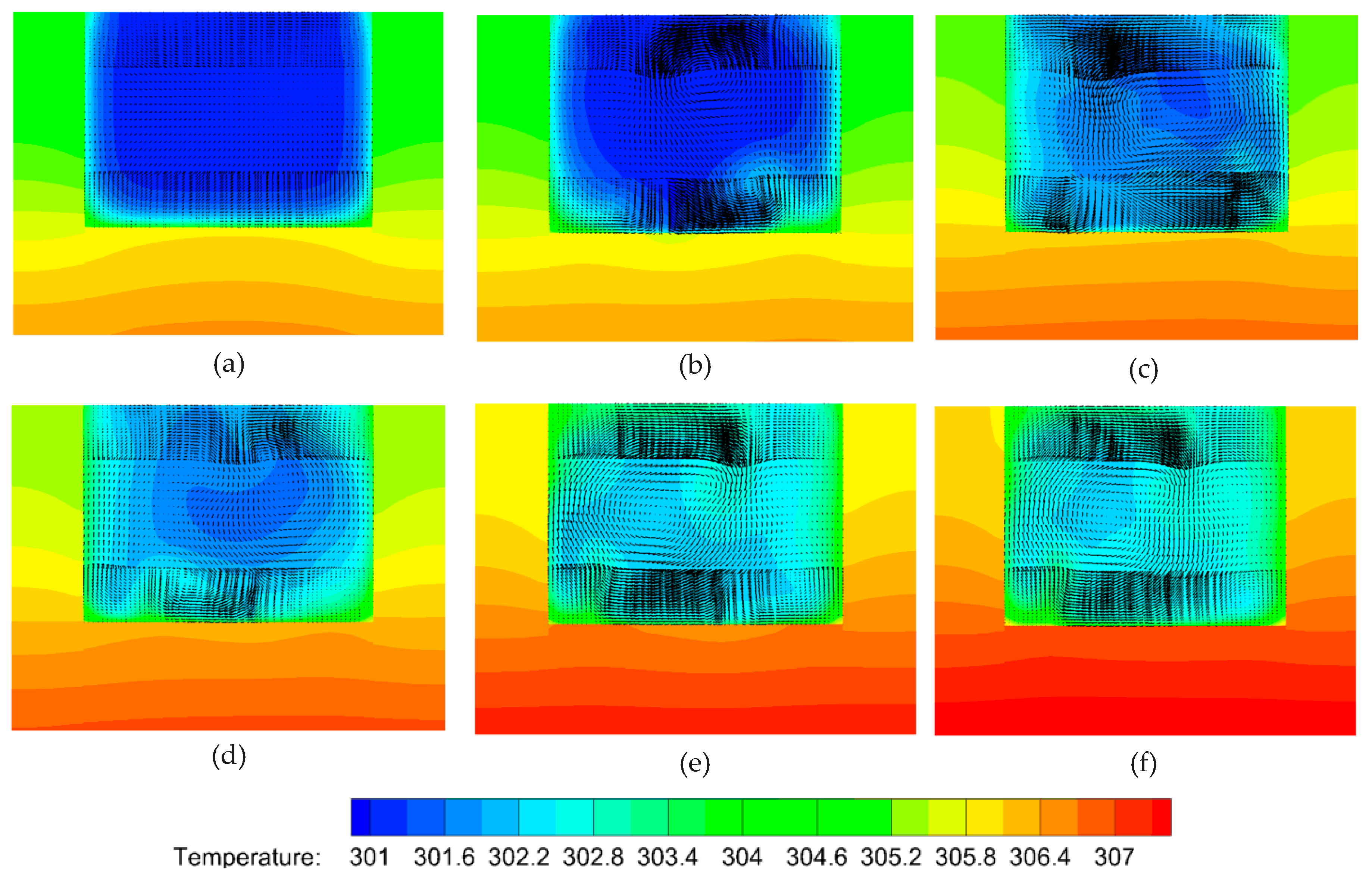
4.6. Comparison of Temperature at Various Heights
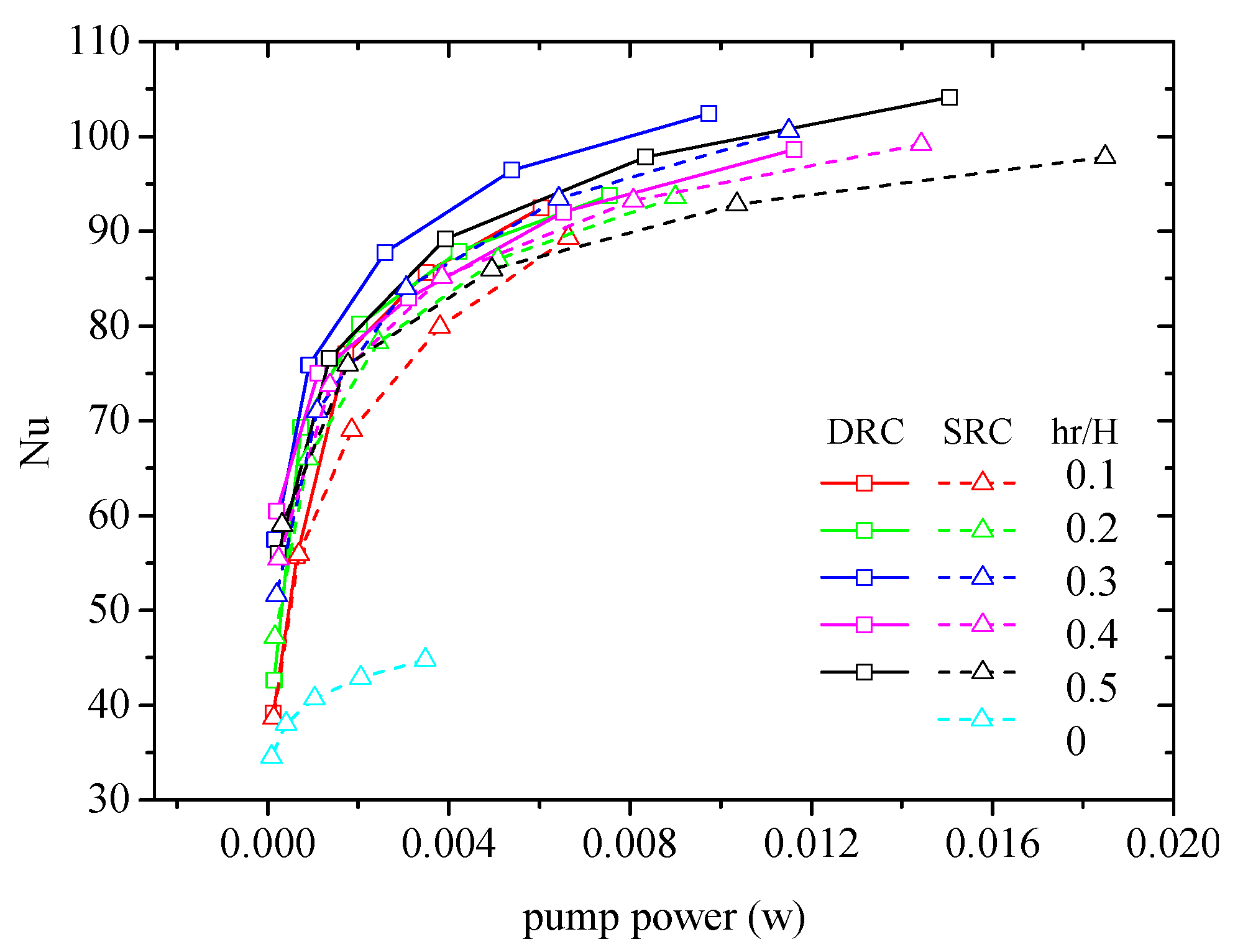
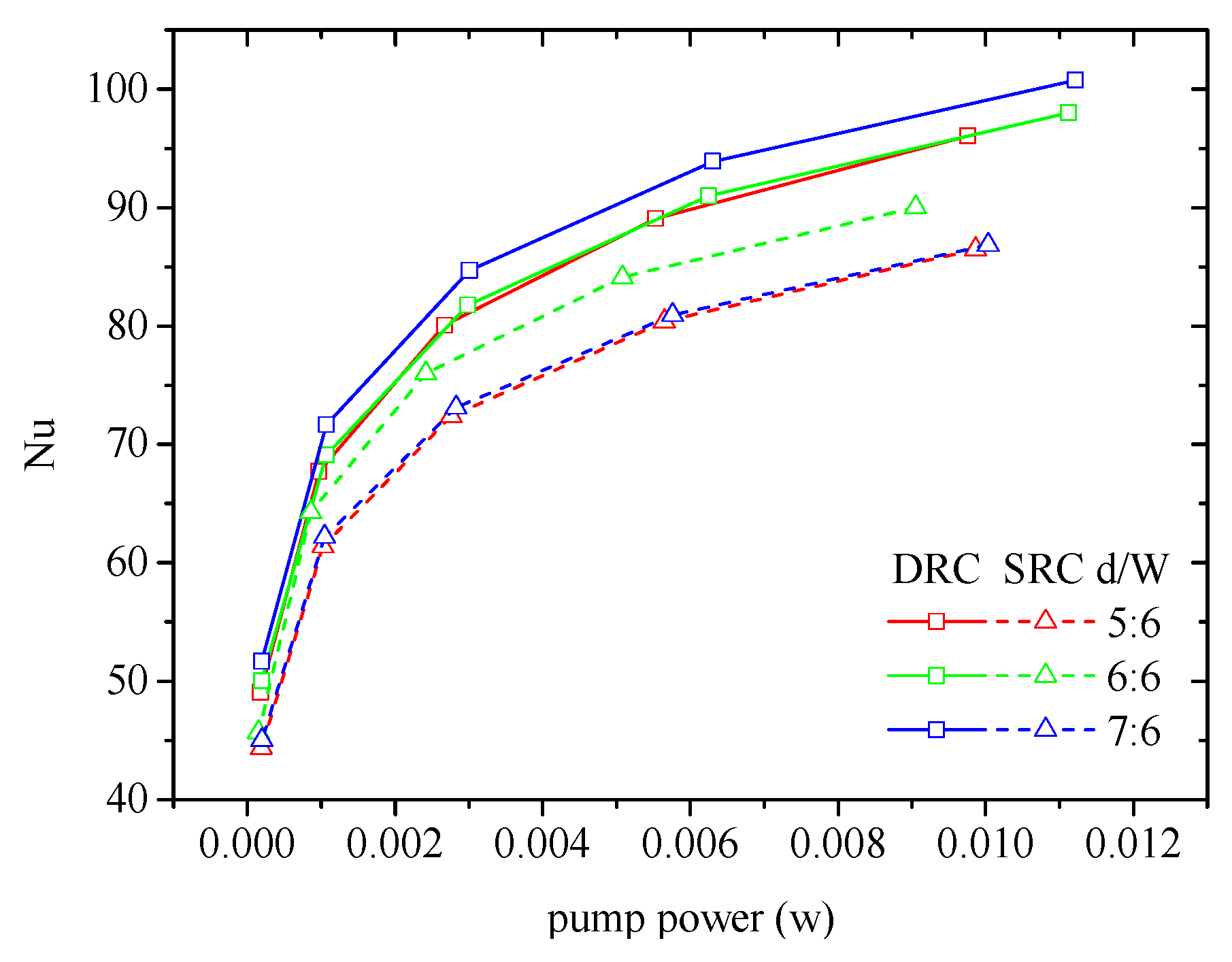
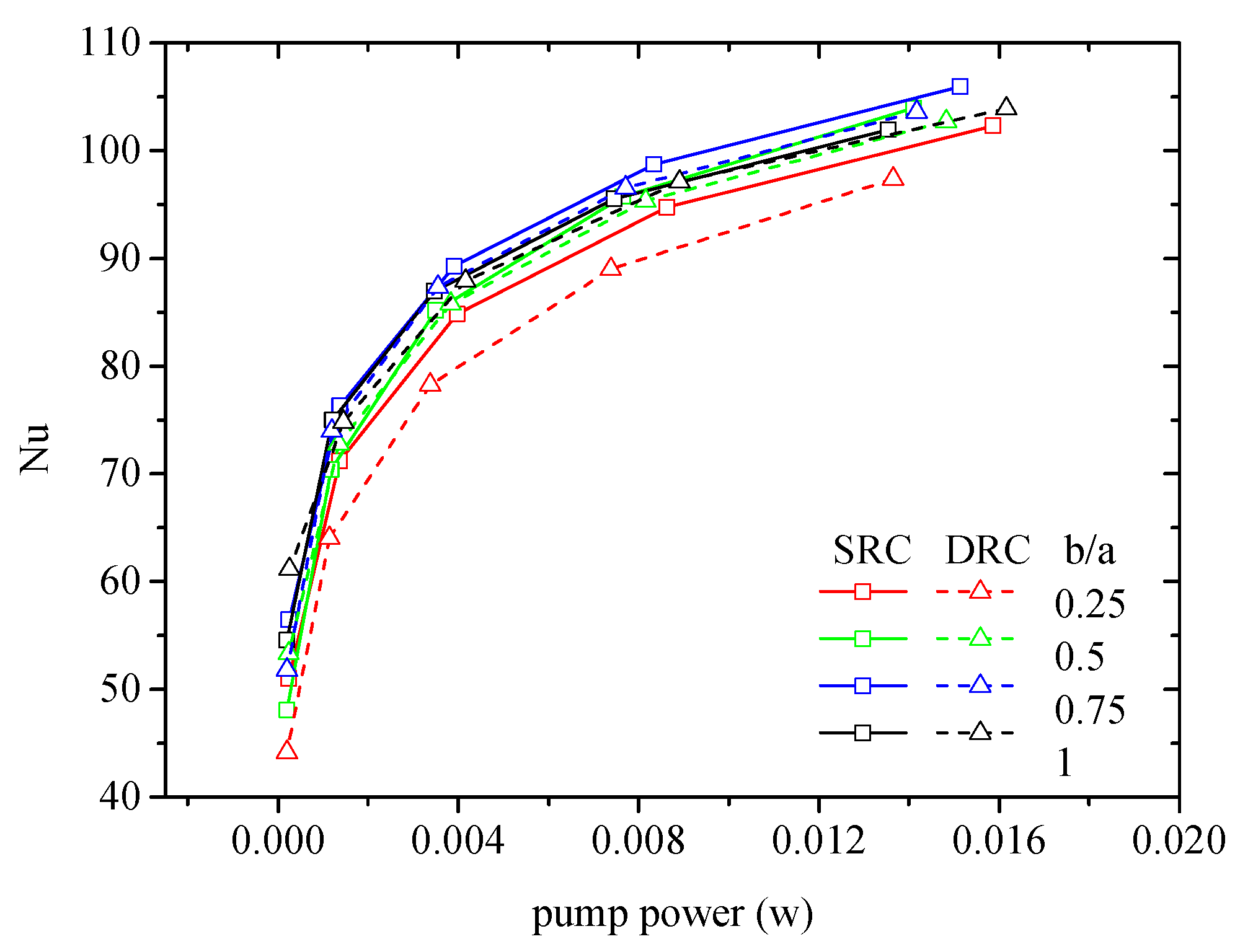
4.7. Parameterized Study of V-ribs
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sathe, T.M.; Dhoble, A. A review on recent advancements in photovoltaic thermal techniques. Renew. Sustain. Energy Rev. 2017, 76, 645–672. [Google Scholar] [CrossRef]
- Modjinou, M.; Ji, J.; Li, J.; Yuan, W.; Zhou, F. A numerical and experimental study of micro-channel heat pipe solar photovoltaics thermal system. Appl. Energy 2017, 206, 708–722. [Google Scholar] [CrossRef]
- Moharram, K.; Abd-Elhady, M.; Kandil, H.; El-Sherif, H.; Kandil, H. Enhancing the performance of photovoltaic panels by water cooling. Ain Shams Eng. J. 2013, 4, 869–877. [Google Scholar] [CrossRef]
- Bahaidarah, H.M.; Baloch, A.A.; Gandhidasan, P. Uniform cooling of photovoltaic panels: A review. Renew. Sustain. Energy Rev. 2016, 57, 1520–1544. [Google Scholar] [CrossRef]
- Rahimi, M.; Karimi, E.; Asadi, M.; Valeh-E-Sheyda, P. Heat transfer augmentation in a hybrid microchannel solar cell. Int. Commun. Heat Mass Transf. 2013, 43, 131–137. [Google Scholar] [CrossRef]
- Barrau, J.; Rosell, J.; Chemisana, D.; Tadrist, L.; Ibáñez, M. Effect of a hybrid jet impingement/micro-channel cooling device on the performance of densely packed PV cells under high concentration. Sol. Energy 2011, 85, 2655–2665. [Google Scholar] [CrossRef]
- Do, K.H.; Kim, T.H.; Han, Y.-S.; Choi, B.-I.; Kim, M.-B. General correlation of a natural convective heat sink with plate-fins for high concentrating photovoltaic module cooling. Sol. Energy 2012, 86, 2725–2734. [Google Scholar] [CrossRef]
- Radwan, A.; Ahmed, M.; Ookawara, S. Performance enhancement of concentrated photovoltaic systems using a microchannel heat sink with nanofluids. Energy Convers. Manag. 2016, 119, 289–303. [Google Scholar] [CrossRef]
- Wang, R.; Wang, W.; Wang, J.; Zhu, Z. Analysis and Optimization of Trapezoidal Grooved Microchannel Heat Sink Using Nanofluids in a Micro Solar Cell. Entropy 2017, 20, 9. [Google Scholar] [CrossRef]
- Tuckerman, D.; Pease, R. High-performance heat sinking for VLSI. IEEE Electron Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Z.; Gao, J. Influence of geometric parameters on flow and heat transfer performance of micro-channel heat sinks. Appl. Therm. Eng. 2016, 107, 870–879. [Google Scholar] [CrossRef]
- Gunnasegaran, P.; Mohammed, H.; Shuaib, N.; Saidur, R. The effect of geometrical parameters on heat transfer characteristics of microchannels heat sink with different shapes. Int. Commun. Heat Mass Transf. 2010, 37, 1078–1086. [Google Scholar] [CrossRef]
- Dehghan, M.; Daneshipour, M.; Valipour, M.S.; Rafee, R.; Saedodin, S. Enhancing heat transfer in microchannel heat sinks using converging flow passages. Energy Convers. Manag. 2015, 92, 244–250. [Google Scholar] [CrossRef]
- Xie, G.; Zhang, F.; Sundén, B.; Zhang, W. Constructal design and thermal analysis of microchannel heat sinks with multistage bifurcations in single-phase liquid flow. Appl. Therm. Eng. 2014, 62, 791–802. [Google Scholar] [CrossRef]
- Leng, C.; Wang, X.-D.; Wang, T.-H. An improved design of double-layered microchannel heat sink with truncated top channels. Appl. Therm. Eng. 2015, 79, 54–62. [Google Scholar] [CrossRef]
- Sarlak, A.; Ahmadpour, A.; Hajmohammadi, M.R. Thermal design improvement of a double-layered microchannel heat sink by using multi-walled carbon nanotube nanofluids with non-Newtonian viscosity. Appl. Therm. Eng. 2018, 147, 205–215. [Google Scholar] [CrossRef]
- Ansari, D.; Kim, K.-Y. Performance Analysis of Double-Layer Microchannel Heat Sinks under Non-Uniform Heating Conditions with Random Hotspots. Micromachines 2017, 8, 54. [Google Scholar] [CrossRef]
- Abdollahi, A.; Sharma, R.N.; Mohammed, H.A.; Vatani, A. Heat transfer and flow analysis of Al2O3-Water nanofluids in interrupted microchannel heat sink with ellipse and diamond ribs in the transverse microchambers. Heat Transf. Eng. 2018, 39, 1461–1469. [Google Scholar] [CrossRef]
- Chai, L.; Wang, L. Thermal-hydraulic performance of interrupted microchannel heat sinks with different rib geometries in transverse microchambers. Int. J. Therm. Sci. 2018, 127, 201–212. [Google Scholar] [CrossRef]
- Sidik, N.A.C.; Muhamad, M.N.A.W.; Japar, W.M.A.A.; Rasid, Z.A. An overview of passive techniques for heat transfer augmentation in microchannel heat sink. Int. Commun. Heat Mass Transf. 2017, 88, 74–83. [Google Scholar] [CrossRef]
- Wang, R.J.; Wang, J.W.; Lijin, B.Q.; Zhu, Z.F. Parameterization Investigation on the Micro- channel Heat Sink with Slant Rectangular Ribs by numerical simulation. Appl. Therm. Eng. 2018, 133, 428–438. [Google Scholar] [CrossRef]
- Behnampour, A.; Akbari, O.A.; Safaei, M.R.; Ghavami, M.; Marzban, A.; Shabani, G.A.S.; Zarringhalam, M.; Mashayekhi, R. Analysis of heat transfer and nanofluid fluid flow in microchannels with trapezoidal, rectangular and triangular shaped ribs. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 91, 15–31. [Google Scholar] [CrossRef]
- Chai, L.; Xia, G.D.; Wang, H.S. Numerical study of laminar flow and heat transfer in microchannel heat sink with offset ribs on sidewalls. Appl. Therm. Eng. 2016, 92, 32–41. [Google Scholar] [CrossRef]
- Li, P.; Zhang, D.; Xie, Y.; Xie, G. Flow structure and heat transfer of non-Newtonian fluids in microchannel heat sinks with dimples and protrusions. Appl. Therm. Eng. 2016, 94, 50–58. [Google Scholar] [CrossRef]
- Duangthongsuk, W.; Wongwises, S. A comparison of the thermal and hydraulic performances between miniature pin fin heat sink and microchannel heat sink with zigzag flow channel together with using nanofluids. Heat Mass Transf. 2018, 54, 3265–3274. [Google Scholar] [CrossRef]
- Wang, S.-L.; Li, X.-Y.; Wang, X.-D.; Lu, G. Flow and heat transfer characteristics in double-layered microchannel heat sinks with porous fins. Int. Commun. Heat Mass Transf. 2018, 93, 41–47. [Google Scholar] [CrossRef]
- Toghraie, D.; Mahmoudi, M.; Akbari, O.A.; Pourfattah, F.; Heydari, M. The effect of using water/CuO nanofluid and L-shaped porous ribs on the performance evaluation criterion of microchannels. J. Therm. Anal. Calorim. 2019, 135, 145–159. [Google Scholar] [CrossRef]
- Akbari, O.A.; Toghraie, D.; Karimipour, A. Numerical simulation of heat transfer and turbulent flow of water nanofluids copper oxide in rectangular microchannel with semi- attached rib. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef]
- Wang, G.; Qian, N.; Ding, G. Heat transfer enhancement in microchannel heat sink with bidirectional rib. Int. J. Heat Mass Transf. 2019, 136, 597–609. [Google Scholar] [CrossRef]
- Ghani, I.A.; Kamaruzaman, N.; Sidik, N.A.C. Heat transfer augmentation in a microchannel heat sink with sinusoidal cavities and rectangular ribs. Int. J. Heat Mass Transf. 2017, 108, 1969–1981. [Google Scholar] [CrossRef]
- Lu, G.; Zhao, J.; Lin, L.; Wang, X.D.; Yan, W.M. A new scheme for reducing pressure drop and thermal resistance simultaneously in microchannel heat sinks with wavy porous fins. Int. J. Heat Mass Transf. 2017, 111, 1071–1078. [Google Scholar] [CrossRef]
- Vinoth, R.; Kumar, D.S. Experimental investigation on heat transfer characteristics of an oblique finned microchannel heat sink with different channel cross sections. Heat Mass Transf. 2018, 54, 3809–3817. [Google Scholar] [CrossRef]
- Ghani, I.A.; Sidik, N.A.C.; Kamaruzaman, N. Hydrothermal performance of microchannel heat sink: The effect of channel design. Int. J. Heat Mass Transf. 2017, 107, 21–44. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective Transport in Nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Li, P.; Zhang, J. Simulating Heat Transfer through Periodic Structures with Different Wall Temperatures: A Temperature Decomposition Method. J. Heat Transf. 2018, 140, 112002. [Google Scholar] [CrossRef]
- Minea, A.A. Uncertainties in modeling thermal conductivity of laminar forced convection heat transfer with water alumina nanofluids. Int. J. Heat Mass Transf. 2014, 68, 78–84. [Google Scholar] [CrossRef]
- Guo, W.W.; Li, G.N.; Zheng, Y.Q. Numerical study of nanofluids thermal and hydraulic characteristics considering Brownian motion effect in micro fin heat sink. J. Mol. Liq. 2018, 264, 38–47. [Google Scholar] [CrossRef]
- Fani, B.; Abbassi, A.; Kalteh, M. Effect of nanoparticles size on thermal performance of nanofluid in a trapezoidal microchannel-heat-sink. Int. Commun. Heat Mass Transf. 2013, 45, 155–161. [Google Scholar] [CrossRef]
- Stroock, A.D.; Dertinger, S.K.W.; Ajdari, A. Chaotic mixer for microchannels. Science 2002, 295, 647–651. [Google Scholar] [CrossRef] [PubMed]
- Brinkman, H.C. The Viscosity of Concentrated Suspensions and Solutions. J. Chem. Phys. 2004, 20, 571. [Google Scholar] [CrossRef]
- Einstein, A. An Investigation on the Theory of Brownian Movement. James Joyce Q. 1956, 35, 155–158. [Google Scholar]
- Chon, C.H.; Kihm, K.D.; Lee, S.P. Empirical correlation finding the role of temperature and particle size for nanofluid (Al2O3), thermal conductivity enhancement. Appl. Phys. Lett. 2005, 87, 153107. [Google Scholar] [CrossRef]
- Knight, R.W.; Hall, D.J.; Goodling, J.S. Heat sink optimization with application to microchannels. IEEE Trans. Compon. Hybrids Manuf. Technol. 1992, 15, 832–842. [Google Scholar] [CrossRef]
- Rosa, P.; Karayiannis, T.; Collins, M. Single-phase heat transfer in microchannels: The importance of scaling effects. Appl. Therm. Eng. 2009, 29, 3447–3468. [Google Scholar] [CrossRef]
- Ho, C.J.; Wei, L.; Li, Z. An experimental investigation of forced convective cooling performance of a microchannel heat sink with Al2O3/water nanofluid. Appl. Therm. Eng. 2010, 30, 96–103. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Gunnasegaran, P.; Shuaib, N.H. Heat transfer in rectangular microchannels heat sink using nanofluids. Int. Commun. Heat Mass Transf. 2010, 37, 1496–1503. [Google Scholar] [CrossRef]
- Stephen, W.; Julio, M.O. Foundations of chaotic mixing. Philos. Trans. R. Soc. Lond. A 2004, 362, 937–970. [Google Scholar]


| Ratio of Side a/b | Flare Angle α (°) | Rib Height hr/H | Rib Thickness t/W | Rib Pitch d/W |
|---|---|---|---|---|
| 0.25–1 | 30–75 | 0.1–0.5 | 0.1 | 5/6–7/6 |
| Parameters | |||
|---|---|---|---|
| Water | 998.2 | 0.6 | 4182 |
| Al2O3 | 3970 | 42 | 880 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Wang, J.; Yuan, W. Analysis and Optimization of a Microchannel Heat Sink with V-Ribs Using Nanofluids for Micro Solar Cells. Micromachines 2019, 10, 620. https://doi.org/10.3390/mi10090620
Wang R, Wang J, Yuan W. Analysis and Optimization of a Microchannel Heat Sink with V-Ribs Using Nanofluids for Micro Solar Cells. Micromachines. 2019; 10(9):620. https://doi.org/10.3390/mi10090620
Chicago/Turabian StyleWang, Ruijin, Jiawei Wang, and Weijia Yuan. 2019. "Analysis and Optimization of a Microchannel Heat Sink with V-Ribs Using Nanofluids for Micro Solar Cells" Micromachines 10, no. 9: 620. https://doi.org/10.3390/mi10090620
APA StyleWang, R., Wang, J., & Yuan, W. (2019). Analysis and Optimization of a Microchannel Heat Sink with V-Ribs Using Nanofluids for Micro Solar Cells. Micromachines, 10(9), 620. https://doi.org/10.3390/mi10090620






