A Gas Mixture Prediction Model Based on the Dynamic Response of a Metal-Oxide Sensor
Abstract
1. Introduction
2. Experiment and Method
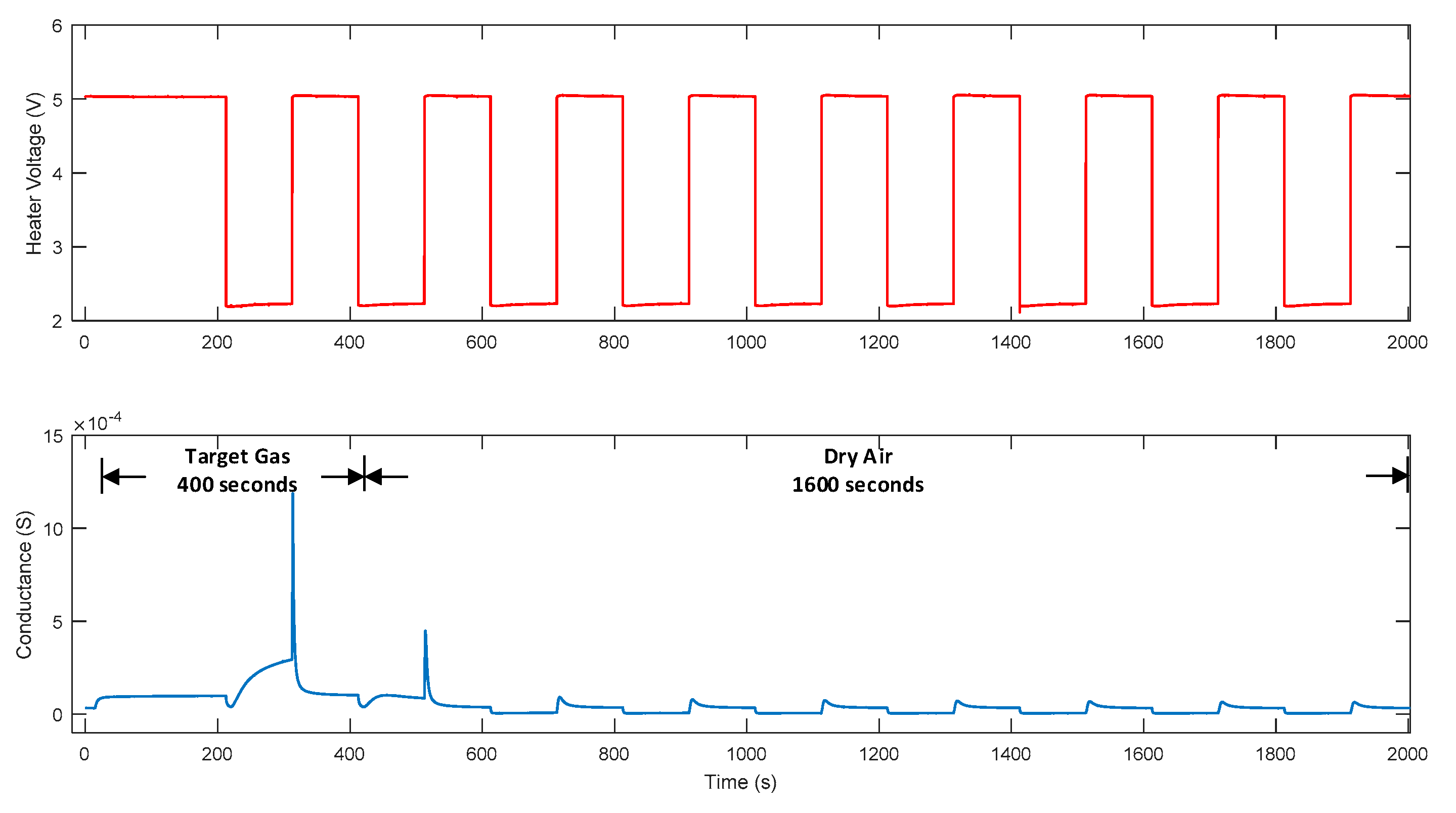
2.1. Temperature Modulation
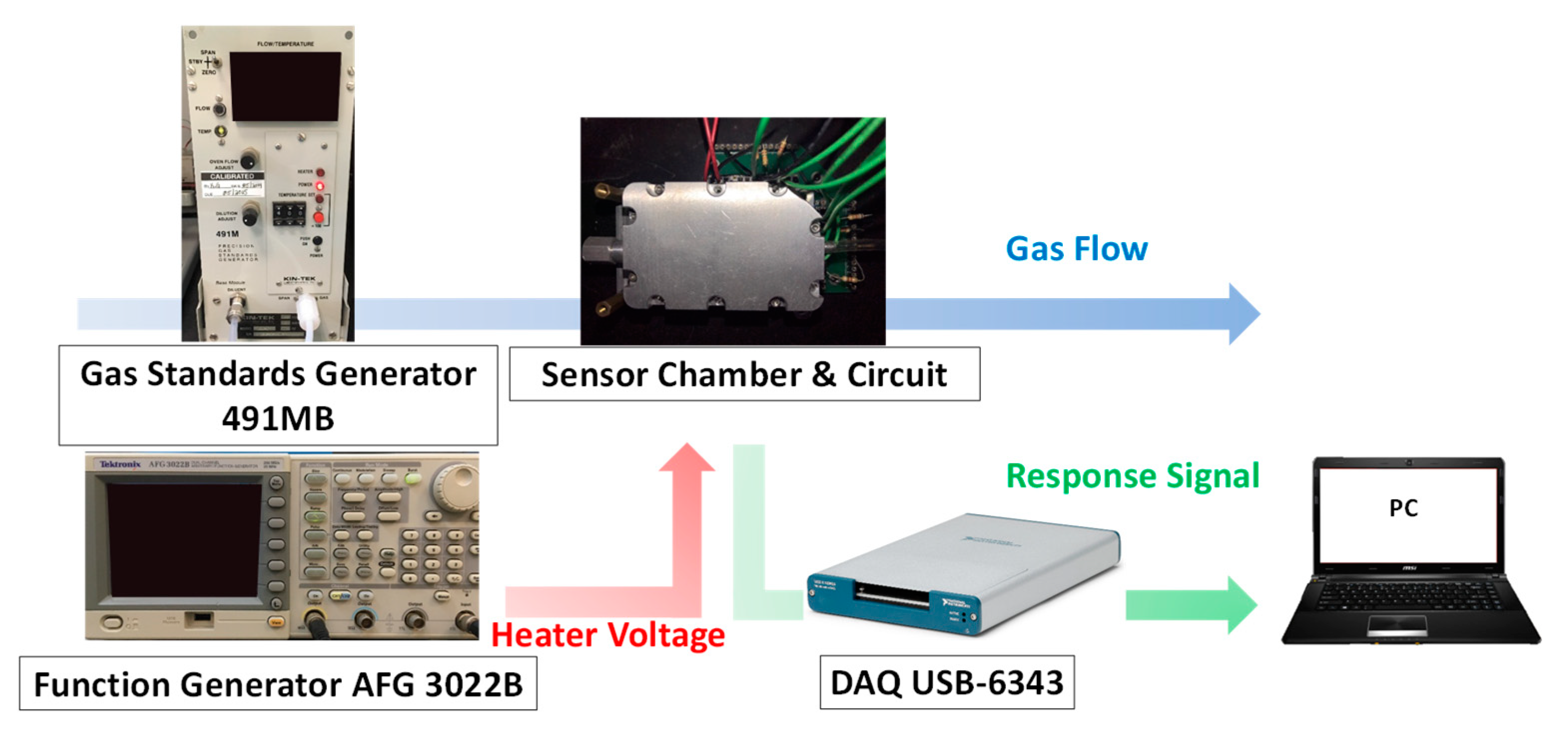
2.2. Experimental Setup
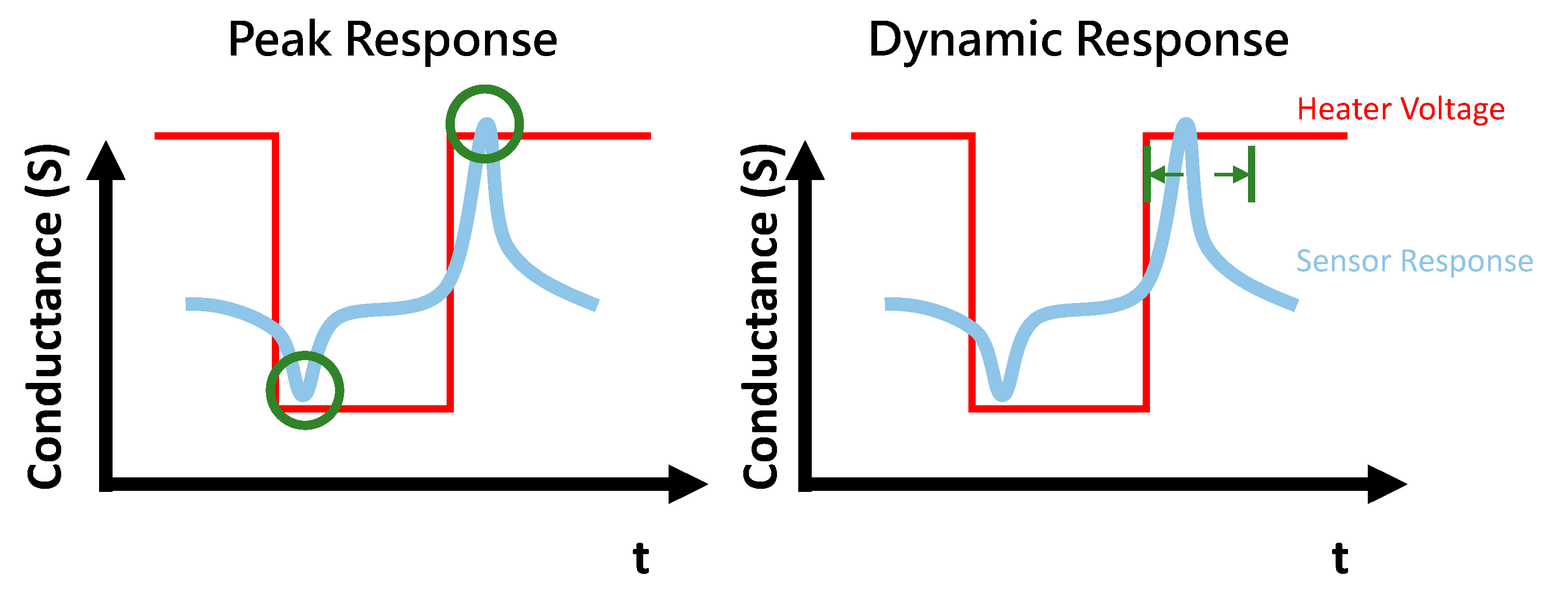
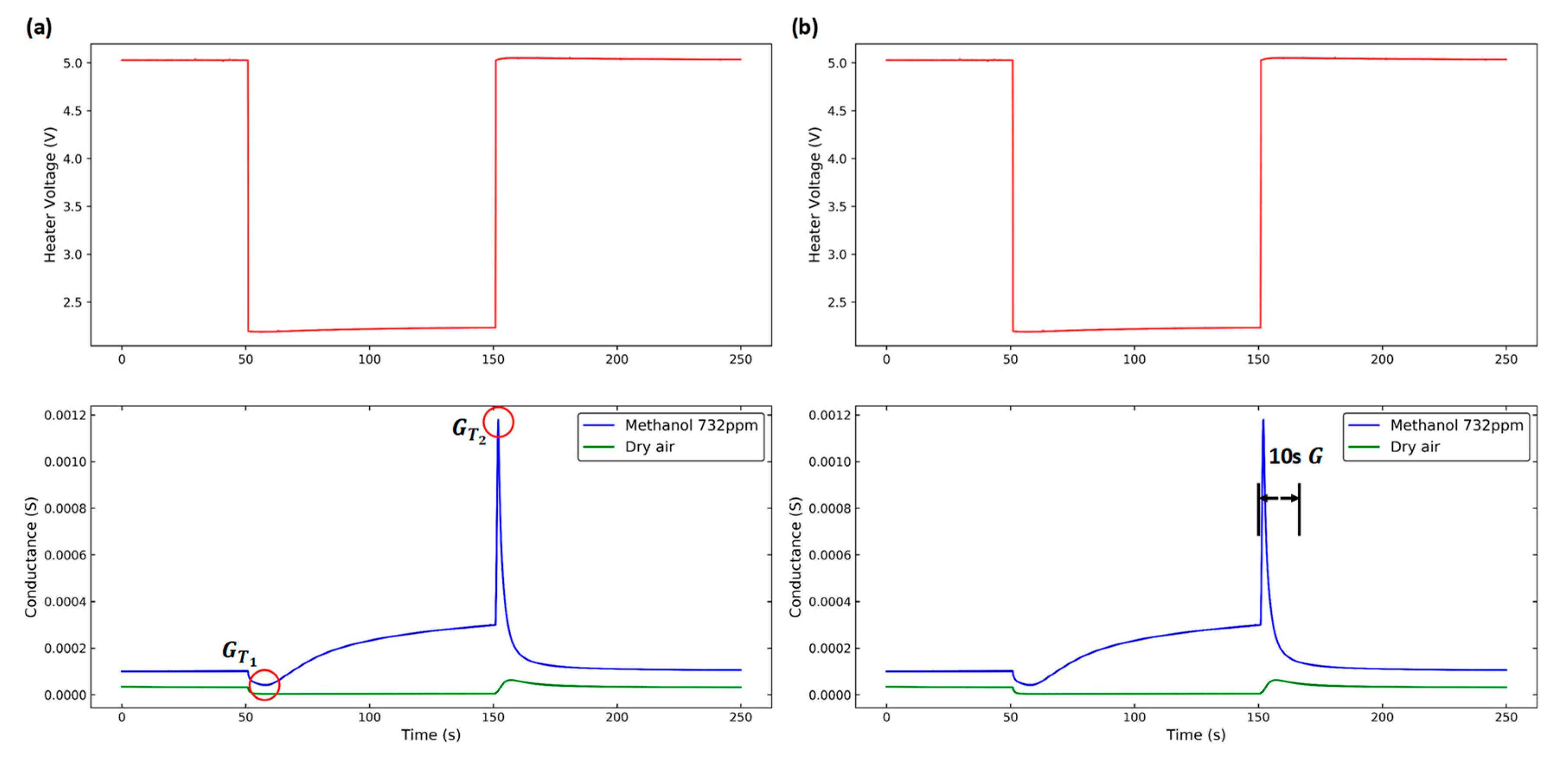
2.3. Feature Extraction
2.4. Dynamic Response
2.5. Mixture Model
2.6. Model Inversion
2.7. Performance Parameter
3. Results
3.1. Data Distribution
3.2. Mixture Model
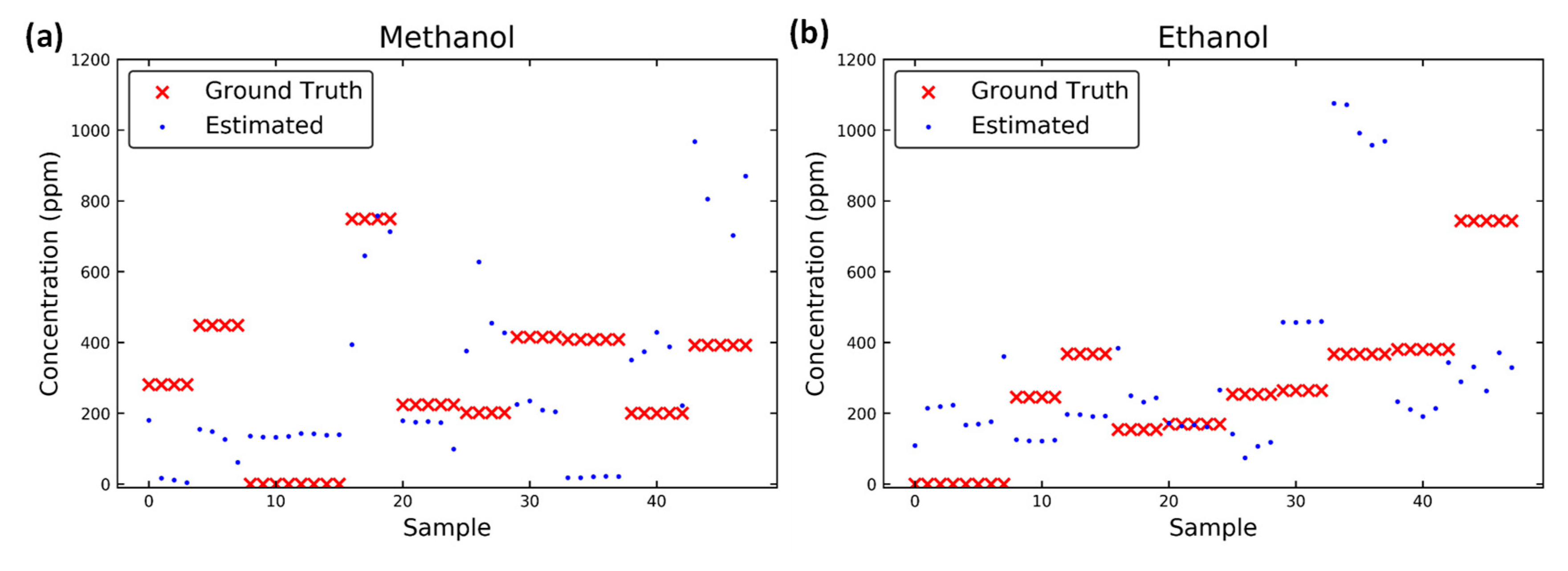
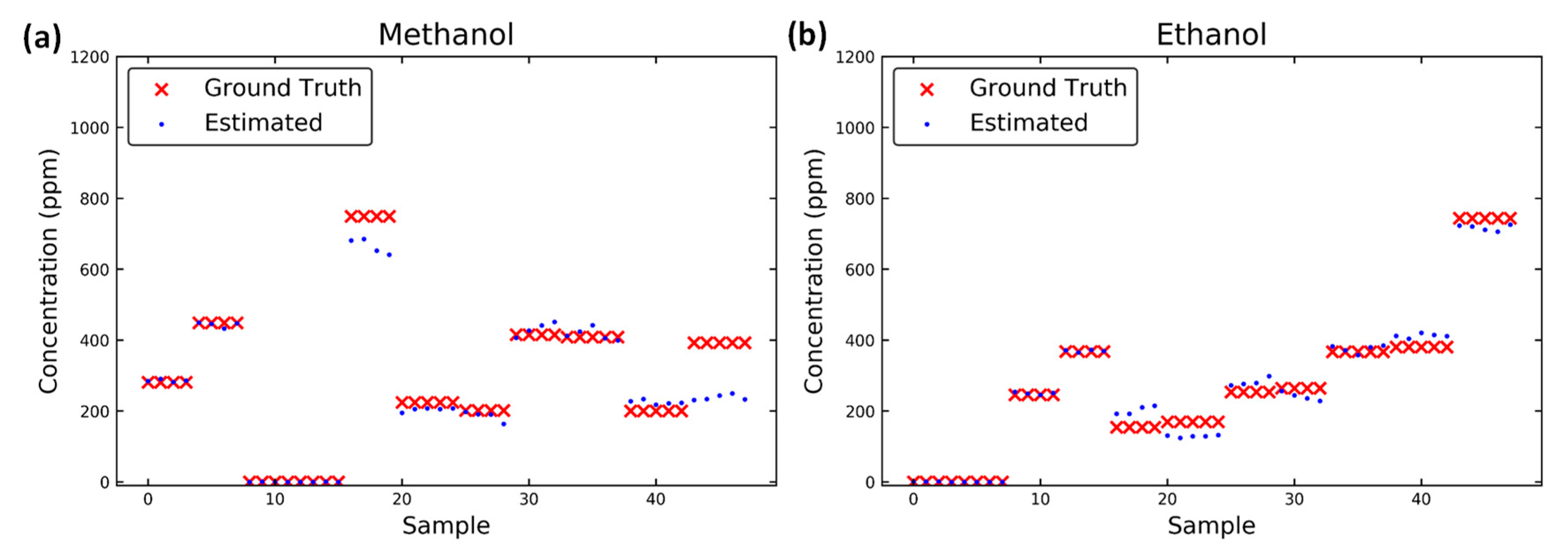
3.3. Results of Predictions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hodgkinson, J.; Tatam, R.P. Optical gas sensing: a review. Meas. Sci. Technol. 2012, 24, 012004. [Google Scholar] [CrossRef]
- Patrizi, B.; de Cumis, M.S.; Viciani, S.; D’Amato, F.; Foggi, P. Characteristic vibrational frequencies of toxic polychlorinated dibenzo-dioxins and-furans. J. Hazard. Mater. 2014, 274, 98–105. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Zhao, X.; Chen, Y.; Zhao, W. Research on a mixed gas recognition and concentration detection algorithm based on a metal oxide semiconductor olfactory system sensor array. Sensors 2018, 18, 3264. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Yin, L.; Zhang, L.; Xiang, D.; Gao, R. Metal oxide gas sensors: sensitivity and influencing factors. Sensors 2010, 10, 2088–2106. [Google Scholar] [CrossRef] [PubMed]
- Tang, K.T.; Lin, Y.S.; Shyu, J.M. A local weighted nearest neighbor algorithm and a weighted and constrained least-squared method for mixed odor analysis by electronic nose systems. Sensors 2010, 10, 10467–10483. [Google Scholar] [CrossRef] [PubMed]
- Ryan, M.A.; Zhou, H.; Buehler, M.G.; Manatt, K.S.; Mowrey, V.S.; Jackson, S.P.; Kisor, A.K.; Shevade, A.V.; Homer, M.L. Monitoring space shuttle air quality using the jet propulsion laboratory electronic nose. Sensors 2004, 4, 337–347. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, J.; Jiang, C.; Liu, A.; Xia, B. Quantitative detection of formaldehyde and ammonia gas via metal oxide-modified graphene-based sensor array combining with neural network model. Sensor Actuat. B. 2017, 240, 55–65. [Google Scholar] [CrossRef]
- Hossein-Babaei, F.; Amini, A. Recognition of complex odors with a single generic tin oxide gas sensor. Sensor Actuat. B. 2014, 194, 156–163. [Google Scholar] [CrossRef]
- Rastkhadiv, A.; Jenabi, A.; Souri, A. Discriminating among different tea leaves using an operating temperature-modulated tin oxide gas sensor. IOP Conf. Ser. Mater. Sci. Eng. 2016, 108, 012019. [Google Scholar] [CrossRef]
- Fort, A.; Gregorkiewitz, M.; Machetti, N.; Rocchi, S.; Serrano, B.; Tondi, L.; Ulivieri, N.; Vignoli, V.; Faglia, G.; Comini, E. Selectivity enhancement of SnO2 sensors by means of operating temperature modulation. Thin Solid Films 2002, 418, 2–8. [Google Scholar] [CrossRef]
- Amini, A.; Bagheri, M.A.; Montazer, G.A. Improving gas identification accuracy of a temperature-modulated gas sensor using an ensemble of classifiers. Sensor Actuat. B. 2013, 187, 241–246. [Google Scholar] [CrossRef]
- Ngo, K.A.; Lauque, P.; Aguir, K. High performance of a gas identification system using sensor array and temperature modulation. Sensor Actuat. B. 2007, 124, 209–216. [Google Scholar] [CrossRef]
- Vainiotalo, S.; Vaaranrinta, R.; Tornaeus, J.; Aremo, N.; Hase, T.; Peltonen, K. Passive monitoring method for 3-ethenylpyridine: a marker for environmental tobacco smoke. Environ. Sci. Technol. 2001, 35, 1818–1822. [Google Scholar] [CrossRef] [PubMed]
- Madrolle, S.; Grangeat, P.; Jutten, C. A Linear-Quadratic Model for the Quantification of a Mixture of Two Diluted Gases with a Single Metal Oxide Sensor. Sensors 2018, 18, 1785. [Google Scholar] [CrossRef] [PubMed]
- Wlodek, S.; Colbow, K.; Consadori, F. Signal-shape analysis of a thermally cycled tin-oxide gas sensor. Sensor Actuat. B. 1991, 3, 63–68. [Google Scholar] [CrossRef]
- Caroline, S.; Baur, T.; Schütze, A.; Sauerwald, T. Facile Quantification and Identification Techniques for Reducing Gases over a Wide Concentration Range Using a MOS Sensor in Temperature-Cycled Operation. Sensors 2018, 18, 744. [Google Scholar]
- Sears, W.M.; Colbow, K.; Consadori, F. General characteristics of thermally cycled tin oxide gas sensors. Semicon. Sci. Tech. 1989, 4, 351. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: implementation and theory. In Numerical Analysis; Springer: Berlin, Germany, 1978; Volume 630, pp. 105–116. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemometr. Intell. lab. 1987, 2, 37–52. [Google Scholar] [CrossRef]
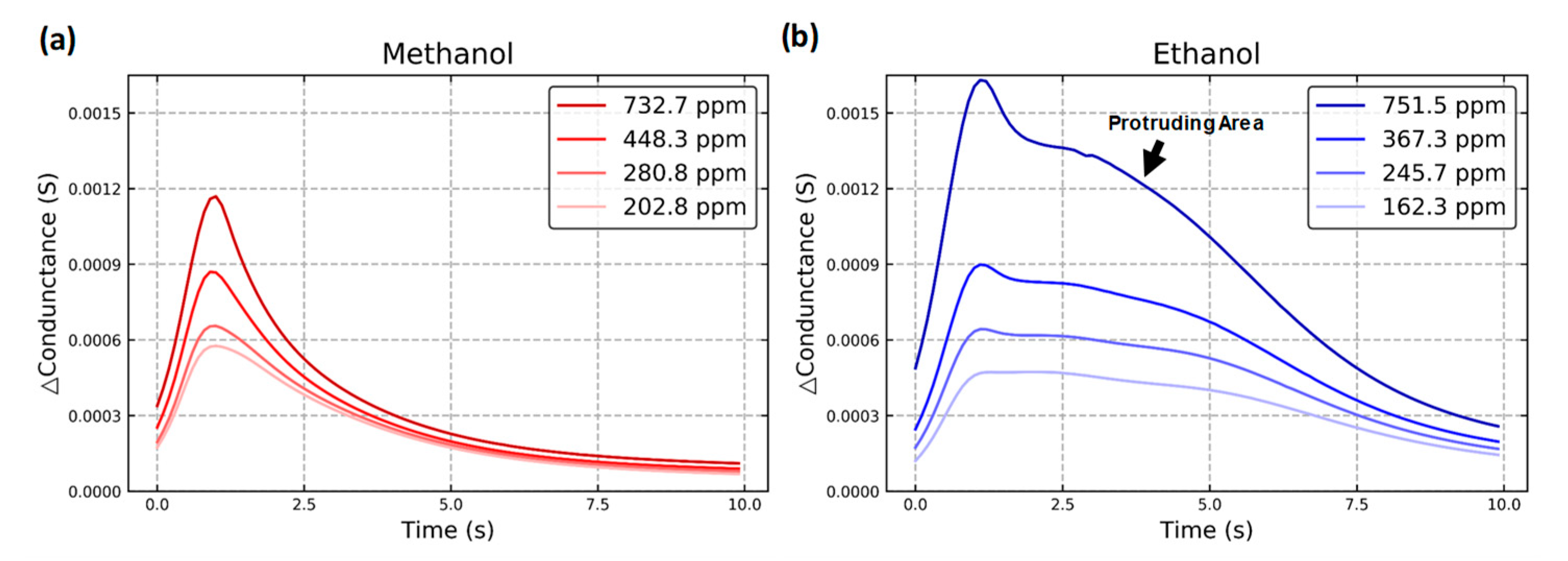
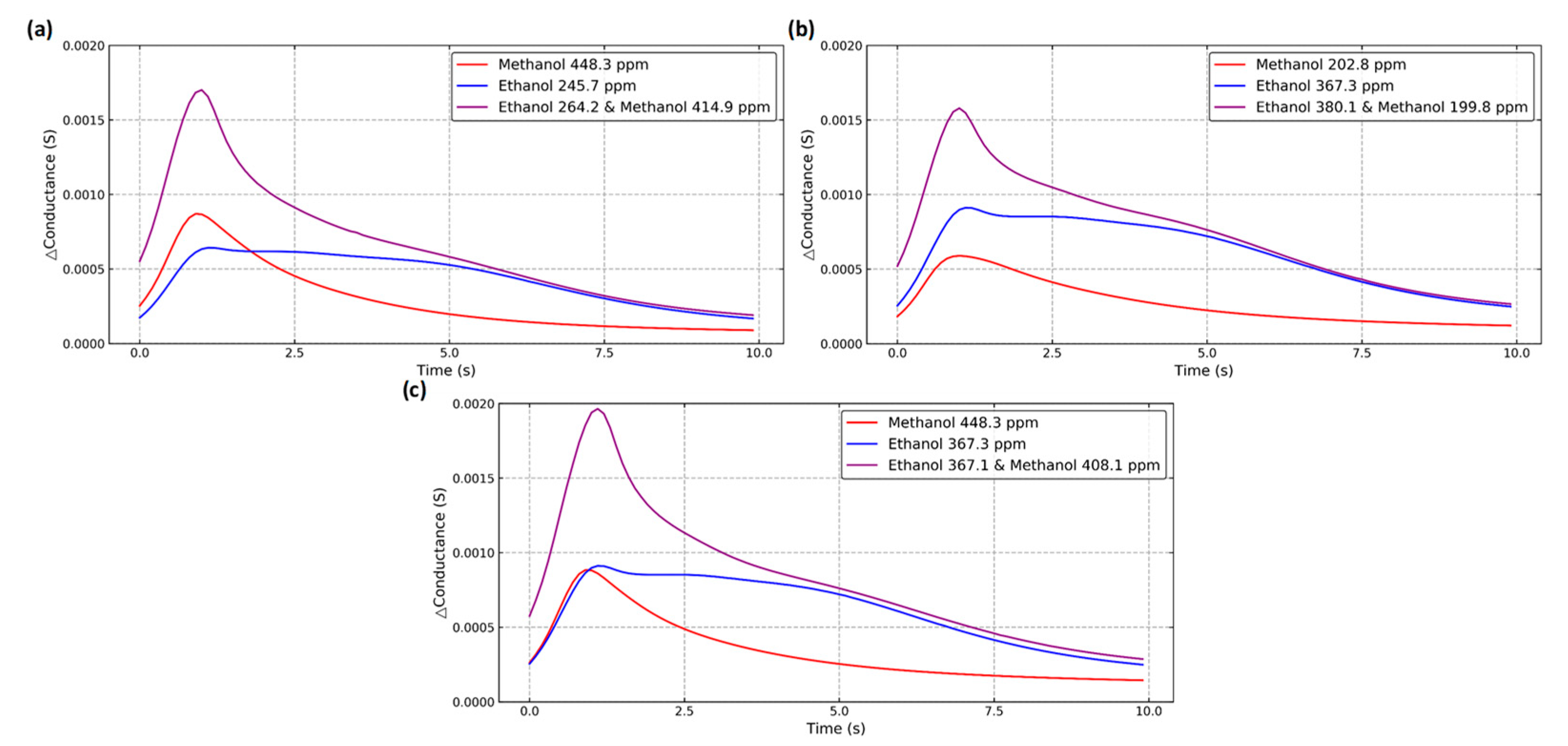
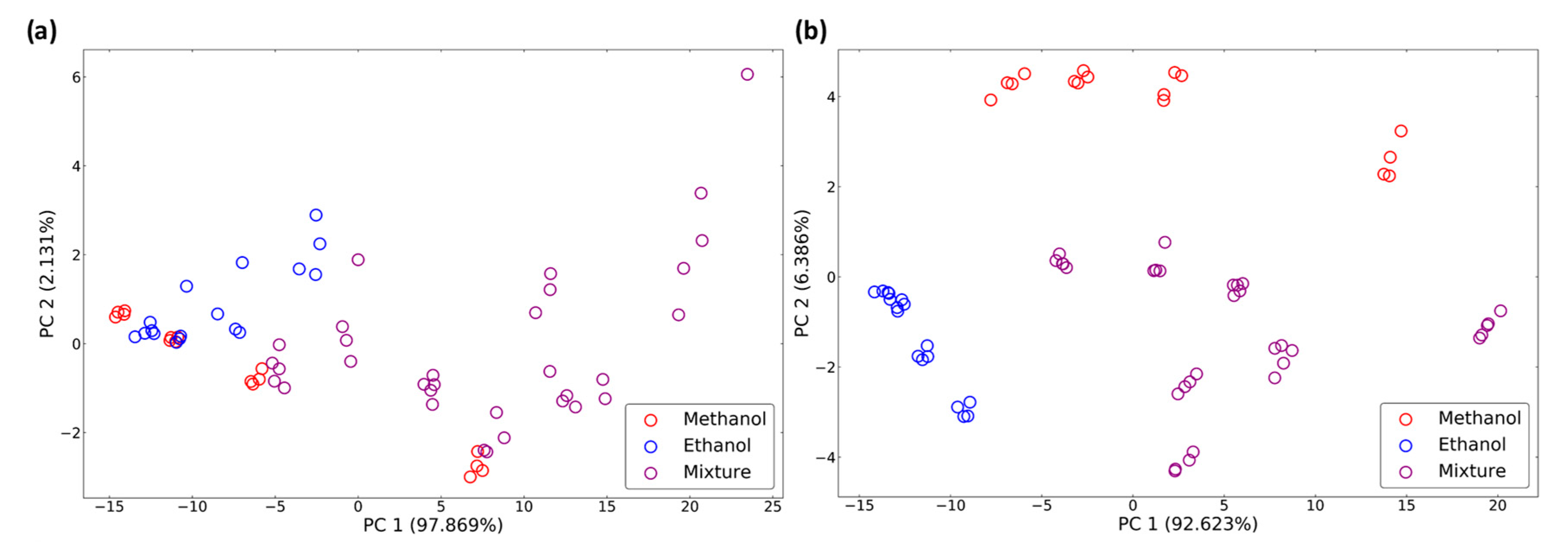
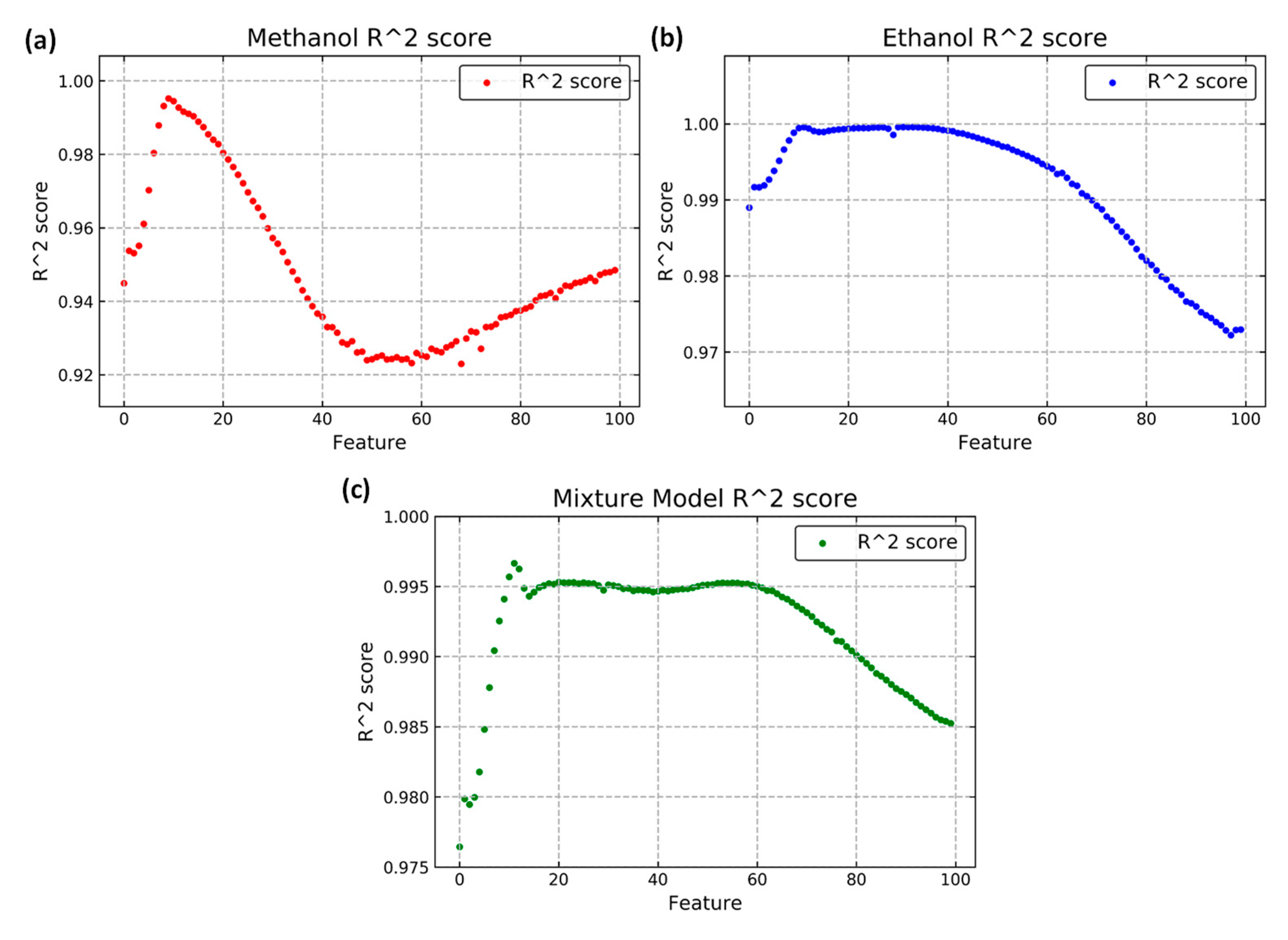
| Gas Type | Methanol Concen-Tration (ppm) | Ethanol Concen-Tration (ppm) | Amount | Gas Type | Methanol Concen-Tration (ppm) | Ethanol Concen-Tration (ppm) | Amount |
|---|---|---|---|---|---|---|---|
| Ethanol | 0 | 162.3 | 5 | Mixture | 392.6 | 743.8 | 5 |
| Ethanol | 0 | 245.7 | 4 | Mixture | 199.8 | 380.1 | 5 |
| Ethanol | 0 | 369.3 | 4 | Mixture | 408.1 | 367.1 | 5 |
| Ethanol | 0 | 751.5 | 4 | Mixture | 414.9 | 264.2 | 4 |
| Methanol | 202.8 | 0 | 4 | Mixture | 201.4 | 253.4 | 5 |
| Methanol | 280.8 | 0 | 4 | Mixture | 224.3 | 169.1 | 4 |
| Methanol | 448.3 | 0 | 4 | Mixture | 748.8 | 154.0 | 4 |
| Methanol | 732.7 | 0 | 4 |
| Class | Peak Response (2 Points) | |||
|---|---|---|---|---|
| Linear-Quadratic Model | Polynomial Interaction Term Model | |||
| Mean Relative Error (%) | ||||
| Methanol | 77.0 | 71.2 | 18.0 | 12.7 |
| Ethanol | 48.6 | 31.3 | 71.5 | 76.8 |
| Methanol in mixture | 76.7 | 48.4 | 88.0 | 92.1 |
| Ethanol in mixture | 70.6 | 51.1 | 72.3 | 118.1 |
| Class | Dynamic Response (100 points) | |||
|---|---|---|---|---|
| Linear-Quadratic Model | Polynomial Interaction Term Model | |||
| Mean Relative Error (%) | ||||
| Methanol | 32.9 | 13.4 | 18.7 | 1.4 |
| Ethanol | 29.2 | 6.7 | 35.0 | 1.3 |
| Methanol in mixture | 32.7 | 20.3 | 30.0 | 13.0 |
| Ethanol in mixture | 15.3 | 14.2 | 29.0 | 12.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, W.-C.; Chou, T.-I.; Tang, K.-T. A Gas Mixture Prediction Model Based on the Dynamic Response of a Metal-Oxide Sensor. Micromachines 2019, 10, 598. https://doi.org/10.3390/mi10090598
Wen W-C, Chou T-I, Tang K-T. A Gas Mixture Prediction Model Based on the Dynamic Response of a Metal-Oxide Sensor. Micromachines. 2019; 10(9):598. https://doi.org/10.3390/mi10090598
Chicago/Turabian StyleWen, Wei-Chih, Ting-I Chou, and Kea-Tiong Tang. 2019. "A Gas Mixture Prediction Model Based on the Dynamic Response of a Metal-Oxide Sensor" Micromachines 10, no. 9: 598. https://doi.org/10.3390/mi10090598
APA StyleWen, W.-C., Chou, T.-I., & Tang, K.-T. (2019). A Gas Mixture Prediction Model Based on the Dynamic Response of a Metal-Oxide Sensor. Micromachines, 10(9), 598. https://doi.org/10.3390/mi10090598





