Molecular Dynamics Simulation of the Influence of Nanoscale Structure on Water Wetting and Condensation
Abstract
1. Introduction
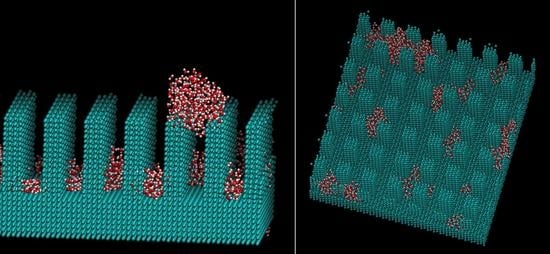
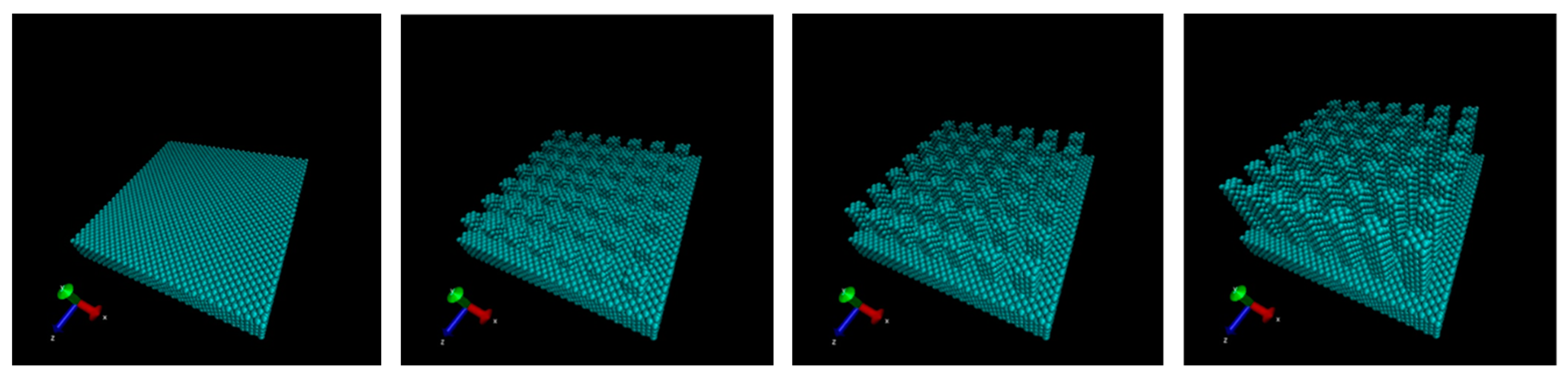
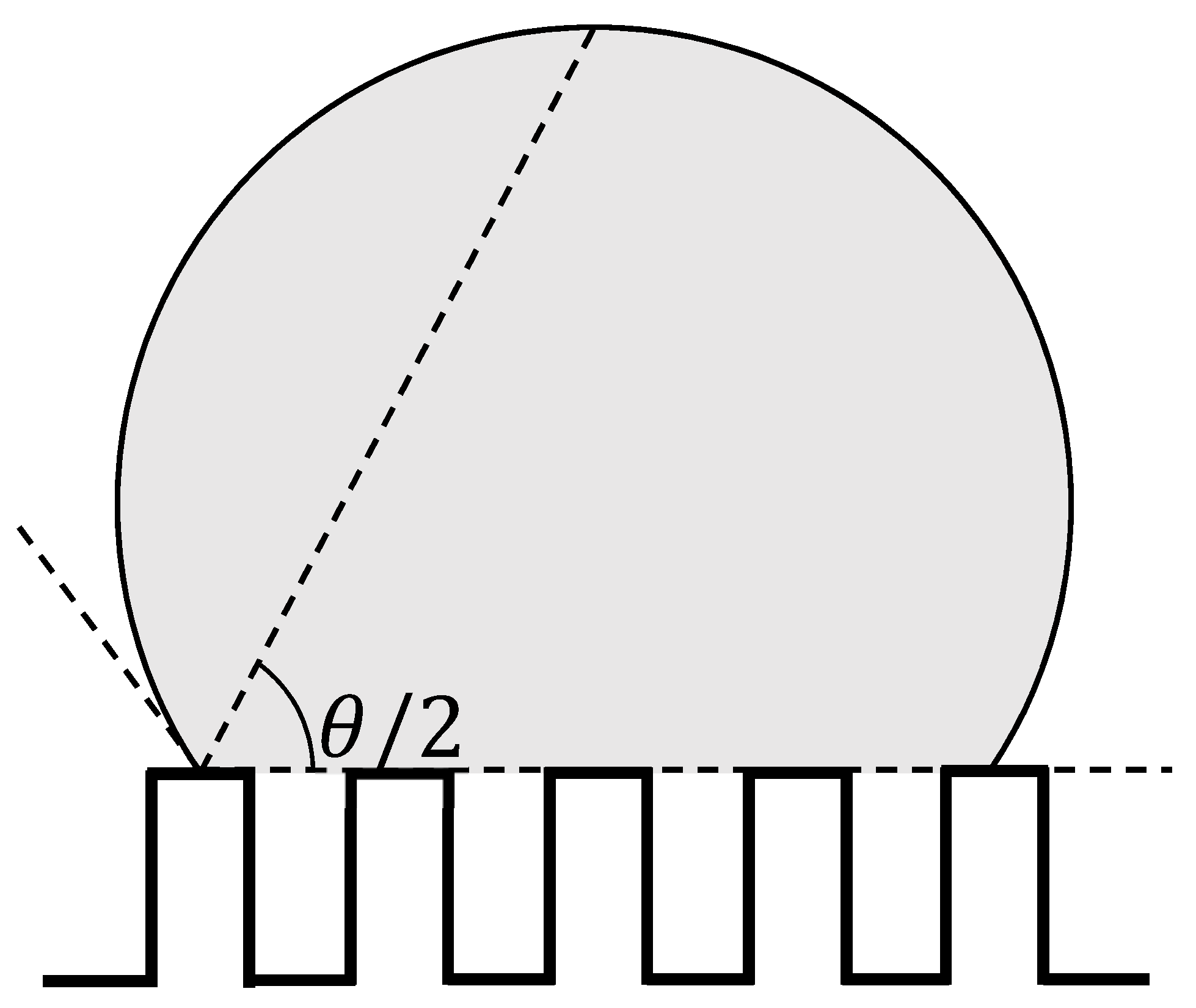
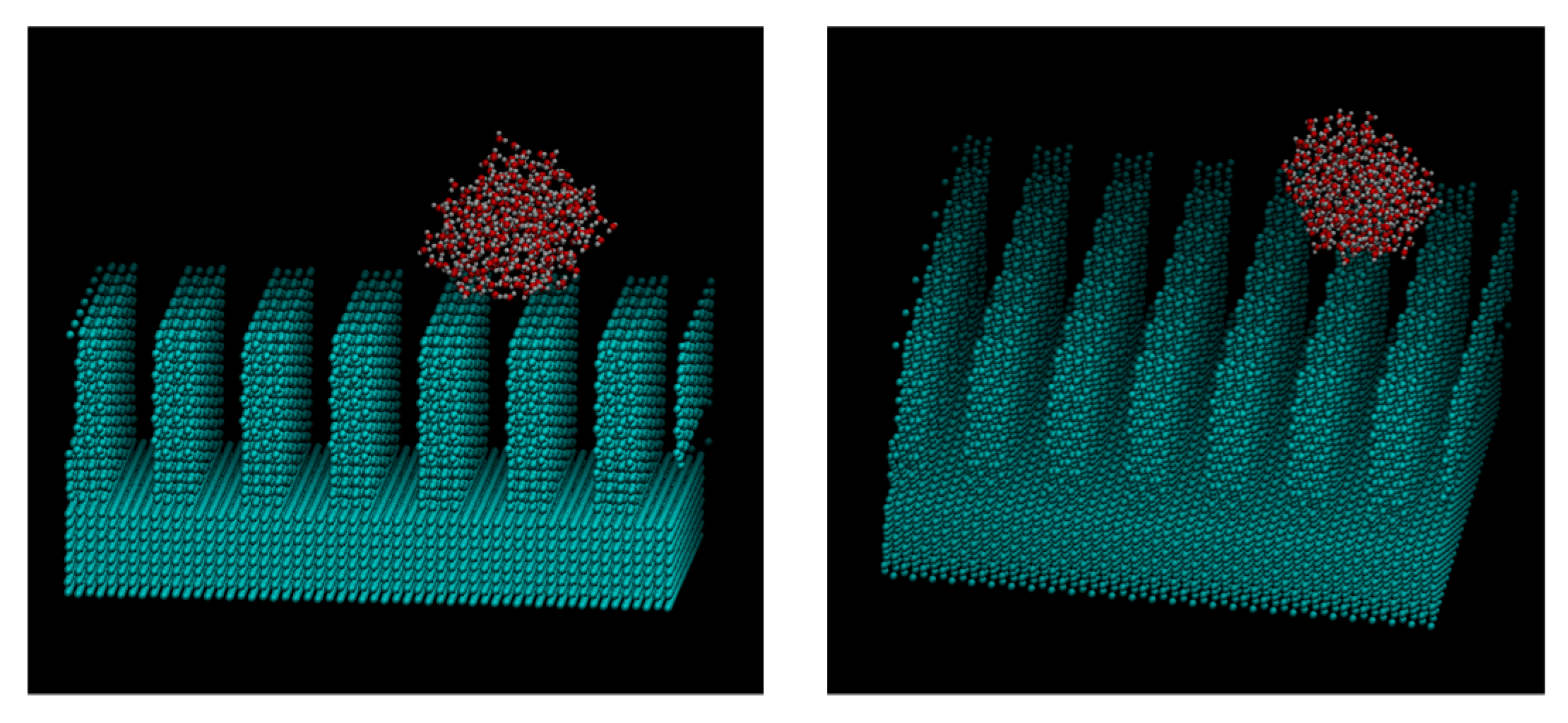
2. Computational Methods
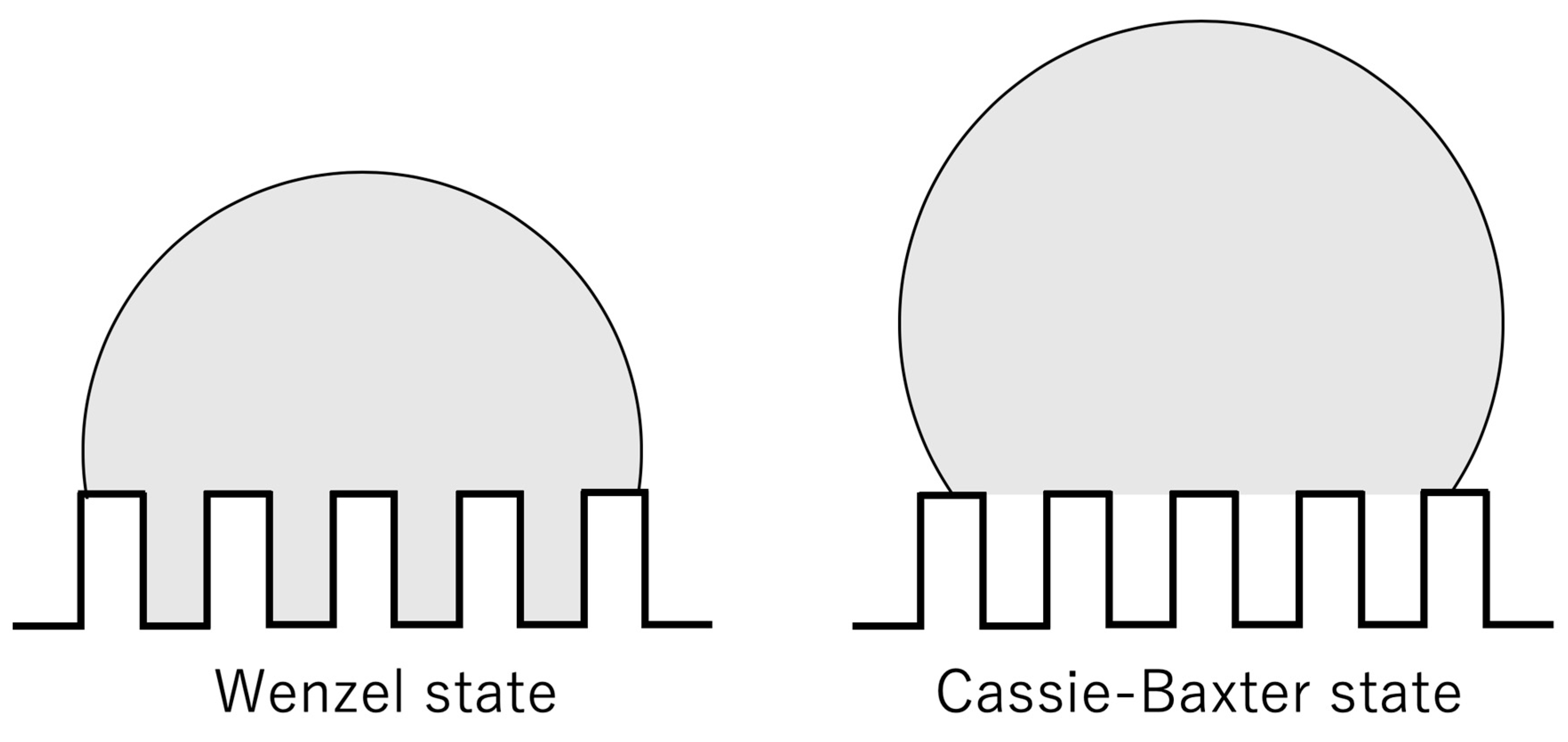
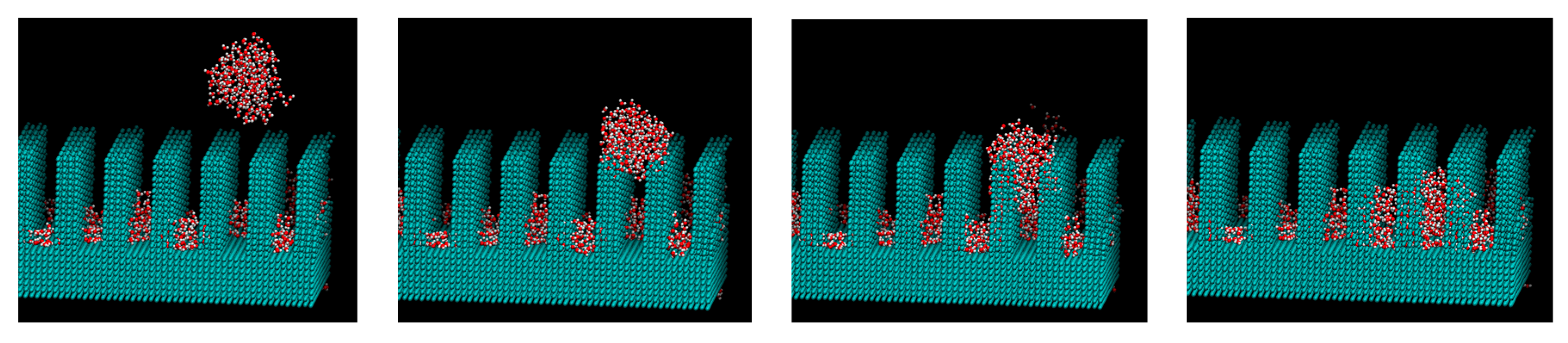
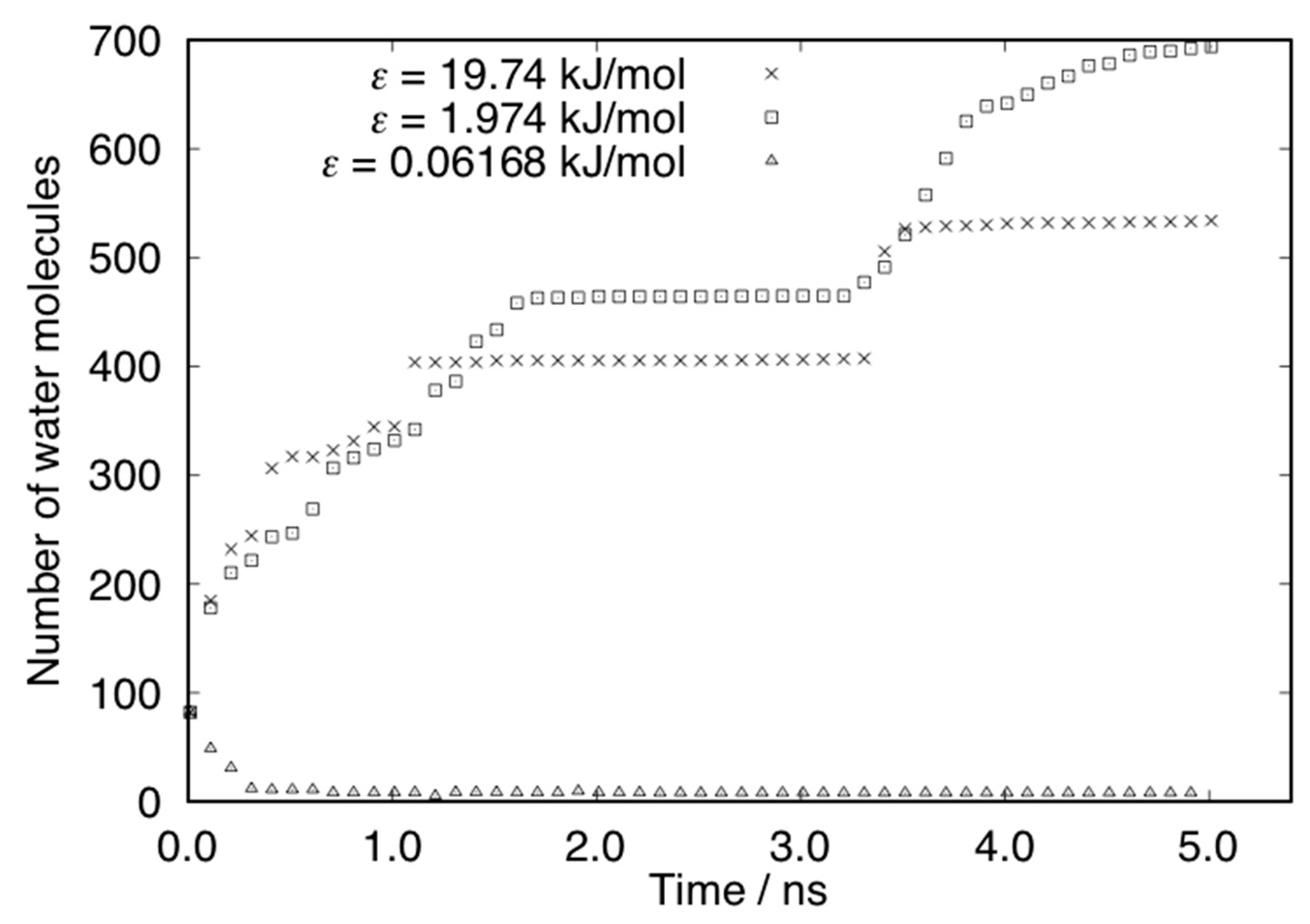
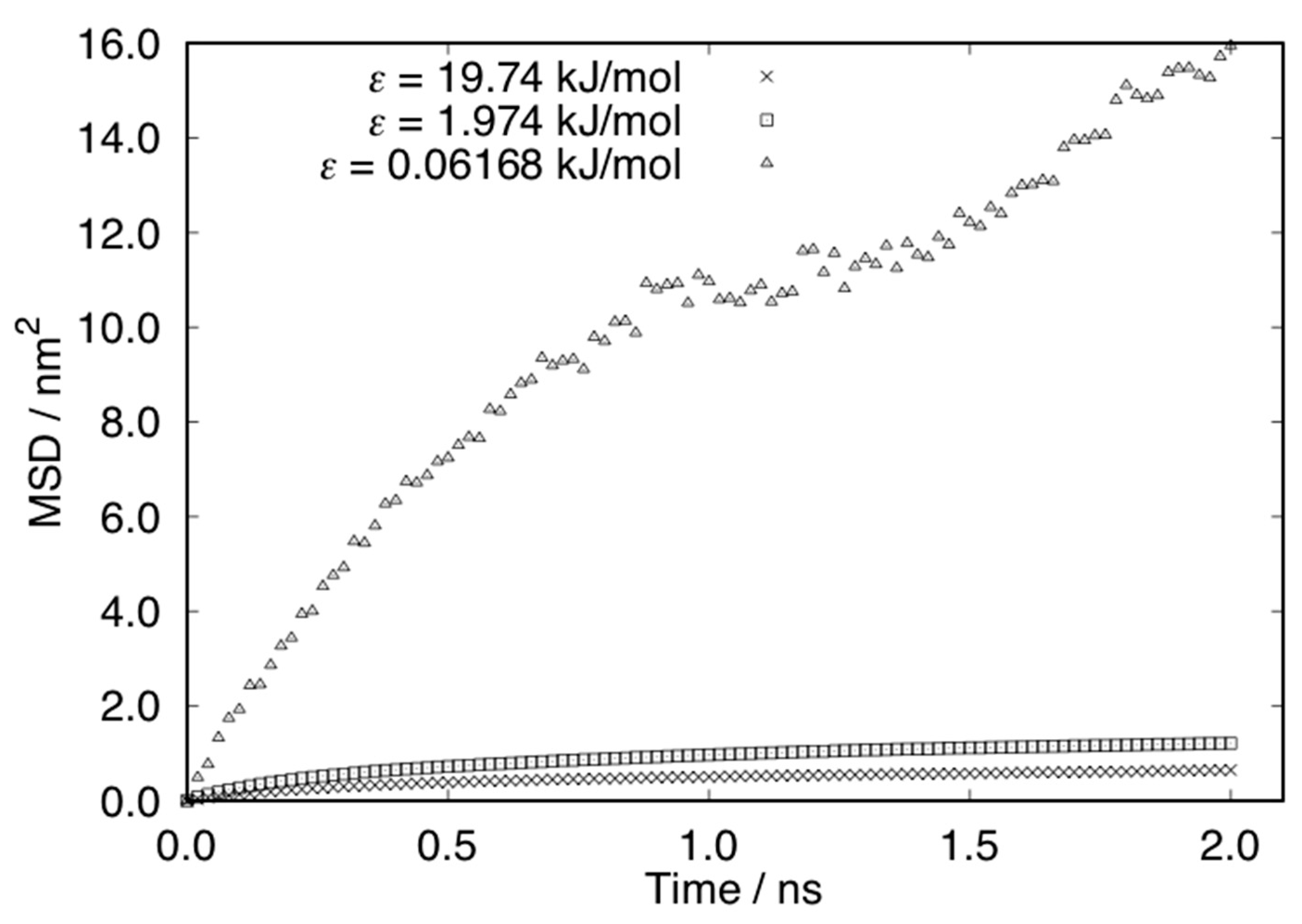
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Biró, L.P.; Nemes-Incze, P.; Lambin, P. Graphene: Nanoscale processing and recent applications. Nanoscale 2011, 4, 1824–1839. [Google Scholar]
- Tan, X.; Tao, Z.; Yu, M.; Wu, H.; Li, H. Anti-Reflectance Optimization of Secondary Nanostructured Black Silicon Grown on Micro-Structured Arrays. Micromachines 2018, 9, 385. [Google Scholar] [CrossRef] [PubMed]
- Meng, J.; Dong, X.; Zhao, Y.; Xu, R.; Bai, X.; Zhou, H. Fabrication of a Low Adhesive Superhydrophobic Surface on Ti6Al4V Alloys Using TiO2/Ni Composite Electrodeposition. Micromachines 2019, 10, 121. [Google Scholar] [CrossRef] [PubMed]
- Yoshimitsu, Z.; Nakajima, A.; Watanabe, T.; Hashimoto, K. Effects of Surface Structure on the Hydrophobicity and Sliding Behavior of Water Droplets. Langmuir 2002, 18, 5818–5822. [Google Scholar] [CrossRef]
- Wang, J.; Liu, M.; Ma, R.; Wang, Q.; Jiang, L. In Situ Wetting State Transition on Micro- and Nanostructured Surfaces at High Temperature. ACS Appl. Mater. Interfaces 2014, 6, 15198–15208. [Google Scholar] [CrossRef]
- Chen, S.; Wang, J.; Chen, D. States of a Water Droplet on Nanostructured Surfaces. J. Phys. Chem. C 2014, 118, 18529–18536. [Google Scholar] [CrossRef]
- Yong, X.; Zhang, L.T. Nanoscale Wetting on Groove-Patterned Surfaces. Langmuir 2009, 25, 5045–5053. [Google Scholar] [CrossRef]
- Introzzi, L.; Fuentes-Alventosa, J.M.; Cozzolino, C.A.; Trabattoni, S.; Tavazzi, S.; Bianchi, C.L.; Schiraldi, A.; Piergiovanni, L.; Farris, S. “Wetting Enhancer” Pullulan Coating for Antifog Packaging Applications. ACS Appl. Mater. Interfaces 2012, 4, 3692–3700. [Google Scholar] [CrossRef]
- Ho, T.A.; Papavassiliou, D.V.; Lee, L.L.; Striolo, A. Liquid water can slip on a hydrophilic surface. Proc. Natl. Acad. Sci. USA 2011, 108, 16170–16175. [Google Scholar] [CrossRef]
- Wang, C.; Wen, B.; Tu, Y.; Wan, R.; Fang, H. Friction Reduction at a Superhydrophilic Surface: Role of Ordered Water. J. Phys. Chem. C 2015, 119, 11679–11684. [Google Scholar] [CrossRef]
- Tocci, G.; Joly, L.; Michaelides, A. Friction of Water on Graphene and Hexagonal Boron Nitride from ab initio Methods: Very Different Slippage Despite Very Similar Interface Structures. Nano Lett. 2015, 14, 6872–6877. [Google Scholar] [CrossRef] [PubMed]
- Lu, P.; Liu, X.; Zhang, C. Electroosmotic Flow in a Rough Nanochannel with Surface Roughness Characterized by Fractal Cantor. Micromachines 2017, 8, 190. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, X.; Han, X.; Shen, C. Role of Solid Wall Properties in the Interface Slip of Liquid in Nanochannels. Micromachines 2018, 9, 663. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Shi, B.; Lu, H.; Xiu, P.; Zhou, R. Dewetfting Transitions in the Self-Assembly of Two Amyloidogenic β-Sheets and the Importance of Matching Surfaces. J. Phys. Chem. B 2011, 115, 11137–11144. [Google Scholar] [CrossRef] [PubMed]
- Weibel, D.E.; Michels, A.F.; Feil, A.F.; Amaral, L.; Teixeira, S.R.; Horowitz, F. Adjustable Hydrophobicity of Al Substrates by Chemical Surface Functionalization of Nano/Microstructures. J. Phys. Chem. C 2010, 114, 13219–13225. [Google Scholar] [CrossRef]
- Miljkovic, N.; Wang, E.N. Condensation heat transfer on superhydrophobic surfaces. MRS Bull. 2013, 38, 397–406. [Google Scholar] [CrossRef]
- Miljkovic, N.; Enright, R.; Wang, E.N. Effect of Droplet Morphology on Growth Dynamics and Heat Transfer during Condensation on Superhydrophobic Nanostructured Surfaces. ACS Nano 2012, 6, 1776–1785. [Google Scholar] [CrossRef]
- Enright, R.; Miljkovic, N.; Al-Obeidi, A.; Thompson, C.V.; Wang, E. Condensation on Superhydrophobic Surfaces: The Role of Local Energy Barriers and Structure Length Scale. Langmuir 2012, 28, 14424–14432. [Google Scholar] [CrossRef]
- Miljkovic, N.; Enright, R.; Nam, Y.; Lopez, K.; Dou, N.; Sack, J.; Wang, E.N. Jumping-Droplet-Enhanced Condensation on Scalable Superhydrophobic Nanostructured Surfaces. Nano Lett. 2013, 13, 179–187. [Google Scholar] [CrossRef]
- Hou, Y.; Yu, M.; Chen, X.; Wang, Z.; Yao, S. Recurrent Filmwise and Dropwise Condensation on a Beetle Mimetic Surface. ACS Nano 2015, 9, 71–81. [Google Scholar] [CrossRef]
- Erb, R.A. Wettability of Metals under Continuous Condensing Conditions. J. Phys. Chem. 1965, 69, 1306–1309. [Google Scholar] [CrossRef]
- Varanasi, K.K.; Hsu, M.; Bhate, N.; Yang, W.; Deng, T. Spatial control in the heterogeneous nucleation of water. Appl. Phys. Lett. 2009, 95, 094101. [Google Scholar]
- Boreyko, J.B.; Chen, C.H. Self-Propelled Dropwise Condensate on Superhydrophobic Surfaces. Phys. Rev. Lett. 2009, 103, 184501. [Google Scholar] [CrossRef] [PubMed]
- Dietz, C.; Rykaczewski, K.; Fedorov, A.G.; Joshi, Y. Visualization of droplet departure on a superhydrophobic surface and implications to heat transfer enhancement during dropwise condensation. Appl. Phys. Lett. 2010, 978, 033104. [Google Scholar]
- Chen, X.; Wu, J.; Ma, R.; Hua, M.; Koratkar, N.; Yao, S.; Wang, Z. Nanograssed Micropyramidal Architectures for Continuous Dropwise Condensation. Adv. Funct. Mater. 2011, 21, 4617–4623. [Google Scholar] [CrossRef]
- Cheng, J.; Vandadi, A.; Chen, C.L. Condensation heat transfer on two-tier superhydrophobic surfaces. Appl. Phys. Lett. 2012, 101, 131909. [Google Scholar] [CrossRef]
- Lee, S.; Cheng, K.; Palmre, V.; Bhuiya, M.D.M.H.; Kim, K.J.; Zhang, B.J.; Yoon, H. Heat transfer measurement during dropwise condensation using micro/nano-scale porous surface. J. Heat Mass Transf. 2013, 65, 619–626. [Google Scholar] [CrossRef]
- Quang, T.S.B.; Leong, F.Y.; An, H.; Tan, B.H.; Ohl, C.D. Growth and wetting of water droplet condensed between micron-sized particles and substrate. Sci. Rep. 2016, 6, 30989. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Ding, Y.; Chen, J.; Song, Y. Spontaneous Uphill Movement and Self-Removal of Condensates on Hierarchical Tower-Like Arrays. ACS Nano 2016, 6, 9456–9462. [Google Scholar] [CrossRef]
- Zhu, C.; Li, H.; Huang, Y.; Zeng, X.C.; Meng, S. Microscopic Insight into Surface Wetting: Relations between Interfacial Water Structure and the Underlying Lattice Constant. Phys. Rev. Lett. 2013, 110, 126101. [Google Scholar] [CrossRef]
- Xu, Z.; Gao, Y.; Wang, C.; Fang, H. Nanoscale Hydrophilicity on Metal Surfaces at Room Temperature: Coupling Lattice Constants and Crystal Faces. J. Phys. Chem. C 2015, 119, 20409–20415. [Google Scholar] [CrossRef]
- Carrasco, J.; Hodgson, A.; Michaelides, A. A molecular perspective of water at metal interfaces. Nat. Matt 2012, 11, 667. [Google Scholar]
- Van Vreumingen, D.; Tewari, S.; Verbeek, F.; van Ruitenbeek, J.M. Towards Controlled Single-Molecule Manipulation Using “Real-Time” Molecular Dynamics Simulation: A GPU Implementation. Micromachines 2018, 9, 270. [Google Scholar] [CrossRef] [PubMed]
- Koishi, T.; Yasuoka, K.; Fujikawa, S.; Ebisuzaki, T.; Cheng, X. Coexistence and transition between Cassie and Wenzel state on pillared hydrophobic surface. Proc. Natl. Acad. Sci. USA 2009, 206, 8435–8440. [Google Scholar] [CrossRef] [PubMed]
- Koishi, T.; Yasuoka, K.; Zeng, X.C. Molecular dynamics simulation of water nanodroplet bounce back from flat and nanopillared surface. Langmuir 2017, 33, 10184–10192. [Google Scholar] [CrossRef]
- Wenzel, R.N. Resistance of Solid Surfaces to Wetting by Water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Cassie, A.B.D.; Baxter, S. Wettability of Porous Surfaces. Trans. Faraday Soc. 1944, 40, 546–551. [Google Scholar] [CrossRef]
- Niu, D.; Tang, G.H. The effect of surface wettability on water vapor condensation in nanoscale. Sci. Rep. 2016, 67, 19192. [Google Scholar] [CrossRef]
- Gao, S.; Liao, Q.; Liu, W.; Liu, Z. Effects of solid fraction on droplet wetting and vapor condensation: A molecular dynamic simulation study. Langmuir 2017, 33, 12379–12388. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Spoel, D.V.D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comp. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef] [PubMed]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [PubMed]
- Nosé, S. A unified formulation of the constant temperature molecular-dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed]
- Gu, H.; Wang, C.; Gong, S.; Mei, Y.; Li, H.; Ma, W. Investigation on contact angle measurement methods and wettability transition of porous surfaces. Surf. Coat. Technol. 2016, 292, 72–77. [Google Scholar] [CrossRef]
- Wang, C.; Lu, H.; Wang, Z.; Xiu, P.; Zhou, B.; Zuo, G.; Wan, R.; Hu, J.; Fang, H. Stable Liquid Water Droplet on a Water Monolayer Formed at Room Temperature on Ionic Model Substrates. Phys. Rev. Lett. 2009, 103, 137801. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhao, Y.P. Precursor Film in Dynamic Wetting, Electrowetting, and Electro-Elasto-Capillarity. Phys. Rev. Lett. 2010, 104, 246101. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Wang, F.; Bai, J.; Xeng, X.C.; Wu, H. Compression Limit of Two-Dimensional Water Constrained in Graphene Nanocapillaries. ACS Nano 2015, 9, 12197–12204. [Google Scholar] [CrossRef]
- Gao, Z.; Giovambattista, N.; Sahin, O. Phase Diagram of Water Confined by Graphene. Sci. Rep. 2018, 8, 6228. [Google Scholar] [CrossRef]

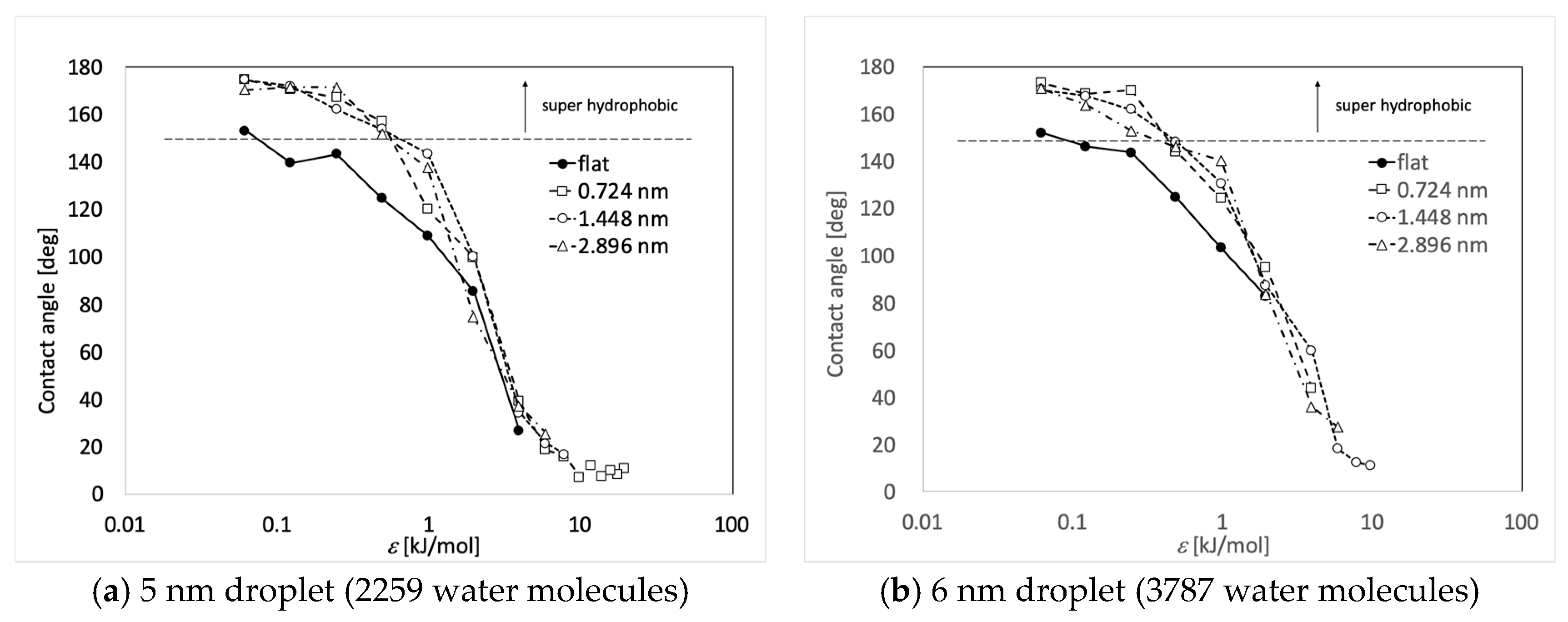
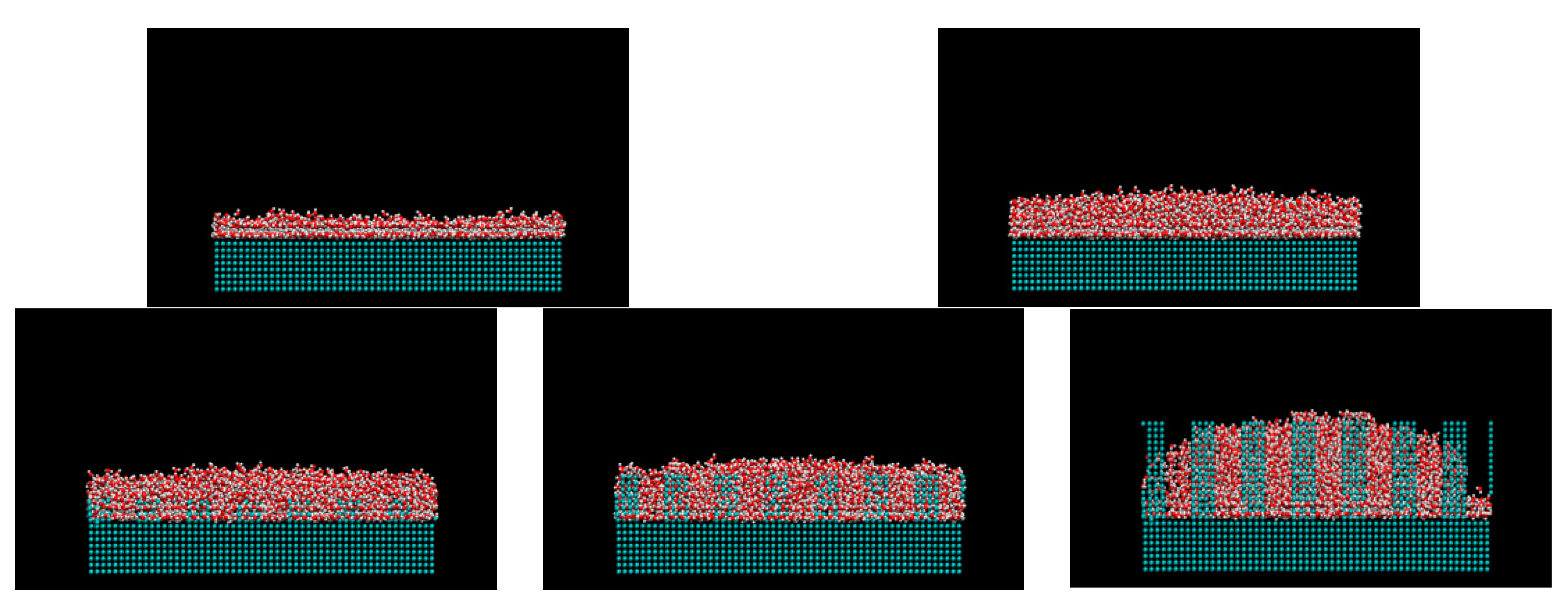


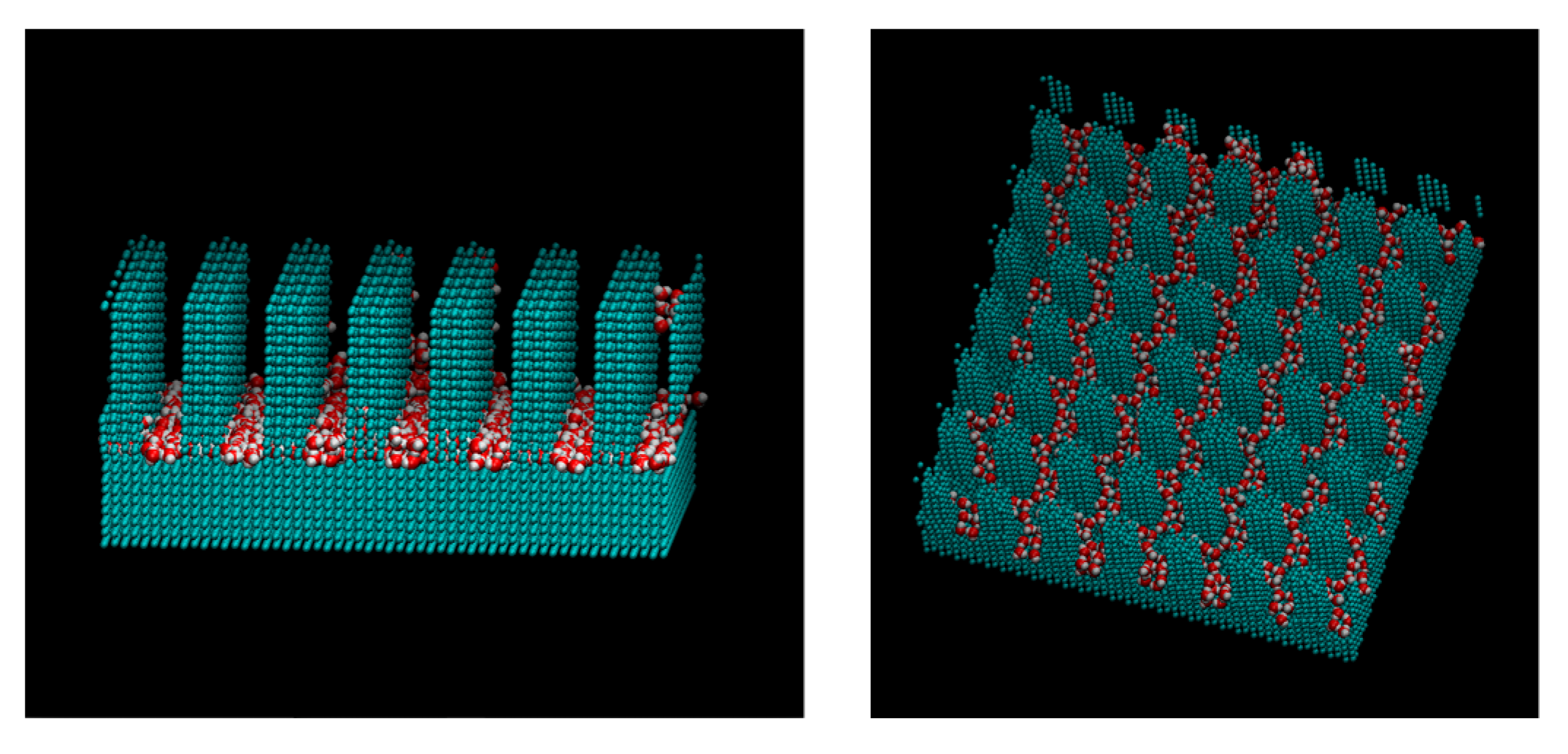
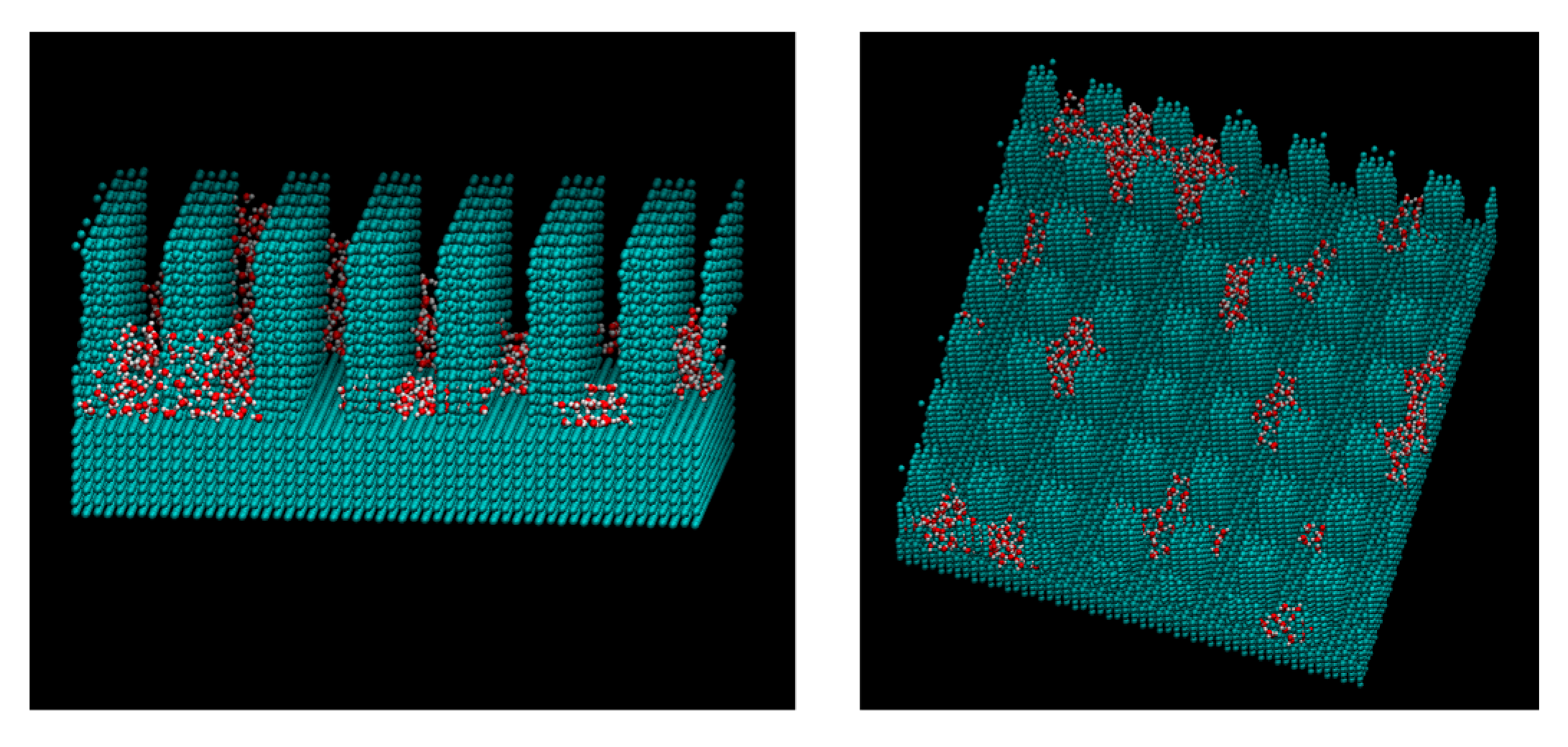

| Ratio | ε (kJ/mol) |
|---|---|
| 1.0 | 19.74 |
| 0.9 | 17.76 |
| 0.8 | 15.79 |
| 0.7 | 13.82 |
| 0.6 | 11.84 |
| 0.5 | 9.869 |
| 0.4 | 7.895 |
| 0.3 | 5.921 |
| 0.2 | 3.948 |
| 0.1 | 1.974 |
| 1/20 | 0.9869 |
| 1/40 | 0.4935 |
| 1/80 | 0.2467 |
| 1/160 | 0.1234 |
| 1/320 | 0.06168 |
| ε (kJ/mol) | Flat | 0.724 nm | 1.448 nm | 2.896 nm |
|---|---|---|---|---|
| 19.74 | - | 10.6 | - | - |
| 17.76 | - | 8.1 | - | - |
| 15.79 | - | 10.0 | - | - |
| 13.82 | - | 7.5 | - | - |
| 11.84 | - | 11.8 | - | - |
| 9.869 | - | 7.0 | - | - |
| 7.895 | - | 15.8 | 16.7 | - |
| 5.921 | - | 18.5 | 21.1 | 25.3 |
| 3.948 | 26.5 | 39.0 | 34.3 | 37.2 |
| 1.974 | 85.4 | 99.7 | 99.9 | 74.4 |
| 0.9869 | 108.8 | 120.0 | 143.4 | 137.5 |
| 0.4935 | 124.4 | 157.1 | 153.7 | 151.8 |
| 0.2467 | 143.3 | 167.0 | 162.0 | 171.3 |
| 0.1234 | 139.6 | 170.5 | 171.9 | 171.4 |
| 0.06168 | 153.0 | 174.5 | 174.6 | 170.5 |
| ε (kJ/mol) | Flat | 0.724 nm | 1.448 nm | 2.896 nm |
|---|---|---|---|---|
| 19.74 | - | - | - | - |
| 17.76 | - | - | - | - |
| 15.79 | - | - | - | - |
| 13.82 | - | - | - | - |
| 11.84 | - | - | - | - |
| 9.869 | - | - | 10.9 | - |
| 7.895 | - | - | 12.3 | - |
| 5.921 | - | - | 18.1 | 27.4 |
| 3.948 | - | 44.0 | 59.6 | 36.0 |
| 1.974 | 82.6 | 95.0 | 87.3 | 83.8 |
| 0.9869 | 103.2 | 124.1 | 130.6 | 140.3 |
| 0.4935 | 124.6 | 144.1 | 148.2 | 145.9 |
| 0.2467 | 143.7 | 170.1 | 161.8 | 153.0 |
| 0.1234 | 146.3 | 168.5 | 167.5 | 163.7 |
| 0.06168 | 152.1 | 173.2 | 170.3 | 170.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hiratsuka, M.; Emoto, M.; Konno, A.; Ito, S. Molecular Dynamics Simulation of the Influence of Nanoscale Structure on Water Wetting and Condensation. Micromachines 2019, 10, 587. https://doi.org/10.3390/mi10090587
Hiratsuka M, Emoto M, Konno A, Ito S. Molecular Dynamics Simulation of the Influence of Nanoscale Structure on Water Wetting and Condensation. Micromachines. 2019; 10(9):587. https://doi.org/10.3390/mi10090587
Chicago/Turabian StyleHiratsuka, Masaki, Motoki Emoto, Akihisa Konno, and Shinichiro Ito. 2019. "Molecular Dynamics Simulation of the Influence of Nanoscale Structure on Water Wetting and Condensation" Micromachines 10, no. 9: 587. https://doi.org/10.3390/mi10090587
APA StyleHiratsuka, M., Emoto, M., Konno, A., & Ito, S. (2019). Molecular Dynamics Simulation of the Influence of Nanoscale Structure on Water Wetting and Condensation. Micromachines, 10(9), 587. https://doi.org/10.3390/mi10090587